Interpretacja tabel
kontyngencji

Dr hab. inż. Jadwiga Stobiecka

Etapy wnioskowania statystycznego

Na piechotę



Wprowadzenie danych



Sformułowanie hipotezy zerowej



Sprawdzenie założeń testu



Obliczenie wartości testu na

podstawie wyników z próby



Znajdowanie wartości krytycznych
z tablic przy ustalonym poziomie

istotności α



Podjęcie decyzji o odrzuceniu/lub
nie hipotezy zerowej przy danym

poziomie istotności



Interpretacja wyników

Z zastosowaniem programów

statystycznych



Wprowadzenie danych



Sformułowanie hipotezy zerowej



Sprawdzenie założeń testu



-



-



Podjęcie decyzji przy możliwie
najlepszym poziomie

wiarygodności hipotezy
alternatywnej



Interpretacja wyników

Analiza tabel zależności
polega na:



Ustaleniu czy istnieje zależność
statystycznie istotna oraz:



Jeśli jest istotna, to należy ustalić,
jaka jest jej siła.

Idea komputerowego poziomu

prawdopodobieństwa

Przy weryfikacji hipotez statystycznych za pomocą programów

komputerowych ważne jest wprowadzenie poza poziomem
istotności α (ex ante) także poziomu p (ex post). Ten drugi poziom
istotności nazywany jest komputerowym poziomem istotności,
poziomem prawdopodobieństwa lub też prawdopodobieństwem
testowym (significance level).

Jeżeli α > p, to na danym poziomie istotności α odrzucamy

hipotezę zerową, natomiast jeśli α < p, to na danym poziomie
istotności α brak jest podstaw do odrzucenia hipotezy zerowej.

Weryfikacja hipotez statystycznych

Hipotezę zerową orzekająca, że cechy X i Y są
niezależne, możemy zweryfikować testem χ

2

.

H

0

: cechy X i Y są niezależne

H

1

:

cechy X i Y są zależne

(O

– E)

2

k p

(n

ij

– E

ij

)

2

χ

2

= ∑---------- = ∑ ∑ ----------

E

i=1 j=1

E

ij

gdzie:
E

– wartość oczekiwana

O

– wartość obserwowana

Założenia testu χ

2

:



Wartość oczekiwana E nie może być
zerem, bo przez zero się nie dzieli!



Najkorzystniej jest, gdy wartość
oczekiwana E

jest większa od 10.



Dla małych tabel (20<N<40 lub tabel
większych, w których występują liczności
poniżej 5 wprowadza się tzw. poprawkę
Yatesa

Wybrane współczynniki siły

związku

Współczynnik Φ – stosowany

dla tabel małych (2x2)

Współczynnik Φ jest miarą zależności między dwiema

zmiennymi w tabeli 2x2.

Jego wartość zmienia się od 0

(brak zależności między zmiennymi) do 1 (całkowita
zależność między zmiennymi).

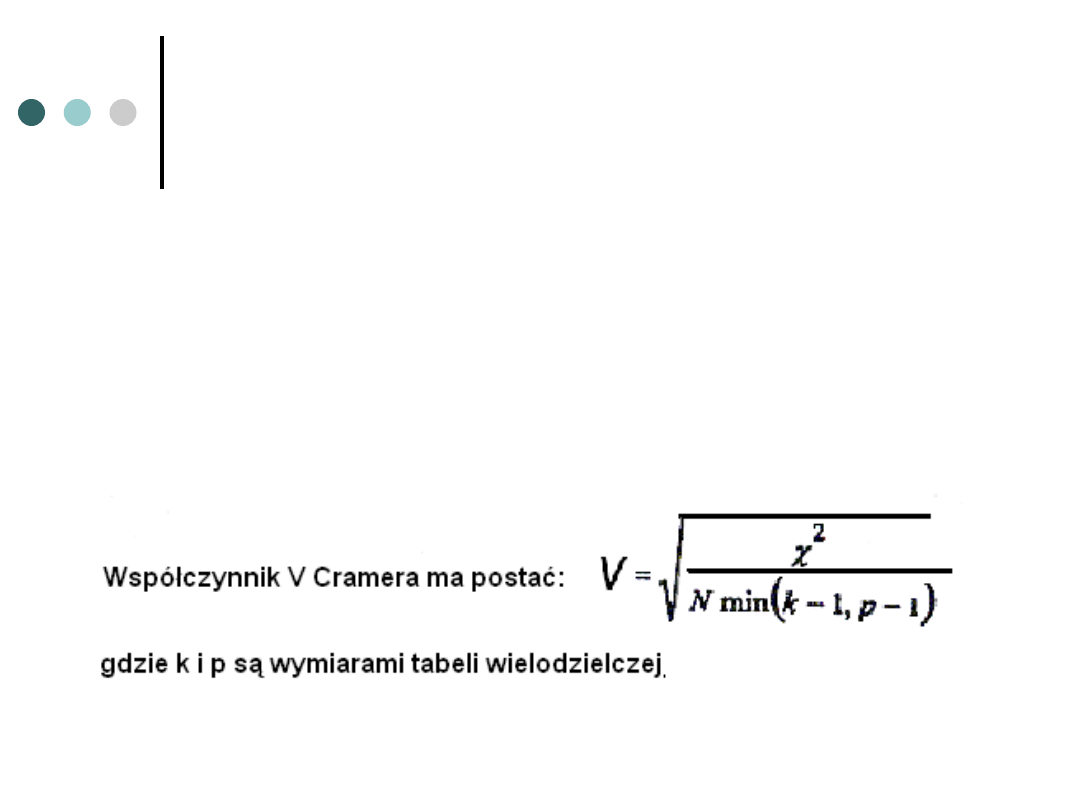
Współczynnik V Cramera – stosowany

dla tabel ze zmienną (zmiennymi)

nominalną

Współczynnik V Cramera jest miarą zależności

pomiędzy dwiema zmiennymi. Przyjmuje on wartość od 0
(brak zależności między zmiennymi) do 1. Im wyższa jest
wartość współczynnika, tym silniejsze jest powiązanie
między analizowanymi cechami.

Współczynnik R Spearmana – stosowany

dla zmiennych porządkowych

Współczynnik korelacji rang Spearmana (R)
można uważać za zwyczajny współczynnik korelacji
Pearsona z tą różnicą, że wykorzystujemy rangi, a nie
wartości. Stosuje się go wtedy, gdy dwie zmienne
mierzone są na skali porządkowej lub nie posiadają
rozkładu normalnego. Przyjmuje on wartości z przedziału
<-1, 1>. Im wartość R jest bliższa 1 lub -1, tym
silniejsza jest analizowana zależność.

Przykład braku zależności

Płeć a częstość korzystania z restauracji

typu fast-food

PŁEC

Nigdy

Rzadko

Często

Wiersz

ogółem

Mężczyzna

80

190

250

520

Kobieta

110

200

300

610

Ogółem

190

390

550

1130

Charakterystyka statystyczna zależności

Chi-kwadr.

df

p

Chi kwadrat

Pearsona

0,2385699

df=2 p=0,88756

Współczynnik

kontyngencji

0,0458998

V Cramera

0,0459482

Interpretacja danych polega na:



Ho: Nie ma zależności pomiędzy płcią a
częstością korzystania z restauracji
typu fast food (zmienne są niezależne).

1. Postawieniu hipotezy zerowej

o niezależności analizowanych zmiennych

2. Postawieniu hipotezy alternatywnej



H1: Istnieje zależność pomiędzy płcią a
częstością korzystania z restauracji
typu fast food

(zmienne są zależne).

3.

Sprawdzeniu założenia testu, w tym

przypadku χ2.

(założenia dla tabeli na

slajdzie 13 są spełnione, dlaczego?)

4. Porównanie prawdopodobiestwa

testowego p

z przyjętym poziomem

istotności α.

Dla p>α - nie ma podstaw do odrzucenia

hipotezy zerowej

Dla p=α - mamy dylemat – przyjąć czy

odrzucić?

Dla p<α - odrzucamy hipotezę zerową na

rzecz alternatywnej

5. Podjęciu decyzji o braku podstaw do

odrzuceniu hipotezy zerowej lub
odrzucenie hipotezy i przyjęcie
alternatywnej

Niech α=0,01,

p=0,88756 (tabela na slajdzie 13)

Ponieważ p>α, nie ma podstaw do odrzucenia

hipotezy zerowej o

niezależności zmiennych.

6. W przypadku odrzucenia hipotezy zerowej,

wybór właściwego współczynnika do określenia

siły zależności (w oparciu o wymiar tabeli i
poziom obu pomiaru zmiennych)

W naszym przypadku to koniec zadania. Gdyby

były podstawy do odrzucenia hipotezy zerowej,

należałoby jeszcze określić siłę związku w

oparciu o właściwy współczynnik. W naszym

przypadku zmienna płeć jest mierzona na skali

nominalnej, zmienna częstość korzystania z
restauracji Fast-

food na skali porządkowej,

wobec tego moglibyśmy zastosować

współczynnik V Cramera.

Zadanie do samodzielnej interpretacji

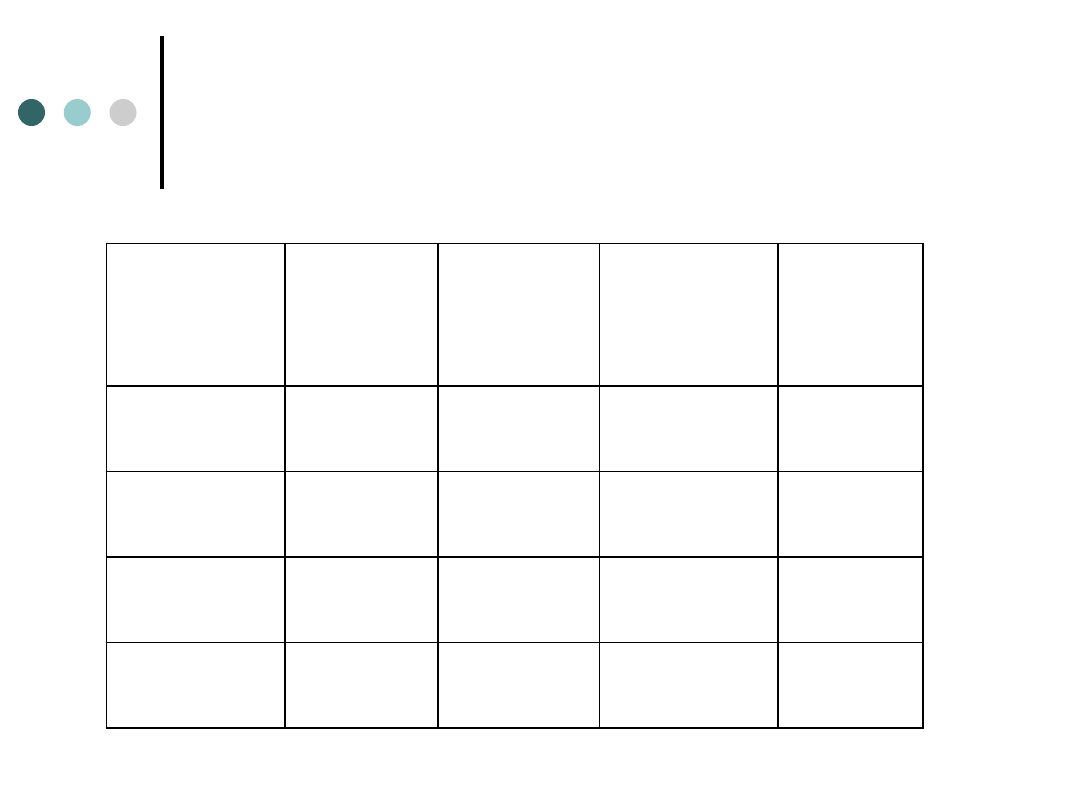
Wiek respondenta a czas posiadania

telefonu komórkowego

WIEK

Do roku 1 do 3 lat Pow. 3 lat Wiersz

do 20 lat

50

150

100

300

21-30 lat

140

610

160

910

31-45 lat

0

170

160

330

Ogółem

1900

930

420

1540

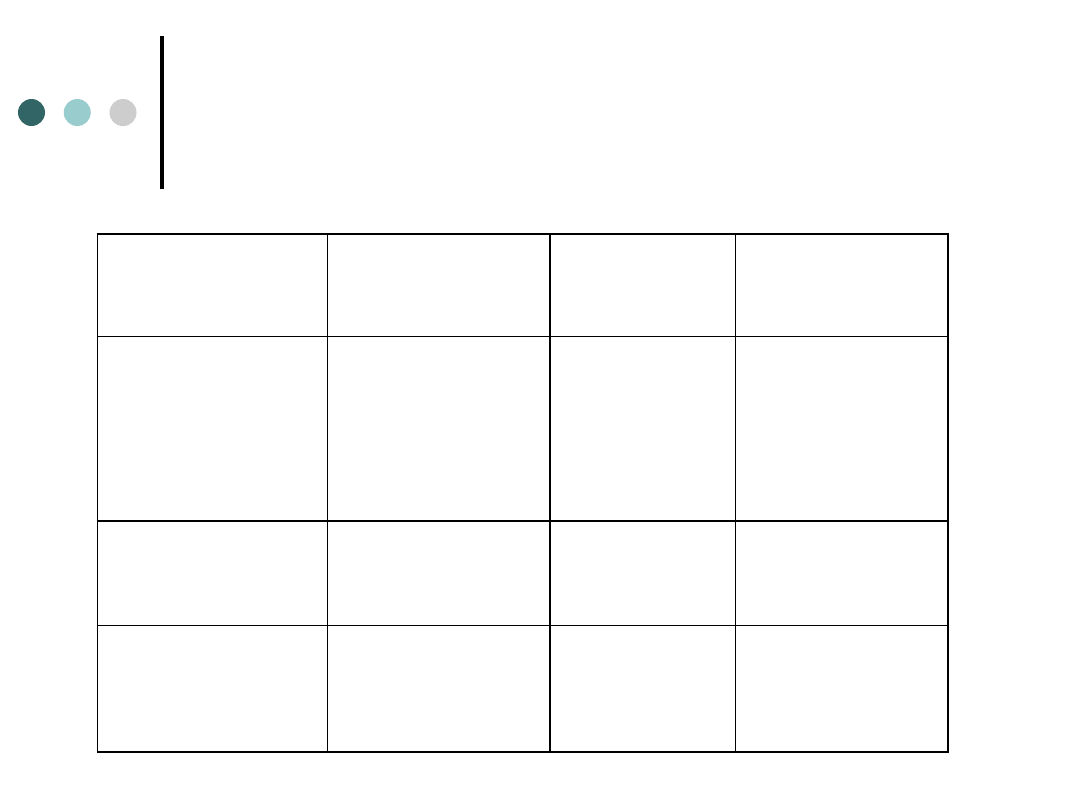
Wiek respondenta

a czas posiadania telefonu komórkowego

(

charakterystyka statystyczna zależności)

Chi-kwadr. df

p

Chi
kwadrat
Pearsona

15,82521

df=4

p=0,00326

V Cramera 0,2266728

R rang
Spearmana

0,1730977 t=2,1668 p=0,03181

Jeszcze jedno zadanie

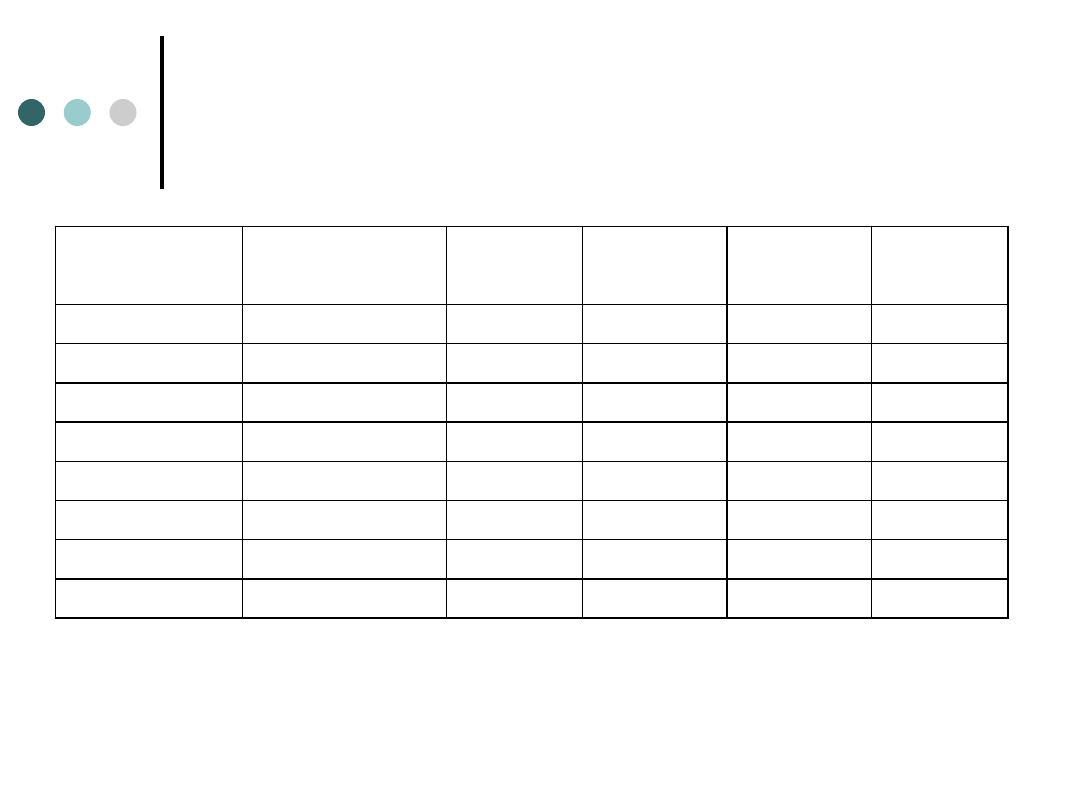
Wiek a znajomość marek rowerów

(procentowanie do kolumn)

ZNAJOMOŚĆ

MAREK

WIEK -

15_24

WIEK -

25_44

WIEK -

45_64

Wiersz

Razem

Liczba

NIE ZNA

7

17

28

52

% z kolumny

10,00%

17,71%

41,18%

Liczba

SŁABO ZNA

18

39

20

77

% z kolumny

25,71%

40,63%

29,41%

Liczba

DOBRZE ZNA

45

40

20

105

% z kolumny

64,29%

41,67%

29,41%

Liczba

Ogółem

70

96

68

234

% z kolumny

100%

100%

100%

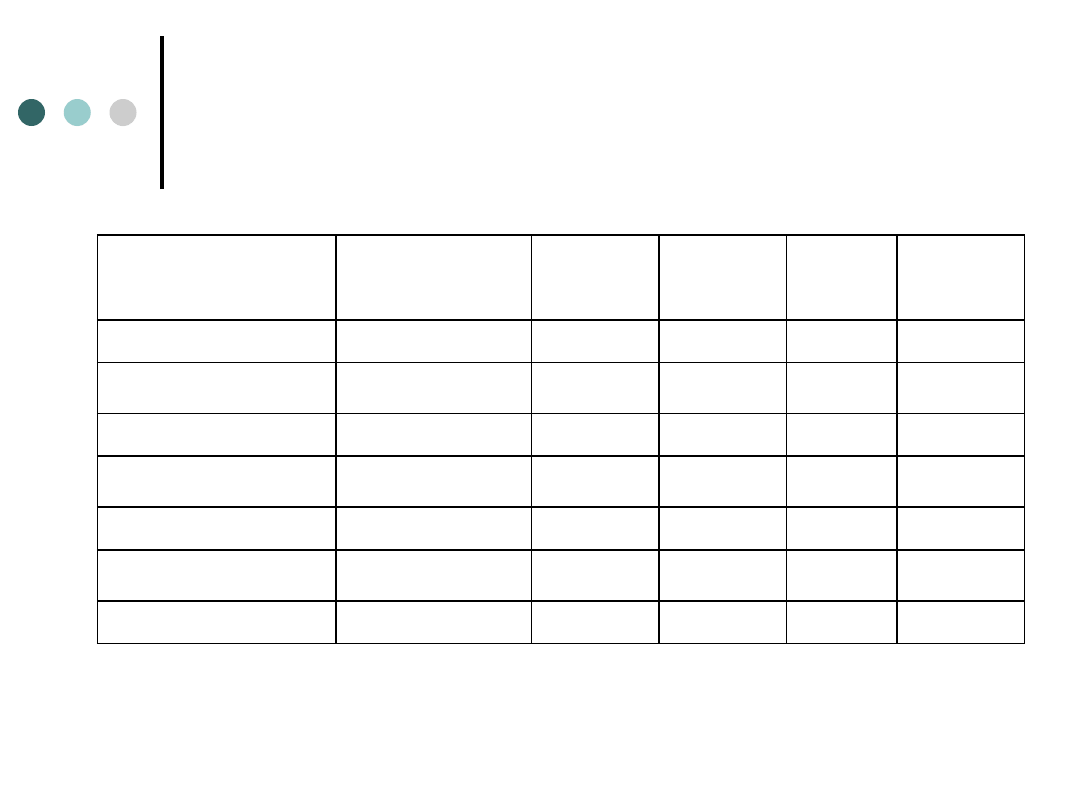
Wiek a znajomość marek rowerów

(procentowanie do wierszy)

ZNAJOMOŚĆ

MAREK

WIEK

–

15-24

WIEK

–

25-44

WIEK

–

45-64

Wiersz

Razem

Liczba

NIE ZNA

7

17

28

52

% z wiersza

13,46%

32,69%

53,85%

100%

Liczba

SŁABO ZNA

18

39

20

77

% z wiersza

23,38%

50,65%

25,97%

100%

Liczba

DOBRZE ZNA

45

40

20

105

% z wiersza

42,86%

38,10%

19,05%

100%

Liczba

70

96

68

234

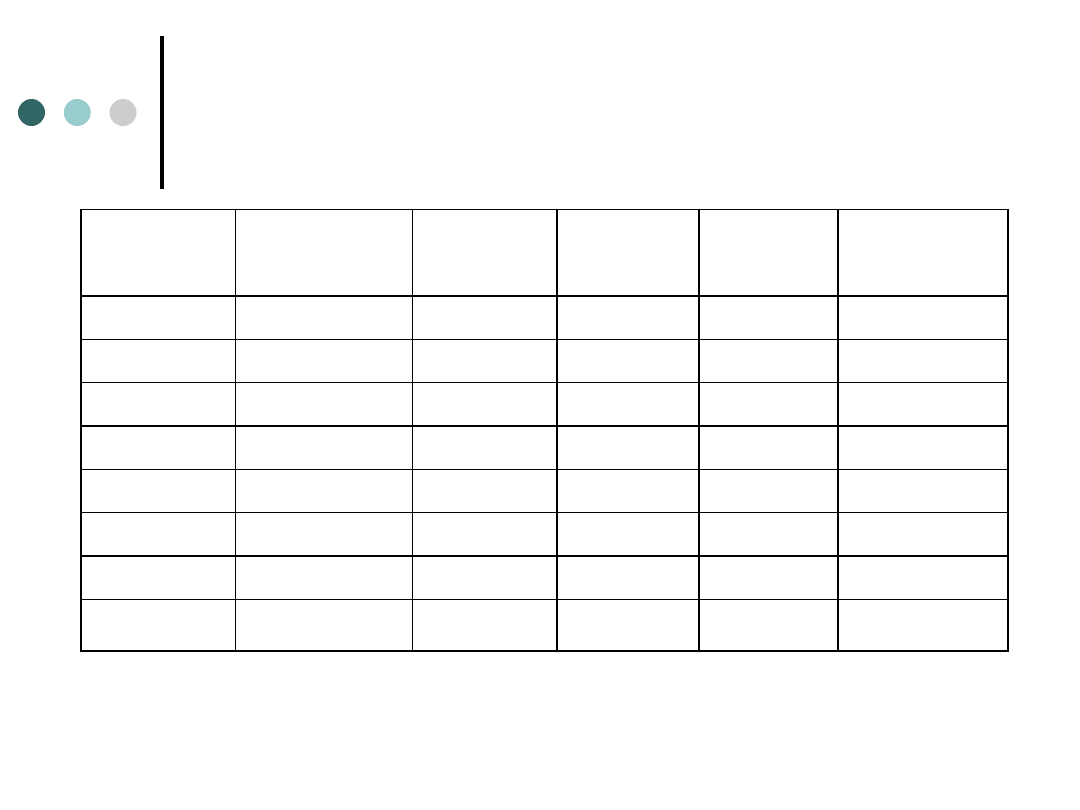
Wiek a znajomość marek rowerów

(procentowanie do całości)

ZNAJOMOŚĆ

MAREK

WIEK -

15_24

WIEK -

25_44

WIEK -

45_64

Wiersz

Razem

Liczba

NIE ZNA

7

17

28

52

% z całości

2,99%

7,26%

11,97%

22,22%

Liczba

SŁABO ZNA

18

39

20

77

% z całości

7,69%

16,67%

8,55%

32,91%

Liczba

DOBRZE ZNA

45

40

20

105

% z całości

19,23%

17,09%

8,55%

44,87%

Liczba

70

96

68

234

% z całości

29,91%

41,03%

29,06%

100%

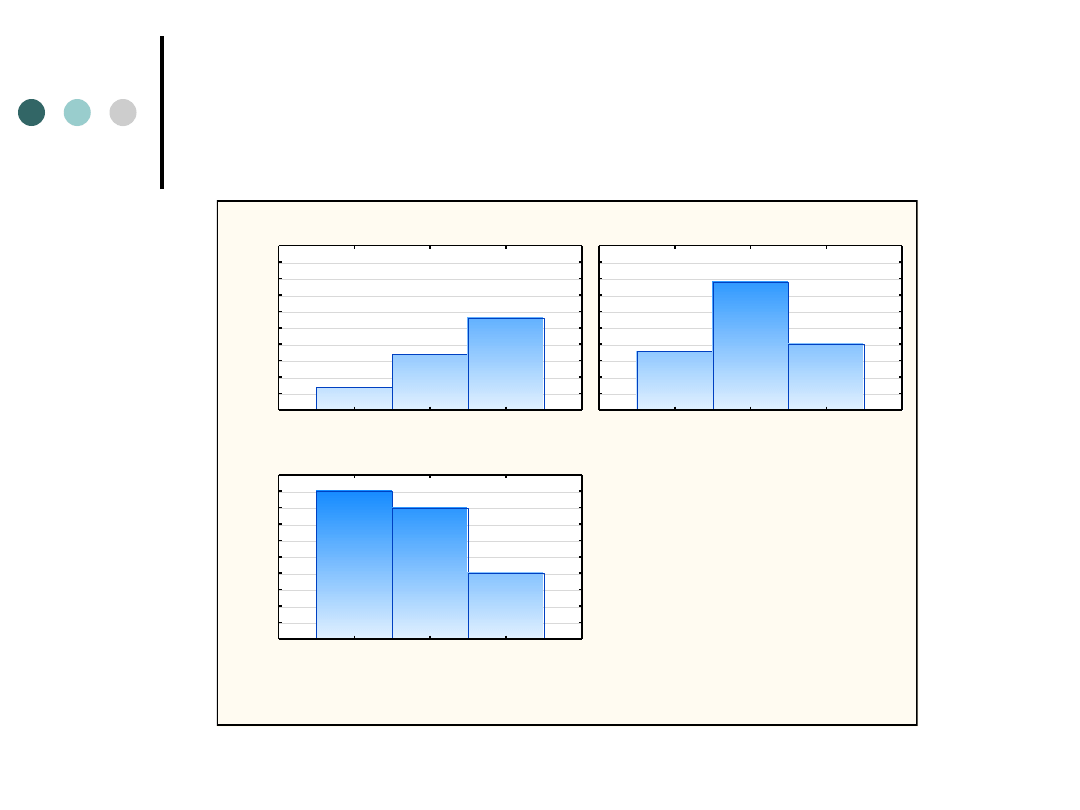
Histogram skategoryzowany

Skategoryz. histogram: ZNAJ_MAR x WIEK

WIEK

L

ic

z

b

a

o

b

s

.

ZNAJ_MAR: N_ZNA

15_24

25_44

45_64

0

5

10

15

20

25

30

35

40

45

50

ZNAJ_MAR: S_ZNA

15_24

25_44

45_64

ZNAJ_MAR: D_ZNA

15_24

25_44

45_64

0

5

10

15

20

25

30

35

40

45

50

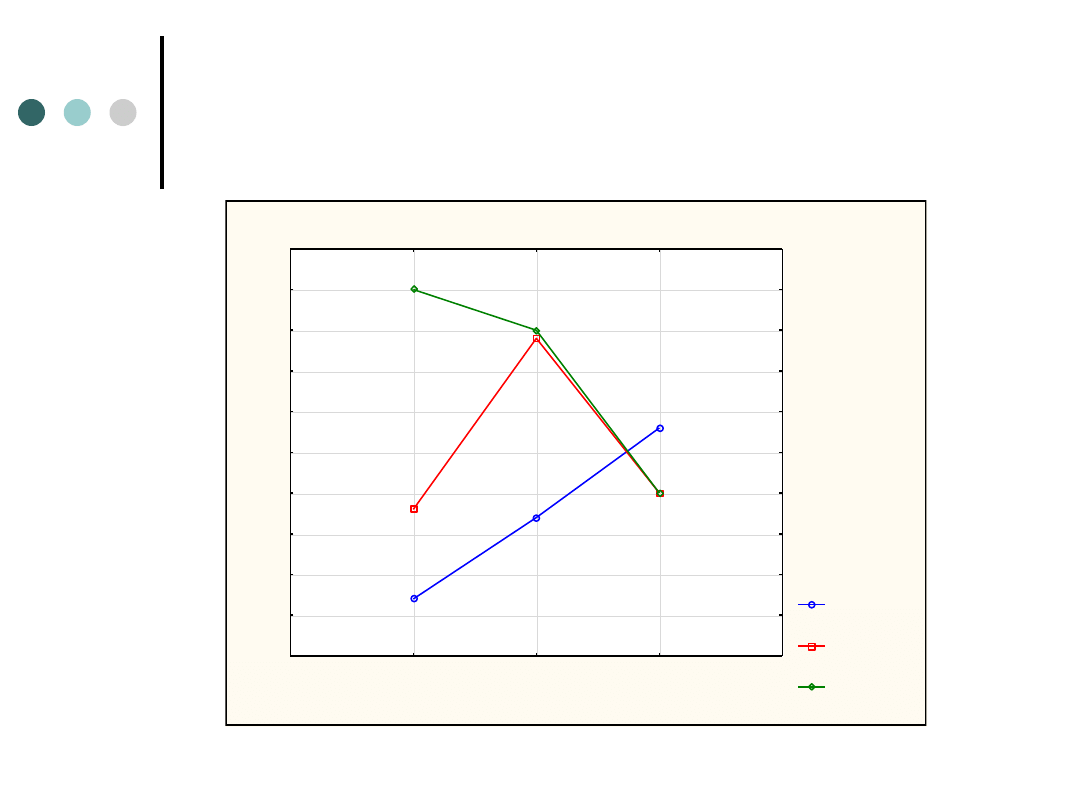
Wykres interakcji

Wykres interakcji: ZNAJ_MAR x WIEK

ZNAJ_MAR

N_ZNA

ZNAJ_MAR

S_ZNA

ZNAJ_MAR

D_ZNA

15_24

25_44

45_64

WIEK

0

5

10

15

20

25

30

35

40

45

50

Li

cz

no

śc

i

Interpretacja statystyczna zależności

Chi-kwadr.

df

p

Chi^2

Pearsona

29,39154

df=4

p=0,00001

Chi^2 NW

28,24119

df=4

p=0,00001

V Craméra

0,2506042

R rang

Spearmana

-0,317159

t=-5,094

p=0,00000