PKM ćwiczenia – wytrzymałość zmęczeniowa

1

Ćwiczenia - wytrzymałość zmęczeniowa

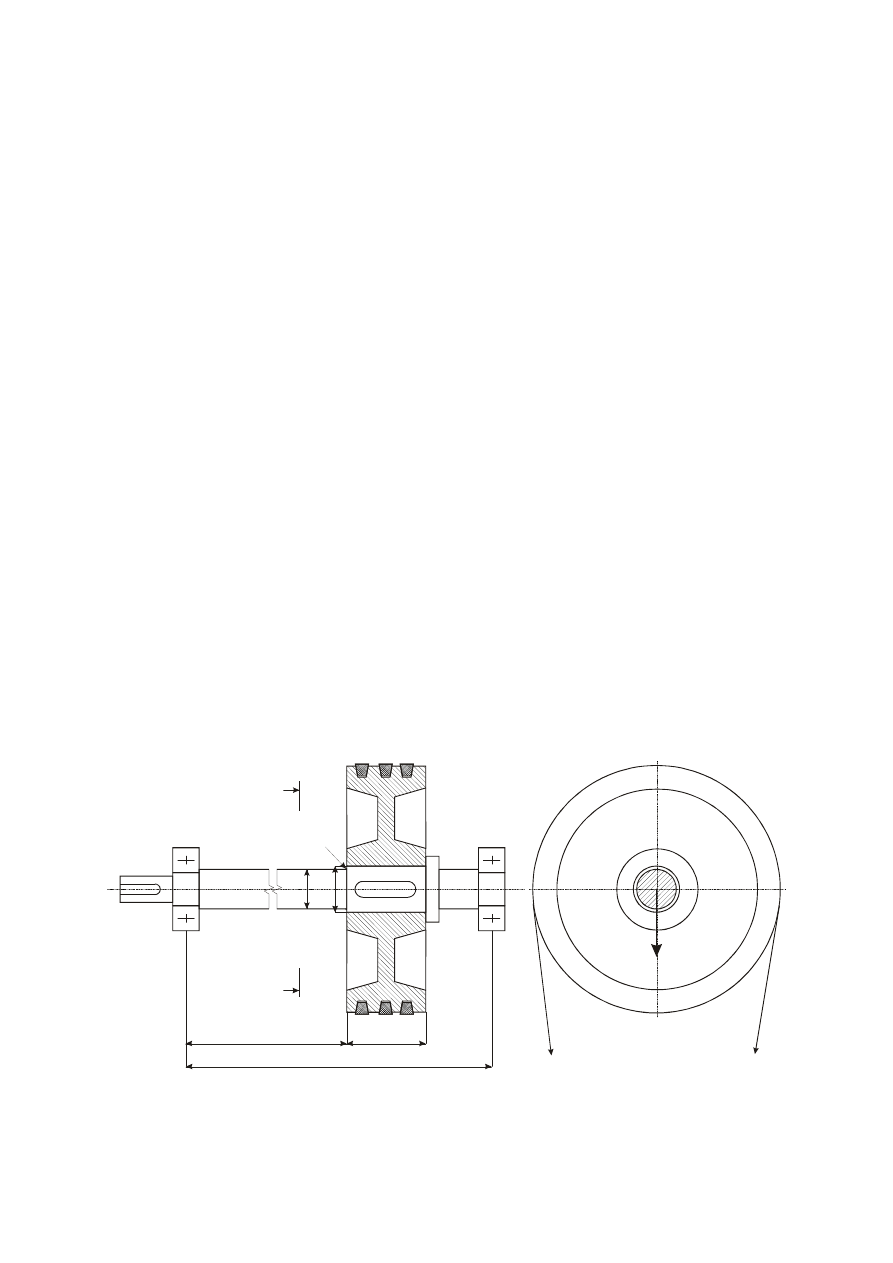
Wał maszyny stolarskiej (por. rys. poniżej) obraca się z prędkością obrotową n.
Napędzany jest on silnikiem elektrycznym poprzez przekładnię z paskami klinowymi.
Kąt opasania wynosi

α. Jeden z końców wału połączono sprzęgłem z elementem

roboczym, który odbiera przekazywaną moc N. Nierównomierność biegu maszyny K

I

.

Na wale osadzono koło pasowe o masie m (masę wału pominąć). Obliczono, że
sumaryczna siła w części czynnej pasów wynosi S

1

a w części biernej S

2

. Wał

wykonano ze stali 45.
Wiedząc, że wymagana liczba bezpieczeństwa wynosi

δ

0

:

1) zweryfikuj wał w przekroju niebezpiecznym,
2) oblicz liczbę bezpieczeństwa przy założeniu, że na kole pasowym powstanie

niewywaga G’ a środek masy niewyważonej znajdzie się na promieniu R’.

δ

0

= 3,0

d = 30 mm

D = 35 mm

ρ = 1,5 mm

L = 400 mm

a = 250 mm

b = 100 mm

S

1

= 1025 N

S

2

= 135 N

α = 173°

ρ = 1,5 mm

m = 33,6 kg

n = 4960 min

-1

N = 1,8 kW

R’ = 160 mm

K

I

= 1,2

G’ = 30 g

Rm = 650 Mpa

Reg = 500 Mpa

Rer = 420 Mpa

Res = 260 Mpa

Zro = 210 Mpa

Zgo = 280 Mpa

Zso = 170 MPa

a

b

L

S

1

Q

S

2

d

D

A

A-A

A

ρ

Symbol

⇐ oznacza, że wartość powinni podać studenci odczytując ją z tablic

PKM ćwiczenia – wytrzymałość zmęczeniowa

2

1. Stan obciążenia

Ponieważ cos

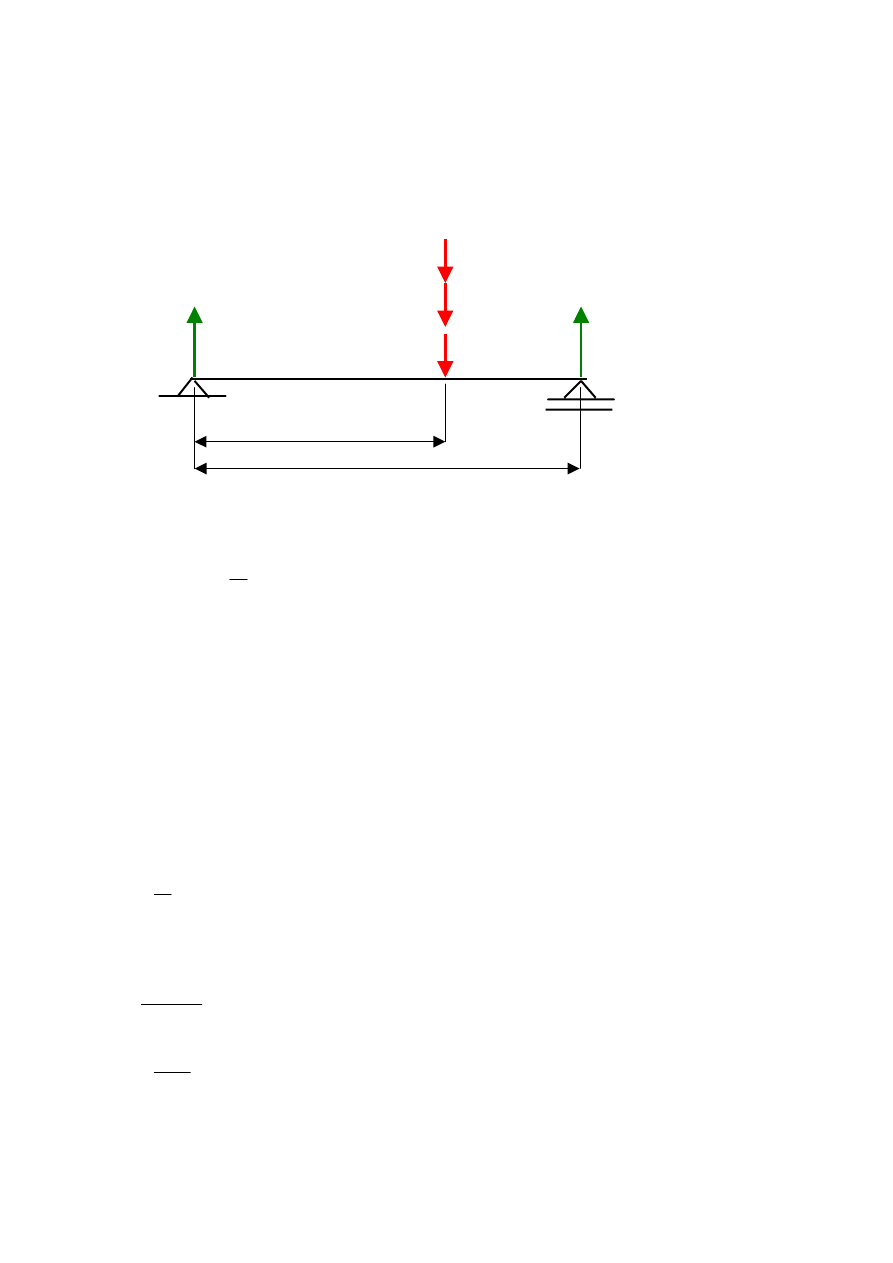
α ≈ -1, kąt opasania można pominąć. Wówczas model

fenomenologiczny wału można przedstawić w sposób następujący:

Gdzie
Q - ciężar koła paskowego:

N

s

m

kg

Q

330

81

,

9

6

,

33

2

=

⋅

=

R

a

– Q – S

1

– S

2

+ R

b

= 0

R

b

L – (Q + S

1

+ S

2

)(a+b/2) = 0

R

b

= 1117,5 N

R

a

=372,5 N

Moment gnący w przekroju niebezpiecznym (tutaj wybrano przekrój A-A):

Mg = R

a

* a

Mg = 372,5 N * 0,25 m = 93,1 Nm

Moment skręcający:

ω

N

M

S

=

n

⋅

=

π

ω

2

gdzie

ω

wyrażana jest w [rad/s] a prędkość obrotowa n podana w [obr/s], zatem:

]

/

[

519

60

4960

2

s

rad

=

=

π

ω

]

[

5

,

3

519

1800

Nm

M

S

=

=

R

a

R

b

Q

a+b/2

S

2

S

1

L

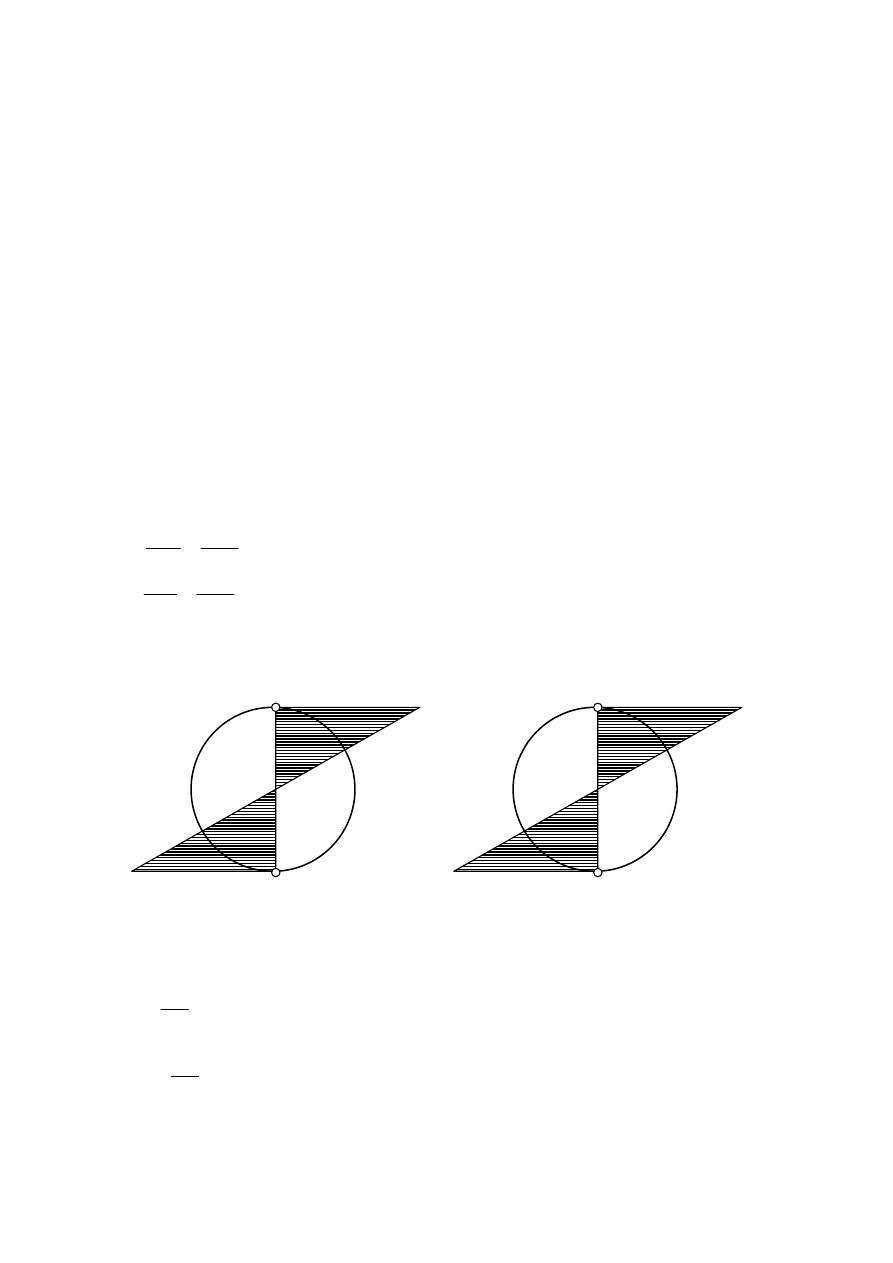
PKM ćwiczenia – wytrzymałość zmęczeniowa

3

Moment skręcający zmienia się zgodnie z przyjętym K

I

:

moment skręcający medialny (średni)

Nm

Ms

m

5

,

3

=

moment skręcający maksymalny:

Nm

Ms

Ms

m

2

,

4

2

,

1

max

=

⋅

=

więc moment skręcający amplitudalny:

Nm

Ms

Ms

Ms

m

a

7

,

0

max

=

−

=

2. Stan naprężeń

3

3

3

2700

30

1

,

0

1

,

0

mm

d

Wx

=

⋅

=

≈

3

3

3

5400

30

2

,

0

2

,

0

mm

d

Wo

=

⋅

=

≈

]

[

65

,

0

5400

3500

MPa

Wo

Ms

m

m

=

=

=

τ

]

[

13

,

0

5400

700

MPa

Wo

Ms

a

a

=

=

=

τ

Naprężenia normalne w przekroju wału rozkładają się w sposób następujący:

Ponieważ wał się obraca a obciążenie ma stałą wartość i stały kierunek, włókna A i B
wału będą naprzemiennie ściskane i rozciągane. Naprężenia w tych włóknach są co
do wartości takie same. Różnią się jedynie znakiem, więc

Wx

Mg

=

max

σ

natomiast

Wx

Mg

−

=

min

σ

A

B

σ

+

σ

-

B

A

σ

+

σ

-

PKM ćwiczenia – wytrzymałość zmęczeniowa

4

Zatem naprężenia medialne (średnie)

0

2

min

max

=

+

=

σ

σ

σ

m

a napężenia amplitudalne

]

[

5

,

34

2700

139750

2

min

max

MPa

Wx

Mg

a

=

=

=

−

=

σ

σ

σ

3. Liczby działania karbu

Wpływ powierzchni (przyjęto, że powierzchnia wału będzie szlifowana)

05

,

1

=

p

β

03

,

1

'

=

p

β

mm

k

5

,

1

=

ρ

⇐

Dla Rm=650MPa

mm

57

,

0

min

=

ρ

)

;

max(

min

ρ

ρ

ρ

k

=

mm

5

,

1

=

ρ

Dla

1

,

0

=

r

ρ

oraz

17

,

1

=

r

R

92

,

1

=

kg

α

⇐

7

,

1

=

ks

α

⇐

78

,

0

=

k

η

⇐

Liczba działania karbu dla zginania

72

,

1

)

1

(

1

=

−

+

=

kg

k

kg

α

η

β

77

,

1

1

=

−

+

=

p

kg

g

β

β

β

Liczba działania karbu dla skręcania

55

,

1

)

1

(

1

=

−

+

=

ks

k

ks

α

η

β

58

,

1

1

'

=

−

+

=

p

ks

s

β

β

β

PKM ćwiczenia – wytrzymałość zmęczeniowa

5

4. Wpływ wielkości elementu

ε

γ

1

=

dla

1

=

k

α

06

,

1

1 =

e

ε

⇐

dla

92

,

1

=

kg

α

28

,

1

1 =

zg

ε

⇐

dla

7

,

1

=

ks

α

27

,

1

1 =

zs

ε

⇐

5. Naprężenia kryterialne

Naprężenia styczne

]

[

1

,

1 MPa

Z

R

a

zs

s

so

es

e

m

=

⋅

⋅

+

=

τ

ε

β

ε

τ

τ

Naprężenia normalne

]

[

4

,

139

MPa

Z

R

a

zg

g

go

eg

e

m

=

⋅

⋅

+

=

σ

ε

β

ε

σ

σ

6. Cząstkowe (umowne, zastępcze) liczby bezpieczeństwa

59

,

3

=

=

σ

δ

eg

gz

R

89

,

239

=

=

τ

δ

es

sz

R

7. Liczba bezpieczeństwa dla obciążeń zmiennych

59

,

3

2

2

=

+

⋅

=

gz

sz

gz

sz

z

δ

δ

δ

δ

δ

wym

z

δ

δ

≥

PKM ćwiczenia – wytrzymałość zmęczeniowa

6

Weryfikacja przy założeniu, że na kole pasowym powstanie niewywaga G’ a środek
masy niewyważonej znajdzie się na promieniu R’.
G’ = 30g = 0,03 kg
R’ = 160 mm = 0,16m

W układzie zmieni się stan obciążenia.

1. Stan obciążenia

Siła odśrodkowa:

]

[

1295

16

,

0

*

)

519

(

*

03

,

0

'

'

2

2

N

R

G

P

≈

=

=

ω

Kierunek działania siły odśrodkowej (od niewywagi) zmienia się. Należy więc
rozpatrzyć dwa skrajne przypadki obciążenia:
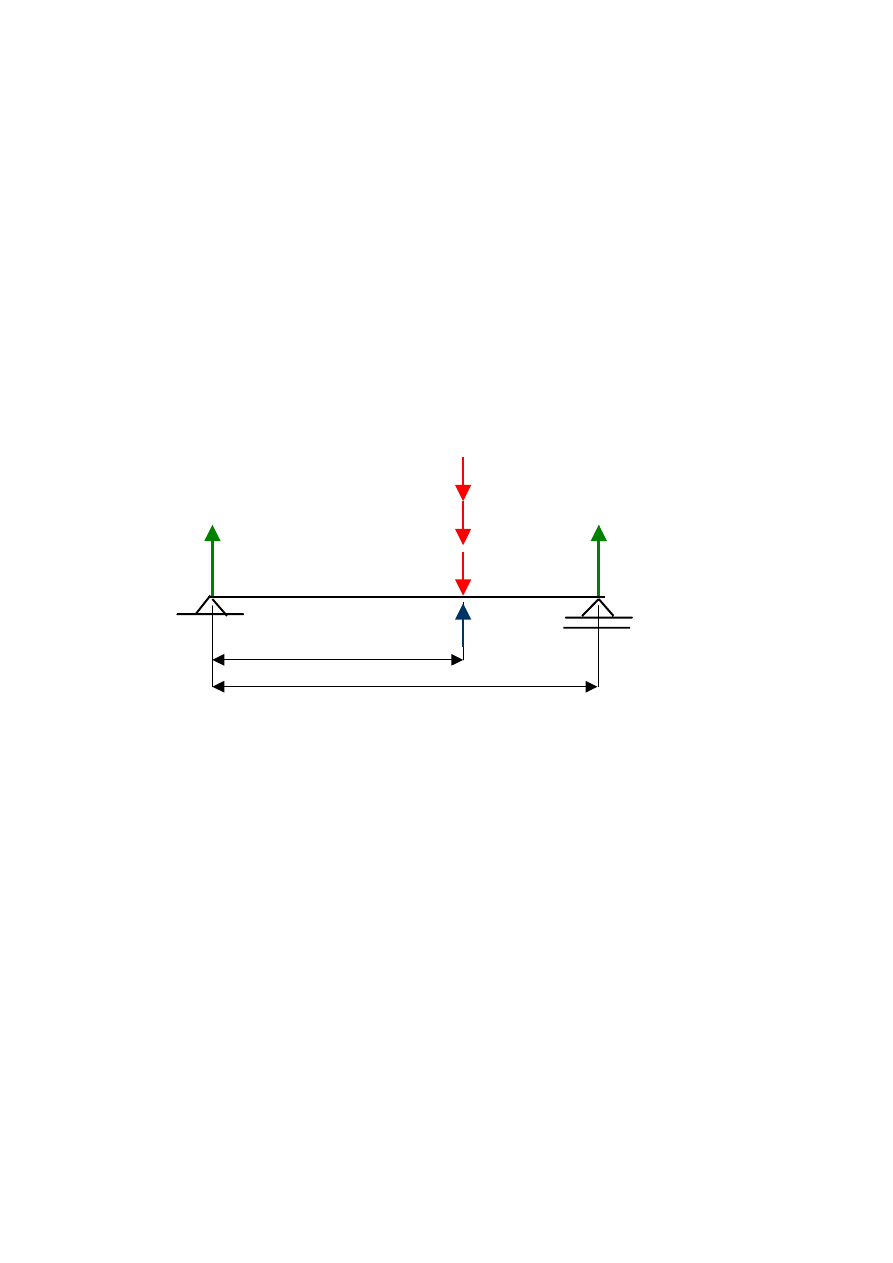
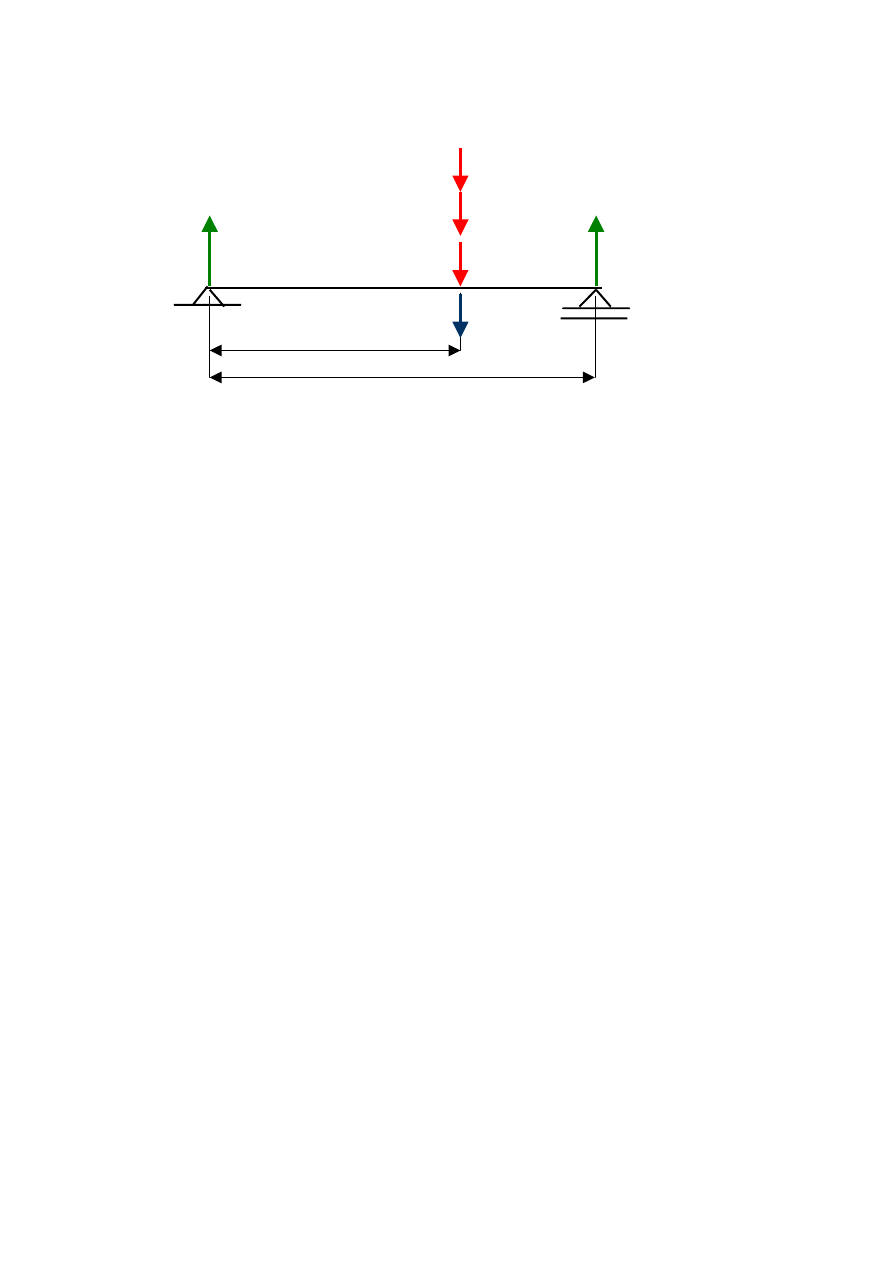
a)

R

a

– Q – S

1

– S

2

+P + R

b

= 0

R

b

L – (Q + S

1

+ S

2

- P)(a+b/2) = 0

R

b

A

= 146,3 N

R

a

A

=48,8 N

R

A

a

R

A

b

Q

a+b/2

S

2

S

1

L

P

PKM ćwiczenia – wytrzymałość zmęczeniowa

7

b)

R

a

– Q – S

1

– S

2

- P + R

b

= 0

R

b

L – (Q + S

1

+ S

2

+ P)(a+b/2) = 0

R

b

B

= 2088,7 N

R

a

B

=696,2 N

Reakcja R

a

zmienia się zatem w granicach:

R

a min

= min(R

a

A

;R

a

B

)

R

a max

= max(R

a

A

;R

a

B

)

Wówczas moment gnący w rozpatrywanym przekroju będzie zmienny od:
Mg

min

= R

a min

* a = R

a

A

* a

Mg

min

= 48,8 N * 0,25 m = 12,2 Nm

do:
Mg

max

= R

a max

* a = R

a

B

* a

Mg

max

= 696,2 N * 0,25 m = 174,1 Nm

Moment skręcający pozostaje bez zmian;
medialny (średni):

Nm

Ms

m

5

,

3

=

amplitudalny:

Nm

Ms

Ms

m

a

7

,

0

%

20

=

⋅

=

R

B

a

R

B

b

Q

a+b/2

S

2

S

1

L

P

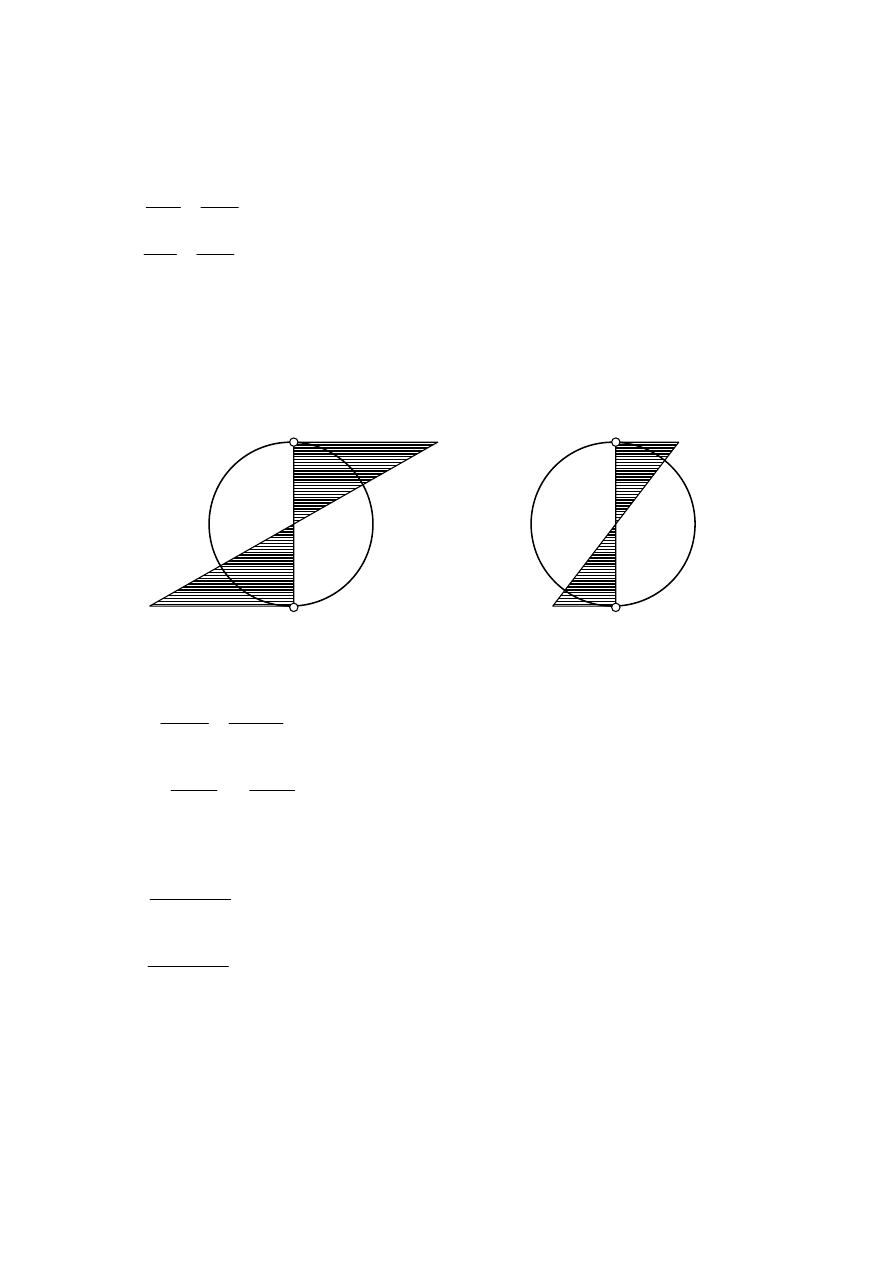
PKM ćwiczenia – wytrzymałość zmęczeniowa

8

2. Stan naprężeń

Naprężenia styczne bez zmian:

]

[

65

,

0

5400

3500

MPa

Wo

Ms

m

m

=

=

=

τ

]

[

13

,

0

5400

700

MPa

Wo

Ms

a

a

=

=

=

τ

Ze względu na to, że wał się obraca a obciążenie zmienia się co do wartości i
kierunku, naprężenia w przekroju niebezpiecznym będą miały różne wartości i znaki.

a) b)

Maksymalne i minimalne naprężenia w danym włóknie wyniosą:

]

[

5

,

64

2700

174100

max

max

MPa

Wx

Mg

=

=

=

σ

]

[

5

,

4

2700

12200

min

min

MPa

Wx

Mg

−

=

−

=

−

=

σ

(minus ze względu na zmianę znaku - ściskanie)

Naprężenia medialne i amplitudalne:

]

[

0

,

30

2

min

max

MPa

m

=

+

=

σ

σ

σ

]

[

5

,

34

2

min

max

MPa

a

=

−

=

σ

σ

σ

3. Liczby działania karbu

Bez zmian

4. Wpływ wielkości elementu

Bez zmian

A

B

σ

max

+

σ

max

-

B

A

σ

min

+

σ

min

-

PKM ćwiczenia – wytrzymałość zmęczeniowa

9

5. Naprężenia kryterialne

Naprężenia styczne

]

[

1

,

1

MPa

Z

R

a

zs

s

so

es

e

m

=

⋅

⋅

+

=

τ

ε

β

ε

τ

τ

Naprężenia normalne

]

[

1

,

171

MPa

Z

R

a

zg

g

go

eg

e

m

=

⋅

⋅

+

=

σ

ε

β

ε

σ

σ

6. Cząstkowe (umowne, zastępcze) liczby bezpieczeństwa

92

,

2

=

=

σ

δ

eg

gz

R

89

,

239

=

=

τ

δ

es

sz

R

7. Liczba bezpieczeństwa dla obciążeń zmiennych

92

,

2

2

2

=

+

⋅

=

gz

sz

gz

sz

z

δ

δ

δ

δ

δ

0

δ

δ

<

z

!

PKM ćwiczenia – wytrzymałość zmęczeniowa

10

PKM ćwiczenia – wytrzymałość zmęczeniowa

11