Podstawy elektroniki

i energoelektroniki

2. ZŁĄCZA

PÓŁPRZEWODNIKOWE

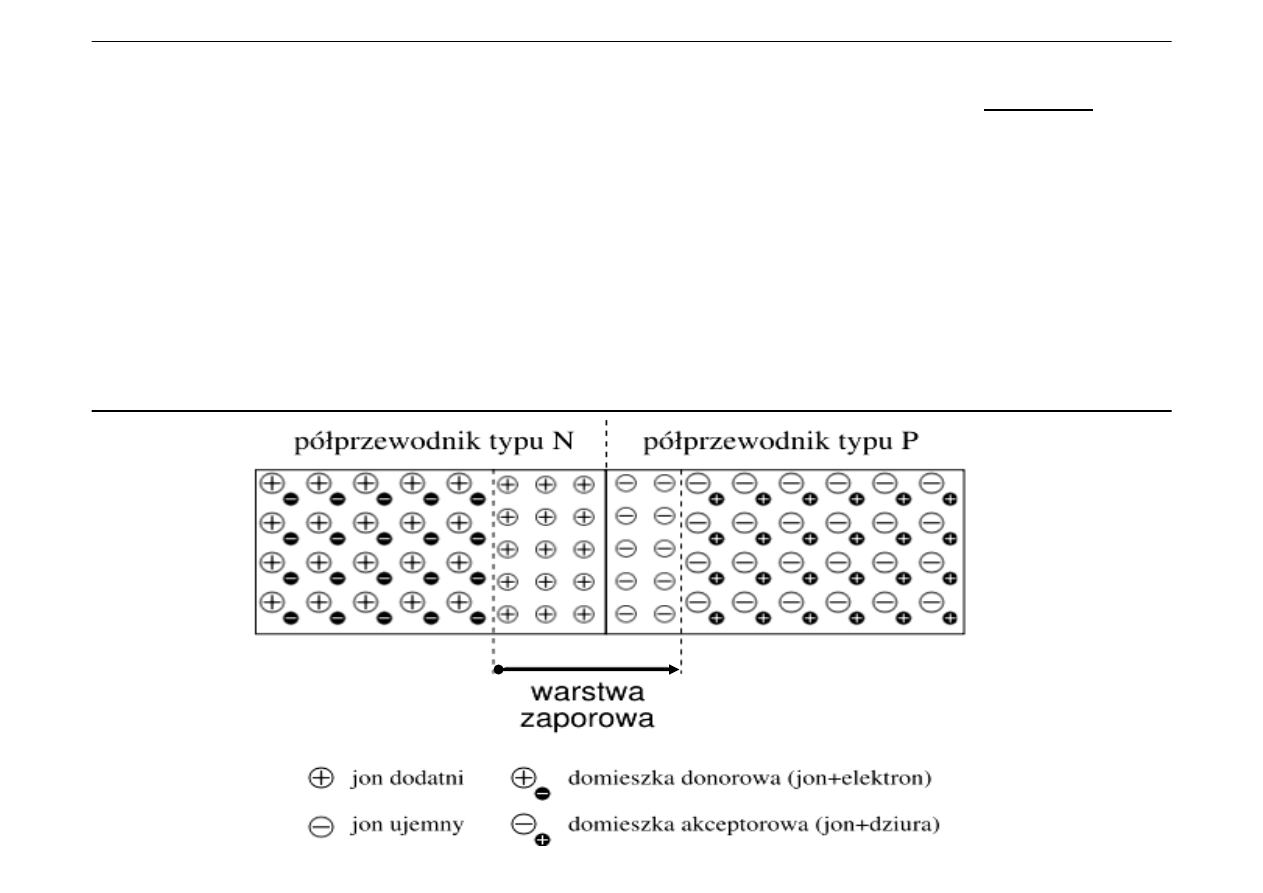
W stanie równowagi termodynamicznej tj. gdy z zewnątrz nie przyłożono żadnego pola
elektrycznego, w pobliżu styku obszarów P i N swobodne nośniki większościowe dyfundują, co
spowodowane jest różnicą

koncentracji nośników.

Gdy elektrony przemieszczą

się

do obszaru typu

P, natomiast dziury do obszaru typu N pojawia się

rekombinacja

z nośnikami większościowymi,

które nie przeszły na drugą

stronę

złącza

.

Rekombinacja „łączy”

elektrony z dziurami, co

powoduje "unieruchomienie" tych dwu swobodnych nośników.

Następuje redukcja nośników

swobodnych po obu stronach złącza, i pojawienie się

nieruchomych jonów: ujemnych

(akceptorowych) i dodatnich (donorowych). Jony te wytwarzają

pole elektryczne, które

zapobiega dalszej dyfuzji

nośników

większościowych.

Mówimy, że w pobliżu złącza powstaje

warstwa ładunku przestrzennego

, nazywana też

warstwą

zubożoną

(tj. praktycznie nie

posiadającą

swobodnych nośników) lub

warstwą

zaporową

.

E

Z

Z

łą

łą

czem p

czem p

-

-

n nazywamy obszar p

n nazywamy obszar p

ó

ó

ł

ł

przewodnika, w kt

przewodnika, w kt

ó

ó

rym

rym

nast

nast

ę

ę

puje zmiana przewodnictwa z typu p na typ n.

puje zmiana przewodnictwa z typu p na typ n.

Właściwości złącza zależą

od rodzaju użytego półprzewodnika

(homozłącze) lub półprzewodników tworzących tzw. heterozłącze, typu
domieszek

i ich rozkładu

(rodzaju zastosowanej technologii).

Z punktu widzenia technologii wytwarzania złącza dzielimy na dyfuzyjne

implantowane, epitaksjalne.

p

n

j

x

d

N

(x)

N

a

)

0

(

N

a

x

a

N

d

N

d

a

-N

N

j

x

x

Rys.2.8. Przykład złącza

dyfuzyjnego i

skokowego otrzymanego

metodą

epitaksji

Stan r

Stan r

ó

ó

wnowagowy z

wnowagowy z

łą

łą

cza

cza

Jak już

opisano bezpośredni kontakt obszarów n oraz p prowadzi do wzajemnej dyfuzji

nośników -

elektronów do obszaru typu p i dziur do obszaru typu n, na skutek istniejących

gradientów koncentracji. W efekcie po obu stronach złącza technologicznego powstają

warstwy

nieruchomego ładunku przestrzennego (jony + i -) tworzące warstwę

dipolową. W

półprzewodniku typu p powstanie warstwa ładunku ujemnego zjonizowanych akceptorów, a w
półprzewodniku typu n warstwa ładunku dodatniego zjonizowanych donorów, rys.2.9.

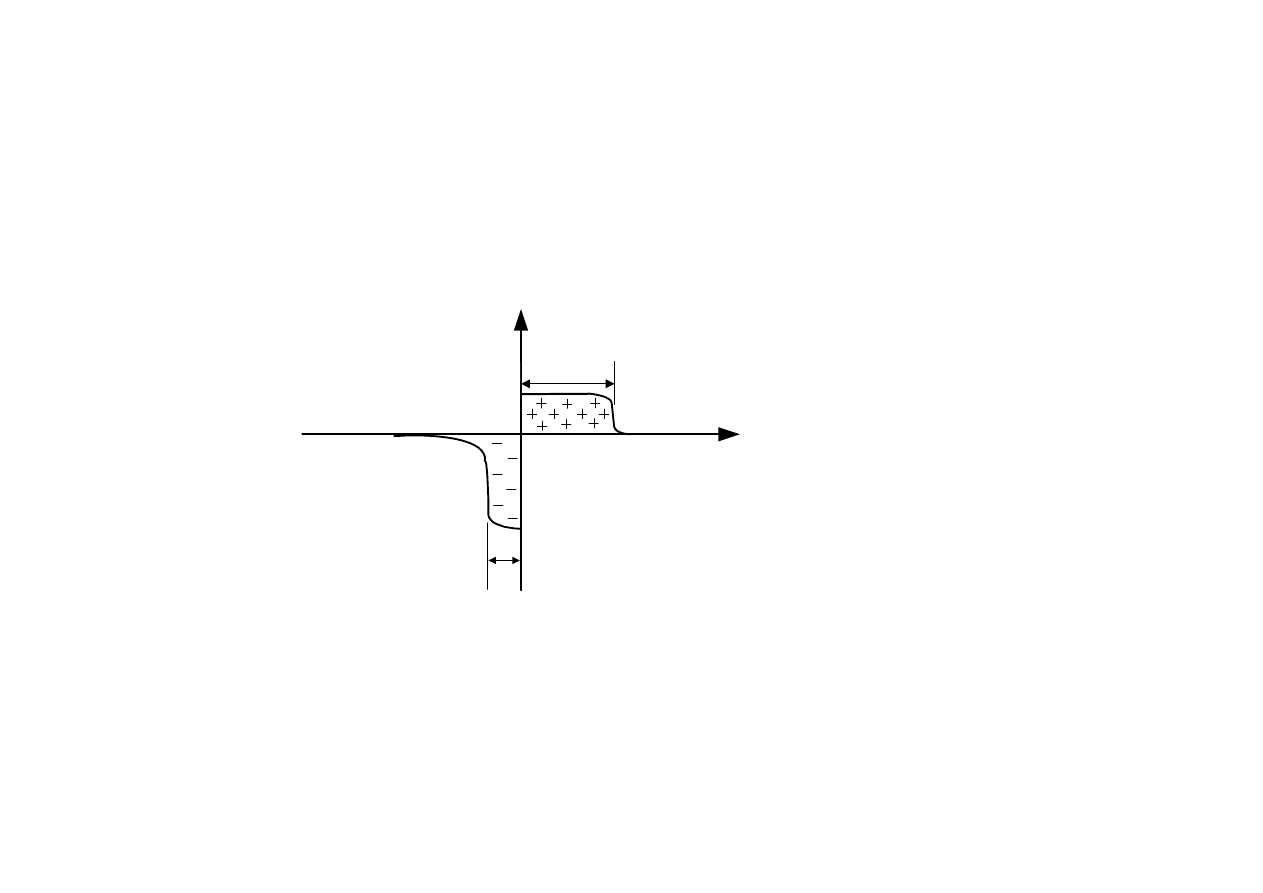
Rys.2.9. Warstwa dipolowa ładunku przestrzennego dla złącza skokowego p-n; w obszarze d

p

+d

n

brak jest

ładunków swobodnych (obszar zubożony)

Całkowity ładunek warstwy dipolowej musi być

jednak równy zero, co dla złącza

przedstawionego na rys.2.9 daje:

(2.8)

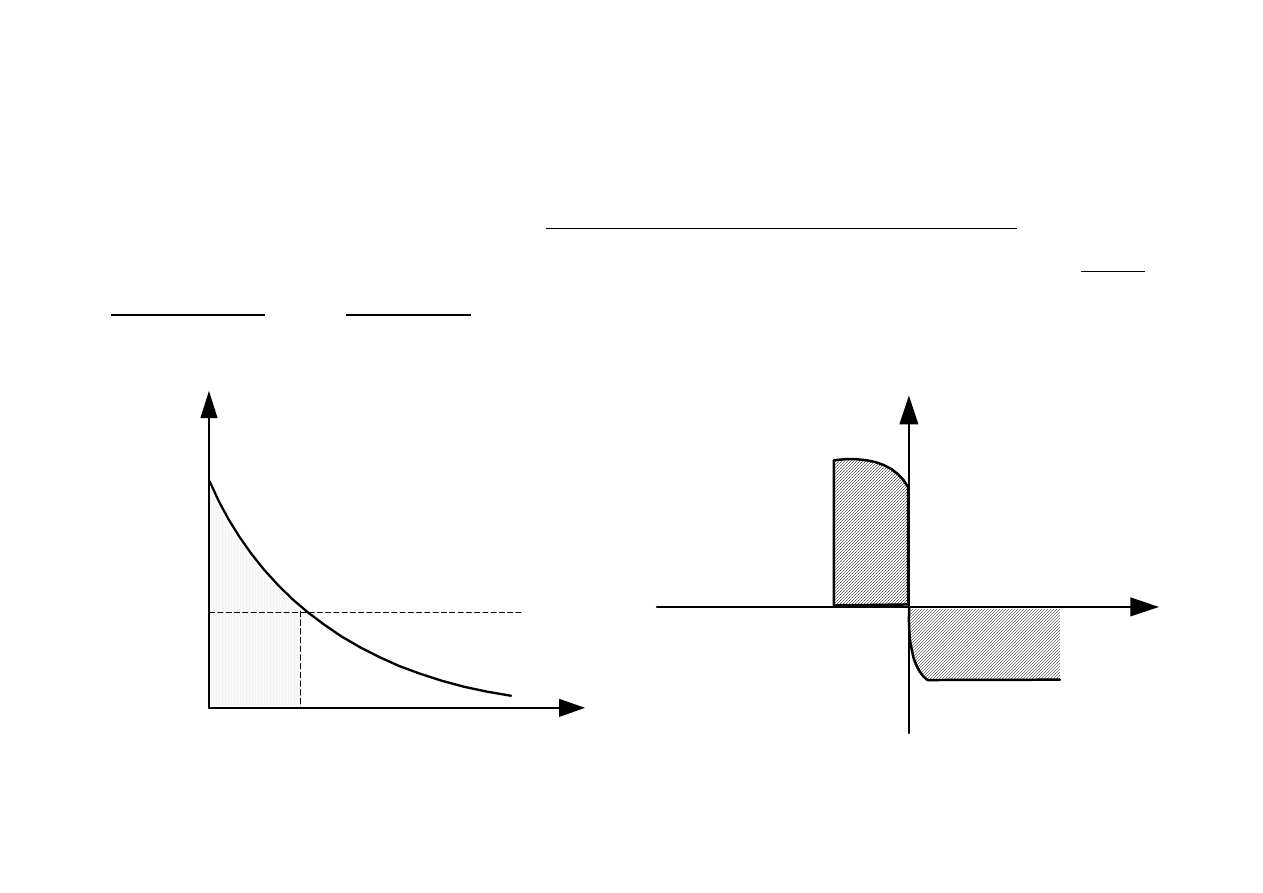
Równanie (2.8) określa głębokość

wnikania warstwy ładunku przestrzennego w obszar półprzewodnika. Wnikanie to

jest tym większe, im mniejsza jest koncentracja domieszki w danym obszarze.

a

-qN

d

qN

n

d

q(x)

x

p

d

0

=

−

a

p

d

n

N

qd

N

qd

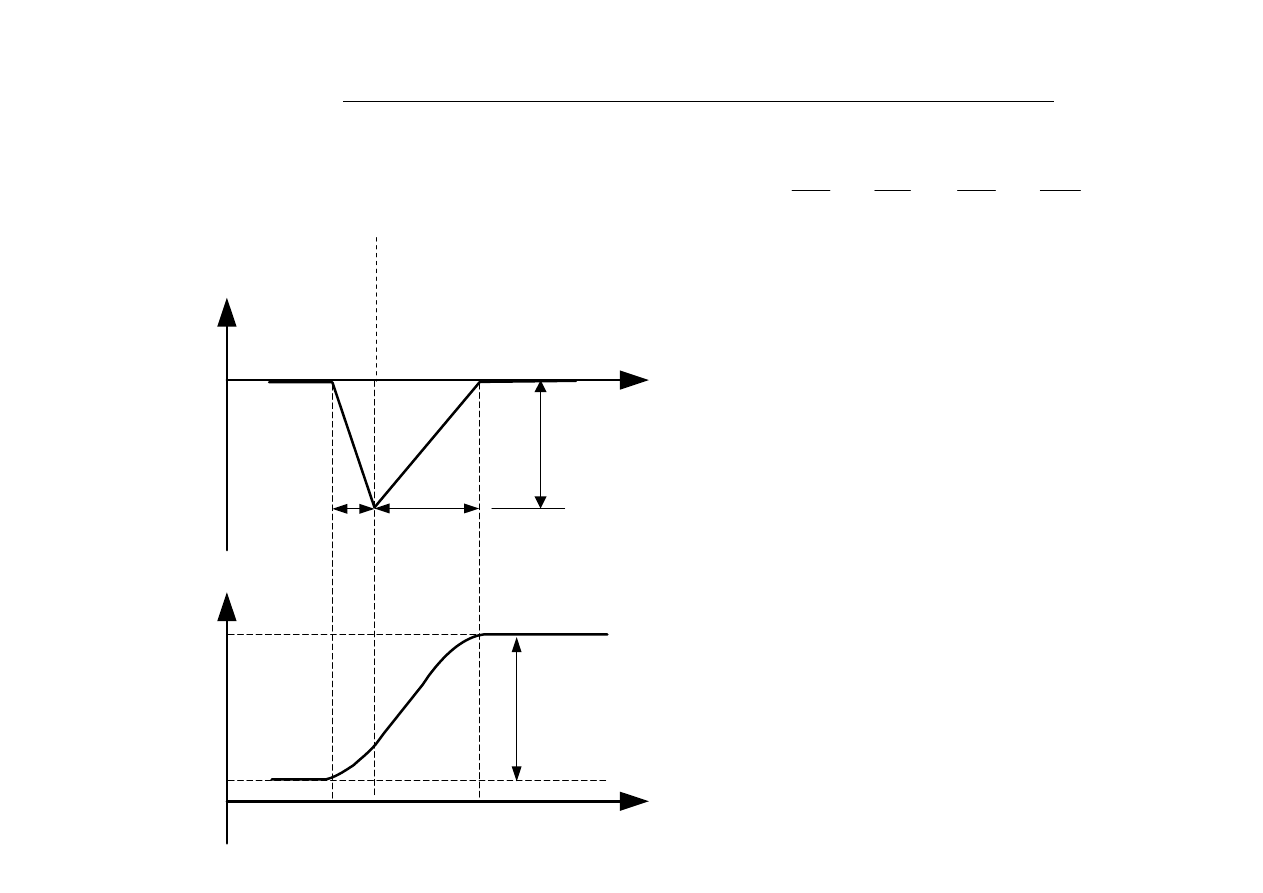
Wbudowane pole elektryczne kierunkuje prądy unoszenia elektronów i dziur, które są

skierowane przeciwnie

do prądów dyfuzyjnych. W stanie równowagi prądy dyfuzyjne i unoszenia muszą

się

równoważyć.

Z analizy domieszkowania można wyliczyć

wysokość

bariery potencjału:

(2.10)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

p

n

p

n

p

p

q

kT

n

n

q

kT

ln

ln

0

ψ

Rys.2.10. Pole elektryczne „wbudowane”

(a);

potencjał

wytworzony w skokowym złączu p-n

w wyniku istnienia ładunku dipolowego (b);

max

E

E(x)

0

p

d

n

d

x

V(x)

(a)

(b)

k

V

p

V

x

x

j

ψ

0

=

−

V

V

k

p

p

n

ψ

0

-

bariera potencjału.

Dla złącza skokowego (rozkład ładunku jak na rys.2.9), przebiegi przedstawione na rys.2.10.

Stan r

Stan r

ó

ó

wnowagowy z

wnowagowy z

łą

łą

cza

cza

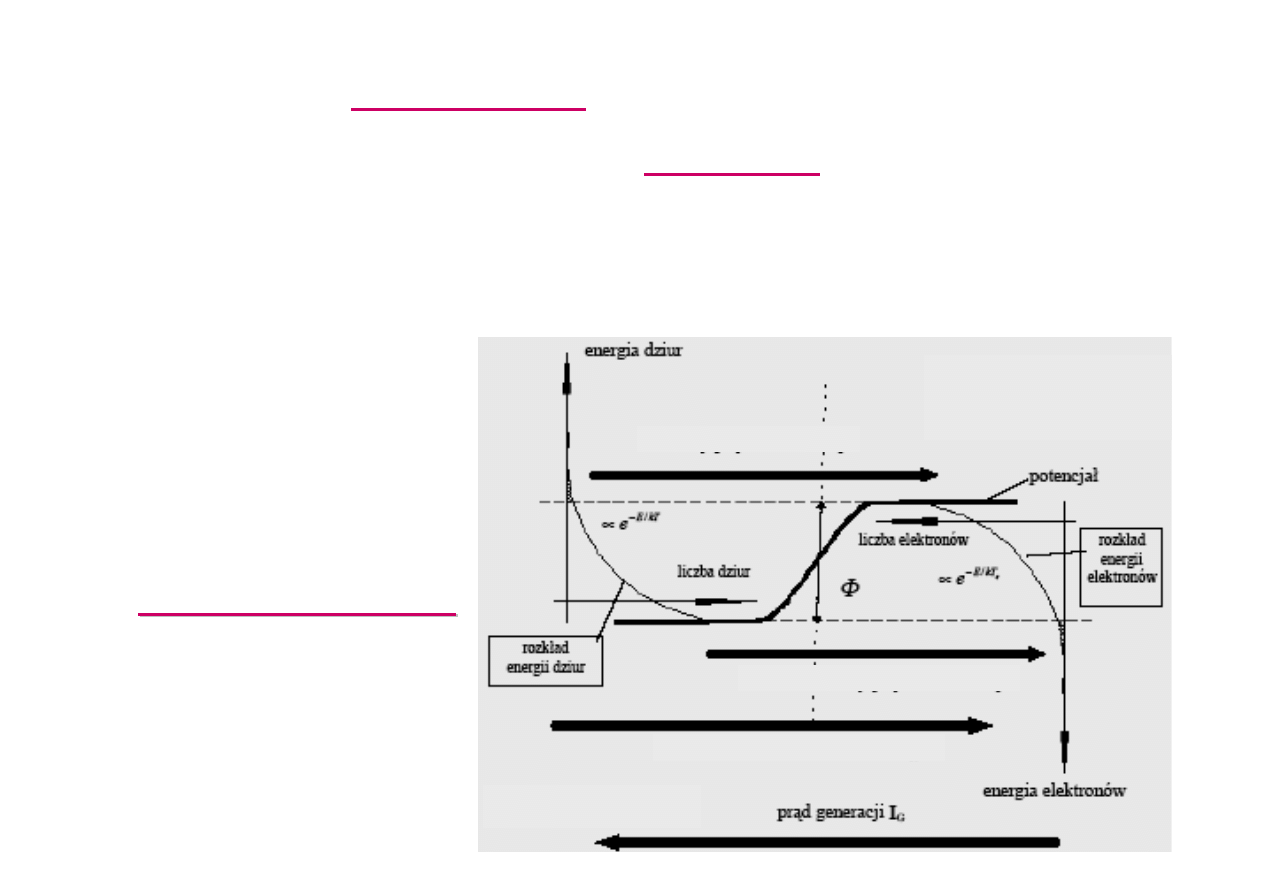
Przepływ nośników większościowych

przez

złącze zachodzący

pod wpływem

dyfuzji

nazywany jest

prądem dyfuzyjnym

(czasem

prądem rekombinacji

).

Przez złącze

pod wpływem pola ładunku przestrzennego

przepływać

mogą

również

nośniki mniejszościowe

– stanowią

one

prąd unoszenia

(lub inaczej prąd generacji) a

jego zwrot jest przeciwny do zwrotu prądu dyfuzyjnego.

Pole elektryczne ładunku przestrzennego jest reprezentowane przez barierę

potencjału.

W złączu niespolaryzowanym jest to

napięcie dyfuzyjne

, którego wartość

zależy głównie od

rodzaju półprzewodnika, koncentracji domieszek i temperatury. Napięcie dyfuzyjne zmniejsza się

wraz ze wzrostem temperatury o ok. 2,3 mV/K.

Rozp

Rozp

ł

ł

yw pr

yw pr

ą

ą

d

d

ó

ó

w

w

w z

w z

łą

łą

czu

czu

niespolaryzowanym:

niespolaryzowanym:

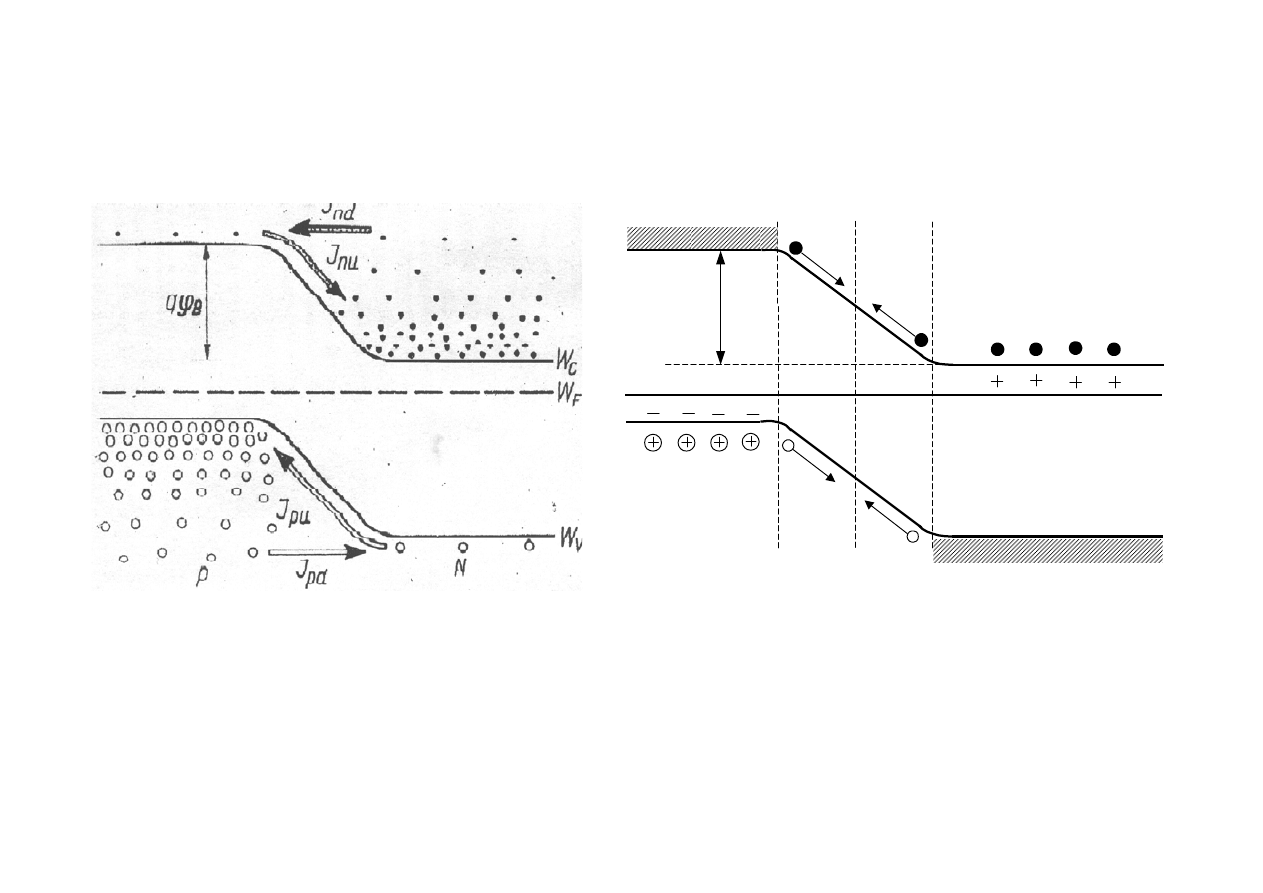
Dziurowy prąd dyfuzji

Elektronowy prąd dyfuzji

Wypadkowy prąd dyfuzji

półprzewodnik „p”

półprzewodnik „n”

Przep

Przep

ł

ł

yw pr

yw pr

ą

ą

du przez z

du przez z

łą

łą

cze p

cze p

-

-

n

n

Złącze niespolaryzowane

W

stanie równowagi (brak napięcia zewnętrznego) prąd wypadkowy przez

złącze jest równy zero, rys.2.11.

Rys.2.11. Złącze p-n

w stanie równowagi (U = 0)

Prąd dyfuzyjny elektronów j

Dn

(prąd nośnikow

większościowych) jest równoważony

przez prąd unoszenia elektronów j

Un

(prąd nośników mniejszościowych) oraz prąd

dyfuzyjny dziur j

Dp

jest równoważony przez prąd unoszenia dziur j

Up

.

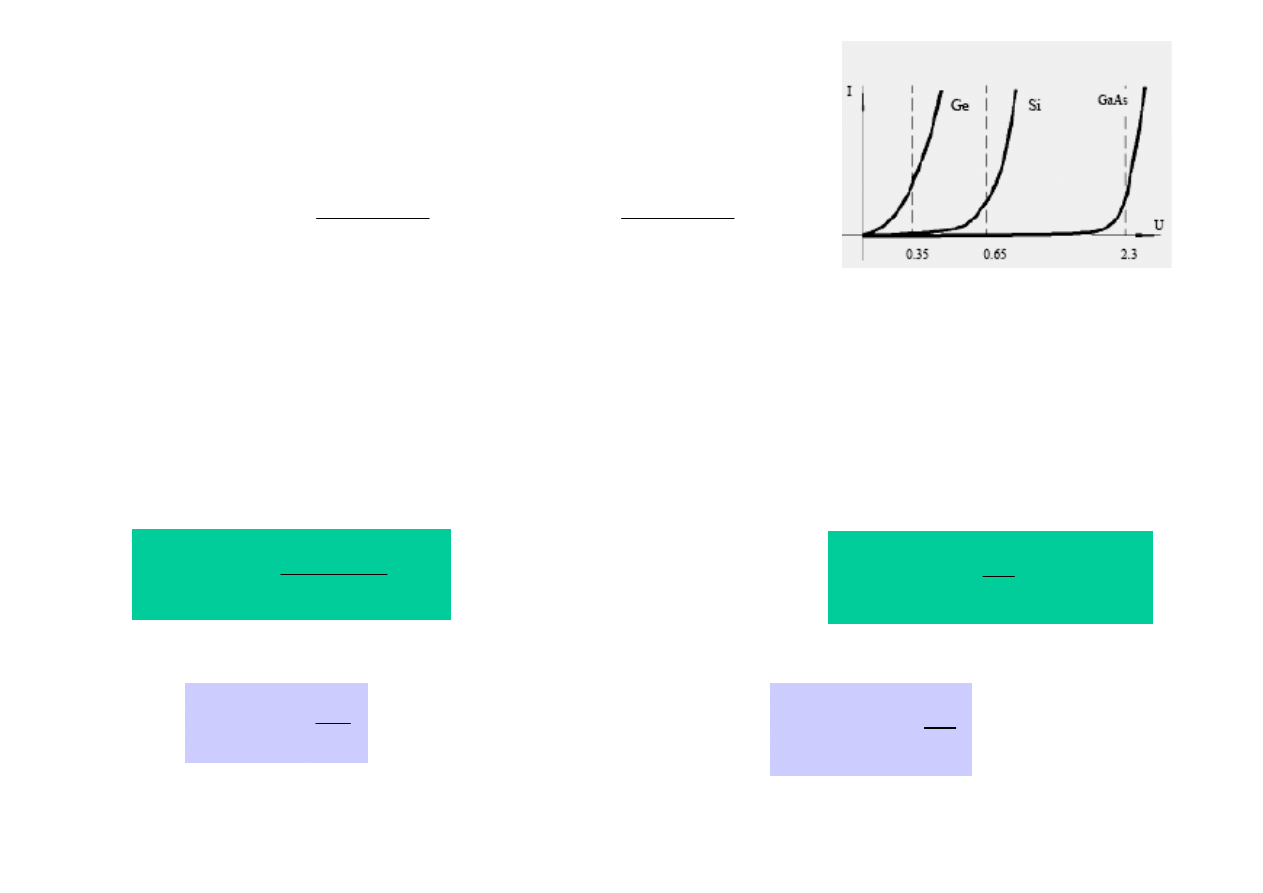
W przypadku

złącz wykonanych z krzemu napięcie U

D

w temperaturze pokojowej ma wartość

rzędu

0,6-0.8 V, natomiast dla złącz germanowych wynosi ok. 0,2-0,3 V.

C

W

F

W

V

W

D

qU

p

n

p

D

j

n

D

-j

p

U

j

n

U

-j

Przep

Przep

ł

ł

yw pr

yw pr

ą

ą

du przez z

du przez z

łą

łą

cze p

cze p

-

-

n

n

Z

Z

łą

łą

cze spolaryzowane zaporowo

cze spolaryzowane zaporowo

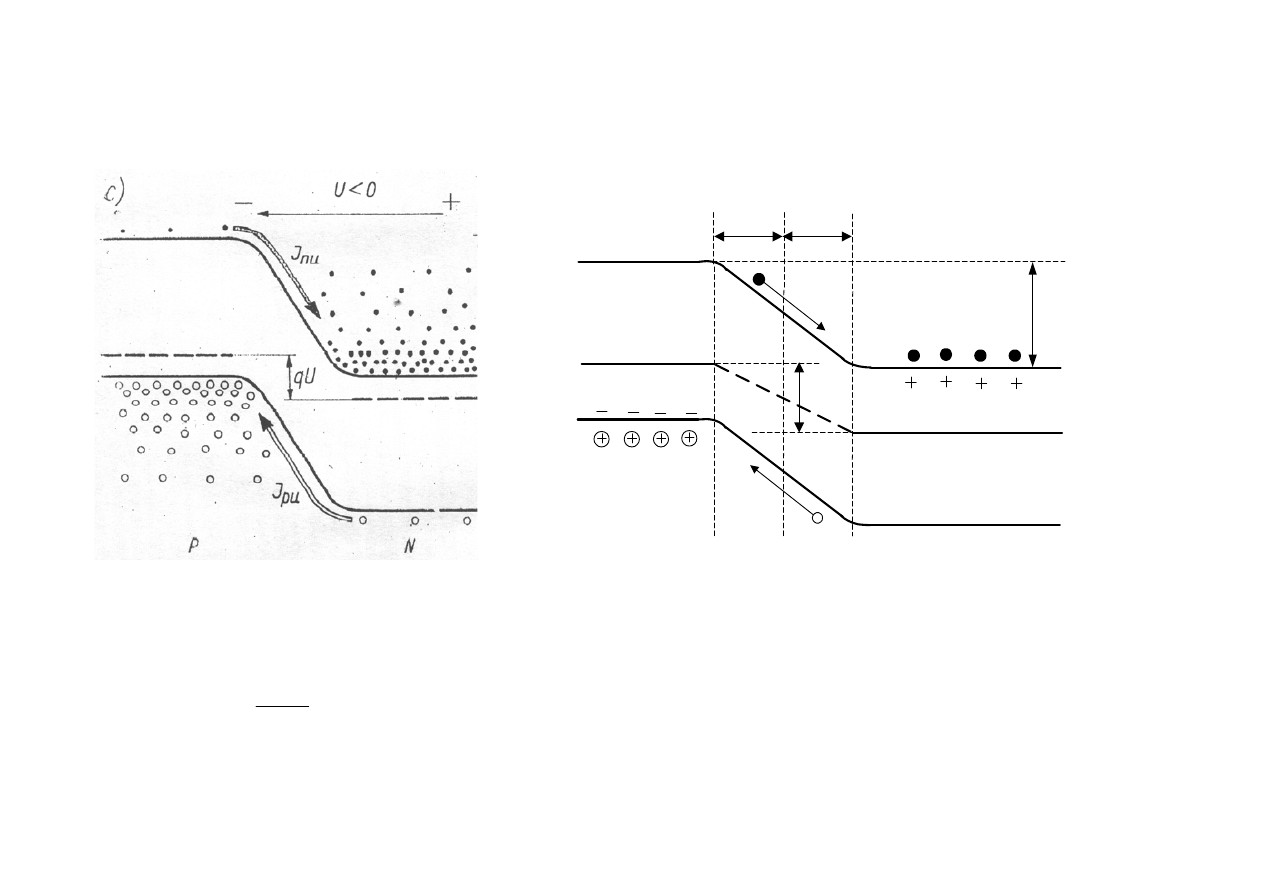
Przyłożenie

napięcia zaporowego

do złącza p-n (rys.2.12) powoduje

wzrost i poszerzenie bariery potencjału

dla nośników większościowych

czyli

zanik prądu dyfuzyjnego

nośników większościowych. Prąd nośników

mniejszościowych (

generacji termicznej

) praktycznie nie zmienia się

i

decyduje o tzw. prądzie zaporowym

.

Jeżeli zaniedba się

zjawiska generacji i rekombinacji nośników w

samym złączu

p-n, co jest

dobrym przybliżeniem dla złącz cienkich,

wyrażenie na prąd płynący przez złącze

spolaryzowane w kierunku zaporowyym

przybiera kształt

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

1

T

S

n

U

I

I

ϕ

exp

gdzie U

jest napięciem polaryzacji złącza, a n

jest tzw. współczynnikiem nieidealności złącza o

wartościach nieco większych od jedności. Współczynnik n

został

wprowadzony, aby upodobnić

charakterystykę

idealnego złącza p-n do złącz rzeczywistych we współczesnych technologiach.

φ

T

= kT/q=26 mV

dla T=300 K

n

C

W

p

F

W

V

W

p

U

j

n

U

-j

n

F

W

p

d

n

d

qU

q

U

(

)

ψ

0

+

p

n

Z

Z

łą

łą

cze spolaryzowane w kierunku przewodzenia

cze spolaryzowane w kierunku przewodzenia

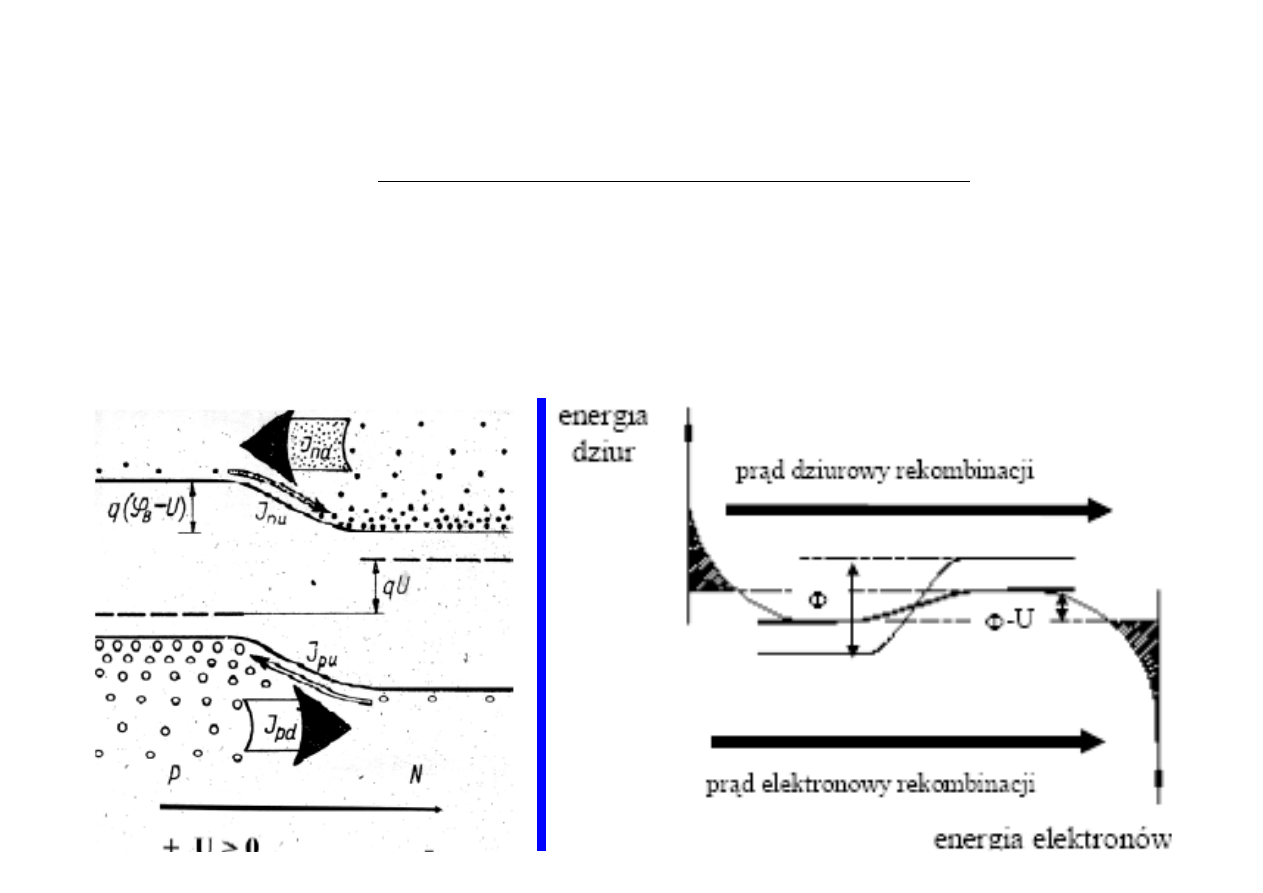
Bariera potencjału zmniejsza się

i zwęża. B

ez przeszkód

następuje dyfuzja

wszystkich nośników większościowych

z obszaru N do P i z P do N. Te dodatkowe

nośniki (nazywane wstrzykniętymi nośnikami mniejszościowymi) częściowo
rekombinują

z nośnikami większościowymi w danym obszarze. Dlatego prąd dyfuzji

jest czasem nazywany prądem rekombinacji. Ale do i ze

źródła zasilania dopływają

wciąż

nowe nośniki większościowe (pod wpływem pola zewnętrznego), zatem

dyfuzja nie zatrzymuje się

i w

efekcie w obwodzie płynie prąd dyfuzyjny

i

praktycznie całkowicie pomijalny prąd unoszenia nośników mniejszościowych
(generacji par dziura-elektron.

Pr

Pr

ą

ą

d diody rzeczywistej w kierunku przewodzenia

d diody rzeczywistej w kierunku przewodzenia

składa się

głównie z dwóch prądów: generacji (unoszenia)

i dyfuzyjnego (3.1):

gdzie:

I

GR

0

-zerowy prąd generacyjno-rekombinacyjny w obszarze złącza p-n przy u

D

=u

F

→0,

I

s

- prąd rewersyjny nasycenia nośników mniejszościowych przy

u

R

≡u

D

≤0,

r

S

-

rezystancja szeregowa diody,

U

T

-

potencjał

termiczny elektronów: U

T

=kT/q

( 25,8 mV

w 300 K),

u

D

-i

D

r

S

-

napięcie bezpośrednio na złączu, przeciwne napięciu dyfuzyjnemu

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

1

1

2

0

T

S

D

D

S

T

S

D

D

GR

D

U

r

i

u

I

U

r

i

u

I

i

exp

exp

W diodach krzemowych

przy u

D

>16 U

T

dominuje już

prąd dyfuzyjny (rów. Shockley’a):

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

1

exp

T

S

D

D

S

D

U

r

i

u

I

i

Dla jeszcze większych napięć

można przyjmować:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

T

D

S

D

U

u

I

i

exp

)

ln(

S

D

T

D

I

i

U

u

=

lub przy poszukiwanym napięciu:

lub przy poszukiwanym napięciu:

S

D

S

D

T

D

r

i

I

i

U

u

+

+

=

)

1

ln(

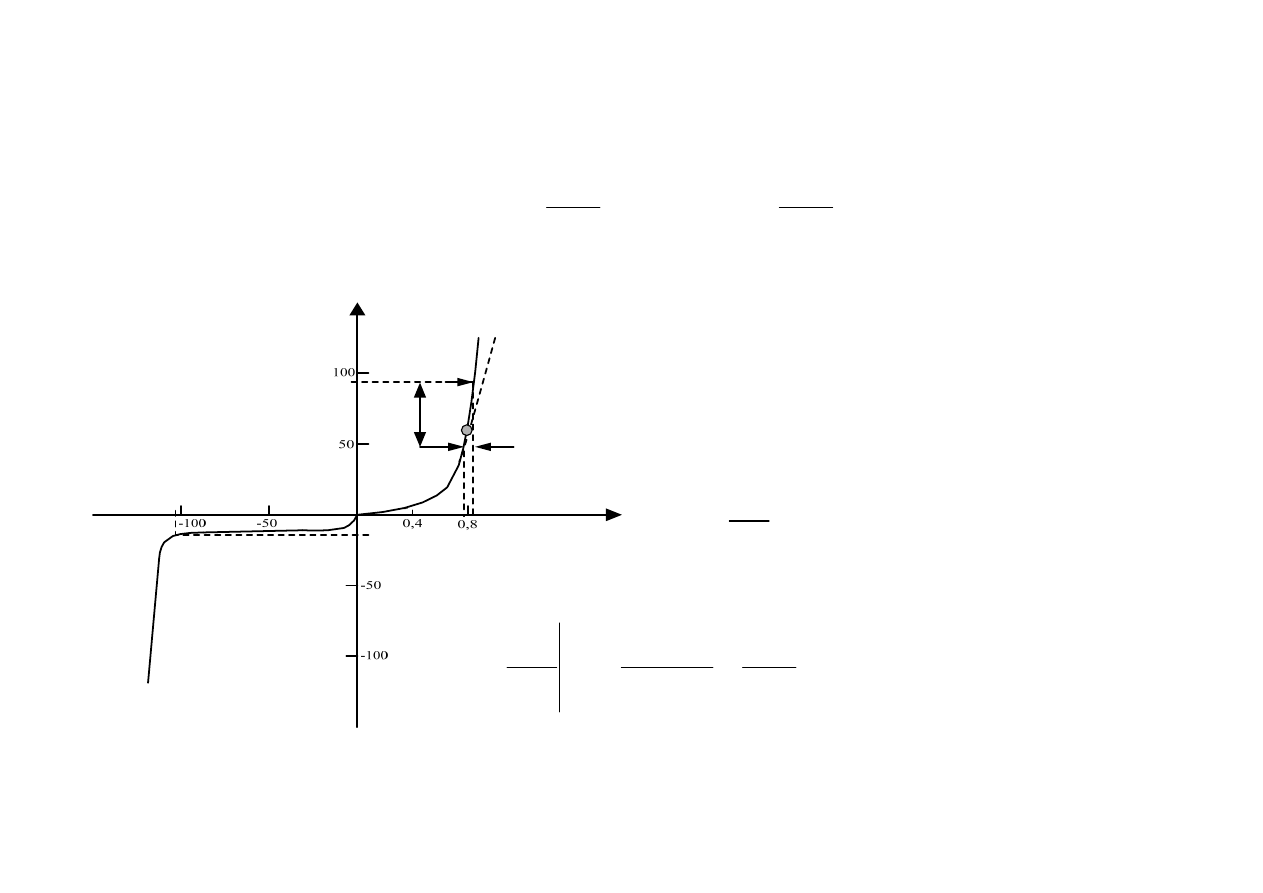
D

I

]

[V

U

D

BR

U

D

I

D

u

Δ

]

[ A

μ

D

U

]

[mA

0

I

D

I

Δ

sz

D

D

r

I

U

+

D

D

S

I

U

R

=

r

du

di

n

I

I

n

I

d

D

D I

T

D

S

T

D

D

≡

=

+

≈

ϕ

ϕ

-

-

d

d

iod

iod

a rzeczywista

a rzeczywista

i

I

u

n

I

u

n

D

S

D

T

S

D

T

=

⎛
⎝

⎜

⎞
⎠

⎟ −

⎡

⎣

⎢

⎤

⎦

⎥ ≈

⎛
⎝

⎜

⎞
⎠

⎟

exp

exp

ϕ

ϕ

1

I

I

S

S

-

-

pr

pr

ą

ą

d nasycenia diody

d nasycenia diody

r

sz

-

rezystancja poza złączowych obszarów diody

-

rezystancja statyczna

-

rezystancja dynamiczna

Charakterystyka diody z

Charakterystyka diody z

łą

łą

czowej

czowej

Interpretacje:

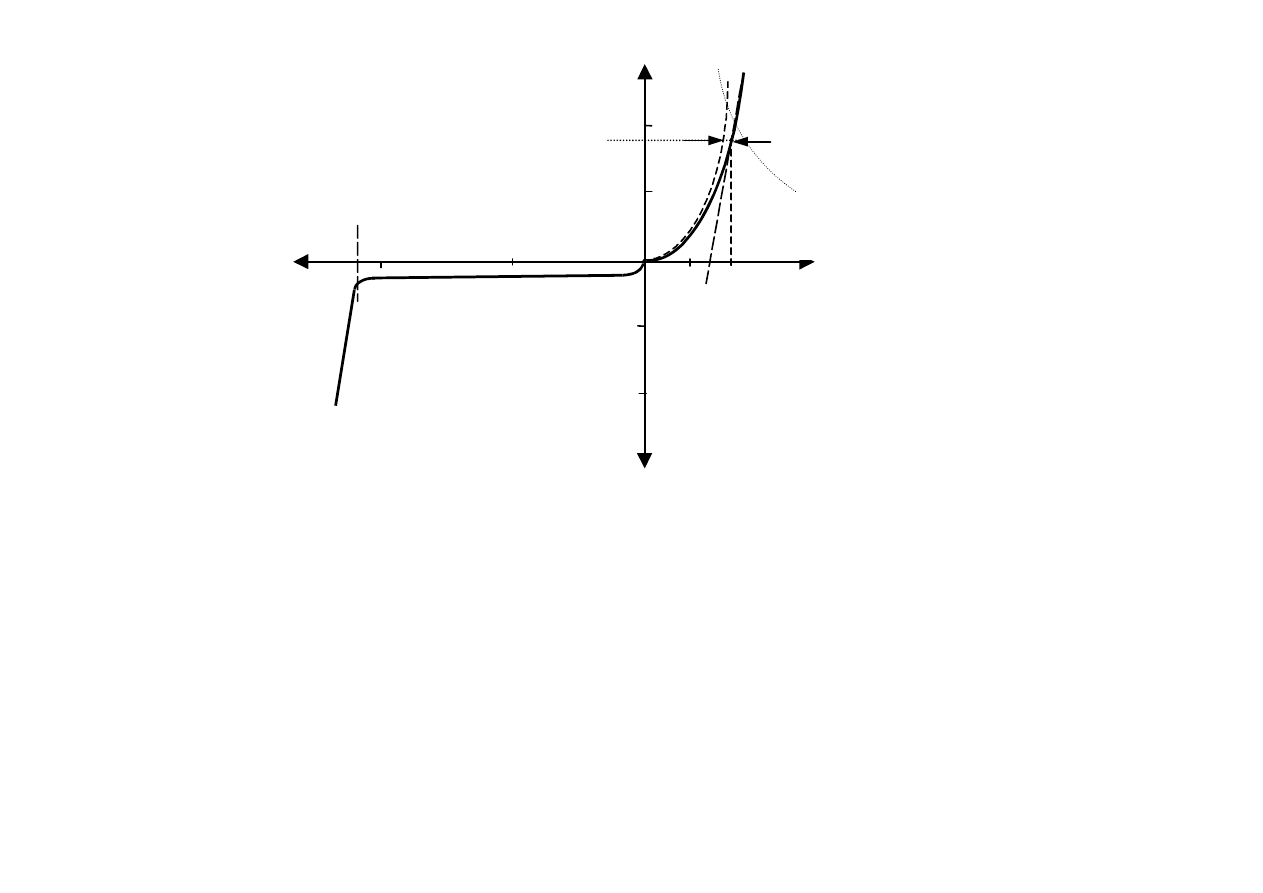
PARAMETRY

PARAMETRY

diody bipolarnej

diody bipolarnej

U

RWM-

-

maksymalne napięcie wsteczne, które może być

wielokrotnie przykładane do diod

U

R-

-

maksymalne stałe napięcie wsteczne,

U

RSM-

-

maksymalne napięcie wsteczne, które niepowtarzalnie może być

przyłożone do dio

I

FSM

-

maksymalny prąd przewodzenia,

U

F

- napięcie przewodzenia przy stałym określonym prądzie,

I

R

- prąd wsteczny przy określonym napięciu rewersyjnym i temperaturze złącza T

j

.

P

a

-

moc admisyjna

Aby ocenić

przydatność

diody w układach elektronicznych określane są

jej maksymalne,

dopuszczalne oraz charakterystyczne prądy i napięcia (parametry):

i

D

[mA]

I

D

100

Δu

D

50

U

BR

u

R [V] 100 50

0,4 0,8 [V]

u

D

U

K

50

100

[

μA]

i

R

Linia mocy admisyjnej

a)

b)

I

BV

(I

0

)

i

D

r

S

i

R

U

BR

r

R

(I

GR0

)

A

K

A

K

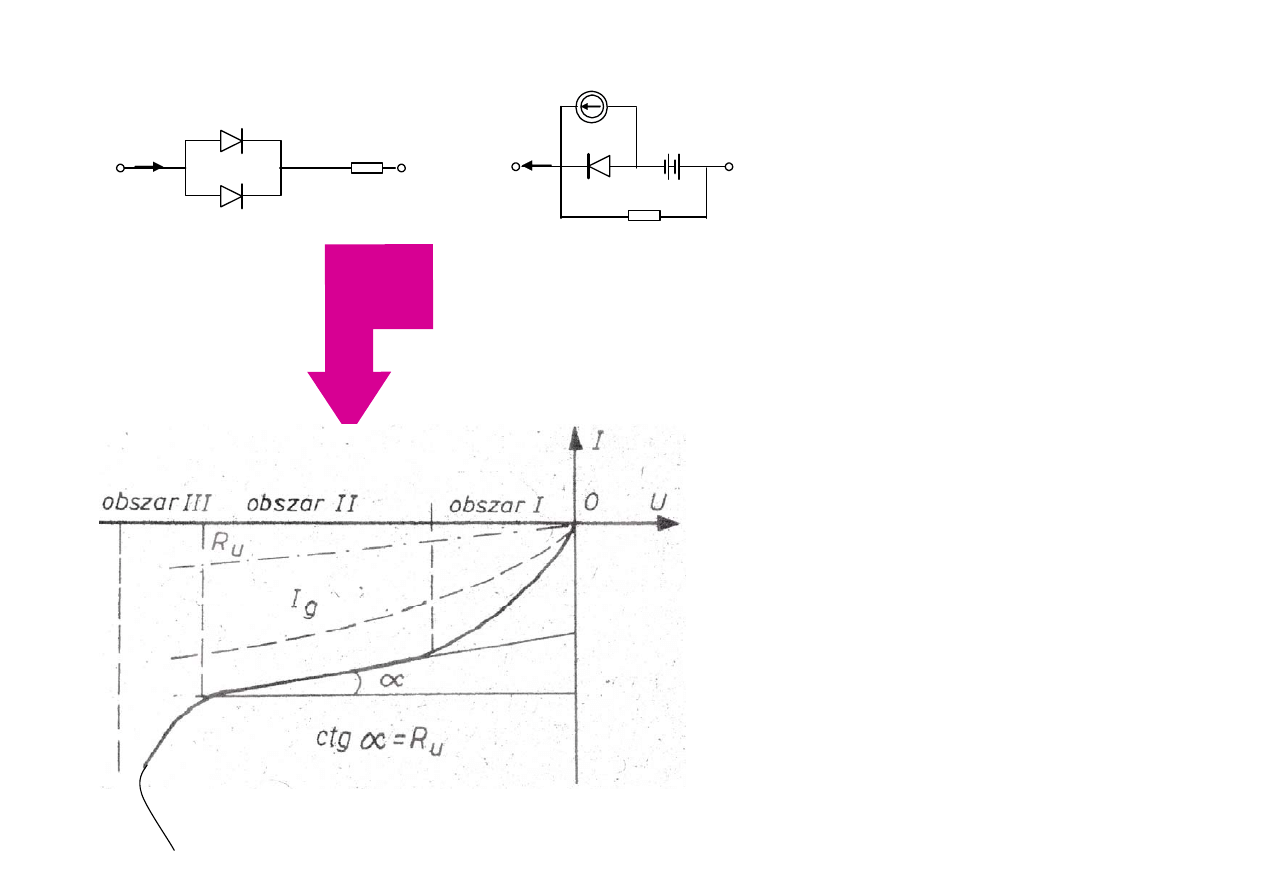
Schemat zast

Schemat zast

ę

ę

pczy diody

pczy diody

rzeczywistej:

rzeczywistej:

a

a

) w kierunku

) w kierunku

przewodzenia,

przewodzenia,

b

b

) w kierunku

) w kierunku

zaporowym

zaporowym

Prąd rewersyjny

I

R

składa się

z

prądu rewersyjnego nośników
mniejszościowych I

0

,

prądu generacji-rekombinacji I

GR0

w warstwie zubożonej oraz prądu
upływności powierzchniowej.

Źródło napięciowe U

BR

reprezentuje napięcie przebicia
lawinowego o całkowitym prądzie
I

BV

R

R

ó

ó

ż

ż

ne

ne

Apro

Apro

ksy

ksy

ma

ma

cje

cje

R

R

ó

ó

wnania Diody

wnania Diody

•

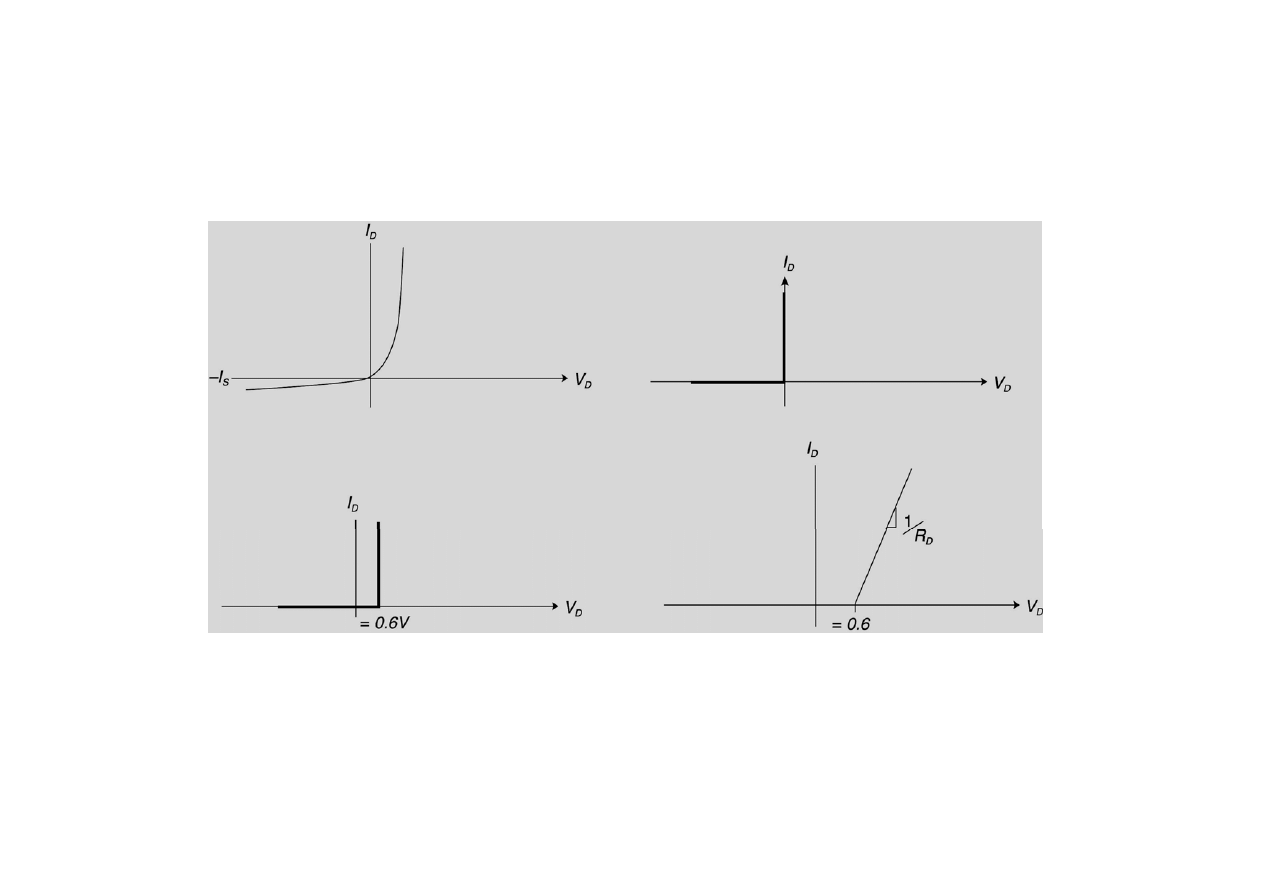
(a) Dioda rzeczywista. (b) Aproksymacja

diody

idealnej,

(c)

Aproksymacja

ze stałym napięciem przewodzenia (0.6V),

(d)

Aproksymacja z uwzględnieniem

szeregowej

rezystancji

diody.

+

-

V

V

d

I

d

R

3.1. Model analityczny diody z

3.1. Model analityczny diody z

łą

łą

czowej

czowej

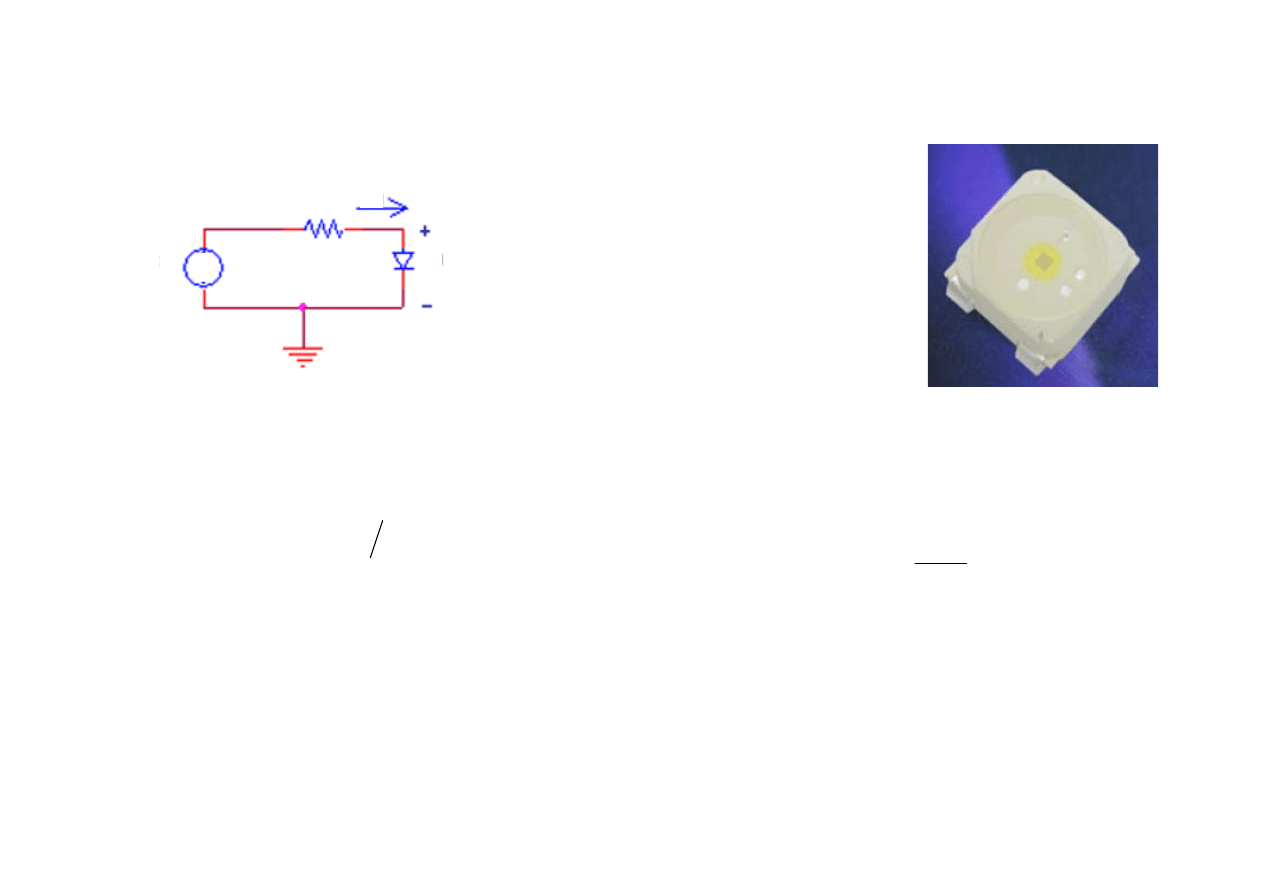
Rys.1. Obwód szeregowego połączenia diody z
rezystorem, zasilany źródłem napięcia stałego

R

I

V

V

d

d

+

=

(1)

Zwi

Zwi

ą

ą

zek pomi

zek pomi

ę

ę

dzy napi

dzy napi

ę

ę

ciem

ciem

V

V

d

d

panuj

panuj

ą

ą

cym na diodzie p

cym na diodzie p

ł

ł

yn

yn

ą

ą

cym

cym

przez ni

przez ni

ą

ą

pr

pr

ą

ą

dem wyra

dem wyra

ż

ż

a r

a r

ó

ó

wnanie

wnanie

Shockley

Shockley

’

’

a

a

:

:

)

1

(

'

−

=

T

d

V

V

s

d

e

I

I

(2)

gdzie

T

T

V

V

η

=

'

η

-współczynnik emisji złącza p-n (nieidealność złącza) nieco większy od 1,

T

V

-potencjał termiczny elektronów (

K

300

w

mV

26

/

=

=

q

kT

V

T

),

I

s

- prąd nasycenia.

)

1

ln(

'

+

=

s

d

T

d

I

I

V

V

(3)

3. Zastosowanie funkcji Lamberta w analizie matematycznej

3. Zastosowanie funkcji Lamberta w analizie matematycznej

uk

uk

ł

ł

ad

ad

ó

ó

w elektronicznych zawieraj

w elektronicznych zawieraj

ą

ą

cych z

cych z

łą

łą

cza p

cza p

-

-

n

n

}

3.1. Uog

3.1. Uog

ó

ó

lnione r

lnione r

ó

ó

wnanie diody

wnanie diody

+

-

V

V

d

I

d

R

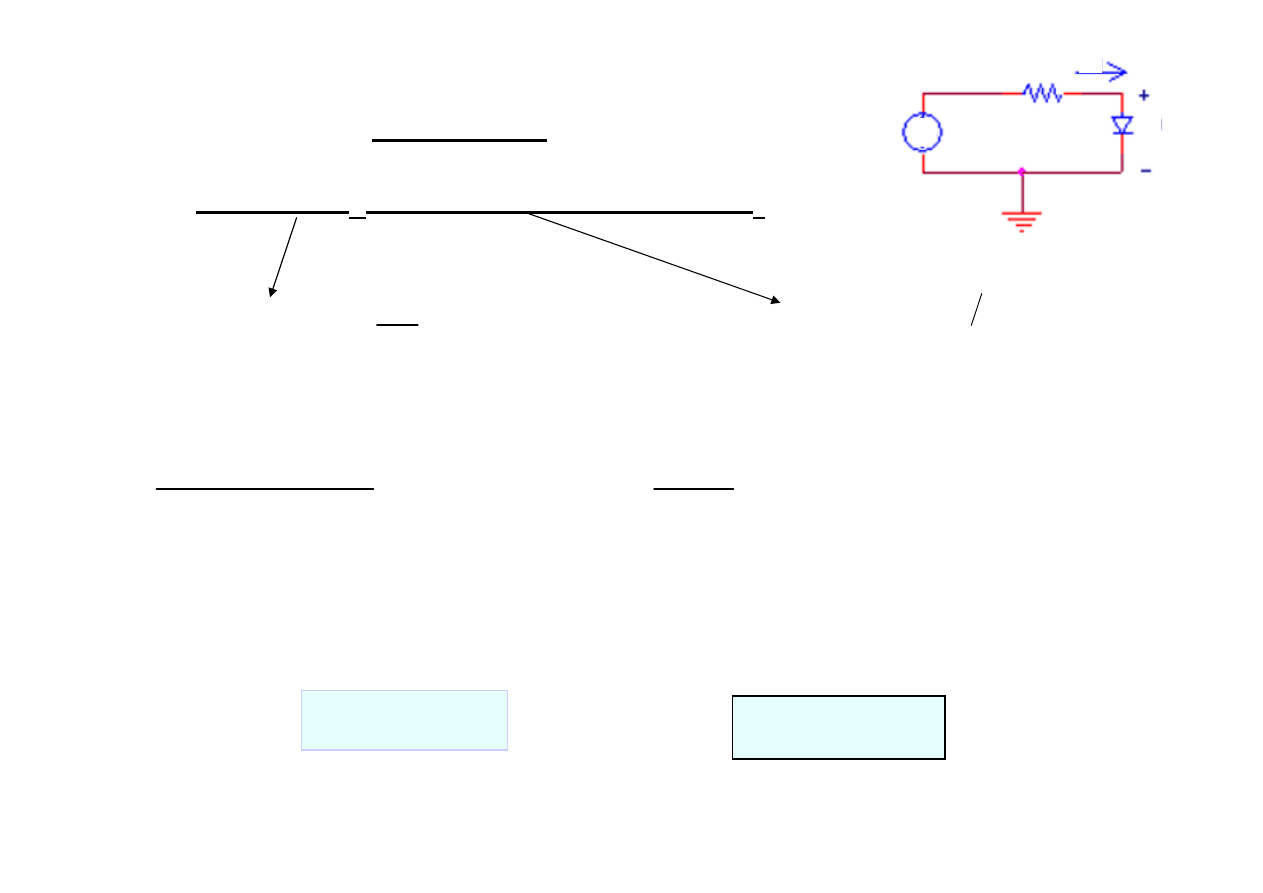
Rys.1.

Związek pomiędzy napięciem V

przyłożonym do

połączenia opornik-dioda i natężeniem prądu płynącego
w tym obwodzie I

d

czy napięciem na diodzie V

d

(4)

)

( d

V

f

d

I

=

∨

V

d

= g(I

d

)

Posta

Posta

ć

ć

algebraiczn

algebraiczn

ą

ą

rozwi

rozwi

ą

ą

zania r

zania r

ó

ó

wna

wna

ń

ń

transcendentalnych (4)

transcendentalnych (4)

mo

mo

ż

ż

na uzyska

na uzyska

ć

ć

korzystaj

korzystaj

ą

ą

c z funkcji specjalnej

c z funkcji specjalnej

W

W

.

.

)

1

ln(

'

+

+

=

s

d

T

d

I

I

V

R

I

V

'

'

/

)

(

'

/

)

(

'

)

(

T

s

T

s

d

V

R

I

V

T

s

V

R

I

I

T

s

d

e

V

R

I

e

V

R

I

I

+

+

=

+

R

e

I

V

V

T

d

V

V

s

d

)

1

(

'

−

+

=

Równania transcedentalne nie mają

rozwiązań

w zakresie funkcji

elementarnych (algebraicznych). Zależności tych nie da się

przekształcić

za pomocą

funkcji elementarnych do wzorów w postaci jawnej:

}

Po uszeregowaniu stronami uzyskuje się

3. Zastosowanie funkcji

3. Zastosowanie funkcji

W

W

Lamberta do analitycznych bada

Lamberta do analitycznych bada

ń

ń

uk

uk

ł

ł

ad

ad

ó

ó

w elektronicznych zawieraj

w elektronicznych zawieraj

ą

ą

cych z

cych z

łą

łą

cza p

cza p

-

-

n

n

(5)

3.2. Rozwi

3.2. Rozwi

ą

ą

zanie uog

zanie uog

ó

ó

lnionego r

lnionego r

ó

ó

wnania diody

wnania diody

Z punktu widzenia uogólnionego równania diody poszukiwaną

gałęzią

funkcji W Lamberta, która spełnia jego założenia jest gałąź

podstawowa, ponieważ

tylko dla niej W

0

(x)=0 dla x=0.

Rozwiązanie uogólnionego równania diody I

d

(V) można zapisać

w postaci symbolicznej jak następuje:

s

V

R

I

V

T

s

s

s

T

d

I

e

V

R

I

W

R

V

V

I

T

s

s

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

+

)

(

)

(

'

0

'

'

gdzie:

'

)

(

0

T

V

V

s

e

I

V

I

≡

-

równanie diody idealnej (dla R

s

=0)

Uproszczone równanie diody (13) przy polaryzacji w kierunku

przewodzenia

(gdy I

d

>>I

s

):

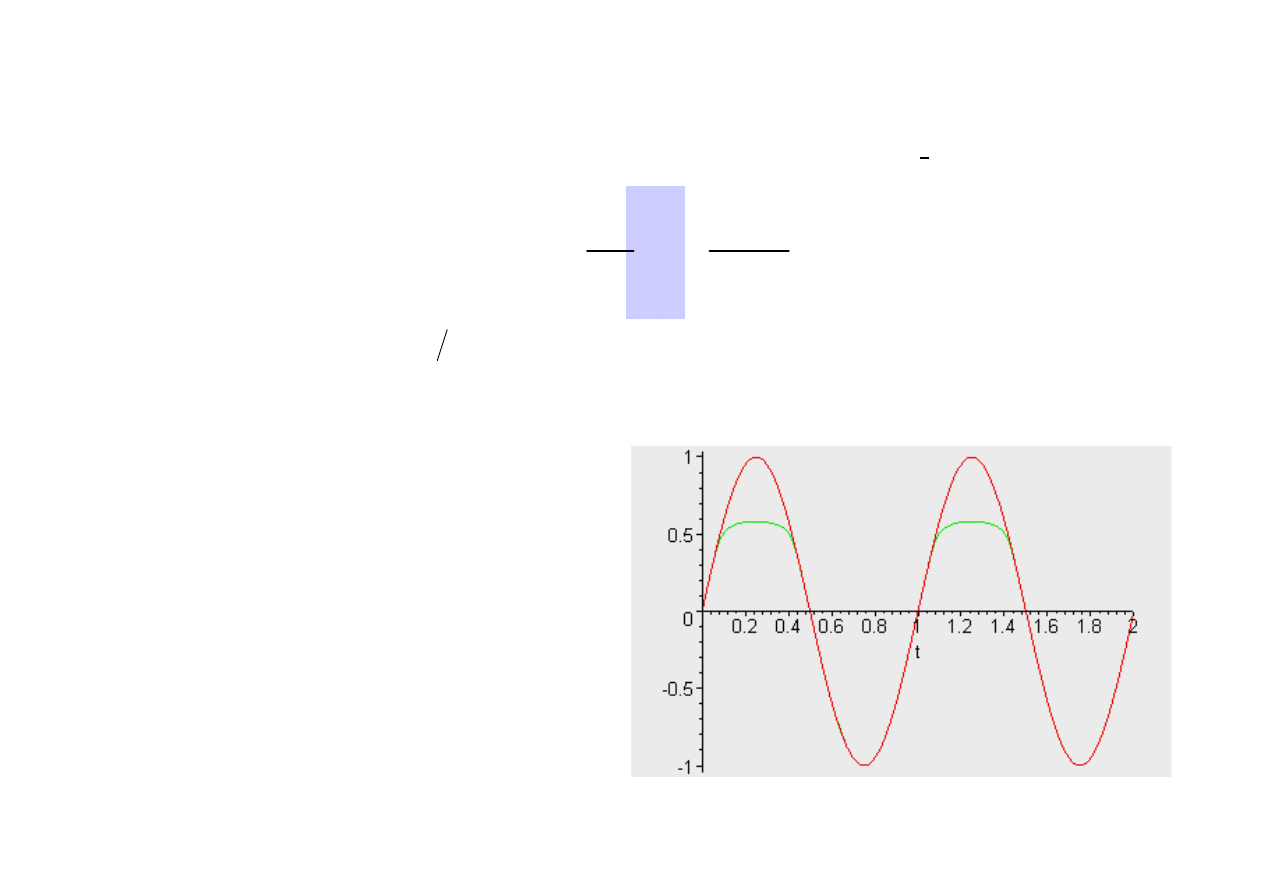
> plot([eval(V, A=1),eval(Vd, A=1)],t=0..2);

(14)

Możliwe stało się łatwe uzyskanie

analitycznych zależności

charakteryzujących wiele

parametrów obejmujących obwody

z tranzystorami bipolarnymi

3.2. Rozwi

3.2. Rozwi

ą

ą

zanie uog

zanie uog

ó

ó

lnionego r

lnionego r

ó

ó

wnania diody

wnania diody

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

'

0

0

'

)

(

T

s

s

T

d

V

R

I

W

R

V

V

I

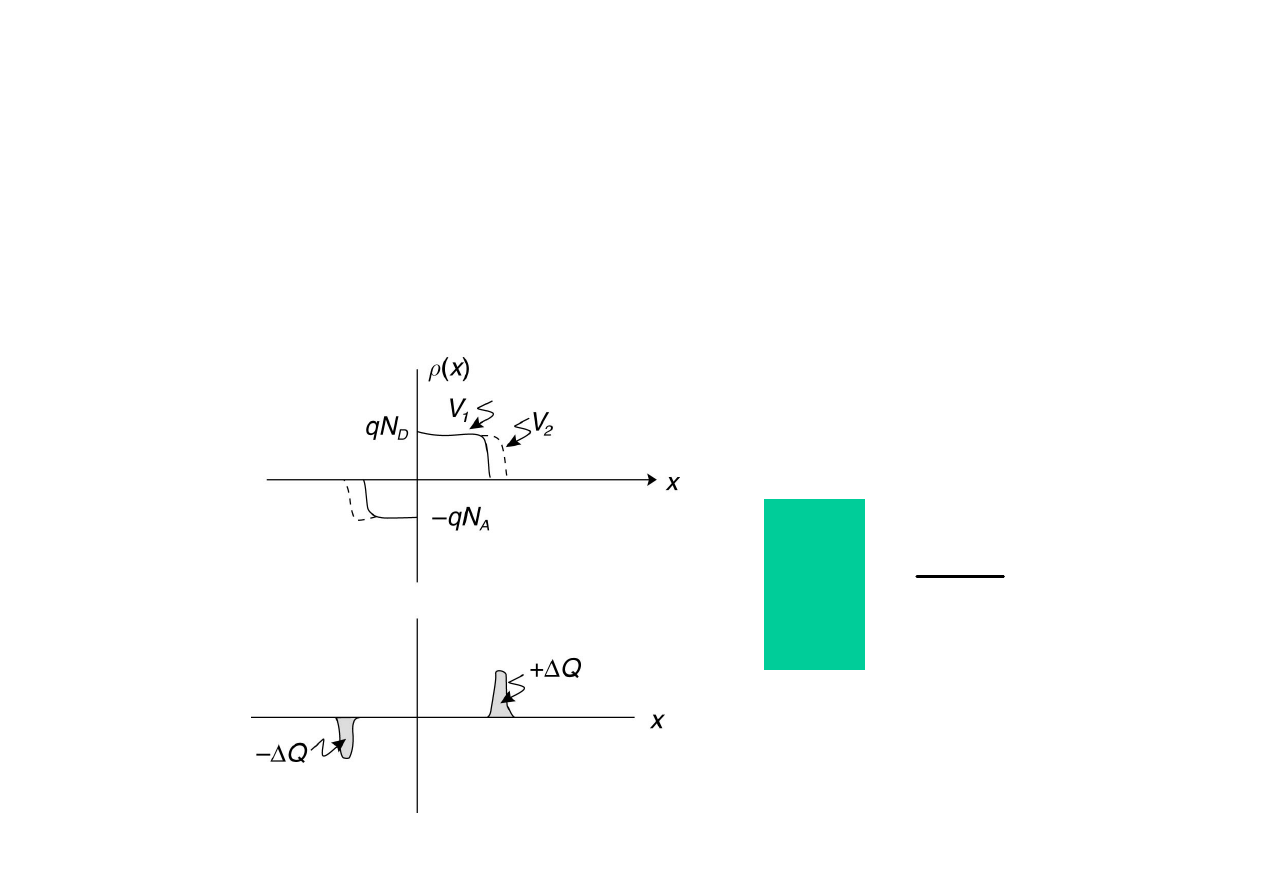
Pojemno

Pojemno

ść

ść

z

z

łą

łą

czowa diody

czowa diody

(polaryzacja zaporowa)

Ładunek zgromadzony w obszarze zubożonym zmienia się

wraz ze zmianami napięcia wstecznego.

dV

dQ

C

j

=

-10

-8

-6

-4

-2

0

2

0

0.5

1

1.5

2

2.5

3

m

bi

D

jo

j

V

C

C

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

φ

1

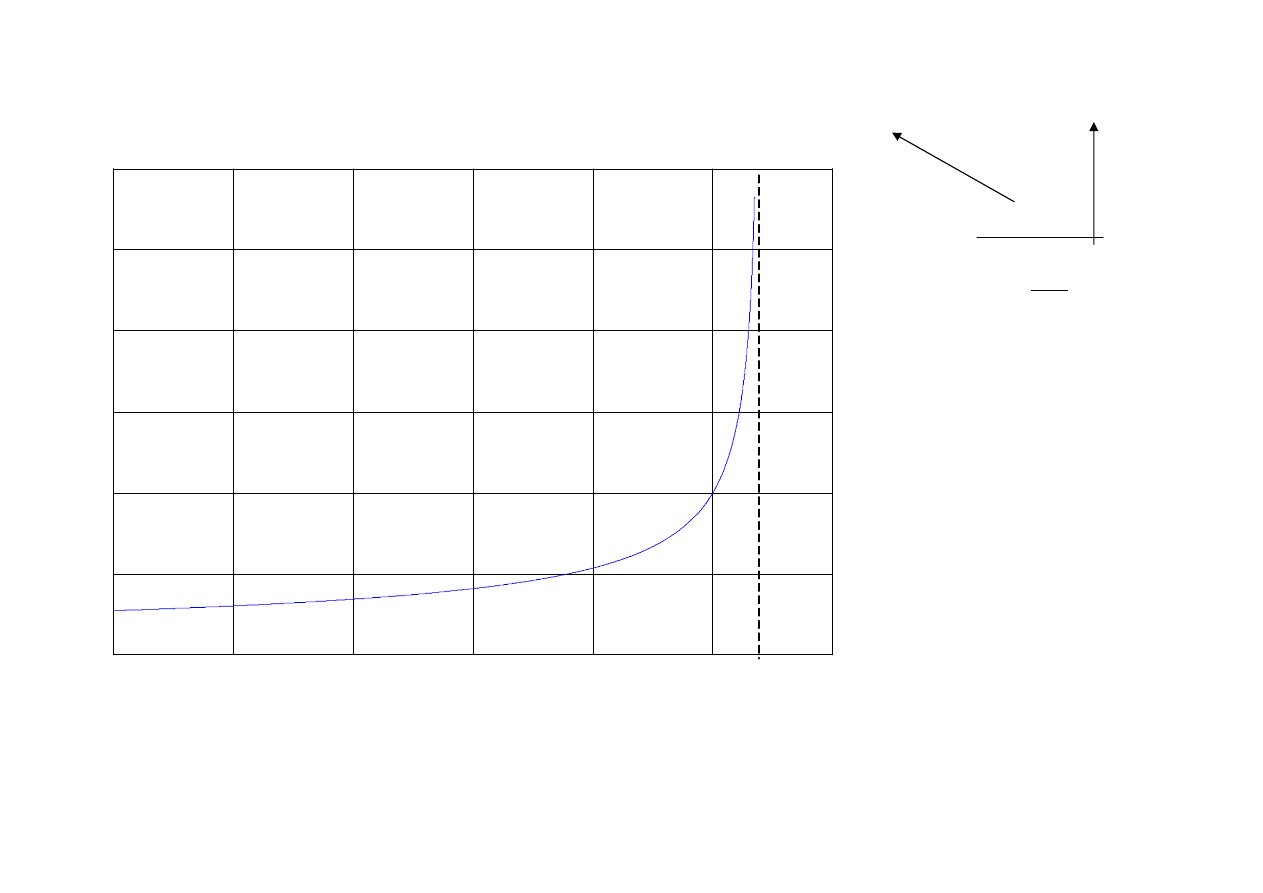
Pojemno

Pojemno

ść

ść

z

z

łą

łą

czowa (

czowa (

cd

cd

.)

.)

Zależność

wielkości pojemności złączowej [pF] od napięcia na diodzie [V]

bi

φ

-

potencjał

złącza (napięcie na złączu

przy braku polaryzacji zewnętrznej)

Pojemność

przy

zerowej polaryzacji

Rodzaj złącza
m=1/3 lub 1/2

×100

Bariera potencjału

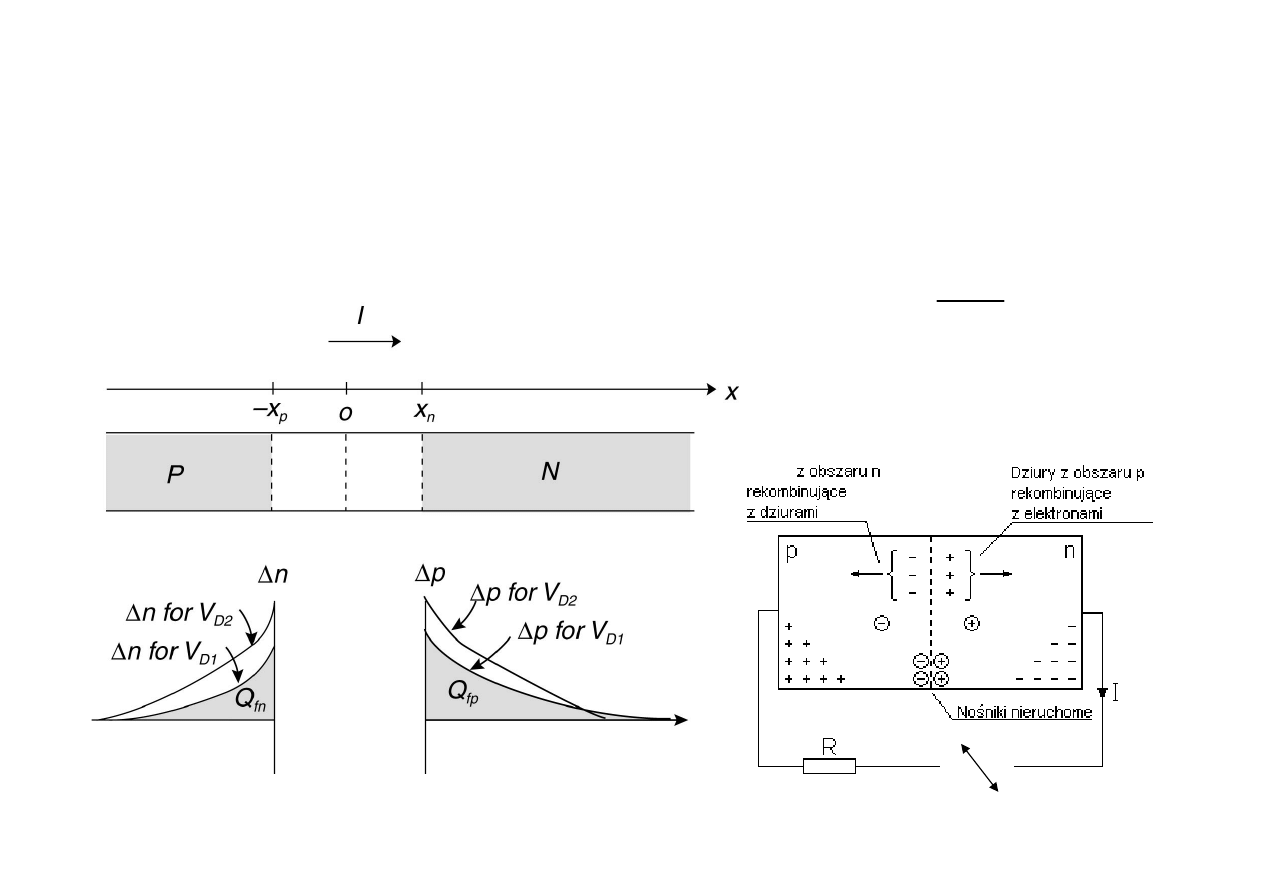
Pojemno

Pojemno

ść

ść

dyfuzyjna

dyfuzyjna

(polaryzacja w kierunku przewodzenia)

(polaryzacja w kierunku przewodzenia)

Ładunki gromadzące się

w obu obszarach diody przy polaryzacji w

kierunku przewodzenia. Wraz ze zmianami napięcia zewnętrznego ładunek
tam zgromadzony ulega zmianie -

zjawisko można zamodelować

za

pomocą

pojemności zwanej dyfuzyjną

C

d

D

d

I

C

∝

+ -

elektrony

dU

dQ

C

d

d

=

•

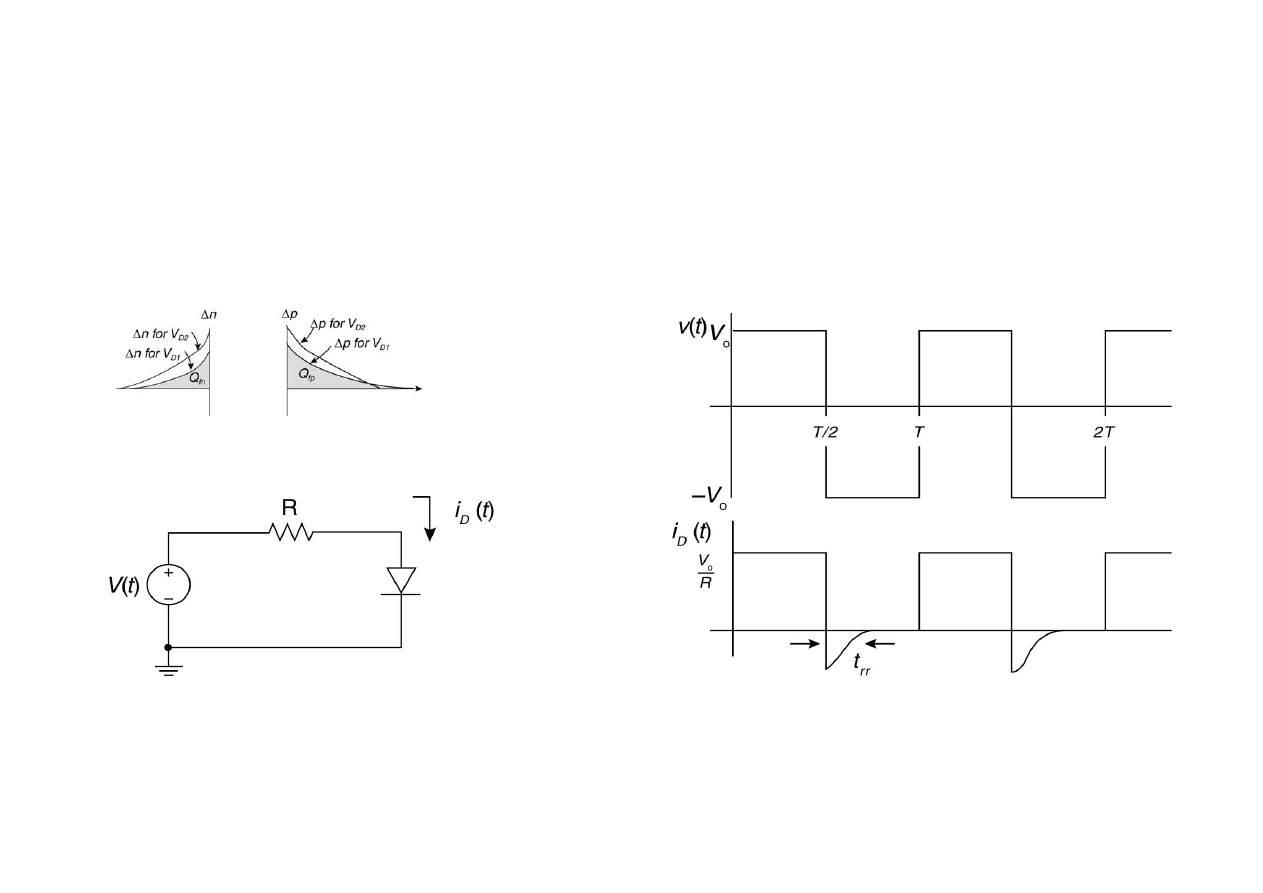
Zanim dioda bipolarna przełączy się

ze stanu przewodzenia

(klucz zamknięty) w stan zatkania (klucz otwarty)

musi nastąpić

usunięcie ładunku zgromadzonego w pojemności dyfuzyjnej
(z obszarów poza-złączowych)

Prze

Prze

łą

łą

czanie diody

czanie diody

t

rr

–czas odzyskania zdolności

przęłączania

do stanu zatkania

(

reverse

recovery

time

)

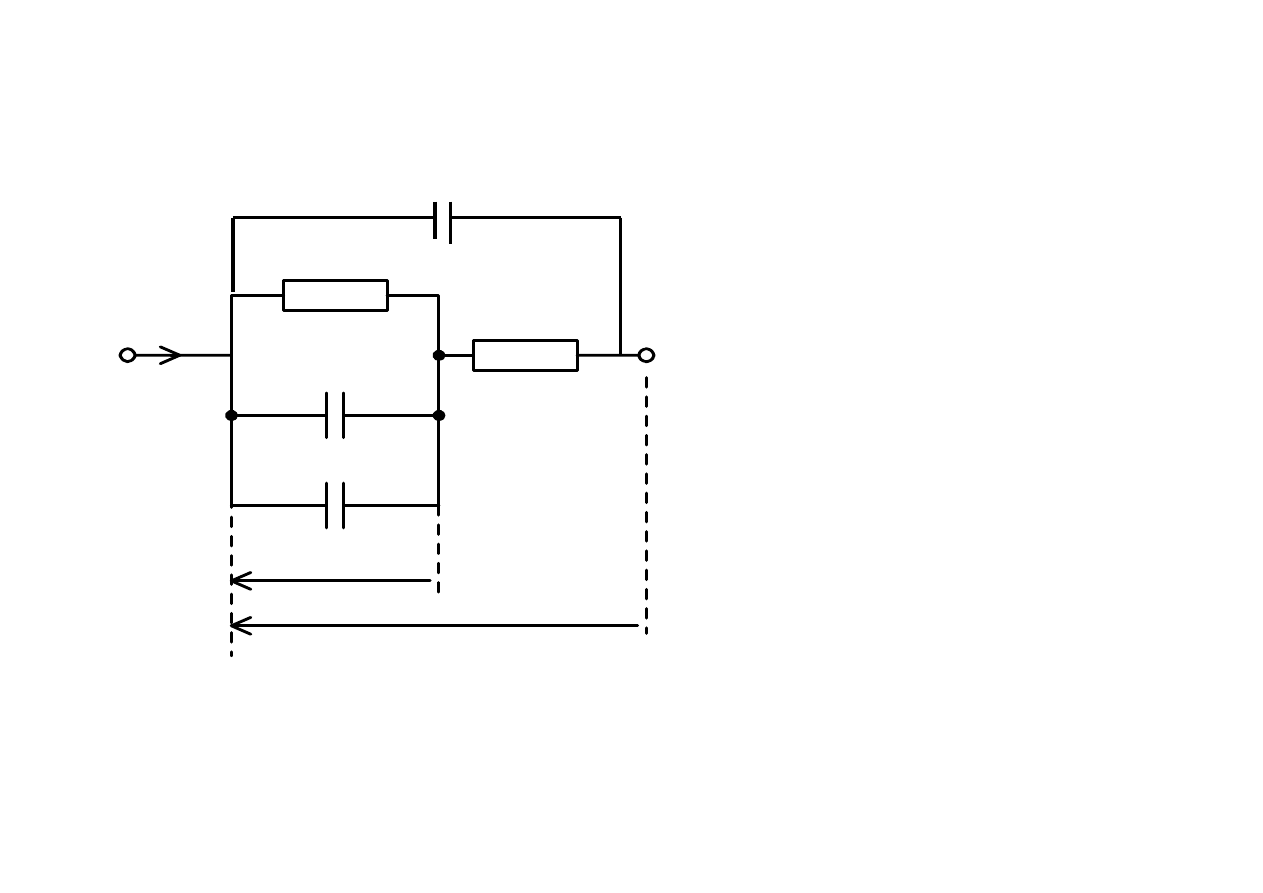
Dioda ze złączem PN

…………..cd

Diod

Diod

a ze z

a ze z

łą

łą

czem

czem

PN

PN

…………..cd

Schemat zast

Schemat zast

ę

ę

pczy dla w.cz.

pczy dla w.cz.

d

r

d

C

S

r

d

U

S

d

d

r

I

U

−

d

I

j

C

C = Cd +

C = Cd +

Cj

Cj

+ Co

+ Co

Ca

Ca

ł

ł

kowita pojemno

kowita pojemno

ść

ść

diody

diody

Co

Co

-

-

pojemno

pojemno

ść

ść

paso

paso

ż

ż

ytnicza

ytnicza

C

o

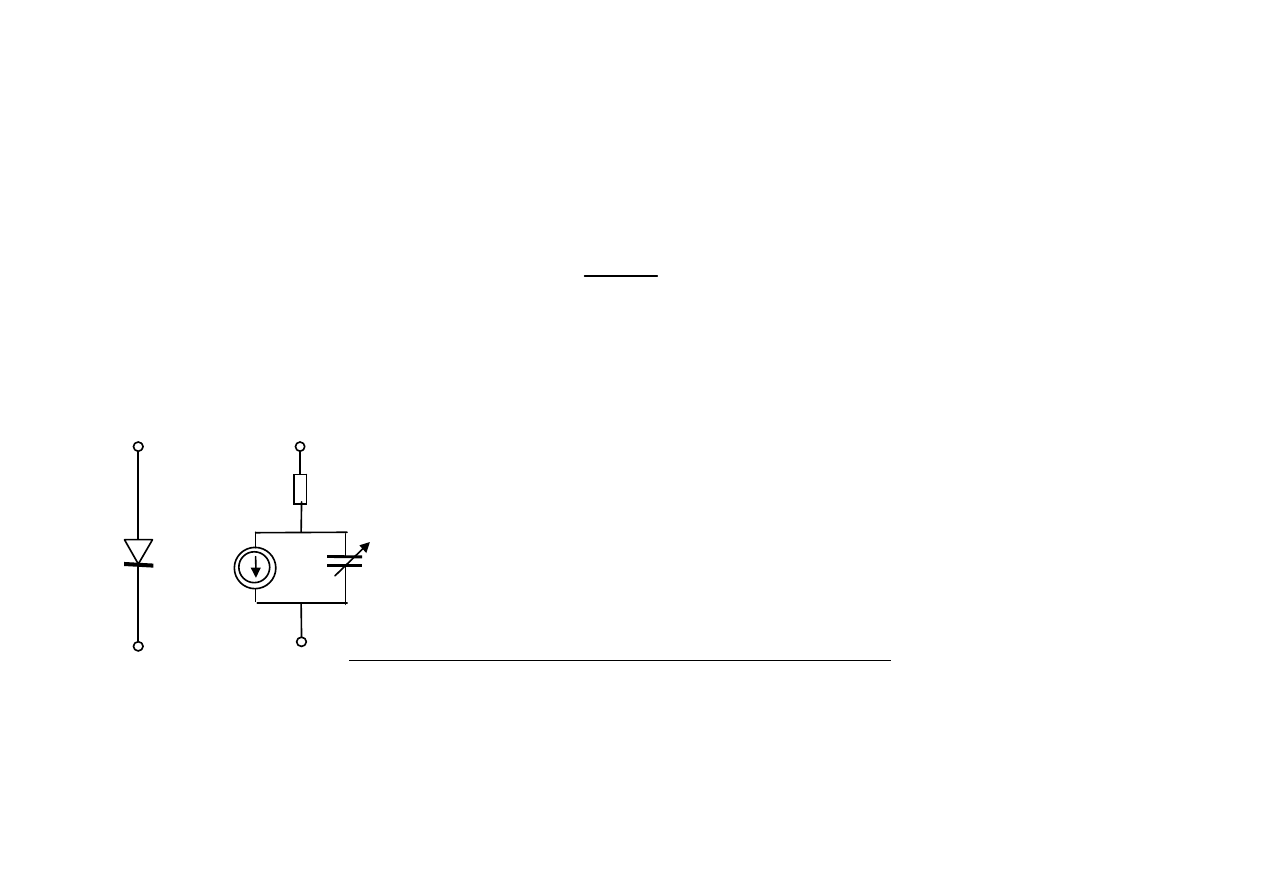
gdzie: IS -

prąd nasycenia w temperaturze nominalnej TNOM=27

o

C (I

S-

), N -

współczynnik

emisji (n) -

parametry komputerowe, które mają

w programie wbudowaną

wartość

–

SPICE

default

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

1

T

D

D

U

u

i

N

exp

IS

Model komputerowy diody (SPICE)

Model komputerowy diody (SPICE)

RS

+

≡ i

D

u

D

C

j

-

Model diody postaci schematu zastępczego w

SPICE/PSPICE

Model –

obiekt zastępczy reprezentujący wybrane cechy obiektu

rzeczywistego z zadowalającą

dokładnością.

Schematy zastępcze, równania, modele mieszane.

Modele dla różnych typów sygnałów i oznaczenia

I

B

; U

BE

-

składowe stałe

i

b

(t); u

be

(t) - składowe zmienne

i

B

(t); u

BE

(t) - wartości chwilowe

I

b

; U

be

– wartości zespolone

Modele: wielkosygnałowe, małosygnałowe statyczne, dynamiczne (stało-

lub zmienno-prądowe)

Diody Zenera

Diody Zenera

W diodach spolaryzowanych zaporowo występują

dwa mechanizmy przebicia

napięciowego różniące się

znakiem temperaturowego współczynnika stabilizacji napięcia

a) Przebicie Zenera

Pod wpływem bardzo

dużego natężenia pola elektrycznego

(gradientu

potencjału) 10

6

-10

8

[V/m] w obszarze złącza następuje

rozrywanie

wiązań

kowalentnych, (generacja par dziura –elektron)

a więc znaczne

zwiększenie ilości nośników mniejszościowych.

Im silniejsze

domieszkowanie tym przy mniejszym napięciu uzyskuje się

wystarczające

do rozrywania wiązań

natężenie pola E

.

Wzrost energii kinetycznej

nośników mniejszościowych ze wzrostem temperatury wspomaga
pole w wytwarzaniu dalszych nośników mniejszościowych czyli
mechanizm przebicia Zenera charakteryzuje się

ujemnym

współczynnikiem temperaturowym.

Obserwuje się

go dla diod o napięciach powyżej 7 woltów.

b) Przebicie lawinowe

b)

Przebicie lawinowe

Wskutek działania cieplnego generowana jest w złączu pewna niewielka

ilość

nośników mniejszościowych.

Nośniki mniejszościowe przy

odpowiednio dużym natężeniu pola E uzyskują

tak dużą

prędkość, że

zdarzając się

z obojętnymi atomami wytwarzają

pary dziura-elektron.

Ponieważ

elektrony są

bardziej ruchliwe większość

nowych nośnikowa

powstaje wskutek uderzeń

elektronów.

Aby zjawisko miało charakter

lawinowy elektrony muszą

osiągać

w czasie przejścia tzw. średniej drogi

swobodnej (średnia odległość

miedzy zderzeniami). wystarczającą

energię

do zjonizowania kolejnego atomu. Energia ta (kinetyczna) musi być

większa od energii pasma zabronionego

.

Wzrost temperatury zmniejsza

średnią

drogę

swobodną

i w efekcie musi być

wyższe napięcie

(natężenie) aby doprowadzić

do podtrzymania przebicia lawinowego.

Efekt dodatniego współczynnika temperaturowego, który charakteryzuje

przebicie lawinowe występuje dla diod o napięciach stabilizacji mniejszych

od 5 woltów.

Pomiędzy 5 a 6 woltów współczynnik temperaturowy diod

stabilizacyjnych jest zbliżony do 0 [V/K].

Diody Zenera

Diody Zenera

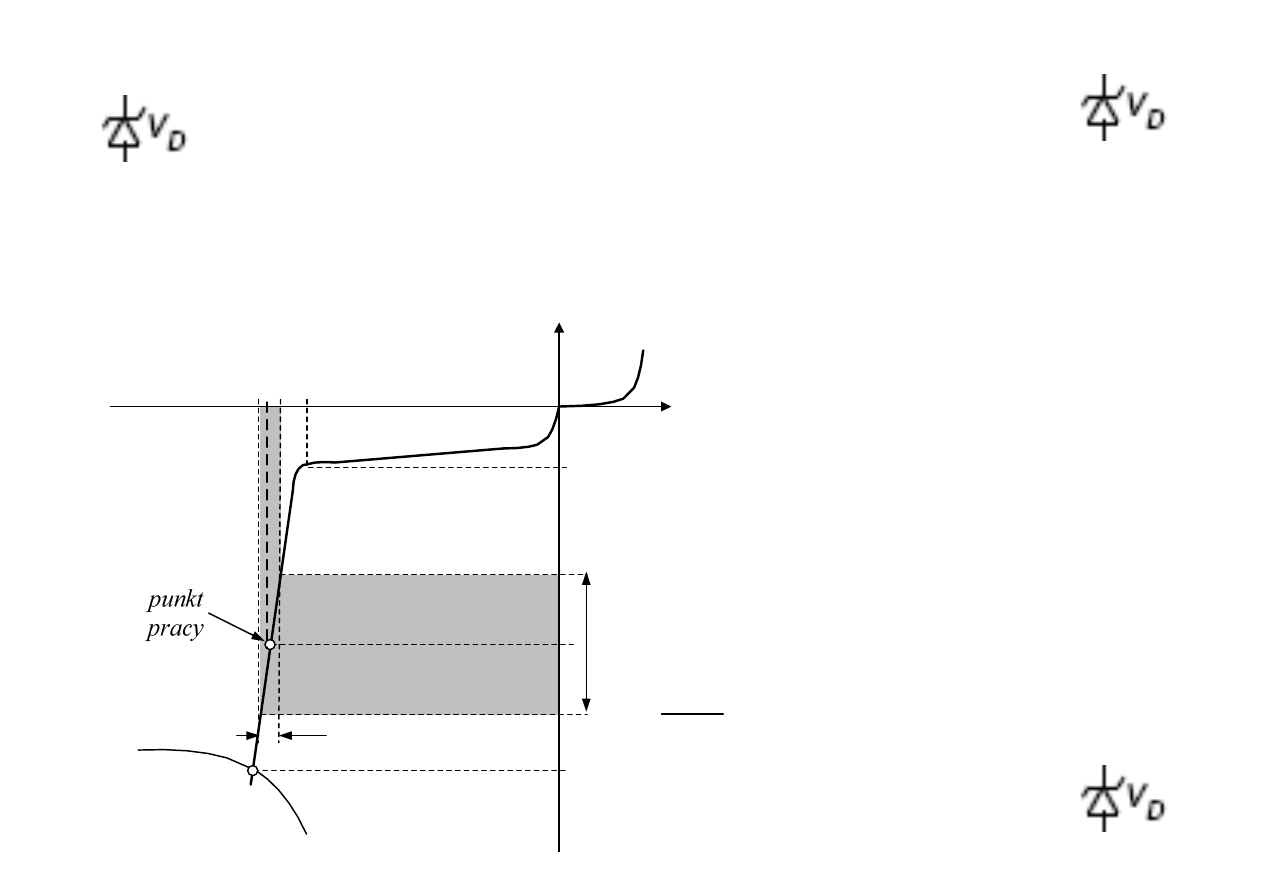
Diody Zenera

Diody Zenera

charakterystyka i parametry

charakterystyka i parametry

Z

U

ZK

U

Z

i

Z

u

Z

I

Z

i

Δ

Z

u

Δ

MIN

I

MAX

I

MAX

P

Z

Z

Z

r

I

U

=

Δ

Δ

rezystancja dynamiczna diody Zenera

Dioda Zenera spolaryzowana w kierunku przewodzenia

zachowuje się

jak zwykła dioda

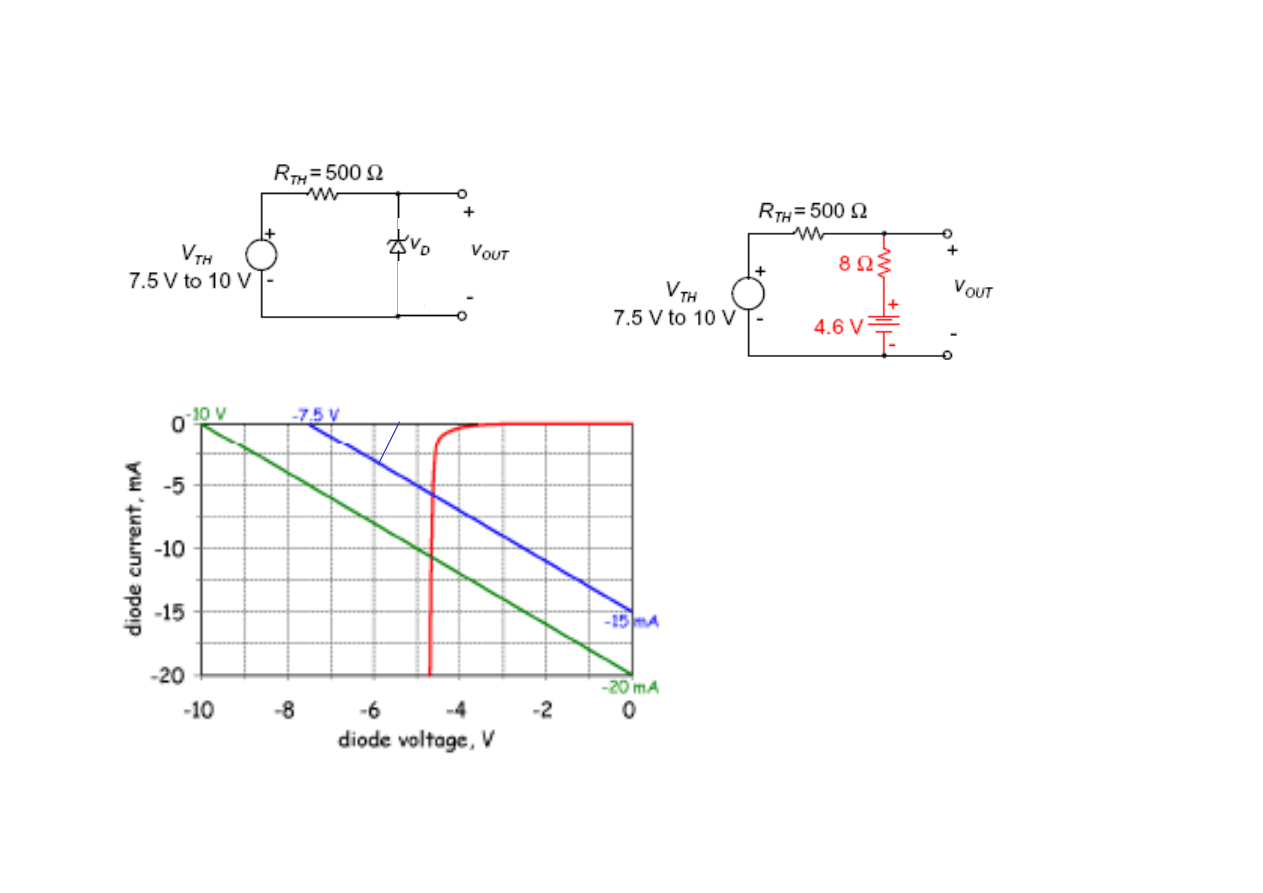
V

out

= V

z

≅

4,7 V

α

500

500

=

⇔

Ω

=

α

ctg

R

TH

Obw

Obw

ó

ó

d z diod

d z diod

ą

ą

Zenera

Zenera

–

–

bez obci

bez obci

ąż

ąż

enia

enia

Obwód z modelem diody

do rozwiązania analitycznego

Rozwiązanie graficzne

Najprostszy stabilizator

Najprostszy stabilizator

bez obci

bez obci

ąż

ąż

enia tzn.

enia tzn.

R

R

L

L

=

=

∞

∞

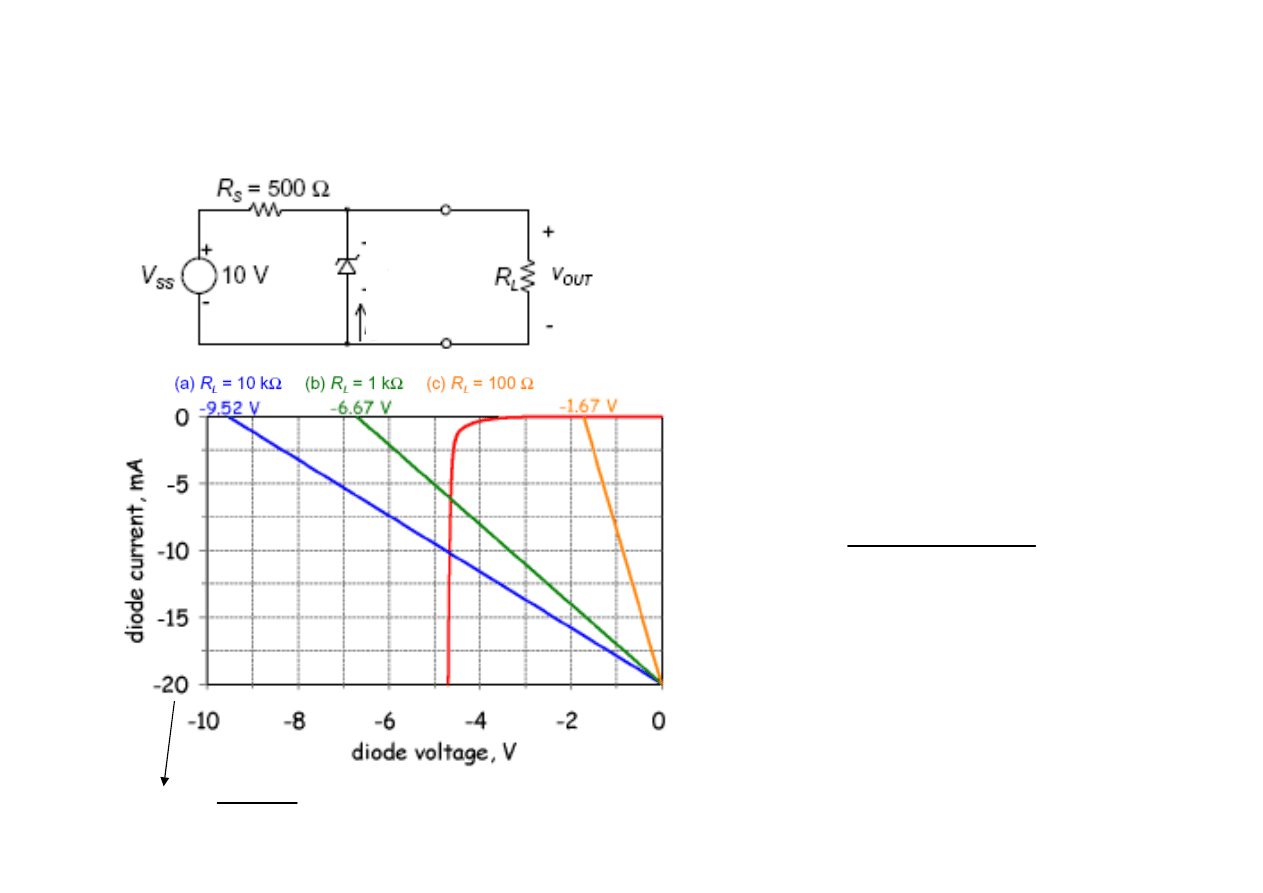
Obwód z diodą

Zenera + obciążenie

Największa moc wydziela się

w diodzie Zenera

gdy napięcie wejściowe jest największe i

rezystancja obciążenia jest maksymalna

(prąd=0).

Moc ta musi być

mniejsza od mocy

dopuszczalnej stosowanej diody.

0

500

10

20

=

Ω

=

L

R

V

mA

Najprostszy stabilizator

Najprostszy stabilizator

z obci

z obci

ąż

ąż

eniem

eniem

R

R

L

L

Z

S

Z

we

Z

str

U

R

U

U

P

)

(

max

max

−

=

Z

Z

strZ

U

I

P

=

Z

str

dopZ

P

P

max

>

0

500

10

20

=

Ω

=

L

R

V

mA

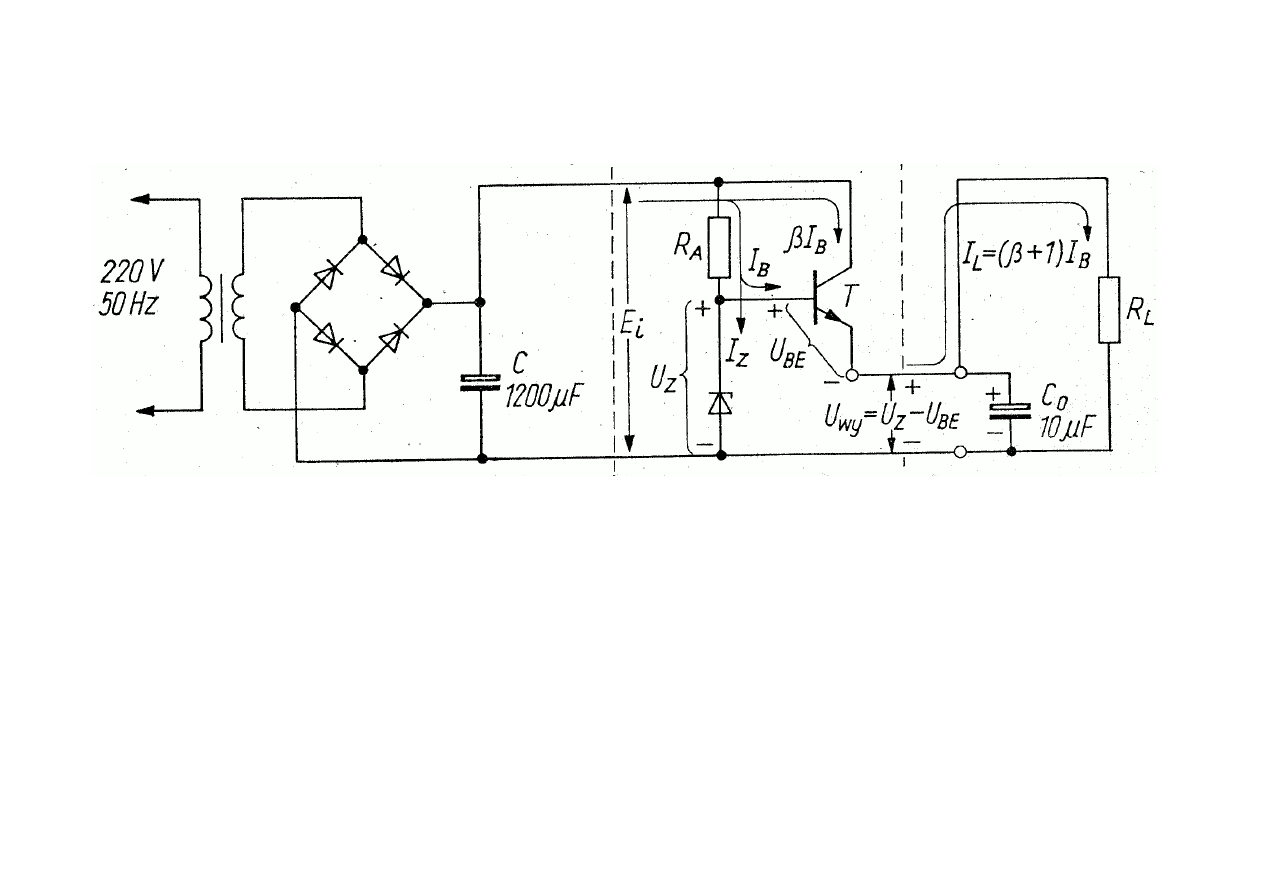
Zastosowanie diody Zenera jako

Zastosowanie diody Zenera jako

ź

ź

r

r

ó

ó

d

d

ł

ł

a napi

a napi

ę

ę

cia odniesienia

cia odniesienia

w zasilaczu stabilizowanym

w zasilaczu stabilizowanym

Prostownik

Stabilizator

Obciążenie

Zasilacz niestabilizowany

Dzięki zastosowaniu tranzystora nie musi być

stosowana

dioda Zenera dużej mocy mimo stosowania dużych obciążeń.
Prąd w diodzie wystarczy, że jest nieco większy niż

I

Bmax

czyli około

β

razy mniejszy niż

wymagany prąd obciążenia.

Uwaga: Jest to piękny przykład wykorzystania tranzystora jako transformatora impedancji
(wtórnik) dla prądu stałego a także jako świetnego układu sterującego (małe zmiany prądu na
wejściu sterują

dużymi zmianami prądu na wyjściu a układ odniesienia pobiera mało mocy)

LITERATURA

„

„

Elementy i uk

Elementy i uk

ł

ł

ady elektroniczne

ady elektroniczne

”

”

, red. St. Kuta;

, red. St. Kuta;

„

„

Uk

Uk

ł

ł

ady p

ady p

ó

ó

ł

ł

przewodnikowe

przewodnikowe

”

”

U. Tietze, Ch.

U. Tietze, Ch.

Schenk

Schenk

„

„

Sztuka Elektroniki

Sztuka Elektroniki

”

”

t1, t2 Horowitz,

t1, t2 Horowitz,

Hill

Hill

Elementy i uk

Elementy i uk

ł

ł

ady p

ady p

ó

ó

ł

ł

przewodnikowe

przewodnikowe

Alley

Alley

,

,

Atwood

Atwood

R

R

ó

ó

wnanie

wnanie

Diod

Diod

y

y

Ideal

Ideal

nej

nej

(

(

Shockley

Shockley

’

’

a

a

)

)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

=

1

kT

qV

s

TOTAL

D

D

e

I

A

J

I

q

kT

V

for

e

I

I

D

kT

qV

s

D

D

/

>>

≈

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

=

1

1

2

kT

qV

S

kT

qV

n

A

n

p

D

p

i

D

D

D

e

I

e

L

N

D

L

N

D

qAn

I

Pominięty przede wszystkim prąd gene-rekombinacji.
Nie obowiązuje przy V

D

< 400 mV

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

+

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

1

exp

1

2

exp

0

T

S

D

D

S

T

S

D

D

GR

D

U

r

i

u

I

U

r

i

u

I

I

q

kT

U

T

/

=

-

potencjał

elektrokinetyczny