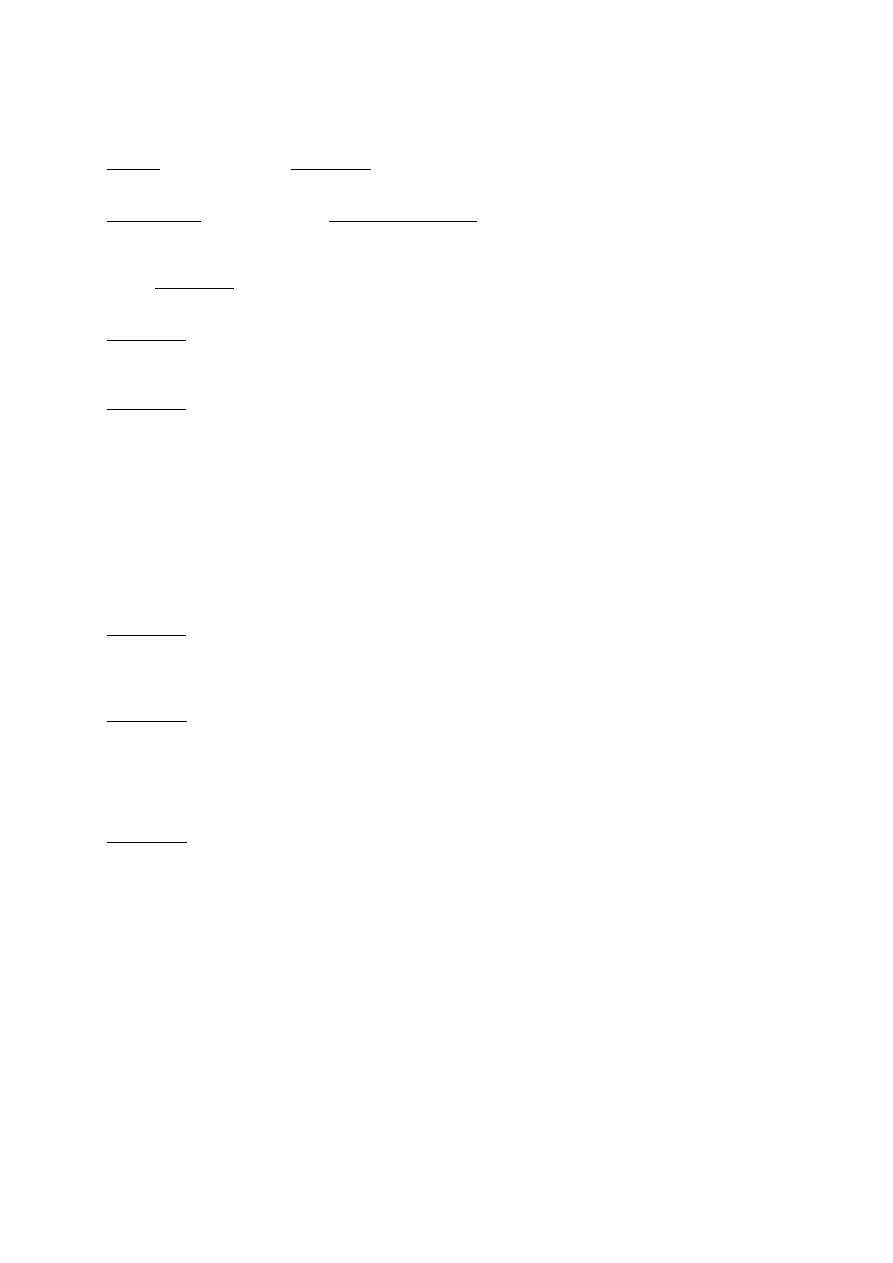
LICZENIE PIERWIASTKA KWADRATOWEGO
Liczenie pierwiastka kwadratowego rozpoczynamy od “podzielenia” liczby pierwiastkowanej na grupy liczb
dwucyfrowych:
7654321
podzielimy tak:
07|65| 43| 21
Gdy liczba posiada część ułamkową to dzielimy ją osobno:
7654321,12345 podzielimy tak:
07|65 |43 |21,|12| 34|50
Kolejnym krokiem jest wyznaczenie pierwszej cyfry wyniku. Jest to największa cyfra, która podniesiona do kwadratu
będzie mniejsza od liczby utworzonej z pierwszej pary liczb.
Np. dla
07|65| 43| 21
pierwszą cyfrą wyniku będzie 2 (
2
2
=4 7 ale 3
2
=9 7
)
Teraz odejmujemy kwadrat wyznaczonej cyfry od pierwszej pary cyfr:
07|65| 43| 21
=2...
−04
03
a do otrzymanej różnicy dopisujemy kolejną parę cyfr (otrzymaną liczbę oznaczmy przez x)
07|65| 43| 21
=2...
−04
03 65
i powtarzamy kolejne kroki:
a) podwojenie dotychczasowego wyniku
b) dopisanie z prawej strony otrzymanej liczby największej takiej cyfry, że otrzymana w ten sposób liczba
pomnożona przez tą cyfrę będzie mniejsza od ostatnio otrzymanej liczby x (zapisując to arytmetycznie: (liczba
z pp a)*
+Ax, gdzie a to szukana cyfra)
c) dopisanie cyfry x do wyniku
d) odjęcie od liczby x liczby otrzymanej przez pomnożenie liczby z pp b przez cyfrę z pp b
Najlepiej zrozumieć to na przykładzie:
07|65| 43| 21
=2...
−04
03 65 4X
⋅X 365 ⇒ X =7 bo 47∗7=329 365
X=7 dopiszemy do wyniku i wartość wyliczoną w poprzednim kroku odejmiemy od poprzedniej reszty:
07|65| 43| 21
=27..
−04
03 65
−3 29
36
Dopisujemy kolejną grupę dwucyfrową i powtarzamy wszystkie kroki:
07|65| 43| 21
=2766
−04
03 65
−3 29
36 43 54X
⋅X 3643 ⇒ X =6 bo 546⋅6=3276 3643
−32 76
3 73 21 552X
⋅X 37321 ⇒ X =6 bo 5526⋅6=33156 37321
−3 31 56
41 65
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
1
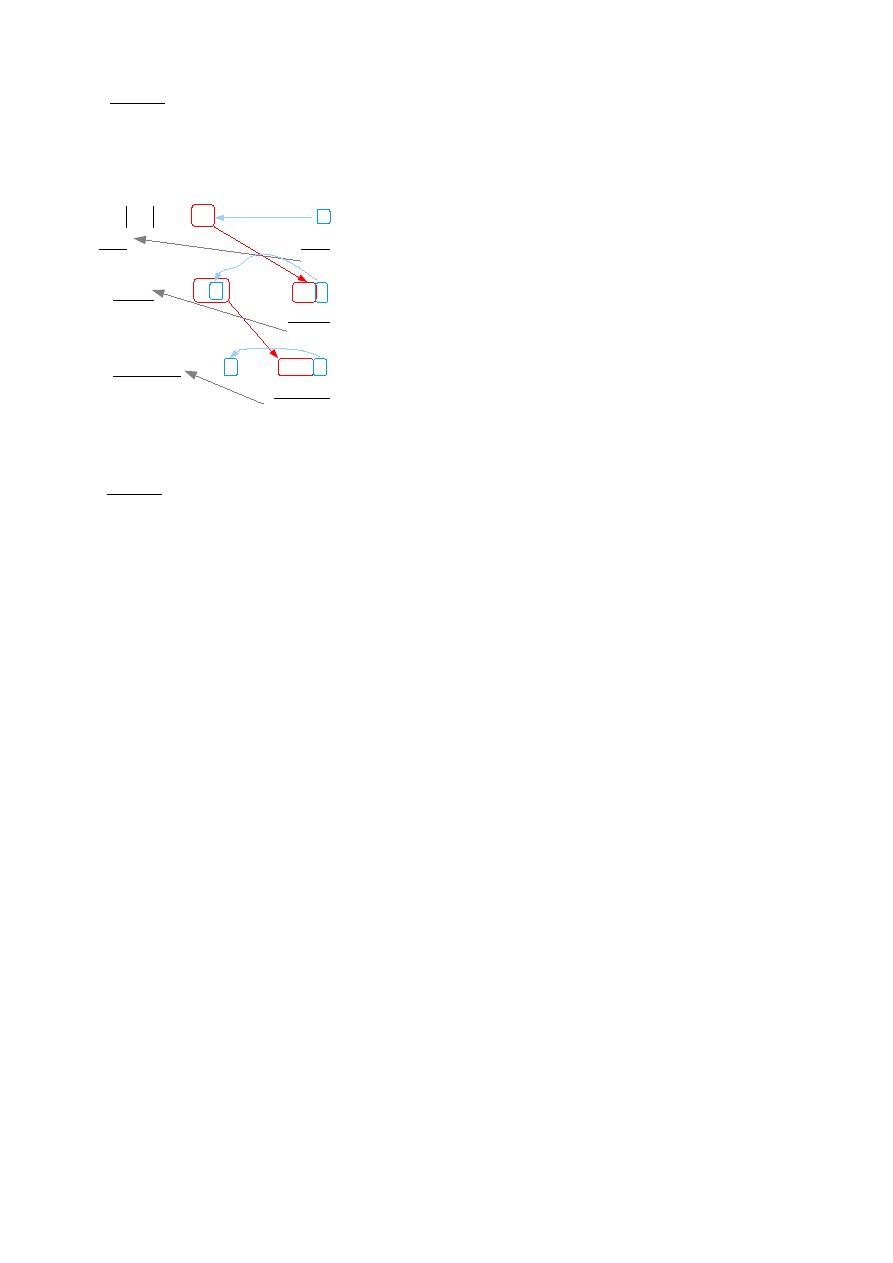
Oto kolejny przykład:
347549
10
postępując w analogiczny sposób dalej moglibyśmy otrzymać lepsze przybliżenie ale na razie to nam wystarczy.
347549
10
≈589
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
2
kolejne reszty
wynik
obliczenia dla
kolejnych cyfr
3 4 7 5 4 9
5
5
- 2 5
5
0 9 7 5
2 5
-
8
1
6
1
4
1 4 9
5 8
1 0 8
*
8
8 6 4
- 1 0 5 2 1
5 8 9
1 1 6 9
0 0 6 2 8
*
9
1 0 5 2 1
pierwsza cyfra to 5 bo
5
2
=25 a już 6
2
=36 więc jest zbyt duże.
odejmujemy kwadrat znalezionej cyfry
dopisujemy kolejna grupę
Do tej pory mieliśmy wynik równy 5.
5*2=10
Musimy dopisać do otrzymanej 10 największą cyfrę taką, że jak otrzymaną liczbę pomnożymy
przez tą cyfrę to wynik będzie mniejszy od reszty. Ta cyfra to 8.
Do tej pory mieliśmy wynik równy 58.
58*2=116
Musimy dopisać do otrzymanej 116 największą cyfrę taką, że jak otrzymaną liczbę pomnożymy
przez tą cyfrę to wynik będzie mniejszy od reszty. Ta cyfra to 9.
*2
*2
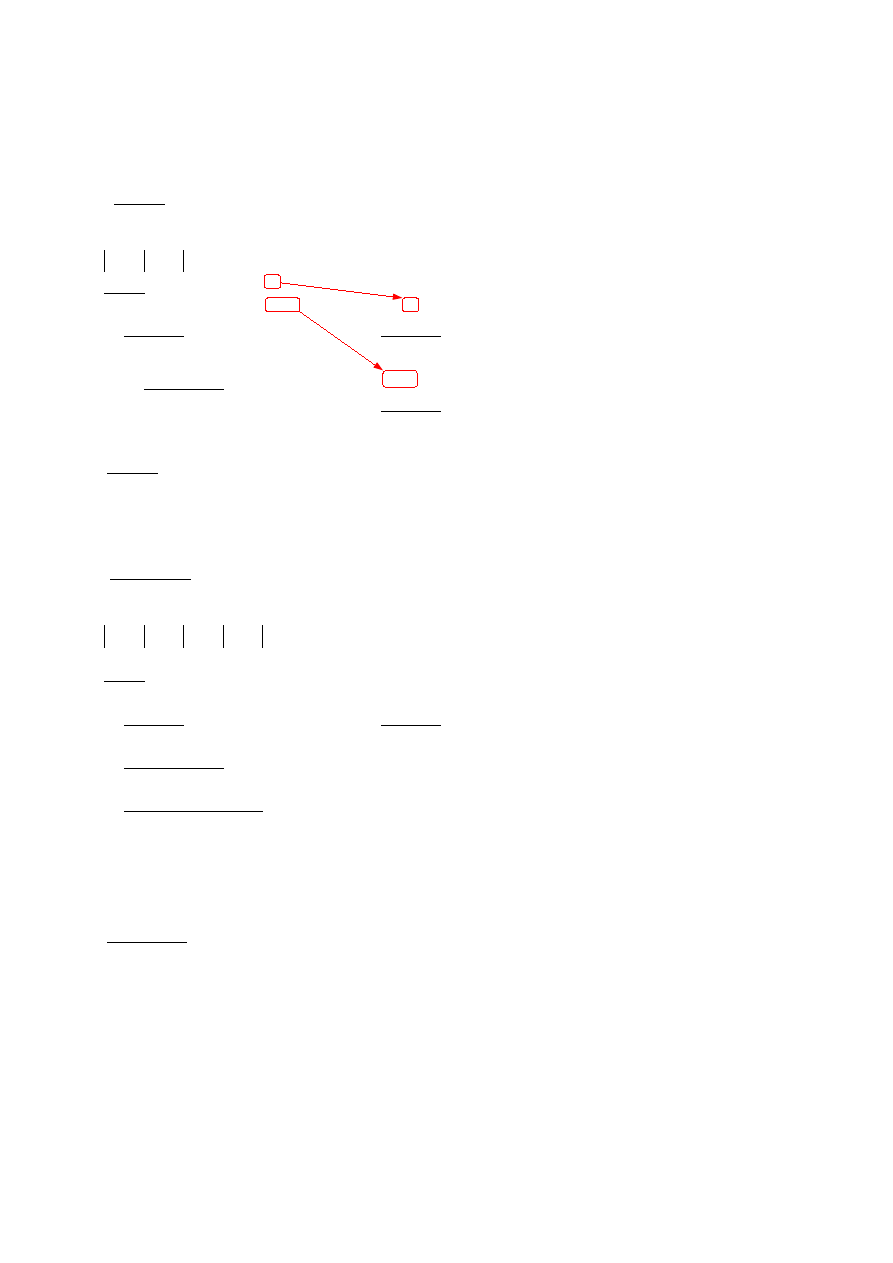
Zobaczmy co się dzieje, gdy liczba pod pierwiastkiem nie jest całkowita. Na początek zauważmy, że zawsze jesteśmy
w stanie od razu stwierdzić ile cyfr będzie miała część całkowita wyniku. Z każdej grupy dwóch cyfr otrzymywaliśmy
kolejną cyfrę wyniku więc część całkowita wyniku będzie zawsze miała dwukrotnie mniej cyfr niż liczba
pierwiastkowana.
Ważne jest również to, że zawsze dzielimy liczbę pod pierwiastkiem poczynając od przecinka w lewo i w prawo.
Nigdy w jednej grupie nie może być cyfra stojąca przed i za przecinkiem. Wystarczy spojrzeć na kolejny przykład:
12,457
10
12,457
10
≈3,52
W innych systemach postępujemy dokładnie tak samo. Rozważmy przykład na systemie dwójkowym:
1001001010
2
1001001010
2
=11000
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
3
1 2, 4
5
7
0
wynik
9
3,
mamy jedną grupę przed przecinkiem a więc część całkowita wyniku
będzie mieć jedną cyfrę
3
4
5
3, 5
6
5
3
2
5
5
0
2
0
7
0
3
2
5
1
4
0
4
3, 5
2
7
0
2
0
6
6
6
0
0
2
1
4
0
4
1
0
0
1
0
0
1
0
1 0
0
1
1
W systemie dwójkowym pierwsza cyfra to zawsze jeden.
W systemie dwójkowym gdy mnożymy przez dwa to dodajemy zero z
prawej strony liczby (przesuwamy wszystkie bity o jeden w lewo)
1
0
1
1
0
1
1
0
1
1 1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1 1
0
0
0
0
0
0
1
0
1 1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1 0
1 1
0
0
0
*2
*2