Artur Szarszewski, POMPY-projekt 1.

Dane projektowe:
Q=50m

3

/h

n=1420obr/min
H=15m

Rozwiązanie:

Zakładam: k=1 (wylot jednostrumieniowy), i=1 (liczba stopni)

Obliczam kinematyczny wyróżnik szybkobieżności pompy:





96

,

21

15

3600

50

min

1420

4

3

3

4

3





















m

h

s

h

m

obr

i

H

k

Q

n

n

q

Obliczam sprawność objętościową oraz hydrauliczną na podstawie wzorów
empirycznych A.Łomakina:





2

1

2

3

2

3

172

,

0

log

42

,

0

1

%

47

,

96

96

,

21

287

,

0

1

1

287

,

0

1

1























zr

h

q

v

d

n





Średnica zredukowana:

%

44

,

86

54

,

85

min

1420

3600

50

10

4

10

4

3

3

3

3

3

1



















h

zr

mm

obr

s

m

n

Q

d



Sprawność całkowitą odczytuję z wykresu:
η=69%

Obliczam strumień objętościowy cieczy:

h

m

h

m

Q

Q

v

th

3

3

81

,

51

9647

,

0

50









Obliczam moc na wale pompy:

W

h

s

s

m

m

h

m

m

kg

g

H

Q

P

n

96

,

2961

69

,

0

3600

81

,

9

15

50

1000

2

3

3

























Przyjmuję, że czynnikiem roboczym w pompie będzie woda: ρ=1000m

3

/kg. Przyśpieszenie

ziemskie g=9,81m/s

2

.

Obliczam teoretyczną moc silnika z uwzględnieniem współczynnika rezerwy mocy δ.
Przyjmuję δ=0,30.









W

W

P

P

n

s

55

,

3850

96

,

2961

3

,

0

1

1















Wybieram silnik 112M-4 o mocy znamionowej P

s

=4000W i prędkości obrotowej

n=1445obr/min.

Koryguję wcześniejsze obliczenia dla prędkości obrotowej n=1445obr/min:
n

q

=22,34, η

v

=96,5%, d

1zr

=85,05mm, η

h

=97,03%, η=69%, Q

th

=51,81m

3

/h.

Obliczam średnicę wału w miejscu osadzenia wirnika:
Zakładam, że wirnik jest łożyskowany z dwóch stron. Przyjmuję k

s

=15MPa.

mm

obr

MPa

kW

n

k

P

d

s

s

w

83

,

20

min

1445

15

4

10

9

,

4

10

9

,

4

3

7

3

7



















Przyjmuję d

w

=22mm.

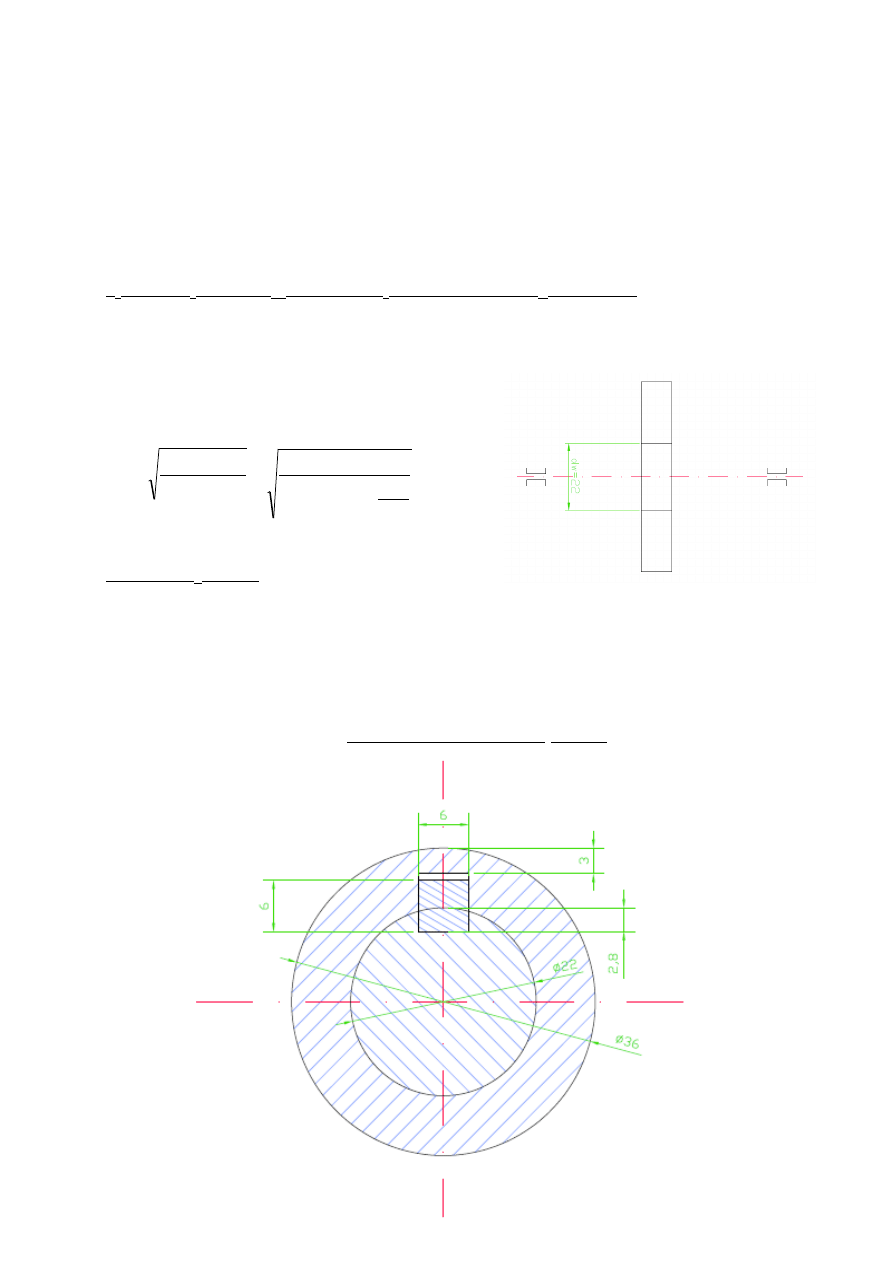
Dla tej średnicy wału wybieram wymiary rowka wpustowego wg normy PN-70/M-85005,
b x h= 6 x 6mm, Δw=3,5mm, Δp=2,8mm, x=3mm

Średnica piasty:









mm

d

d

mm

mm

mm

mm

x

p

d

d

w

p

w

p

8

,

30

4

,

1

6

,

33

3

8

,

2

2

22

2























Należy przyjąć większą wartość, przyjmuję średnicę piasty d

p

=36mm.

Obliczam średnią prędkość na wylocie wirnika:

s

m

obr

h

s

h

m

n

Q

c

th

w

17

,

2

min

1445

3600

81

,

51

07

,

0

07

,

0

3

2

3

3

2

1



























Odczytuję z wykresu współczynniki prędkości K

cm1

=0,15, K

cm2

=0,11, a następnie

prędkości merydionalne c

m1

i c

m2

:

s

m

m

s

m

i

H

g

K

c

s

m

m

s

m

i

H

g

K

c

cm

m

cm

m

89

,

1

15

81

,

9

2

11

,

0

2

57

,

2

15

81

,

9

2

15

,

0

2

2

2

2

2

1

1





























Obliczam pole powierzchni przekroju wlotowego A

w1

:

2

3

3

1

1

10

613

,

6

17

,

2

3600

81

,

51

m

s

m

h

s

h

m

c

Q

A

w

th

w













Obliczam średnicę d

w1

:









mm

m

m

d

d

A

d

d

d

A

w

p

w

w

p

w

w

6

,

98

0986

,

0

036

,

0

10

613

,

6

4

4

4

2

2

3

1

2

1

1

2

2

1

1































Przyjmuję średnicę d

w1

=100mm

Wyznaczam średnicę d

1

, zakładam, że łopatki są prostokreślne.

d

1

=95mm

Obliczam prędkość obwodową u

1

:

s

m

s

obr

m

n

d

u

19

,

7

min

60

min

1445

095

,

0

60

1

1



















Obliczam kąt napływu bezuderzeniowego β

1

:

0

1

1

1

67

,

19

19

,

7

57

,

2











































s

m

s

m

arctg

u

c

arctg

m



Kąt napływu z uwzględnieniem kąta natarcia:
Przyjmuję kąt natarcia δ=3,33

0

.

0

1

'

1

23













Dalsze założenia projektowe:
Liczba łopatek z=7
Grubość łopatek s=4mm
Kąt strug na wylocie z wirnika

0

'

2

2

2

30















łop

Obliczam współczynnik doświadczalny ψ:

85

,

0

30

sin

6

,

0

55

,

0

sin

6

,

0

55

,

0

0

2

















Obliczam poprawkę Pffeiderera p:

2

2

1

1

1

2























d

d

z

p

Do pierwszego przybliżenia, korzystam z tablic:

45

,

0

2

1



d

d

Obliczam pierwszą poprawkę Pffeiderera:

305

,

0

45

,

0

1

1

7

85

,

0

2

2











p

Obliczam prędkość obwodową u

2

:









s

m

s

m

m

tg

s

m

tg

s

m

Hg

p

tg

c

tg

c

u

h

m

m

63

,

16

8644

,

0

81

,

9

15

305

,

0

1

30

2

89

,

1

30

2

89

,

1

1

2

2

2

2

0

0

2

2

2

2

2

























































Średnica wylotowa wirnika d

2

:

mm

m

obr

s

m

n

u

d

4

,

219

2194

,

0

min

1445

63

,

16

60

60

2

2



















Przyjmuję średnicę wirnika d

2

=220mm- jest to wymiar znormalizowany.

Koryguję wyniki dla średnicy d

2

=220mm

43

,

0

220

95

66

,

16

min

60

min

1445

22

.

0

60

2

1

2

2



















mm

mm

d

d

s

m

s

obr

m

n

d

u





Obliczam drugą poprawkę Pffeidenera:

298

,

0

43

,

0

1

1

7

85

,

0

2

1

1

2

2

2

2

1

































d

d

z

p

Druga poprawka Pffeidenera nie mieści się w przedziale 0.3….0.36. W celu osiągnięcia
wymaganej wartości poprawki p, zmniejszam liczbę łopatek do z=6.

Obliczam od nowa pierwszą poprawkę Pffeidenera:

347

,

0

43

,

0

1

1

6

85

,

0

2

2











p

Obliczam prędkość obwodową u

2

dla nowej poprawki p:









s

m

s

m

m

tg

s

m

tg

s

m

Hg

p

tg

c

tg

c

u

h

m

m

87

,

16

8644

,

0

81

,

9

15

347

,

0

1

30

2

89

,

1

30

2

89

,

1

1

2

2

2

2

0

0

2

2

2

2

2

























































Obliczam średnicę wylotową wirnika d

2

:

mm

m

obr

s

m

n

u

d

223

222

,

0

min

1445

81

,

16

60

60

2

2





















Przyjmuję średnicę wylotową d

2

=240mm – jest to wymiar znormalizowany.

Dla średnicy d

2

=240mm:

40

,

0

240

95

2

1





d

d

Obliczam drugą poprawkę Pffeidenera:

337

,

0

40

,

0

1

1

6

85

,

0

2

2











p

Nowa poprawka mieści się w przedziale p=0,3….0,36.

Podsumowując: d

2

=240mm, u

2

=16,81m/s

Obliczam podziałki łopatek:

mm

mm

z

d

t

mm

mm

z

d

t

66

,

125

6

240

74

,

49

6

95

2

2

1

1





























Obliczam współczynniki przesłonięcia:

068

,

1

30

sin

4

66

,

125

66

,

125

sin

259

,

1

23

sin

4

74

,

49

74

,

49

sin

0

2

2

2

2

0

'

1

1

1

1























mm

mm

mm

s

t

t

mm

mm

mm

s

t

t









Obliczam szerokość wirnika na wlocie i wylocie:

mm

m

s

m

m

h

s

h

m

c

d

Q

b

mm

m

s

m

m

h

s

h

m

c

d

Q

b

m

th

m

th

8

,

10

0108

,

0

89

,

1

240

,

0

3600

81

,

51

068

,

1

6

,

23

0236

,

0

57

,

2

095

,

0

3600

81

,

51

259

,

1

3

2

2

2

2

3

1

1

1

1





















































Przyjmuję: b

1

=24mm, b

2

=12mm.

Skorygowane prędkości merydionalne:

s

m

m

m

h

s

h

m

b

d

Q

c

s

m

m

m

h

s

h

m

b

d

Q

c

th

m

th

m

7

,

1

012

,

0

24

,

0

3600

81

,

51

068

,

1

53

,

2

024

,

0

095

,

0

3600

81

,

51

259

,

1

3

2

2

2

2

3

1

1

1

1

















































Stosunek prędkości merydionalnych:

67

,

0

53

,

2

7

,

1

1

2





s

m

s

m

c

c

m

m

Sprawdzam poprawność obliczeń:

Wysokość podnoszenia:









m

tg

s

m

s

m

s

m

s

m

tg

c

u

u

p

g

H

m

h

obl

36

,

15

30

7

,

1

81

,

16

81

,

16

337

,

0

1

81

,

9

8644

,

0

1

0

2

2

2

2

2

































































Zapas wysokości podnoszenia:

%

4

,

2

15

36

,

0

36

,

0

15

36

,

15



















m

m

H

H

m

m

m

H

H

H

obl

Zapas wysokości podnoszenia 2,4% jest wystarczający, nie ma więc potrzeby zmieniać
wymiarów projektowych pompy.

Obliczam moc silnika dla nowej wysokości podnoszenia:

W

W

m

m

W

P

s

4000

96

,

3942

15

36

,

15

55

,

3850









Wybrany poprzednio silnik wystarcza dla naszej pompy, nie ma potrzeba go zamieniać
innym. Pozostaje więc silnik 112M-4 o mocy znamionowej P

s

=4000W i prędkości obrotowej

n=1445obr/min.

Obliczam prędkości względne na wlocie i wylocie z wirnika:

s

m

s

m

c

w

s

m

s

m

c

w

m

m

4

,

3

30

sin

7

,

1

sin

58

,

6

23

sin

57

,

2

sin

0

2

2

'

2

0

'

1

1

'

1



















Nowa wartość wyróżnika szybkobieżności n

q

=21,95 nieznacznie różni się od poprzedniej

(n

q

=22,34), nie ma więc konieczności korygowania wyników.

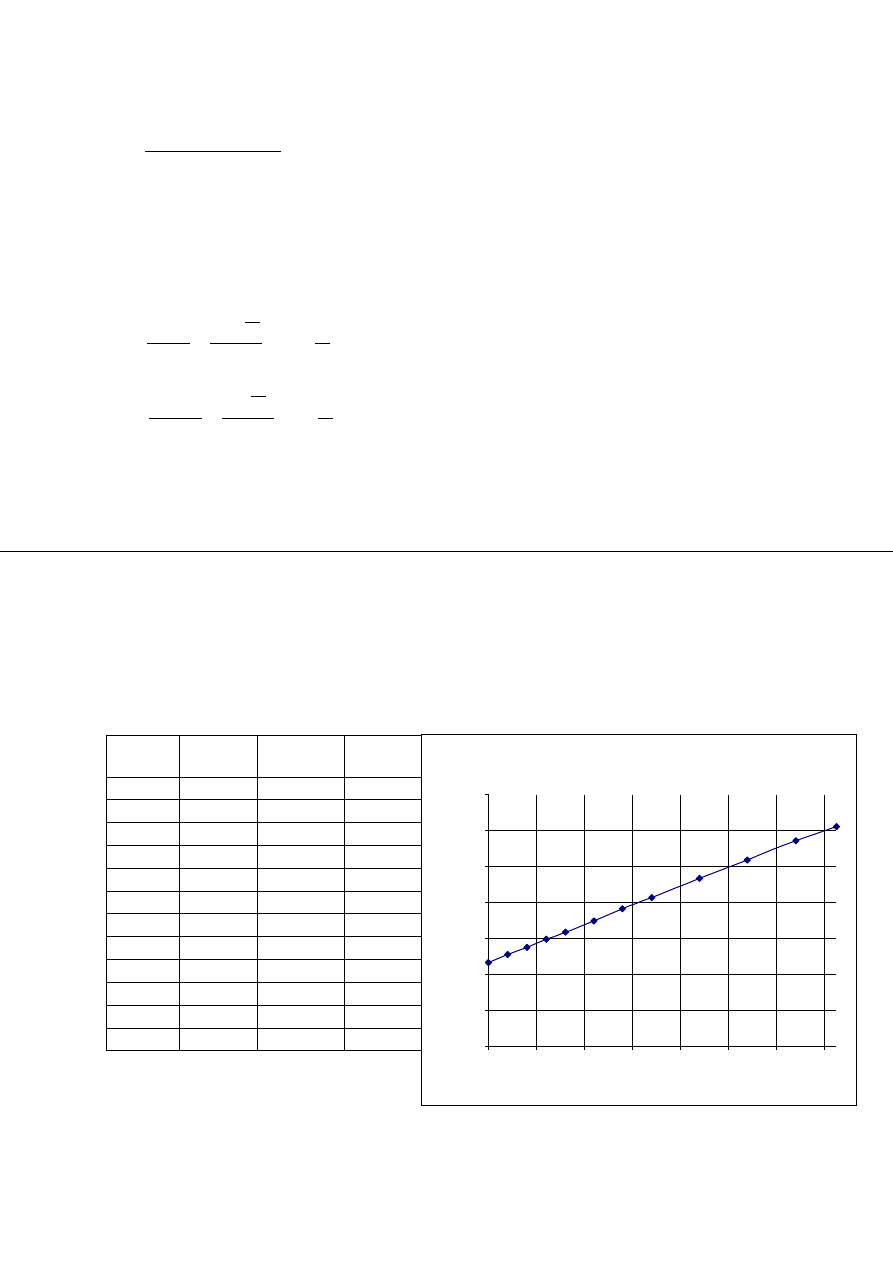
Profiluję kanał w przekroju południkowym.
Wyznaczam najpierw „na oko” środkową linią prądu. Następnie koryguję średnicę b

i

, aby

uzyskać w miarę prawidłowy rozkład funkcji f=A

n

(r

i

)

r

i

[mm] b

i

[mm]

π

A

n

[mm2]

47,5

24

3,1415927 7162,831

51,5

22,4759 3,1415927 7272,843

55,5

21,1528 3,1415927 7376,335

59,5

20,01772 3,1415927 7483,615

63,5

19,0088 3,1415927 7584,175

69,5

17,74589 3,1415927 7749,299

75,5

16,67439 3,1415927 7910,006

81,5

15,74834 3,1415927 8064,403

91,5

14,48968 3,1415927 8330,285

101,5

13,4675 3,1415927 8588,805

111,5

12,63617 3,1415927 8852,584

120

12

3,1415927 9047,787

f=An(ri)

6000

6500

7000

7500

8000

8500

9000

9500

47,5

57,5

67,5

77,5

87,5

97,5

107,5

117,5

ri [m m ]

A

n

[

m

m

2

]

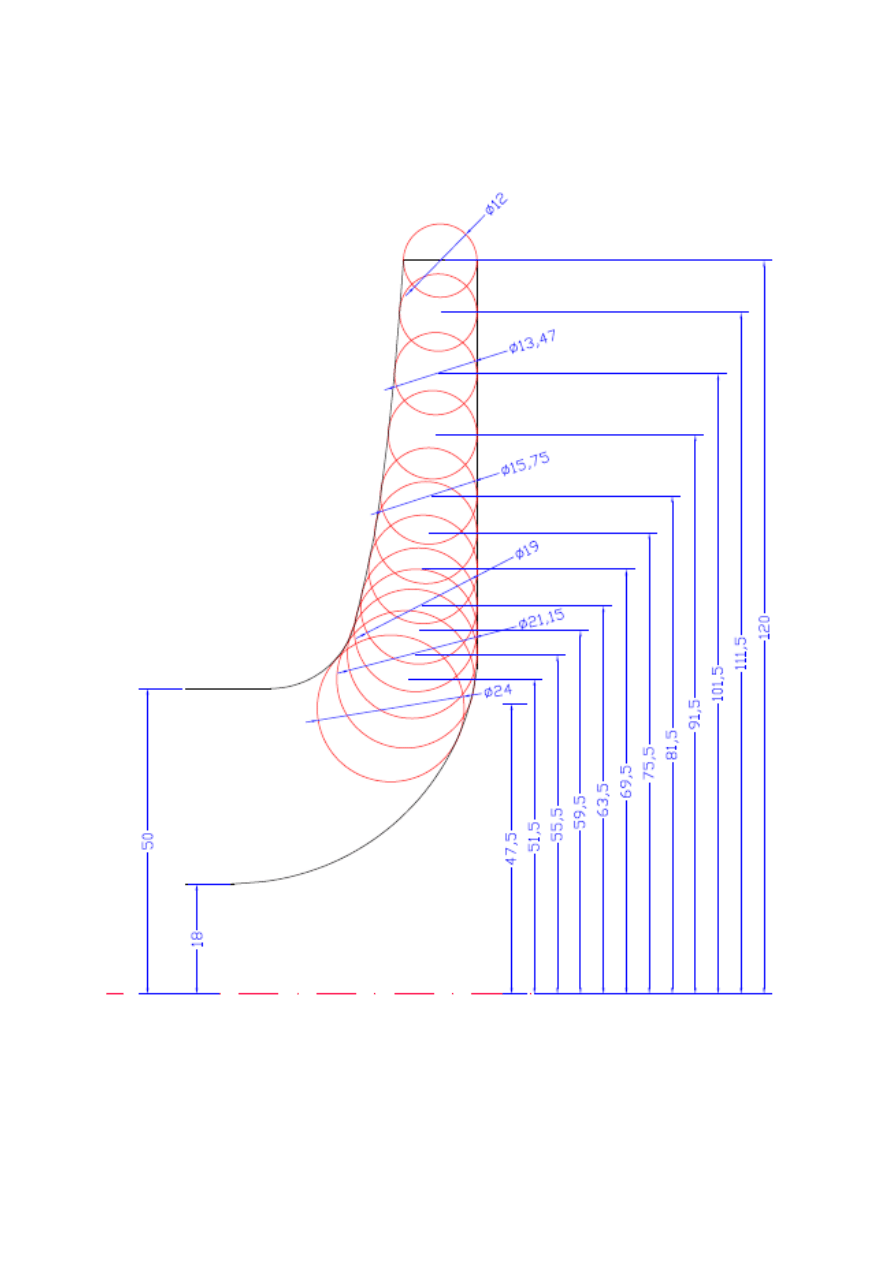
Po skorygowaniu średnic b

i

otrzymuję następujący przekrój kanału. Na rysunku nie

zwymiarowano wszystkich średnic b

i

, w celu lepszej przejrzystości przekroju.

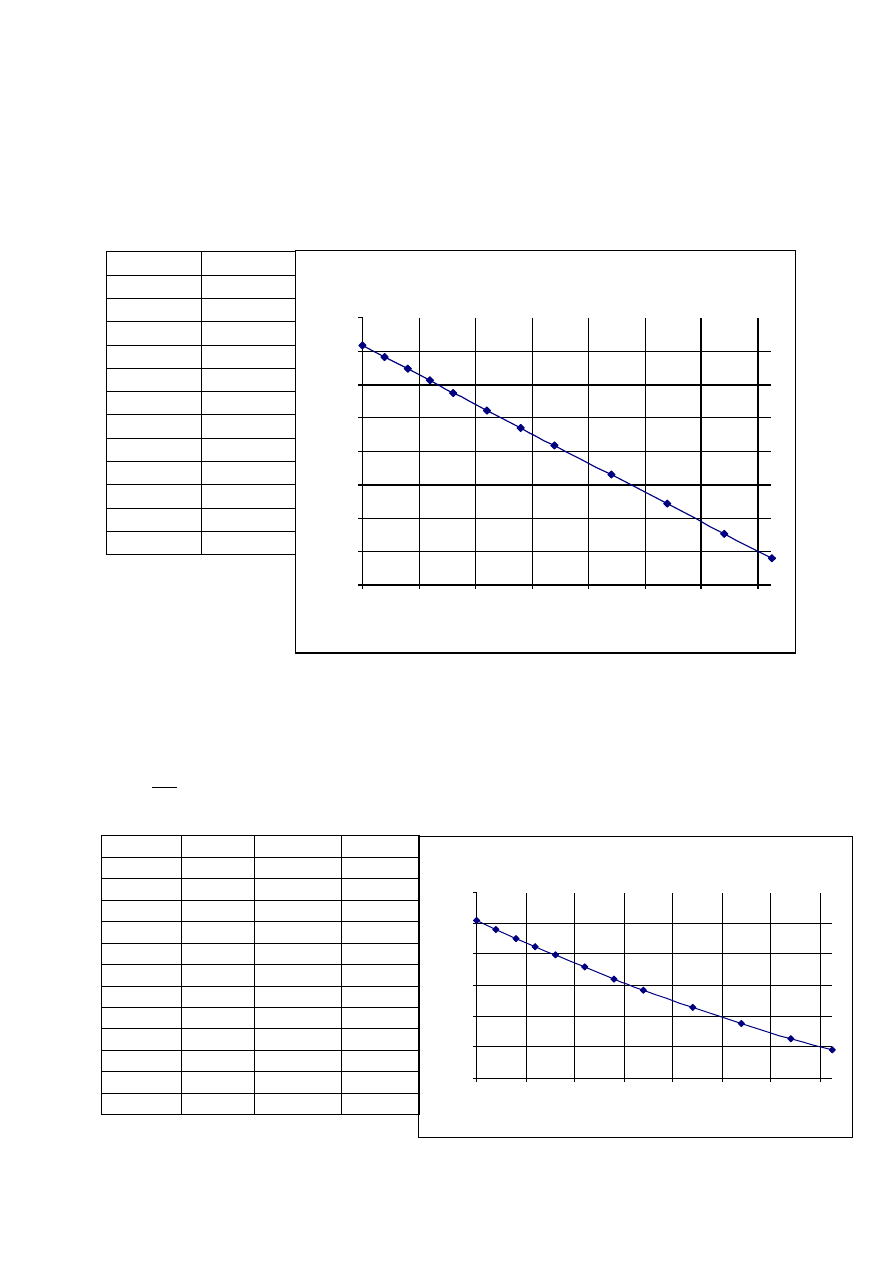
cmn=f(ri)

1,5

1,6

1,7

1,8

1,9

2

2,1

47,5

57,5

67,5

77,5

87,5

97,5

107,5

117,5

ri [m m ]

c

m

n

[

m

/s

]

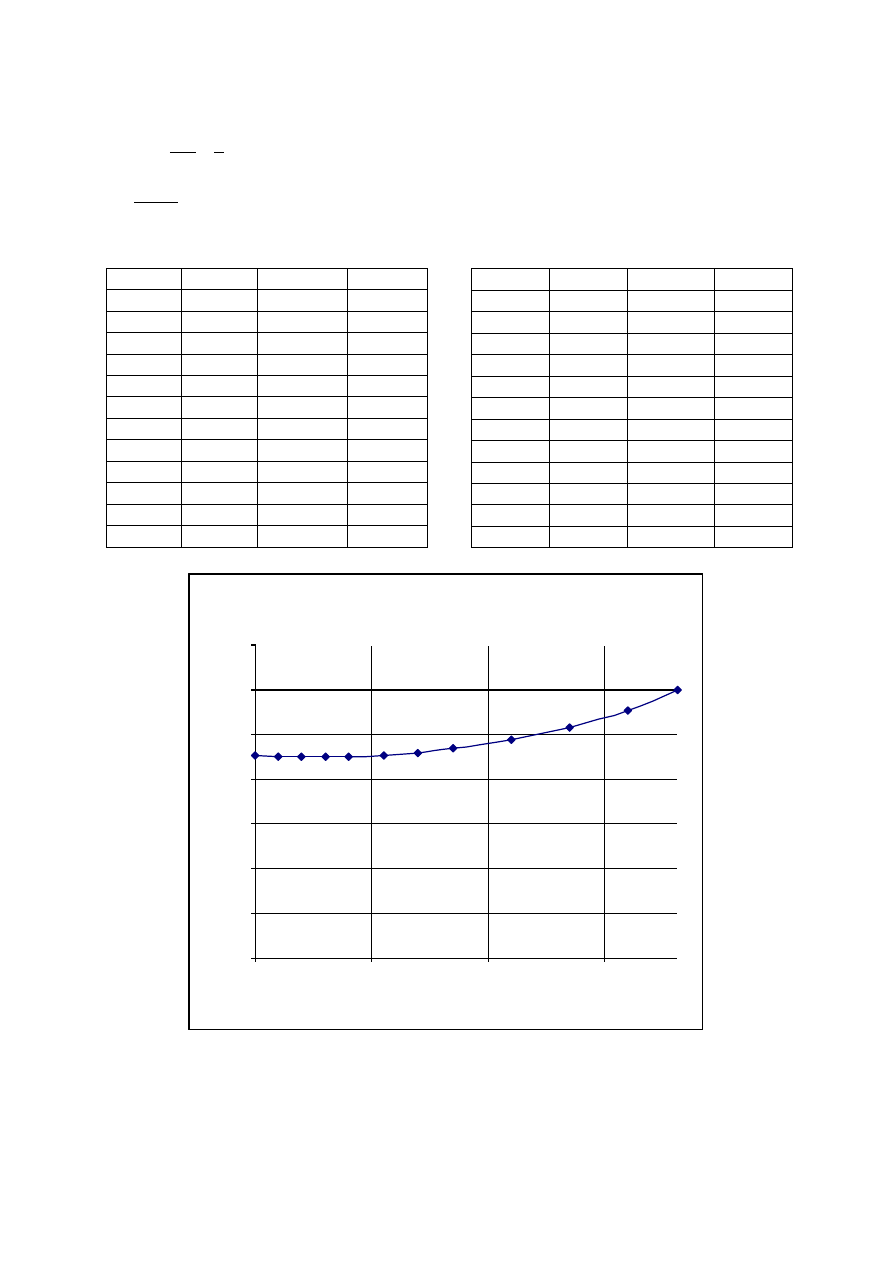
Wyznaczam kształt łopatki o pojedynczej krzywiźnie metodą punktową:

Wykres prędkości względnych:
Przyjmuję że funkcja w’=f(r

i

) ma charakter liniowy.

r

i

[mm]

w' [m/s]

47,5

6,580003

51,5

6,404555

55,5

6,229107

59,5

6,053659

63,5

5,878211

69,5

5,615039

75,5

5,351867

81,5

5,088695

91,5

4,650075

101,5

4,211455

111,5

3,772835

120

3,400008

Zależność c

mn

od promienia r

i

:

n

th

mn

A

Q

c



Q

th

[m3/s] r

i

[mm]

A

n

[m2]

c

mn

[m/s]

0,014392

47,5

0,0071628 2,009215

0,014392

51,5

0,0072728 1,978823

0,014392

55,5

0,0073763 1,951059

0,014392

59,5

0,0074836 1,92309

0,014392

63,5

0,0075842 1,897592

0,014392

69,5

0,0077493 1,857157

0,014392

75,5

0,00791 1,819426

0,014392

81,5

0,0080644 1,784592

0,014392

91,5

0,0083303 1,727632

0,014392

101,5

0,0085888 1,675631

0,014392

111,5

0,0088526 1,625702

0,014392

120

0,0090478 1,590628

w'=f(ri)

3

3,5

4

4,5

5

5,5

6

6,5

7

47,5

57,5

67,5

77,5

87,5

97,5

107,5

117,5

ri [m m ]

w

'

[m

/s

]

Obliczam zależność β

’

od promienia r

i

:

mm

s

z

r

t

t

s

w

c

i

mn

4

2

sin

'

'















z

r

i

[mm]

π

t

i

[mm]

6

47,5

3,1415927 49,74188

6

51,5

3,1415927 53,93067

6

55,5

3,1415927 58,11946

6

59,5

3,1415927 62,30825

6

63,5

3,1415927 66,49704

6

69,5

3,1415927 72,78023

6

75,5

3,1415927 79,06342

6

81,5

3,1415927 85,3466

6

91,5

3,1415927 95,81858

6

101,5

3,1415927 106,2906

6

111,5

3,1415927 116,7625

6

120

3,1415927 125,6637

B'=f(ri)

0

5

10

15

20

25

30

35

47,5

67,5

87,5

107,5

ri [m m ]

B

'

[o

]

s/t

i

c

mn

/w

sinβ'

β'

0,080415 0,305352 0,3857668 22,69563
0,074169 0,308971 0,3831404 22,53259
0,068824 0,313217 0,3820403 22,46436
0,064197 0,317674 0,381871 22,45386
0,060153 0,322818 0,3829709 22,52208

0,05496 0,330747 0,385707 22,69192

0,050592 0,339961 0,3905532 22,99326
0,046868 0,350697 0,397565 23,43046
0,041746 0,371528 0,4132733 24,41523
0,037633 0,397875 0,4355072 25,82245
0,034258 0,430897 0,4651543 27,72544
0,031831 0,467831 0,4996617 29,98328

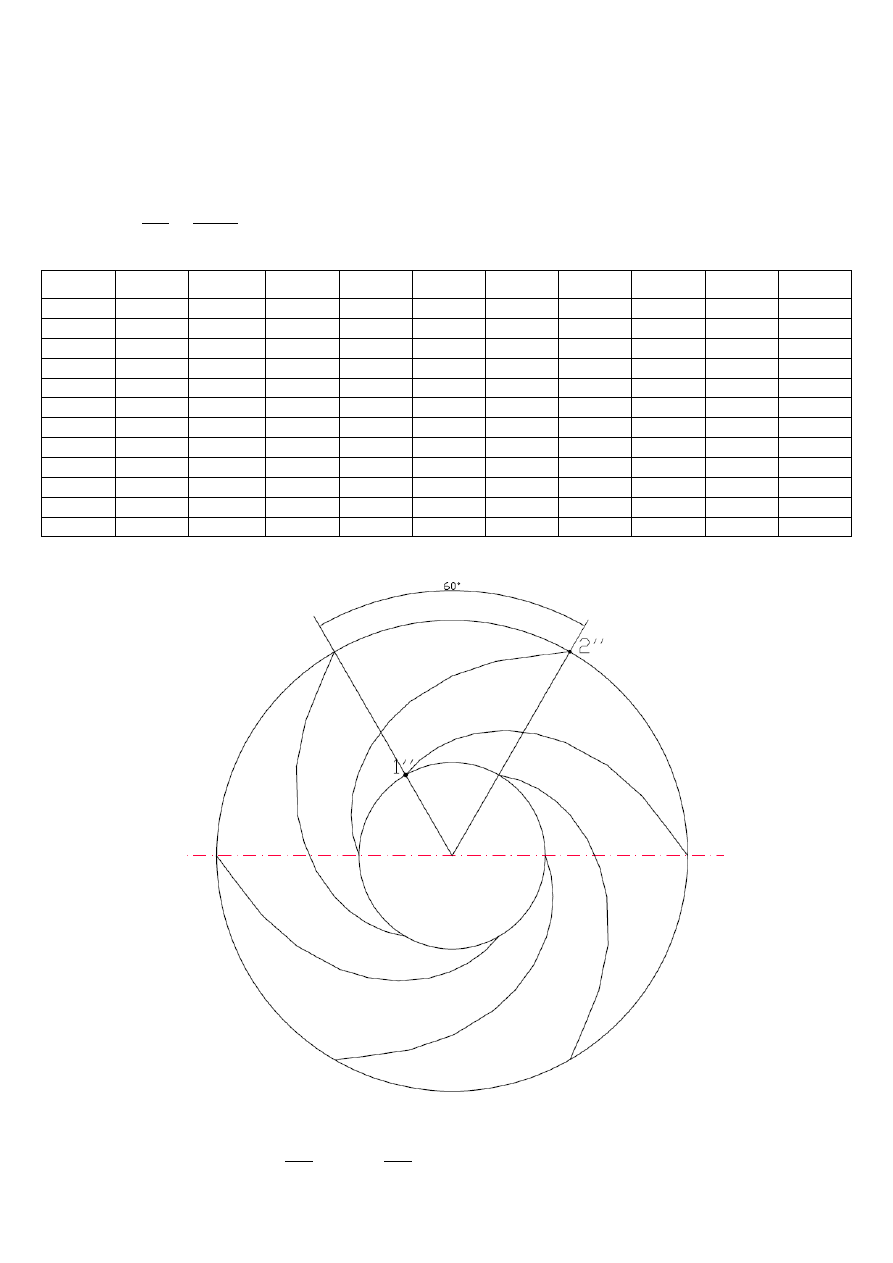
Obliczam kąt υ

i

dla poszczególnych promieni, następnie nanoszę na układ współrzędnych

kolejno punkty (r

i

, υ

i

) w celu wyznaczenia kształtu łopatki.













k

i

i

i

i

i

tg

r

r

tg

tg

1

''

'

''

180

cos













β'

tgβ'

ε

cosε

tgβ''

r

i

*tgβ''

r

i

[mm]

1/rtgβ''

Δf

∑Δf

i



22,69563 0,41822

27

0,891007 0,372636

0,0177

47,5

56,49646

0

0

0

22,53259 0,41488

14

0,970296 0,402556 0,020732

51,5

48,23541 0,209464 0,198809 11,3909

22,46436 0,413485

8

0,990268 0,409461 0,022725

55,5

44,00424 0,184479 0,383288 21,96079

22,45386 0,41327

7

0,992546 0,41019 0,024406

59,5

40,97303 0,169955 0,553243 31,69847

22,52208 0,414665

7

0,992546 0,411574 0,026135

63,5

38,26292 0,158472 0,711714 40,77824

22,69192 0,418143

4

0,997564 0,417125 0,02899

69,5

34,49445 0,218272 0,929987 53,28431

22,99326 0,424336

3

0,99863 0,423754 0,031993

75,5

31,25638 0,197253 1,127239 64,58604

23,43046 0,43337

2

0,999391 0,433106 0,035298

81,5

28,3301 0,178759 1,305999 74,82821

24,41523 0,453941

1

0,999848 0,453872 0,041529

91,5

24,07942 0,262048 1,568046 89,84243

25,82245 0,483902

0

1

0,483902 0,049116

101,5

20,35993 0,222197 1,790243 102,5734

27,72544 0,525578

0

1

0,525578 0,058602

111,5

17,06427 0,187121 1,977364 113,2946

29,98328 0,576961

0

1

0,576961 0,069235

120

14,44349 0,133908 2,111272 120,967

Kąt pokrycia

0

0

60

6

360

120

360











z

cała



