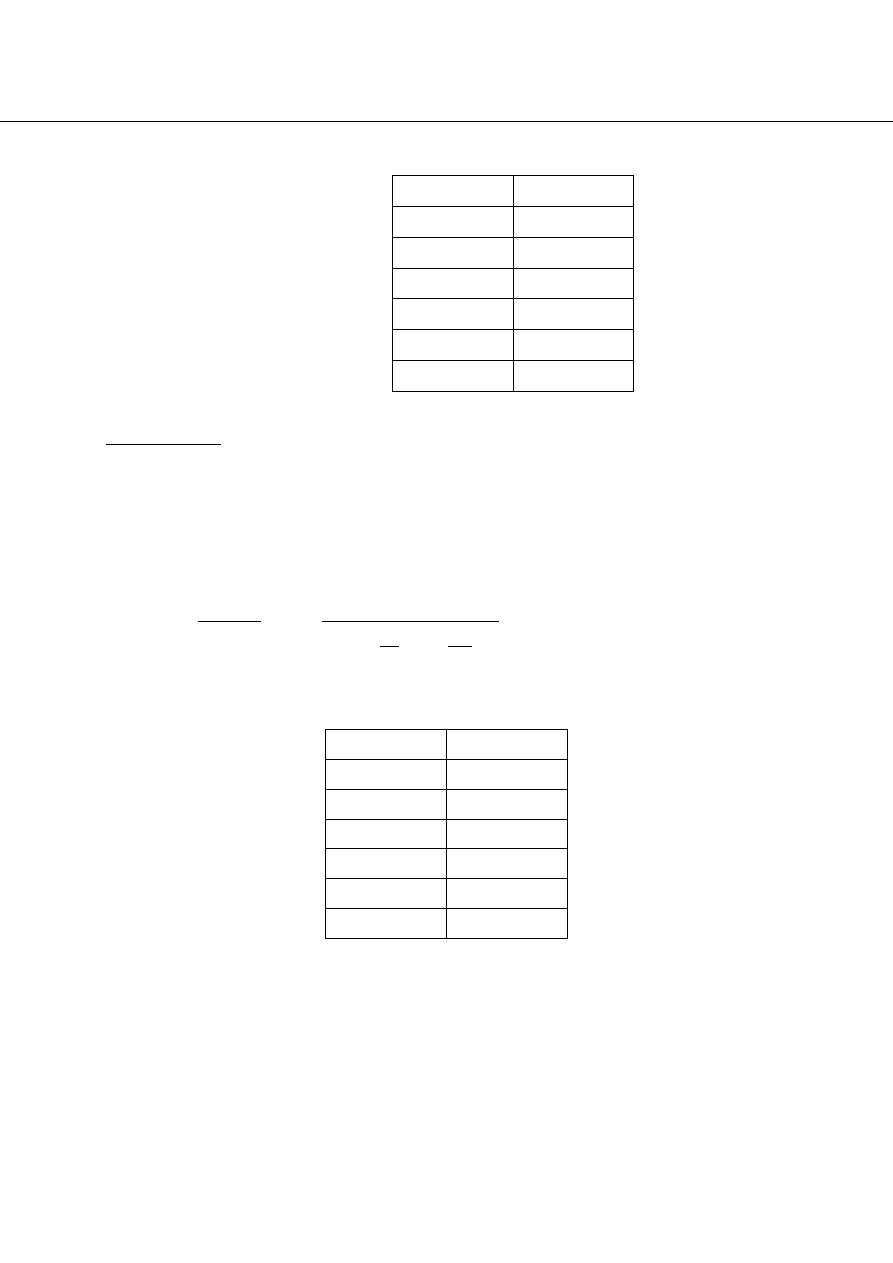
Artur Szarszewski, POMPY-projekt 2.
Zestaw 27.
Dane projektowe:
d
2
=345mm
η
1
=0,8
n=1460obr/min
η
1A
=0,75
H
z
=5m
η
1B
=0,7
p
g
=0,1981MPa
p
d
=0,1MPa
ρ=1000kg/m
3
H
dyn
=2000Q
2
Q
2
=0,8Q
1
Rozwiązanie:
Wyznaczam punkt pracy w układzie pompowym:
Na wykres H=f(Q) nanoszę dane z tabeli umieszczonej powyżej – jest to charakterystyka
przepływu pompy
Na ten sam wykres nanoszę charakterystykę rurociągu, przedstawioną równaniem
H
r
=H
st
+H
dyn.
m
m
kg
s
m
Pa
Pa
m
g
p
p
H
H
d
g
z
st
15
1000
81
,
9
10
1
,
0
1981
,
0
5
3
2
6
H
dyn
zmienia się wg zależności H
dyn
=2000Q
2
, wyniki przedstawia tabela:
Q[m3/s]
Hdyn
0,015
15,45
0,04
18,2
0,07
24,8
0,1
35
0,12
43,8
0,14
54,2
Punkt pracy układu pompowego to punkt przecięcia się krzywych charakterystyk rurociągu i
przepływu pompy, pokazany na wykresie:
Odczytuję z wykresu punkt pracy:
Q=0,1m
3
/s
H=35m
Q[m3/s]
H[m]
0,015
52,5
0,04
49
0,07
44
0,1
35,5
0,12
29
0,14
21,5
A)
Obliczam do jakiej wartości n’ należy zmniejszyć prędkość obrotową wirnika, aby
uzyskać wydajność Q
2
=0,8Q
1
:
Q
2
=0,08m
3
/s
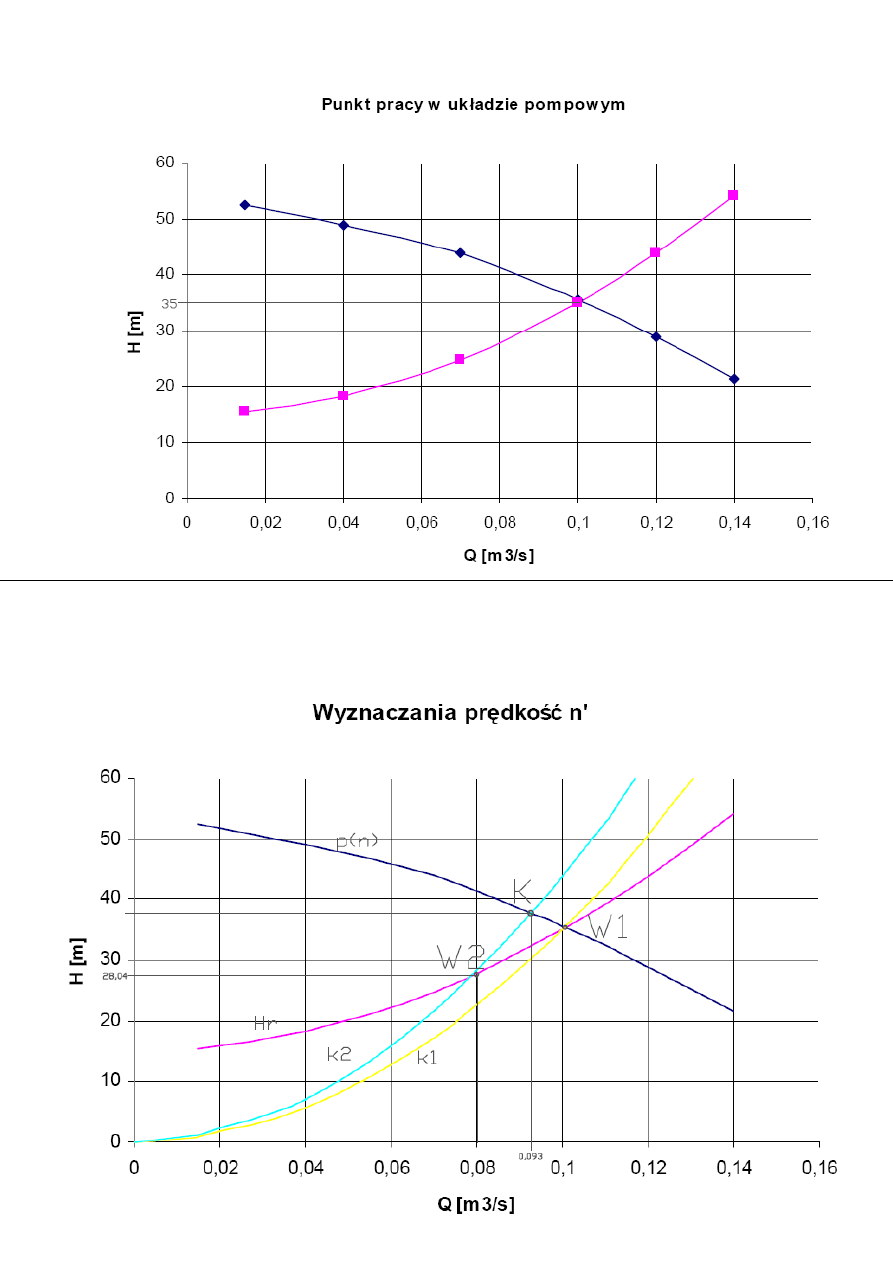
Prowadzę parabolę k1 przechodzącą przez punkt W1 i początek układu współrzędnych, oraz
parabolę k2 przechodzącą przez punkt W2 (przecięcie krzywych charakterystyki rurociągu z
prostą Q=0,08m
3
/s) i początek układu współrzędnych.
Parabole opisane są równaniami:
k1=3500Q
2
k2=4381,8Q
2
Z wykresu odczytuję wartość Q
k
=0,093m
3
/s, H
2
=28,04m, Q
2
=0,08m
3
/s
Obliczam prędkość obrotową n’:
min
1256
093
,
0
08
,
0
min
1460
'
3
3
2
1
obr
s
m
s
m
obr
Q
Q
n
n
k
Przyjmuję, że prędkość obrotowa n’=1260obr/min
B)
Obliczam średnicę d
2
’, do której należy zmniejszyć średnicę zewnętrzną wirnika d
2
poprzez stoczenie, aby otrzymać wartość Q
2
=0,8Q
1
.
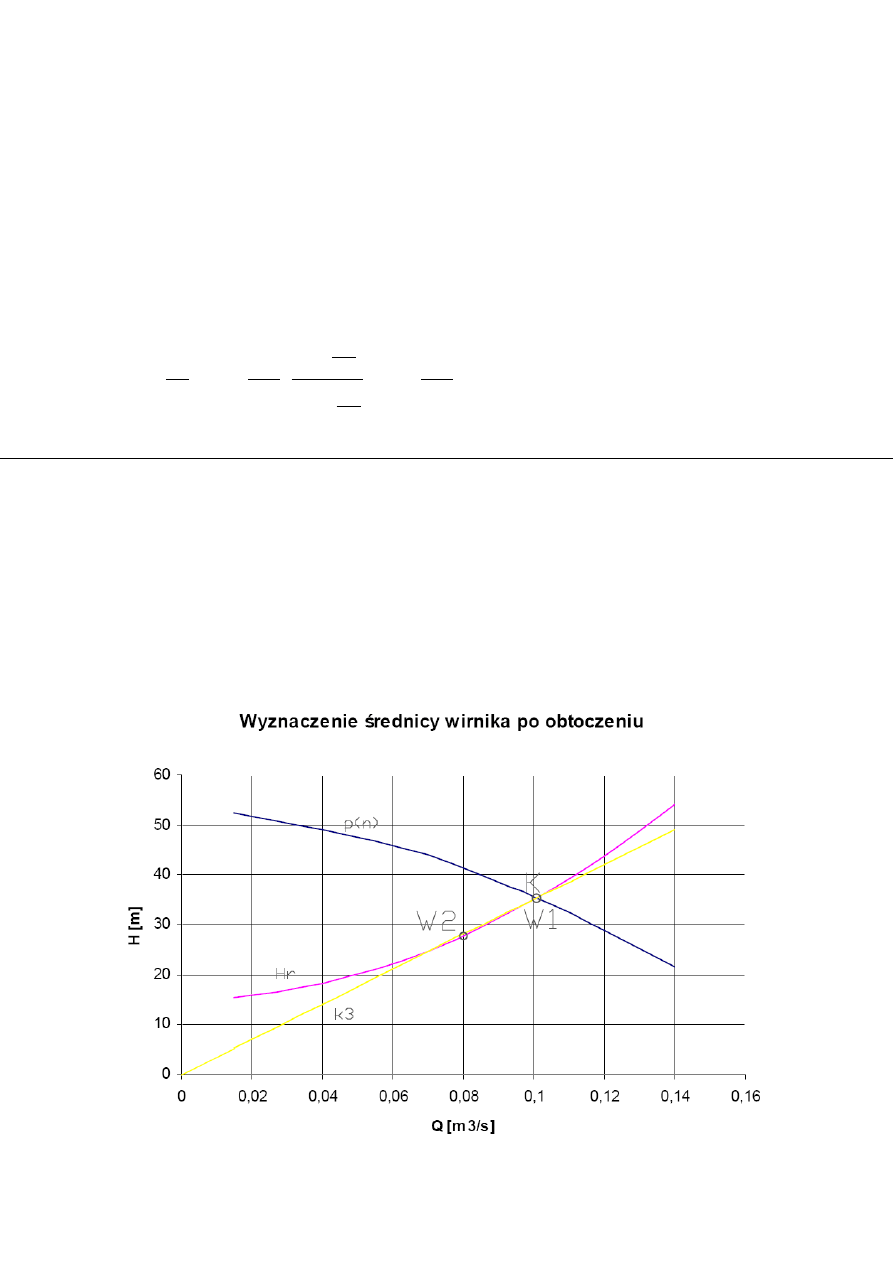
Prowadzę prostą k3, przechodzącą przez punkt W2 (przecięcie krzywych charakterystyki
rurociągu z prostą Q=0,08m
3
/s) i początek układu współrzędnych, odczytuję wartość
wydajności objętościowej Q
k
.
Równanie prostej k3:
k3=305,5Q
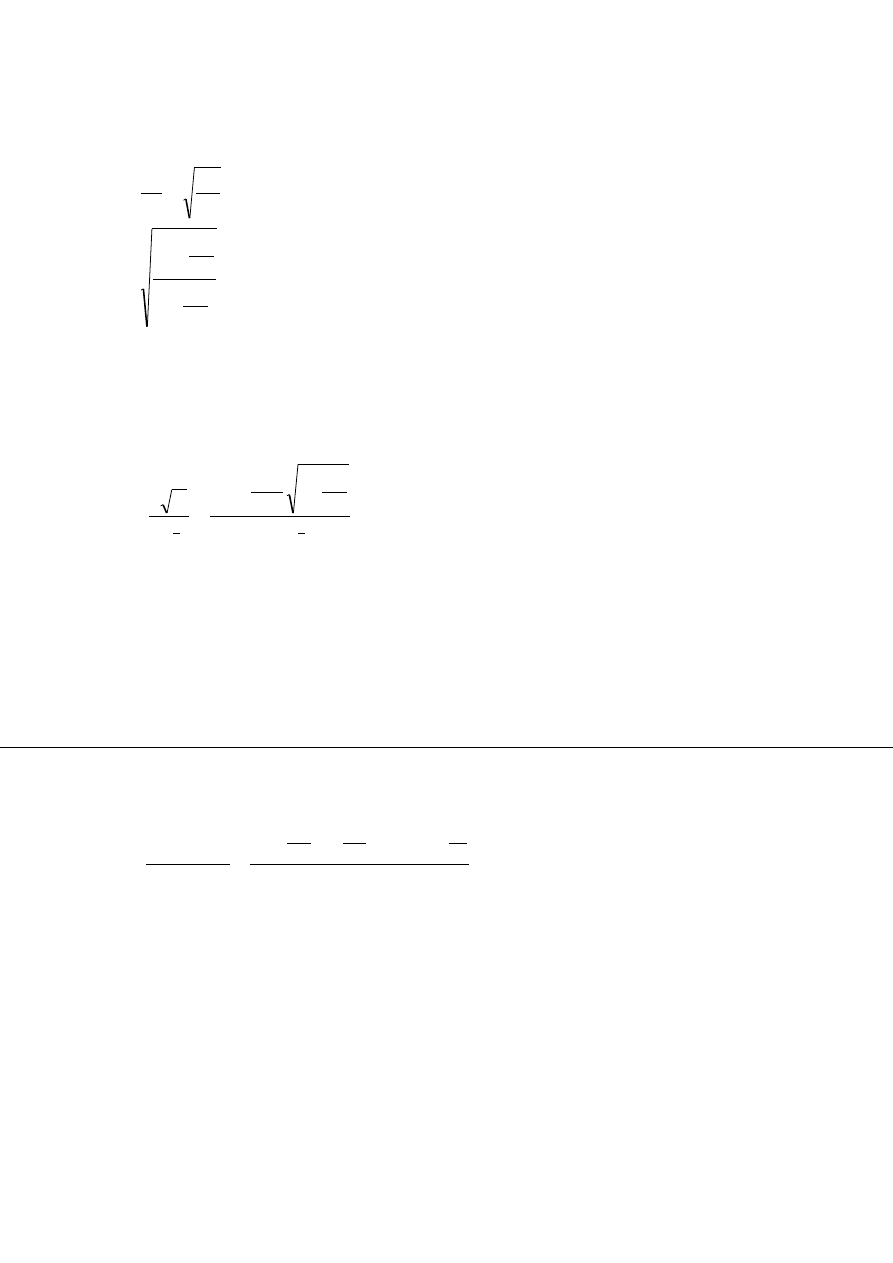
Q
k
=0,1m
3
/s
Obliczam względną wartość obtoczenia:
894
,
0
1
,
0
08
,
0
3
3
2
2
'
2
s
m
s
m
Q
Q
d
d
k
Zmniejszenie średnicy zewnętrznej:
1
2
2
d
k
d
Obliczam kinematyczny wyróżnik szybkobieżności pompy:
08
,
32
35
1
,
0
min
1460
4
3
3
4
3
m
s
m
obr
H
Q
n
n
q
Dla danego współczynnika szybkobieżności n
q
, przyjmuję współczynnik korekcyjny k=0,8
mm
mm
mm
d
d
d
mm
mm
d
74
,
315
26
,
29
345
26
,
29
894
,
0
1
345
8
,
0
2
2
'
2
2
Przyjmuję że średnica wirnika po obtoczeniu d
2
’=315mm
C)
Pobór mocy P
1
:
Obliczam moc na wale pompy:
W
s
m
m
s
m
m
kg
g
H
Q
P
n
8
,
42918
8
,
0
81
,
9
35
1
,
0
1000
2
3
3
1
Obliczam teoretyczną moc silnika z uwzględnieniem współczynnika rezerwy mocy f.
Przyjmuję f=0,10.
W
W
f
P
P
n
47211
1
,
0
1
8
,
42918
)
1
(
Zakładam że pompę będzie napędzać silnik elektryczny klatkowy.
Obliczona powyżej moc jest mocą którą teoretycznie silnik będzie oddawał na wał pompy.
Zakładam, że silnik elektryczny, użyty do napędu pompy będzie miał sprawność 94%
(osiągalną przez współczesne silniki) i znamionową prędkość obrotową 1460obr/min
Dla tej sprawności moc silnika będzie wynosić:
W
W
P
s
5
,
50224
94
,
0
47211
Przyjmuję, że silnik elektryczny będzie miał parametry:
P
silnika
= P
sieci
=52kW, n=1460obr/min
Nie należy zapominać o tym, że silniki indukcyjne pobierają z sieci nie tylko moc czynną,
lecz również moc bierną, za którą również trzeba płacić. Możliwe jest zainstalowanie przed
silnikiem urządzeń do kompensacji mocy biernej, jak np. baterie kondensatorowe. W takim
wypadku nie pobieramy mocy biernej z sieci. Zakładam, że nasz silnik nie ma urządzeń do
kompensacji mocy biernej.
Moc bierną P
q
obliczam z trójkąta mocy:
sieci
q
P
P
tg
Z tabeli odczytuje wartość cosφ=0,91.
Obliczam kąt φ=arccos0,91=24,5
0
.
Var
tg
W
tg
P
P
sieci
q
23698
5
,
24
52000
0
Ostatecznie: moc czynna: 52kW, moc bierna 23698Var – są to wartości dla pracy
znamionowej
Pobór mocy P
2A
:
Obliczam moc na wale pompy:
W
s
m
m
s
m
m
kg
g
H
Q
P
A
n
1
,
29341
75
,
0
81
,
9
04
,
28
08
,
0
1000
2
3
3
1
2
2
Obliczam teoretyczną moc silnika z uwzględnieniem współczynnika rezerwy mocy f.
Przyjmuję f=0,10.
W
W
f
P
P
n
2
,
32275
1
,
0
1
1
,
29341
)
1
(
Zakładam że pompę będzie napędzać silnik elektryczny klatkowy.
Obliczona powyżej moc jest mocą którą teoretycznie silnik będzie oddawał na wał pompy.
Zakładam, że silnik elektryczny, użyty do napędu pompy będzie miał sprawność 94%
(osiągalną przez współczesne silniki) i znamionową prędkość obrotową 1260obr/min
Dla tej sprawności moc silnika będzie wynosić:
W
W
P
s
1
,
34335
94
,
0
2
,
32275
Przyjmuję, że silnik elektryczny będzie miał parametry:
P
silnika
= P
sieci
=35kW, n=1260obr/min
Zakładam, że nasz silnik nie ma urządzeń do kompensacji mocy biernej.
Moc bierną P
q
obliczam z trójkąta mocy:
sieci
q
P
P
tg
Z tabeli odczytuje wartość cosφ=0,91.
Obliczam kąt φ=arccos0,91=24,5
0
.
Var
tg
W
tg
P
P
sieci
q
4
,
15950
5
,
24
35000
0
Ostatecznie: moc czynna: 35kW, moc bierna 15950,4Var – są to wartości dla pracy
znamionowej
Pobór mocy P
2B
:
Obliczam moc na wale pompy:
W
s
m
m
s
m
m
kg
g
H
Q
P
B
n
8
,
31436
7
,
0
81
,
9
04
,
28
08
,
0
1000
2
3
3
1
2
2
Obliczam teoretyczną moc silnika z uwzględnieniem współczynnika rezerwy mocy f.
Przyjmuję f=0,10.
W
W
f
P
P
n
5
,
34580
1
,
0
1
8
,
31436
)
1
(
Zakładam że pompę będzie napędzać silnik elektryczny klatkowy.
Obliczona powyżej moc jest mocą którą teoretycznie silnik będzie oddawał na wał pompy.
Zakładam, że silnik elektryczny, użyty do napędu pompy będzie miał sprawność 94%
(osiągalną przez współczesne silniki) i znamionową prędkość obrotową 1460obr/min
Dla tej sprawności moc silnika będzie wynosić:
W
W
P
s
8
,
36787
94
,
0
5
,
34580
Przyjmuję, że silnik elektryczny będzie miał parametry:
P
silnika
= P
sieci
=38kW, n=1460obr/min
Zakładam, że nasz silnik nie ma urządzeń do kompensacji mocy biernej.
Moc bierną P
q
obliczam z trójkąta mocy:
sieci
q
P
P
tg
Z tabeli odczytuje wartość cosφ=0,91.
Obliczam kąt φ=arccos0,91=24,5
0
.
Var
tg
W
tg
P
P
sieci
q
6
,
17317
5
,
24
38000
0
Ostatecznie: moc czynna: 38kW, moc bierna 17317,6Var – są to wartości dla pracy
znamionowej.