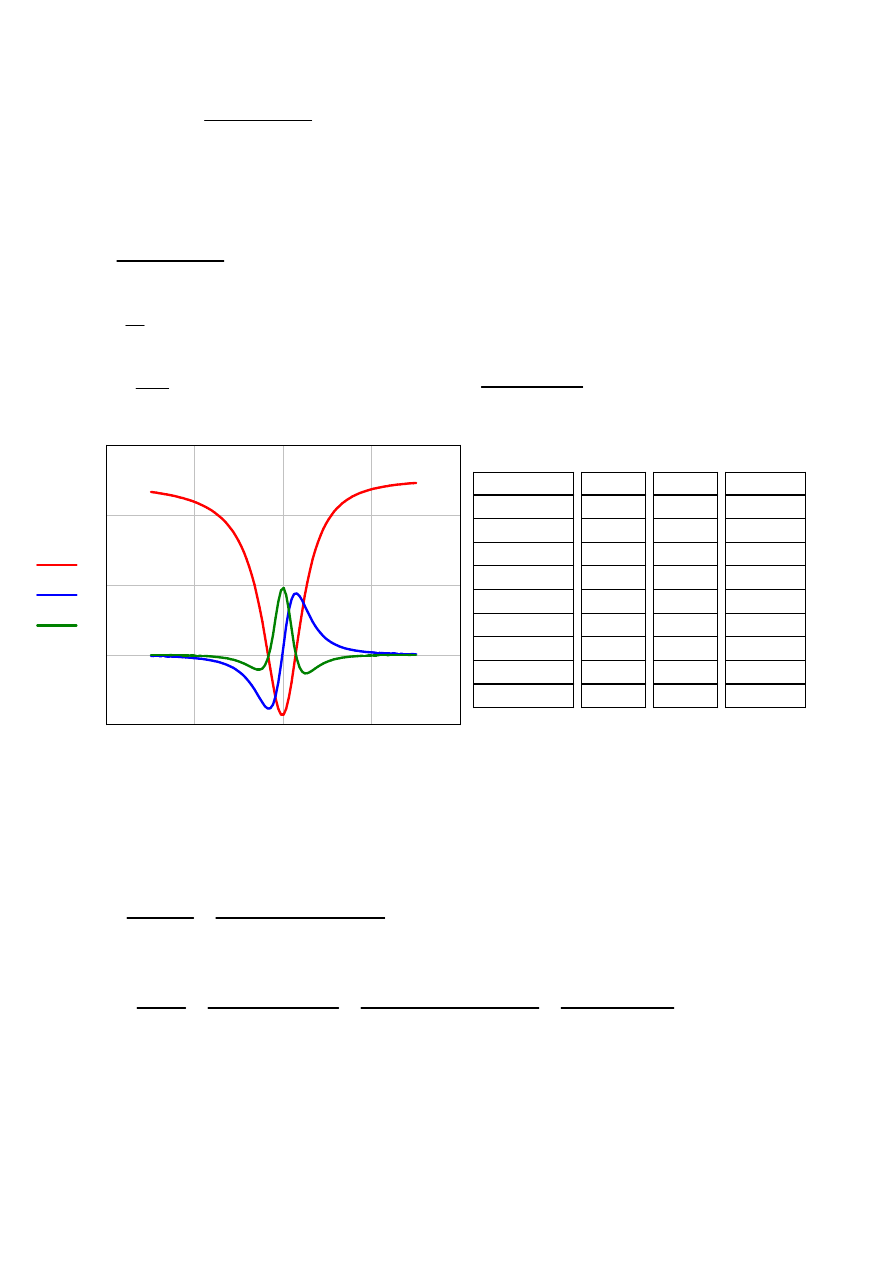
1. Pochodne
PRZYKŁAD
Dana jest funkcja f(x)=
5x
2
2x
+
12
−
x
2
7
+
w przedziale -15<x<15:
1. Wyznaczy
ć
pochodn
ą
funkcji df(x)
2. Sporz
ą
dzi
ć
tabelki, wspólne wykresy dla x, f(x), df(x)
3. Wykona
ć
przekształcenia symboliczne wykonaj ponownie wykresy
xmin
15
−
:=
f x
( )
5x
2
2x
+
12
−
x
2
7
+
:=
xmax
15
:=
df x
( )
x
f x
( )
d
d
:=
d2f x
( )
2
x
f x
( )
d
d
2
:=
x
xmin xmin
xmax xmin
−
100
+
,
xmax
..
:=
20
−
10
−
0
10
20
2
−
0
2
4
6
f x
( )
df x
( )
d2f x
( )
x
x
-15
-14.7
-14.4
-14.1
-13.8
-13.5
-13.2
-12.9
-12.6
...
=
f x
( )
4.668
4.658
4.646
4.635
4.622
4.609
4.595
4.58
4.564
...
=
df x
( )
-0.034
-0.036
-0.038
-0.04
-0.043
-0.045
-0.048
-0.051
-0.054
...
=
d2f x
( )
-0.00601
-0.00646
-0.00696
-0.00751
-0.00811
-0.00877
-0.0095
-0.01031
-0.01121
...
=
Wyznaczanie pochodnych- przekształcenia symboliczne
x
x
:=
<--- Ponowna definicja zmiennej "x" wył
ą
cza zdefiniowan
ą
wcze
ś
niej zmienn
ą
zakresow
ą
df x
( )
10 x
⋅
2
+
x
2
7
+
2 x
⋅
5 x
2
⋅
2 x
⋅
+
12
−
(
)
⋅
x
2
7
+
(
)
2
−
→
d2f x
( )
10
x
2
7
+
10 x
2
⋅
4 x
⋅
+
24
−
x
2
7
+
(
)
2
−
8 x
2
⋅
5 x
2
⋅
2 x
⋅
+
12
−
(
)
⋅
x
2
7
+
(
)
3
+
4 x
⋅
10 x
⋅
2
+
(
)
⋅
x
2
7
+
(
)
2
−
→
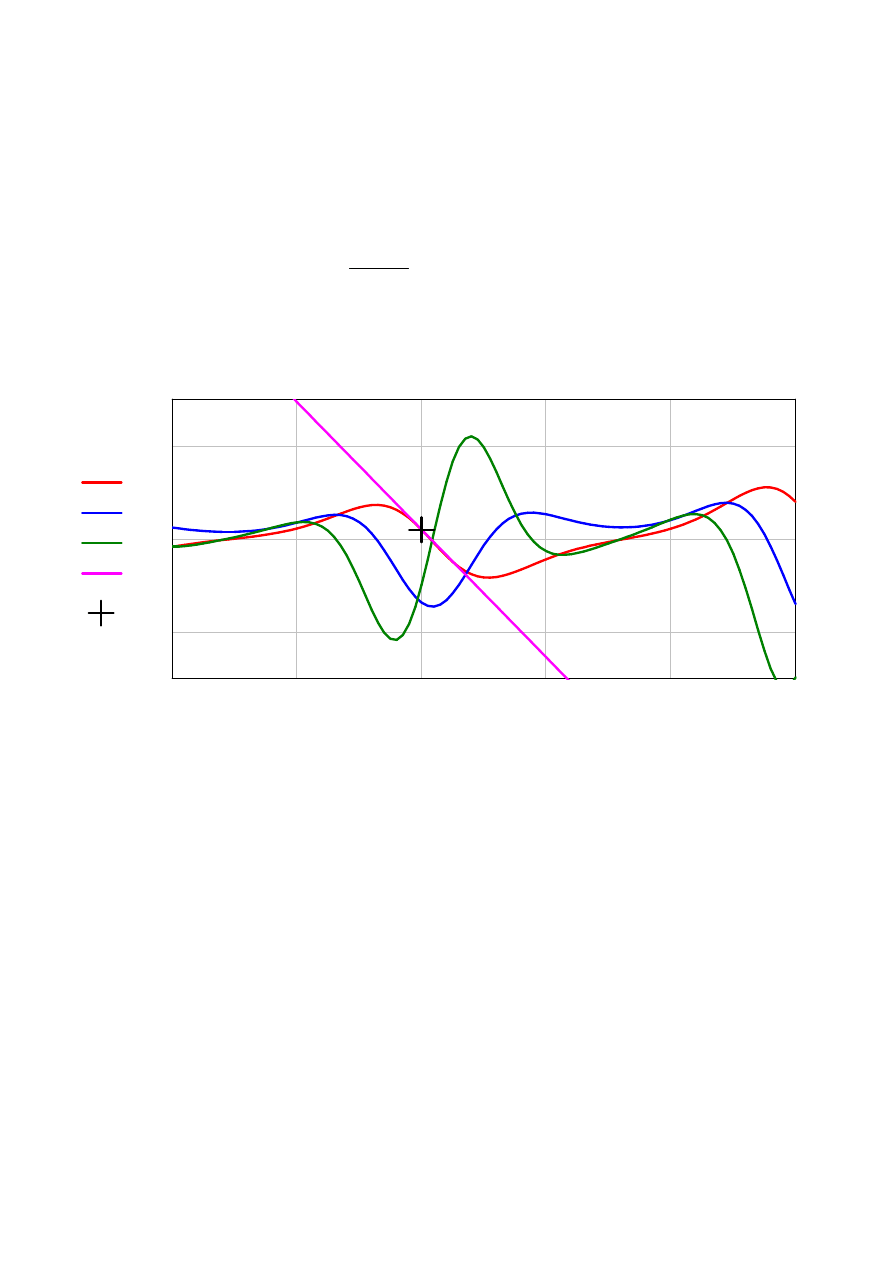
Zadanie 1
Dana jest funkcja f(x) w przedziale 10<x<20:
1. Wyznaczy
ć
pochodne funkcji df(x), d2f(x)
2. Sporz
ą
dzi
ć
tabelki i wspólny wykres funkcji
3. Wykona
ć
przekształcenia symboliczne wykonaj ponownie wykresy
4. Oblicz współczynnik kierunkowy dla stycznej w wybranym punkcie
oraz napisz równanie linii stycznej - wstaw na wykres funkcji razem z x, f(x),
df(x)
Wskazówka:
f x
( )
2x
3
cos x
( )
x
2
11
+
⋅
e
sin x
( )
⋅
:=
s x
( )
df p
( ) x
p
−
(
)
⋅
f p
( )
+
:=
10
12
14
16
18
20
100
−
0
100
f x
( )
df x
( )
d2f x
( )
s x
( )
f p
( )
x x
,
x
,
x
,
p
,
Wynik:
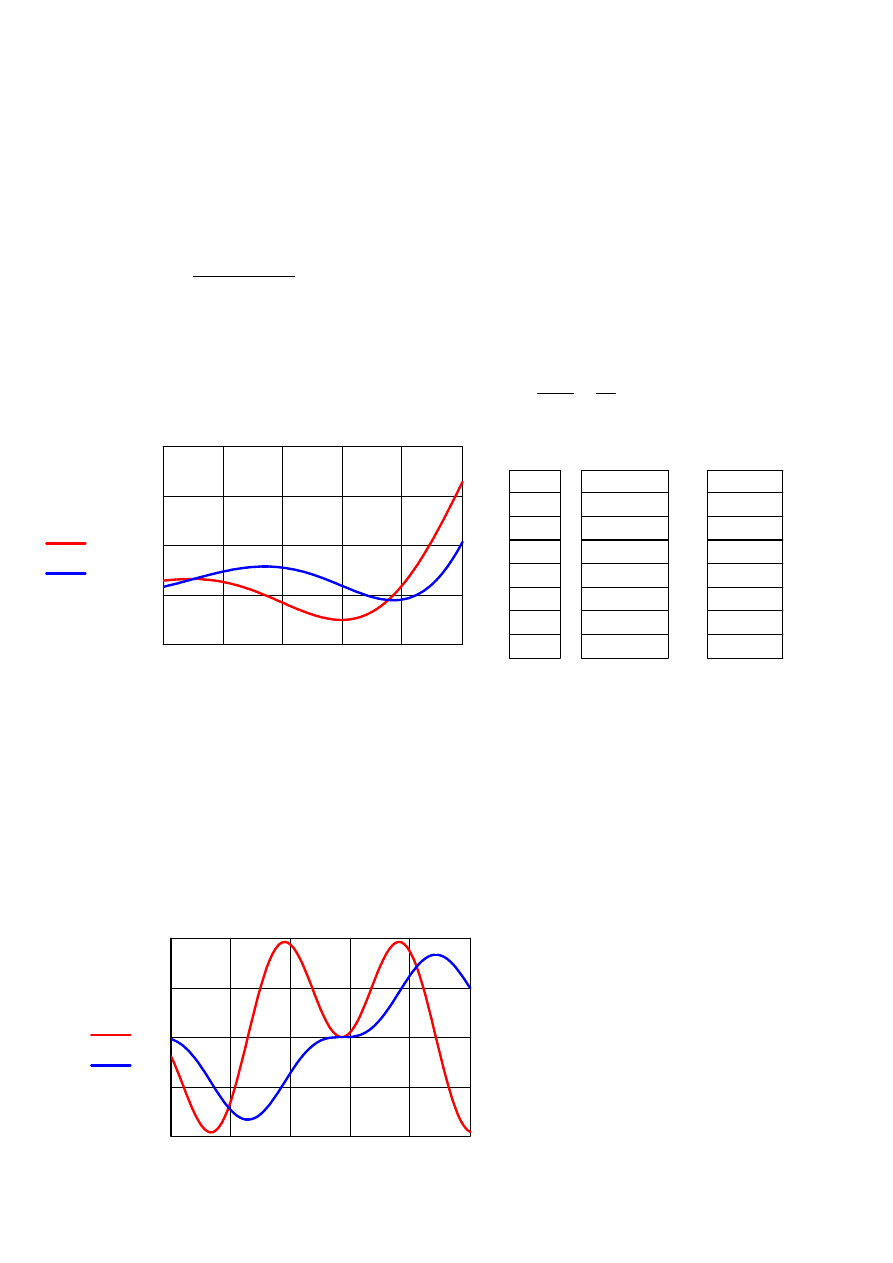
2. Całki
PRZYKŁAD
Dana jest funkcja g(x) w przedziale 5<x<10:
1. Wyznaczy
ć
całk
ę
funkcji cg(x)
2. Sporz
ą
dzi
ć
tabelki, wspólne wykresy dla x, g(x), cg(x)
3. Wyznacz warto
ść
całki oznaczonej dla wybranego podprzedziału
4. Wykona
ć
przekształcenia symboliczne
xmin
5
:=
xmax
10
:=
x
xmin xmin
xmax xmin
−
100
+
,
xmax
..
:=
g x
( )
x
3
4 x
2
⋅
−
x
3
sin x
( )
⋅
−
:=
cg x
( )
x
g x
( )
⌠
⌡
d
6 sin x
( )
⋅
x
3
cos x
( )
⋅
+
3 x
2
⋅
sin x
( )
⋅
−
4 x
3
⋅
3
−
x
4
4
+
6 x
⋅
cos x
( )
⋅
−
→
:=
5
6
7
8
9
10
500
−
0
500
1 10
3
×
1.5 10
3
×
g x
( )
cg x
( )
x
x
5
5.05
5.1
5.15
5.2
5.25
5.3
...
=
g x
( )
144.866
148.295
151.421
154.22
156.669
158.744
160.422
...
=
cg x
( )
82.697
90.027
97.521
105.164
112.938
120.825
128.805
...
=
0
10
x
g x
( )
⌠
⌡
d
537.9
=
Zadanie 2
Dana jest funkcja k(a) = sin a
( ) cos a
( )
2
w przedziale 5<a<10:
1. Wyznaczy
ć
całk
ę
funkcji ck(a)
2. Sporz
ą
dzi
ć
tabelki i wspólne wykresy dla a, k(a), ck(a)
3. Wyznacz warto
ść
całki oznaczonej dla wybranego podprzedzi
5
6
7
8
9
10
0.4
−
0.2
−
0
0.2
0.4
k a
( )
ck a
( )
a
Wynik:
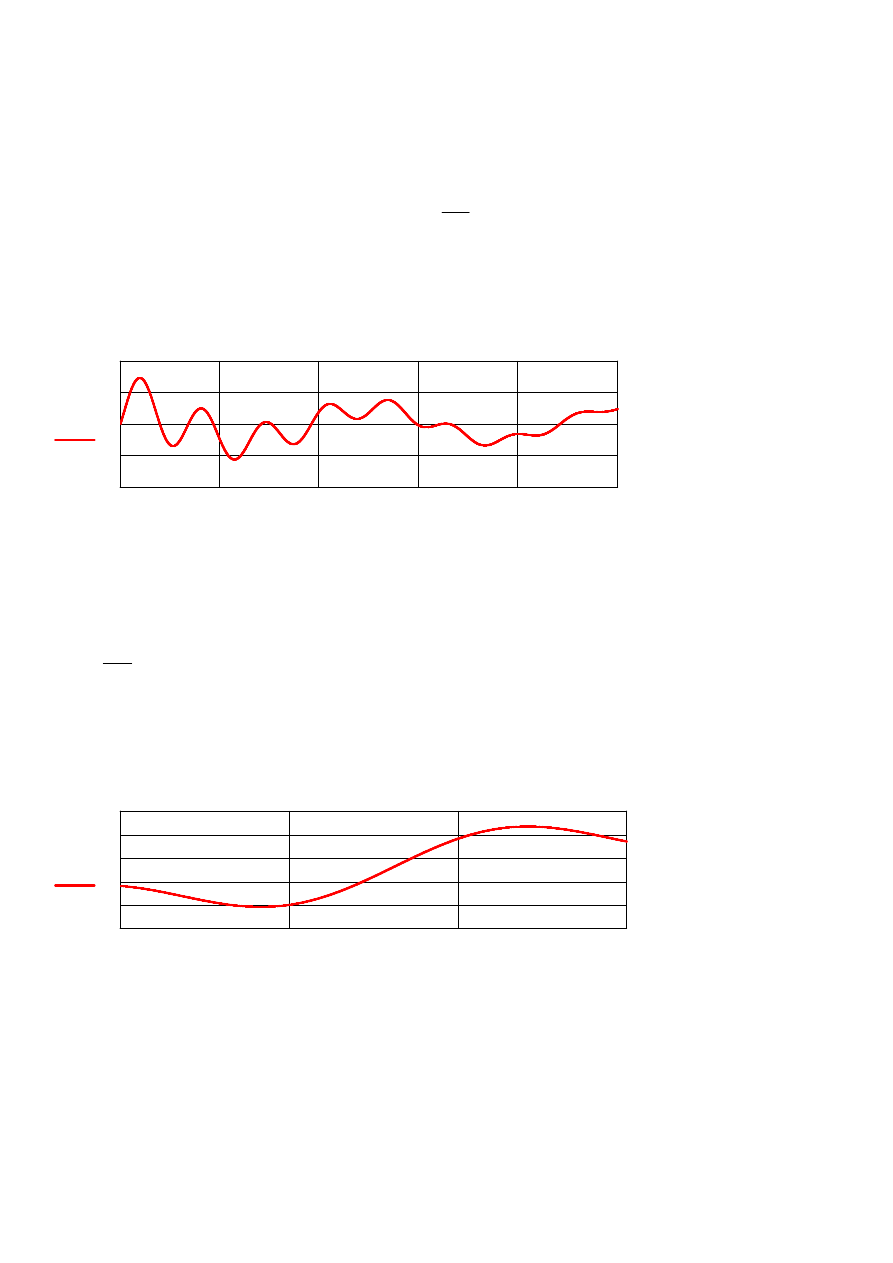
3. Równania ró
ż
niczkowe
I Sposób
"prim" uzyskiuje si
ę
przez Ctrl+[F7]
Given
x
0 0.01
,
50
..
:=
100 y'' x
( )
⋅
10 y' x
( )
⋅
+
101 y x
( )
⋅
+
50 cos
x 1
⋅
4
⋅
=
y 0
( )
0
=
y' 0
( )
1
=
y
Odesolve x 220
,
(
)
:=
0
10
20
30
40
50
2
−
1
−
0
1
2
y x
( )
x
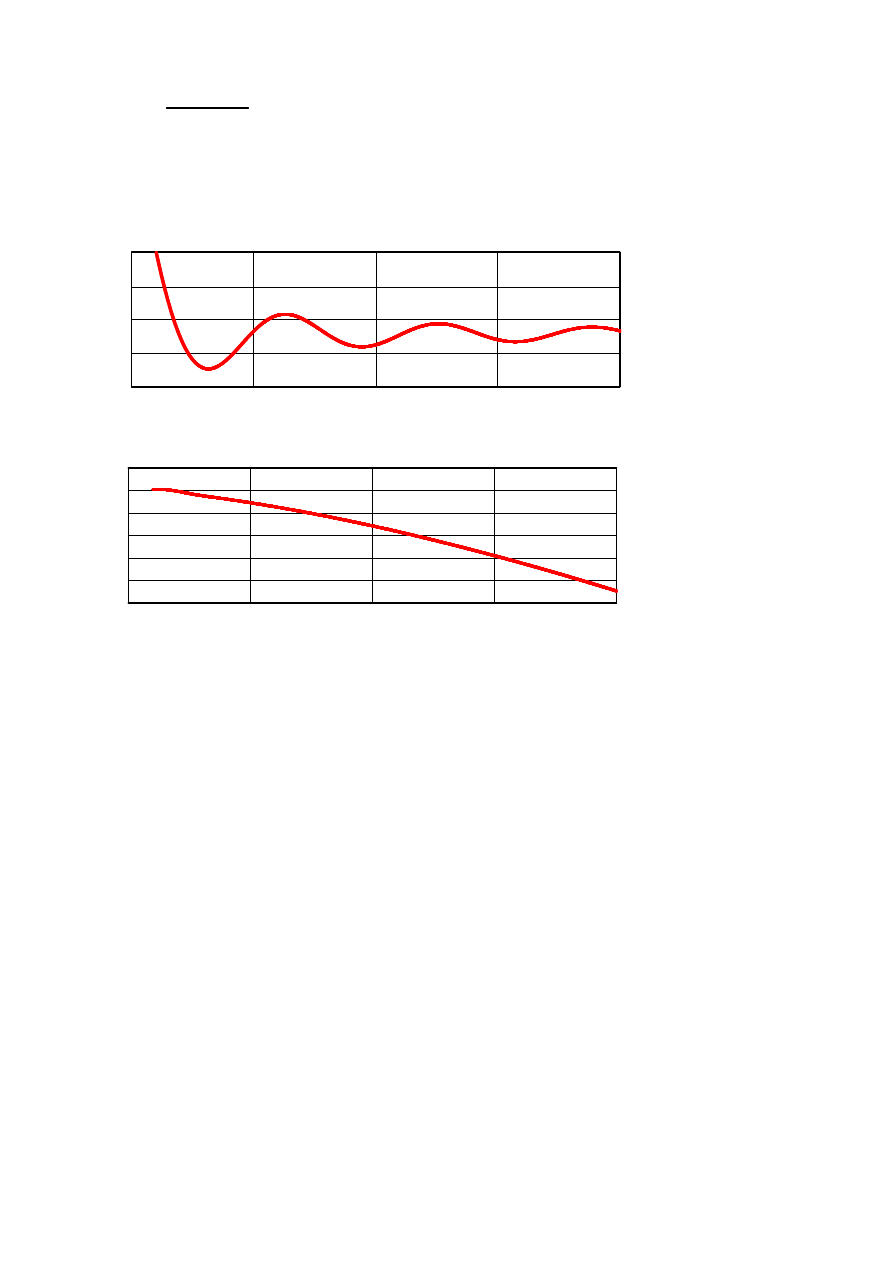
II Sposób
Given
t
0 0.01
,
15
..
:=
4
2
t
f t
( )
d
d
2
⋅
f t
( )
+
t
=
f 0
( )
4
=
f 15
(
)
13.5
=
f
Odesolve t 15
,
(
)
:=
0
5
10
15
5
−
0
5
10
15
20
f t
( )
t
Zadanie 3
Rozwi
ąż
równiania ró
ż
niczkowe
a) 5 y' x
( )
⋅
y x
( ) sin x
( )
2x
+
0
=
dla y(1)=2
b) 2
−
y' x
( )
⋅
y x
( )
2
+
x
3
=
dla y(1)=1
Wynik
a)
0
5
10
15
20
1.8
1.85
1.9
1.95
2
b)
0
5
10
15
20
100
−
80
−
60
−
40
−
20
−
0
20

4. Upraszczanie i przekształcanie wyra
ż
e
ń
algebraicznych
Simplify - upraszczenie wyra
ż
e
ń
c
2
c
+
2
−
c
2
+
(
) c
⋅
simplify
1
1
c
−
→
Explicit- podmiana zmiennej
y
2 a
⋅
3
+
:=
y
3
2 y
⋅
+
18 y
2
⋅
−
explicit y
,
2 a
⋅
3
+
3
2 2 a
⋅
3
+
(
)
⋅
+
18 2 a
⋅
3
+
(
)
2
⋅
−
→
Substitute-Podstawienie
w
3
2 w
⋅
+
18 w
2
⋅
−
substitute w
2 c
⋅
3
+
=
,
72 c
2
⋅
−
634 c
⋅
3
−
155
−
→
w
3
2 w
⋅
+
18 w
2
⋅
−
substitute w
1
3
=
,
11
9
−
→
Factor-Postac ilocznynowa
x
2
x
−
2
−
factor
x
1
+
(
) x
2
−
(
)
⋅
→
2 x
3
⋅
8 x
⋅
−
3 x
2
⋅
−
12
+
factor
2 x
⋅
3
−
(
) x
2
+
(
)
⋅
x
2
−
(
)
⋅
→
Expand -Postac wykładnicza
x
1
+
(
) x
2
−
(
)
⋅
expand
x
2
x
−
2
−
→
2 x
⋅
3
−
(
) x
2
+
(
)
⋅
x
2
−
(
)
⋅
expand
2 x
3
⋅
3 x
2
⋅
−
8 x
⋅
−
12
+
→
Coeffs-współczynniki wielomianu
2 x
3
⋅
3 x
2
⋅
−
8 x
⋅
−
12
+
coeffs
12
8
−
3
−
2
→
Collect- grupowanie wyrazów i wyci
ą
ganie wspólnego czynnika przed nawias
3s
2
d
5s
2
d
2
+
7s d
2
⋅
+
collect s
,
5 d
2
⋅
3 d
⋅
+
(
)
s
2
⋅
7 d
2
⋅
s
⋅
+
→
Convert to Partial Fraction- przedstawienie wyra
ż
enia jako sum
ę
ułamków prostych
c
3
−
(
) c
6
+
(
)
⋅
c
2
−
(
) c
5
+
(
)
⋅
parfrac
8
7 c
5
+
(
)
⋅
8
7 c
2
−
(
)
⋅
−
1
+
→
Series-rozwijanie w szereg
sin b
( ) series
b
b
3
6
−
b
5
120
+
→
sin b
( ) series 12
,
b
b
3
6
−
b
5
120
+
b
7
5040
−
b
9
362880
+
b
11
39916800
−
→
Assume-zało
ż
enia
2 x
⋅
3
−
(
) x
2
+
(
)
⋅
x
2
−
(
)
⋅
solve
2
2
−
3
2
→
2 x
⋅
3
−
(
) x
2
+
(
)
⋅
x
2
−
(
)
⋅
solve
assume x
0
>
,
2
3
2
→
2 x
⋅
3
−
(
) x
2
+
(
)
⋅
x
2
−
(
)
⋅
solve
assume x
integer
=
,
2
2
−
→
Fully-szczegółowe informacje o rozwi
ą
zaniu
7b
2
−
(
)x
1
=
solve x
,
1
7 b
⋅
2
−
→
7b
2
−
(
)x
1
=
solve x
,
fully
,
1
7 b
⋅
2
−
b
2
7
≠
if
undefined
b
2
7
=
if
→
sin x
( )
cos x
( )
=
solve
π
4
→
sin x
( )
cos x
( )
=
solve fully
,
π
4
π
_n
⋅
+
_n
∈ ℤ
if
undefined otherwise
→
Obliczanie granic funkcji
∞
x
1
x
lim
→
0
→
∞
n
1
5
n
−
n
lim
→
e
5
−
→
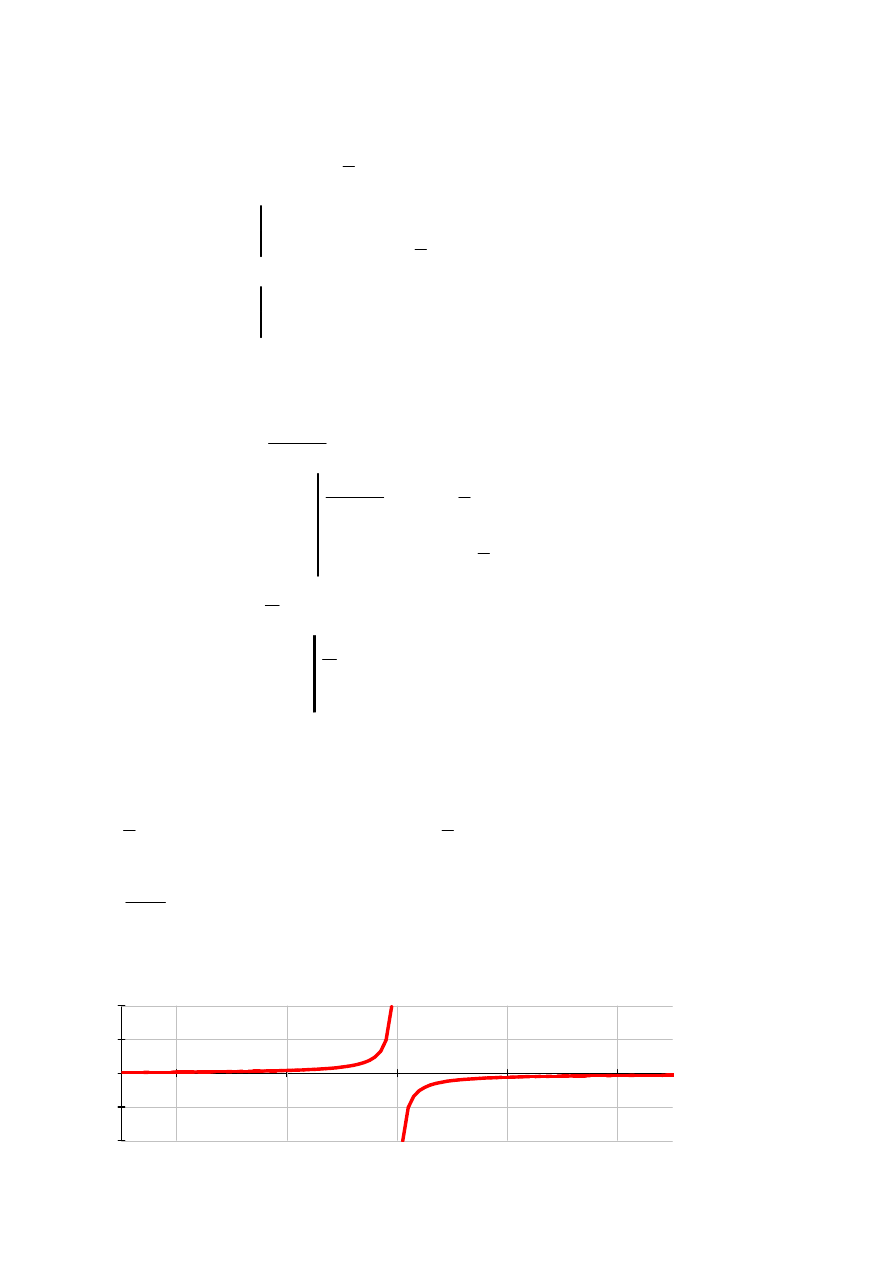
f x
( )
x
1
x
−
:=
1
x
f x
( )
lim
+
→
∞
−
→
1
x
f x
( )
lim
−
→
∞
→
0.6
0.8
1
1.2
1.4
100
−
50
−
50
100

Zadanie 4
a) Upro
ś
ci
ć
wyra
ż
enia
23
x
2
−
(
)
3
5
2x
+
(
)
4
−
2 x
4
−
(
)
3
−
sin
2
x
( )
cos
2
x
( )
+
a
4 b
⋅
−
(
)
2
2 b
⋅
a
+
(
)
3
−
7 a
3
⋅
−
b) Pogrupowa
ć
składowe wyra
ż
enia ze wzgl
ę
du na "z"
z
5
7x z
⋅
+
100 z
2
⋅
−
12 x
⋅
+
z
+
6x
8z
−
(
)
2
−
z
1
−
(
)
2
x
⋅
z
2
+
4 z
⋅
−
z
1
+
(
)
2
−
c) W wyra
ż
eniu:
h
2
h
3
+
h
1
−
(
)
3
+
4
zast
ą
p zmienn
ą
"b" przez wyra
ż
enie "h=6+2c"
Nast
ę
pnie upro
ść
wyra
ż
enie
d) Przedstaw wyra
ż
enie jako sum
ę
ułamków
18 x
⋅
40
+
2 x
2
⋅
8x
−
e) Oblicz granic
ę
oraz przedstaw interpretacj
ę
graficzn
ą
nast
ę
puj
ą
cych wyra
ż
e
ń
∞
n
1
5
−
n
n
lim
→
0
x
x
4
+
2
−
sin 5 x
⋅
(
)
lim
→
Metody rozwi
ą
zywania równa
ń
Metoda 1
v
x
2
3x
−
7
−
coeffs
7
−
3
−
1
→
:=
polyroots v
( )
1.541
−
4.541
=
Metoda 2
x
2
3x
−
7
−
0
=
solve
37
2
3
2
+
3
2
37
2
−
→
37
2
3
2
+
3
2
37
2
−
4.541
1.541
−
=
Metoda 3
Given
0
x
2
3x
−
7
−
=
Find x
( )
37
2
3
2
+
3
2
37
2
−
→
Wyszukiwarka
Podobne podstrony:
KWP cw3
PG cw3
cw3
cw3 rezystancja id 123348 Nieznany
cw3 odp
cw3 2014 notatki
LA cw3
cw3 9
CW3 INST
korespondencja polecenia, Weterynaria Lublin, INFORMATYKA, cw3, cw2
SK-cw3 2h Konfigurowanie sieci WLAN, Sieci Komputerowe
szymikowski OPTO cw3 (ndkn)
ćw3 zmk
Ćw3 jak w kserówkach
metody cw3
więcej podobnych podstron