Ć

wiczenie nr ........

Dynamiczne równania ruchu – ruch postępowy i obrotowy

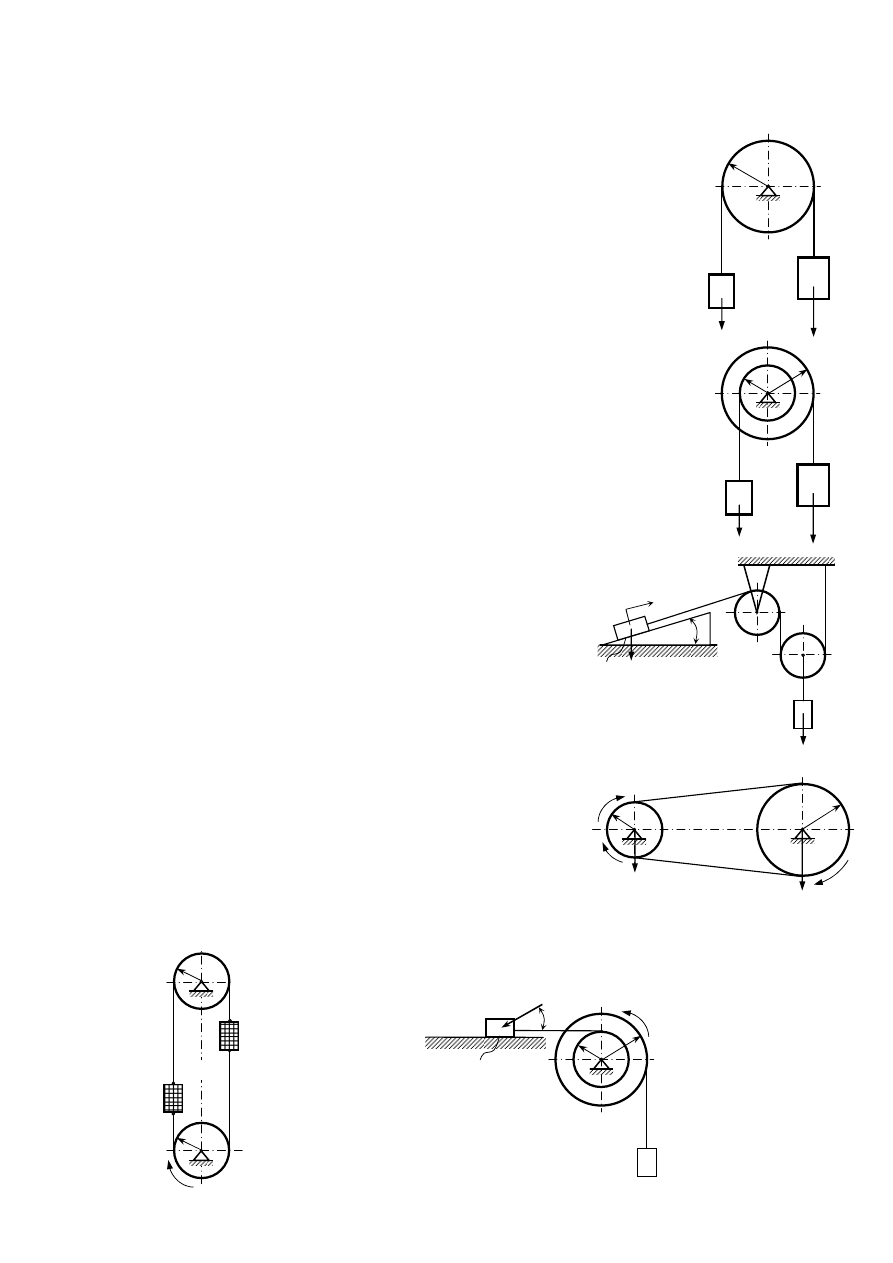
1)

Przez krążek o promieniu r przerzucona jest nierozciągliwa nić do której końców
przymocowane są ciała M

1

o ciężarze P

1

i M

2

o ciężarze P

2

. Zakładając, że P

2

>P

1

określić przyspieszenie ciał (a) oraz napięcie nici (T):
a)

pomijając masę krążka

b)

uwzględniając masę krążka którego ciężar wynosi Q

2)

Dwa ciała: M

1

o ciężarze P

1

i M

2

o ciężarze P

2

podwieszone są na dwóch

nierozciągliwych linkach nawiniętych na współosiowo połączone bębny o
promieniach wynoszących odpowiednio r

1

i r

2

oraz ciężarach Q

1

i Q

2

. Określić

przyspieszenie kątowe bębnów (

εεεε

) oraz napięcia linek (T

1

oraz T

2

), jeżeli:

P

1

=200 N

P

2

=340 N

Q

1

=40 N

Q

2

=80 N

r

1

=5 cm

r

2

=10 cm

3)

Znajdujące się na równi pochyłej ciało A o ciężarze Q połączono linką poprzez układ
dwóch krążków z ciałem B o takimż samym ciężarze Q. Współczynnik tarcia na równi
pochyłej wynosi

µµµµ

, a kąt jej wzniosu

αααα

. Pomijając masy krążków obliczyć wartości

przyspieszeń ciał A i B (odpowiednio a

A

i a

B

) oraz naciąg linki (T).

4)

Dwa koła jak na rysunku o promieniach R

1

i R

2

oraz ciężarach P

1

i P

2

połączono pasem. Znaleźć przyspieszenie kątowe obu kół
(odpowiednio

εεεε

1

i

εεεε

2

) jeżeli pierwsze z nich obciążone jest momentem

obrotowym M

0

. Tarcie w łożyskach, ciężar pasa oraz jego poślizg

pominąć.

5)

Do dolnej tarczy C podnośnika przyłożony jest moment obrotowy M.
Obliczyć przyspieszenie podnoszonego do góry ciała A o ciężarze P

1

,

jeżeli ciężar przeciwwagi B wynosi P

2

. Tarcze C i D są jednorodnymi

walcami o promieniu r i ciężarze Q każda. Masę liny pominąć.

6)

Dwa ciała: A o masie m

A

i B o masie m

B

przymocowane są jak na

rysunku do końców dwóch nierozciągliwych linek nawiniętych na
współosiowo połączone bębny o promieniach wynoszących
odpowiednio r

1

i r

2

oraz masach m

1

i m

2

. Na ciało A znajdujące się

na poziomej płaszczyźnie działa pod kątem

αααα

siła P, wymuszająca

ruch tego ciała zgodny ze zwrotem swej poziomej składowej.
Współczynnik tarcia pomiędzy płaszczyzną a ciałem A wynosi

µµµµ

.

Obliczyć przyspieszenie ciała A (a

A

).

r

M

2

M

1

P

2

P

1

P

2

>P

1

zad. 1

r

1

M

2

M

1

P

2

P

1

r

2

zad. 2

B

α

Q

zad. 3

Q

A

µµµµ

X

A

M

0

R

2

zad. 4

R

1

εεεε

1

εεεε

2

P

2

P

1

A

M

r

r

zad. 5

B

C

D

P

µµµµ

r

1

r

2

zad. 6

m

1

m

2

φφφφ

B

A

αααα