Wybrane charakterystyki układów

drgających

Marcin Graba

POLITECHNIKA ŚWIĘTOKRZYSKA W KIELCACH

WYDZIAŁ

MECHATRONIKI I BUDOWY MASZYN

KATEDRA PODSTAW KONSTRUKCJI MASZYN

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Cel ćwiczenia

•

Definicja drgań

wg Newton’a

•

Drgania w codzienności –

zalety i wady

•

Ogólna metoda pomiaru drgań

•

Przetworniki drgań

mechanicznych

•

Przetworniki mechaniczno-elektryczne i nieelektryczne

•

Przetwornik indukcyjny

•

Przetwornik potencjometryczny dwustronny

•

Drgania belki bez tłumienia

•

Drgania belki ze słabym tłumieniem

•

Drgania belki z tłumieniem krytycznym

•

Drgania belki z tłumieniem nadkrytycznym

•

Wykonanie ćwiczenia

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Definicja drgań

wg Newton’a

Jest to taki
proces, w którym
jakakolwiek
wielkość

fizyczna

charakteryzująca
ten proces
doznaje kolejno
wzrostu i
obniżania swej
wartości w funkcji
pewnej innej
wielkości, którą

zazwyczaj jest
czas.

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Definicja drgań

wg Newton’a

Jest to taki
proces, w którym
jakakolwiek
wielkość

fizyczna

charakteryzująca
ten proces
doznaje kolejno
wzrostu i
obniżania swej
wartości w funkcji
pewnej innej
wielkości, którą

zazwyczaj jest
czas.

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Drgania w codzienności –

zalety i wady

•

w

odlewnictwie

stosuje się

wibrujące platformy (jeśli kadź

z roztopionym metalem postawimy na

platformie to drgania kadzi sprzyjają

wydzielaniu gazu i oddzieleniu żużli); w transporcie znane

są

od dawna przenośniki wibracyjne;

•

w budownictwie stosowane są

urządzenia wykorzystujące drgania do zagęszczania, mieszania,

formowania i wybijania mas formierskich, wbijania pali, mielenia

czy ubijania;

najpopularniejszym obecnie przyrządem wykorzystującym opisywane zjawisko jest młot
pneumatyczny oraz jego liczne hybrydy jak przecinaki, nitowniki,

kilofy;

•

w budowie maszyn drgania wykorzystywane są

w urządzeniach do polerowania (szlifierka

oscylacyjna) i docierania;

•

w naszym laboratorium spotkaliśmy się

już

z drganiami; służyły one do zainicjowania w

próbkach pęknięcia zmęczeniowego;

•

innym przykładem zastosowania drgań

mechanicznych jest metoda wyznaczania momentu

bezwładności metodą

wahadła trójnitkowego, jak też

badania zdolności tłumienia drgań;

•

statystyka wykazuje, że około 70-80% pęknięć

i

awarii

w maszynach jest wynikiem właśnie

drgań;

•

co jakiś

czas gdzieś

na świecie pojawia się

trzęsienie ziemi -

spektakularny przykład

katastrofalnego wpływu drgań;

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

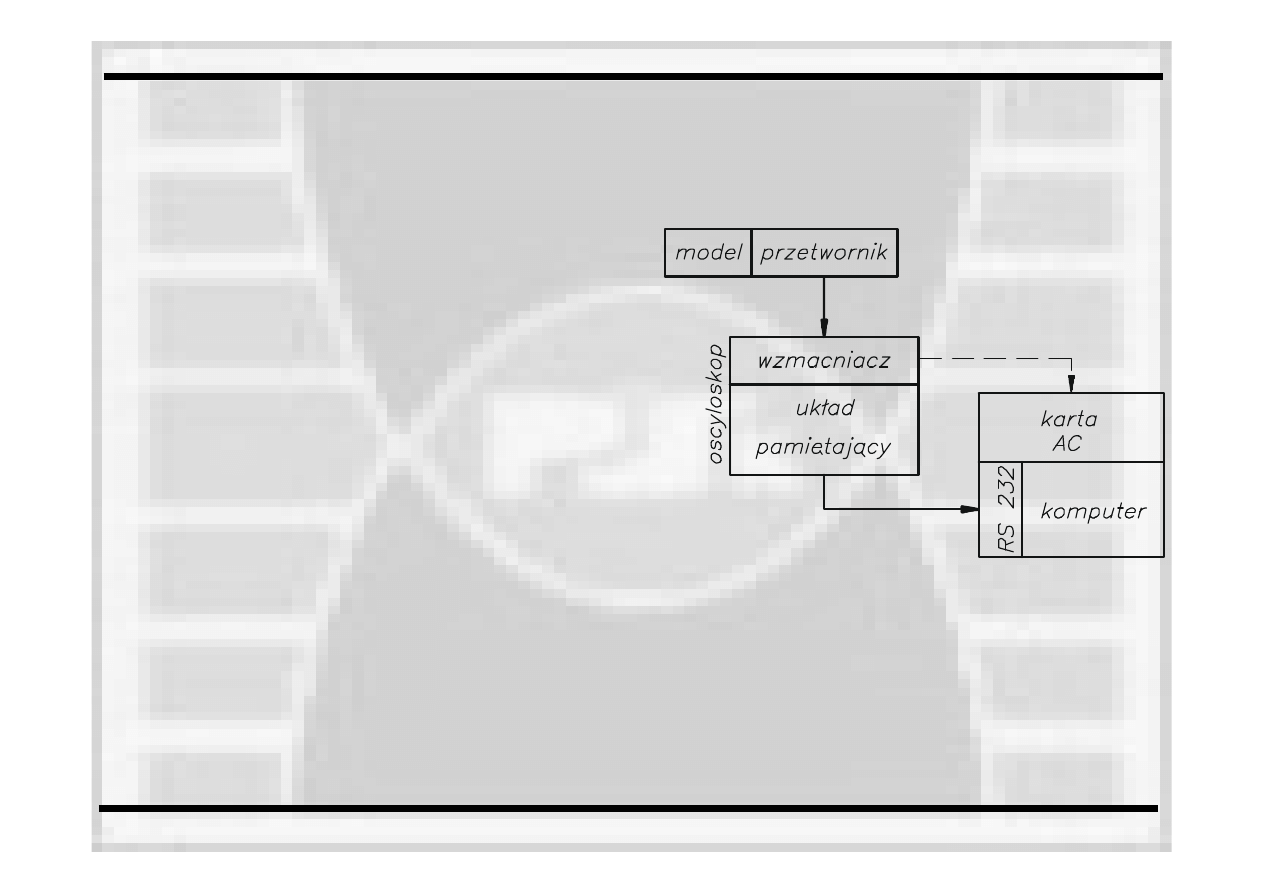
Ogólna metoda pomiaru drgań

Wykorzystywany w laboratorium model do
pomiaru drgań, zawiera przetwornik, który
zamieni drgania układu na sygnały elektryczne.
Sygnały te z kolei muszą

być

wzmocnione do

odpowiedniego poziomu i zapamiętane. Te dwie
funkcje w naszym układzie spełnia oscyloskop.
Jest to bardzo korzystne rozwiązanie, gdyż

umożliwia zapamiętanie szybkozmiennych w
czasie sygnałów. Dla wolniejszych przebiegów
zamiast oscyloskopu wykorzystujemy kartę

AC

i komputer. Sygnał

z oscyloskopu przesyłany

jest do komputera za pomocą

portu

szeregowego RS232 i programu sterującego
połączeniem oscyloskop-komputer.

Pomiar drgań

przeprowadza się

w dwóch etapach. Pierwsza część, to analiza geometryczna polegająca

na wyznaczeniu postaci drgań

ich charakteru, punktów, które przy danej postaci nie biorą

udziału w

drganiach oraz tych o największej amplitudzie drgań. W drugiej fazie przeprowadza się

analizę

czasową,

tzn. bada się

zmienność

poszczególnych wielkości (przemieszczenia liniowego i kątowego, odkształcenia

wzdłużnego i poprzecznego) w czasie oraz ich pierwszych i drugich pochodnych.
Jeśli zmiany są

okresowe, to należy wyznaczyć

parametry tych zmian (np.:

częstość, współczynnik

tłumienia), zaś

w przypadku przebiegu nieustalonego należy opisać

je statystycznie.

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Przetworniki drgań

mechanicznych

Czujnik umożliwiający zamianę

sygnału mechanicznego (np. przemieszczenia) na sygnał

elektryczny (np. napięcie) jest najważniejszym elementem całego układu. Od jego
właściwości zależy wynik pomiarów. Zależnie od zjawiska wykorzystywanego w procesie
przetwarzania sygnałów można przetworniki można podzielić

na kilka grup.

Generujące

Parametryczne

*

Indukcyjne:

*

Elektrodynamiczne

*

Elektromagnetyczne

*

Piezoelektryczne

*

Fotoelektryczne zaworowe

*

Elektrolityczne

*

Elektrokinetyczne

*

Indukcyjne

*

Dławikowe

*

Transformatorowe

*

Pojemnościowe

*

Fotoelektryczne z efektem zewn. i wewn.

*

Oporowe

*

Potencjometryczne

*

Oporowo-węglowe

*

Tensometryczne

*

Elektronowe

*

Akustyczne

*

Ultradźwiękowe

*

Magnetosprężyste

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Przetworniki mechaniczno-elektryczne

i nieelektryczne

Przetworniki mechaniczno-elektryczne cyfrowe mają

przewagę

nad przetwornikami

nieelektrycznymi dzięki wielu zaletom, do których zaliczamy:

•

wysoka jakość

zapisu (sygnał

nie jest zakłócony przez urządzanie zapamiętująco-

rejestrujące, którym w przypadku przetworników mechanicznych analogowych jest
pisak),

•

możliwość

wzmacniania i przekształcania sygnału,

•

zwartość

budowy i mały ciężar (jest to bardzo ważne, gdyż

zapobiega to

powstawaniu dodatkowych znacznych co do wartości sił

bezwładności),

•

możliwość

działania na odległość

(przetwornik jest oddzielony od pozostałych

elementów układu pomiarowego i może być

sterowany poprzez przewody lub drogą

radiową),

•

możliwość

jednoczesnej rejestracji sygnałów z kilku czujników,

•

wysoka niezawodność,

•

łatwy montaż

i obsługa.

Powyższe zalety spowodowały wyparcie wszelkich przyrządów zarówno mechanicznych jak
i optycznych, choć

te ostatnie dzięki rozwojowi techniki są

często wykorzystywane w

technice laboratoryjnej.

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

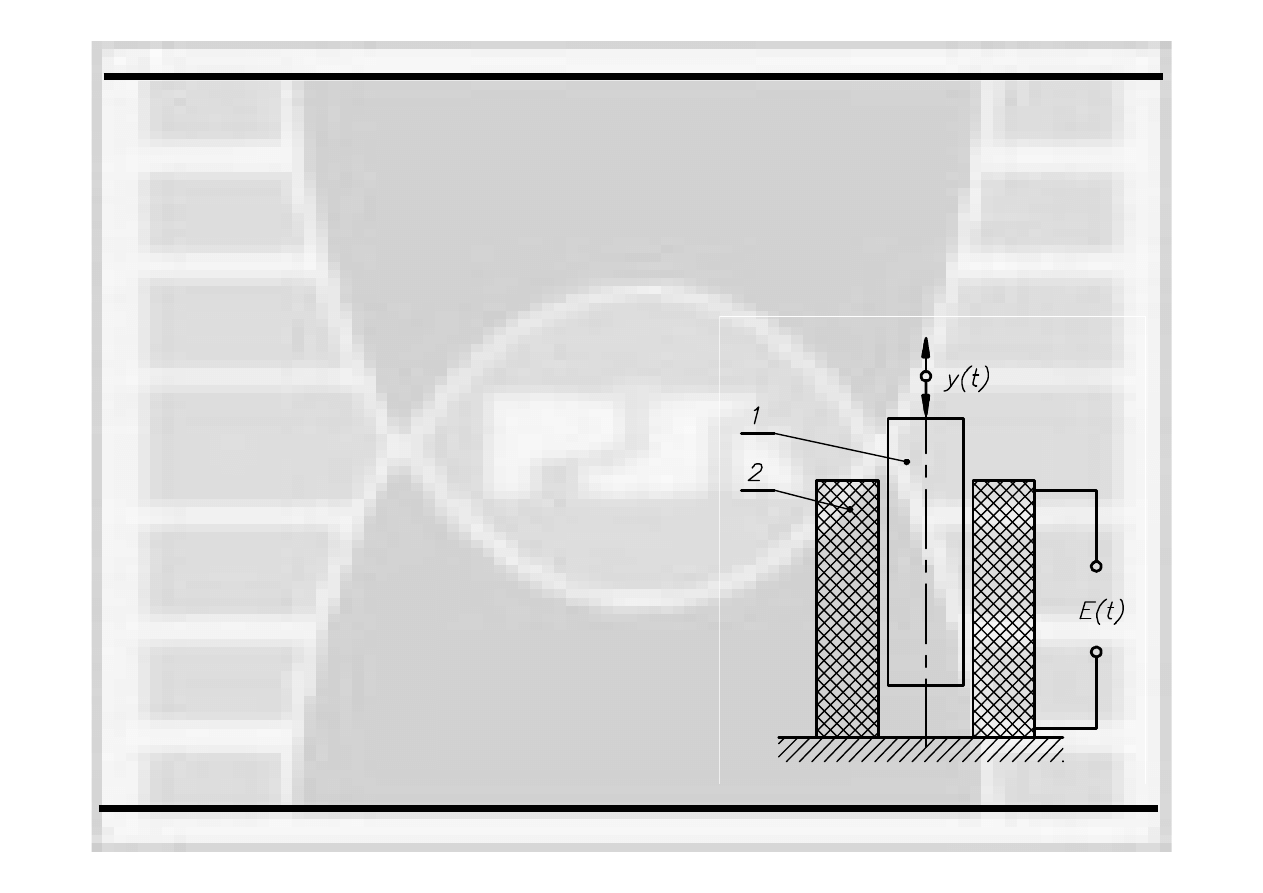
Przetwornik indukcyjny

•

magnes trwały 1, poruszając się

wewnątrz

nieruchomej cewki 2, indukuje w obwodzie
cewki napięcie zmienne, którego znak zależy od
kierunku ruchu rdzenia, a wartość

od położenia

rdzenia względem cewki;

•

w

pewnych

sytuacjach zamiast rdzenia porusza

się

cewka;

•

podobną

budowę

i

sposób

działania ma czujnik

bierny, ale tu rdzeń

jest po prostu

przewodnikiem elektryczności (np.żelazo), a
układ wymaga źródła zasilania;

•

położenie rdzenia wpływa na wartość

indukcyjności, a przez to na wartość

napięcia

wyjściowego czujnika;

Zasada działania przetwornika indukcyjnego czynnego (w czasie pracy wytwarza

sygnał

-

zmienną

w czasie siłę

elektromotoryczną):

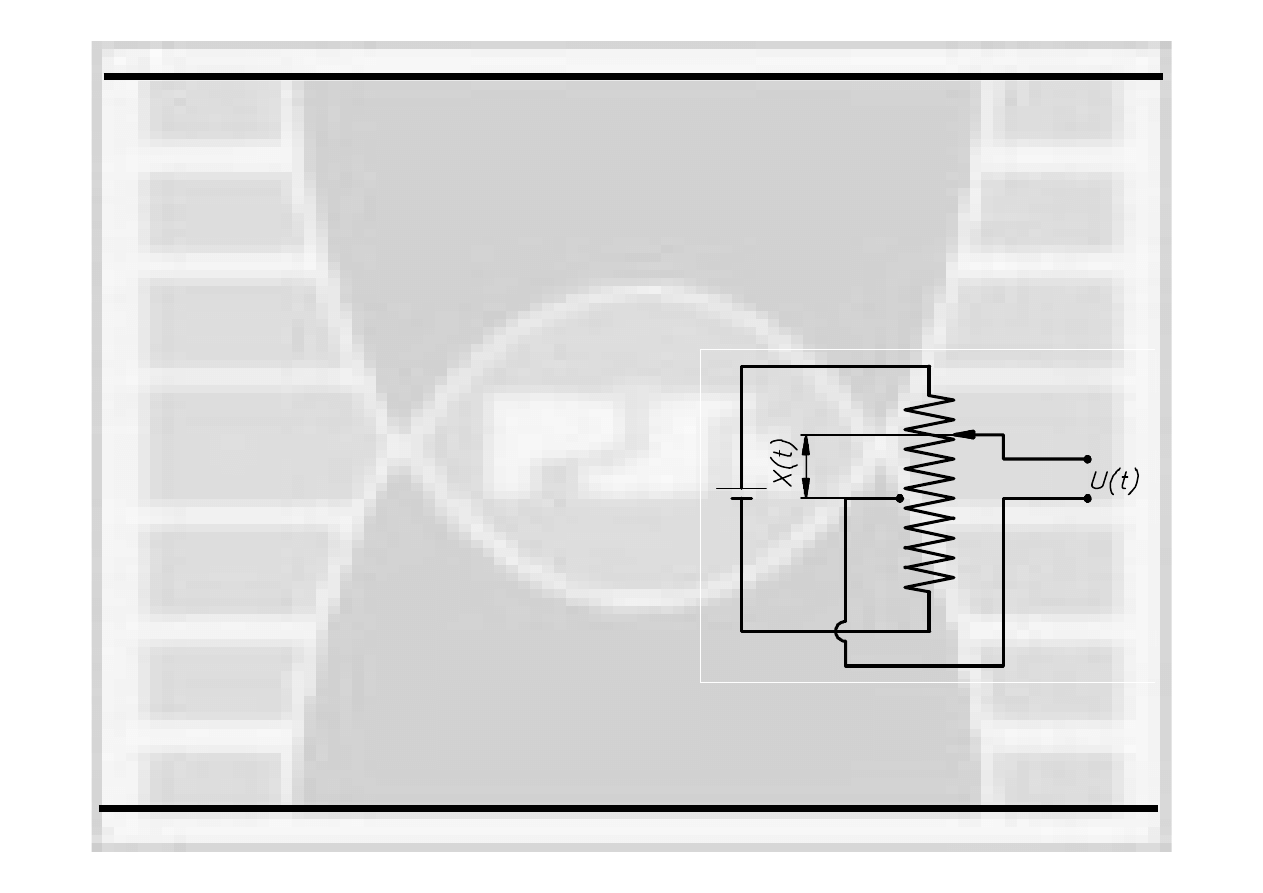
www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Przetwornik potencjometryczny

dwustronny

•

nadają

się

one do pomiaru amplitudy drgań

rzędu 1cm i częstotliwości do 10 Hz;

•

podstawowym elementem układu jest element
oporowy z suwakiem;

•

od położenia suwaka na elemencie oporowym
zależy wartość

napięcia odbieranego przez

dalszą

część

układu;

•

do grupy przetworników oporowych należą

również

tensometry, wykorzystywane do

pomiarów odkształceń

metodą

tensometrii

oporowej;

Innym prostym i niezawodnym w działaniu typem przetworników są

czujniki

potencjometryczne należące do grupy oporowych:

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

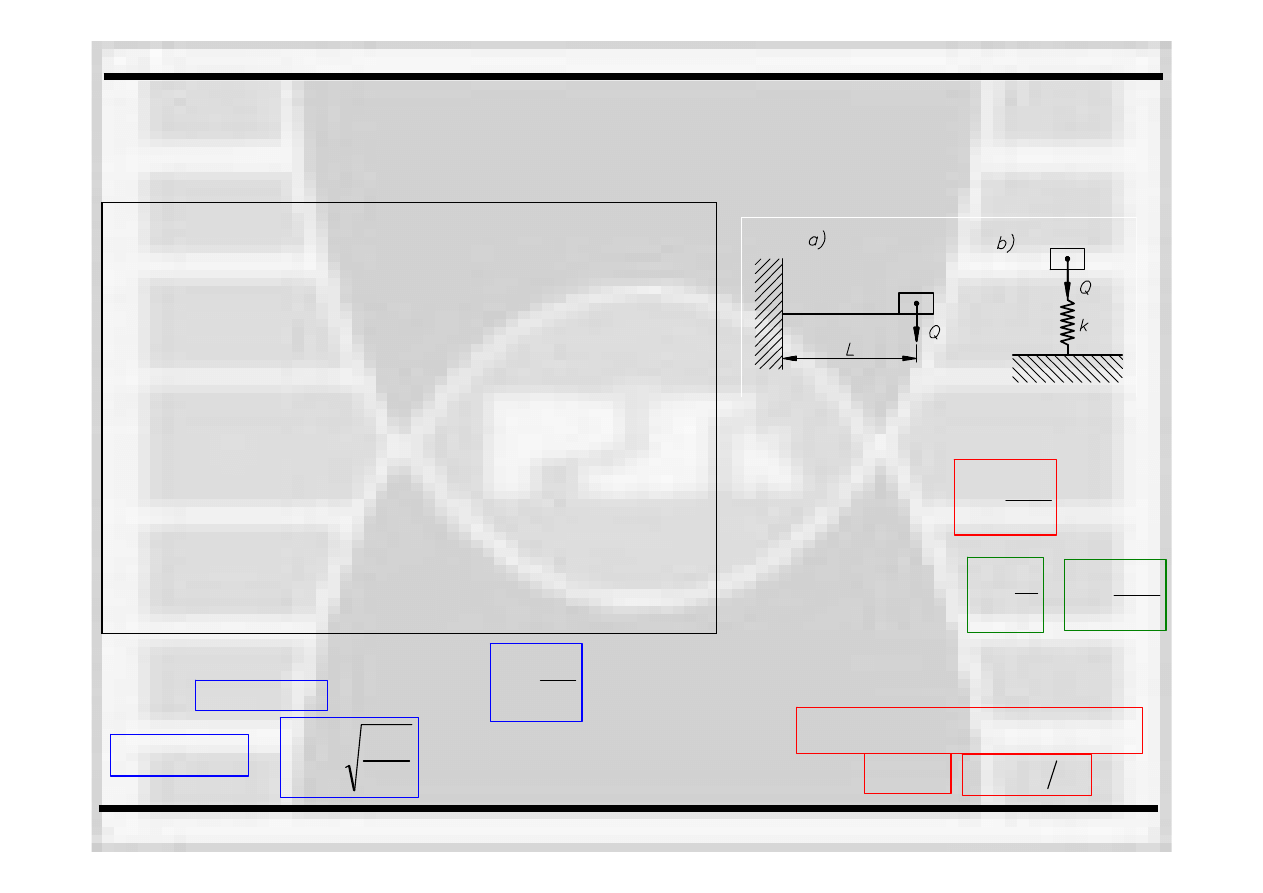
Drgania belki bez tłumienia

•

rozważamy belką

utwierdzoną

w jednym końcu i

obciążoną

masą

na drugim końcu; belkę

wykonano ze stali dla której moduł

Younga

wynosi E=2,15

⋅105MPa;

•

posiada ona długość

L

, szerokość

b

oraz

wysokość

h

;

•

w naszym układzie wstępnie przyjmiemy, że
belka jest nieważka (nie ma ciężaru) oraz
pominiemy tłumienie;

•

aby wyznaczyć

równanie ruchu masy,

rzeczywisty układ zastąpimy równoważnym
składającym się

z masy zawieszonej na sprężynie

o sztywności k;

Belka z obciążeniem (a) i jej model (b)

Strzałka ugięcia

belki

f

QL

EI

=

3

3

Sztywność

sprężyny zastępczej

k

Q

f

=

k

EI

L

=

3

3

Równanie opisujące ruch masy

mx

kx

&& +

= 0

&&x

x

+

=

ω

0

2

0

ω

0

3

3

=

EI

mL

Å

jest to częstością drgań

nietłumionych

T

=

2

0

π

ω

Å

jest to okres

drgań

nietłumionych

( )

( )

( )

x t

C

t

C

t

=

+

1

0

2

0

cos

sin

ω

ω

C

x

1

0

=

0

0

2

ω

V

C

=

Trajektoria ruchu masy dla x

0

i V

0

-

odpowiednio

położenia i prędkości dla czasu t=0

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

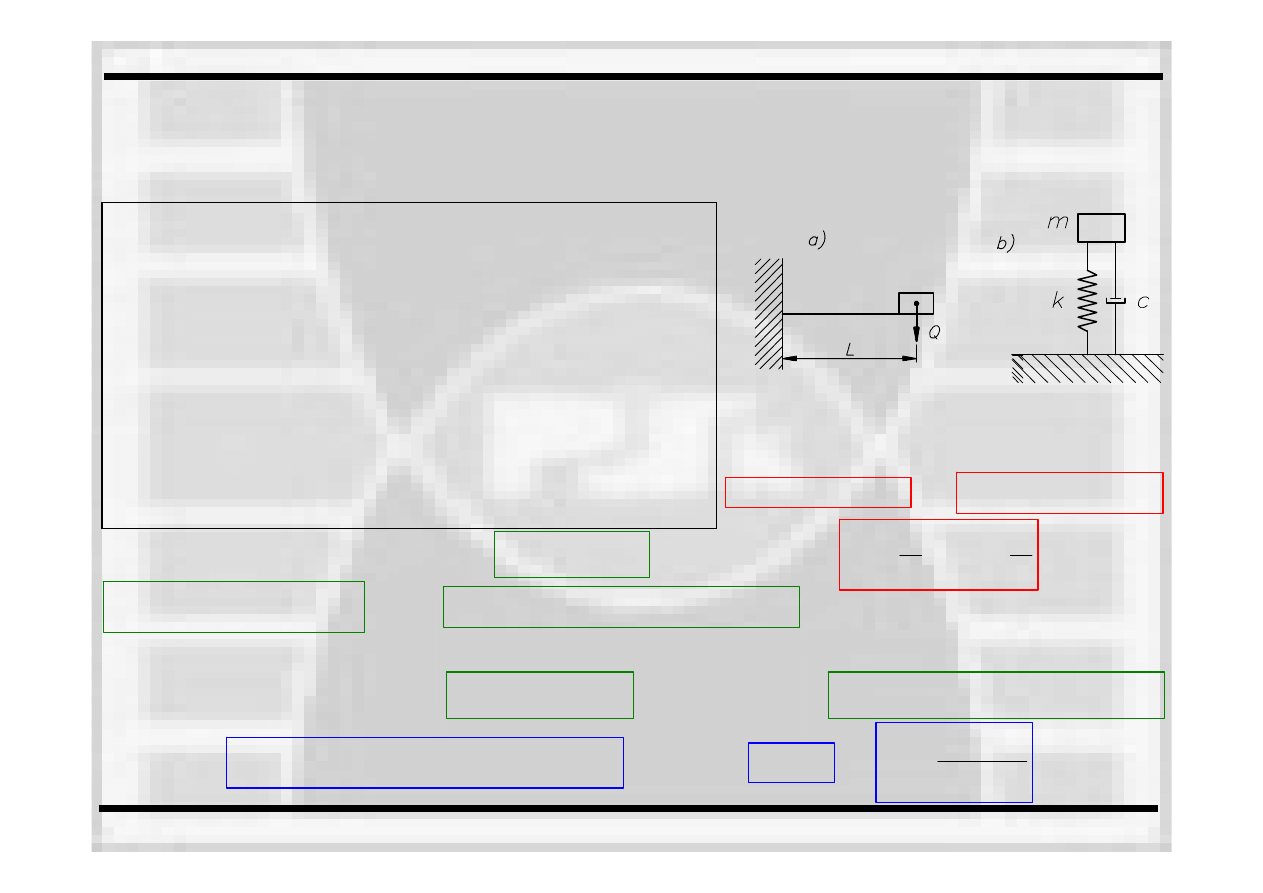
Drgania belki ze słabym tłumieniem

•

rozważamy belką

utwierdzoną

w jednym końcu i

obciążoną

masą

na drugim końcu; belkę

wykonano ze

stali dla której moduł

Younga

wynosi E=2,15

⋅105MPa;

•

posiada ona długość

L

, szerokość

b

oraz wysokość

h

;

•

w naszym układzie przyjmiemy, że belka ma ciężar
własny, więc rozważamy układ z tłumieniem;

•

tłumienie zależy od własności medium w którym porusza
się

badany obiekt, kształt badanego obiektu, siły tarcia

zarówno tego zewnętrznego (wynikającego z kontaktu z
innymi przedmiotami) jak i wewnętrznego (wynikającego
z ruchu cząsteczek materiału względem siebie);

Belka z obciążeniem (a) i jej model (b)

Równanie ruchu z uwzględnioną

siłą

oporu

mx

cx

kx

&&

&

+

+

= 0

lub

&&

&

x

hx

x

+

+

=

2

0

0

2

ω

2

0

2

h

c

m

k

m

=

=

ω

Zakłada się

rozwiązanie postaci

( ) ( )

x t

t e

ht

=

−

ξ

( )

(

)

( )

&&

ξ

ω

ξ

t

h

t

+

−

=

0

2

2

0

jeżeli

ω

ω

ω

0

2

2

0

2

2

2

0

>

⇒

−

=

>

h

h

*

to mamy do czynienia z tłumieniem podkrytycznym (słabym)

( )

( )

&&

*

ξ

ω ξ

t

t

+

=

2

0

Równanie ruchu przyjmuje postać

( )

( )

( )

ξ

ω

ω

t

C

t

C

t

=

+

1

2

cos

sin

*

*

a jego rozwiązanie

Zatem:

( )

( )

( )

(

)

x t

C

t

C

t e

ht

=

+

−

1

2

cos

sin

*

*

ω

ω

C

x

0

0

=

C

V

hx

2

0

0

=

+

ω

*

gdzie

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Drgania belki ze słabym tłumieniem

Belka z obciążeniem (a) i jej model (b)

Równanie ruchu z uwzględnioną

siłą

oporu

mx

cx

kx

&&

&

+

+

= 0

lub

&&

&

x

hx

x

+

+

=

2

0

0

2

ω

2

0

2

h

c

m

k

m

=

=

ω

-1,5

- 1

-0,5

0

0,5

1

1,5

0

2

4

6

A (t)=A e

0

-h t

A

A

1

2

x

t

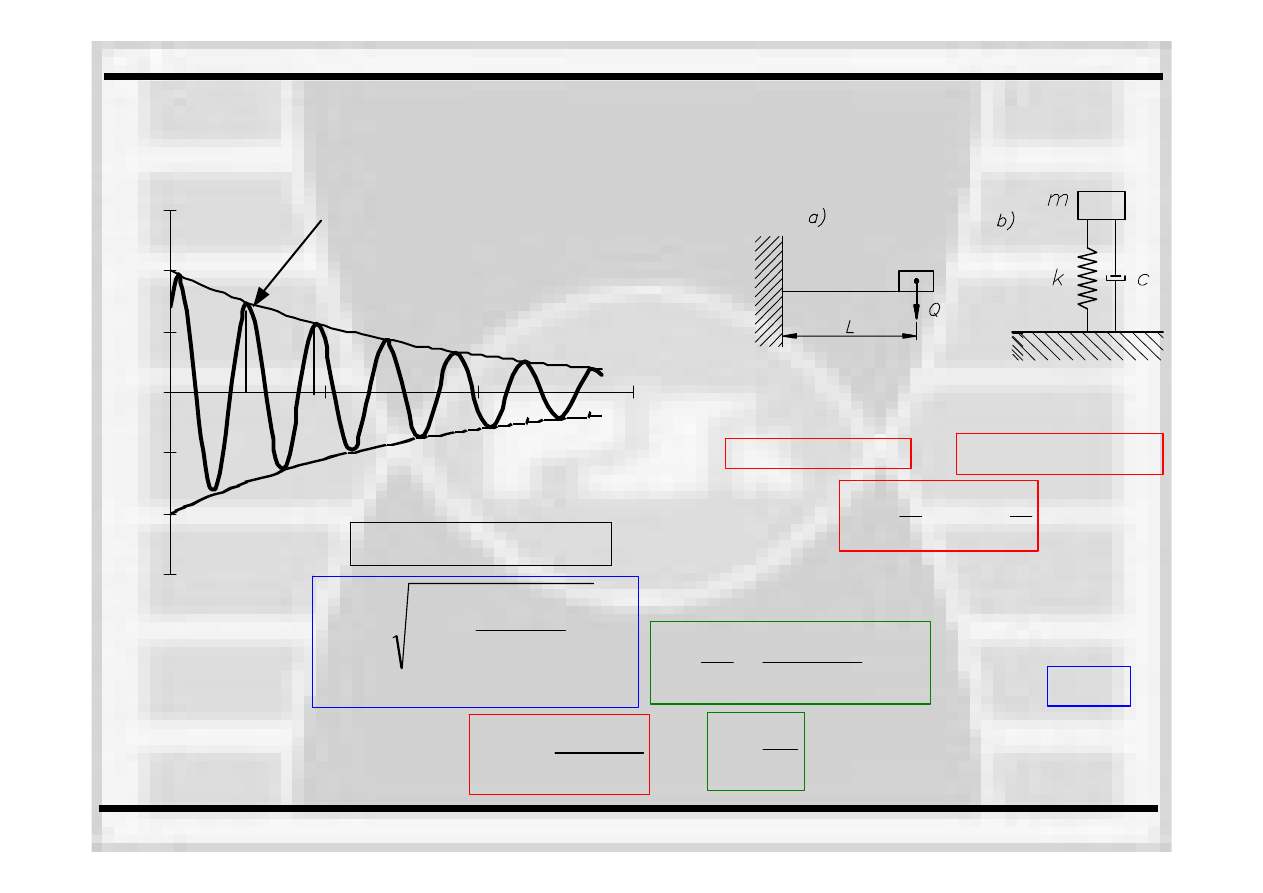
Równanie drgań

belki ze

słabym tłumieniem

( )

( )

(

)

x t

A t

t

=

+

sin

*

ω

β

Zmiana amplitudy

w czasie

( )

A t

x

V

hx

e

A

ht

=

+

+

⎛
⎝

⎜

⎞
⎠

⎟

−

0

2

0

0

2

0

ω

*

1

2

444

3

444

Kąt przesunięcia

fazowego

tan

*

β

ω

=

+

x

V

hx

0

0

0

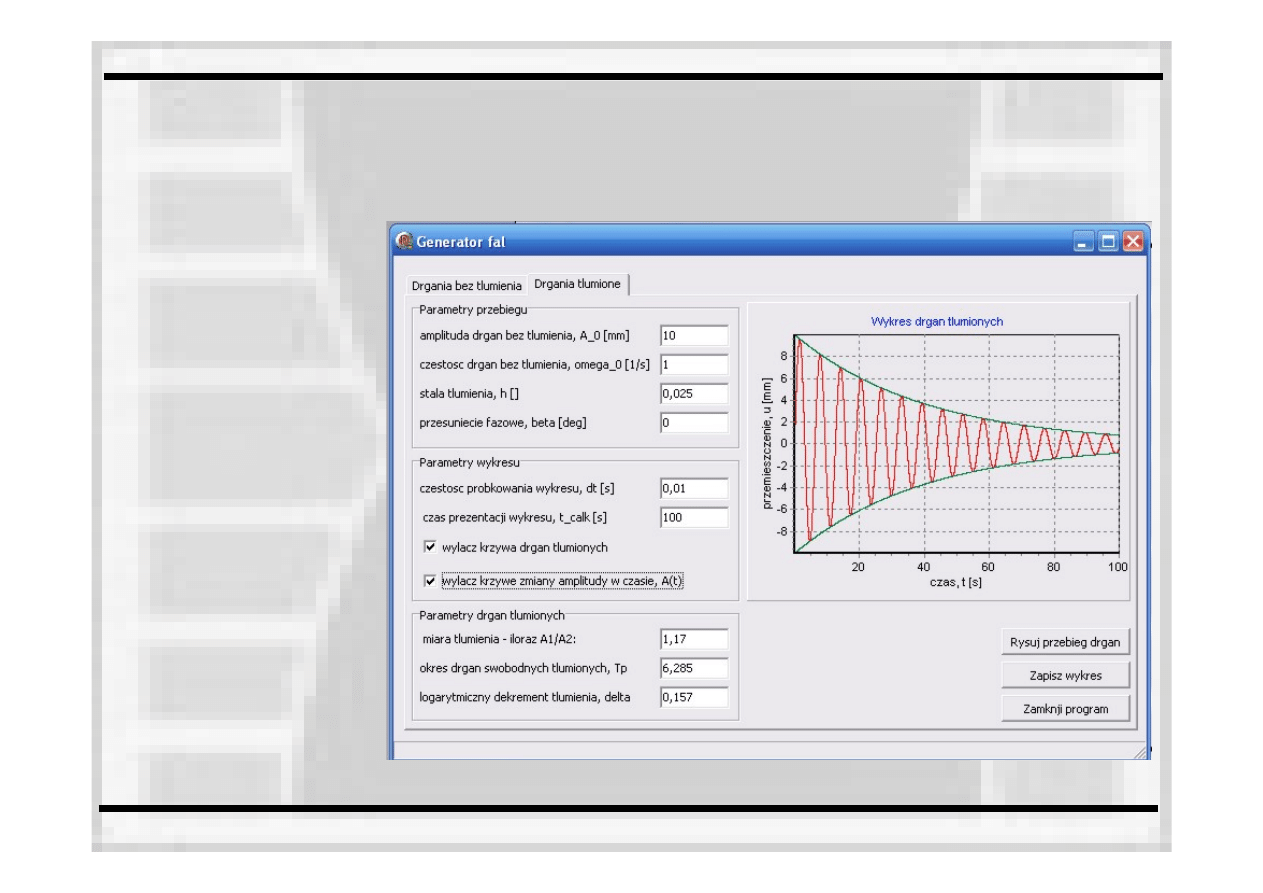
Miarą

tłumienia w układzie może być

iloraz dwóch

amplitud A1 i A2 odległych od siebie o jeden okres.

(

)

Δ =

=

=

−

−

+

A

A

Ae

Ae

e

ht

h t T

hT

1

2

*

*

T

*

*

=

2

π

ω

Å

okres drgań

swobodnych,

tłumionych

δ

= hT

*

logarytmiczny

dekrement

tłumienia

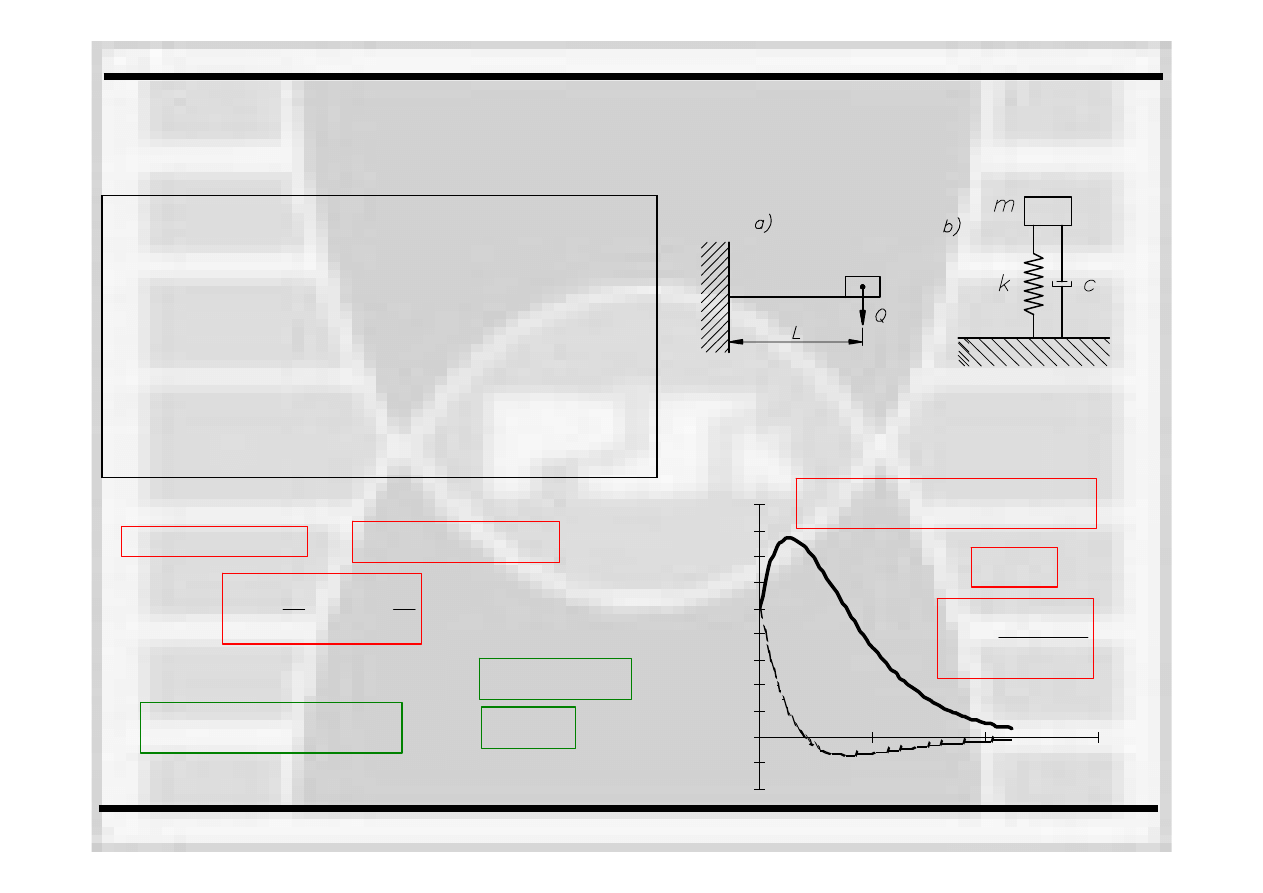
-0,04

-0,02

0

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

0,18

0

5

10

15

x

t

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Drgania belki z tłumieniem krytycznym

•

rozważamy belką

utwierdzoną

w jednym końcu i obciążoną

masą

na drugim końcu; belkę

wykonano ze stali dla której

moduł

Younga

wynosi E=2,15

⋅105MPa;

•

posiada ona długość

L

, szerokość

b

oraz wysokość

h

;

•

w naszym układzie przyjmiemy, że belka ma ciężar własny,
więc rozważamy układ z tłumieniem;

•

tłumienie zależy od własności medium w którym porusza
się

badany obiekt, kształt badanego obiektu, siły tarcia

zarówno tego zewnętrznego (wynikającego z kontaktu z
innymi przedmiotami) jak i wewnętrznego (wynikającego z
ruchu cząsteczek materiału względem siebie);

Belka z obciążeniem (a) i jej model (b)

Równanie ruchu z uwzględnioną

siłą

oporu

mx

cx

kx

&&

&

+

+

= 0

lub

&&

&

x

hx

x

+

+

=

2

0

0

2

ω

2

0

2

h

c

m

k

m

=

=

ω

Zakłada się

rozwiązanie postaci

( ) ( )

ht

e

t

t

x

−

=

ξ

( )

(

)

( )

&&

ξ

ω

ξ

t

h

t

+

−

=

0

2

2

0

jeżeli

to mamy do czynienia z tłumieniem krytycznym

Rozwiązanie równania ruchu w

tym wypadku ma postać:

C

x

0

0

=

C

V

hx

2

0

0

=

+

ω

*

gdzie

ω

0

2

2

= h

(

)

[

]

x t

e

x

hx

V t

ht

o

( )

=

+

+

−

0

0

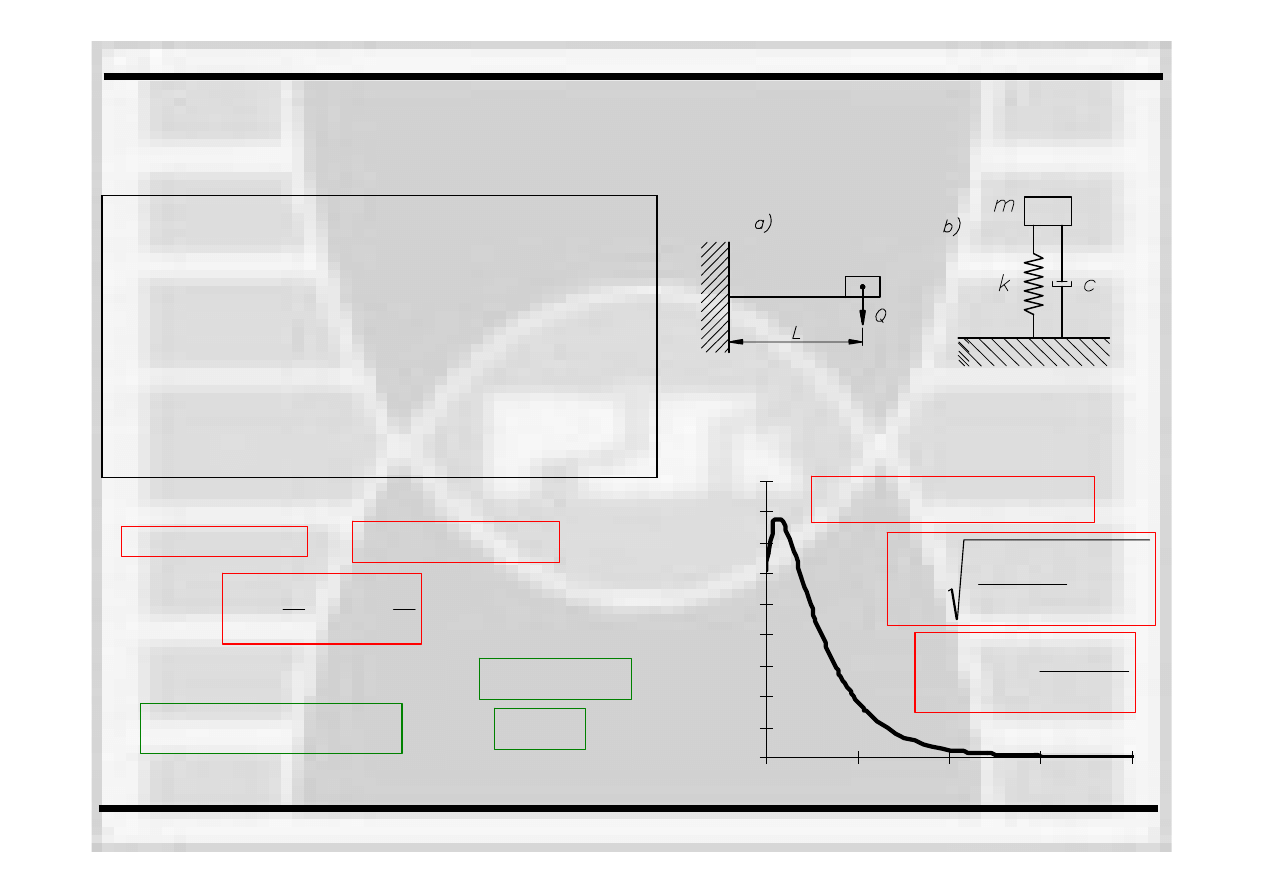
0

0 ,0 5

0 ,1

0 ,1 5

0 ,2

0 ,2 5

0 ,3

0 ,3 5

0 ,4

0 ,4 5

0

1 0

2 0

3 0

4 0

x

t

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Drgania belki z silnym tłumieniem

•

rozważamy belką

utwierdzoną

w jednym końcu i obciążoną

masą

na drugim końcu; belkę

wykonano ze stali dla której

moduł

Younga

wynosi E=2,15

⋅105MPa;

•

posiada ona długość

L

, szerokość

b

oraz wysokość

h

;

•

w naszym układzie przyjmiemy, że belka ma ciężar własny,
więc rozważamy układ z tłumieniem;

•

tłumienie zależy od własności medium w którym porusza
się

badany obiekt, kształt badanego obiektu, siły tarcia

zarówno tego zewnętrznego (wynikającego z kontaktu z
innymi przedmiotami) jak i wewnętrznego (wynikającego z
ruchu cząsteczek materiału względem siebie);

Belka z obciążeniem (a) i jej model (b)

Równanie ruchu z uwzględnioną

siłą

oporu

mx

cx

kx

&&

&

+

+

= 0

lub

&&

&

x

hx

x

+

+

=

2

0

0

2

ω

2

0

2

h

c

m

k

m

=

=

ω

Zakłada się

rozwiązanie postaci

( ) ( )

ht

e

t

t

x

−

=

ξ

( )

(

)

( )

&&

ξ

ω

ξ

t

h

t

+

−

=

0

2

2

0

jeżeli

to mamy do czynienia z silnym tłumieniem (nadkrytycznym)

Rozwiązanie równania ruchu w

tym wypadku ma postać:

gdzie

ω

0

2

2

< h

( )

(

)

x t

A e

t

ht

=

+

−

0

1

sinh

α β

A

hx

V

0

0

0

2

2

=

+

⎛
⎝⎜

⎞
⎠⎟

−

α

α

( )

tanh

β

α

1

0

0

0

=

+

x

hx

V

www.tu.kielce.pl/~mgraba

Copyright

©2009 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

WYBRANE CHARAKTERYSTYKI UKŁADÓW DRGAJĄCYCH

Wykonanie ćwiczenia -

sporządzenie

sprawozdania

•

Rejestracja drgań

nietłumionych

za pomocą

oscyloskopa

–

plik

tekstowy;

•

Opis zarejestrowanej trajektorii równaniem postaci:
x(t)=A+B

⋅sin(ω⋅t+ϕ), podanie wartości parametrów oraz okresu

drgań; sporządzić

wykres x(t);

•

Opis trajektorii drgań

nietłumionych

zadanej przez prowadzącego

równaniem postaci:

x(t)=A+B

⋅sin(ω⋅t+ϕ), podanie wartości parametrów oraz okresu

drgań; sporządzić

wykres x(t);

•

Opis trajektorii drgań

tłumionych: rozpoznać

rodzaj tłumienia,

napisać

wszelki niezbędne równania, obliczyć

wszystkie parametry

krzywej x(t), wyznaczyć

krzywe zmiany amplitudy w czasie A(t),

wyznaczyć

wszelkie parametry tłumienia; sporządzić

wykres x(t);

nanieść

na wykres krzywą

zmiany amplitudy w czasie;

•

Wnioski końcowe –

własne i rozsądne;