1

Dynamiczna alokacja pamięci,
biblioteka

stdlib.h

Funkcja

malloc

void* malloc (size_t size);

Przydziela pamięć o wielkości

size

bajtów. Obszar nie jest

inicjowany. Zwraca wskaźnik do nowo przydzielonego

bloku pamięci.

W przypadku niepowodzenia (np. nie ma wystarczająco

dużo miejsca w pamięci lub

size=0

) zwraca NULL oraz

do zmiennej

errno

wpisany jest kod błędu.

Przykład:

#include <stdlib.h>

int r = 10;
float* tab;

tab = malloc ( r * sizeof(float) );
tab[5] = 9;

lub
tab = malloc ( r * sizeof *tab );

2

Kontrola typów

Powyższy przykład jest poprawny dla języka C, nie jest
jednak poprawny dla języka C++

W C++ w stosunku do C została zaostrzona kontrola typów,
co wymaga stosowania jawnego rzutowania. Konwersja z

void*

na inne typy wskaźnikowe nie jest domyślna.

Język ten oferuje nowe sposoby alokacji pamięci (

new

,

delete

).

Kod poprawny dla C+++:

tab = (float*) malloc( r*sizeof(float) );

3

Funkcja

calloc

void *calloc (size_t n, size_t size);

Przydziela pamięć dla

n

elementów o rozmiarze

size

bajtów każdy i zeruje przydzieloną pamięć.

Jeżeli przydzielanie pamięci się powiodło, zwraca wskaźnik

do nowo przydzielonego bloku pamięci, w przeciwnym

przypadku zwraca NULL (i w zmiennej

errno

zapisuje

kod błędu).

Przykład:

#include <stdlib.h>

int r = 10;

float *tab;

tab=calloc(r, sizeof *tablica);

Uwaga: Podstawową różnicą pomiędzy funkcjami

malloc

i

calloc

jest to, że ta druga zeruje wartość przydzielonej

pamięci (do wszystkich bajtów wpisuje wartość 0).

4

Przykład: tablica wskaźników

int **tab = calloc(100,sizeof *tab);

Pomimo wyzerowania bajtów, nie możemy założyć, że

wszystkiego wskaźniki tablicy

tab

mają wartość NULL.

Nie możemy bowiem założyć, że w reprezentacji wskaźnika

NULL występują same zera, a tak nie musi być.

Bezpiecznie zainicjowana dynamiczna tablica wskaźników:

int **tab = malloc(100* sizeof *tab);

int i = 0;

while (i<100) tab [i++] = NULL;

5

Definicje makra NULL

stddef.h, locale.h, stdio.h, stdlib.h, string.h, time.h

#define NULL 0

#define NULL 0L

#define NULL ((void *) 0)

6

Funkcja

realloc

void *realloc(void *wsk, size_t size);

Zmienia rozmiar przydzielonego wcześniej bloku pamięci

wskazywanego przez

wsk

na

size

bajtów.

Dodatkowy obszar pamięci nie jest inicjowany.

Funkcja zwraca wskaźnik na nowy przydzielonego bloku

pamięci. Może to być wartość inna niż

wsk

.

Jeśli żądamy zwiększenia rozmiaru, a za zaalokowanym

aktualnie obszarem nie ma wystarczająco dużo wolnego

miejsca, funkcja znajdzie nowe miejsce i przekopiuje tam

starą zawartość. Wywołanie tej funkcji może więc

kosztować dużo czasu.

Przykład:

tab = realloc (tab, 2*r*sizeof *tab);

Jeżeli

tab

było równa NULL, funkcja zachowuje się tak

samo jako

malloc

.

Jeśli działanie funkcji nie powiedzie się, zwracany jest

NULL i w

errno

jest kod błędu

7

Funkcja

free

void free (void* wsk);

Zwalnia blok pamięci wskazywany przez

wsk

przydzielony

przez

malloc

,

calloc

lub

realloc (

a także

strdup

z biblioteki

string.h)

.

Jeżeli

wsk

ma wartość NULL funkcja nie robi nic.

Uwaga 1

Należy pamiętać o zwalnianiu pamięci - inaczej dojdzie do

tzw. wycieku pamięci - program będzie rezerwował nową

pamięć, ale nie zwracał jej z powrotem i w końcu pamięci

może mu zabraknąć.

Uwaga 2

Po wywołaniu

free

wskaźnik nie zmienia wartości

(pamięta wskazywany adres). Ale nie należy już się do niej

odwoływać. Dla bezpieczeństwa warto po wywołaniu

funkcji

free

przypisać wskaźnikowi wartość NULL.

Uwaga 3

Nie należy dwa razy zwalniać tego samego miejsca.

8

Przykład: Odczyt liczb

int size = 64;

int num = 0;

float *tab, tmp;

tab = malloc(size * sizeof *tab);

if (tab!=NULL) {perror("malloc");return 1;}

while (scanf("%f", &tmp)==1)

{

if (num==size)

{ /* trzeba zwi

ę

kszy

ć

tablice*/

float *wsk = realloc (tab,

(size *= 2) * sizeof *wsk);

if (wsk!=NULL) {

free (tab);

perror("realloc"); return 1;

}

tab = wsk;

}

tab[num++] = tmp;

}

while (num) printf ("%f\n", tab[--num]);

/* Zwolnienie pamieci */

free (tab);

9

Dynamiczne tablice wielowymiarowe

Tablica dwuwymiarowa — tablica wskaźników do tablic

Przykład – tabliczka mnożenia

int n;
int i, j;
int** tab;

printf("Podaj rozmiar: ");
scanf("%i", &n);

tab = malloc (n * sizeof *tab);

for (i=0; i<n; ++i)
tab [i] = malloc(n* sizeof **tab);

for (i=0; i<n; ++i)
for (j=0; j<n; ++j)
tab[i][j] = (i+1)*(j+1);

. . .

for (i = 0; i<n; ++i) free(tab[i]);

free(tab);

10

Możemy

alokować

inne

tablice

niż

normalne,

"kwadratowe", np.

Tablica trójkątna:

0123456789

…

0123

012

01

0

int** tab = malloc(10*sizeof *tab);

for (i = 9; i>=0; ++i)

tab [i] = malloc (i*sizeof **tab);

...

for (i = 0; i<10; ++i) free(tab[i]);

free(tab);

11

Tablica o dowolnym rozkładzie długości wierszy

const int wymiary[10] =

{ 2, 4, 6, 8, 1, 3, 5, 7, 9 };

int i;

int **tab = malloc(10*sizeof *tab);

for (i = 0; i<10; ++i)

tab [i] =

malloc (wymiary[i] * sizeof **tab);

12

Na tablicach dynamicznych można wykonywać różne

operacje, np. zamiana wierszy miejscami:

Przykład: Zamiana wierszy miejscami
Tablica:

int** tab

0123456789
…
012
01
0

int i = 0
int j = 9;
int* temp;

while (i<j)
{
temp = tab [i];
tab [i] = tab [j];
tab [j] = tab [i];
i++; j--;
}

Tablica:

0
01
012
…
0123456789

13

Tablice wielowymiarowe

- analogicznie, zwiększa się tylko liczba poziomów,

Przykład:

Tablica trójwymiarowa

int X = 100, Y = 10, Z = 10;

int x, y;

int ***tab;

tab = (int***)malloc(X*sizeof(int**));

for (x = 0; x < X ; ++x)

{

tab[x]=(int**)malloc (Y * sizeof(int*));

for (y = 0; y < Y; ++y)

tab[x][y]=(int*) malloc(Z*sizeof(int));

}

/* u

ż

ycie - jak tablicy trójwymiarowej */

tab[5][6][1] = 1;

int b = tab [5][6][1];

/* czyszczenie pami

ę

ci: */

for (x = 0; x < X; ++x)

{

for(y = 0; y < Y; ++y) free(tab[x][y]);

free(tab [x]);

}

free(tab);

14

Inne funkcje związane z pamięcią

Funkcja

memset,

plik

string.h

void* memset(void* tab, int c,size_t n);

Funkcja wypełnia kolejne

n

bajtów pamięci o adresie

tab

ustaloną wartością

c

. Zwraca wskaźnik na

tab

. Zasadniczo

stosowana dla napisów.

Przykład 1

#include <string.h>

int main()
{
char napis[10] ;
memset(napis, 'a', 5);
memset(napis+5, '-', 1);
memset(napis+6, 'b', 5);

puts(napis);
return 0;
}

Wynik działania:

aaaaa-bbbb

15

Przykład 2:

Nie możemy stosować tej funkcji dla tablicy liczb, chyba, że
chcemy ta tablicę wyzerować.

#include <stdio.h>
#include <string.h>

int main()
{
int i;
int t[5] ;

memset( t, 2 ,5*sizeof(int) );
for (i=0;i<5;i++) printf(“%d ”,t[i]);
printf(“\n”);

memset( t, 0 ,5*sizeof(int) );
for (i=0;i<5;i++) printf(“%d ”,t[i]);
printf(“\n”);

return 0;
}

Wynik działania:

33686018 33686018 33686018 33686018 33686018

0 0 0 0 0

16

Funkcja

memcpy,

plik

string.h

void *memcpy
(void* to, const void* from, size_t s);

Funkcja kopiuje

s

bajtów z pamięci o adresie

from

do

pamięci o adresie

to

. Zwraca wskaźnik do

to

Uwaga: Pod adresem to powinno być zaalokowane
dostatecznie dużo pamięci, co najmniej s bajtów.

Przykład

int t1[] = {1,2,3,4,5,6,7,8,9,10};

int* t2 = malloc(10 * sizeof(int));

memcpy ( t2, t1, 10*sizeof(int) );

for (i=0;i<10;i++) printf("%d ", t2[i]);

printf("\n");

Wynik:

1 2 3 4 5 6 7 8 9 10

17

Funkcja

memmove,

plik

string.h

void *memmove
(void* to, const void* from, size_t s);

Funkcja kopiuje

s

bajtów z pamięci o adresie

from

do

pamięci o adresie

to

. Zwraca wskaźnik do

to.

Różni się

od

memcpy

tym, że obszar odpowiadające adresom

from

oraz

to

mogą się częściowo pokrywać

.

Przykład

int t[] = {1,2,3,4,5,6,7,8,9,10};

memcpy ( t+4, t, 6*sizeof(int) );

Wynik:

1 2 3 4 1 2 3 4 1 2

memmove ( t+4, t, 6*sizeof(int) );

Wynik:

1 2 3 4 1 2 3 4 5 6

18

Pamięć

Dwa rodzaje pamięci: stos i sterta.

Stos (ang. stack)

1. Przechowuje zmienne programu:

•

rezerwacja pamięci dokonywana jest, gdy program

wchodzi

do

bloku,

w

którym

zmienne

są

zadeklarowane, a

•

zwalnianie pamięci dokonywane jest, kiedy program

opuszcza blok

•

dla zmiennych globalnych w momencie uruchomienia i

zakończenia programu.

2. Przechowuje informacje o wywoływanych funkcjach

(parametry, zmienne, wartość zwracana)

Każde wywołanie rekurencyjne funkcji wymaga pamiętania

na stosie:

•

Adresu powrotu,

•

parametry przekazane do funkcji

•

wartości zmiennych lokalnych

19

Przykład

int f(int n)
{
int b = 1;
if (n==1) return 1;
b = f(n-1)*n; /* adres 2 */
return b;
}

int main()
{
int n =4;
int a = f(n); /* adres 1 */
}

b=1

1

Wywołanie

f(1)

adres 2

Adres powrotu do funkcji f

b=1

2

Wywołanie

f(2)

adres 2

Adres powrotu do funkcji f

b=1

3

Wywołanie

f(3)

adres 2

Adres powrotu do funkcji f

b=1

4

Parametr dla funkcji f, Wywołanie

f(4)

adres 1

Adres powrotu do funkcji

main

a

n=4

Stos dla wywołań funkcji f

20

Rozmiar stosu

Zależy od kompilatora i systemu.

Pod linuxem można to sprawdzić (albo ustawić) za

pomocą:

ulimit –s

ulimit –s 65536

Błąd

przepełnienia stosu ( ang

.

stack overflow ).

Występuje zwykle wtedy, gdy pamięć stosu jest pełna a

chcemy zaalokować nowy obszar, np.

•

próba alokacji dużej tablicy statycznej

•

nastąpiło zbyt wiele wywołań funkcji (na ogół zbyt

głęboka

rekursja

lub

nieskończone

wywołania

rekurencyjne).

21

Sterta (ang. heap)

Obszar pamięci udostępniany przez system operacyjny

wykonującym się procesom.

Przechowywane są w nim zmienne „dynamiczne”, ich czas

ż

ycia nie jest związany z poszczególnymi blokami.

Programista sam rezerwuje dla nich miejsce i to miejsce

zwalnia.

Uwaga:

Rezerwowanie i zwalnianie pamięci na stercie zajmuje

więcej czasu niż analogiczne działania na stosie.

Sterta utrzymuje specjalną strukturę, w której trzymane są

wolne partie (może to być np. lista).

22

Błąd przepełnienia sterty

(ang. heap overflow)

Pojawia się przy próbie alokacji zmiennej dynamicznej, dla

której na stercie nie ma już miejsca (najczęściej z powodu

wycieku pamięci albo nieoptymalnego wykorzystania

pamięci przez program)

Wyciek pamięci

(ang. memory leak)

Pojawia się najczęściej, gdy program nie zwalnia

przydzielonej pamięci, przestaje o niej „pamiętać” i

rezerwuje nową.

Program z wyciekiem pamięci zajmuje coraz więcej

pamięci, ale nie jest w stanie jej wykorzystać ani zwolnić.

Przykład 1

int cos1()

{

int* wsk = malloc( sizeof int );

*wsk = 20;

return *wsk; //zamiast return wsk;

}

23

Przykład 2

void cos2 (struct osoba* os1)

{

struct osoba* os2 =

malloc(sizeof (struct osoba));

os2 = os1;

/* albo: os2 = NULL; */

return;

}

Przykład 3

int* cos3(int *a, int n)

{

int *b = malloc ( 10* sizeof int);

for (i=0; i<n; i++) b[i]=a[i]*a[i];

return b;

}

int *a = malloc(10*sizeof(int));

a = cos3(a, 10)

24

Popularne błędy

1.

Próba wykonania operacji na wskaźniku NULL.

2.

Brak sprawdzania, czy dany wskaźnik nie ma wartości

NULL.

3.

Odwołania się do obszaru pamięci po jego zwolnieniu. Po

wykonaniu funkcji

free

nie możemy już wykonywać

ż

adnych odwołań do zwolnionego obszaru. Warto wpisać

tam NULL.

4.

Odwołania do adresów pamięci, które są poza

przydzielonym obszarem

.

5.

Wyciek pamięci, czyli nie zwalnianie całej, przydzielonej

wcześniej pamięci

25

Przykłady struktur dynamicznych

Zbiór osób:

typedef struct {
char *imie;
char *nazwisko;
int wiek, zarobki;
} osoba;

int size = 5000;
osoba *tab;

tab =malloc(size * sizeof *tab);

w razie potrzeby:

wsk = realloc(tab,
(size *= 2) * sizeof *tab);

Problemy:

1. Zwiększanie rozmiaru jest czasochłonne – może

wymagać kopiowania…

2. Jak usuwać osoby ze środka tablicy?

3. Jak dodawać osoby do środka tablicy posortowanej?

26

Lista -

Abstrakcyjna struktura danych, w której

elementy uporządkowane są w sposób liniowy oraz na

której mogą być wykonywane różne operacje, tj. dodawanie

elementów w dowolne miejsce listy, usuwanie z dowolnego

miejsca, wyszukiwanie, itp.

Typowe operacje wykonywane na liście:

dodaj (element, gdzie, lista) - wstawia element na odpowiednia

pozycję w liście

usun (pozycja, lista) - kasuje element z określonej pozycji.

szukaj (element, lista) - znajduje element w liście i zwraca jego

pozycję

pierwszy (lista) - zwraca pozycję pierwszego elementu na

liście

ostatni (lista) - zwraca pozycję za ostatnim elementem w liście

poprzedni (pozycja, lista) - zwraca pozycję elementu

poprzedniego

nastepny (pozycja, lista) - zwraca pozycję elementu

następnego

czysc (lista) - czyści listę

27

Implementacje:

1.

Przykładem listy jest zwykła tablica. Porządek elementów

wyznaczają wówczas indeksy.

2.

Wskaźnikowa pojedynczo wiązana (jednokierunkowa)

3.

Wskaźnikowa podwójnie wiązana (dwukierunkowa)

4.

Kursorowa

Lista wskaźnikowa jednokierunkowa

Struktura składająca się ze struktur, w której porządek

wyznaczają

wskaźniki(adresy)

związane

z

każdym

elementem listy, inaczej mówiąc każdy element listy „zna”

adres swojego następnika.

Po liście możemy poruszać się w kierunku od pierwszego

do ostatniego.

Na takiej liście można „łatwo” dodawać/usuwać elementy.

Lista jest wskaźnikiem na swój pierwszy element.

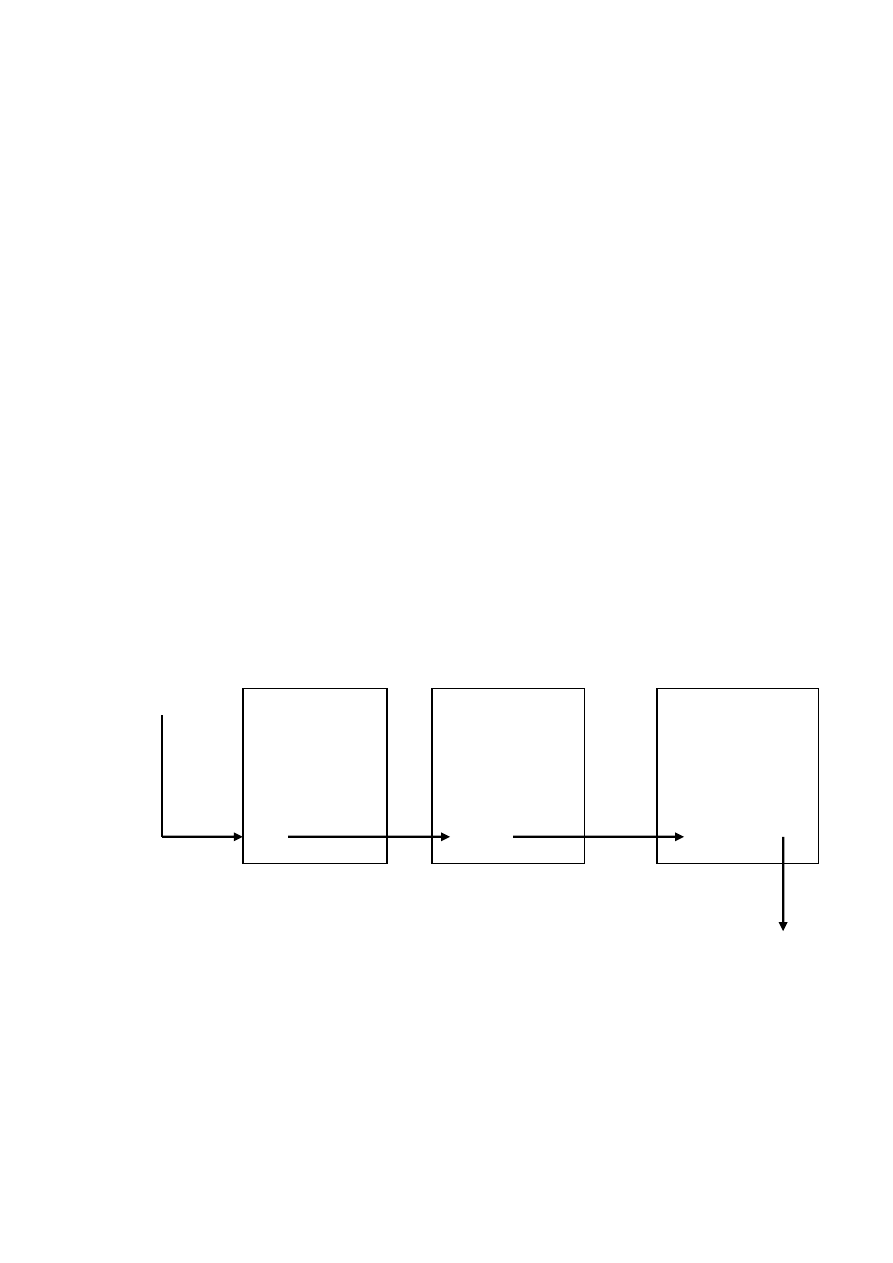
28

Struktury odwołujące się do samych siebie

typedef struct os

{

char *imie;

char *nazwisko;

int wiek, zarobki;

struct os *nast;

} osoba;

osoba *lista;

Inicjowanie listy pustej

osoba *lista = NULL;

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista

NULL

29

Tworzenie listy:

osoba *lista = malloc(sizeof osoba);

lista->imie = ”Ala”;
/* równowa

ż

nie (*lista).imie = ”Ala” */

lista->nazwisko = ”Kowalska”;
lista->wiek = 30;
lista->pensja = 3000;

osoba *temp = malloc(sizeof osoba);

temp->imie = ”Józek”;
temp->nazwisko = ”Malinowski”;
temp->wiek = 35;
temp->pensja = 3000;

lista->nast = temp;

temp = malloc(sizeof osoba);

temp->imie = ”Genowefa”;
temp->nazwisko = ”Wisniewska”;
temp->wiek = 50;
temp->pensja = 3500;
temp->nast = NULL;

lista->nast->nast = temp;

30

Przeglądanie listy:

/* ustawiamy si

ę

na pocz

ą

tku listy */

osoba *p = lista;

while (p != NULL)

{

/*jaka

ś

operacja na elemencie listy*/

visit(p)

/* przej

ś

cie do kolejnego elementu */

p = p->nast;

}

/* teraz p == NULL */

31

Wyszukiwanie elementu na liście

– wersja iteracyjna

osoba *szukaj(osoba *lista, int wiek)

{

osoba *p = lista;

while ((p != NULL) && (p->wiek !=wiek))

p = p->nast;

return p;

}

Jeśli

p == NULL

elementu szukanego nie ma,

Jeśli

p!=NULL

to wskazuje na szukany element.

Wyszukiwanie elementu na liście

– wersja rekurencyjna

osoba *szukaj(osoba *lista, int wiek)

{

if (lista == NULL) return NULL;

if (lista->wiek == wiek) return lista;

return szukaj(lista->nast, wiek );

}

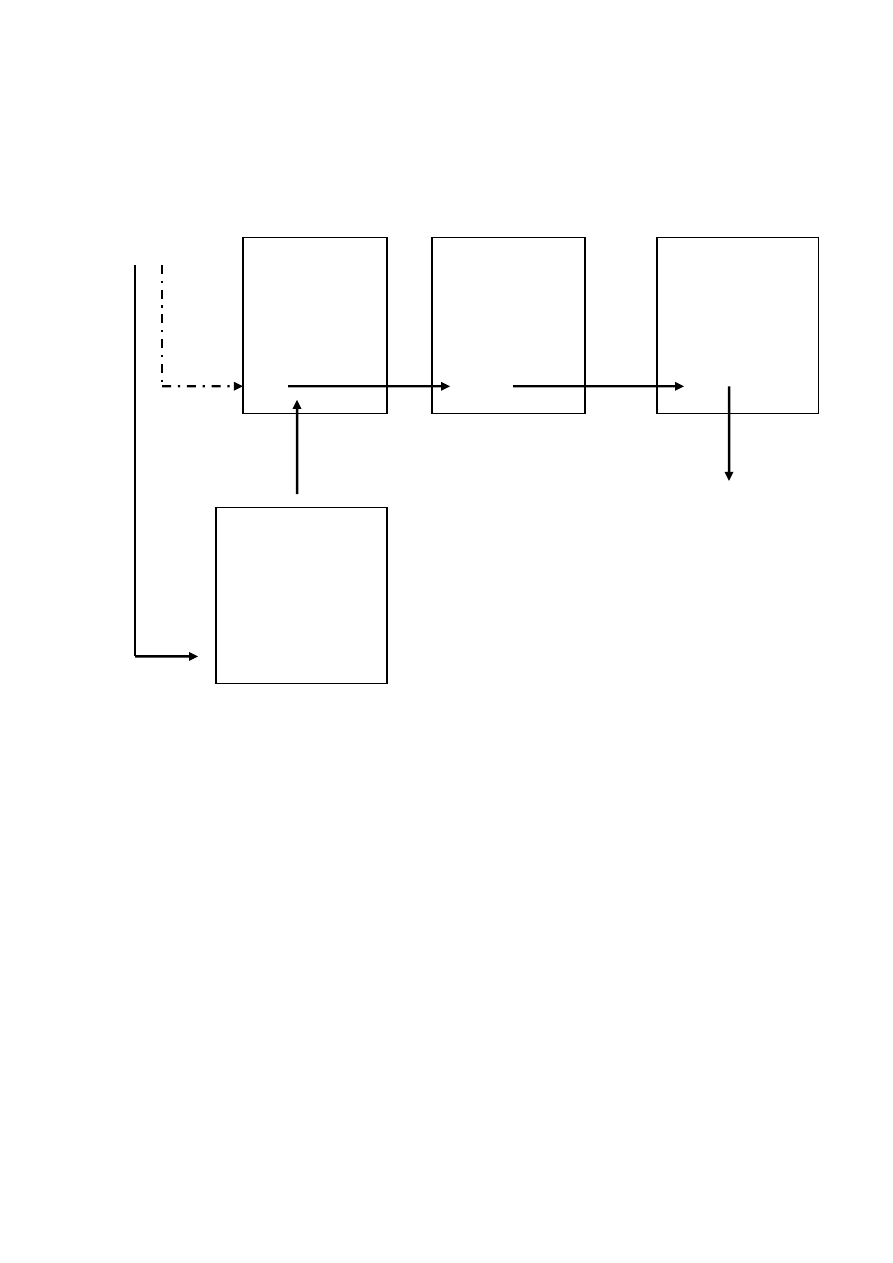
32

Dodawanie elementu na początek listy:

void dodaj_p (osoba **lista, char *imie,
char *nazwisko, int wiek, int pensja)
{
osoba *temp = malloc(sizeof osoba);
temp->imie = strdup(imie);
temp->nazwisko = strdup(nazwisko);
temp->wiek = wiek;
temp->pensja = pensja;
temp->nast = *lista;

*lista = temp;
}

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista

NULL

Marek
Nowakowski
45
3200

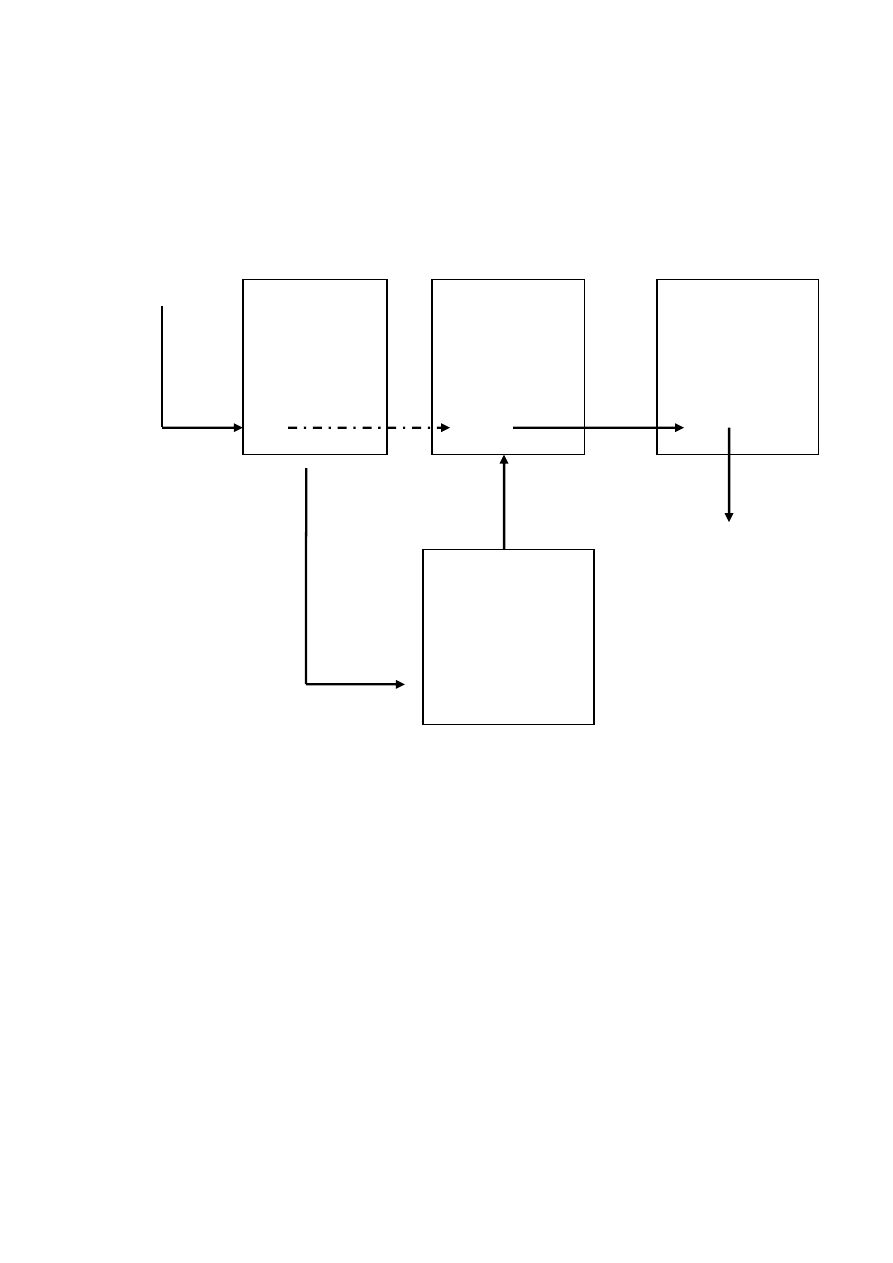
33

Dodawanie elementu w środek listy:

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista

NULL

Marek
Nowakowski
45
3200

34

void dodaj (osoba *poprzednik,

char *imie, char *nazwisko,

int wiek, int pensja)

/* dodaj nowy element za struktur

ą

wskazywan

ą

przez poprzednik */

{

osoba *temp = malloc(sizeof osoba);

temp->imie = strdup(imie);

temp->nazwisko = strdup(nazwisko);

temp->wiek = wiek;

temp->pensja = pensja;

temp->nast = poprzednik->nast;

poprzednik->nast = temp;

}

Uwaga:

Kolejność instrukcji jest istotna. Poniższy fragment jest

błędny:

poprzednik->nast = temp;

temp->nast = poprzednik->nast;

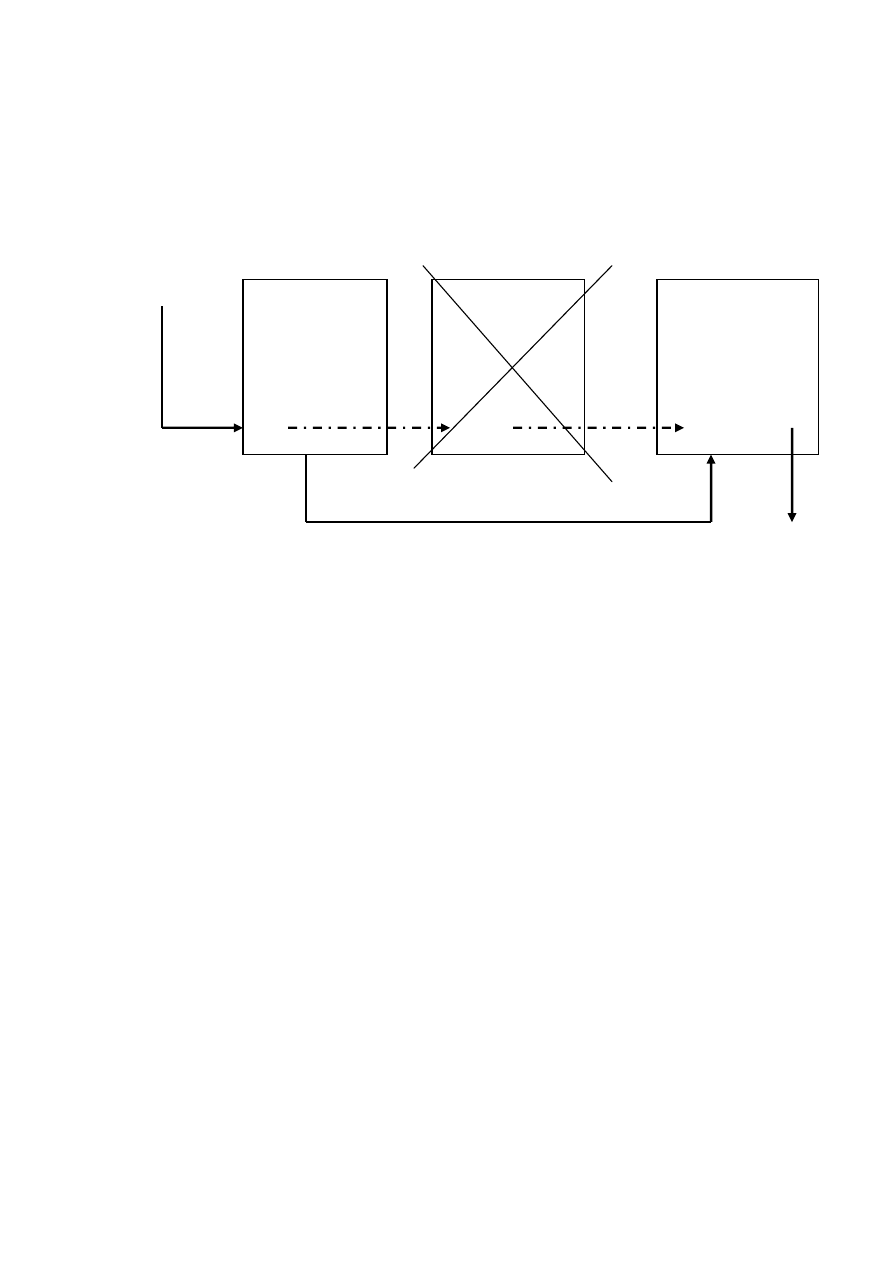
35

Usuwanie elementy ze środka listy:

void usun (osoba *poprzednik)

{

/* usu

ń

element za struktur

ą

wskazywan

ą

przez poprzednik */

poprzednik->nast=poprzednik->nast->nast;

}

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista

NULL

36

Funkcja

usun

jest niepoprawna, powoduje wyciek pamięci.

void usun2 (osoba *poprzednik)

{

/* usun element za struktur

ą

wskazywan

ą

przez poprzednik */

osoba *temp = poprzednik->nast;

poprzednik->nast = temp->nast;

free(temp);

}

Nadal jest wyciek pamięci…

void usun3 (osoba *poprzednik)

{

/* usun element za struktur

ą

wskazywan

ą

przez poprzednik */

osoba *temp = poprzednik->nast;

poprzednik->nast = temp->nast;

free(temp->imie);

free(temp->nazwisko);

free(temp);

}

Jak usunąć element, jeśli nie znamy jego poprzednika?

Należy go najpierw wyszukać – przebiec całą listę…

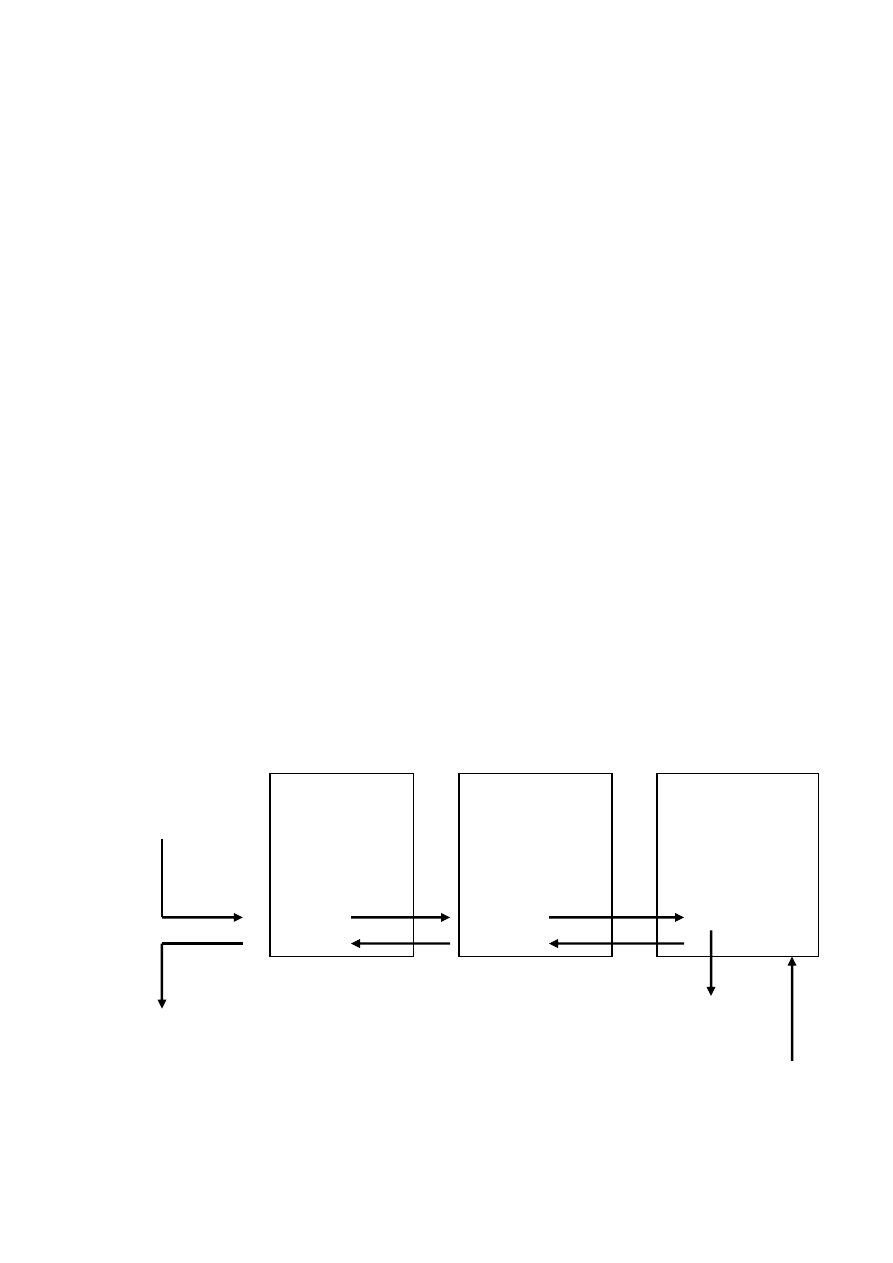
37

Lista wskaźnikowa dwukierunkowa

Lista wskaźnikowa, w której jest możliwość poruszania się

w obu kierunkach. Oznacza to, że każdy element listy

posiada wskaźnik do swojego poprzednika i wskaźnik do

swojego następnika.

typedef struct os

{

char *imie;

char *nazwisko;

int wiek, zarobki;

struct os *nast;

struct os *poprz;

} osoba;

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista.
first

NULL

NULL

lista.
last

38

Lista jest pamiętana jako 2 wskaźniki:

adres elementu pierwszego i adres elementu ostatniego

Lista jest strukturą.

typedef struct

{

first *osoba

last *osoba

} Tlista;

Tlista lista;

Inicjowanie listy pustej

lista.first = NULL;

lista.last = NULL;

39

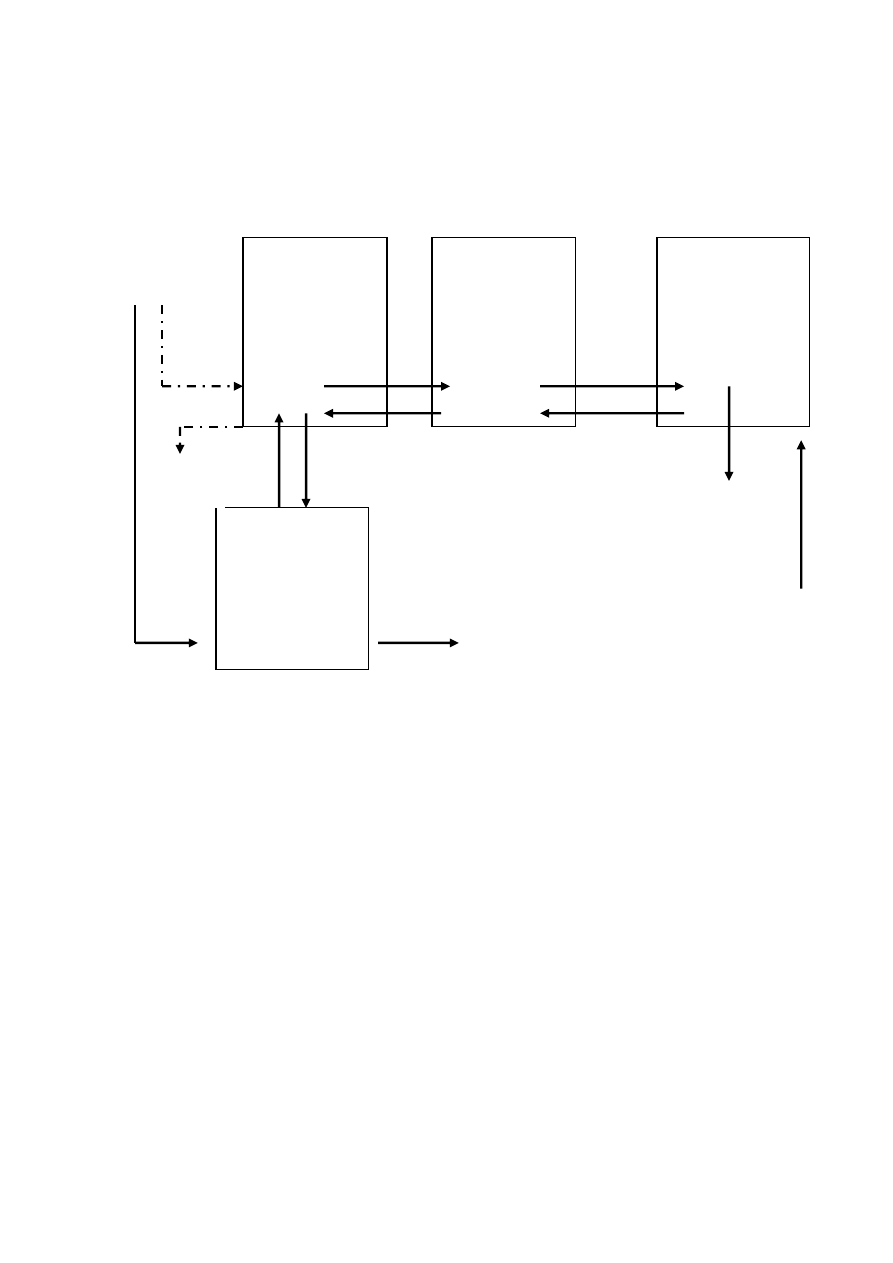
Dodawanie elementu na początek listy:

void dodaj_p (Tlista *lista, char *imie,
char *nazwisko, int wiek, int pensja)
{
osoba* temp = malloc(sizeof osoba);
temp->nazwisko = strdup(nazwisko);
temp->imie = strdup(imie);
temp->wiek = wiek;
temp->pensja = pensja;

temp->nast = lista->first;
temp->poprz = NULL;
lista->first = temp;
}

Ala
Kowalska
30
3000

Józek
Malinows
ki
35
3000

Genowefa
Wiśniewsk
a
50
3500

lista.
first

NULL

Marek
Nowakows
ki
45
3200

lista.
last

NULL

NULL

40

Poprawiona funkcja

dodaj

:

void dodaj_p (Tlista *lista, char *imie,

char *nazwisko, int wiek, int pensja)

{

osoba *temp = malloc(sizeof osoba);

temp->nazwisko = strdup(nazwisko);

temp->imie = strdup(imie);

temp->wiek = wiek;

temp->pensja = pensja;

temp->nast = lista->first;

temp->poprz = NULL;

if (lista->first != NULL)

lista->first->poprz = temp;

else lista->last = temp;

lista->first = temp;

}

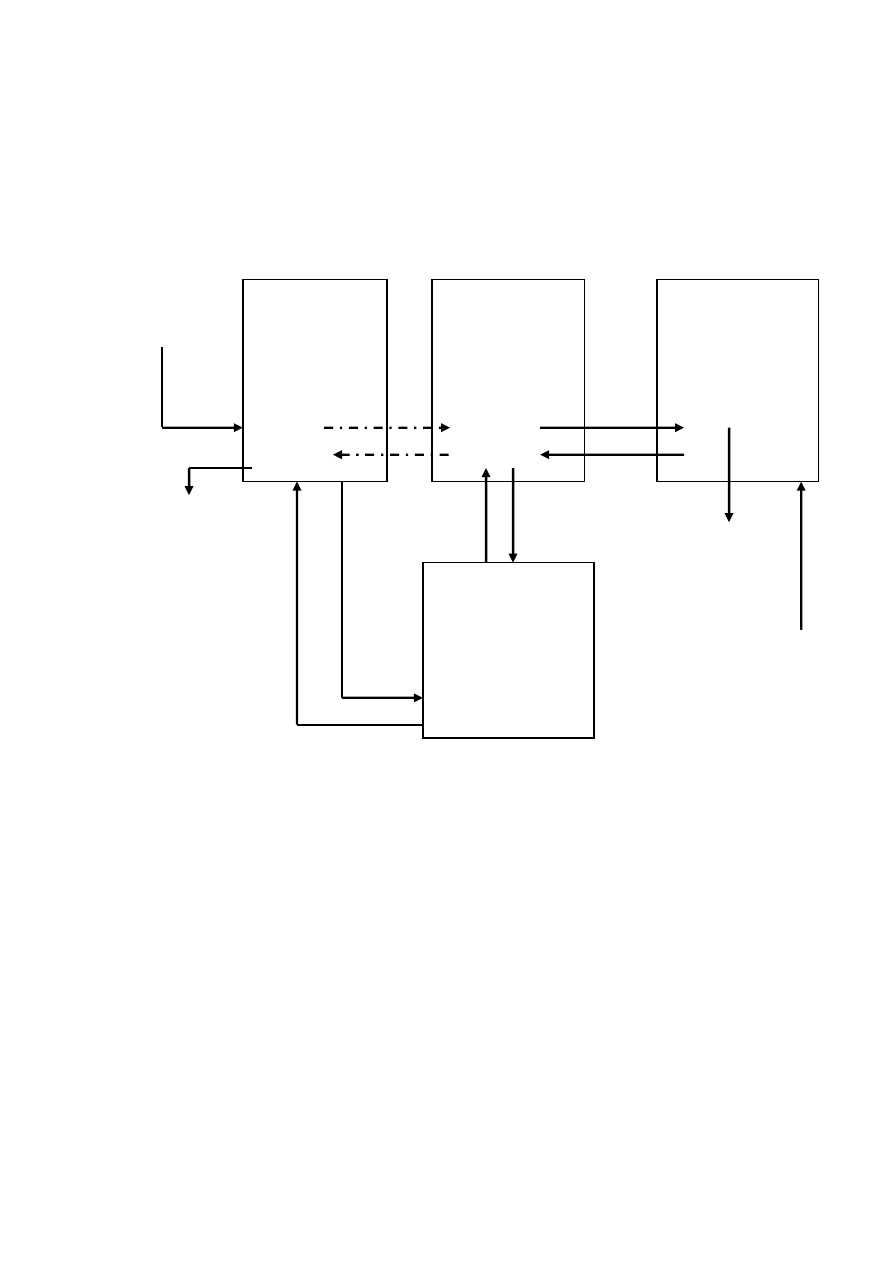
41

Dodawanie elementu w środek listy:

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista.
first

NULL

Marek
Nowakowski
45
3200

lista.
last

NULL

42

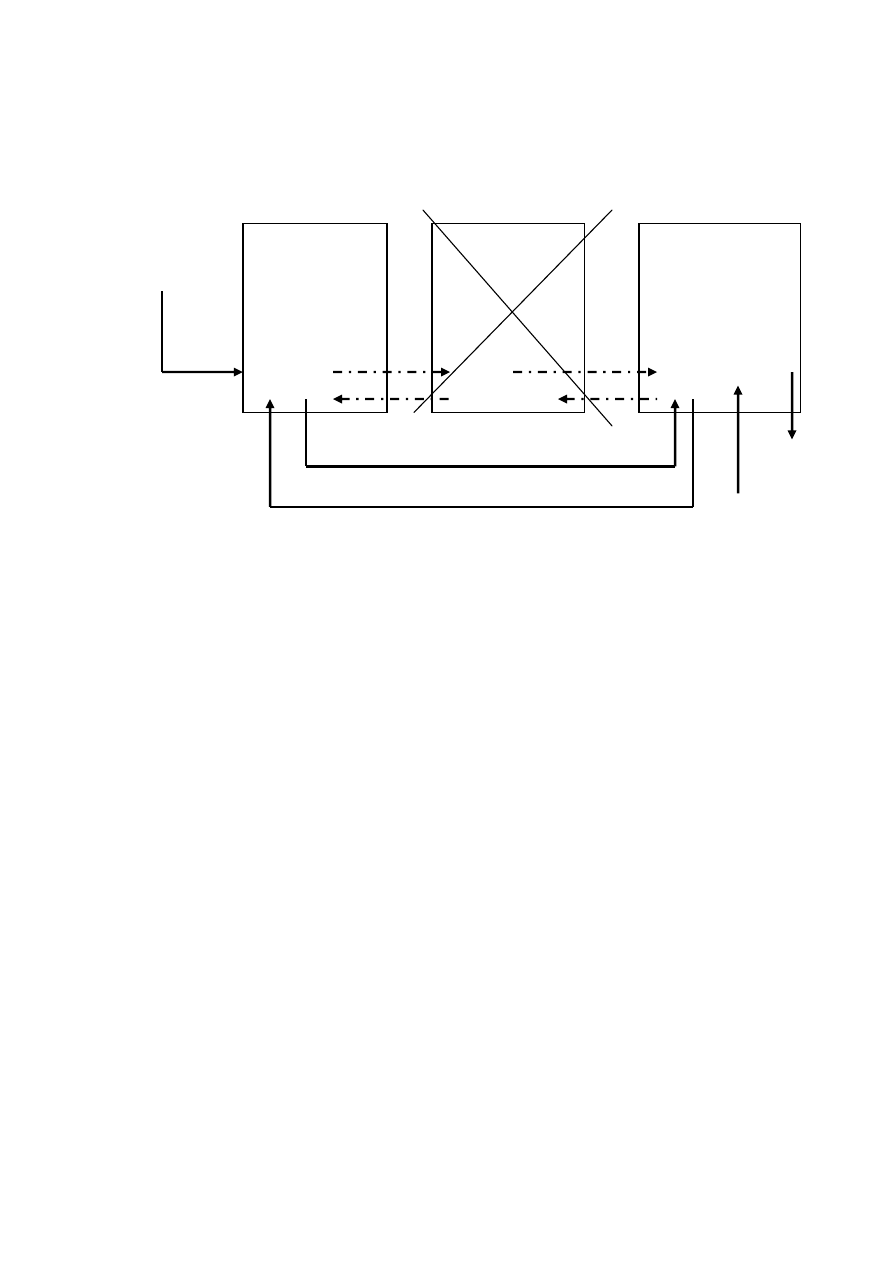
Usuwanie elementy ze środka listy:

void usun (Tlista *lista, osoba *wsk)

/* usun element wskazywany przez wsk */

{

osoba *temp = wsk->poprz;

if (temp!=NULL) temp->nast=wsk->nast;

else lista->first = wsk->nast;

temp = wsk->nast;

if (temp!=NULL) temp->poprz=wsk->poprz;

else lista->last = wsk->poprz;

free(temp->imie);

free(temp->nazwisko);

free(temp);

}

lista
.last

Ala
Kowalska
30
3000

Józek
Malinowski
35
3000

Genowefa
Wiśniewska
50
3500

lista.
first

NULL

wsk

43

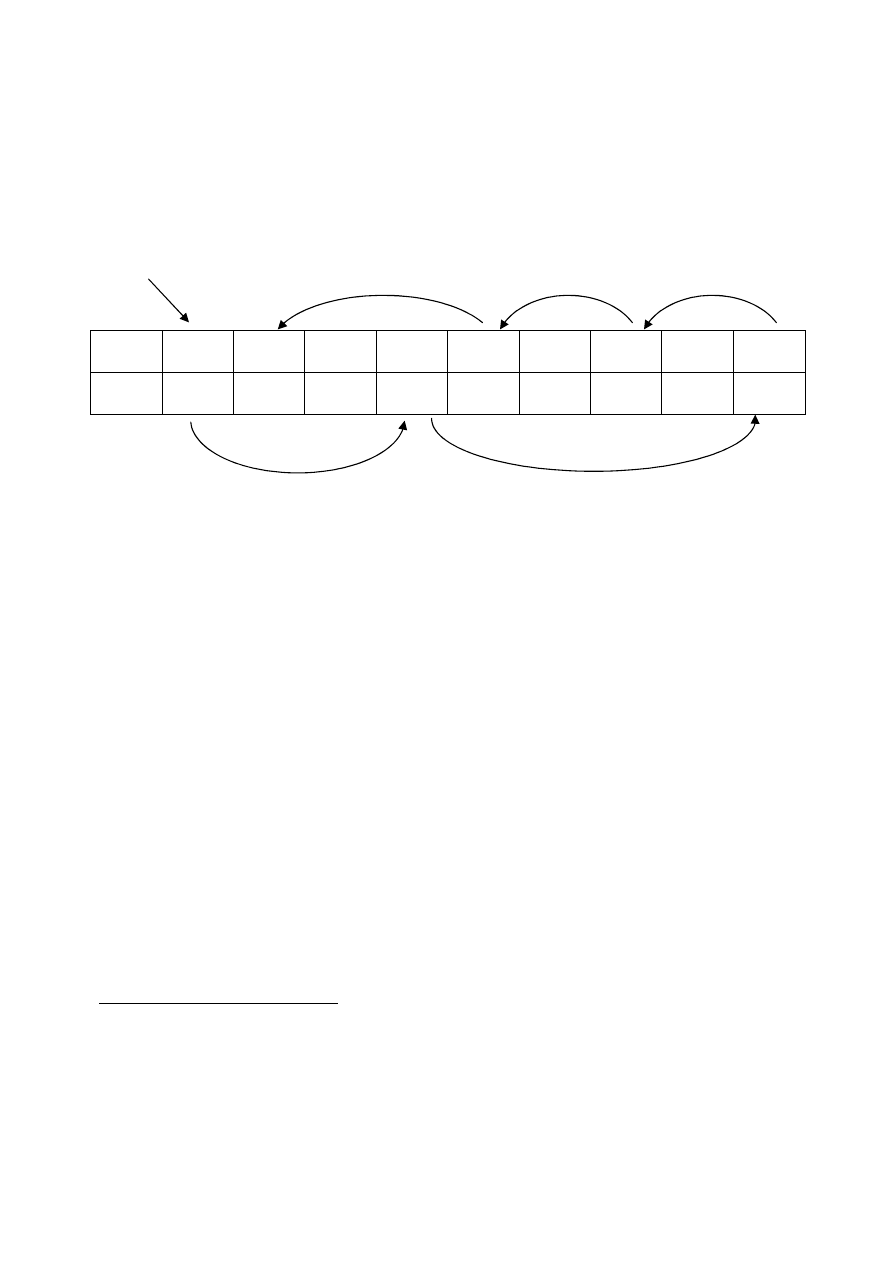
Lista kursorowa –

symulacja wskaźników w tablicy

lista

4

-1

9

2

5

7

struct

{

char* nazwisko;

int wiek

int next;

} tab[100];

int lista; //indeks komórki

pierwszego elementu listy

Lista jest indeksem.

Ostatni element listy ma „wskaźnik”/kursor

next

ustawiony na

-1

.

44

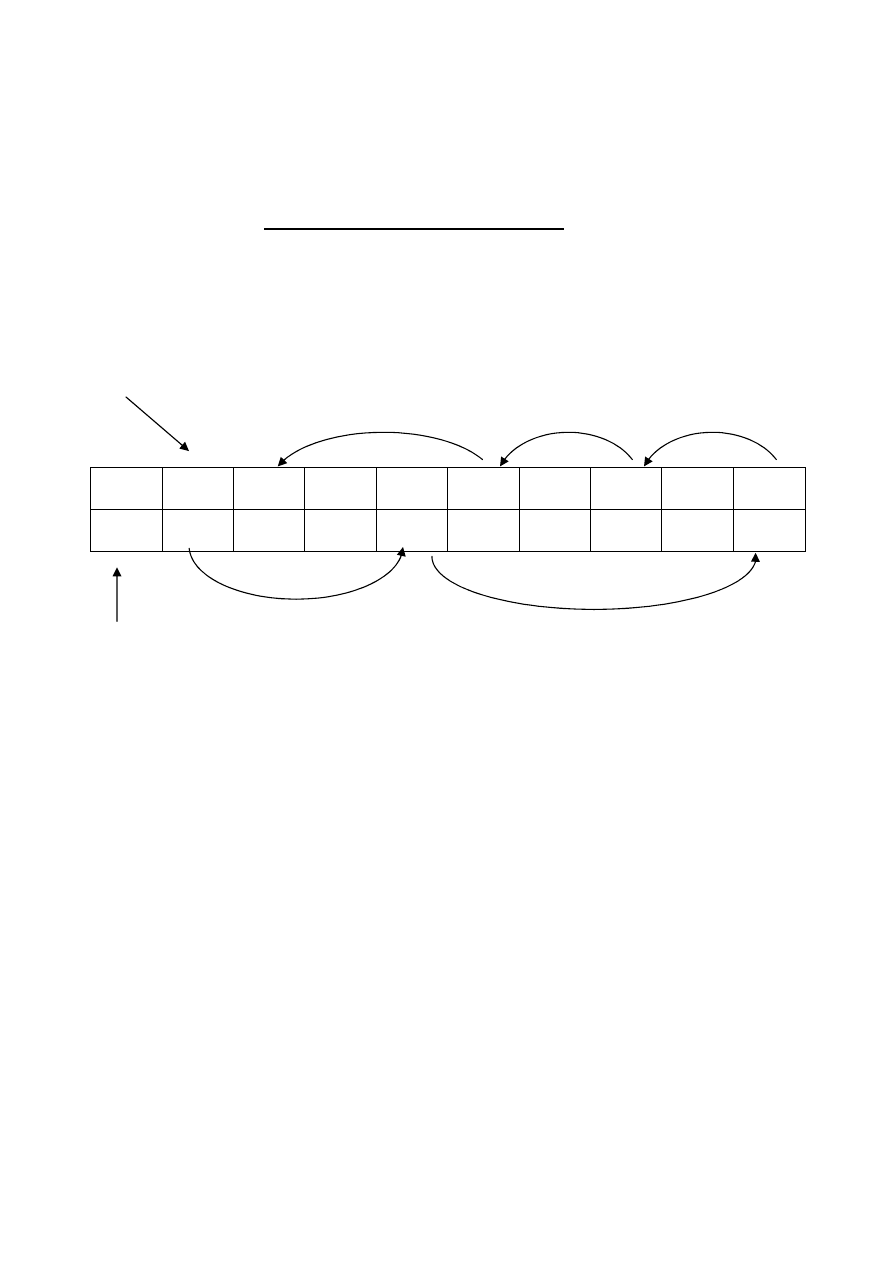
Lista elementów wolnych

Wszystkie wolne komórki tablicy – nienależące do listy są

powiązane w listę elementów wolnych.

int wolne; //indeks wolnej komórki

lista = 1

3

4

-1

6

9

2

8

5

-1

7

wolne = 0

Przygotowanie

Inicjalizacja_tablicy (),

Funkcja wiąże wszystkie elementy w listę elementów
wolnych oraz ustawia zmienną

wolne

na 0.

Funkcję należy wykonać na początku działania programu.

Inicjalizacja listy

lista = -1;

45

Operacje

Algorytmy operacji są analogiczne jak te dla list

wskaźnikowych, tyle, że

•

zamiast pracować na wskaźnikach operujemy na

indeksach (kursorach)

•

wskaźnik pusty (NULL) identyfikowany jest przez -1

•

podczas dodawania do listy nowego elementu –

usuwamy pierwszy element z listy elementów wolnych,

o ile to możliwe. W przeciwnym przypadku dodawania

nie można wykonać.

•

podczas usuwania elementu z listy – dodajemy usunięty

element do na początek listy elementów wolnych

W jednej tablicy można przechowywać jednocześnie wiele

różnych list kursorowych.

46

Przykład 1: Wyszukiwanie

int szukaj(int lista, int wiek)

{

int p = lista;

while ((p != -1) && (p.wiek !=wiek))

p = p.nast;

return p;

}

Jeśli

p == -1

elementu szukanego nie ma, w przeciwnym

razie

p>-1 i

wskazuje na szukany element.

Przykład 2: Dodawanie na początek

int dodaj_p (int lista, char *nazwisko,

int wiek){

if (wolne == -1) return 0;

temp = wolne;
wolne = tab[wolne].next;

tab[temp].nazwisko = strdup(nazwisko);
tab[temp].wiek = wiek;
tab[temp].nast = lista;
lista = temp;
}

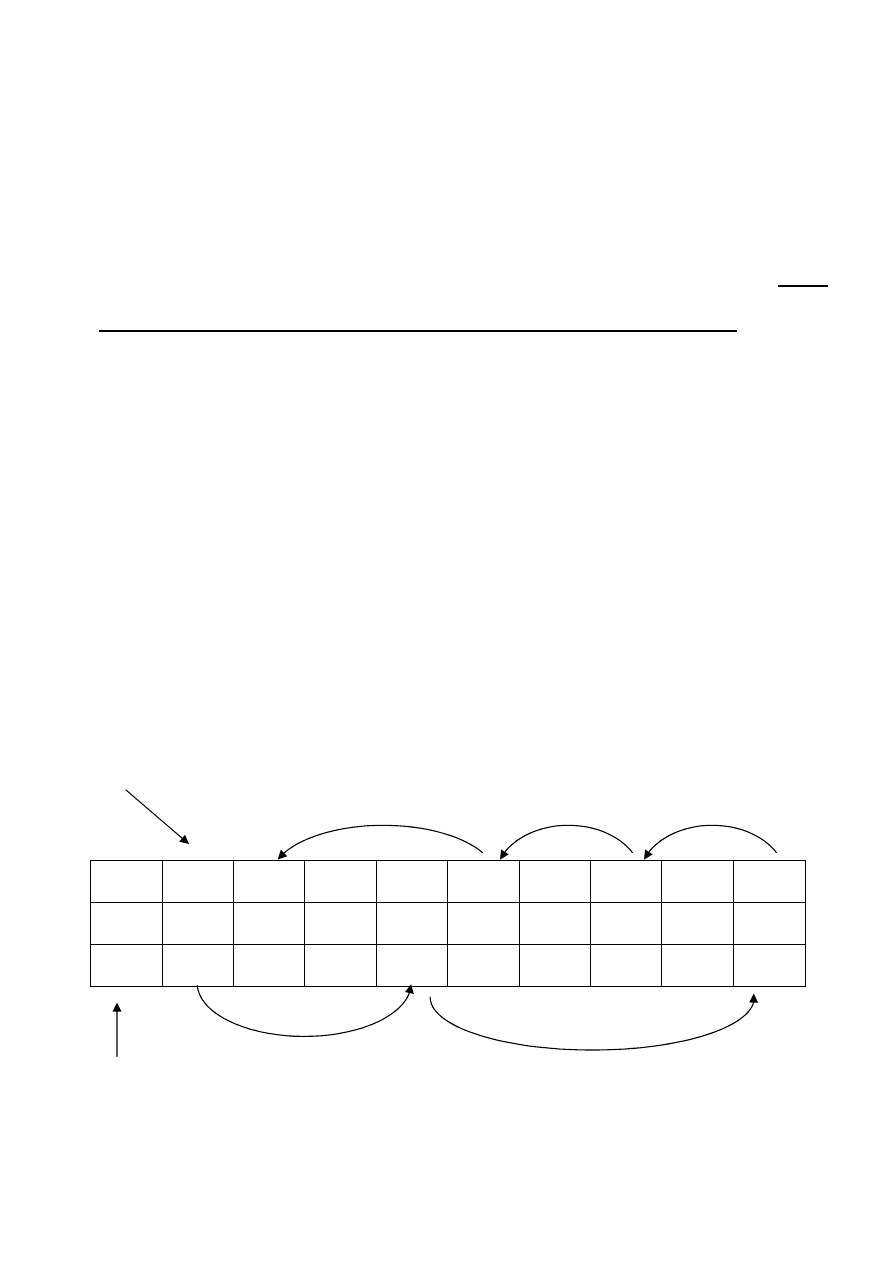
47

Lista kursorowa dwukierunkowa

Analogiczna do listy wskaźnikowej dwukierunkowej.

Każda komórka tablicy przechowuje dodatkowo dwa

indeksy – indeks poprzednika oraz indeks następnika.

struct

{

char* nazwisko;

int wiek

int next;

int prev;

} tab[100];

lista = 1

3

4

-1

6

9

2

8

5

-1

7

-1

5

1

7

9

4

wolne = 0

48

Przygotowanie

Inicjalizacja_tablicy ()

Przygotowanie jest takie samo jak w przypadku listy

kursorowej jednokierunkowej.

Funkcja wiąże wszystkie elementy w listę elementów

wolnych oraz ustawia zmienną

wolne

na 0.

Lista elementów wolnych może być listą jednokierunkową:

dodawanie do niej i usuwanie zawsze odbywa się dla

pierwszego elementu.

Definicja listy

typedef struct

{

int first;

int last;

} Tlista;

Tlista lista;

Inicjalizacja listy:

lista.first = -1;
lista.last = -1;

49

Drzewo

Struktura danych, w której na elementy narzucona jest

pewna drzewiasta struktura, na której wykonywane są

operacje:

•

dodawania,

•

usuwania,

•

przeszukiwania,

•

czasem łączenie

Drzewa nieukorzenione

Drzewa ukorzenione

Drzewa wielodzietne (wieloarne)

Drzewa binarne

Implementacja wskaźnikowa

Implementacja kursorowa

Implementacja „left-child, right-sibling”

50

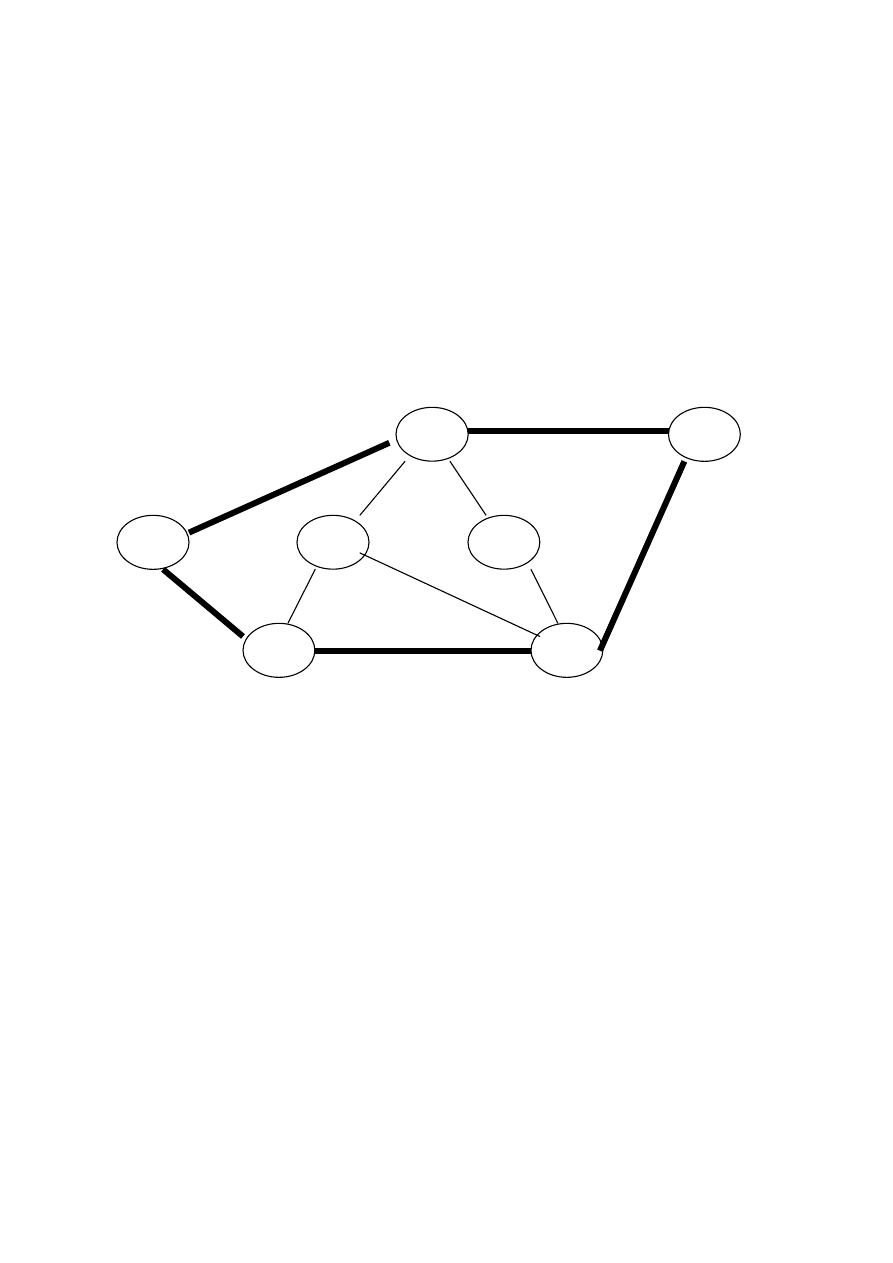
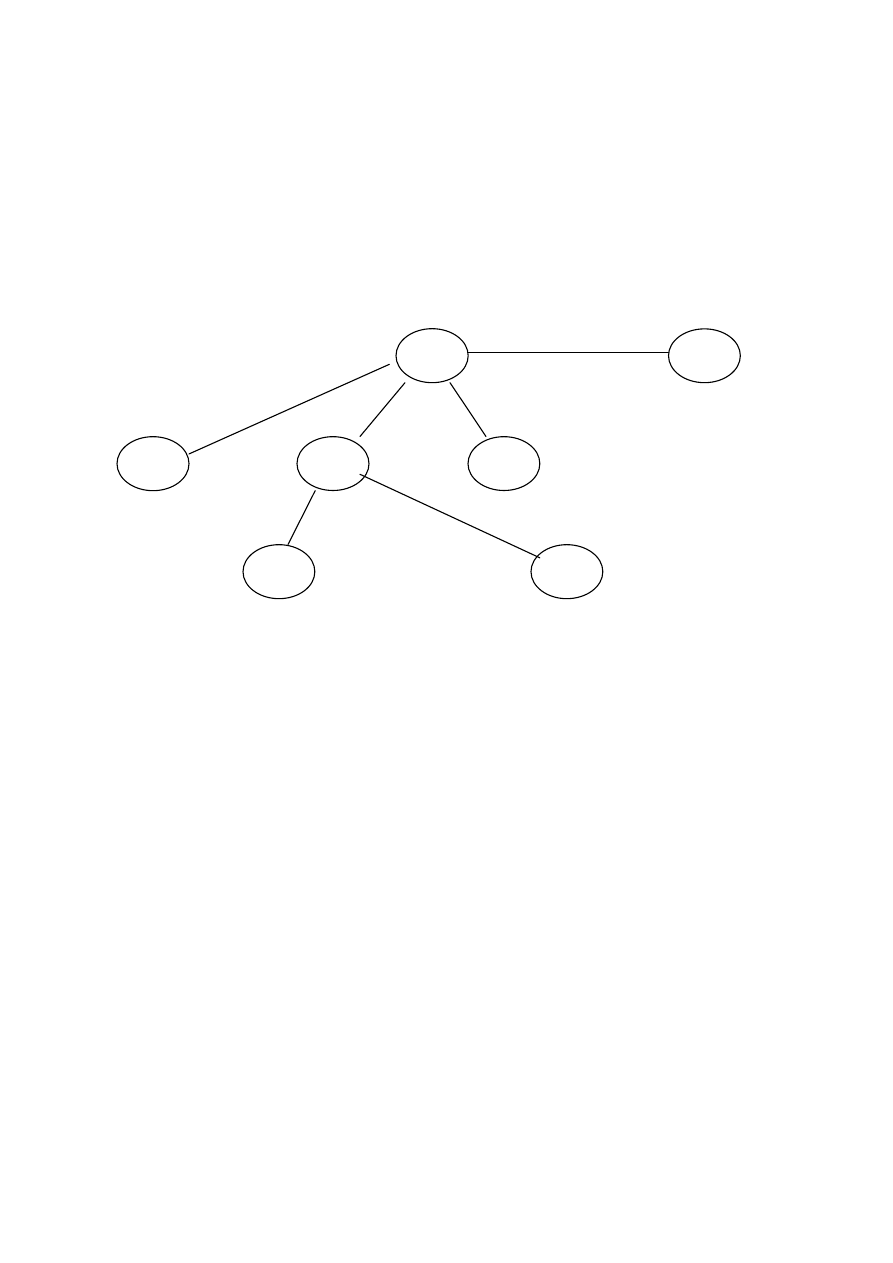
Graf

– struktura danych, składająca się ze zbioru

wierzchołków V i zbioru krawędzi E, czyli połączeń między

wierzchołkami.

Jeśli krawędzie mają określony kierunek graf nazywamy

skierowanym, w przeciwnym wypadku mówimy że jest ona

nieskierowany

Ś

cieżka - czyli ciąg wierzchołków, między którym

przechodzimy za pomocą krawędzi, np. abzx

Cykl –ścieżka, której pierwszy wierzchołek jest zarazem

wierzchołkiem ostatnim, np. abcxd

Graf spójny – graf, w którym między każdymi dwom

wierzchołkami istnieje ścieżka.

x

z

a

b

c

y

d

51

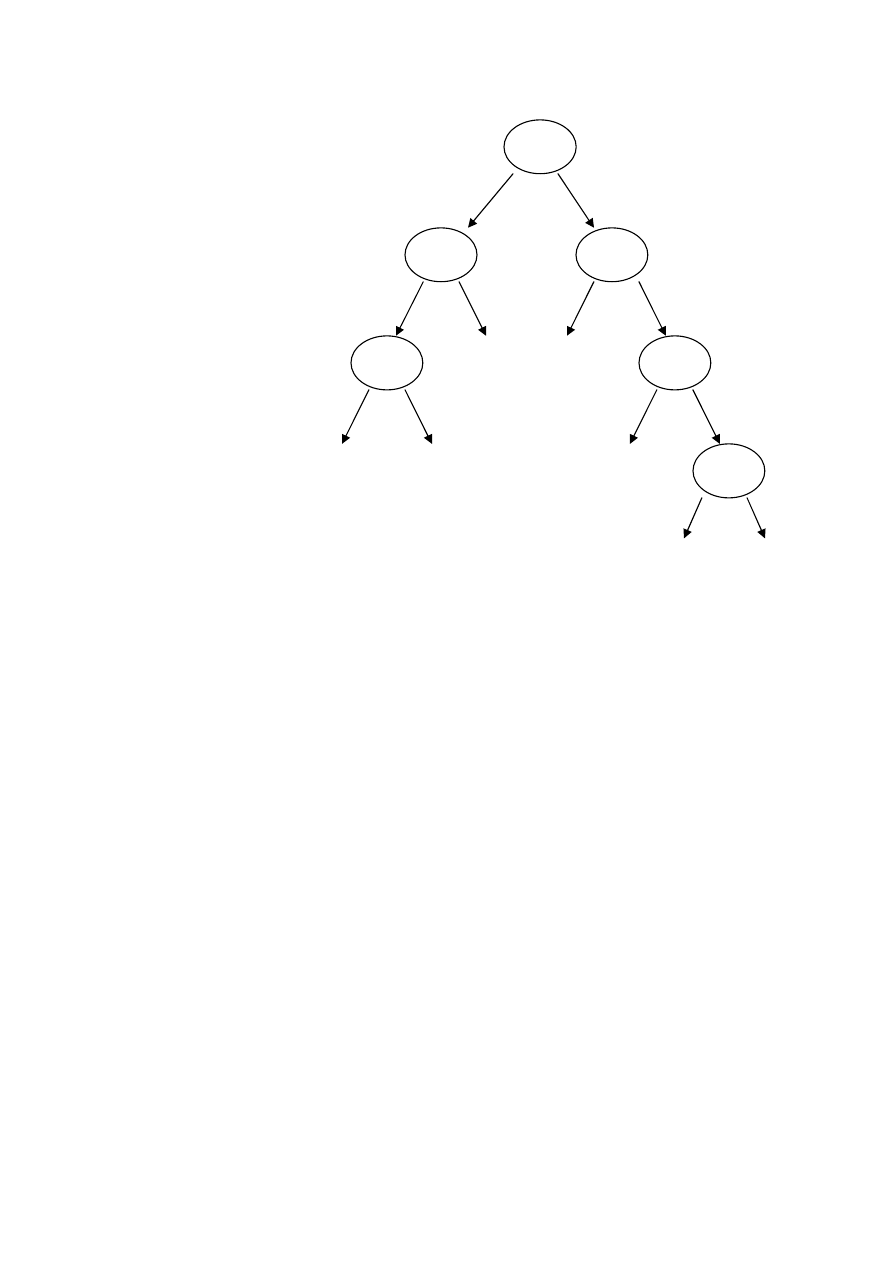
Drzewo nieukorzenione

Nieskierowany grafy spójny nie zawierający cykli

Wierzchołki drzewa często nazywamy węzłami.

Drzewo ukorzenione

Drzewo, w którym jeden z wierzchołków został wyróżniony

i nazywany jest korzeniem oraz krawędzie zostają

skierowane w taki sposób, że każdy węzeł, z wyjątkiem

korzenia ma dokładnie jedna krawędź wchodząca.

x

z

a

b

c

y

d

52

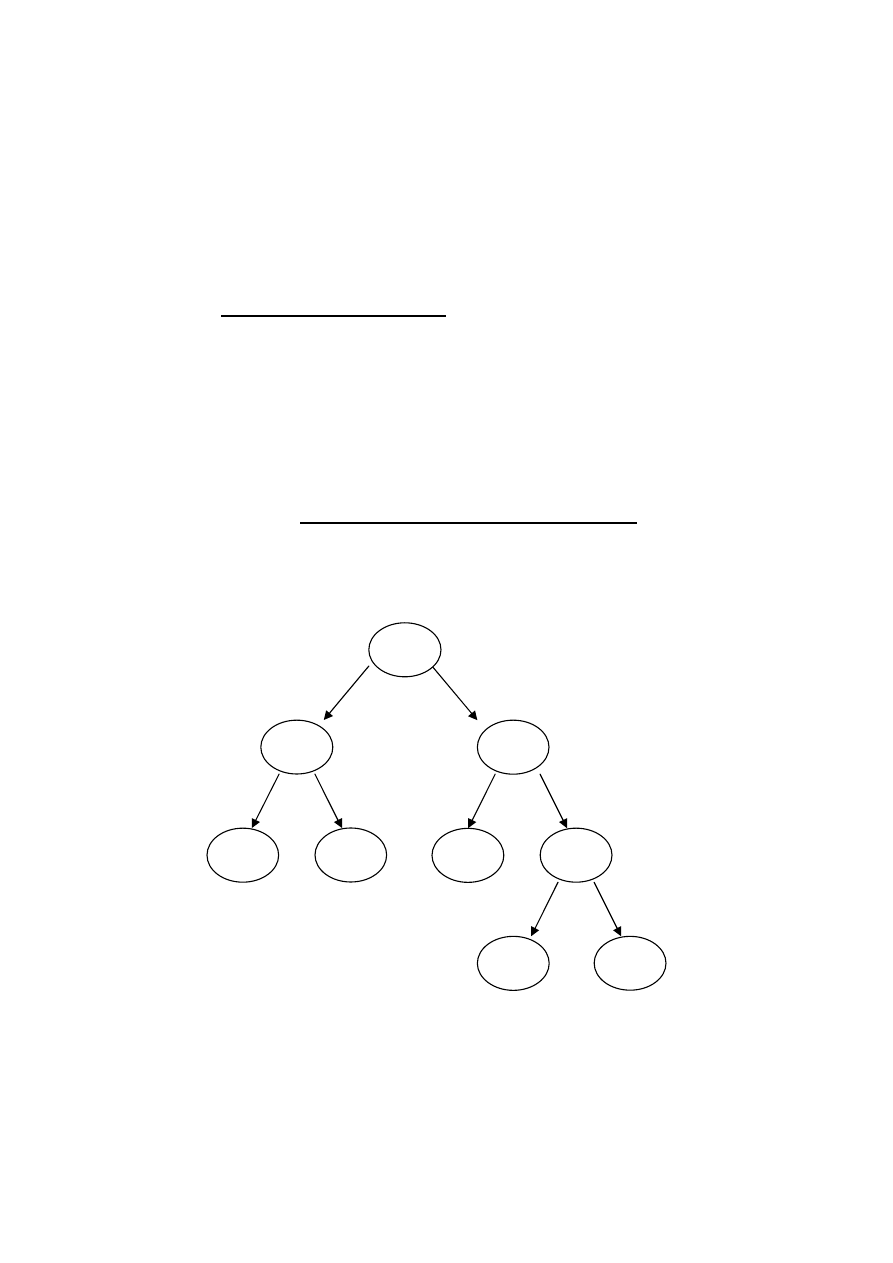
Przykład:

Pojęcia:

węzeł drzewa – element drzewa

ojciec (rodzic) węzła y – węzeł x, który wskazuje na
element y, np.

x->left

== y lub

x->right ==y

korzeń drzewa – węzeł, który nie ma ojca

syn (dziecko) węzła y – element wskazywany przez y

brat elementu y – węzeł, który ma z

y

wspólnego ojca

liść – węzeł który nie posiada dzieci (jego wskaźniki

left

i

right

mają wartość NULL)

poddrzewo o korzeniu y – fragment drzewa zawierający

węzeł

y

, jego dzieci, dzieci, itd.

x

z

NULL

NULL

a

b

NULL

NULL

NULL

NULL

c

NULL

y

53

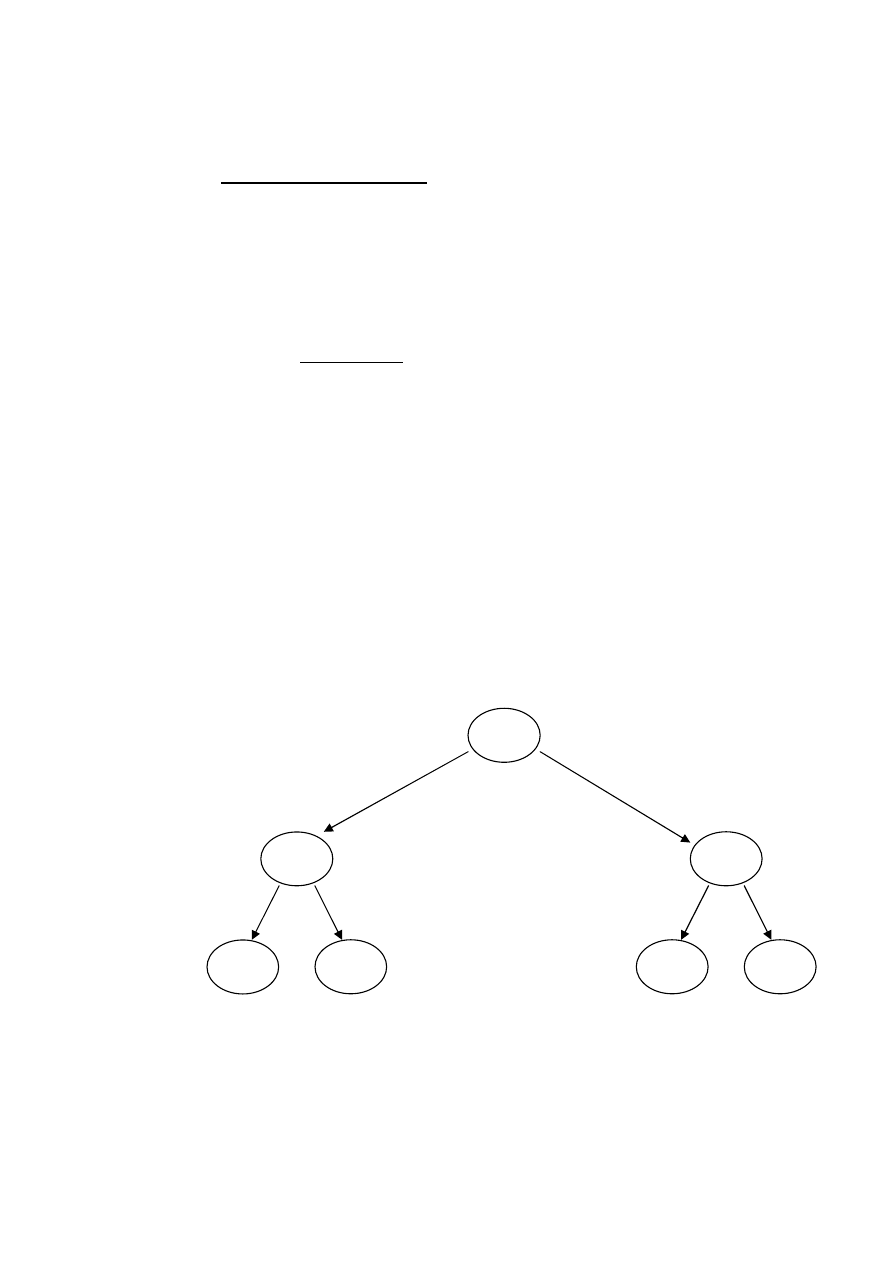
Rodzaje drzew

Drzewo binarne – drzewo ukorzenione, w którym każdy

węzeł ma co najwyżej dwoje dzieci.

Drzewo binarne regularne – drzewo binarne, w którym

każdy węzeł ma albo dwoje albo zero dzieci.

x

z

a

d

f

y

b

c

e

54

Drzewo trzyarne – drzewo ukorzenione, w którym każdy

węzeł ma co najwyżej troje dzieci

Drzewo wielodzietne – drzewo ukorzenione, w którym

każdy węzeł ma dowolną liczbę dzieci

Drzewo binarne (trzyarne) pełne – drzewo binarne

(trzyarne) regularne, którego wszystkie liście znajdują się na

tym samym poziomie (tzn. dla wszystkich liści w drzewie,

długość ich najkrótszej ścieżki od korzenia jest taka sama)

x

a

y

b

a

y

b

55

Przeglądanie drzewa binarnego (inorder)

1. przeglądnij lewe poddrzewo węzła

x

(rekurencyjnie)

2. wypisz wartość węzła x (albo wykonaj inną akcje na
węźle x)

3.· przeglądnij prawe poddrzewo węzła

x

(rekurencyjnie)

Wynik przeglądania:

2, 16, 6, 17, 9, 1, 12, 15, 20, 5, 3

1

17

15

16

5

9

6

2

3

12

20

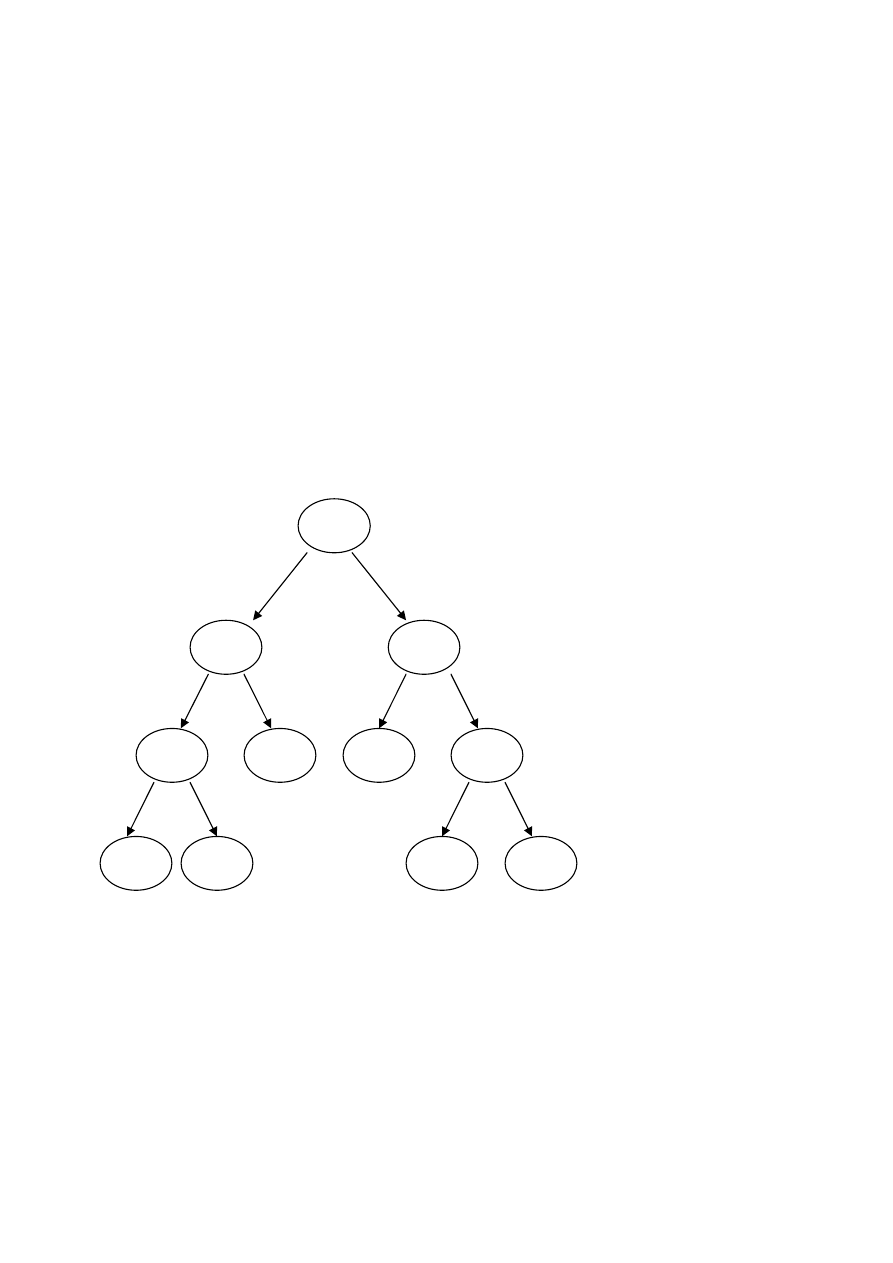
56

Przeglądanie drzewa binarnego (preorder)

1. wypisz wartość węzła x (albo wykonaj inną akcje na
węźle x)

2. przeglądnij lewe poddrzewo węzła

x

(rekurencyjnie)

3.· przeglądnij prawe poddrzewo węzła

x

(rekurencyjnie)

Wynik przeglądania:

1, 17, 16, 2, 6, 9, 15, 12, 5, 20, 3

1

17

15

16

5

9

6

2

3

12

20

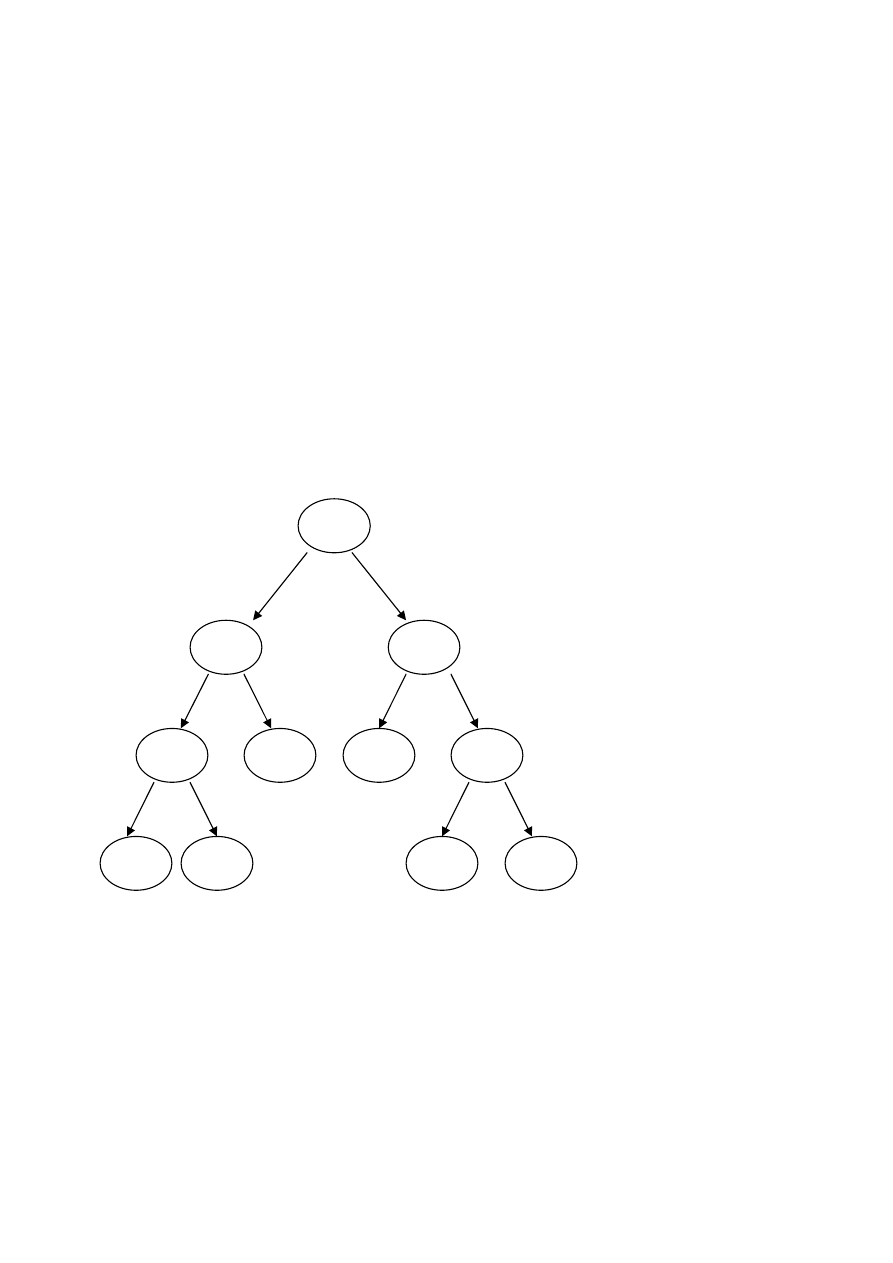
57

Przeglądanie drzewa binarnego (postorder)

1. przeglądnij lewe poddrzewo węzła

x

(rekurencyjnie)

2.· przeglądnij prawe poddrzewo węzła

x

(rekurencyjnie)

3. wypisz wartość węzła x (albo wykonaj inną akcje na
węźle x)

Wynik przeglądania:

2, 6, 16, 9, 17, 12, 20,3, 5, 15, 1

1

17

15

16

5

9

6

2

3

12

20

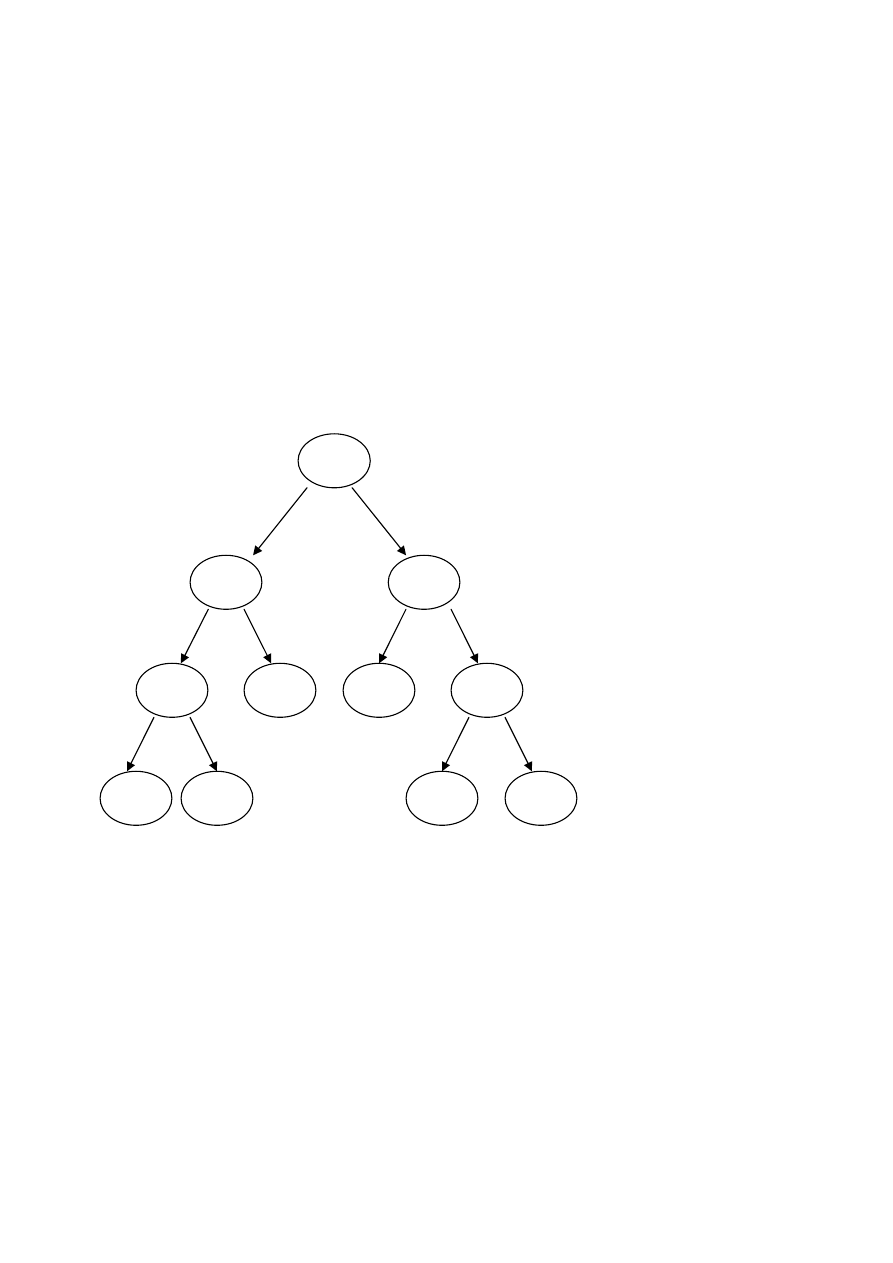
58

Przeglądanie drzewa binarnego poziomami

1.

Dla każdego poziomu wypisz kolejno węzły na tym

poziomie. Wypisywanie rozpocznij od poziomu na

którym znajduje się korzeń

Wynik przeglądania:

1, 17, 15, 16, 9, 12, 5, 2, 6, 20, 3

1

17

15

16

5

9

6

2

3

12

20

59

Drzewo binarne – implementacja wskaźnikowa

typedef struct os

{

int liczba;

struct os *lewy;

struct os *prawy;

} osoba;

osoba *korzen;

Inicjowanie drzewa pustego

osoba *korzen = NULL;

Czasem drzewo jest wzbogacone o wskaźnik do „rodzica”

typedef struct os

{

int liczba;

struct os *lewy;

struct os *prawy;

struct os *ojciec;

} osoba;

60

Drzewo binarne – implementacja kursorowa

struct os

{

int liczba;

int lewy;

int prawy;

} tab[100];

Drzewo wzbogacone o kursor do „rodzica”

struct os

{

int liczba;

int lewy;

int prawy;

int ojciec;

}tab[100];

61

Przygotowanie

Inicjalizacja_tablicy (),

Przygotowanie jest takie samo jak w przypadku list

kursorowych.

Łączymy

w

listę

(jednokierunkową)

wszystkie elementy tablicy

Inicjowanie drzewa pustego

int korzen = -1;

W jednej tablicy może być kilka struktur kursorowych,

zarówno list (jedno i dwukierunkowych) jak i kilka drzew.

62

Drzewo poszukiwań binarnych

Drzewo BST (binary search tree),

Drzewo BST to drzewo binarne, dla którego wartość
przechowywana w węźle jest większa od wartości
przechowywanej w lewym synu i mniejsza od wartości
przechowywanej w prawym synu
(relacja może być odwrócona).

Fakt.

Dla dowolnych węzłów drzewa x, y zachodzi:

jeśli x jest w lewym poddrzewie o korzeniu y, to x<y

jeśli x jest w prawym poddrzewie o korzeniu y, to x>y

10

7

15

5

25

9

6

2

30

12

20

63

Przeglądanie drzewa (inorder)

1. przeglądnij lewe poddrzewo węzła

x

(rekurencyjnie)

2. wypisz wartość węzła x
3.· przeglądnij prawe poddrzewo węzła

x

(rekurencyjnie)

Wynik przeglądania:

2, 5, 6, 7, 9, 10, 12, 15, 20, 25, 30

Fakt.

Drzewo binarne jest drzewem BST wtedy i tylko wtedy gdy

lista jego węzłów w porządku inorder jest ciągiem

rosnącym.

10

7

15

5

25

9

6

2

30

12

20

64

Wyszukiwanie w drzewie

Szukamy w drzewie węzła o wartości

x

:

Porównujemy wartość

x

z wartością aktualnego węzła

k

x == k

– cieszymy się, że znaleźliśmy

x < k

– szukamy w lewym poddrzewie

x > k

– szukamy w prawym poddrzewie

typedef struct os
{
int liczba;
struct os *lewy;
struct os *prawy;
} osoba;

osoba *szukaj (osoba *korzen, int k)
{
osoba *temp = korzen;
while (temp!=NULL && temp->liczba!=k)
{

if (temp->liczba<k) temp=temp->lewy;
else temp=temp->prawy;
}
return temp;
}

Jeśli dojdziemy w ten sposób do pustego drzewa
(

temp==NULL

) elementu nie ma w drzewie.

65

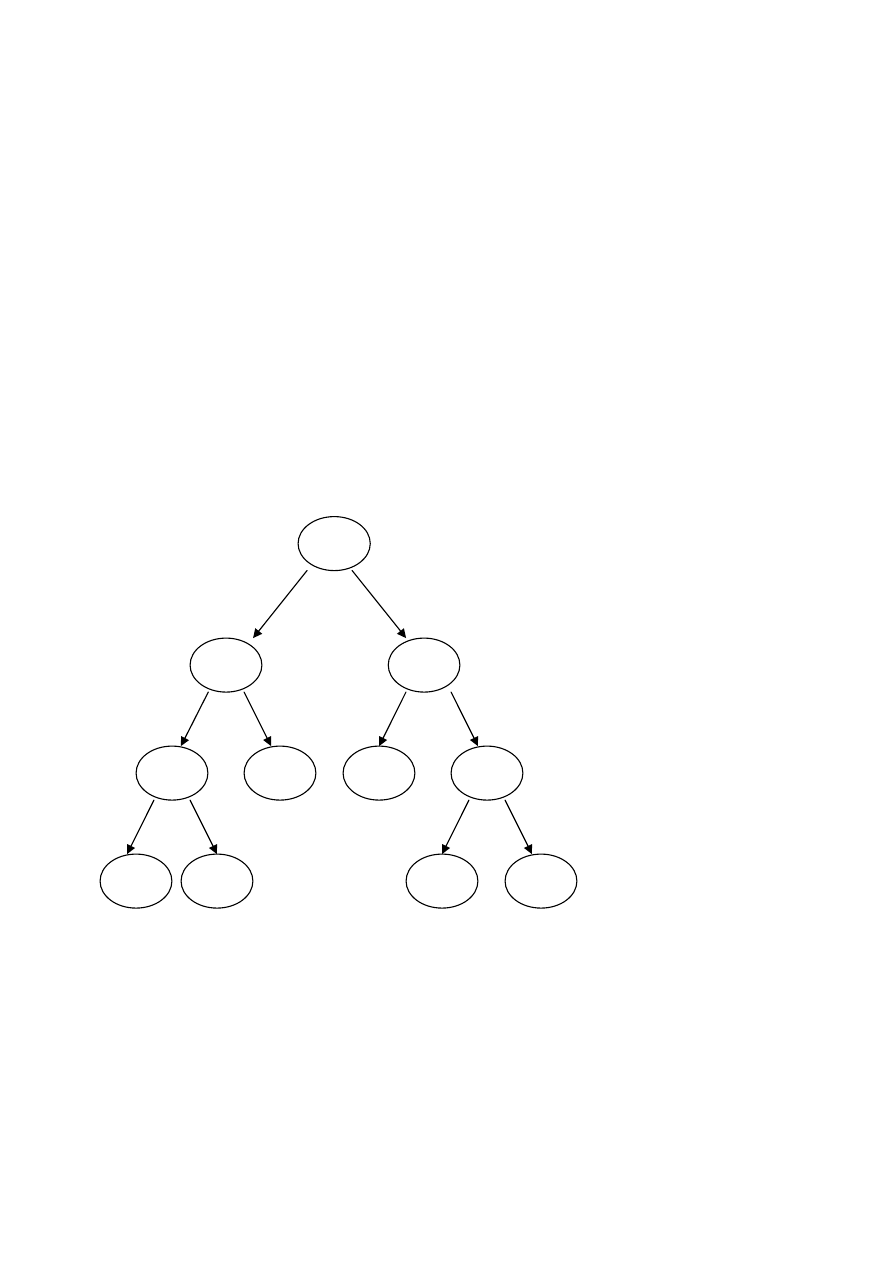
Dodawanie do drzewa:

Postępujemy jak przy wyszukiwaniu i nowy element

wstawiamy w liściach

10

7

15

5

25

9

6

2

30

12

20

11

66

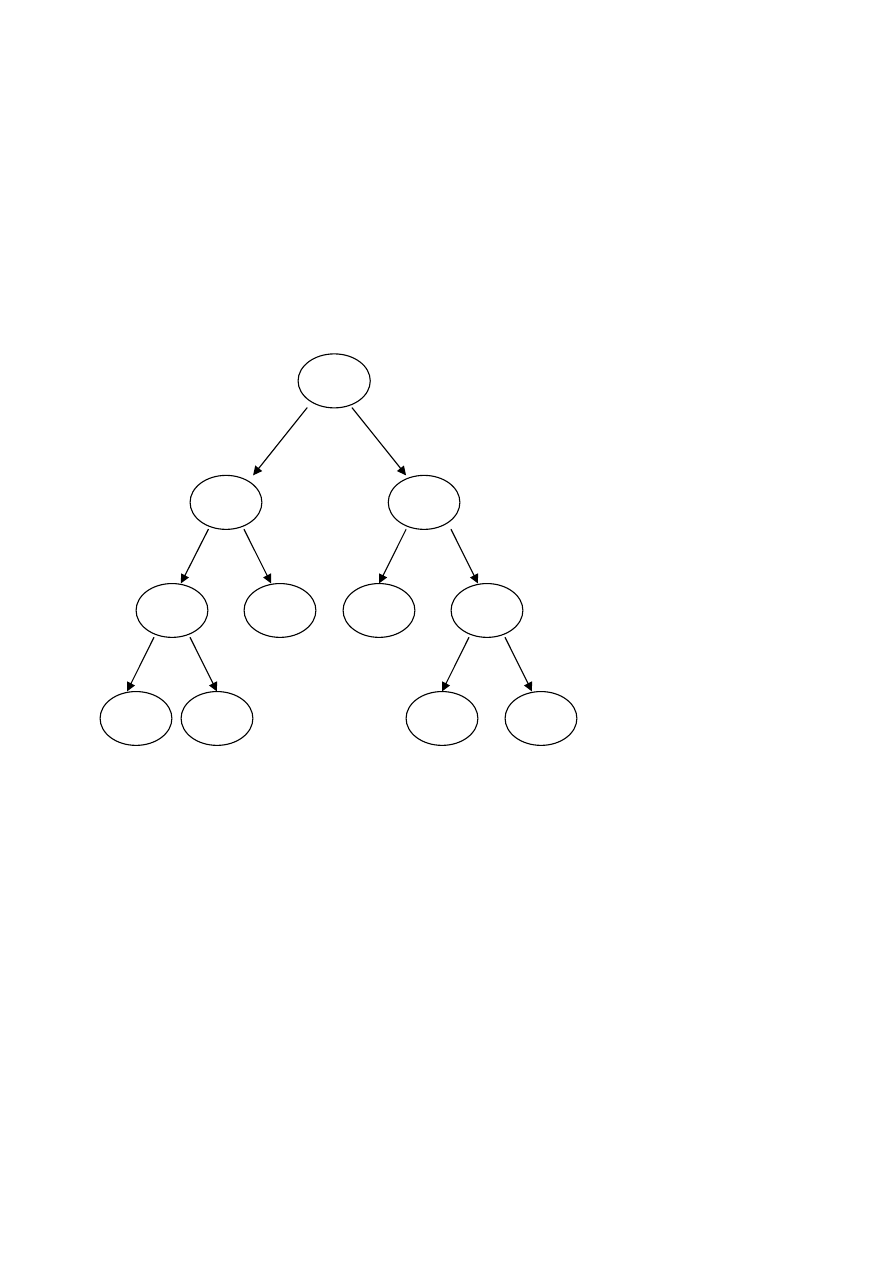
Usuwanie całego drzewa

void usunDrzewo(osoba *korzen)

{

/* wersja rekurencyjna

if (korzen != NULL) {

usunDrzewo(korzen->lewy);

usunDrzewo(korzen->prawy);

free(korzen);

}

return;

}

usunDrzewo(korzen);

korzen = NULL:

67

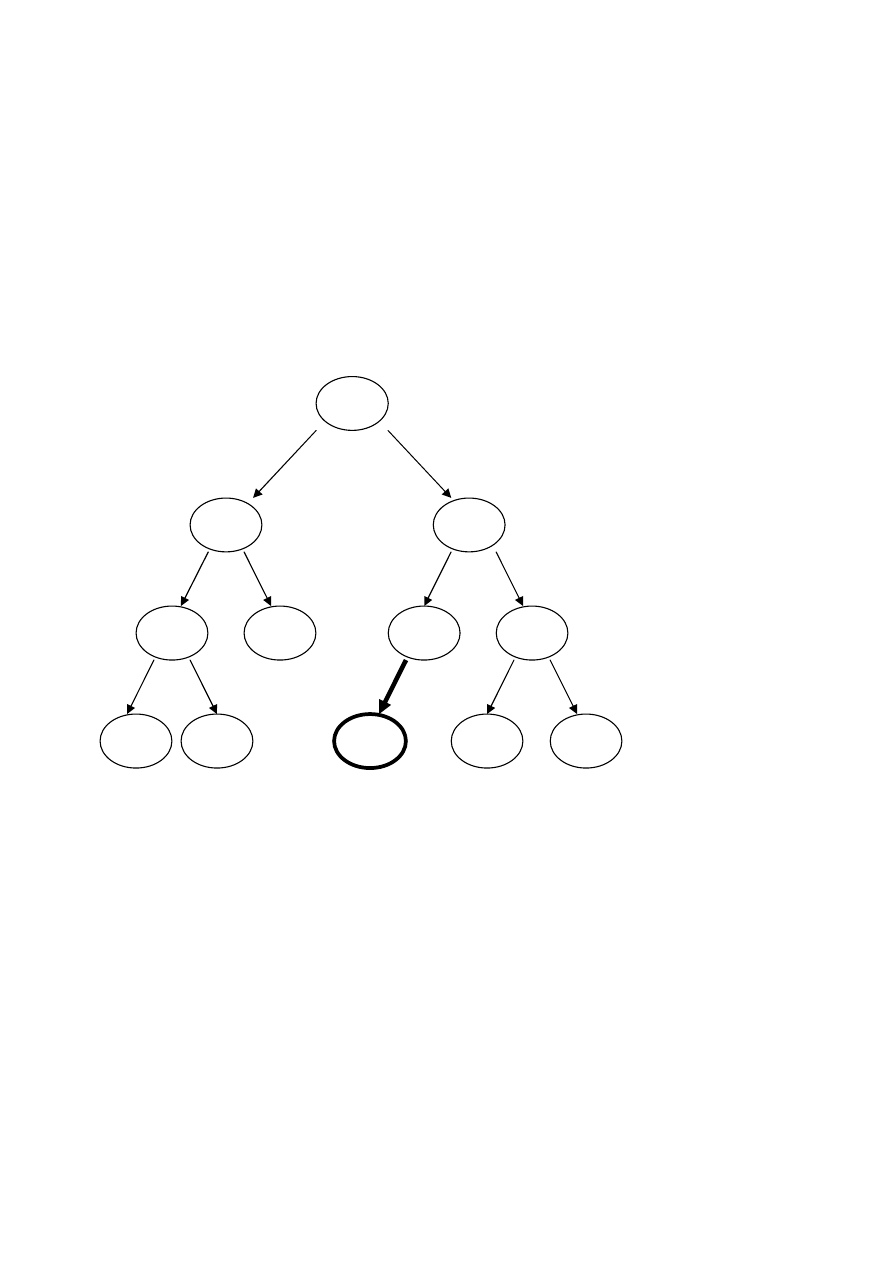
Usuwanie jednego węzła w drzewie

10

7

15

5

25

9

6

2

30

12

20

11

23

18

19

10

7

18

5

25

9

6

2

30

12

20

11

23

19

68

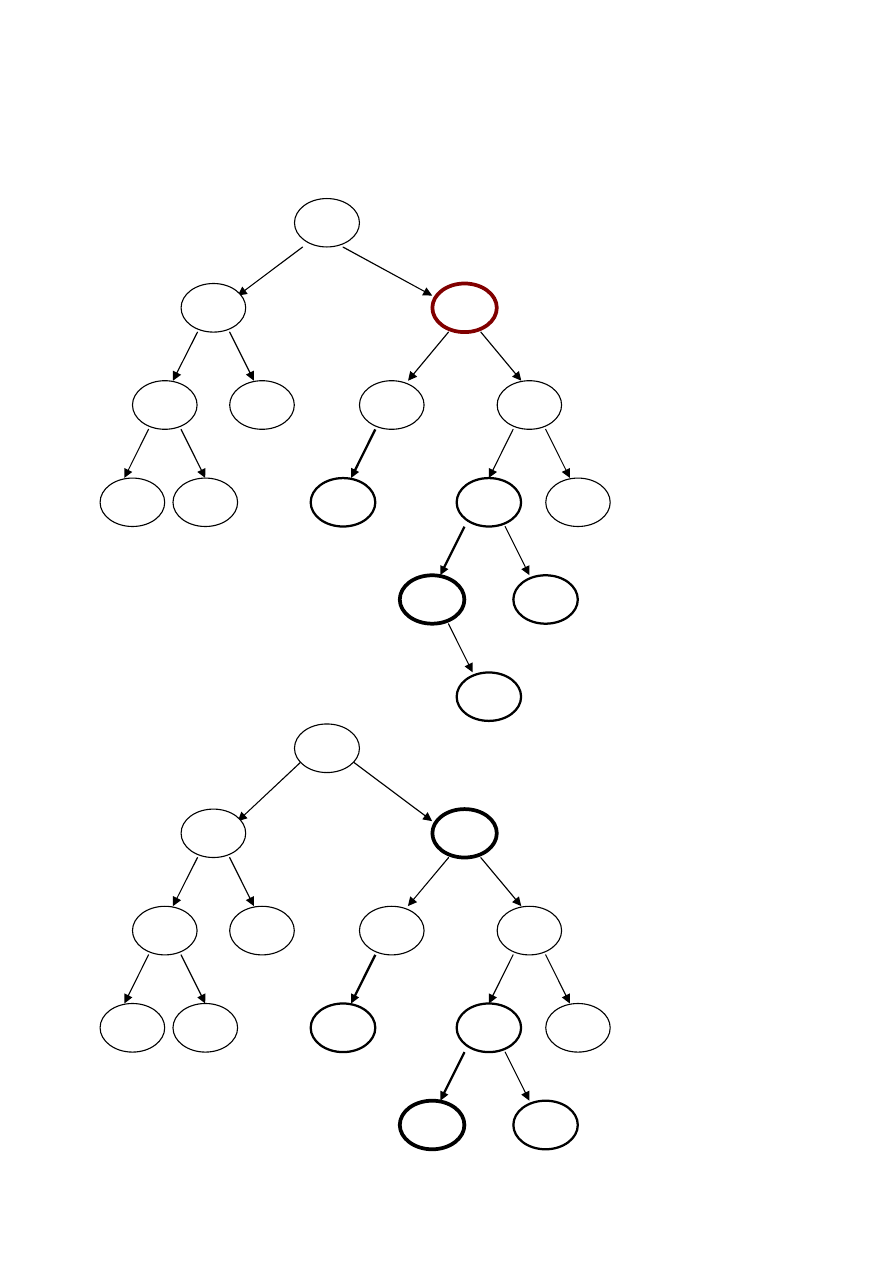
Usuwanie jednego węzła w drzewie

1.

Znajdujemy węzeł

x

, który chcemy usunąć.

2.

Rozpatrujemy przypadki:

a.

jeśli

x

nie ma dzieci – usuwamy go

b.

jeśli

x

ma tylko jedno dziecko – zastępujemy go

własnym dzieckiem

c.

jeśli

x

ma dwoje dzieci:

•

znajdujemy następnik

y

(najbardziej lewy element w

prawym poddrzewie

x

)

•

zastępujemy zawartość węzła

x

przez zawartość

węzła

y

•

usuwamy węzeł

y

(syn

y

stanie się synem swojego

„dziadka”)

Możliwa wersja druga:

•

znajdujemy poprzednik

y

(najbardziej prawy

element lewego podrzewa)

•

dalej tak samo

69

Drzewo trzyarne

– implementacje analogiczne

do binarnych

typedef struct os

{

int liczba;

struct os *pierwszy;

struct os *drugi;

struct os *trzeci;

struct os *ojciec;

} osoba;

osoba* korzen = NULL;

struct os

{

int liczba;

int pierwszy;

int drugi;

int trzeci;

int ojciec;

} tab[100];

int korzen = -1;

70

Drzewo wielodzietne

1. Implementacja poprzez tablicę lub listę
dzieci

1. Drzewo jest wskaźnikiem (kursorem) na korzeń drzewa.

2.

Każdy węzeł „pamięta” wskaźnik na tablicę lub listę

zawierająca wskaźniki do swoich dzieci.

3.

Wszystkie węzły mogą być stablicowane. Wówczas

zamiast wskaźników mogą być pamiętane indeksy dzieci.

2. Implementacja poprzez wskaźnik na rodzica

1. Wszystkie węzły drzewa są stablicowane.

2. Każdy węzeł „pamięta” wskaźnik (albo kursor) na

swojego rodzica.

3.

Dodatkowo może być pamiętana lista (tablica) liści

drzewa.

4.

Przy tym podejściu chodzimy po drzewie „od dołu”.

71

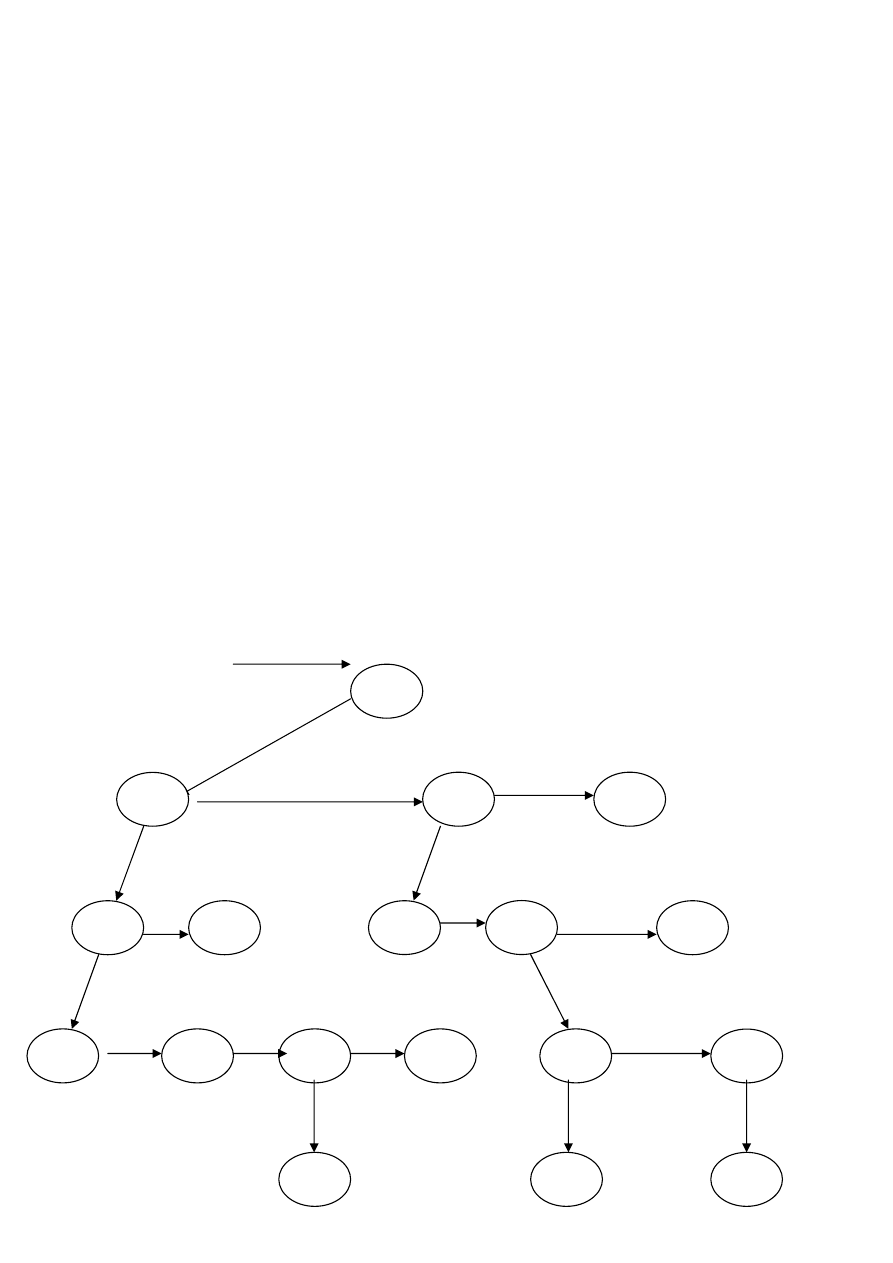
3. Implementacja „left-child, right-sibling”

==

implementacja

za

pomocą

drzewa

binarnego

(wskaźnikowego lub kursorowego)

1. Drzewo jest wskaźnikiem na korzeń.

2. Każdy węzeł struktury „pamięta” dwa wskaźniki

•

wskaźnik na swoje pierwsze dziecko

•

wskaźnik na swojego brata

Przykład

korzen

a

c

e

h

n

b

f

d

i

o

g

m

l

k

j

p

q

r

72

Implementacja wskaźnikowa:

typedef struct os

{

int liczba;

struct os *first_child;

struct os *next_sibling;

struct os *parent;

//ewent.

} osoba;

osoba* korzen = NULL;

Implementacja kursorowa:

struct os

{

int liczba;

int first_child;

int next_sibling;

int parent; //ewent.

} tab[100];

int korzen =-1;