Makroekonomia Gospodarki Otwartej
WNE UW, 2009

Efekt Balassy-Samuelsona, model Dornbuscha przestrzelenia
kursu walutowego

Zadanie 1
Załóżmy, że świat składa się z dwóch gospodarek: kraju i zagranicy (oznaczonej

∗

). Przyjmijmy,

iż stopa inflacji jest średnią ważoną stóp zmian cen dóbr handlowych (sektor T ) i niehandlowych
(sektor N), przy czym wagami są udziały tych dóbr w referencyjnym koszyku konsumpcyjnym.
Niech α będzie udziałem dóbr handlowych w koszyku. Załóżmy początkowo, że α = α

∗

= 0,5.

Wzrost cen w danym sektorze jest równy różnicy między wzrostem płac nominalnych a wzro-

stem wydajności pracy w danym sektorze: π

i

= ˆ

w − ˆa

i

, gdzie i = T, N. Analogicznie za granicą:

π

∗

i

= ˆ

w

∗

− ˆ

a

∗

i

, gdzie i = T, N.

(a) Z jakiego założenia wynika to, iż stopa wzrostu wynagrodzeń nominalnych nie jest zróż-

nicowana między sektorami? Jak myślisz, w jakim stopniu założenie to jest spełnione
w rzeczywistości?

(b) Zapisz inflację w kraju i za granicą (π oraz π

∗

) jako średnią ważoną inflacji w sektorze

dóbr handlowych i niehnaldowych.

(c) Załóżmy, że płace nominalne w kraju rosną o 10%, zaś za granicą – o 5%, wydajność pra-

cy w sektorze dóbr handlowych w kraju o 7%, zaś w sektorze dóbr niehandlowych o 4%.
Za granicą wydajność pracy w sektorze dóbr handlowych rośnie o 3%, zaś w sektorze
dóbr niehandlowych – o 1%. Oblicz średni poziom inflacji w kraju i za granicą.

(d) Jakiej zmiany kursu walutowego możemy się spodziewać w świetle parytetu siły nabyw-

czej?

(e) Z jaką zmianą realnego kursu mamy do czynienia w naszym przypadku? Sformułuj wnio-

sek dotyczący wpływu zmian w wydajności w sektorze dóbr handlowych i niehandlowych
w kraju i za granicą na realny kurs walutowy. Zapisz wyrażenie opisujące zmianę realne-
go kursu walutowego jako funkcję różnic w tempach wzrostu wydajności. Wykorzystaj
fakt, że z prawa jednej ceny, które jest zachowane w sektorze dóbr handlowych wynika,
że ˆe = π

T

− π

∗

T

, gdzie ˆe to stopa zmiany kursu nominalnego.

(f) Dotychczas zakładaliśmy, że udział dóbr handlowych w koszyku referencyjnym wynosi

50% i jest taki sam w kraju i za granicą. W Polsce w 2003, usługi stanowiły ok. 63%
PKB. W krajach OECD jest to średnio ok. 70%. Zastanów się, jak uwzględnienie tego
w modelu (zróżnicowanie wartości parametru α, przy czym α > α

∗

) wpłynie na wnioski.

Jak sądzisz, jakiej zmiany wartości parametru α można się spodziewać w Polsce wraz
z procesem doganiania krajów wyżej rozwiniętych? Jak to może wpłynąć na wnioski
z modelu?

(g) Poniższa tabela zawiera dane dotyczące średnich rocznych stóp zmian zatrudnienia, pro-

duktywności oraz cen w sektorze dóbr handlowych i niehandlowych w Polsce i w krajach
strefy euro w okresie 1996-2007. Wykresy ilustrują zmiany względnej produktywności
oraz zmiany realnego kursu złotego wobec ecu/euro w tym okresie.

Czy w przypadku Polski spełnione są przesłanki efektu Balassy-Samuelsona? Czy zaobserwo-

wano zmiany kursu realnego przewidywane na gruncie teoretycznym? Jakie skutki mogło to mieć
dla konkurencyjności polskiego eksportu? Jeśli odchylenie różnicy we wzroście wydajności pracy
w sektorze dóbr handlowych i niehandlowych w Polsce i UE utrzyma się w najbliższych latach,
jakie może mieć to konsekwencje dla możliwości spełnienia kryteriów konwergencji dotyczących
stabilności kursu walutowego oraz utrzymania inflacji na wyznaczonym poziomie?

1

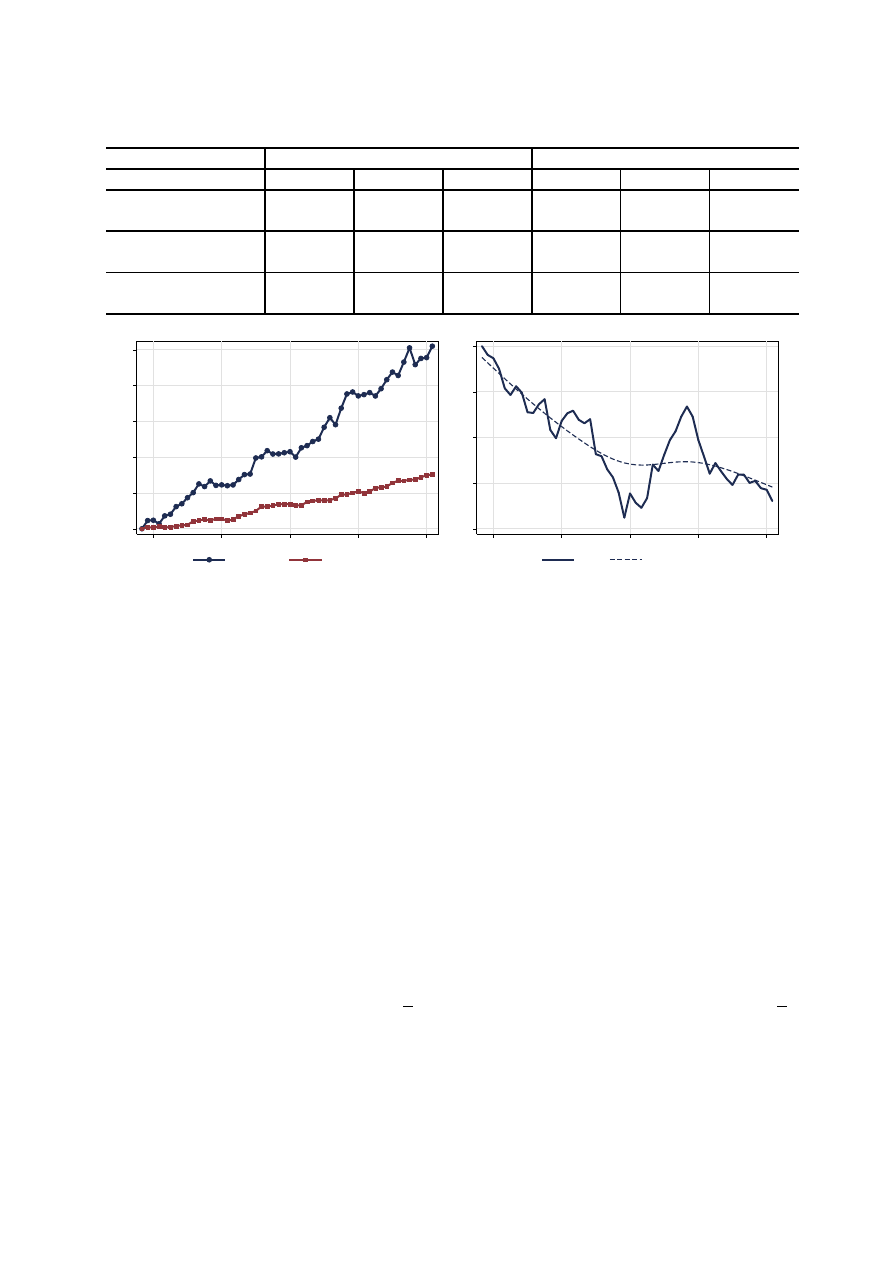
Tabela 1

Średnioroczne tempa wzrostu wybranych zmiennych w Polsce i krajach strefy euro, 1996-2007

Polska

Eurozone

1996-2004 2005-2007 1996-2007 1996-2004 2005-2007 1996-2007

Zatrudnienie (T)

−3.48

2.19

−2.06

−0.21

−0.02

−0.16

Zatrudnienie (N)

0.92

4.07

1.71

2.02

1.96

2.01

Produktywność (T)

8.40

4.08

7.32

2.37

2.72

2.45

Produktywność (N)

2.59

0.64

2.10

0.36

0.44

0.38

Inflacja (T)

5.82

1.78

4.72

1.56

2.06

1.70

Inflacja (N)

9.22

2.56

7.40

2.26

2.25

2.26

100

120

140

160

180

200

1995q3

1998q3

2001q3

2004q3

2007q3

LP T/N PL

LP T/N EUR

60

70

80

90

100

1995q3

1998q3

2001q3

2004q3

2007q3

RER

trend HP l(1600)

Rysunek 1
Względna wydajność pracy (T/N) w Polsce i krajach strefy euro, 1995 = 100 (lewy wykres)
oraz realny kurs złotego względem ecu/euro, 1995 = 100 (prawy wykres, spadek oznacza realną
aprecjację złotego).

Zadanie 2
Posługując się modelem parytetu stóp procentowych i modelem rynku pieniężnego, powiedz, jak
zmieni się bieżący kurs walutowy w krótkim i w długim okresie (przy nieelastycznych cenach
w krótkim okresie i przy w pełni elastycznych – w długim) pod wpływem obniżenia przez bank
centralny krajowej podaży pieniądza, przy założeniu, że:

(a) inwestorzy postrzegają zmianę w podaży pieniądza jako przejściową

(b) przy założeniu, że postrzegają ją jako zmianę trwałą

Odpowiedź przedstaw graficznie na schemacie rynku walutowego i pieniężnego. Pokaż także,

jak zmieniać się będzie nominalna podaż pieniądza, poziom cen, stopa procentowa oraz kurs
walutowy w czasie (posługując się diagramami fazowymi).

Zadanie 3
Rozważamy uproszczony model przestrzelenia kursu walutowego Dornbuscha. Załóżmy, że popyt
na pieniądz dany jest przez: m

d

= −ai + by, gdzie i jest krajową nominalną stopą procentową, y

jest krajowym potencjalnym dochodem (przy pełnym zatrudnieniu), zaś a, b – pół-elastyczność
i elastyczność popytu na pieniądz. Wszystkie zmienne pisane małymi literami (z wyjątkiem
elastyczności i stopy procentowej) wyrażone są w logarytmach.

Równowaga na rynku pieniądza zachodzi, gdy: m

− p = m

d

, gdzie m jest nominalną podażą

pieniądza, zaś p to poziom cen. Zakładamy doskonałą mobilność kapitału oraz parytet stóp
procentowych: i = i

∗

+ ˙e, gdzie ˙e oznacza oczekiwaną stopę aprecjacji waluty zagranicznej.

2

Uwaga: ponieważ e = ln E, to

˙

E
E

= ˙e (czyli jest to stopa wzrostu kursu waluty zagranicznej).

Dostosowanie cen w gospodarce do długookresowej równowagi zachodzi powoli (ceny są

sztywne w krótkim okresie i elastyczne w długim) w odpowiedzi na nadwyżkowy popyt za-
gregowany. Opisuje to równanie: ˙p = α(y

d

− y

s

), gdzie α > 0 jest miarą szybkości dostosowań.

Funkcja zagregowanego popytu ma następującą, uproszczoną postać: y

d

= u + λ(e − p), gdzie

λ > 0, (e − p) jest realnym kursem walutowym, czyli względną ceną dóbr zagranicznych (dla

wygody ceny zagraniczne znormalizowano do jedności), u > 0 jest egzogenicznym składnikiem
zagregowanego popytu. Zagregowana podaż w długim okresie jest ustalona na poziomie pełnego
zatrudnienia: y

s

= y.

(a) Zapisz układ równań różniczkowych opisujących zachowanie się kursu walutowego i po-

ziomu cen ( ˙e oraz ˙p).

(b) Narysuj w przestrzeni (e, p) linie przedstawiające ˙e = 0 oraz ˙p = 0.

(c) Znajdź punkt równowagi stacjonarnej i zaznacz go na wykresie.

(d) Narysuj pole wektorowe dla tego układu równań różniczkowych i przedyskutuj problem

stabilności równowagi.

(e) Przy pomocy wykresu odpowiedz, co stanie się z poziomem kursu walutowego oraz po-

ziomem cen w wyniku egzogenicznego zwiększenia podaży pieniądza. Jakie będą skutki
tego wydarzenia w krótkim i długim okresie i jak będzie wyglądało przejście do no-
wej równowagi stacjonarnej w długim okresie? Podaj wyjaśnienie ekonomiczne takiego
przejścia do nowej równowagi stacjonarnej.

(f) Narysuj diagramy fazowe dla kluczowych zmiennych modelu (m, i, p, e).

3