Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
1
/
27
POLITECHNIKA POZNAŃSKA
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW
W OKRESIE USZKODZEŃ STARZENIOWYCH
ODWZOROWYWANYM
ROZKŁADEM TRÓJKĄTNYM
Prognostyczne modele uszkodzeń i wymian nieodnawianych obiektów poljazdów
Materiały pomocnicze do wykładu (v1)
f
n
(t)
A
B C
t

Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
2
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE
MODELE MATEMATYCZNE
Założenia i przyjęte oznaczenia
Prognostyczny model parametrów rozkładu trójkątnego jako rozkładu
uszkodzeń starzeniowych
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
PODSUMOWANIE
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
3
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
1
)
1
2
3
4
5
6
O
b
i
e
k
t
y
t
1
t
2
t
3
t
N
1
0
2
0
3
t = 0
.
.
.
.
.
0
.
0
T
f
n
(t)
A
B
C
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
czas pracy do
uszkodzenia obiektu
t
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
4
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
2
)
7
8
9
10
11
12
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
T
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
5
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
3
)
13
14
15
16
17
18
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
6
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
4
)
19
20
21
22
23
24
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
7
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
5
)
25
26
27
28
29
30
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
8
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
6
)
31
32
33
34
35
36
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
1
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
9
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
7
)
37
38
39
40
41
42
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
2
1
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
10
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
8
)
43
44
45
46
47
48
t
1
t
2
t
3
t
N
1
2
3
t = 0
O
b
i
e
k
t
y
.
.
.
.
.
.
0
0
0
0
f
n
(t)
A
B
C
t
( )
( )
...
,
,
i
t
N
t
n
t
f
i
i
n
2
1
,
=
Δ
⋅
Δ
=
T
czas pracy do
uszkodzenia obiektu
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
11
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
WPROWADZENIE (
9
) – O ROZKŁADZIE TRÓJKĄTNYM
Funkcja gęstości prawdopodobieństwa TR(a,b,c)
)
(
)
(
)
(
2
a
b
a
c
a
t
−
⋅
−
−
⋅
dla
]
,
( b
a
t
∈
)
,
,
;
(
c
b
a
t
f
TR
)
(
)
(
)
(
2
b
c
a
c
t
c
−
⋅
−
−
⋅
dla
]
,
( c
b
t
∈
dla
0
]
,
( c
a
t
∉
Dystrybuanta TR(a,b,c)
dla
0
a
t
≤
)
(
)
(
)
(
2
a
b
a
c
a
t
−
⋅
−
−
dla
b
t
a
≤
<
)
(
)
(
2
2
b
c
a
c
t
ct
ac
bc
ab
−
⋅
−
−
+
−
−
dla
c
t
b
≤
<
)
,
,
;
(
c
b
a
t
F
TR
dla
1
c
t
>
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
12
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
MODELE MATEMATYCZNE
Założenia i przyjęte oznaczenia (
1
)
1.
Obserwowana jest grupa N nieodnawianych obiektów typu mechanicznego. Zakłada się podział tej
grupy obiektów na dwie frakcje
(rys. 1)
. Pierwszą z nich
− o liczności
π
− stanowią obiekty, które
ulegają uszkodzeniom wczesnym i przypadkowym. Drugą frakcję obiektów
− o liczności N
s
− stano-
wią te, które ulegają uszkodzeniom na skutek starzenia. Chwile czasowe przewidywanych uszkodzeń
obiektów tworzą szereg pozycyjny:
( ) ( )
( ) (
)
( )
N
t
t
t
t
t
,
...
,
,
,
...
,
,
1
2
1
+
π
π
.
(1)
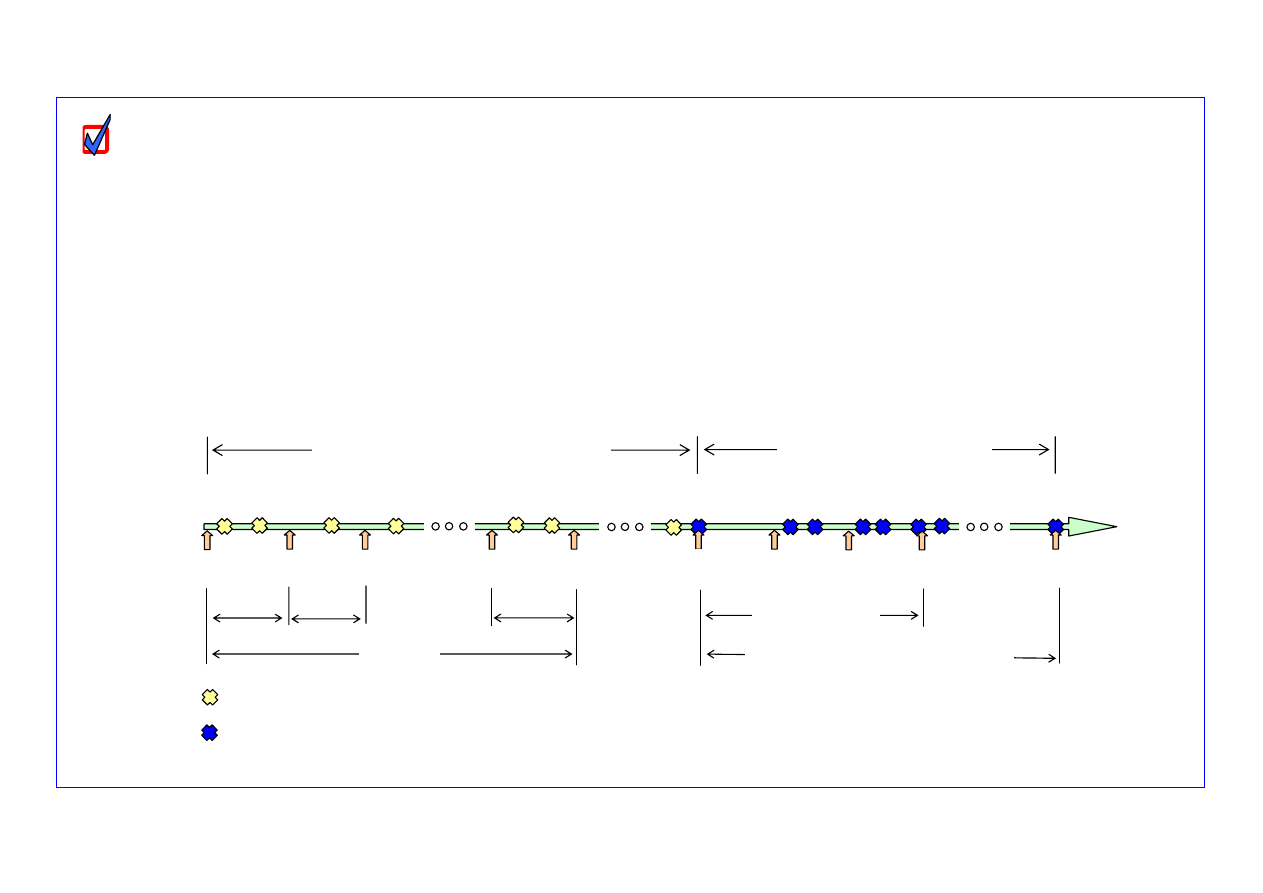
Rys. 1. Schemat wybranych oznaczeń w formułach modeli matematycznych
n(
Δ
t
i-1,i
)
n(
Δ
t
1,2
)
n(
Δ
t
0,1
)
t
i-1
t
i
t
0
t
1
t
2
t
p
t
k
t
(1)
t
(2)
t
(3)
t
(4)
t
(N)
t
(
π
)
t
(
π
+1)
t
(
π
+
κ
)
κ
= n(
Δ
t
p,k
)
N
s
= N -
π
= n(
Δ
t
p,k+r
)
n
sk
(t
i
)
−
oznaczenie chwil uszkodzeń obiektów przed okresem uszkodzeń starzeniowych
−
oznaczenie chwil uszkodzeń obiektów w okresie uszkodzeń starzeniowych
t
k+r
Frakcja pierwsza obiektów
Frakcja druga obiektów
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
13
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
Założenia i przyjęte oznaczenia (
2
)
2.
Czas obserwacji uszkodzeń obiektów podzielono na przedziały o równej długości (rys. 1):
...
1,2,
,
,
...
,
,
...
,
,
...
,
2
,
1
,
1
,
1
=
>
+
=
−
=
−
−
r
p,
k
r
k
k
p
i
t
t
Δt
i
i
i
i
.
(2)
3.
W kolejnych przedziałach czasu rejestruje się liczby n(
Δ
t
i-1,i
) uszkodzeń obiektów, a w chwilach
pokrywających się z górnymi granicami przedziałów czasowych wyznacza się skumulowane
liczby uszkodzeń (rys. 1):
( )
(
)
...
1,2,
,
,
...
,
,
...
,
,
...
,
2
,
1
,
1
,
1
=
>
+
=
=
∑
=
−
r
p,
k
r
k
k
p
i
Δt
n
t
n
i
i
sk
ν
ν
ν
.
(3)
4.
Zakłada się, że rozkład czasu T do uszkodzeń obiektów nieodnawianych zaliczonych do frakcji
drugiej jest rozkładem trójkątnym TR(a,b,c).
5.
Przyjmuje się, że początek uszkodzeń starzeniowych przypada na chwilę t
p
(rys. 1), tzn. przyjmu-
je się, że uszkodzenie pierwszego obiektu będące wynikiem jego starzenia pokrywa się z chwilą
t
p
. Zakłada się, że proces starzenia przebiega tak, że wszystkie N
s
obiektów drugiej frakcji
uszkadza się do chwili t
k+r
. Z założeń tych wynika, że:
( )
N
...
,
,
m
t
t
t
r
k
p
m
,
2
1
,
,
+
+
=
∈
+
π
π
.
(4)
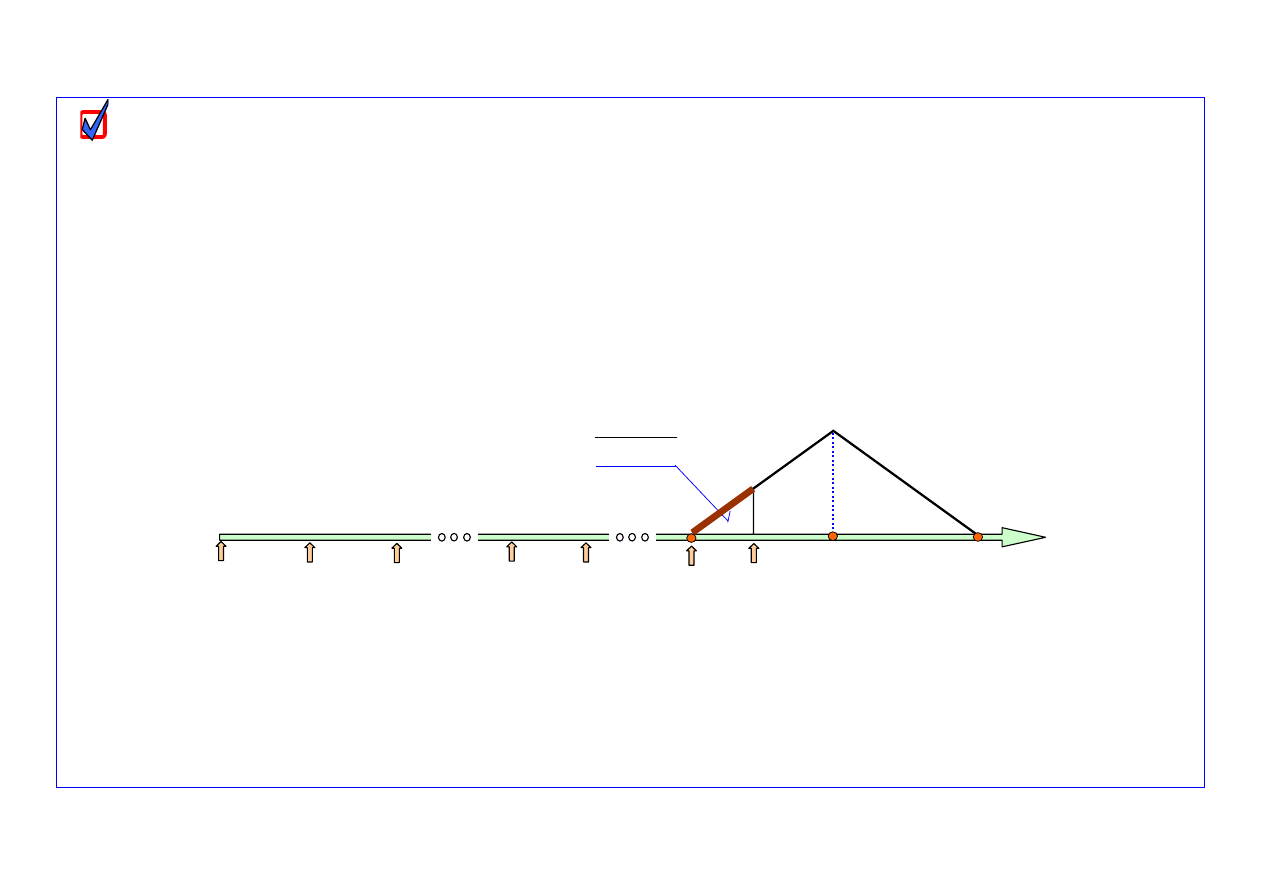
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
14
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
MODELE MATEMATYCZNE
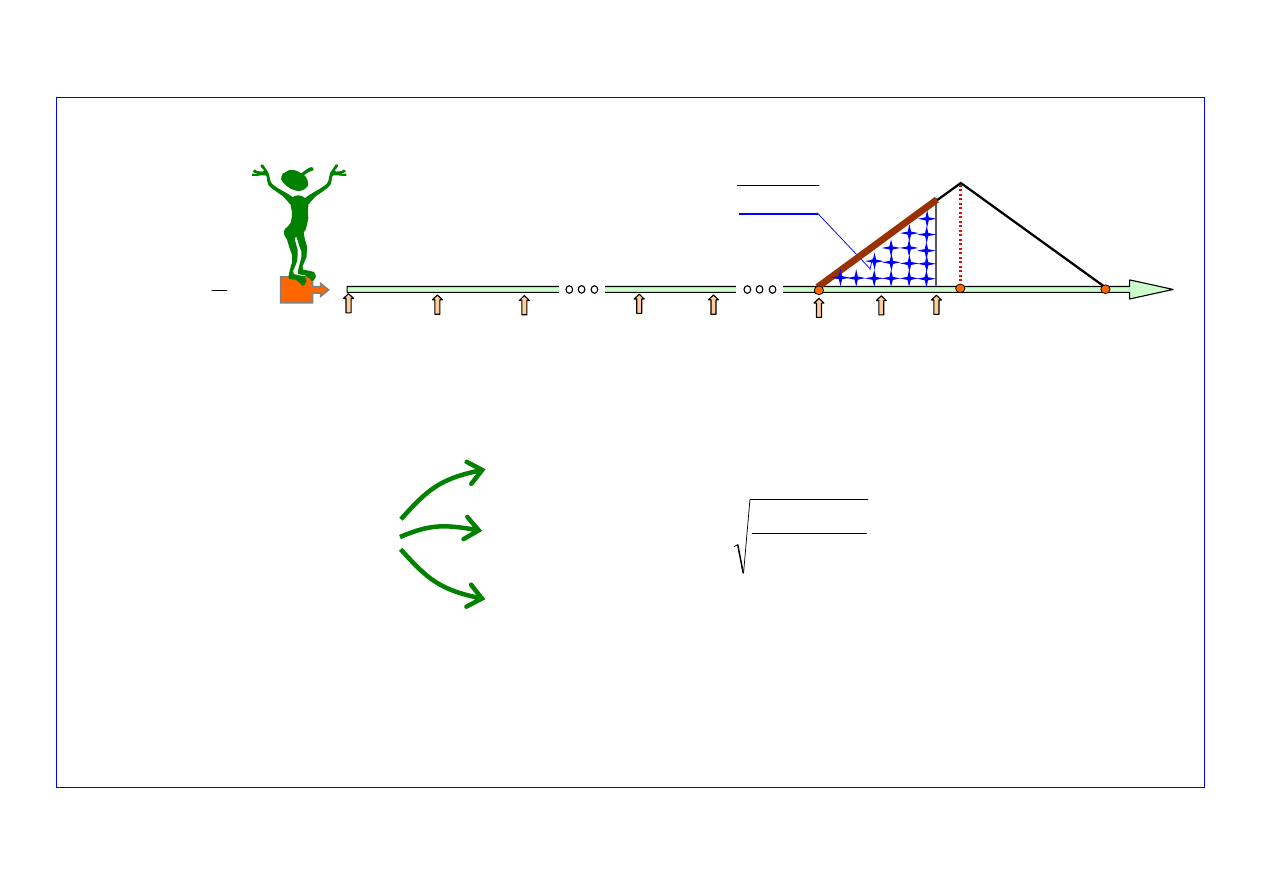
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
1
)
Prognostyczny model parametrów rozkładu obiektów to formuły matematyczne na estymatory
parametrów rozkładu czasu
T
do uszkodzeń starzeniowych obiektów (rozkład trójkątny
TR(a,b,c)
). Es-
tymatory te oszacowuje się na podstawie liczby
n(
Δt
p,k
)
uszkodzeń obiektów w okresie od chwili
t
p
do
chwili
t
k
oraz liczności
N
s
obiektów, dla których przewiduje się, że ulegną uszkodzeniom na skutek ich
starzenia. Schemat ideowy tego prognostycznego modelu przedstawiono na
rys. 2
.
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
czas
n(
Δt
p,k
)
N
s
b
c
Rys. 2. Schemat ideowy prognostycznego modelu parametrów rozkładu uszkodzeń obiektów
w okresie uszkodzeń starzeniowych
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
15
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
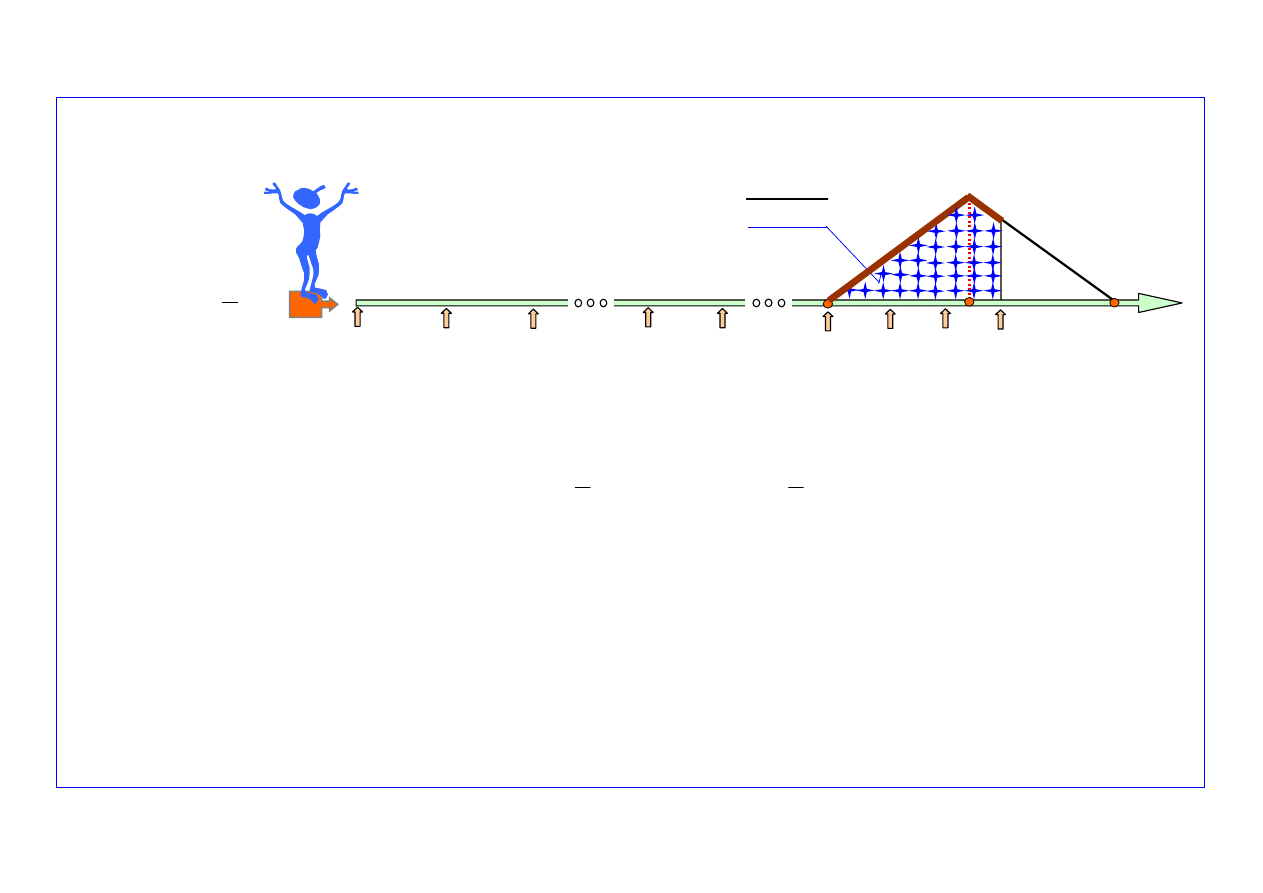
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
2
)
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
2
)
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k-1
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
czas
n(
Δt
p,k
)
N
s
b
c
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
≤
1
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k-2
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
czas
n(
Δt
p,k
)
N
s
b
c
t
k-1
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
>
2
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
16
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
3
)
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
3
)
(
)
( )
1
=
⋅
−
b
f
t
b
p
( )
p
t
b
b
f
−
=
1
( )
( )
b
f
t
b
t
f
t
t
p
k
p
k
−
=
−
( )
p
p
k
p
k
t
b
t
b
t
f
t
t
−
−
=
−
1
( )
(
)
1
2
p
k
p
k
t
b
t
f
t
t
−
=
−
( )
k
p
k
p
t
f
t
t
t
b
−
=
−
( )
k
p
k
p
t
f
t
t
t
b
−
+
=
t
i-1
n(
Δt
p,k
)
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
t
i
t
0
t
1
t
2
a, t
p
t
k-1
czas
N
s
b
c
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
≤
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
17
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
ale
ale
(
)
s
k
p
k
p
N
t
n
P
,
,
Δ
=
Δ
(
)
( )
2
,
k
p
k
k
p
t
f
t
t
P
⋅
−
=
Δ
(
) (
)
( )
2
,
k
p
k
s
k
p
t
f
t
t
N
t
n
⋅
−
=
Δ
( )
(
)
(
)
p
k
s
k
p
k
t
t
N
t
n
t
f
−
⋅
Δ
⋅
=
,
2
a stąd
( )
k
p
k
p
t
f
t
t
t
b
−
+
=
(
)
(
)
p
k
s
k
p
p
k
p
t
t
N
t
n
t
t
t
b
−
⋅
Δ
⋅
−
+
=
,
2
(
)
(
)
k
p
p
k
s
p
t
n
t
t
N
t
b
,
2
2
Δ
⋅
−
⋅
+
=
(
)
(
)
k
p
s
p
k
p
t
n
N
t
t
t
b
,
2
Δ
⋅
⋅
−
+
=
a stąd
(
)
(
)
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
Δ
⋅
⋅
−
+
=
5
,
0
2
ent
ˆ
,k
p
s
p
k
p
t
n
N
t
t
t
b
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
18
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
p
Estymatory parametrów rozkładu dla przypadku
1
:
Estymatory parametrów rozkładu dla przypadku
1
:
p
t
a
=
ˆ
TR(a,b,c)
(
)
(
)
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
Δ
⋅
⋅
−
+
=
5
,
0
2
ent
ˆ
,k
p
s
p
k
p
t
n
N
t
t
t
b
(
)
a
b
t
c
p
−
⋅
+
=
2
ˆ
t
i-1
n(
Δt
p,k
)
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
t
i
t
0
t
1
t
2
a, t
p
t
k-1
czas
N
s
b
c
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
≤
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
19
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
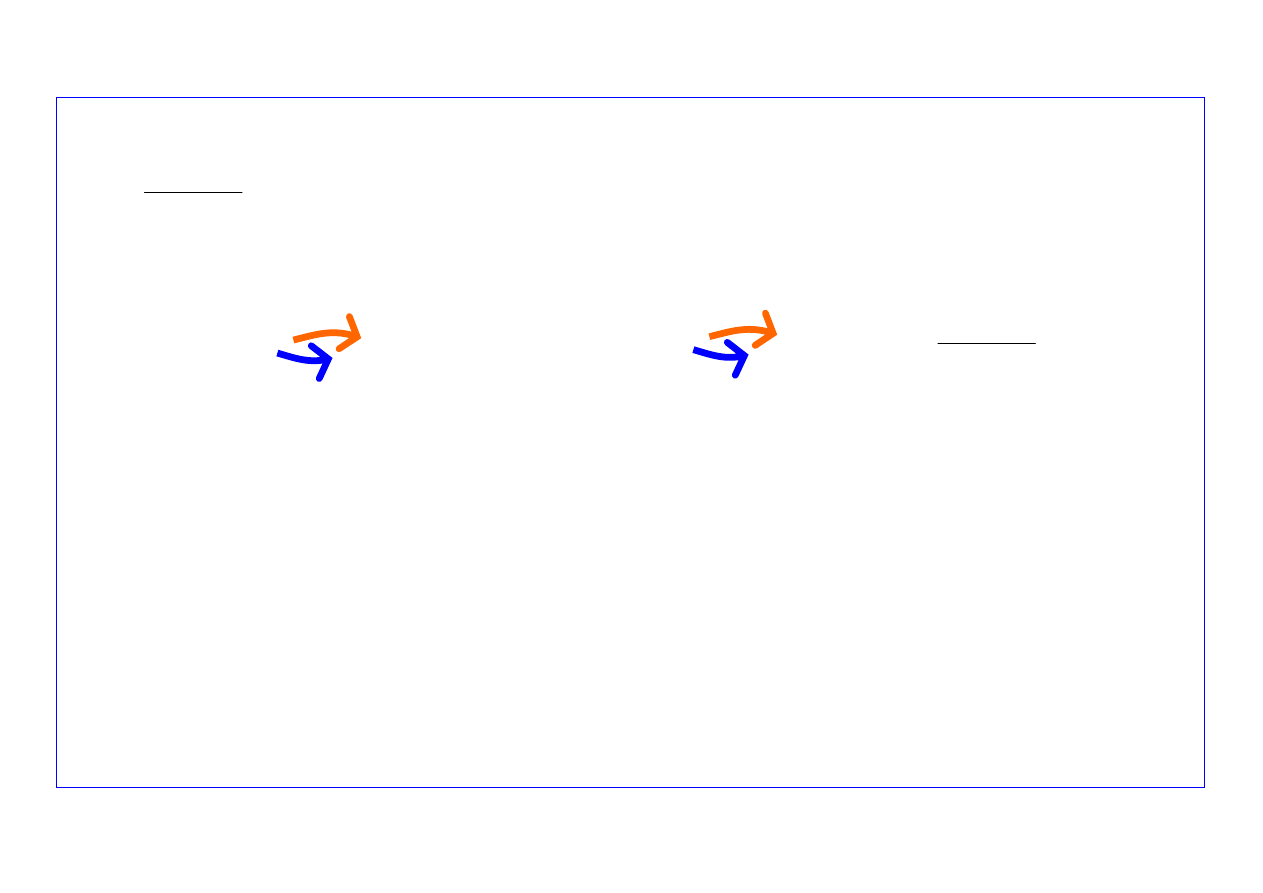
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
4
)
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
4
)
Poszukuje się przedziału czasu
(t
i-1
, t
i
]
życia grupy obiektów, dla którego spełnione są warunki:
Poszukuje się przedziału czasu
(t
i-1
, t
i
]
życia grupy obiektów, dla którego spełnione są warunki:
(
)
s
i
p
N
t
n
2
1
1
,
<
Δ
−
i
( )
s
i
p
N
t
n
2
1
,
≥
Δ
Jeżeli:
1
,
1
−
−
−
=
Δ
i
i
i
i
t
t
t
(
)
( )
( )
1
,
1
−
−
−
=
Δ
i
sk
sk
b
i
t
n
b
n
t
n
( )
( )
(
)
5
,
0
5
,
0
ent
+
⋅
+
=
s
p
sk
sk
N
t
n
b
n
t
i-1
n(
Δt
p,k
)
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
t
i
t
0
t
1
t
2
a, t
p
t
k-2
czas
N
s
b
c
t
k-1
t
i-1
t
i
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
>
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
20
/
27
A. KADZIŃSKI,
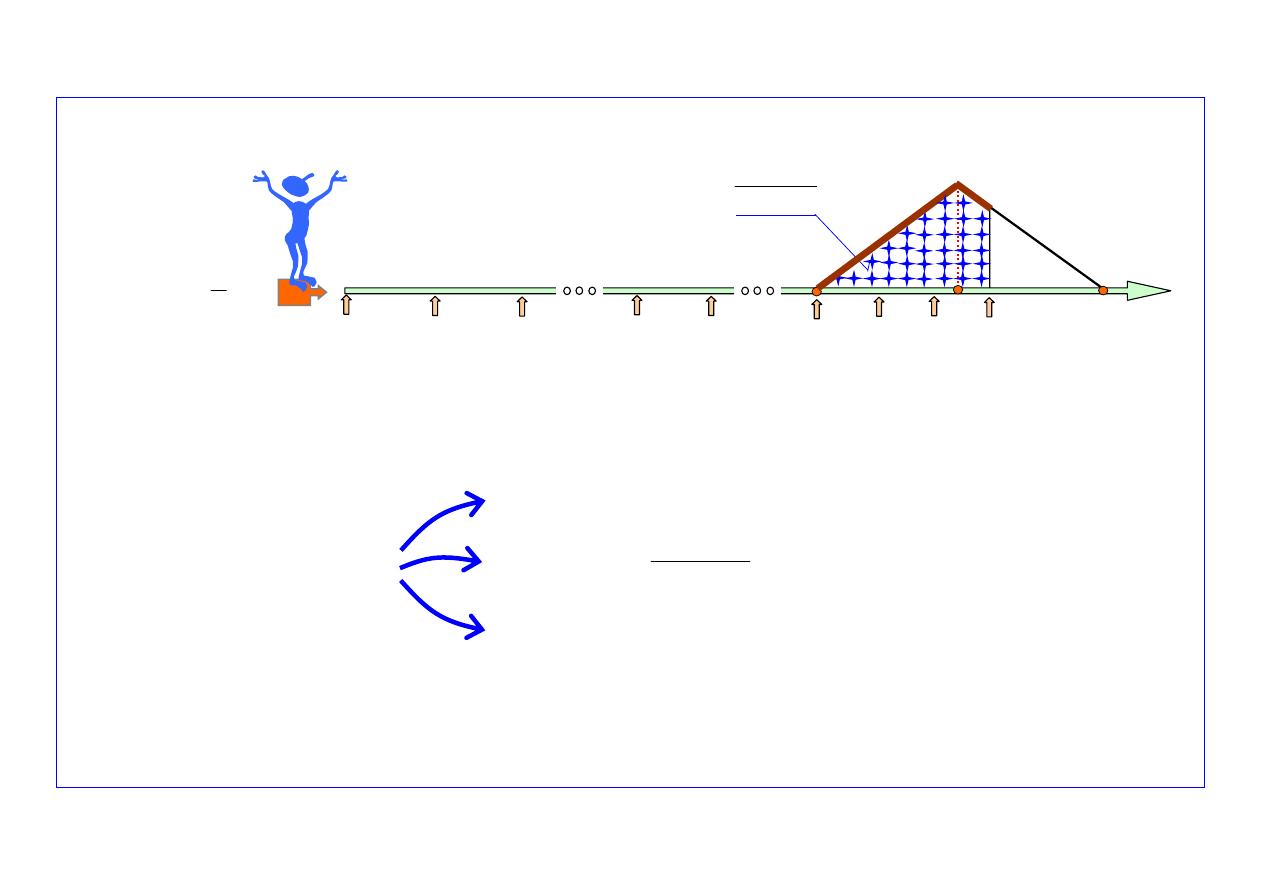
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
(
)
(
)
i
i
b
i
t
n
t
n
w
,
1
,
1
−
−
Δ
Δ
=
to:
b
i
i
t
t
b
,
1
1
−
−
Δ
+
=
(
)
5
,
0
ent
,
1
1
+
Δ
⋅
+
=
−
−
i
i
i
t
w
t
b
(
)
(
)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
Δ
⋅
Δ
Δ
+
=
−
−
−
−
5
,
0
ent
,
1
,
1
,
1
1
i
i
i
i
b
i
i
t
t
n
t
n
t
b
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
21
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
p
t
a
Estymatory parametrów rozkładu dla przypadku
2
:
Estymatory parametrów rozkładu dla przypadku
2
:
p
t
a
=
ˆ
TR(a,b,c)
(
)
(
)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
Δ
⋅
Δ
Δ
+
=
−
−
−
−
5
,
0
ent
ˆ
,
1
,
1
,
1
1
i
i
i
i
b
i
i
t
t
n
t
n
t
b
(
)
a
b
t
c
p
−
⋅
+
=
2
ˆ
t
i-1
n(
Δt
p,k
)
{n(
Δt
p,k
), N
s
}Ö
TR(a,b,c)
t
i
t
0
t
1
t
2
a, t
p
t
k-2
czas
N
s
b
c
t
k-1
t
i-1
t
i
t
k
(
)
s
k
p
N
t
n
2
1
Δ
,
>

Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
22
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
Prognostyczny model parametrów rozkładu uszkodzeń starzeniowych (
5
)
Obserwując uszkodzenia obiektów w kolejnych przedziałach czasu można wskazać chwilę
t
p
po-
czątku uszkodzeń starzeniowych. Pomocnym w tym względzie może być śledzenie przebiegów empi-
rycznych postaci funkcji
f
n
(t)
gęstości prawdopodobieństwa czasu
T
do uszkodzenia obiektów i funkcji
λ
n
(t)
intensywności uszkodzeń. Wartości tych funkcji na końcach przedziałów czasowych wyznacza
się z zależności:
( )
( )
( )
(
)
( )
...
,
,
i
t
N
t
n
t
t
N
t
n
t
n
t
f
i
i
i
i
sk
i
sk
i
n
2
1
,
1
1
=
Δ
⋅
Δ
=
−
⋅
−
=
−
−
,
(7)
( )
( )
( )
( )
[
]
(
)
( )
( )
[
]
...
,
,
i
t
t
n
N
t
n
t
t
t
n
N
t
n
t
n
t
i
sk
i
i
i
i
sk
i
sk
i
sk
i
n
2
1
,
1
1
1
1
=
Δ
⋅
−
Δ
=
−
⋅
−
−
=
−
−
−
−
λ
.
(8)
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
23
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
MODELE MATEMATYCZNE
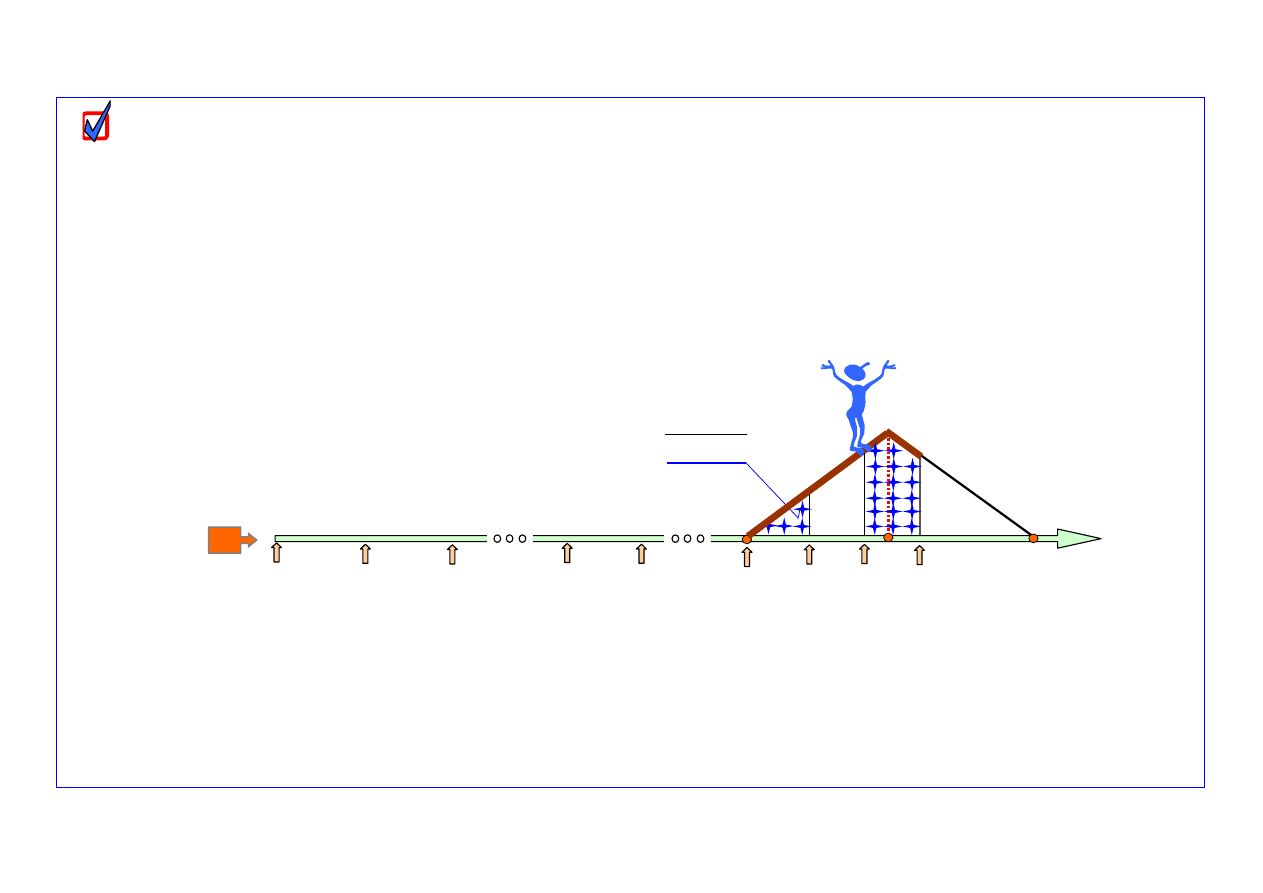
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
Idea prognostycznego modelu liczb uszkodzeń obiektów w okresie ich starzenia opiera się na
oszacowanych wcześniej wartościach parametrów rozkładu uszkodzeń starzeniowych i znajomości
liczby uszkodzonych obiektów od chwili
t
p
do chwili
t
k+j-1
początku okresu dokonywania prognozy.
Schemat ideowy algorytmu modelu prognozowania uszkodzeń pokazano na
rys. 3
.
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k
czas
n(
Δt
p,k
)
N
s
b
c
t
k+j-1
t
k+j
Rys. 3. Schemat ideowy prognostycznego modelu liczb uszkodzeń obiektów w okresie uszkodzeń starzeniowych
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
24
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
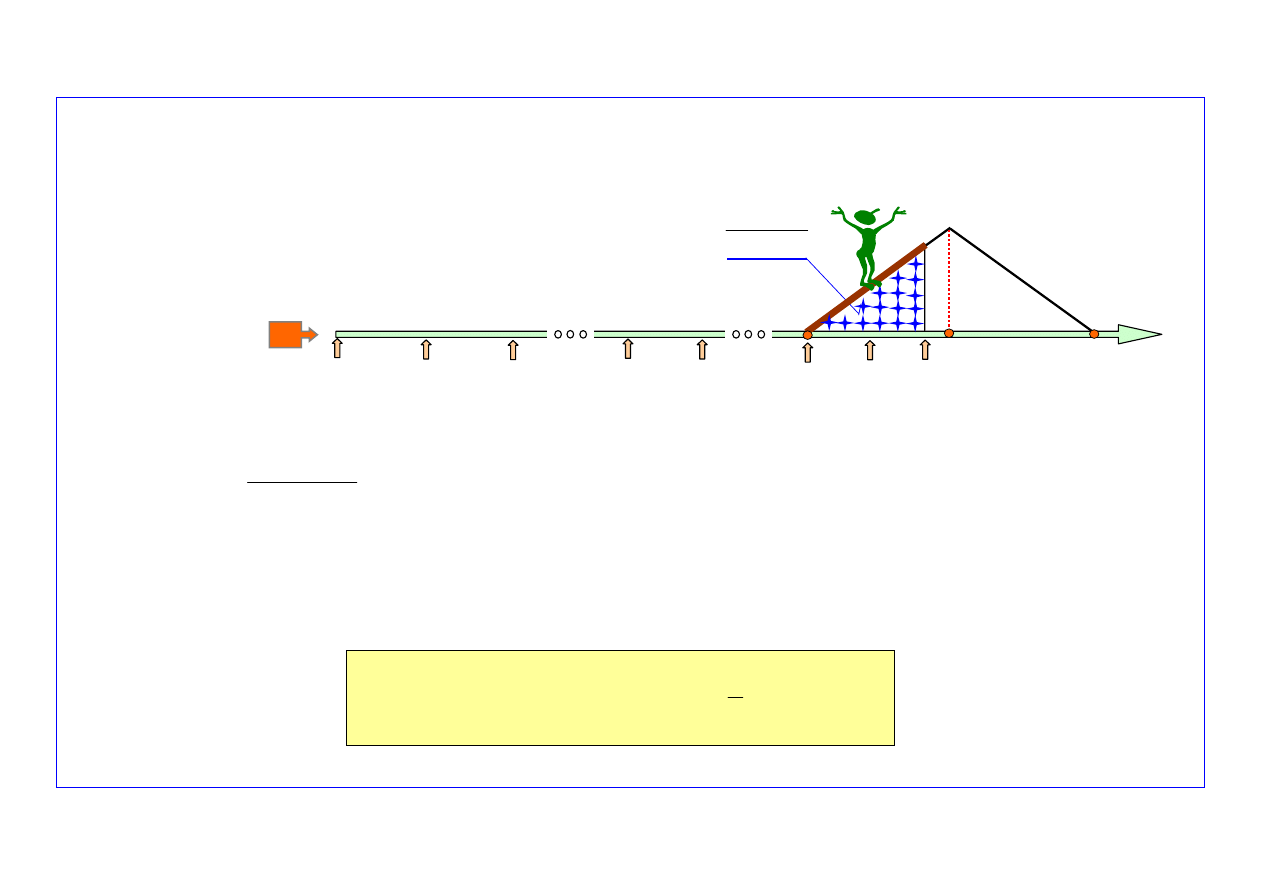
Krok 1-szy. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k
, t
k+1
)
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k
b
c
t
k+1
n(
Δt
p,k+1
)
N
s
czas
Wiadomo, że:
(
)
(
)
1
1
,
+
+
=
Δ
k
TR
s
k
p
t
F
N
t
n
(
)
(
)
1
1
,
+
+
⋅
=
Δ
k
TR
s
k
p
t
F
N
t
n
,
(19)
a gdy zauważy się, że:
(
) (
)
(
)
1
,
,
1
,
+
+
Δ
+
Δ
=
Δ
k
k
k
p
k
p
t
n
t
n
t
n
,
(20)
to liczbę uszkodzeń obiektów w przedziale czasu
(t
k
, t
k+1
)
można wyznaczyć z zależności:
(
)
(
)
(
)
k
p
k
TR
s
k
k
t
n
t
F
N
t
n
,
1
1
,
2
1
ent
Δ
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
+
+
.
(21)
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
25
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
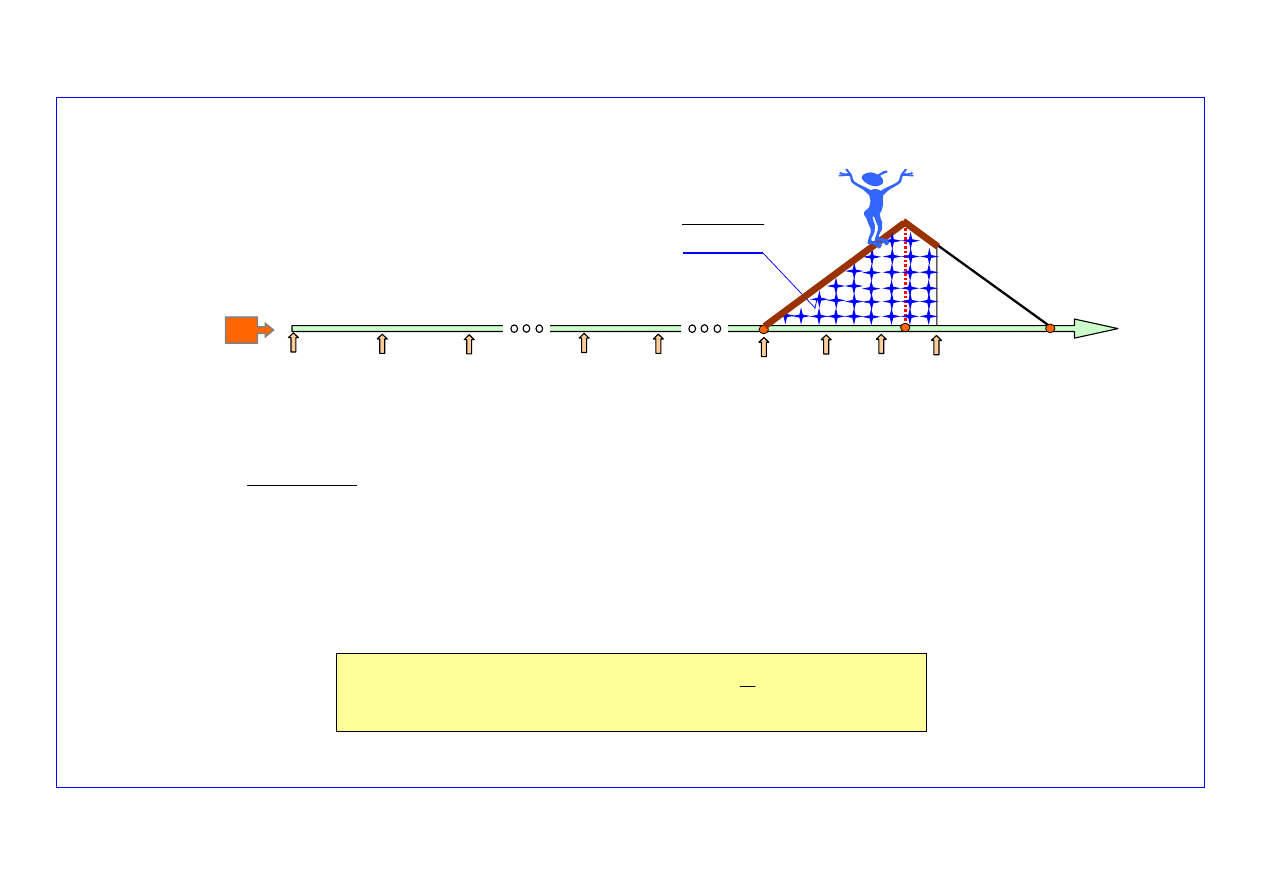
Krok 2-gi.
Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+1
, t
k+2
)
Krok 2-gi.
Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+1
, t
k+2
)
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k
czas
n(
Δt
p,k+2
)
N
s
b
c
t
k+1
t
k+2
Wiadomo, że:
Wiadomo, że:
(
)
(
)
2
2
,
+
+
=
Δ
k
TR
s
k
p
t
F
N
t
n
(
)
(
)
2
2
,
+
+
⋅
=
Δ
k
TR
s
k
p
t
F
N
t
n
,
(19)
a gdy zauważy się, że:
(
) (
)
(
)
2
,
1
1
,
2
,
+
+
+
+
Δ
+
Δ
=
Δ
k
k
k
p
k
p
t
n
t
n
t
n
,
(20)
to liczbę uszkodzeń obiektów w przedziale czasu
(t
k+1
, t
k+2
)
można wyznaczyć z zależności:
(
)
(
)
(
)
1
,
2
2
,
1
2
1
ent
+
+
+
+
Δ
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
Δ
k
p
k
TR
s
k
k
t
n
t
F
N
t
n
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
26
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
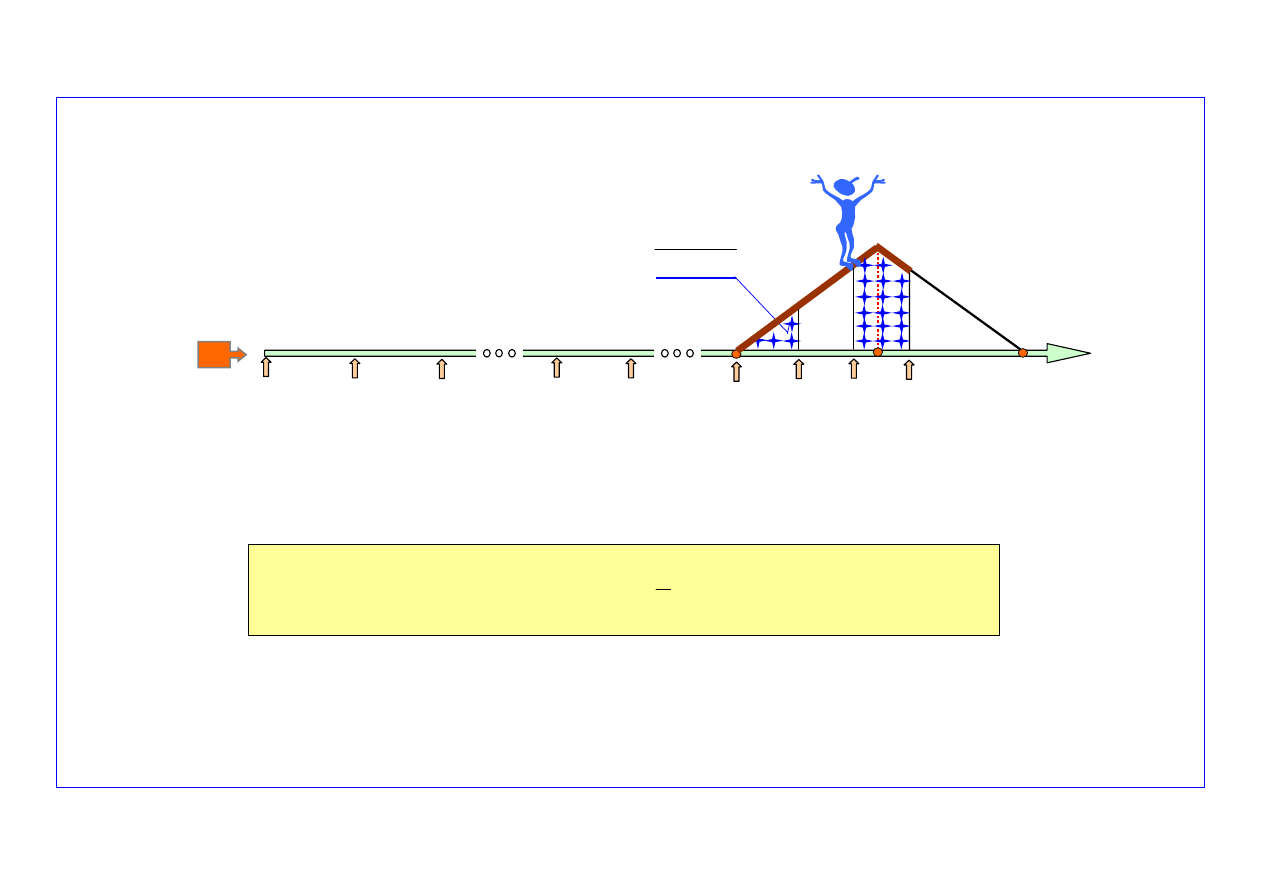
Krok j-ty. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+j-1
, t
k+j
)
Krok j-ty. Prognozowanie liczby uszkodzeń obiektów w przedziale czasu (t
k+j-1
, t
k+j
)
t
i-1
t
i
t
0
t
1
t
2
a, t
p
t
k
czas
n(
Δt
p,k
)
N
s
b
c
t
k+j-1
t
k+j
Uogólniając wyniki obliczeń uzyskane w krokach 1-szym i 2-gim, można zauważyć, że liczbę
uszkodzeń obiektów w przedziale czasu
(t
k+j-1
, t
k+j
)
,
j =1,2, ... , r,
(rys. 3) wskazuje zależność:
Uogólniając wyniki obliczeń uzyskane w krokach 1-szym i 2-gim, można zauważyć, że liczbę
uszkodzeń obiektów w przedziale czasu
(t
k+j-1
, t
k+j
)
,
j =1,2, ... , r,
(rys. 3) wskazuje zależność:
(
)
( )
(
)
r
...
,
,
j
t
n
t
F
N
t
n
j
k
p
j
k
TR
s
j
k
j
k
,
2
1
,
Δ
2
1
ent
Δ
1
,
,
1
=
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
=
−
+
+
+
−
+
,
(23)
Plik:
PP_Rozkład_trójkątny_Modele_Starzenie_obiektów_nieodnawianych_s_p_[v3]
27
/
27
A. KADZIŃSKI,
ANALIZA USZKODZEŃ OBIEKTÓW SYSTEMÓW W OKRESIE USZKODZEŃ STARZENIOWYCH ODWZOROWYWANYM ROZKŁADAM TRÓJKĄTNYM
PODSUMOWANIE
MODELE MATEMATYCZNE
Założenia
Prognostyczny model parametrów rozkładu trójkątnego jako rozkładu
uszkodzeń starzeniowych
Prognostyczny model liczby uszkodzeń obiektów w okresie ich starzenia
Document Outline
Wyszukiwarka
Podobne podstrony:
NiBS 2 Modele Starzenie obiektow nieodnawianych
modele starzenia się
2 0 Dla TR Sem3 Obiekty nieodnawiane charakterystyki niezawodnosci OT v1
Trójkąt Ossana starzenie
Obiekty techniczne jako obiekty eksploatacji ulegają starzeniu
8 Modele Obiektów i Układu Sterowania
17. Modele obliczeniowe konstrukcji obiektĂłw budowlanych, egzamin inz
Tarot - Rozkład Krzyża i Trójkąta [skrót], @ - Chirologia, Numerologia, I Ching itp, Tarot
NiBS 5 Zerowy czas odnowy Obiekty odnawiane
AUTOMATYKA, Liniowe modele obiektów i sposoby ich opisów1, POLITECHNIKA OPOLSKA
Obiekty techniczne jako obiekty eksploatacji ulegają starzeniu
Rozkład Krzyża i Trójkąta(2)
ROGOZ STANISŁAW EADI2 MODELE OBIEKTOW ZAD7
39 KP Modele obliczeniowe konstrukcji obiektów budowlanych
więcej podobnych podstron