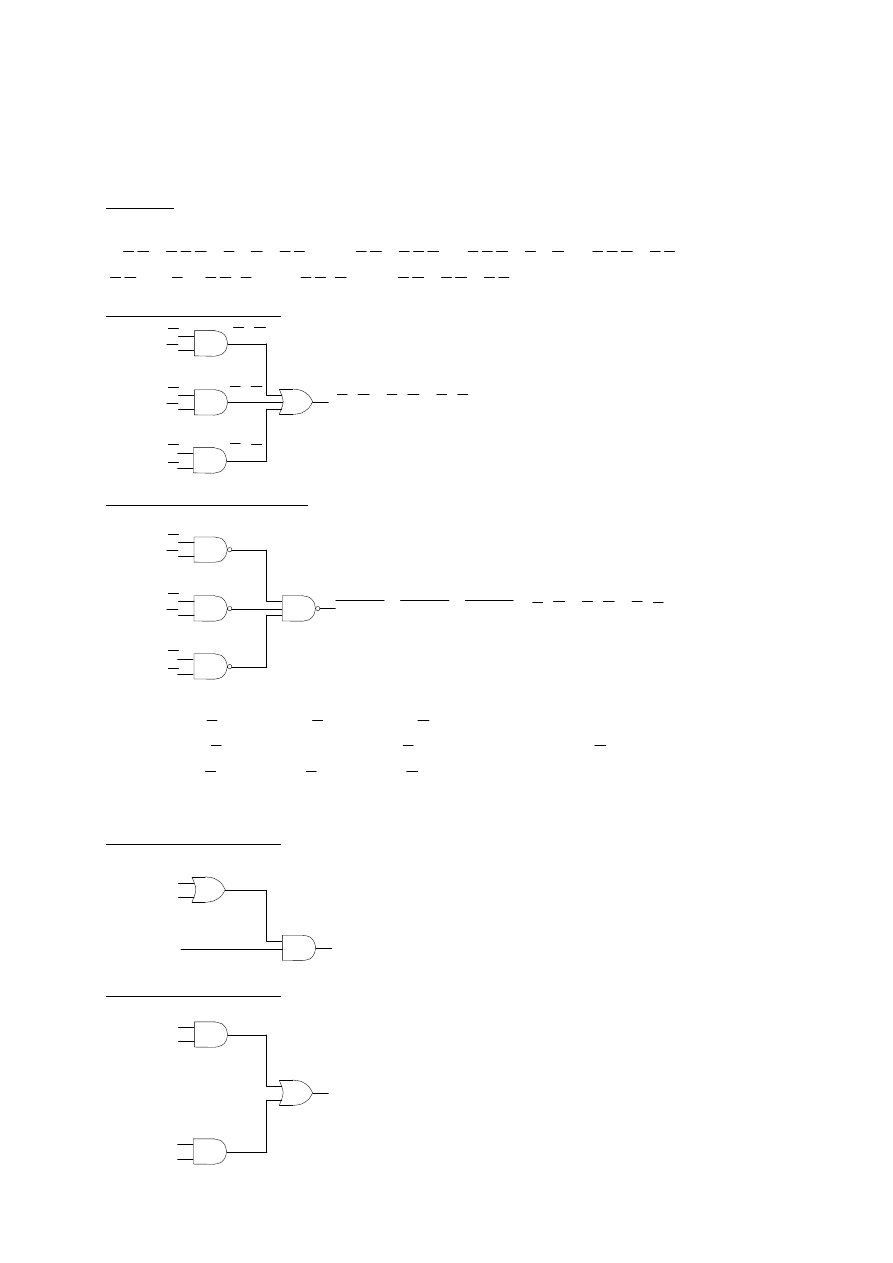
13
Ćwiczenia z algebry Boole’a
Rozwiążemy serię zadań dotyczących dotychczas omówionej problematyki.
Ćwiczenie.
Uprościć wyrażenie algebry Boole’a oraz podać jego realizację przy pomocy bramek:
a)
)
(
)
(
)
(
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
.
)
(
)
(
)
(
B
A
C
A
C
B
C
C
B
A
B
B
C
A
A
A
C
B
Realizacja typu And-to-Or:
Realizacja typu Nand-to-Nand:
b)
)
(
)
(
)
(
)
(
C
B
A
C
B
A
C
B
A
C
B
A
A
)
(
)
(
)
(
)
(
)
(
)
(
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
A
)
(
)
(
)
(
)
(
)
(
)
(
B
A
C
A
C
B
A
C
C
B
A
B
B
C
A
A
A
C
B
A
.
)
(
)
(
)
(
)
(
)
(
lub
C
A
B
A
C
B
A
A
A
C
B
B
A
A
C
A
A
C
B
Realizacja typu Or-to-And:
Realizacja typu And-to-Or:
C
B
C
A
C
B
C
A
B
A
C
A
C
B
A
B
B
A
C
B
A
B
A
)
(
C
B
A
B
A
B
A
AC
B
A
A
C
C
A
C
B
C
A
C
B
C
A
B
A
C
A
C
B
B
A
C
A
C
B
)
(
)
(
)
(
A
B
B
A
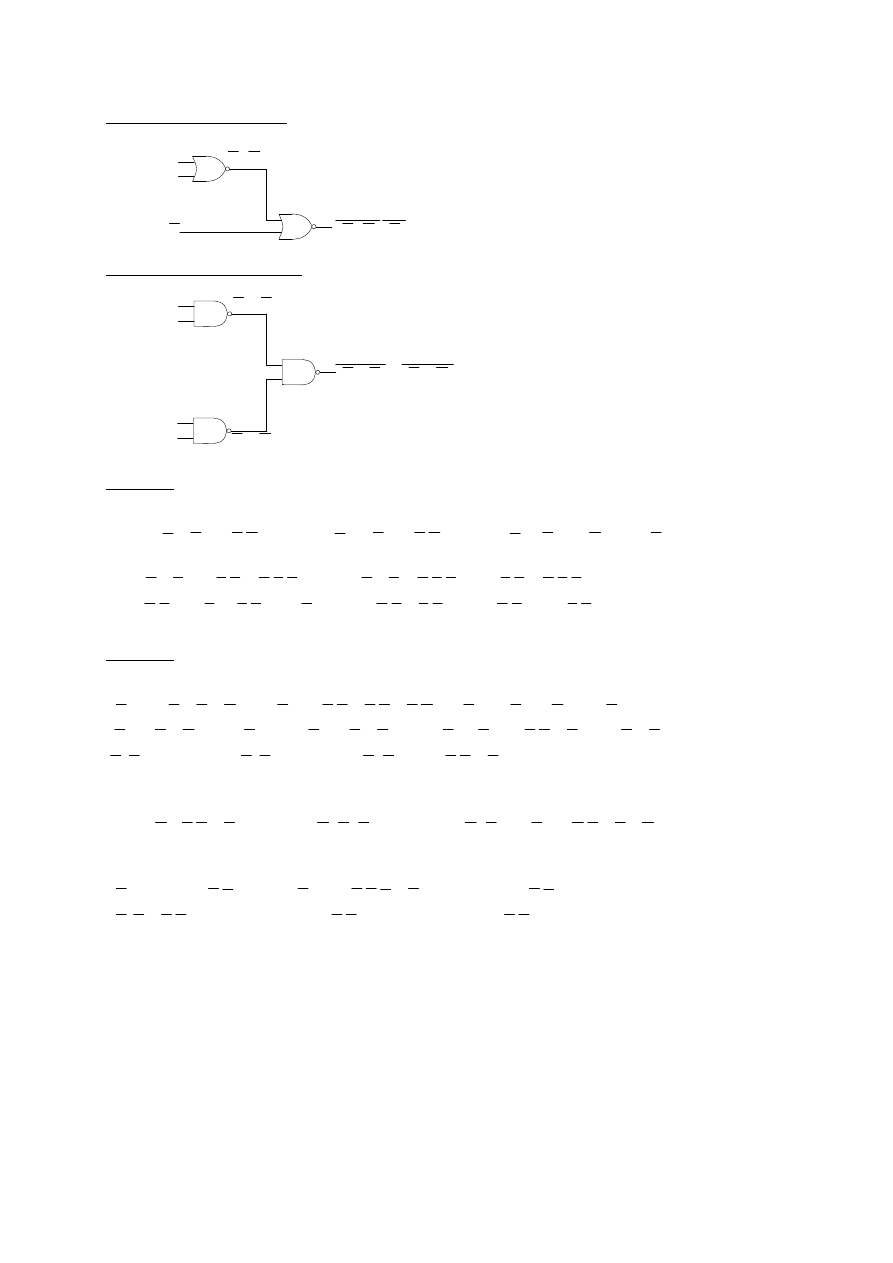
14
Realizacja typu Nor-to-Nor:
Realizacja typu Nand-toNand:
Ćwiczenie.
Uprościć wyrażenie algebry Boole’a:
a)
.
1
)
(
)
(
)
(
)
(
A
A
C
C
A
B
B
A
C
A
C
A
B
A
B
A
C
A
C
A
B
A
B
A
b)
)
(
)
(
)
(
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
Y
X
.
0
0
0
)
(
)
(
)
(
Z
Y
Y
X
Z
X
Y
X
Z
Y
Z
X
Y
X
X
X
Z
Y
Y
Y
Z
X
Y
X
Ćwiczenie.
Przekształcić wyrażenie do najprostszej postaci sumy iloczynów:
a)
)
(
)
(
)
(
)
(
)
(
B
A
C
C
B
C
A
C
C
A
B
A
A
A
B
A
C
B
A
C
A
)
(
)
(
)
(
)
(
)
1
(
B
C
B
A
C
B
B
A
A
A
B
A
C
B
A
B
A
C
B
C
C
B
A
.
)
(
)
1
(
)
(
C
B
B
A
C
A
B
A
C
A
B
C
C
A
A
B
b)
.
)
(
)
(
)
(
)
(
)
(
C
B
A
A
C
B
A
A
A
C
B
A
B
B
A
C
B
A
B
A
B
A
C
B
A
c)
C
A
C
B
A
C
B
A
C
C
A
A
B
A
A
B
A
A
C
A
B
A
B
A
C
A
)
(
)
(
.
)
1
(
)
1
(
)
(
)
(
C
A
B
A
B
C
A
C
B
A
C
A
C
B
A
C
B
A
B
A
B
A
B
A
C
A
B
A
C
A
B
A
)
(
)
(
A
C
C
A
C
B
A
C
B
A
C
B
A
C
B
)
(
)
(
)
(
15
Ćwiczenie.
Zaprojektować możliwie najprostsze wyrażenie logiczne w postaci kanonicznej sumy iloczynów,
przedstawić jego możliwe realizacje przy pomocy bramek:
Input
Output
X
Y
Z
A
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
0
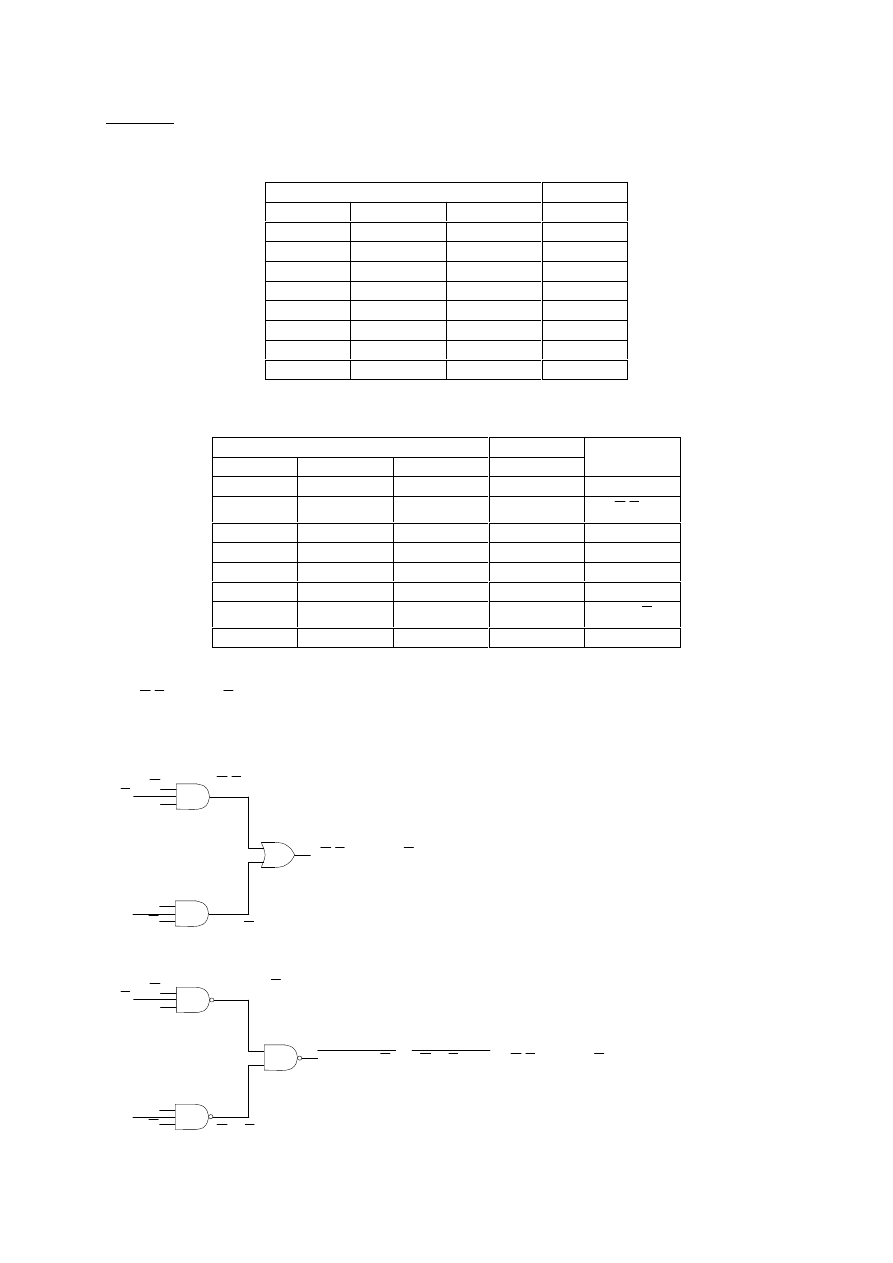
Dodajemy do tabeli definicyjnej dodatkową kolumnę iloczynów:
Input
Output
X
Y
Z
A
Iloczyny
0
0
0
0
0
0
1
1
Z
Y
X
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
Z
Y
X
1
1
1
0
Stąd szukane wyrażenie ma postać|:
.
Z
Y
X
Z
Y
X
A
Może być ono zrealizowane przy pomocy układu bramek typu And-to-Or lub Nand-to-Nand:
X
Z
Z
X
Y
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
Y
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
)
(
)
(
Z
Y
X
Z
X
Y
X
Z
Y
16
Ćwiczenie.
Zaprojektować możliwie najprostsze wyrażenie logiczne w postaci kanonicznej iloczynu sum,
przedstawić jego możliwe realizacje przy pomocy bramek:
Input
Output
A
B
C
Z
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
0
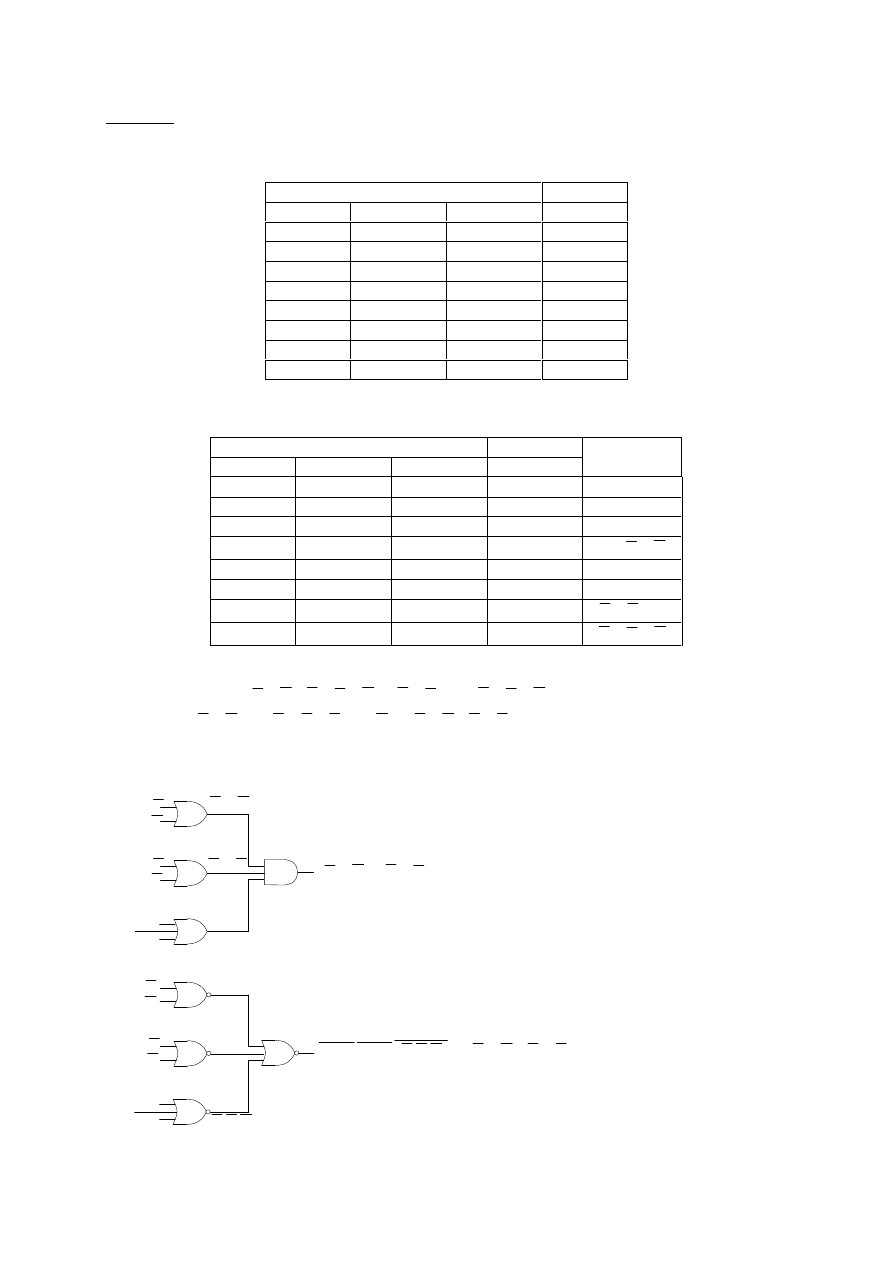
Dodajemy do tabeli definicyjnej dodatkową kolumnę sum:
Input
Output
A
B
C
Z
Sumy
0
0
0
0
C
B
A
0
0
1
1
0
1
0
1
0
1
1
0
C
B
A
1
0
0
1
1
0
1
1
1
1
0
0
C
B
A
1
1
1
0
C
B
A
Stąd szukane wyrażenie ma postać|:
)
(
)
(
)
(
)
(
)
(
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
A
).
(
)
(
)
(
)
(
)
(
)
(
C
B
A
B
A
C
B
C
C
B
A
A
A
C
B
C
B
A
Może być ono zrealizowane przy pomocy układu bramek typu Or-to-And lub Nor-to-Nor:
C
B
B
A
B A
C
C
B
B
A
)
(
)
(
)
(
C
B
A
B
A
C
B
C
B
A
C
B
C
B
B
A
C
B
A
)
(
)
(
)
(
)
(
)
(
)
(
C
B
A
B
A
C
B
C
B
A
B
A
C
B
B AC
B
A

17
Ćwiczenie.
Przekształcić wyrażenie do najprostszej postaci kanonicznej iloczynu sum, w przypadku b) podać jego
realizacje przy pomocy bramek:
a)
.
)
0
(
)
0
(
)
(
)
0
(
)
(
)
0
(
)
(
)
(
B
A
C
B
B
A
C
B
B
B
A
A
C
B
B
A
B
A
W
b)
.)
(
)
(
C
A
B
A
C
B
A
W
Wyjściowa postać wyrażenia W nie jest w żadnej postaci kanonicznej i dlatego przekształcimy
najpierw wyrażenie W do najprostszej postaci sumy iloczynów:
C
B
A
B
C
A
C
B
A
C
B
A
B
C
A
A
A
C
B
A
C
A
B
A
C
B
A
W
)
(
)
(
)
(
)
(
)
(
)
(
)
1
(
A
C
B
B
A
A
C
B
C
A
A
A
C
B
B
A
C
A
C
B
B
A
B
C
A
.
)
1
(
)
1
(
B
A
C
A
C
B
A
B
C
A
A stąd stosując prawa de’Morgana otrzymujemy szukane rozwiązanie:
.)
(
)
(
)
(
B
A
C
A
W
W
Może być ono zrealizowane przy pomocy układu bramek typu Or-to-And lub Nor-to-Nor:
c)
.)
(
)
(
D
B
C
B
A
B
A
W
Postępujemy w analogiczny sposób jak w poprzednim rozwiązaniu:
D
B
B
C
B
B
A
B
D
B
A
C
B
A
A
A
D
B
C
B
A
B
A
W
)
(
)
(
,
)
1
(
)
(
B
A
C
B
D
B
A
B
A
D
B
A
A
C
B
A
B
D
B
A
C
B
C
B
A
0skąd
.)
(
)
(
)
(
B
A
C
B
D
B
A
W
C
A
C
A
B
B
A
C
A
B
A
A
C
C
A
B
A
C
A
B
A
C
A
B
A
A
A
B

18
Mapy Karnaugh
Omówimy pewną metodę definiowania i upraszczania wyrażeń algebry Boole’a, która
wykorzystuje tzw. mapy Karnaugh. Opiszemy ja przy pomocy przykładów.
Przykłady
a) Przykładem mapy Karnaugh dla dwóch zmiennych wejściowych
Y
X , i zmiennej wyjściowej A
jest tabliczka
0
1
0
1
przedstawiana alternatywnie w postaci
0
1
0
1
Definiuje ona wyrażenie
.
Y
X
Y
X
A
b) Przykładem mapy Karnaugh dla trzech zmiennych wejściowych
Z
Y
X
,
,
i zmiennej wyjściowej A
jest tabliczka
1
0
0
1
0
1
1
0
przedstawiana alternatywnie w postaci
1
0
0
1
0
1
1
0
Definiuje ona wyrażenie
.
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
A
c) Przykładem mapy Karnaugh dla czterech zmiennych wejściowych
Z
Y
X
W
,
,
,
i zmiennej wyjścio-
wej A jest tabliczka
1
0
0
1
0
1
1
0
1
1
0
0
1
1
0
1
przedstawiana alternatywnie w postaci
Definiuje ona wyrażenie
.
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
A
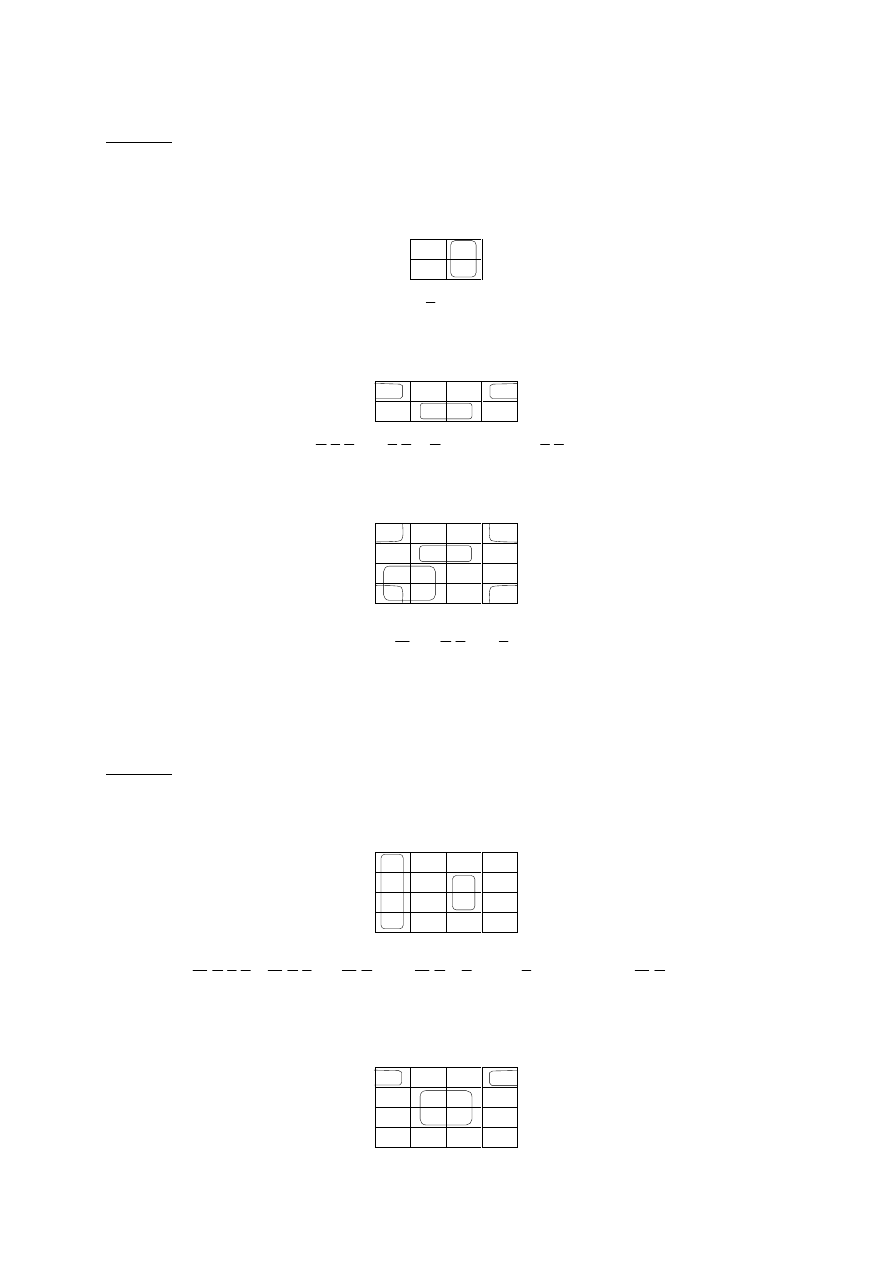
Na potrzebę upraszczania wyrażeń algebry Boole’a wyróżnia się grupy komórek tworzące
tzw. subcubes (z języka angielskiego). Ilość takich komórek musi się wyrażać liczbą naturalną będącą
potęgą całkowitą liczby 2 i muszą one tworzyć figurę w kształcie prostokąta z uwzględnieniem efektu
zawijania mapy.
1
0
0
1
0
1
1
0
1
1
0
0
1
1
0
1
X
Y
X
X
Y
Y
Y
1
0
0
1
Y
Y
X
Y
X
Y
X
Y
X
Z
Z
00 01 11 10
X Y
0
1
Z
X
W
X
W
X
W
X
W
Z
Y
00 01 11 10
W X
Z
Y
Z
Y
Z
Y
00
01
11
10
Y Z
19
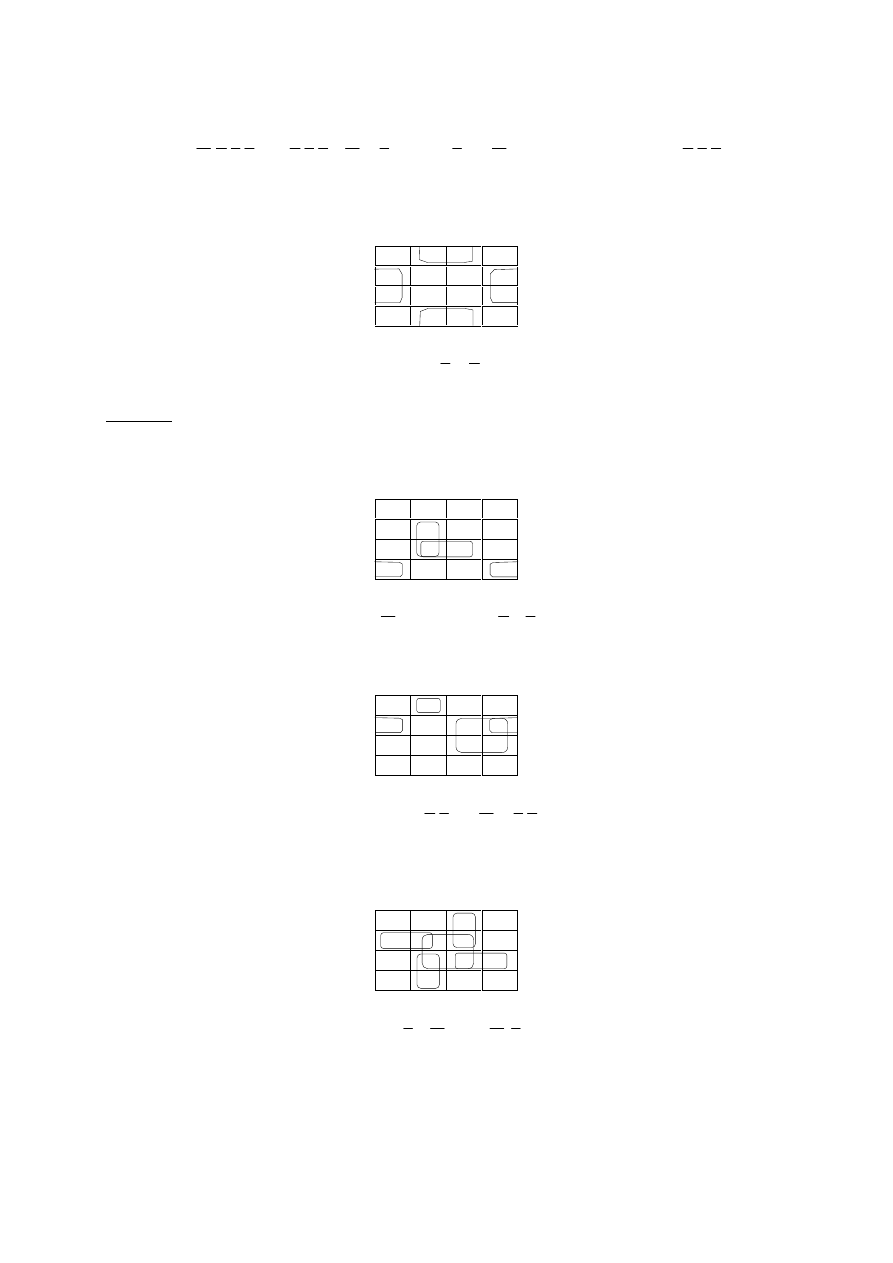
Przykłady
Zademonstrujemy zdefiniowane wyżej pojęcie subcube upraszczając wyrażenia z poprzedniego
przykładu.
a)
0
1
0
1
Stąd
.
X
Y
X
Y
X
A
b)
1
0
0
1
0
1
1
0
Stąd
.
Z
Y
Z
Y
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
A
c)
Stąd
.
Z
Y
X
Z
X
Y
W
A
Prześledzimy serię przykładów ilustrujących proces redukcji wyrażeń algebry Boole’a przy
pomocy map Karnaugh. Na razie ograniczymy się do przypadku wyrażeń w postaci kanonicznej sumy
iloczynów.
Przykłady.
a)
Stąd
.
Z
X
W
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
A
b)
1
0
0
1
0
1
1
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
X
Y
1
0
0
1
Y
00 01 11 10
X Y
0
1
Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
20
Stąd
.
Z
Y
X
Z
X
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
A
c)
Stąd
.
Z
X
Z
X
A
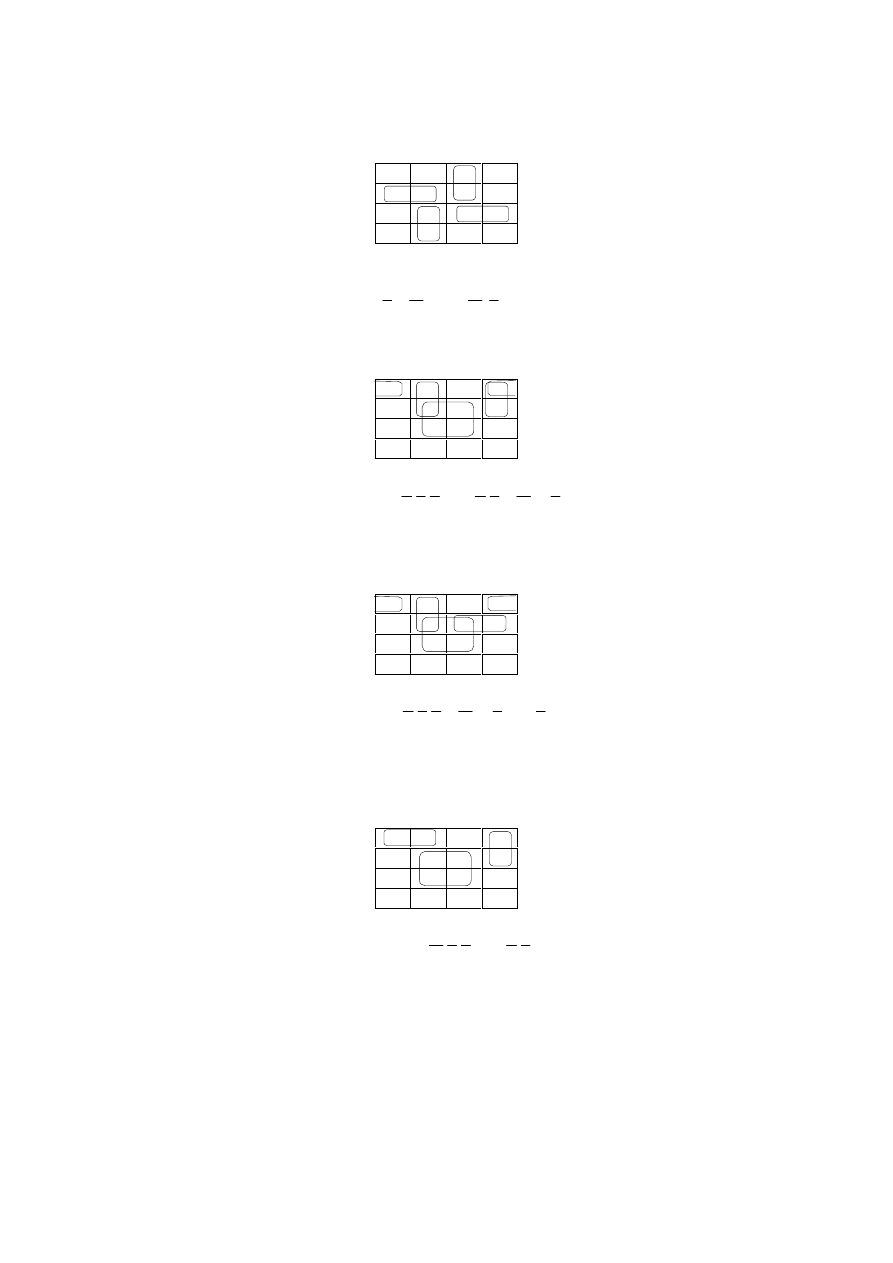
Przykłady.
a)
Stąd
.
Z
Y
X
Z
Y
X
Z
X
W
A
b)
Stąd
.
Z
Y
X
W
Z
Y
X
Z
W
A
c)
Stąd
.
Z
Y
W
Z
Y
W
Y
X
W
Y
X
W
Z
X
A
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
21
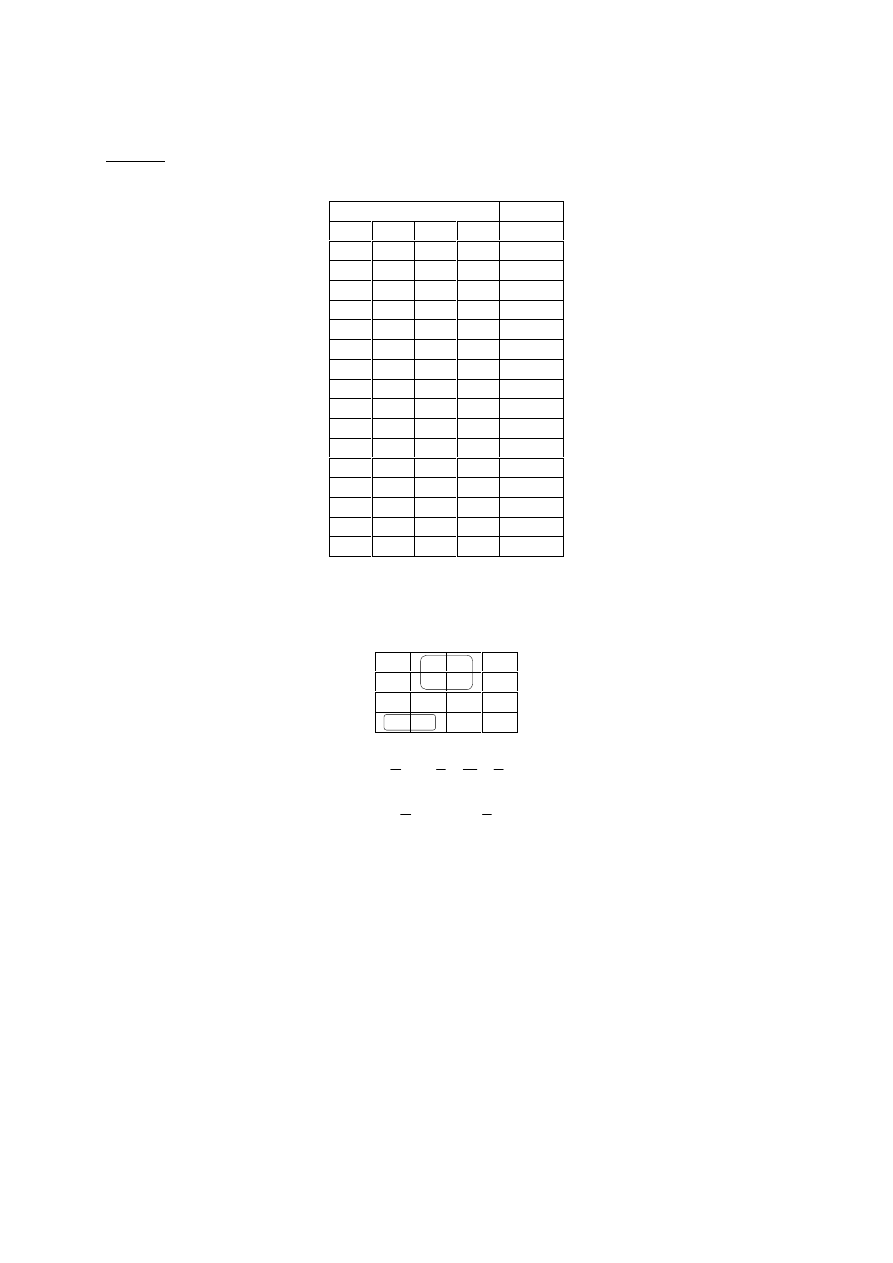
Inne rozwiązanie:
Stąd
.
Z
Y
W
Z
Y
W
Y
X
W
Y
X
W
A
d)
Stąd
.
Y
X
W
Y
X
W
Z
Y
X
Z
X
A
Inne rozwiązanie:
Stąd
.
Z
Y
W
Y
X
W
Z
Y
X
Z
X
A
Najprostsze rozwiązanie:
Stąd
.
Y
X
W
Z
Y
W
Z
X
A
Mapy Karnaugh mogą być zastosowane również do projektowania i upraszczania wyrażeń
w postaci kanonicznej iloczynu sum. Wykorzystuje się tu fakt, że dopełnienie wyrażenia każdej z pos-
taci kanonicznych jest wyrażeniem drugiej z tych postaci. Dlatego w omawianym przypadku stosuje
się następujące postępowanie:
1
0
Tworzy się mapę wpisując we właściwych komórkach zera.
2
0
Upraszcza się wyróżnione w ten sposób komórki tak, jak się to robiło dla „jedynek”.
3
0
Otrzymane w ten sposób wyrażenie jest dopełnieniem wyrażenia szukanego i dlatego
wystarczy na koniec zastosować prawa de’Morgana.
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
22
Zilustrujmy zapowiedzianą metodę.
Przykład
Zaprojektujemy najprostsze wyrażenie w postaci iloczynu sum spełniające założenia:
Input
Output
W
X
Y
Z
A
0
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
0
1
0
1
1
0
1
1
1
1
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
Tworzymy mapę Karnaugh szukanego wyrażenia uwidoczniając położenie zer i ją upraszczamy:
Stąd
Z
Y
W
Y
X
A
i dlatego
.)
(
)
(
Z
Y
W
Y
X
A
Często spotykaną sytuacją jest przypadek projektów, kiedy wartość wyjściowa dla niektórych
danych wejściowych jest nieistotna, np. wtedy, gdy wartości takie nigdy nie wystąpią. W takich
przypadkach mamy swobodę wyboru wartości wyjściowych, co można wykorzystać w celu uzyskania
możliwie najprostszego rozwiązania.
0
0
0
0
0
0
00 01 11 10
W X
00
01
11
10
Y Z
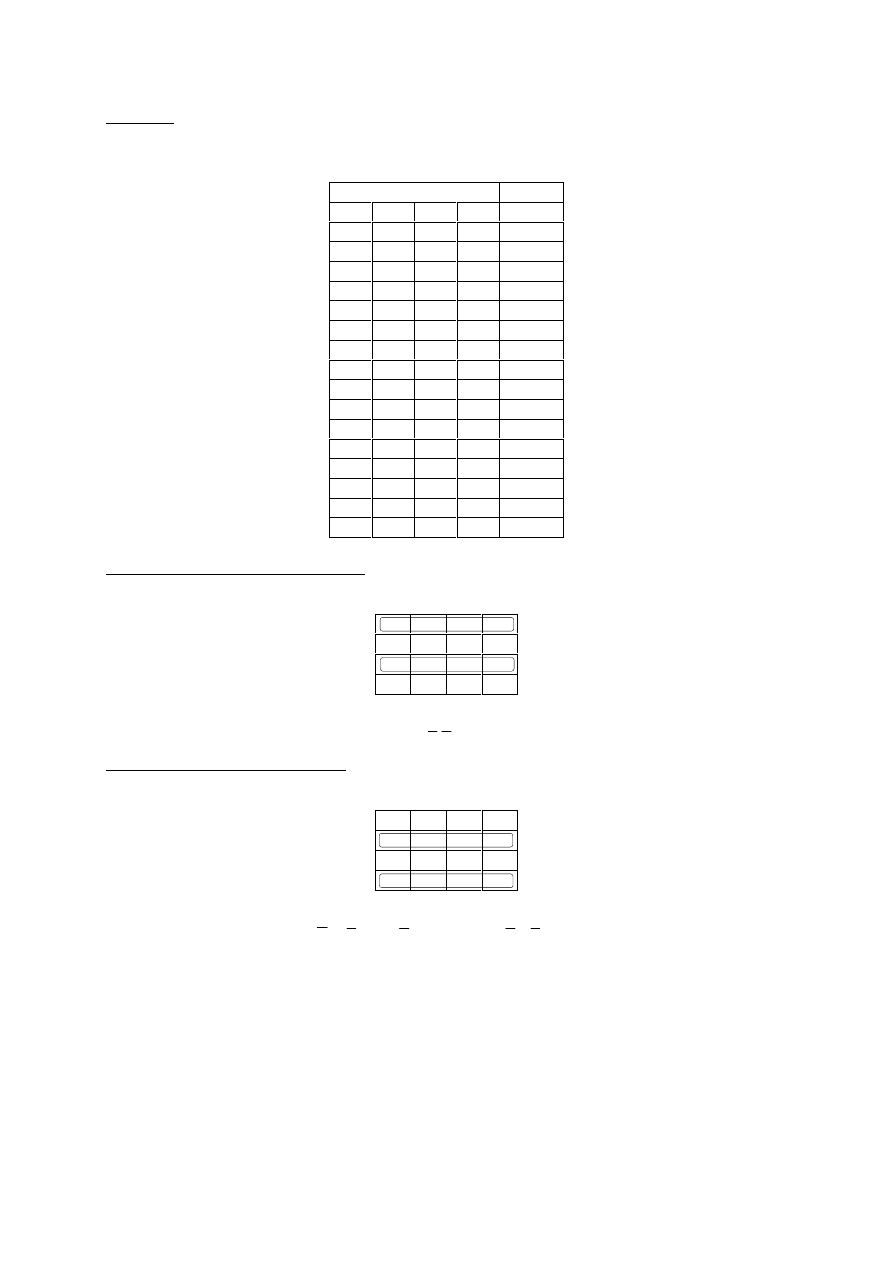
23
Ćwiczenie
Zaprojektujemy najprostsze wyrażenia w postaci sumy iloczynów i iloczynu sum spełniające
założenia:
Input
Output
W
X
Y
Z
A
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
1
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
d
1
0
1
1
d
1
1
0
0
d
1
1
0
1
d
1
1
1
0
d
1
1
1
1
d
gdzie d oznacza wartość dowolną, tj. 0 lub 1.
Rozwiązanie w postaci sumy iloczynów:
Stąd
.
Z
Y
Z
Y
A
Rozwiązanie w postaci iloczynu sum:
Stąd
.)
(
)
(
Z
Y
Z
Y
A
Z
Y
Z
Y
A
1
1
d
1
d
1
1
d
d
d
d
d
0
0
d
0
d
d
0
0
d
d
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z

24
Ćwiczenia podsumowujące
Rozwiążemy serię zadań utrwalających i uzupełniających omówioną tematykę.
Ćwiczenie.
Zaznacz grupy komórek tworzących subcube dla danego wyrażenia zależnego od zmiennych
W, X, Y, Z wyznaczające po redukcji wskazaną wartość:
a)
.
X
b)
.
Z
Y
X
c)
.
Z
W
d)
.
Z
Y
X
W
Ćwiczenie.
Narysować mapę Karnaugh wyrażenia zależnego od zmiennych X, Y, Z i, jeżeli trzeba, uprościć je:
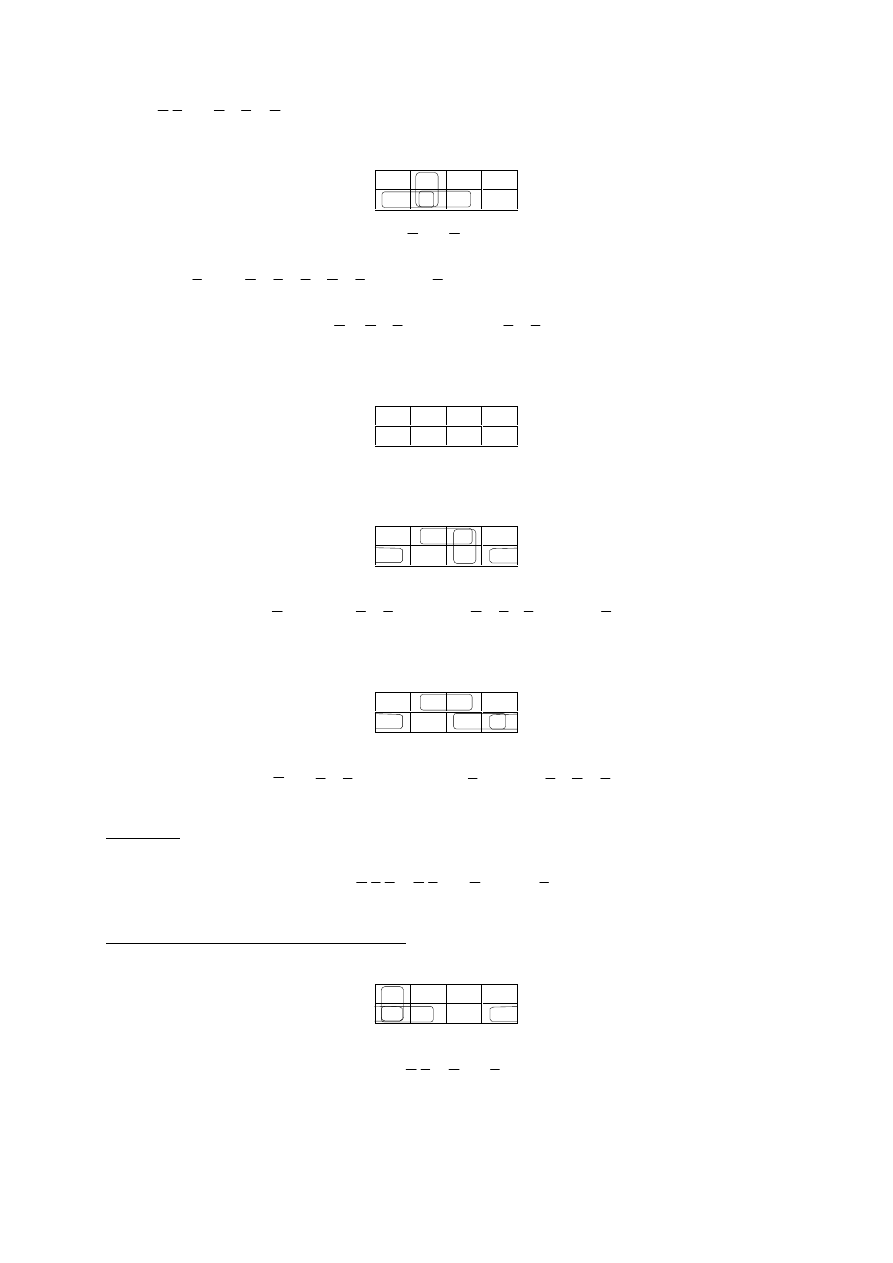
a)
.
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
A
1
1
1
1
Stąd
.
Z
X
Y
X
A
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
X Y
0
1
Z
25
b)
.
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
A
1
1
1
1
Stąd
.
Z
Y
Z
X
Y
X
A
c)
.)
(
)
(
)
(
)
(
Z
Y
Z
Y
X
Z
Y
X
Z
Y
X
A
Mamy
,
Z
Y
Z
Y
X
Z
Y
X
Z
Y
X
A
skąd mapa ma postać:
0
0
0
0
0
Jednym z możliwych uproszczeń jest
0
0
0
0
0
i wtedy
.)
(
)
(
)
(
Z
Y
Z
Y
Y
X
A
Z
Y
Z
Y
Y
X
A
Innym uproszczeniem jest
0
0
0
0
0
i wtedy
.)
(
)
(
)
(
Z
X
Z
Y
Z
Y
A
Z
X
Z
Y
Z
Y
A
Ćwiczenie.
Narysować mapy Karnaugh wyrażenia A zależnego od zmiennych X, Y, Z i przy ich pomocy znaleźć
jego najprostsze postacie sumy iloczynów i iloczynu sum:
.
Z
Y
X
Z
Y
X
Z
Y
X
Z
Y
X
A
Mapa i uproszczenie dla sumy iloczynów:
1
1
1
1
Stąd
.
Z
Y
Z
X
Y
X
A
0
00 01 11 10
X Y
0
1
Z
00 01 11 10
X Y
0
1
Z
00 01 11 10
X Y
0
1
Z
00 01 11 10
0
1
Z
00 01 11 10
X Y
0
1
Z
26
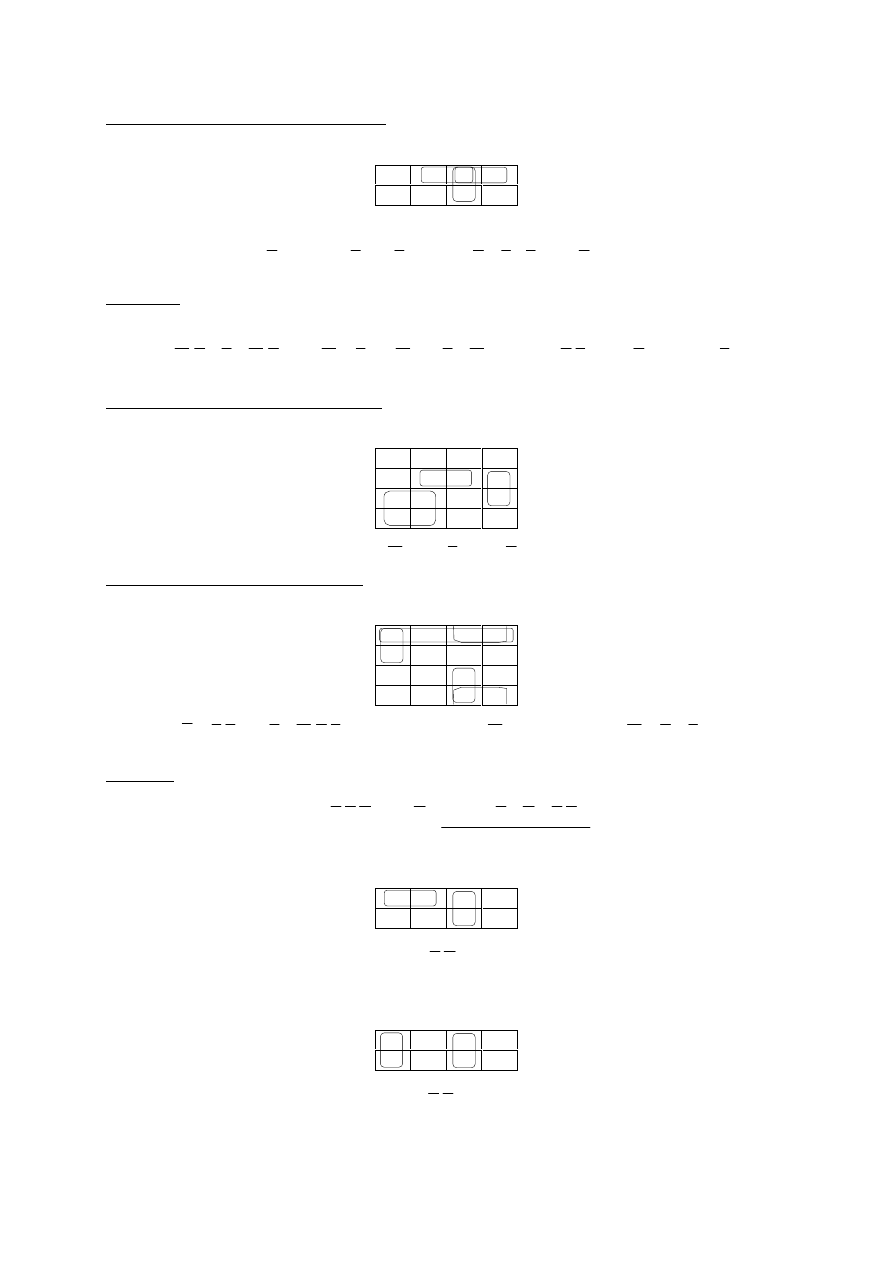
Mapa i uproszczenie dla iloczynu sum:
0
0
0
0
Stąd
.)
(
)
(
)
(
Z
X
Z
Y
Y
X
A
Z
X
Z
Y
Y
X
A
Ćwiczenie.
Narysować mapy Karnaugh wyrażenia A zależnego od zmiennych W, X, Y, Z i przy ich pomocy
znaleźć jego najprostsze postacie sumy iloczynów i iloczynu sum:
.
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
Z
Y
X
W
A
Mapa i uproszczenie dla sumy iloczynów:
Stąd
.
Z
X
W
Z
Y
X
Y
W
A
Mapa i uproszczenie dla iloczynu sum:
Stąd
.)
(
)
(
)
(
)
(
Y
X
W
Y
X
W
Z
W
Z
Y
Y
X
W
Y
X
W
Z
W
Z
Y
A
Ćwiczenie
Uprościć wyrażenie zakładając, że każdy składnik części podkreślonej może, ale nie musi wystąpić:
.
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
W
Mapa Karnaugh wyrażenia ma postać:
1
d
1
d
d
Stąd
B
A
C
A
W
Inna wersja rozwiązania (nie jedyna):
1
d
1
d
d
Stąd
.
B
A
B
A
W
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
00 01 11 10
X Y
0
1
Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
W X
00
01
11
10
Y Z
00 01 11 10
0
1
C
Z
A B
00 01 11 10
0
1
C
A B

27
Ćwiczenie
Uprościć wyrażenie zakładając, że każdy czynnik części podkreślonej może, ale nie musi wystąpić:
.)
(
)
(
)
(
)
(
)
(
)
(
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
W
Mapa Karnaugh wyrażenia ma postać:
Stąd
.
B
A
W
B
A
W
Powyższe rozwiązanie otrzymuje się, jeżeli uwzględnia się dwa pierwsze czynniki części
podkreślonej:
)
(
)
(
)
(
)
(
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
W
.
)
(
)
(
)
(
)
(
)
(
B
A
C
C
B
A
C
B
A
C
B
A
D
D
C
B
A
D
D
C
B
A
d
d
d
d
0
0
00 01 11 10
00
01
11
10
CD
Y Z
Y Z
AB
Wyszukiwarka
Podobne podstrony:
Algebra Boole'a
ALGEBRA BOOLE
Algebra Boole
Algebra Boole'a 1
Prawa logiczne w algebrze Boole'a
Podstawy algebry Boole
Algebra Boole, Informatyka
F1-18 Algebra Boole'a 2
F1-17 Algebra Boole'a 1
Prawa logiczne w algebrze Boole'a
F1 17 Algebra Boole'a 1
Zerówki, ściąga elektronika, Algebra Boole'a - zbiór B, wyróżniony jego podzbiór O i I oraz operacje
ALGEBRA BOOLE’A; SYNTEZA UKŁADÓW KOMBINACYJNYCH
Algebra Boole'a
Prawa logiczne w algebrze Boole a
Algebra Boole a
więcej podobnych podstron