Autor opracowania: Marek Walesiak

1

PROJEKT B – MODEL LINIOWY

z dwiema zmiennymi objaśniającymi

Nazwisko i imię studenta 1: ..........................................
Kierunek i rok studiów studenta 1: ......
Numer grupy studenta 1: .....

Nazwisko i imię studenta 2: ..........................................
Kierunek i rok studiów studenta 2: ......
Numer grupy studenta 2: .....

Uwagi dla studentów:

1. Program R należy pobrać ze strony: http://cran.r-project.org/
2. Co najmniej jeden projekt (A, B, C, D) należy przesłać na e-mail prowadzącego laboratoria
3. Projekty można wykonywać osobiście lub w zespołach dwuosobowych (liczba zrealizowanych

projektów oraz jakość i estetyka wykonania będzie decydować o ocenie z laboratorium dla
przedmiotu Ekonometria)

4. Liczba obserwacji (dane w postaci szeregów przekrojowych z roku 2009 lub 2010) w projekcie

A, B oraz C musi wynosić co najmniej 12, a w projekcie D co najmniej 30. Dla danych staty-
stycznych należy koniecznie podać źródło

5. Nie wolno w projektach stosować zmiennych użytych w przykładowych projektach prezentowa-

nych na laboratoriach (nie dotyczy projektu C)

6. Wraz z każdym projektem opracowanym w edytorze Word (może też być jego odpowiednik z

pakietu OpenOffice) należy przesłać:
a) plik (pliki) danych w formacie csv
b) odpowiednie procedury w programie R

7. Termin przesłania projektu (projektów): do 03 stycznia 2012 roku
8. Proszę przesyłać projekty z własnych e-maili podając w e-mailu skład zespołu (imię i nazwisko,

rok i forma studiów, numer grupy lub specjalność)

9. Warunkiem przyjęcia projektu (projektów) jest uzyskanie pozytywnej odpowiedzi od prowadzą-

cego laboratoria

10. Odpowiedzi na e-maile informujące o akceptacji projektu lub projektów będą przesyłane w cią-

gu siedmiu dni od ich nadesłania

11. Odrzucane będą projekty, które wykonali inni studenci

Autor opracowania: Marek Walesiak

2

PROJEKT B – MODEL LINIOWY

z dwiema zmiennymi objaśniającymi

1. Zebrać z Roczników Statystycznych co najmniej 12 obserwacji na zmiennej objaśnianej i

dwóch zmiennych objaśniających (dane w postaci szeregów przekrojowych)

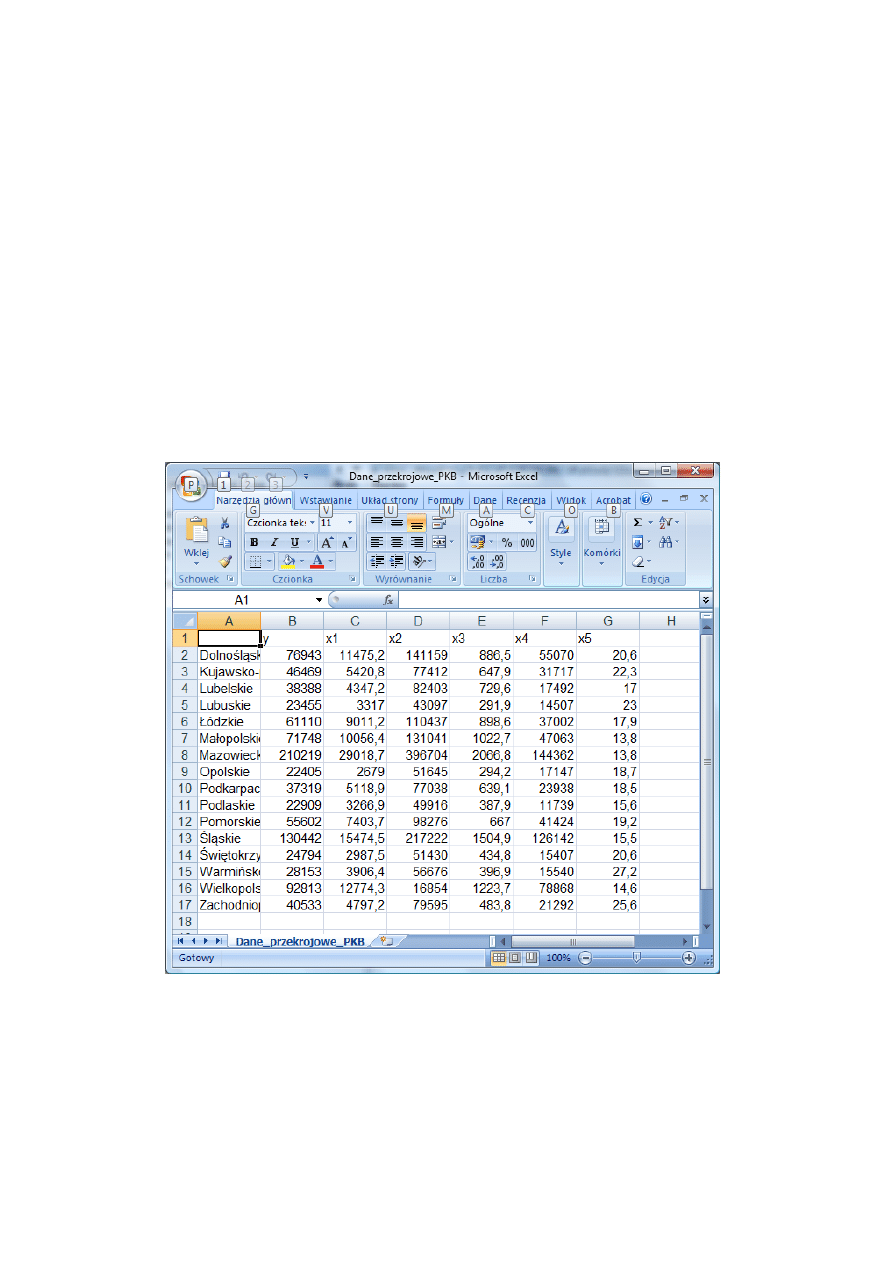
Dane przekrojowe (wg województw Polski w roku 2005)

y – produkt krajowy brutto województwa Polski w mln zł (ceny bieżące),
x1 – nakłady inwestycyjne w województwie w mln zł (ceny bieżące),
x2 – wartość brutto środków trwałych województwa w mln zł (bieżące ceny ewidencyjne),
x3 – pracujący w województwie w tys. osób,
x4 – produkcja sprzedana przemysłu województwa w mln zł (ceny bieżące),
x5 – stopa bezrobocia rejestrowanego w województwie w %.
Źródło: dane dotyczące produktu krajowego brutto są z Rocznika statystycznego województw 2007, pozo-

stałe z Rocznika statystycznego województw 2006.

a) wprowadzić dane statystyczne do programu EXCEL w następującym układzie:

Plik Dane_przekrojowe_PKB

Autor opracowania: Marek Walesiak

3

b) zapisać dane w formacie csv na dysku

(podać nazwę pliku Dane_przekrojowe_PKB.csv)

2. Wykorzystując w programie R procedurę

Reg_wieloraka_model_liniowy_plaszczyzna_2010.r:
a) oszacować metodą najmniejszych kwadratów parametry strukturalne modelu zmiennej y w

zależności od zmiennych x1 i x4. Zapisać postać modelu z oszacowanymi parametrami poda-
jąc w nawiasach pod ocenami estymatorów parametrów ich błędy. Podać interpretację para-
metrów strukturalnych oraz błędów estymatorów parametrów strukturalnych,

b) zinterpretować obliczone parametry struktury stochastycznej (standardowy błąd oceny, współ-

czynnik determinacji, skorygowany współczynnik determinacji),

c) za pomocą testów t i F sprawdzić istotność współczynników regresji,
d) przedstawić wykres płaszczyzny regresji,
e) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych,
f) wykorzystując test Shapiro-Wilka sprawdzić czy składnik losowy ma rozkład normalny,
g) sprawdzić za pomocą VIF czy w modelu nie występuje problem przybliżonej współliniowo-

ści,

h) wykorzystując test Goldfelda-Quandta sprawdzić czy nie występuje niejednorodność warian-

cji składników losowych,

i) za pomocą testów Durbina-Watsona oraz Breuscha-Godfreya zbadać czy w modelu nie wy-

stępuje autokorelacja pierwszego stopnia,

j) sprawdzić czy w zbiorze danych występują obserwacje nietypowe,
k) sprawdzić, które obserwacje są wpływowe, a które nie są wpływowe.

ODPOWIEDZI Z WYKORZYSTANIEM obliczeń w programie R

a) oszacować metodą najmniejszych kwadratów parametry strukturalne modelu zmiennej

y w zależności od zmiennych x1 (zm1) i x4 (zm2)

[1] Wyniki estymacji MNK

Call:
lm(formula = y ~ zm1 + zm2, data = d, x = TRUE, y = TRUE)

Residuals:
Min 1Q Median 3Q Max
-5860,7 -1433,0 -734,5 1773,8 6486,7

Autor opracowania: Marek Walesiak

4

Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2,790e+03 1,457e+03 1,915 0,07771 .
zm1 5,263e+00 4,356e-01 12,083 1,92e-08 ***
zm2 3,562e-01 7,351e-02 4,845 0,00032 ***
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1

Residual standard error: 3619 on 13 degrees of freedom
Multiple R-squared: 0.9954, Adjusted R-squared: 0.9947
F-statistic: 1404 on 2 and 13 DF, p-value: 6,511e-16

a) zapisać postać modelu z oszacowanymi parametrami podając w nawiasach pod ocenami

estymatorów parametrów ich błędy

4

)

074

,

0

(

1

)

436

,

0

(

)

1457

(

356

,

0

263

,

5

2790

ˆ

x

x

y







a) Podać interpretację parametrów strukturalnych oraz błędów estymatorów parametrów

strukturalnych

263

,

5

ˆ

1



b

– wzrost (spadek) wartości nakładów inwestycyjnych województwa (wartości zmien-

nej objaśniającej x1) o 1 mln zł spowoduje wzrost (spadek) produktu krajowego brutto wojewódz-
twa (zmienna objaśniana y) średnio o 5,263 mln zł (ceteris paribus);

356

,

0

ˆ

4



b

– wzrost (spadek) produkcji sprzedanej przemysłu województwa (wartości zmiennej

objaśniającej x4) o 1 mln zł spowoduje wzrost (spadek) produktu krajowego brutto województwa
(zmienna objaśniana y) średnio o 0,356 mln zł (ceteris paribus);

2790

ˆ

0



b

(wyraz wolny) – brak w tym przypadku interpretacji ekonomicznej.

1457

)

ˆ

(

0



b

S

– szacując parametr

0

b , gdybyśmy mogli wiele razy pobrać próbę z tej samej popu-

lacji generalnej, mylimy się średnio in plus i in minus o 1457 (

1457

2790

0





b

),

436

,

0

)

ˆ

(

1



b

S

– szacując parametr

1

b , gdybyśmy mogli wiele razy pobrać próbę z tej samej po-

pulacji generalnej, mylimy się średnio in plus i in minus o 0,436 (

436

,

0

263

,

5

1





b

),

074

,

0

)

ˆ

(

4



b

S

– szacując parametr

4

b , gdybyśmy mogli wiele razy pobrać próbę z tej samej po-

pulacji generalnej, mylimy się średnio in plus i in minus o 0,074 (

074

,

0

356

,

0

4





b

),

b) zinterpretować obliczone parametry struktury stochastycznej (standardowy błąd oceny,

współczynnik determinacji, skorygowany współczynnik determinacji),

standardowy błąd oceny (Residual standard error: 3619) – wartości empiryczne

zmiennej objaśnianej (produkt krajowy brutto województwa) odchylają się od wartości teore-
tycznych przeciętnie o 3619 mln zł.

współczynnik determinacji (Multiple R-Squared: 0.9954) – 99,54% zmienności zmiennej

objaśnianej (produkt krajowy brutto województwa) zostało wyjaśnionych przez zbudowany mo-
del.

skorygowany współczynnik determinacji (Adjusted R-squared: 0.9947) – 99,47% wa-

riancji zmiennej objaśnianej (produkt krajowy brutto województwa) zostało wyjaśnionych przez
zbudowany model.

Autor opracowania: Marek Walesiak

5

c) za pomocą testów t i F sprawdzić istotność współczynników regresji

Test t
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2,790e+03 1,457e+03 1,915 0,07771 .
zm1 5,263e+00 4,356e-01 12,083 1,92e-08 ***
zm2 3,562e-01 7,351e-02 4,845 0,00032 ***

Z uwagi na to, że dla

0

b

07771

,

0

05

,

0







nie ma podstaw do odrzucenia hipotezy zerowej.

Oznacza to, że parametr

0

b nieistotnie różni się od zera.

Z uwagi na to, że dla

1

b

08

92

,

1

05

,

0







e



(0,0000000192) hipotezę zerową odrzucamy.

Oznacza to, że parametr

1

b istotnie różni się od zera. Zmienna objaśniająca x1 ma istotny wpływ na

zmienną objaśnianą y.

Z uwagi na to, że dla

4

b

00032

,

0

05

,

0







hipotezę zerową odrzucamy. Oznacza to, że para-

metr

4

b istotnie różni się od zera. Zmienna objaśniająca x4 ma istotny wpływ na zmienną objaśnia-

ną y.

Test F
F-statistic: 1404 on 2 and 13 DF, p-value: 6,511e-16

Z uwagi na to, że

16

511

,

6

05

,

0







e



(UWAGA!

16



e

oznacza przesunięcie przecinka w

lewo o 16 miejsc) hipotezę zerową należy odrzucić. Oznacza to, że regresja jako całość jest istotna.

d) przedstawić wykres płaszczyzny regresji

zm1

10000

20000

30000

zm

2

0

50000

100000

150000

y

50000

100000

150000

200000

e) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych

[1] Przedziały ufności dla parametrów
2,5 % 97,5 %
(Intercept) -356,8646924 5936,3854523
zm1 4,3224163 6,2045676
zm2 0,1973624 0,5149773

Autor opracowania: Marek Walesiak

6

Z prawdopodobieństwem 0,95 przedział





385

,

5936

865

,

356

;



pokryje nieznaną wartość para-

metru

0

b z modelu











4

4

1

1

0

x

b

x

b

b

y

.

Z prawdopodobieństwem 0,95 przedział





205

,

6

322

,

4

;

pokryje nieznaną wartość parametru

1

b z

modelu











4

4

1

1

0

x

b

x

b

b

y

.

Z prawdopodobieństwem 0,95 przedział





515

,

0

;

197

,

0

pokryje nieznaną wartość parametru

4

b z

modelu











4

4

1

1

0

x

b

x

b

b

y

.

Węższe (szersze) przedziały ufności można uzyskać poprzez zmniejszenie (zwiększenie) pozio-

mu ufności.

f) wykorzystując test Shapiro-Wilka sprawdzić czy składnik losowy ma rozkład normalny

[1] Wyniki testu Shapiro-Wilka
Shapiro-Wilk normality test
data: reg$residuals
W = 0,9512, p-value = 0,509

Z uwagi na to, że

0,509

value









p

05

,

0



nie ma podstaw do odrzucenia hipotezy o nor-

malności rozkładu składnika losowego.

g) sprawdzić za pomocą VIF czy w modelu nie występuje problem przybliżonej

współliniowości

[1] VIF - czynnik inflacji wariancji
zm1 zm2
10,00626 10,00626

Wartości

1



j

VIF

informują ile razy wariancja estymatora parametru jest większa od wariancji

prawdziwej (tzn. nie zakłóconej współliniowością statystyczną). Wartości

20



j

VIF

wskazują na

problemy związane ze współliniowością. W analizowanym modelu w zasadzie nie występuje pro-
blem związany ze współliniowością zmiennych objaśniających.

h) wykorzystując test Goldfelda-Quandta sprawdzić czy nie występuje niejednorodność

wariancji składników losowych

[1] Wyniki testu Goldfelda-Quandta
Goldfeld-Quandt test
data: reg
GQ = 0,472, df1 = 4, df2 = 3, p-value = 0,7594

Nie ma podstaw do odrzucenia hipotezy zerowej, że składnik losowy jest homoskedastyczny

(

0,7594

value









p

05

,

0



).

i) za pomocą testów Durbina-Watsona oraz Breuscha-Godfreya zbadać czy w modelu nie

występuje autokorelacja pierwszego stopnia

[1] Wyniki testów Durbina-Watsona oraz Breuscha-Godfreya na auto-
korelację pierwszego stopnia
lag Autocorrelation D-W Statistic p-value
1 -0,1673144 1,991318 0,48
Alternative hypothesis: rho < 0

Breusch-Godfrey test for serial correlation of order 1
data: reg
LM test = 0,55, df = 1, p-value = 0,4583

Autor opracowania: Marek Walesiak

7

Oba testy potwierdzają brak w modelu autokorelacji reszt pierwszego stopnia, z uwagi na to, że

value







p

05

,

0



.

j) sprawdzić czy w zbiorze danych występują obserwacje nietypowe (rys. z lewej strony)

5

10

15

-4

-2

0

2

4

numer obserwacji

re

szt

y

st

u

d

e

n

tyzo

w

a

n

e

Mazowieckie

5

10

15

0

,2

0

,4

0

,6

0

,8

1

,0

1

,2

numer obserwacji

h

a

t

va

lu

e

s

Mazowieckie

Śląskie

Obserwacje nietypowe (outliers) charakteryzują się dużą resztą. Tego typu obserwacje wpływają

na pogorszenie dopasowania modelu do danych. Dla szacowanego modelu











4

4

1

1

0

x

b

x

b

b

y

jest jedna reszta nietypowa (woj. mazowieckie). W przypadku wystąpienia reszt nietypowych model
należy oszacować i zweryfikować powtórnie z pominięciem obserwacji nietypowych.

j) sprawdzić, które obserwacje są wpływowe, a które nie są wpływowe (rys. z prawej stro-

ny)

Obserwacje wpływowe (influential observations) silnie oddziałują na oszacowane parametry

strukturalne. Włączenie do zbioru danych tych obserwacji powoduje, że znacznie zmieniają się
oszacowane parametry modelu. Dla szacowanego modelu











4

4

1

1

0

x

b

x

b

b

y

obserwacje doty-

czące woj. mazowieckiego i śląskiego są wpływowe. Należy więc oszacować i zweryfikować po-
wtórnie model z pominięciem tych dwóch województw.