Autor opracowania: Marek Walesiak
1
PROJEKT D – MODELOWANIE I PROGNOZOWANIE
ZMIENNYCH JAKOŚCIOWYCH
Nazwisko i imię studenta 1: ..........................................
Kierunek i rok studiów studenta 1: ......
Numer grupy studenta 1: .....
Nazwisko i imię studenta 2: ..........................................
Kierunek i rok studiów studenta 2: ......
Numer grupy studenta 2: .....
Uwagi dla studentów:
1. Program R należy pobrać ze strony: http://cran.r-project.org/
2. Co najmniej jeden projekt (A, B, C, D) należy przesłać na e-mail prowadzącego laboratoria
3. Projekty można wykonywać osobiście lub w zespołach dwuosobowych (liczba zrealizowanych
projektów oraz jakość i estetyka wykonania będzie decydować o ocenie z laboratorium dla
przedmiotu Ekonometria)
4. Liczba obserwacji (dane w postaci szeregów przekrojowych z roku 2009 lub 2010) w projekcie
A, B oraz C musi wynosić co najmniej 12, a w projekcie D co najmniej 30. Dla danych staty-
stycznych należy koniecznie podać źródło
5. Nie wolno w projektach stosować zmiennych użytych w przykładowych projektach prezentowa-
nych na laboratoriach (nie dotyczy projektu C)
6. Wraz z każdym projektem opracowanym w edytorze Word (może też być jego odpowiednik z
pakietu OpenOffice) należy przesłać:
a) plik (pliki) danych w formacie csv
b) odpowiednie procedury w programie R
7. Termin przesłania projektu (projektów): do 03 stycznia 2012 roku
8. Proszę przesyłać projekty z własnych e-maili podając w e-mailu skład zespołu (imię i nazwisko,
rok i forma studiów, numer grupy lub specjalność)
9. Warunkiem przyjęcia projektu (projektów) jest uzyskanie pozytywnej odpowiedzi od prowadzą-
cego laboratoria
10. Odpowiedzi na e-maile informujące o akceptacji projektu lub projektów będą przesyłane w cią-
gu siedmiu dni od ich nadesłania
11. Odrzucane będą projekty, które wykonali inni studenci
Autor opracowania: Marek Walesiak
2
PROJEKT D – MODELOWANIE I PROGNOZOWANIE
ZMIENNYCH JAKOŚCIOWYCH
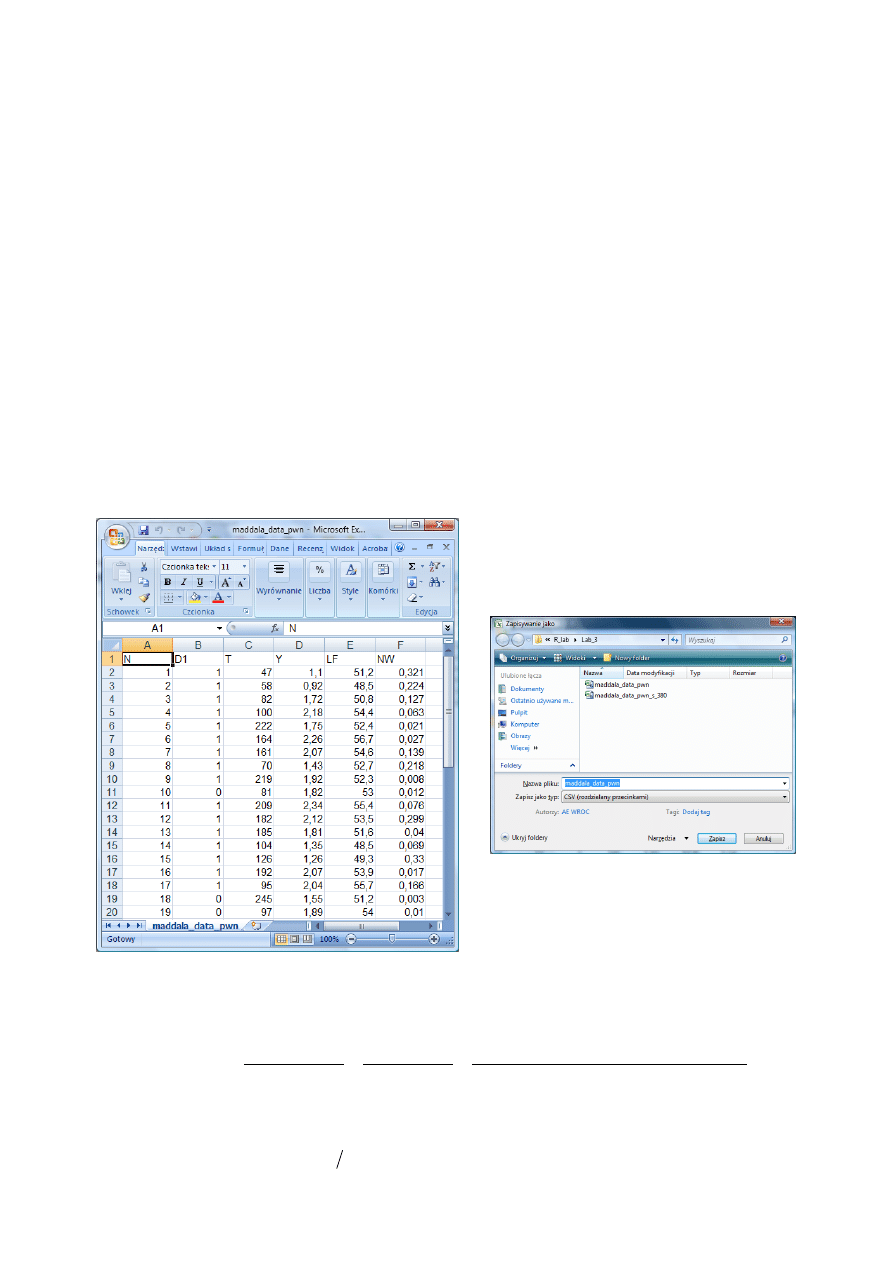
1. Dane przekrojowe dla stanów USA w 1950 r.
D1 – skłonność danego stanu do utrzymywania w stanowym kodeksie karnym kary śmierci (1 – dla stanów,
w których występuje kara śmierci, 0 – dla stanów bez kary śmierci),
T – mediana czasu spędzonego w więzieniu przez skazanych zabójców zwolnionych w 1951 r. (w miesią-
cach),
Y – mediana dochodu rodzin w 1949 r. (w tys. $),
LF – stopa zatrudnienia w 1950 r. (w %),
NW – udział osób nie-białych w populacji.
Źródło: Maddala [2006], s. 380.
a) wprowadzić dane statystyczne do programu EXCEL w następującym układzie
(plik maddala_data_pwn)
b) zapisać dane w formacie csv na dysku
(podać nazwę pliku maddala_data_pwn.csv)
Plik maddala_data_pwn
maddala_data_pwn.csv
W modelu logitowym prawdopodobieństwo przyjmowania przez zmienną
i
y jednej z dwóch
możliwych wartości jest funkcją
b
x
T
i
(i – numer obserwacji):
)
exp(
1
)
exp(
)
exp(
1
)
exp(
)
exp(
1
1
)
(
4
3
2
1
0
4
3
2
1
0
NW
b
LF
b
Y
b
T
b
b
NW
b
LF
b
Y
b
T
b
b
F
P
T
i
T
i
T
i
T
i
i
b
x
b
x
b
x
b
x
,
gdzie: F – dystrybuanta rozkładu logistycznego.
Wartości funkcji odwrotnej do F dla tego modelu nazywa się logitami:
NW
b
LF
b
Y
b
T
b
b
P
P
P
F
T
i
i
i
4
3
2
1
0
1
1
)
1
ln(
)
(
b
x
Autor opracowania: Marek Walesiak
3
2. Wykorzystując w programie R procedurę logit.r (dla modelu logitowego):
a) oszacować parametry modeli logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
. Zapi-
sać postać modelu logitowego z oszacowanymi parametrami podając w nawiasach pod oce-
nami estymatorów parametrów ich błędy,
b) podać interpretację parametrów modelu logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
(interpretacja w kategoriach prawdopodobień-
stwa oraz interpretacja ilorazu szans
i
i
P
P
1
),
c) za pomocą testu z sprawdzić istotność współczynników regresji, a za pomocą testu ilorazu
wiarygodności sprawdzić istotność całego modelu logitowego,
d) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych modelu logito-
wego,
e) obliczyć i ocenić dopasowanie modelu logitowego,
f) wyznaczyć prognozy na podstawie modelu logitowego:
– prognozę prawdopodobieństwa
i
P dla obserwacji znajdujących się w próbie,
– prognozę prawdopodobieństwa
i
P dla obserwacji znajdujących się poza próbą
– prognozę wartości
i
y (1 lub 0), tj. prognozę zmiennej objaśnianej dla i-tej obserwacji –
próba zbilansowana,
– prognozę wartości
i
y (1 lub 0), tj. prognoza zmiennej objaśnianej dla i-tej obserwacji –
próba niezbilansowana
ODPOWIEDZI Z WYKORZYSTANIEM obliczeń w programie R
a) oszacować parametry modeli logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
[1] Wyniki estymacji
Call:
glm(formula = D1 ~ T + Y + LF + NW, family = binomial(link = "logit"),
data = d, x = TRUE, y = TRUE)
Deviance Residuals:
Min 1Q Median 3Q Max
-2,072e+00 1,119e-05 2,934e-02 2,479e-01 1,822e+00
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 16,566989 19,639238 0,844 0,3989
T 0,016516 0,009611 1,718 0,0857 .
Y 9,131548 5,053148 1,807 0,0707 .
LF -0,715389 0,479267 -1,493 0,1355
NW 85,361600 35,854424 2,381 0,0173 *
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 44,584 on 43 degrees of freedom
Residual deviance: 18,215 on 39 degrees of freedom
AIC: 28,215
Number of Fisher Scoring iterations: 9
a) zapisać postać modelu logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
z oszacowa-
nymi parametrami podając w nawiasach pod ocenami estymatorów parametrów ich błędy
NW
LF
Y
T
P
P
i
i
)
854
,
35
(
)
479
,
0
(
)
053
,
5
(
)
010
,
0
(
)
639
,
19
(
362
,
85
715
,
0
132
,
9
017
,
0
567
,
16
)
1
ln(
Autor opracowania: Marek Walesiak
4
b) podać interpretację parametrów modelu logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
(interpretacja w kategoriach prawdopodobień-
stwa oraz interpretacja ilorazu szans
i
i
P
P
1
),
Interpretacja w kategoriach prawdopodobieństwa
Znak oszacowanego parametru przy zmiennej
j
X
(kolumna 3) określa kierunek wpływu zmien-
nej
j
X
na prawdopodobieństwo
i
P :
– dla dodatniego
j
b
wzrost (spadek)
j
X
wiąże się ze wzrostem (spadkiem) szans na to, że
1
i
y
;
– dla ujemnego
j
b
wzrost (spadek)
j
X
wiąże się ze spadkiem (wzrostem) szans na to, że
1
i
y
.
Zmienna
Parametr
Znak pa-
rametru
Iloraz szans
Kolej-
ność
T
1
b
=0,016516
+
017
,
1
)
exp(
1
b
3
Y
2
b
=9,131548
+
321
,
9242
)
exp(
2
b
2
LF
3
b
=–0,715389
–
489
,
0
)
exp(
3
b
4
NW
4
b
=85,3616
+
37
181
,
1
)
exp(
4
e
b
(przecinek 37 miejsc w prawo)
1
Interpretacja ilorazu szans
i
i
P
P
1
[1] Interpretacja parametrów modelu logitowego - iloraz szans Pi(1-Pi)
(Intercept) T Y LF NW
1,566577e+07 1,016654e+00 9,242321e+03 4,890017e-01 1,180516e+37
Dla jednostkowego przyrostu zmiennej objaśniającej
ij
x (ceteris paribus)
)
exp(
j
b pokazuje
krotność o jaką się zmienia iloraz szans (stosunek szansy (prawdopodobieństwa) na to, że
1
i
y
do
szansy na to, że
0
i
y
).
Największy iloraz szans występuje dla parametru przy zmiennej NW, najmniejszy zaś przy
zmiennej LF.
c) za pomocą testu z sprawdzić istotność współczynników regresji dla modelu logitowego
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
Test z
Estimate Std. Error z value Pr(>|z|)
(Intercept) 16,566989 19,639238 0,844 0,3989
T 0,016516 0,009611 1,718 0,0857 .
Y 9,131548 5,053148 1,807 0,0707 .
LF -0,715389 0,479267 -1,493 0,1355
NW 85,361600 35,854424 2,381 0,0173 *
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1
Z uwagi na to, że dla
0
b
3989
,
0
10
,
0
nie ma podstaw do odrzucenia hipotezy zerowej.
Oznacza to, że parametr
0
b nieistotnie różni się od zera.
Z uwagi na to, że dla
1
b
0857
,
0
10
,
0
hipotezę zerową odrzucamy. Oznacza to, że parametr
1
b istotnie różni się od zera. Zmienna objaśniająca T ma istotny wpływ na zmienną objaśnianą.
Z uwagi na to, że dla
2
b
0707
,
0
10
,
0
hipotezę zerową odrzucamy. Oznacza to, że parametr
2
b istotnie różni się od zera. Zmienna objaśniająca Y ma istotny wpływ na zmienną objaśnianą.
Autor opracowania: Marek Walesiak
5
Z uwagi na to, że dla
3
b
1355
,
0
10
,
0
nie ma podstaw do odrzucenia hipotezy zerowej. Za-
tem parametr
3
b nieistotnie różni się od zera i zmienna objaśniająca LF ma nieistotny wpływ na
zmienną objaśnianą.
Z uwagi na to, że dla
4
b
0173
,
0
10
,
0
hipotezę zerową odrzucamy. Oznacza to, że parametr
4
b istotnie różni się od zera. Zmienna objaśniająca NW ma istotny wpływ na zmienną objaśnianą.
c) za pomocą testu ilorazu wiarygodności sprawdzić istotność całego modelu logitowego
:
0
H
0
1
m
b
b
,
:
1
H
przynajmniej jeden
0
j
b
(
m
j
,
,
1
).
Statystyka testu ma postać:
R
UR
L
L
LR
ln
2
,
gdzie:
UR
L
– maksimum funkcji wiarygodności, przy maksymalizacji względem wszystkich para-
metrów (dla pełnego modelu),
R
L – maksimum funkcji wiarygodności przy maksymalizacji z warunkiem
0
j
j
b
(dla mo-
delu tylko z wyrazem wolnym).
Statystyka
LR
ma rozkład chi-kwadrat z liczbą stopni swobody równą liczbie zmiennych obja-
śniających modelu pełnego.
[1] Test ilorazu wiarygodności dla badania istotności całego modelu
(LR=2*Lur/Lr)
Likelihood ratio test
Model 1: D1 ~ T + Y + LF + NW
Model 2: D1 ~ 1
#Df LogLik Df Chisq Pr(>Chisq)
1 5 -9,1076
2 1 -22,2921 -4 26,369 2,666e-05 ***
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1
Z uwagi na to, że dla
e
,
05
666
2
10
,
0
(0,00002666) hipotezę zerową odrzucamy. Ozna-
cza to, że regresja jako całość jest istotna.
d) wyznaczyć i zinterpretować przedziały ufności dla parametrów strukturalnych dla mo-
delu logitowego (dla
10
,
0
)
[1] Przedziały ufności dla parametrów
p_uf_d p_uf_g
(Intercept) -1,573668e+01 48,87066062
T 7,075145e-04 0,03232541
Y 8,198601e-01 17,44323651
LF -1,503714e+00 0,07293508
NW 2,638632e+01 144,33687905
Z prawdopodobieństwem 0,90 przedział
871
,
48
737
,
15
;
pokryje nieznaną wartość parametru
0
b z modelu
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
.
Z prawdopodobieństwem 0,90 przedział
032
,
0
0007
,
0
;
pokryje nieznaną wartość parametru
1
b
z modelu
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
.
Z prawdopodobieństwem 0,90 przedział
443
,
17
;
820
,
0
pokryje nieznaną wartość parametru
2
b
z modelu
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
.
Autor opracowania: Marek Walesiak
6
Z prawdopodobieństwem 0,90 przedział
073
,
0
;
504
,
1
pokryje nieznaną wartość parametru
3
b
z modelu
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
.
Z prawdopodobieństwem 0,90 przedział
337
,
144
;
639
,
2
pokryje nieznaną wartość parametru
4
b z modelu
NW
b
LF
b
Y
b
T
b
b
P
P
i
i
4
3
2
1
0
)
1
ln(
.
Węższe (szersze) przedziały ufności można uzyskać poprzez zmniejszenie (zwiększenie) pozio-
mu ufności.
e) obliczyć i ocenić dopasowanie modelu logitowego
[1] Miary dopasowania
[1] Kwadrat współczynnika korelacji między wartościami empirycznymi i
teoretycznymi
[1] 0,5982244
[1] R kwadrat Efrona
[1] 0,5981534
[1] R kwadrat Nagelkerke
[1] 0,7077272
[1] R kwadrat McFaddena
[1] 0,5914449
Miara dopasowania
2
R
Wartość miary
Kwadrat współczynnika korelacji między wartościami empirycznymi
i
y i
teoretycznymi
i
yˆ .
0,5982244
Miara Efrona
0,5981534
Miara Nagelkerke
0,7077272
Miara McFaddena
0,5914449
Miara Nagelkerke pokazuje na dobre dopasowanie modelu logitowego do danych empirycznych.
Pozostałe miary wskazują, że model jest dość dobrze dopasowany do danych.
f) wyznaczyć prognozy na podstawie modelu logitowego:
– prognozę prawdopodobieństwa
i
P dla obserwacji znajdujących się w próbie
[1] 1a. Prognoza prawdopodobieństwa Pi dla obserwacji znajdujących się w próbie
1 2 3 4 5 6 7
0,99999999 0,99996803 0,99970456 0,98990940 0,62715799 0,83958907 0,99998215
8 9 10 11 12 13 14
0,99999162 0,72803895 0,08571948 0,99973662 1,00000000 0,93407318 0,85886041
15 16 17 18 19 20 21
1,00000000 0,82231552 0,99998469 0,16736354 0,08708977 0,98157700 1,00000000
22 23 24 25 26 27 28
0,37526162 0,99999798 0,51856108 0,88313819 0,99862342 0,97188050 0,96284709
29 30 31 32 33 34 35
0,99940984 0,99839702 0,98885441 0,19028138 0,99710860 0,11119749 1,00000000
36 37 38 39 40 41 42
0,85525045 0,99853555 0,98312092 0,79876223 0,99999693 0,92817998 0,16669814
43 44
0,99836037 0,15447486
Autor opracowania: Marek Walesiak
7
f) wyznaczyć prognozy na podstawie modelu logitowego:
– prognozę prawdopodobieństwa
i
P dla obserwacji znajdujących się poza próbą
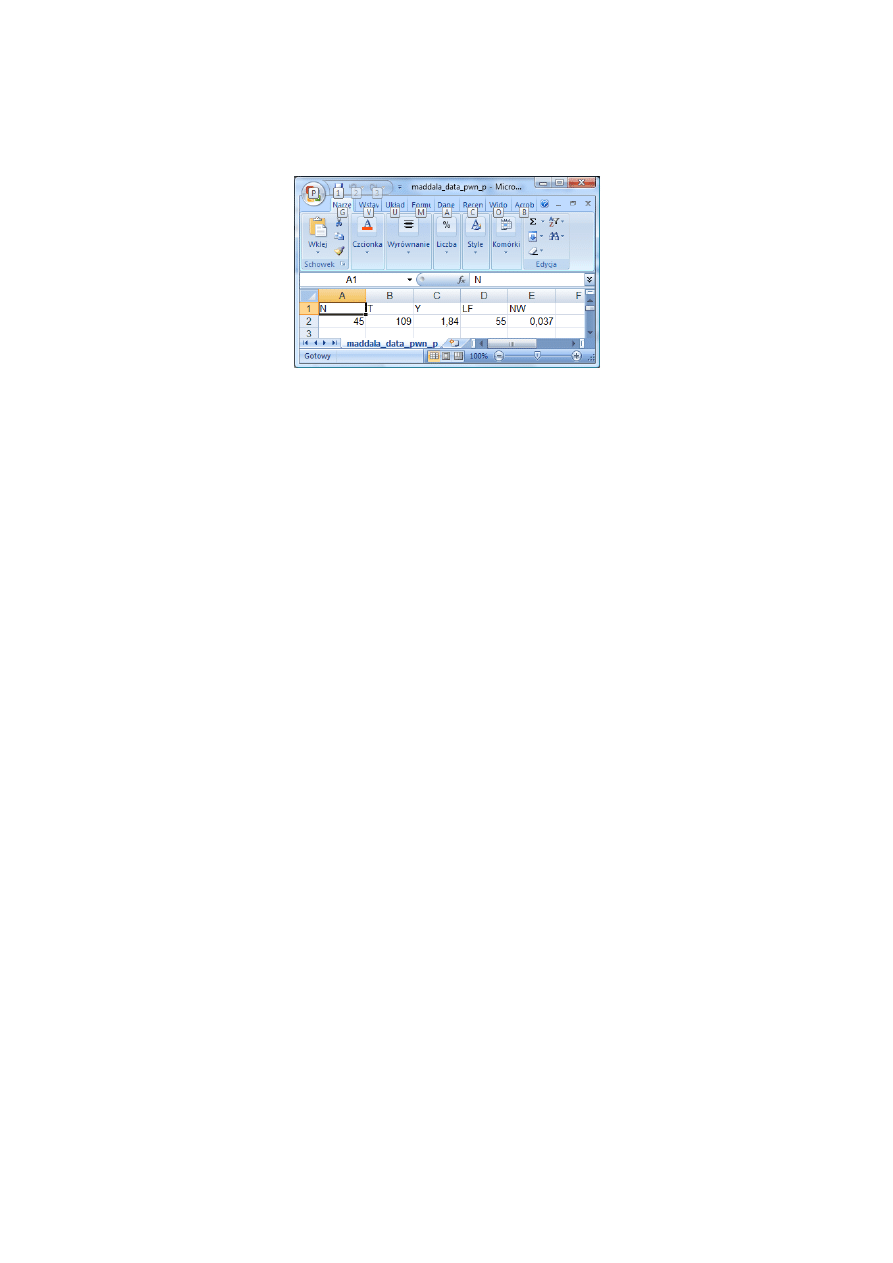
Przyjęto założenie, że dla pewnego stanu USA obserwacje na zmiennych objaśniających będą w
okresie prognozowanym następujące (zob. plik maddala_data_pwn_p.csv):
[1] 1b. Prognoza prawdopodobieństwa Pi dla obserwacji znajdujących się poza pró-
bą
45
0,2652799
Zatem dla tego stanu prognozuje się, że będzie niewielka skłonność do umieszczenia kary śmier-
ci w stanowym kodeksie karnym (
2653
,
0
ˆ
i
P
).
f) wyznaczyć prognozy na podstawie modelu logitowego:
– prognozę wartości
i
y (1 lub 0), tj. prognozę zmiennej objaśnianej dla i-tej obserwacji – próba
zbilansowana,
[1] 2a. Prognoza wartości yi (1 lub 0), tj. prognoza zmiennej objaśnianej
dla i-tej obserwacji – próba zbilansowana
[1] Tablica trafności
przewidywane
faktyczne 0 1
0 7 2
1 1 34
[1] Mierniki dokładności prognoz - próba zbilansowana
[1] Procentowa trafność prognozowania
[1] 93,18182
[1] Iloraz szans
[1] 119
f) wyznaczyć prognozy na podstawie modelu logitowego:
– prognozę wartości
i
y (1 lub 0), tj. prognoza zmiennej objaśnianej dla i-tej obserwacji – próba
niezbilansowana (w próbie obejmującej 44 stany dla zmiennej
D1
jest 35 „1” i 9 „0”. Jest to więc
próba niezbilansowana)
[1] 2b. Prognoza wartości yi (1 lub 0), tj. prognoza zmiennej objaśnianej
dla i-tej obserwacji – próba niezbilansowana
[1] Tablica trafności - próba niezbilansowana
przewidywane_n
faktyczne 0 1
0 7 2
1 4 31
[1] Mierniki dokładności prognoz - próba niezbilansowana
[1] Procentowa trafność prognozowania
[1] 86,36364
[1] Iloraz szans
[1] 27,125