WYTRZYMAŁOŚĆ MATERIAŁÓW C15 sem. III WILIŚ

WYTRZYMAŁOŚĆ MATERIAŁÓW C15 sem. III WILIŚ

Kolokwium nr 1 24 listopada 2005 godz. 18.30

Kolokwium nr 1 24 listopada 2005 godz. 18.30

- propozycje zadań z rozwiązaniami -

- propozycje zadań z rozwiązaniami -

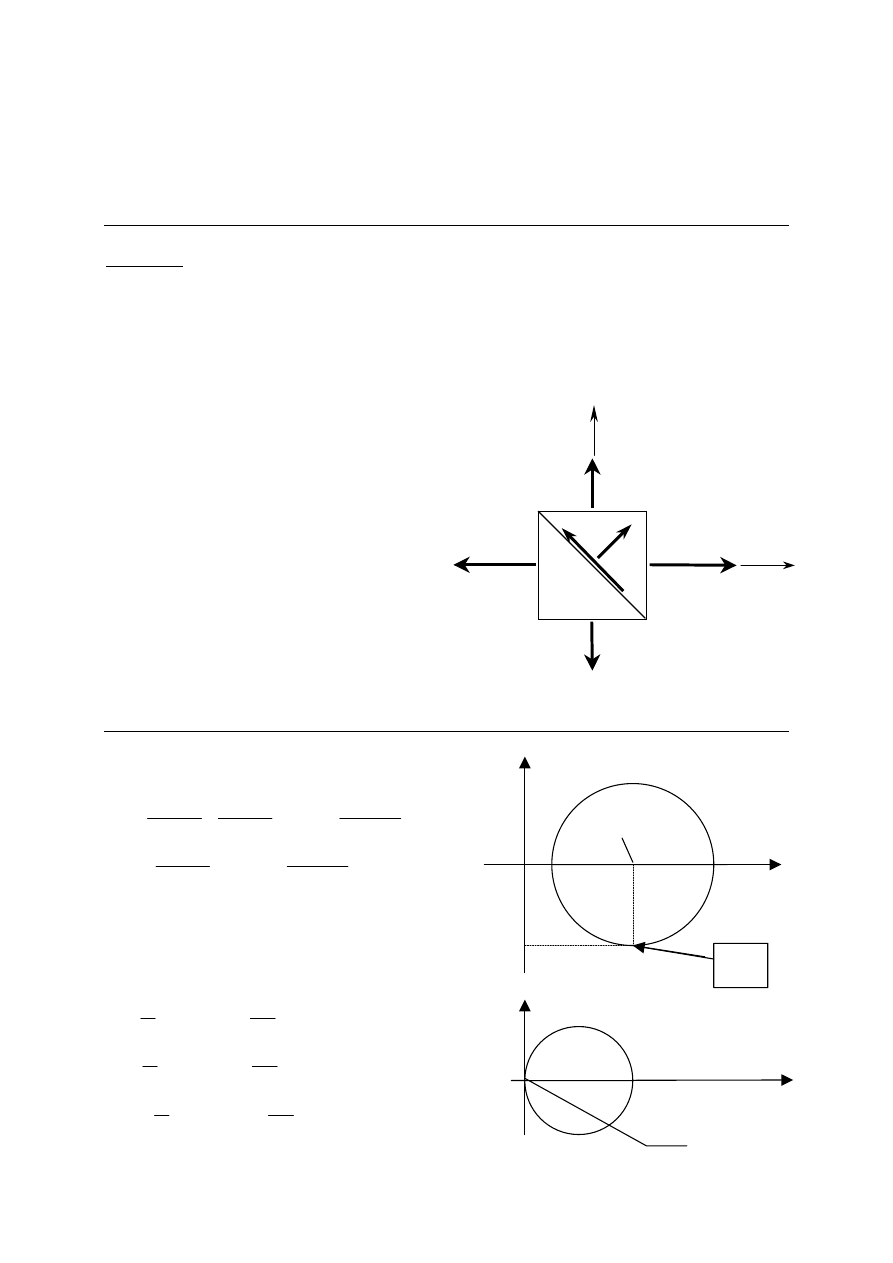
Zadanie 1. W płaskim stanie naprężenia dane są naprężenia główne:

σ

1

= 100 [MPa]

i

σ

2

= 20 [MPa]

Obliczyć naprężenia normalne

σ

φ

i styczne

τ

φ

w przekroju o normalnej nachylonej pod

kątem

φ

= 45 [º] do osi głównej (1) (rys. 1). Narysować koło Mohra dla naprężeń,

zinterpretować powyższy stan naprężenia jako punkt (M) na rysunku koła Mohra,

σ

2

2

σ

1

τ

φ

Obliczyć odkształcenia główne. Narysować koło Mohra dla odkształceń (w płaszczyźnie

wyznaczonej przez osie 1 i 2).
Dane są stałe materiałowe: E = 100 [GPa],

ν

= 0.2.

Rys. 1.

σ

τ

20

100

−40

ε

0.5γ

ε1 = 0.00096

ε

2

= 0

Rozwiązanie:

1

2

1

2

1

2

100 20

cos 2

60[

]

2

2

2

100 20

sin 2

40[

]

2

2

MPa

MPa

ϕ

ϕ

σ σ

σ σ

σ

ϕ

σ σ

τ

ϕ

+

−

+

=

+

=

=

−

−

= −

= −

= −

(

)

(

)

(

)

(

)

(

)

(

)

4

1

1

2

5

2

2

1

5

4

3

1

2

5

1

1

100 0.2 20

9.6 10 [ ]

10

1

1

20 0.2 100

0

10

0.2

100 20

2.4 10 [ ]

10

E

E

v

E

ε

σ νσ

ε

σ νσ

ε

σ σ

−

−

=

−

=

−

⋅

=

⋅

=

−

=

−

⋅

=

= −

+

= −

+

= −

⋅

−

−

1

σ

φ

M

60

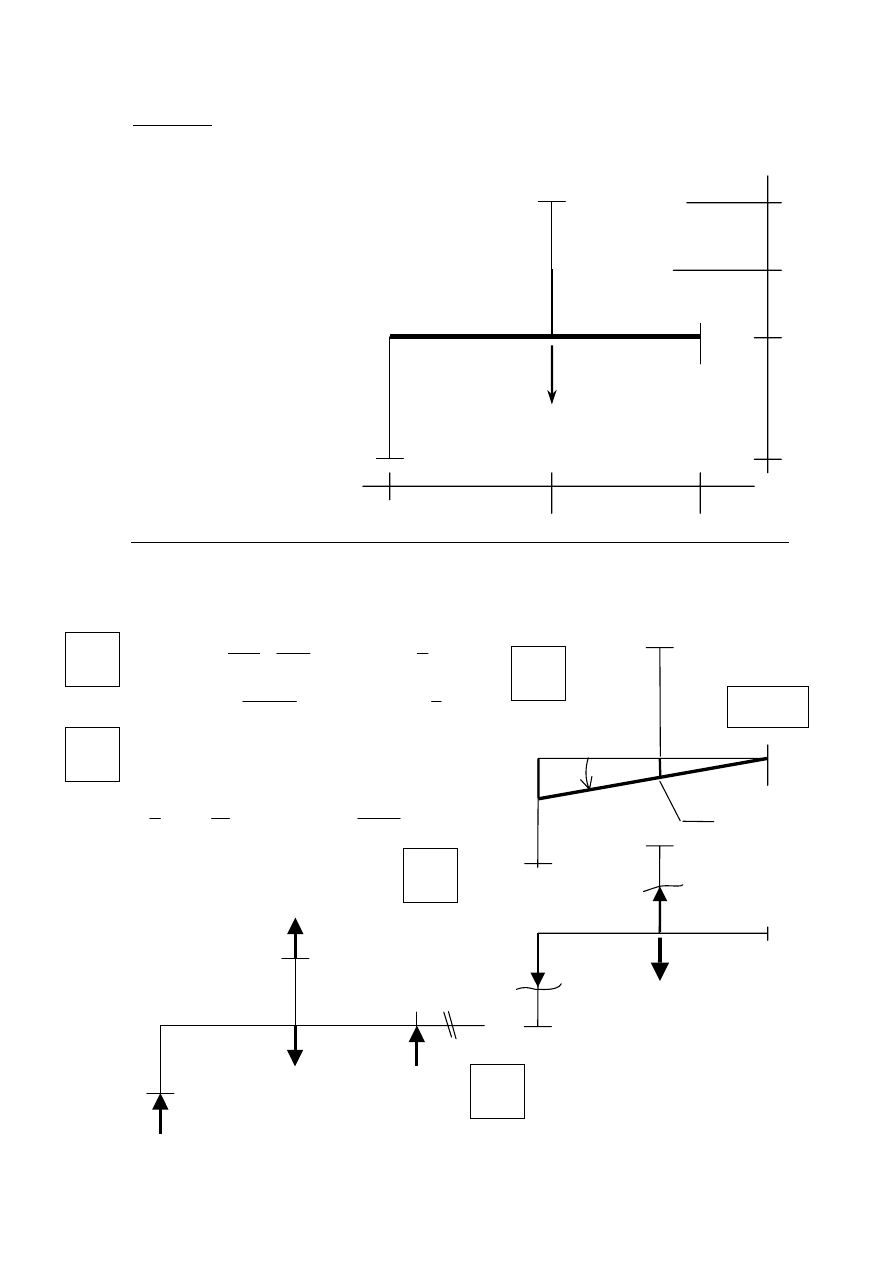
Zadanie 2. Obliczyć siły w prętach i reakcje podporowe w układzie złożonym z
nieskończonej sztywnej belki i prętów kratowych (rys. 2)

A

1

2

A

2A

P

2l

2l

1.5l

l

l

φ

∆

l

1

∆

l

2

S

2

S

1

P

P

0.4P

0.2P

0.4P

A

Rys. 2

Rozwiązanie:
Stan przemieszczeń układu określony jest przez kąt obrotu belki

φ

(rys.)

1

1

1

2

2

2

2

1,5

4

S l

S l

l

l

EA

EA

S

l

l

l

EA

ϕ

ϕ

⋅

⋅

∆ = ⋅ =

+

⋅

∆ = ⋅ = −

⇒

1

2

4
3

8
3

S

EA

S

EA

ϕ

ϕ

⎧ =

⎪⎪

⎨

⎪ = −

⎪⎩

1

2

0

2

4

2

A

M

S

l

S

l

P

l

= ⇒

⋅ −

⋅ − ⋅ =

∑

0

stąd

4

16

3

3

3

20

P

EA

EA

P

EA

φ

φ

φ

+

=

⇒

=

4 p.

2 p.

1

2

0.2 ,

0.4

S

P

S

P

=

= −

8 p.

4 p.

4 p.

3 p.

4 4 4

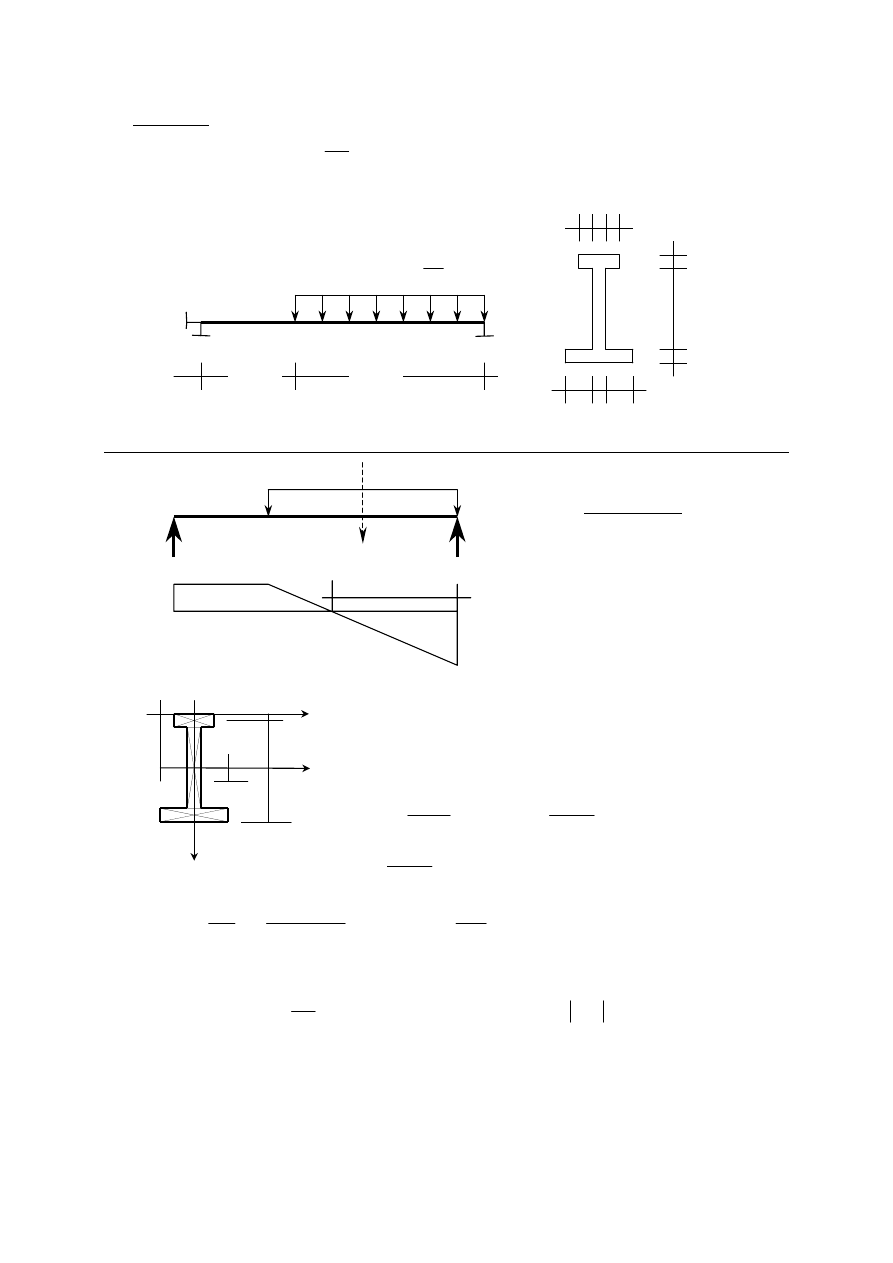
Zadanie 3. Sporządzić wykres ekstremalnych naprężeń normalnych w belce poddanej

działaniu obciążenia

1

kN

q

m

=

(rys. 3). Ile wynosi maksymalna wartość bezwymiarowego

mnożnika obciążenia m, przy której nie zostaną przekroczone naprężenia dopuszczalne

200

dop

g

K

MPa

σ

≡

=

?

1

kN

m

8 4 8 [cm]

4


24

4

+

-

2.667 kN

5.333 kN

5.333 m

8 kN

x’

y’= y

x

12

16

18

2

Rys. 3

Rozwiązanie:

8 m

4 m

=

max

0.5 5.333 5.333

14.222

1422.22

x

M

M

kNm

kNcm

=

=

⋅

⋅

=

=

(

)

2

3

'

3

3

2

2

3

2

4

4 12 24 20

224

4 12 2 4 24 16 4 20 30 4032

18

12 4

4 24

12 4 16

4 24 2

12

12

20 4

20 4 12

28970.667

12

x

C

x

A

cm

S

c

y

cm

I

cm

=

+

+

=

= ⋅ ⋅ + ⋅

⋅ + ⋅

⋅

=

=

⋅

⋅

m

=

+ ⋅ ⋅

+

+ ⋅

⋅ +

⋅

+

+

⋅ ⋅

=

( )

[

]

2

1422.22

,

0.04909

0.4909

28970.667

x

x

M

kN

x y

y

y

y

M

I

cm

σ

⎡

⎤

=

=

=

=

⎢

⎥

⎣

⎦

Pa

14

6.873

18

8.837

d

g

y

cm

MPa

y

cm

MPa

σ

σ

=

⇒

=

= −

⇒

= −

Przy obciążeniu

1

kN

q

m

=

ekstremalne naprężenia są równe

8.837

extr

MPa

σ

=

Przy obciążeniu m-krotnie większym ekstremalne naprężenia wynoszą

[

]

8.837

m

M

Pa

⋅

Warunek wytrzymałościowy:

[

]

[

]

8.837

200

22.633

g

m

MPa

K

MPa

m

⋅

≤

=

⇒

≤

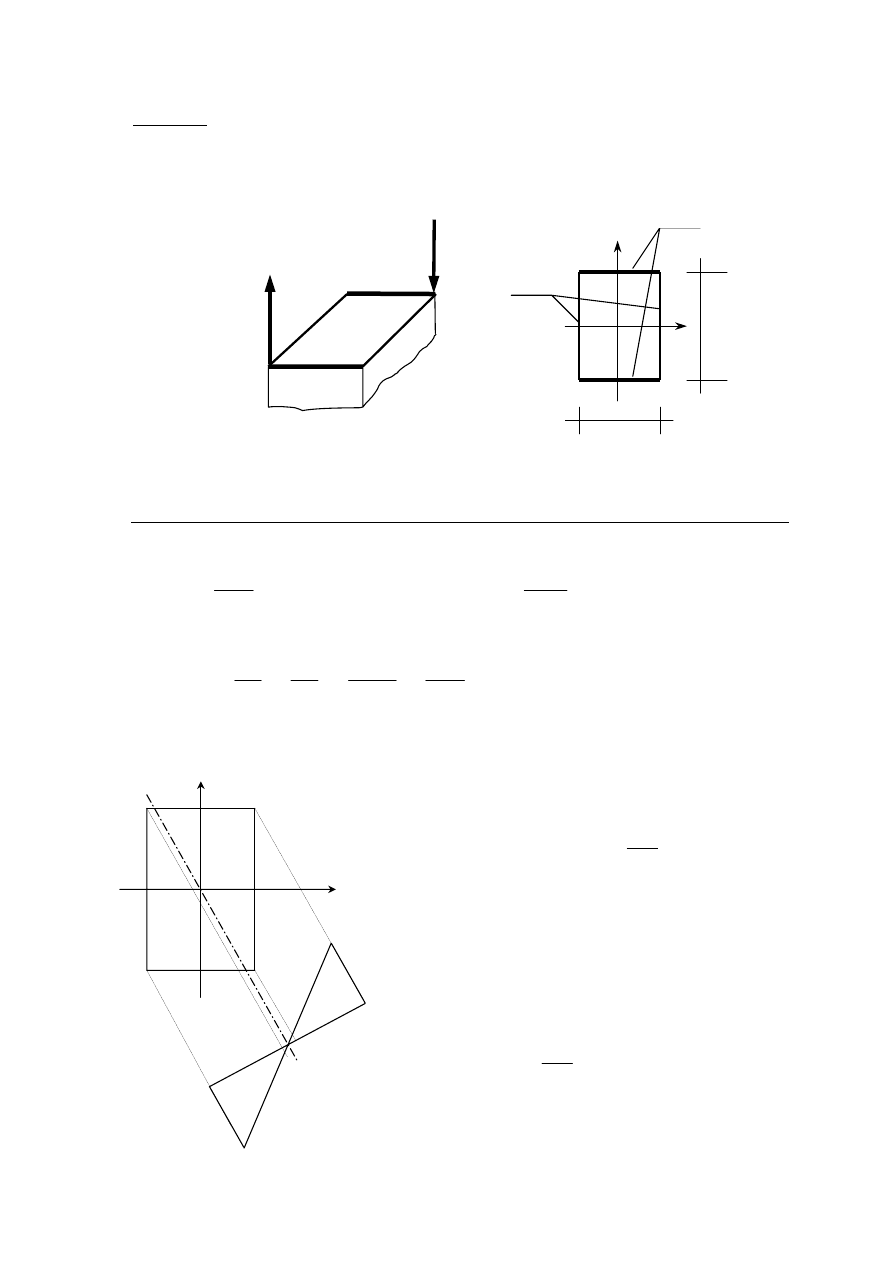
Zadanie 4. Sporządzić wykres naprężeń normalnych w przekroju cienkościennym słupa
jak na rys. 4. Podać równanie osi obojętnej, obliczyć wartości naprężeń w czterech
wierzchołkach przekroju (linii środkowej).

60 kN

60 kN

1

4

2

3

18

x

y

12

1 cm

+

-

4.3076

4.3076

2

1

3

4

x

y

Rys. 4

Rozwiązanie:

[

]

[

]

3

3

2

4

2

1 18

2 12

2

2 12 2 9

4860

,

2

2 1 18 6

1872

12

12

18 60

1080

,

12 60

720

x

y

x

y

4

I

cm

I

cm

M

kNcm

M

kNcm

⋅

⋅

⎡

⎤

⎡

= ⋅

+ ⋅ ⋅ ⋅

=

= ⋅

+ ⋅ ⋅ ⋅

=

⎤

⎣

⎦

⎣

= − ⋅

= −

= − ⋅

= −

⎦

( )

1080

720

,

0.222

0.3846

4860

1872

y

x

x

y

M

M

x y

y

x

y

x

y

I

I

σ

−

−

=

+

=

+

= −

−

x

Oś obojętna:

( )

1.731

6

10.38

y

x

y

= −

= −

cm

(

)

( )

(

)

(

)

1

2

2

3

4

6,9

0.3076

6,9

4.3076

6, 9

0.3076

6, 9

4.3076

kN

cm

σ

σ

σ

σ

σ

σ

σ

σ

=

−

=

⎫

⎪

=

= −

⎪ ⎡

⎤

⎬ ⎢

⎥

=

−

= −

⎣

⎦

⎪

⎪

=

− −

=

⎭

naprężenia normalne,

2

kN

cm

⎡

⎤

⎢

⎥

⎣

⎦

2 cm