Wprowadzenie do teorii pasmowej ciał stałych

Kryształy doskonałe (monokryształy) są ciałami ograniczonymi prawidłowymi
płaszczyznami, o budowie wykazującej okresową powtarzalność identycznych
elementów struktury zwanych komórkami elementarnymi.

Kryształy mogą być zbudowane z
jonów, atomów lub cząsteczek,
których położenie w krysztale zależą
od ich wzajemnych oddziaływań.

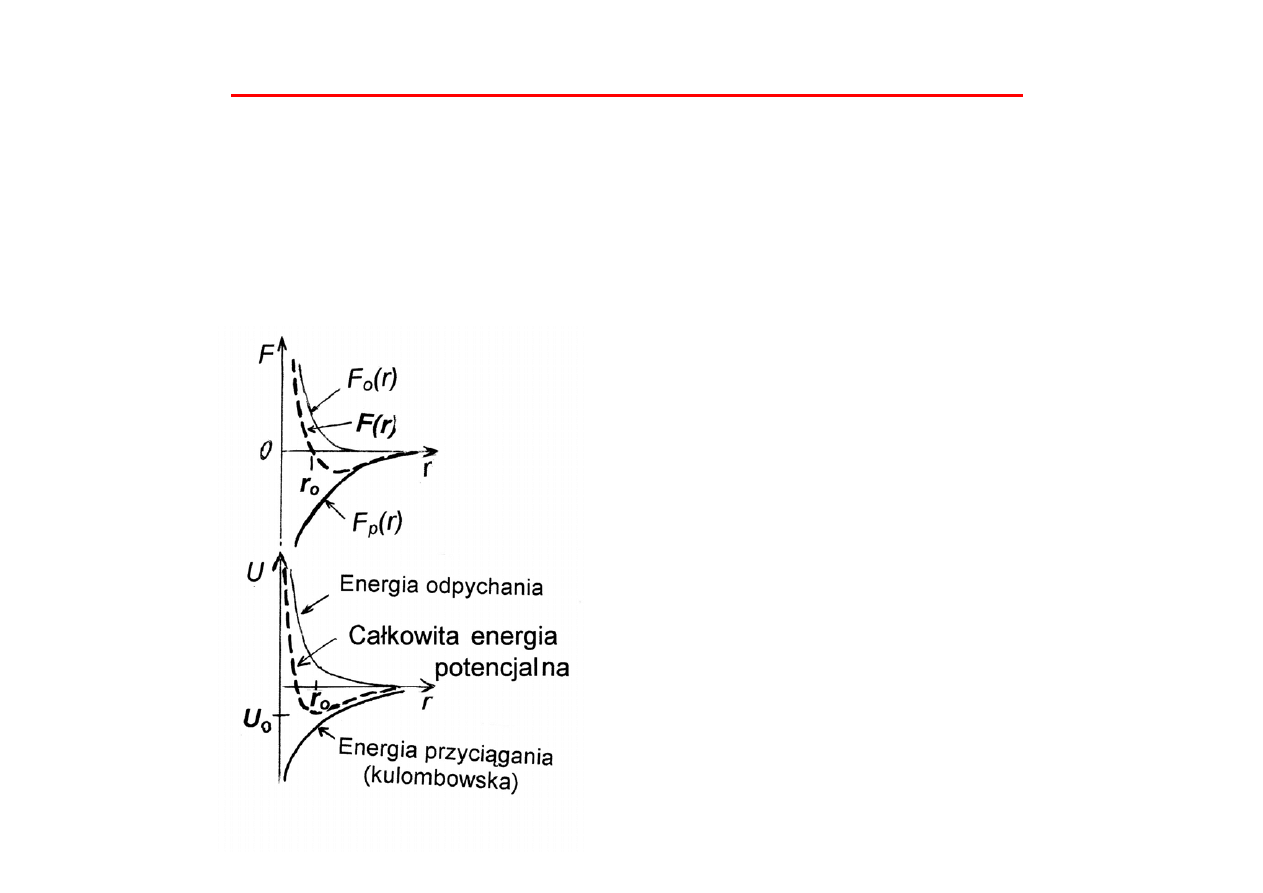
W wyniku nałożenia się siły
przyciągania F

p

(r) i siły odpychania

F

o

(r) siła wypadkowa F(r) jest równa

zero dla r = r

o

Całkowita energia potencjalna U
wzajemnego oddziaływania cząstek
dla r = r

o

ma wartość minimalną,

zwaną energią sieciową lub energią
wiązania U

o

. r

o

określa położenie

równowagi.

Przestrzenne sieci krystaliczne

Periodyczność struktury kryształu można opisać za pomocą
operacji translacji (przesunięć równoległych). Współrzędne
dowolnej cząstki określa wektor :

= m + n + p (m, n, p - liczby całkowite)

Wektory ,

i

nazywamy podstawowymi wektorami

translacji, a ich długości nazywamy stałymi sieci.

Sieć przestrzenną nazywamy siecią Bravais’go.

→

T

→

T

→

a

→

b

→

c

→

a

→

b

→

c

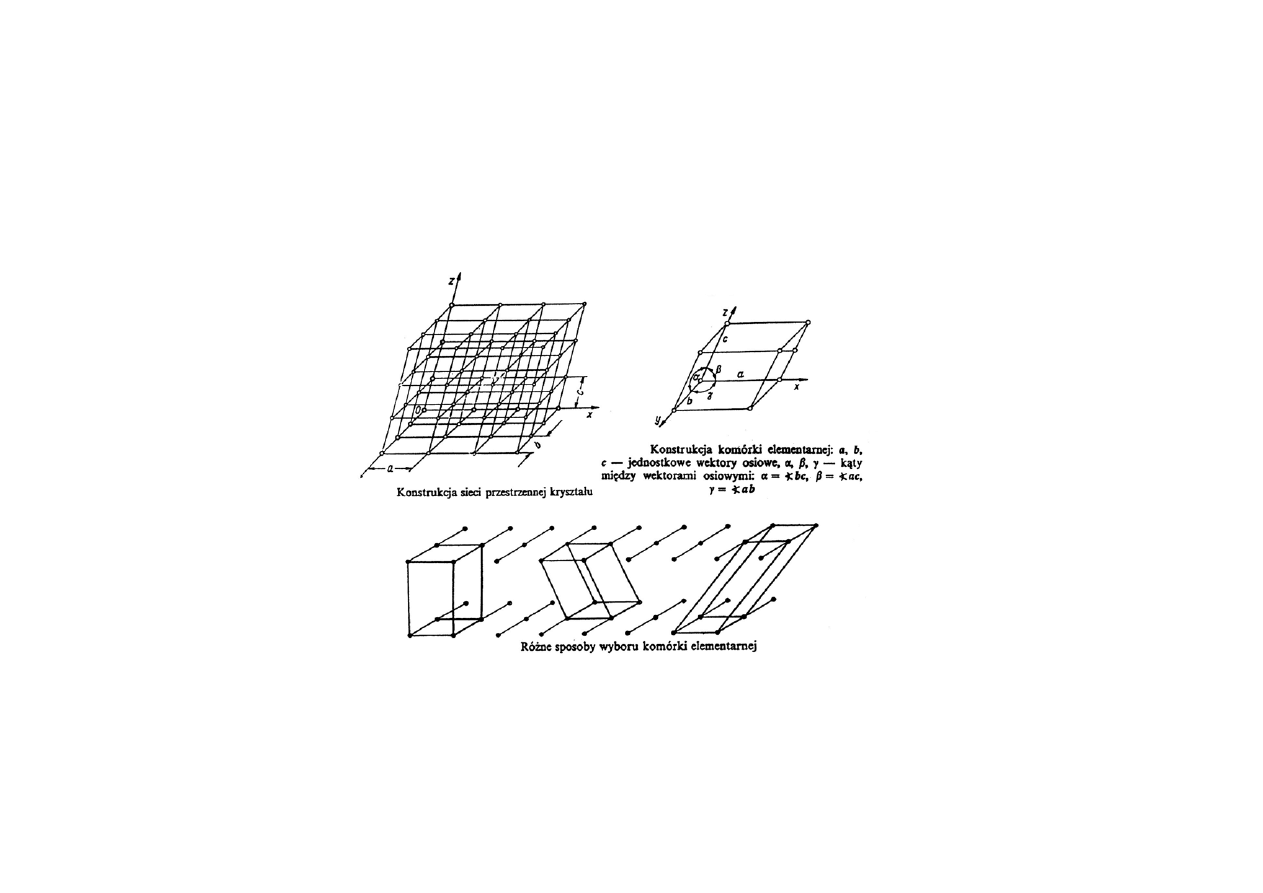
Równoległościan zbudowany na wektorach ,

i

tworzy

komórkę

elementarną.

W sieci przestrzennej można wybrać różne komórki elementarne.

Natomiast komórka elementarna jednoznacznie określa sieć.

→

a

→

b

→

c

Jeśli komórka elementarna zawiera cząstki tylko w węzłach, nazywamy ją

komórkę prymitywną

(węzły to punkty określane wektorem

i stanowiące

naroża komórki elementarnej).

Jeśli cząstki występują nie tylko w węzłach, to komórkę elementarną
nazywamy złożoną. Komórki złożone mogą być

centrowane przestrzennie,

o centrowanej podstawie i centrowane płasko

(ściennie).

→

T

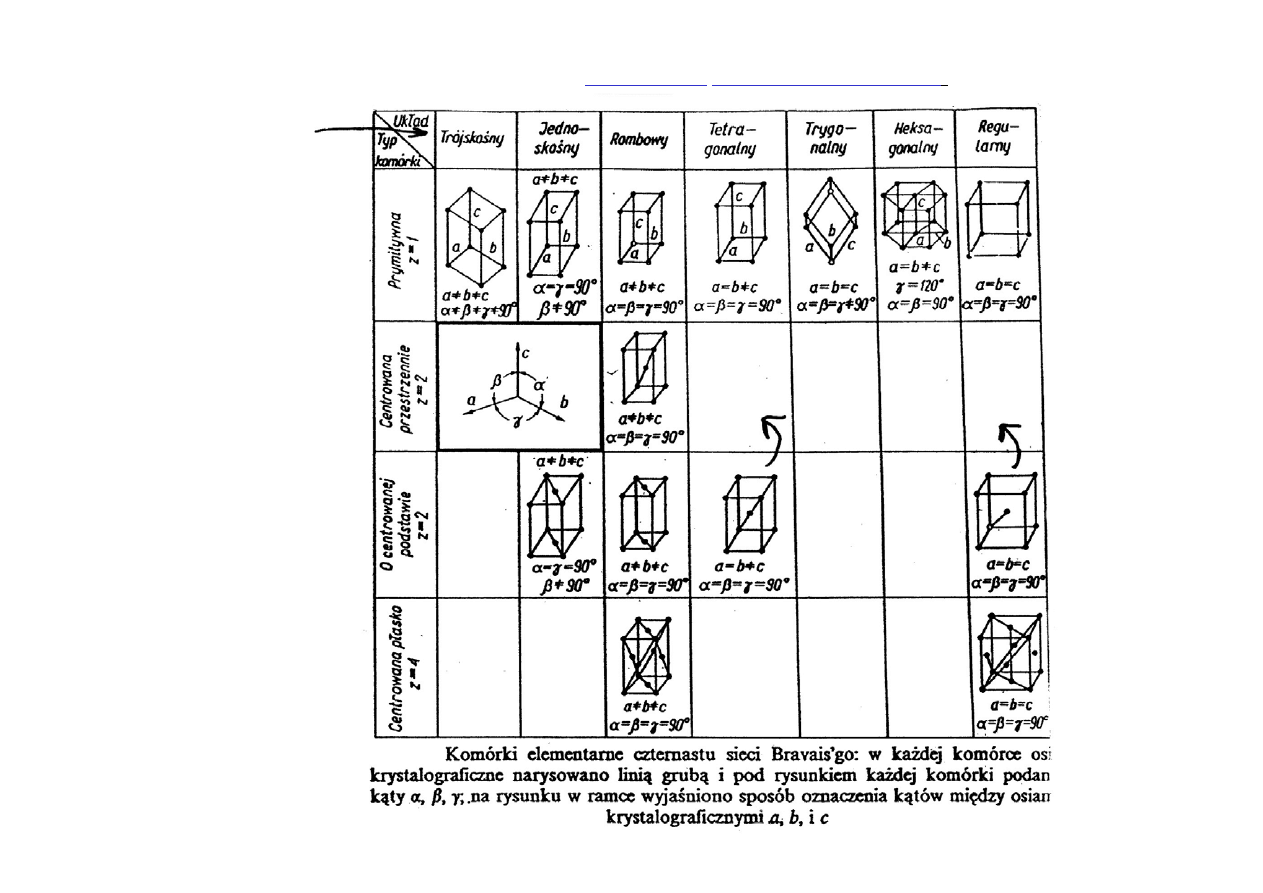
Można wyróżnić

7 układów krystalograficznych

.

Liczba z określa ilość
węzłów przypadających
na jedną komórkę
elementarną.

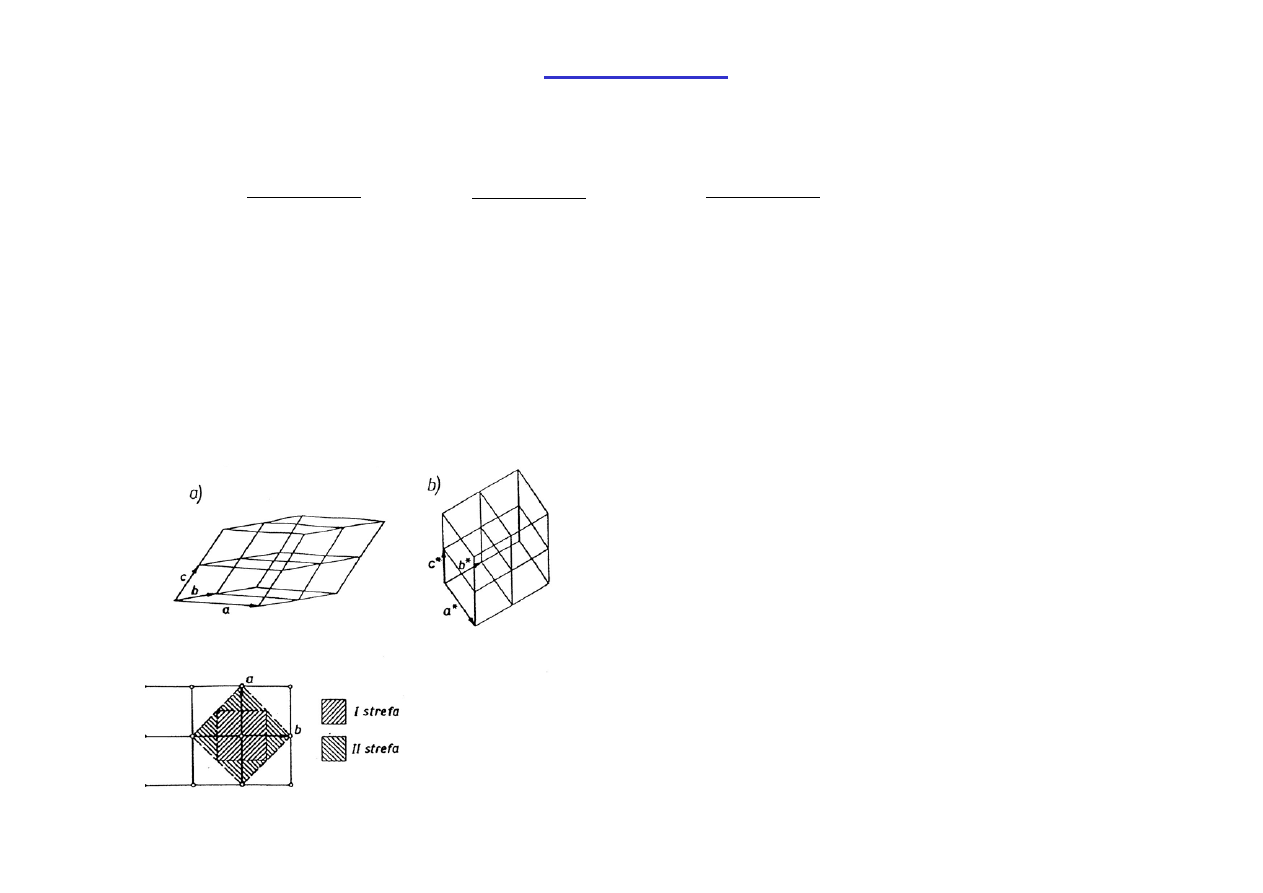
Sieć odwrotna

Do opisu kryształu często stosuje się sieć odwrotną, której podstawowe
wektory

*

,

*

i

*

są zdefiniowane zależnościami:

*

=

,

*

=

,

*

=

(v =

*

(

x

) jest objętością komórki elementarnej.

Przez analogię

, w sieci odwrotnej jest określony wektor :

*

= h

*

+ k

*

+ l

*

h, k, l - liczby całkowite

Przykład sieci prostej (a) i odpowiadającej
jej sieci odwrotnej (b)

Dla sieci odwrotnej określa się też
komórkę prymitywną, tzw. strefę
Brillouina.

Przykład wyznaczenia I i II strefy Brillouina dla sieci kwadratowej.

→

a

→

b

→

c

→

a

2 ( b x c )

v

π

→ →

→

b

2 ( c x a)

v

π

→ →

→

c

2 ( a x b)

v

π

→ →

→

a

→

b

→

c

→

T

→

T

→

a

→

b

→

c

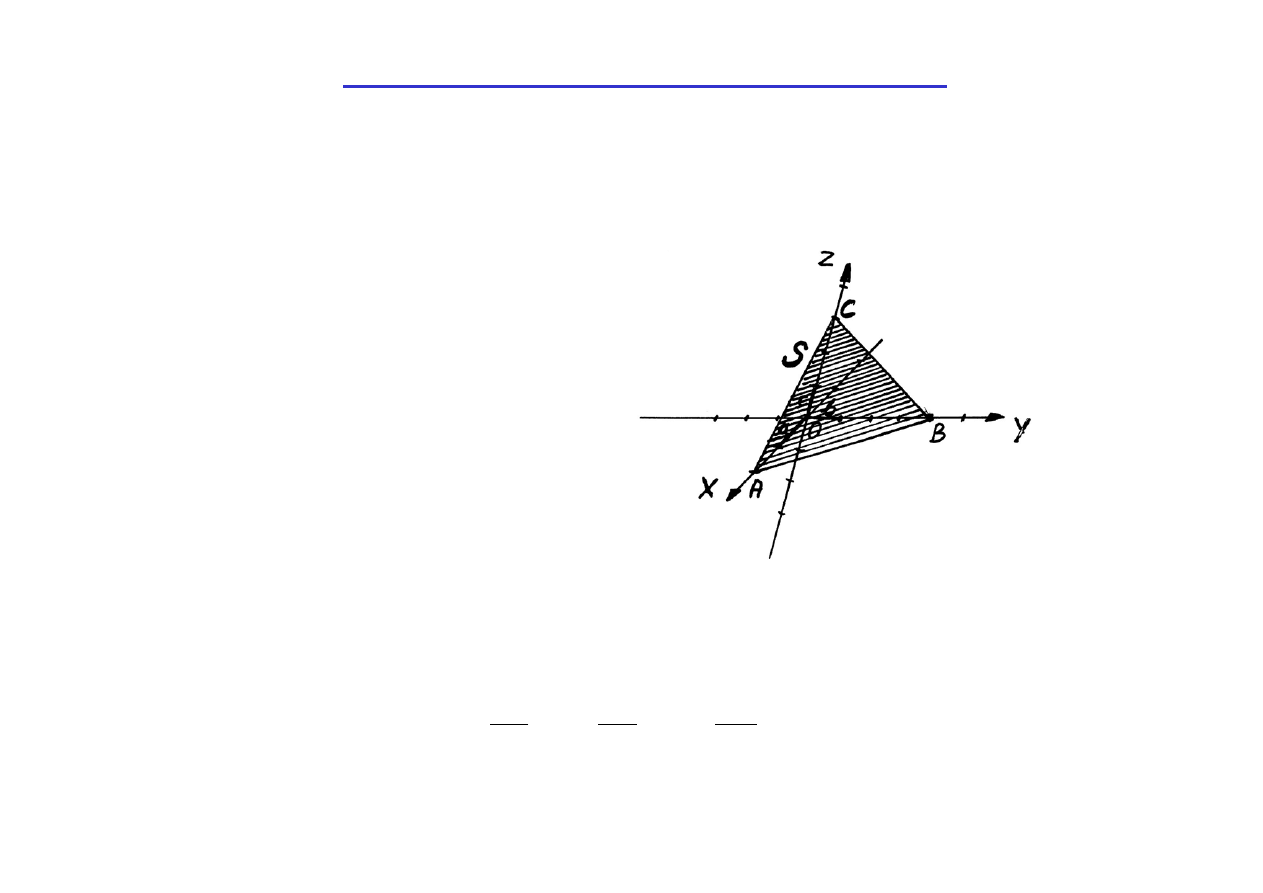
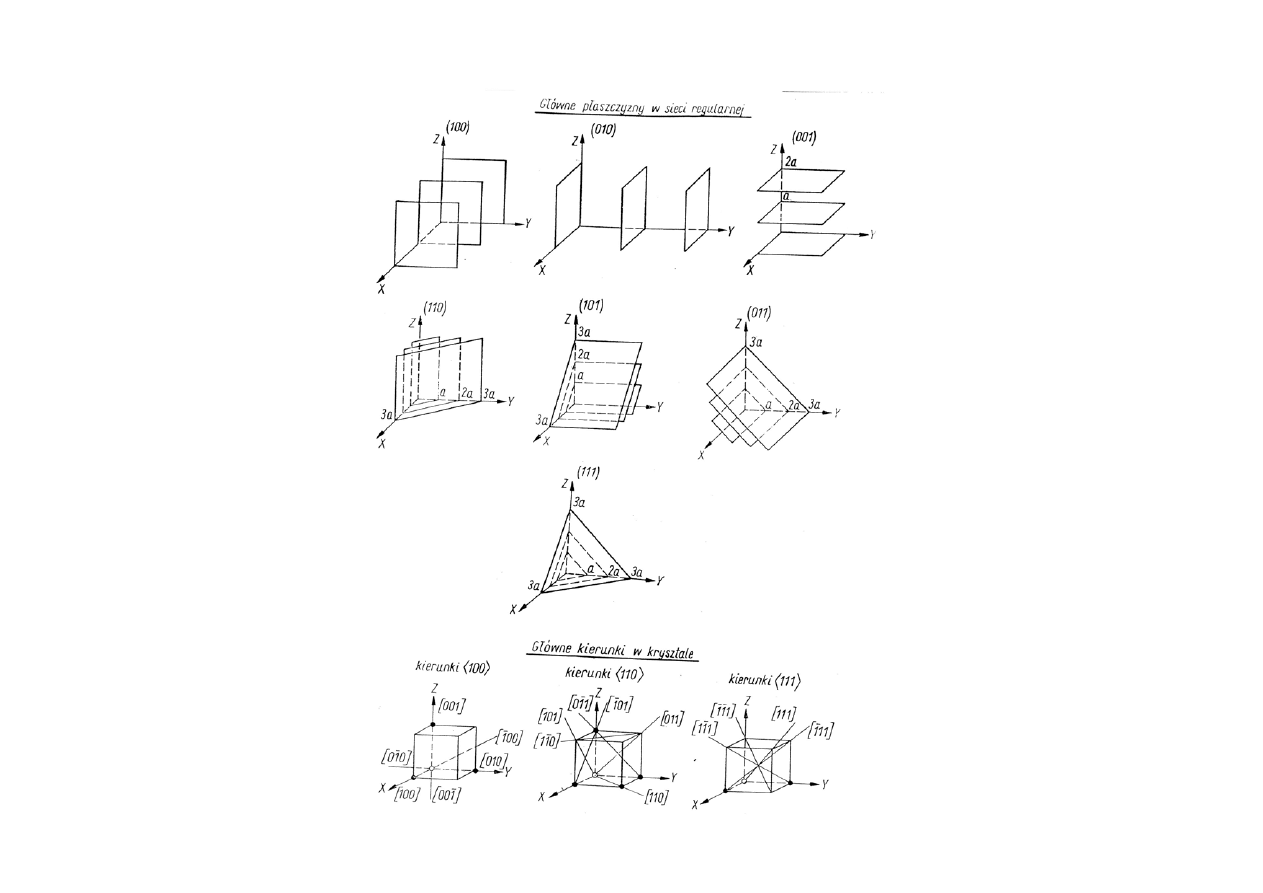
Oznaczanie płaszczyzn i kierunków w krysztale

Położenie każdej płaszczyzny jest określone przez dowolne trzy punkty
na tej płaszczyźnie (nie leżące na jednej prostej). W krysztale wygodnie
jest przyjąć te punkty, w których płaszczyzna przecina osie
krystalograficzne :

na rysunku :

m = 2

n = 4

p = 3

Płaszczyzna S odcina na osiach odcinki m, n, p wyrażone w jednostkach
stałych sieci a, b, c

m = n = p =

Trzy liczby m, n, p całkowicie określają położenie płaszczyzny S, jednak
wygodniej jest używać wskaźników Millera.

OA

a

OB

b

OC

c

Weźmy stosunek odwrotności liczb m, n, p :

:

: = h : k : l

i wyraźmy go przez stosunek najmniejszych liczb całkowitych h, k, l.
W naszym przykładzie :

:

: = :

:

= 6 : 3 : 4

Liczby h, k, l są

wskaźnikami Millera

dla płaszczyzn, które zapisuje się w

nawiasach okrągłych, bez przecinków (h k l) W przykładzie z poprzedniej
płaszczyzna S jest określona symbolem (634) (czytaj : sześć trzy cztery).

Jeśli płaszczyzna jest równoległa do jakieś osi (punkt przecięcia w

∞), to

odpowiedni wskaźnik Millera jest równy zero.
Jeśli odcinek m, n lub p ma wartość ujemną, to odpowiedni wskaźnik
Millera będzie ujemny (minus piszemy nad wskaźnikiem, np. (10 )

1

m

1

n

1

p

1

2

1

4

1

3

6

12

3

12

4

12

2

Wskaźniki Millera danej płaszczyzny sieciowej są równe współrzędnym h,
k, l najkrótszego wektora sieci odwrotnej prostopadłego do tej płaszczyzny.
Czyli płaszczyzna (h k l) jest prostopadła do wektora sieci odwrotnej :

h

*

+ k

*

+ I

*

Wskaźniki kierunkowe

u, v, w w krysztale określa się jako najmniejsze

liczby całkowite których stosunek jest równy stosunkowi rzutów wektora o
danym kierunku na osie krystalograficzne (rzuty wyrażone w jednostkach
stałych sieci a, b, c).

Wskaźniki zapisuje się w nawiasach kwadratowych, bez przecinków [u v
w].

Np. kierunek osi x oznaczymy:
[100] - zwrot dodatni, i [ 00] - zwrot ujemny; dla osi y będzie to
odpowiednio [010] i [0

0], a dla osi z [001] i [00 ]

→

a

→

b

→

c

1

1

1

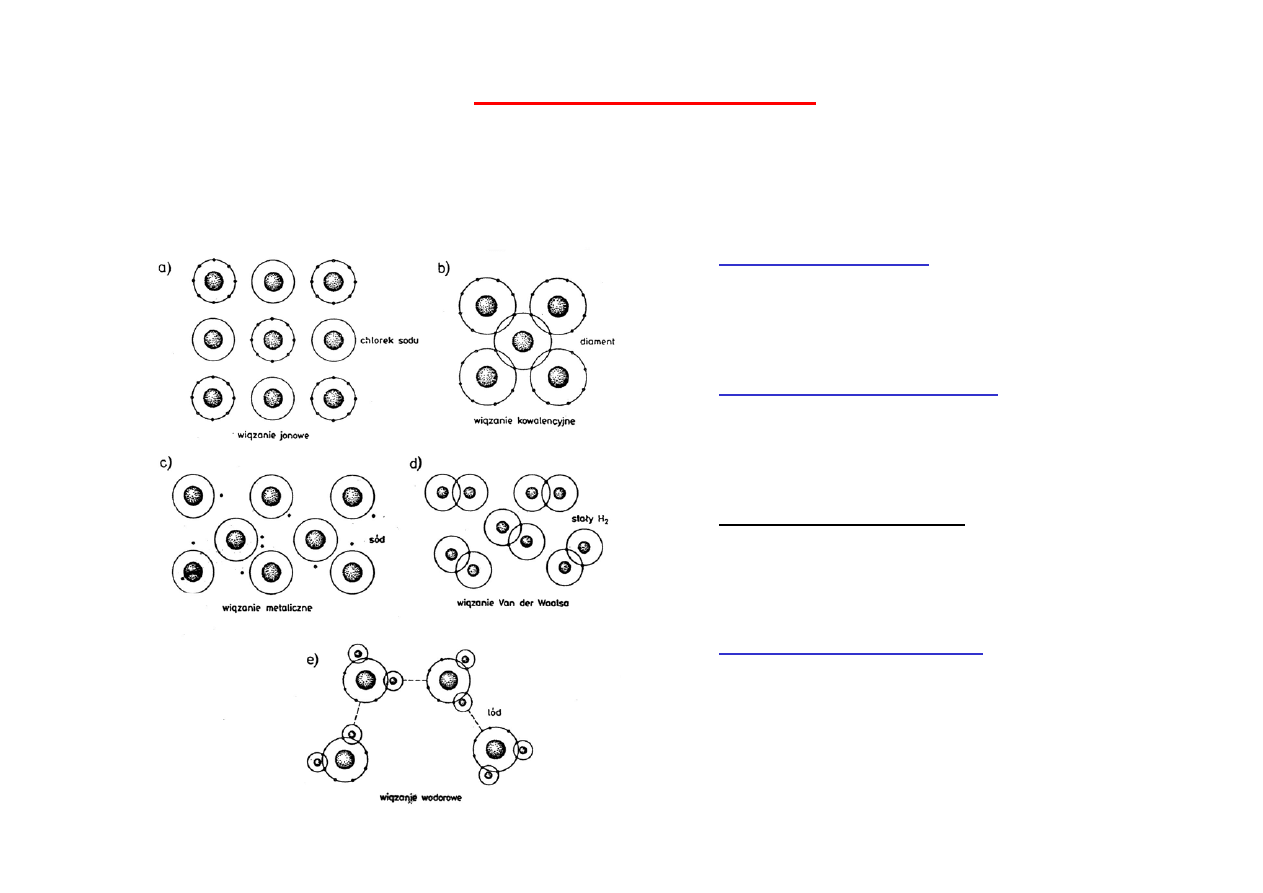
Typy wiązań w kryształach

Kryształy można klasyfikować nie tylko ze względu na ich strukturę geometryczną,
ale również ze względu na typ wiązań. Za wiązania w krysztale odpowiedzialne są
oddziaływania elektromagnetyczne (siły grawitacyjne są bardzo małe, a jądrowe i
słabe mają bardzo mały zasięg).

1)

Kryształy jonowe

są budowane z jonów dodatnich i
ujemnych (siły elektrostatyczne)

2)

Kryształy kowalencyjne

są związane chemicznymi wiązaniami

konwalencyjnymi.

3) Kryształy metaliczne
„Gaz” elektronowy wiąże jony
dodatnie.

4)

Kryształy molekularne

są

zbudowane z cząsteczek,
oddziaływania van der Waalsa
(polaryzacyjne) - dość słabe; w
niektórych przypadkach - silne
wiązania wodorowe.

Energia wiązania kryształu to energia konieczna do rozłożenia kryształu na
elementy składowe (atomy, jony lub cząsteczki), wyrażana na ogół w
J/kmol.

Typowe energie wiązań kryształów:

1) Jonowych: 7,5 x 10

8

J/kmol dla NaCl

2) Kowalencyjnych: 3,5 x 10

8

J/kmol dla diamentu

3) Metaliczne: 1,1 x 10

8

J/kmol dla Na

3,94 x 10

8

J/kmol dla Fe

4) Molekularne: 10

7

J/kmol dla CH

4

(siły van der Waalsa)

5 x 10

7

J/kmol dla H

2

0 (wiązania wodorowe).

Stany elektronów w krysztale w opisie mechaniki kwantowej

Twierdzenie Plancka

- emisja lub absorpcja promieniowania zachodzi porcjami o

wielkości:

E = h

ν

= h c/

λ

ν

= c/

λ

(częstotliwość fali o długości

λ)

h = 6,625 x 10

-34

Js (stała Plancka)

- poprawny opis promieniowania ciała doskonale czarnego.

Zjawisko fotoelektryczne zewnętrzne

potwierdziło kwantową

naturę

promieniowania (zjawisko to polega na wyrzucaniu elektronów z powierzchni
ciała stałego przez padające promieniowanie):
i. natężenie promieniowania nie ma wpływu na energię kinetyczną wybijanych
elektronów.
ii. energia kinetyczna elektronów rośnie wraz z częstotliwością promieniowania.
iii. dla każdego ciała stałego istnieje częstotliwość progowa

ν

o

, poniżej której

zjawisko fotoelektryczne nie występuje.

Wyjaśnienie -

równanie Einsteina

h

ν

=

ϕ

+ E

kmax

ϕ

- praca wyjścia elektronu

E

kmax

- energia kinetyczna najszybszych elektronów.

Dla częstotliwości progowej E

kmax

= 0, czyli h

ν

o

=

ϕ

Promieniowanie elektromagnetyczne ma charakter dualistyczny

:

w niektórych zjawiskach zachowuje się jak fala (dyfrakcja, interferencja),
a w niektórych jak strumień cząstek (zjawisko fotoelektryczne).
Kwant światła - foton - o energii E = h

ν

ma masę określoną z zasady

równoważności masy i energii

E = m c

2

:

m =

i odpowiednio pęd:

p = m c = =

Z relatywistycznej zależności masy od prędkości:

m =

po przekształceniu:

= 1 -

⇒ fotony mają prędkość u = c co możliwe jest tylko dla

m

o

= 0

⇒ masa spoczynkowa fotonu jest równa 0.

h

c

2

ν

h

c

ν

h

ν

m

1 u

c

o

2

2

−

u

c

2

2

o

2

2

m

m

Twierdzenie de Broglie

’

a

Skoro światło ma naturę dualistyczną, to także materia powinna mieć
taką naturę i wykazywać również właściwości falowe.

Skoro p =

, to:

λ

=

gdzie

λ

jest falą materii cząstki o pędzie p.

Każdej poruszającej się cząstce materialnej można przypisać falę
materii o długości danej wzorem de Broglie

’

a.

Potwierdzenie: dyfrakcja wiązki elektronów przechodzących przez
kryształ. Warunek:

λ

< d , więc elektron musi mieć odpowiednią

energię. Np. dla elektronu o energii 10 eV, długość fali de Broglie

’

a

wynosi

λ

= 3,9 x 10

-10

m (tego rzędu są odległości międzyatomowe w

krysztale). Dla cząstek o dużej masie długość

λ

jest bardzo mała, fale

są nieobserwowalne.

h

c

h

ν

λ

=

h

p

h

mu

=

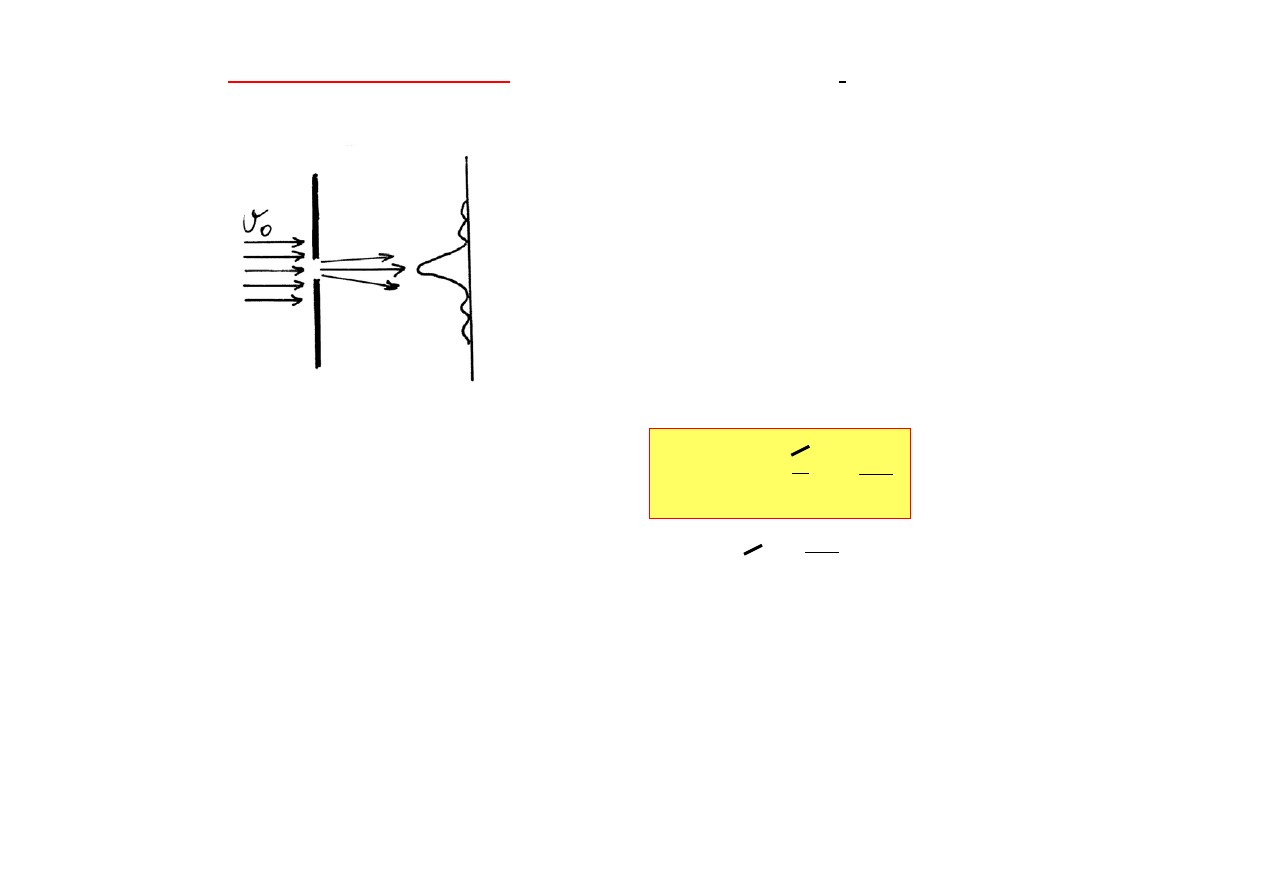
Zasada nieoznaczności

jest konsekwencją falowo - cząsteczkowej

natury materii.

Jeśli wiązka monoenergetycznych
elektronów pada na szczelinę, to ulega
ugięciu. Jeśli chcemy zmierzyć
jednocześnie pęd i położenie jakiegoś
wybranego elektronu, to z praw dyfrakcji
oraz z długości fali de Broglie

’

a wynika,

że nieokreśloność położenia

∆

x i

nieokreśloność pędu

∆

p będą takie, że:

∆

x

⋅ ∆

p

>

=

gdzie h =

Nie można jednocześnie zmierzyć x i p z dowolną dokładnością.
Elektronu nie możemy więc przedstawiać jako ładunku punktowego,
ale jako „chmurę” elektronową o różnej gęstości. Duża gęstość
oznacza duże prawdopodobieństwo znalezienia elektronu.

h

2

h

4

π

h

2

π

”Chmura Rozkład gęstości Warstwice Kontur
elektronowa” w ”chmurze”

gęstości ”chmury”

wzdłuż wybranego ładunku
kierunku

„Chmurę” elektronową można przedstawiać graficznie w różny sposób.
Chemicy na ogół posługują się konturem - na zewnątrz konturu
prawdopodobieństwo znalezienia elektronu jest bardzo małe.

Kształty i rozkład gęstości ładunku w „chmurach” elektronowych w
atomach, cząsteczkach chemicznych i innych układach atomów (np. w
kryształach) opisują tzw.

funkcje falowe

ψ

(x, y, z, t)

, co odzwierciedla

falowe właściwości elektronu. Funkcja falowa zależy od współrzędnych
wszystkich elektronów opisywanego układu (w ogólności zależy też od
położeń jąder).

Kwadrat modułu funkcji

ψ

(x, y, z, t), jest równy

gęstości

prawdopodobieństwa p (x, y, z, t)

, znalezienia cząstki (np.elektronu)

w chwili t w punkcie przestrzeni (x, y, z, t)

|

ψ

|

2

= p

Z definicji prawdopodobieństwa wynika, że całka po całej przestrzeni

pdV = 1

Czyli

dV = 1, a prawdopodobieństwo znalezienia cząstki w

elemencie

∆ V wynosi:

P = p

∆V = |

ψ

|

2

∆x ∆y ∆z

Funkcja falowa

ψ

opisuje zachowanie cząstek w sposób statystyczny.

Funkcja

ψ

jest rozwiązaniem równania różniczkowego, tzw.

równania

Schrödingera

.

Równanie takie można napisać dla dowolnego układu, ale ścisłe
rozwiązanie otrzymuje się tylko dla atomu wodoru; już dla atomu helu
możliwe jest tylko przybliżenie.

∫

∫

|

ψ

|

2

Jeśli

ψ

nie jest zależne od czasu, to

równanie Schrödingera

dla cząstki o

masie m ma postać :

∇

2

ψ +

[ E - U(x,y,z)]

ψ = 0

gdzie :

∇

2

ψ =

+ +

(

∇

2

jest operatorem, tzw. laplasjanem)

E - całkowita energia cząstki
U(x,y,z) - energia potencjalna cząstki (zależy od sił działających na cząstkę)

Z użyciem liczby falowej k

k =

(bo pęd p =

oraz p

2

= 2mE

k,

a E

k

= E - U)

równanie Schrödingera

można przedstawić w postaci:

∇

2

ψ

+ k

2

ψ

= 0

Liczba falowa k nie jest stała, zależy od (x, y, z).
Rozwiązanie równania Schrödingera polega na znalezieniu

ψ

i wartości

energii cząstki E.

8

2

2

π m

h

∂ ψ

∂

2

2

x

∂ ψ

∂

2

2

y

∂ ψ

∂

2

2

z

2

2

2

2

2

2

π

λ

π

π

π

=

=

=

−

p

h

h

mE

h

m E U

k

(

)

h
λ

Nie dla każdej wartości energii całkowitej E istnieje funkcja falowa

ψ

spełniająca równanie Schrödingera. Właściwe rozwiązanie tego równania
otrzymuje się tylko dla określonych wartości energii całkowitej E

1

, E

2

, E

n

,

którym odpowiadają funkcje falowe

ψ

1

,

ψ

2

,

ψ

n

. Mówimy, że

wartości

całkowitej energii elektronu w atomie są skwantowane

. Stan o niższej

energii nazywamy stanem podstawowym. Stany o wyższych energiach -
stanami wzbudzonymi.
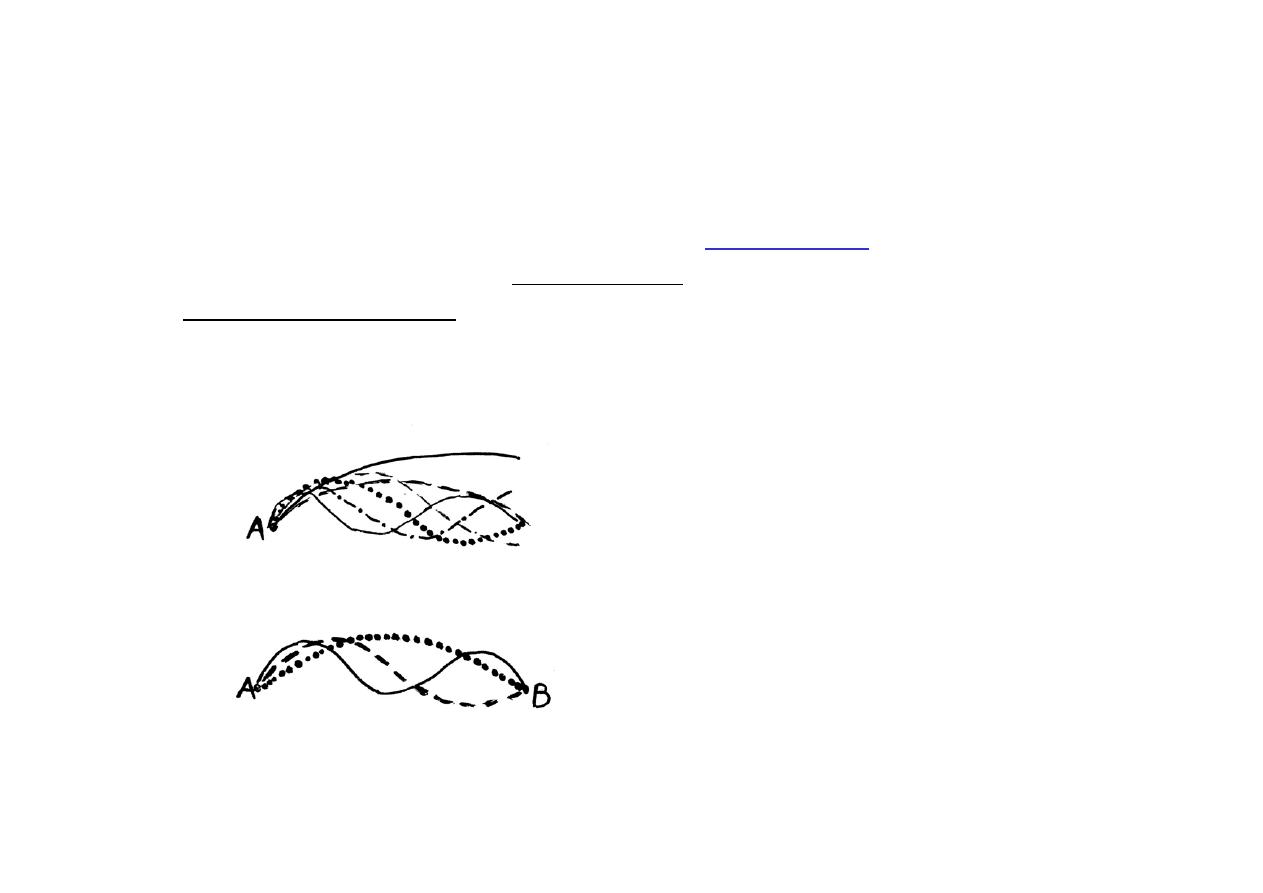
Również w fizyce klasycznej są przypadki „skwantowania” pewnych
wielkości, np. długości fal na strunie obustronnie umocowanej :

Gdy umocowany jest tylko jeden
koniec struny, każde drganie, dla
którego A jest nieruchome, jest
możliwe.

Gdy umocowane są oba końce, to
pomiędzy A i B muszą się zmieścić
całkowite wielokrotności

λ

/2

W mechanice kwantowej sytuacja jest bardzo podobna.

Rozwiązanie równania Schrödingera dla atomu wodoru

Energia potencjalna elektronu w polu elektrycznym protonu :

U(x,y,z) = -

Zatem równanie Schrödingera dla atomu wodoru :

∇

2

ψ +

[ E +

]

ψ = 0

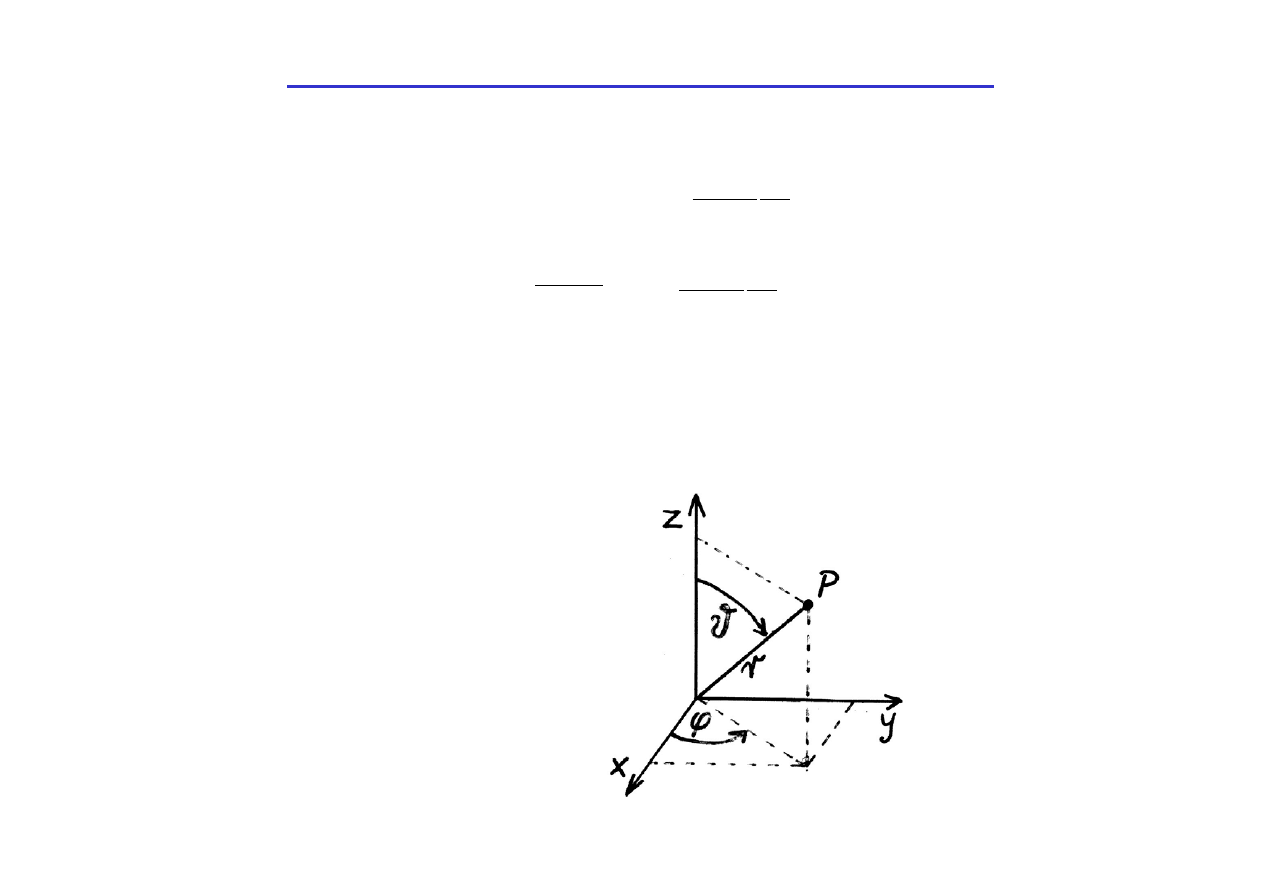
Ponieważ pole, w którym porusza się elektron, jest polem
centralnym (energia potencjalna jest określona przez współrzędną r -
promień wodzący, a nie przez współrzędne kartezjańskie x, y, z),
wygodniej jest zapisać równanie Schrödingera we współrzędnych
sferycznych :

r - promień wodzący

- kąt biegunowy

ϕ

- kąt azymutalny

x = r sin

ϑ

cos

ϕ

y = r sin

ϑ

sin

ϕ

z = r cos

ϑ

1

4

e

r

o

2

π ε

8

2

2

π m

h

1

4

e

r

o

2

π ε

ϑ

Równanie Schrödingera dla atomu wodoru zapisane we współrzędnych
sferycznych (również operator Laplace

’

a zapisany we współrzędnych

sferycznych):

+

+

+

+

[ E +

] =

0

Równanie to ma rozwiązanie (tzn. istnieją dla niego funkcje falowe

ψ

o

odpowiednich właściwościach : jednoznaczne, skończone i ciągłe) dla:
1) dowolnych dodatnich wartości E
2) dla dyskretnych (skwantowanych) ujemnych wartości E równych:

E

n

= -

( n = 1, 2, 3, ..) (h =

)

1 = ∂

∂

∂Ψ

∂

2

2

r

r r

r

(

)

1

2

r s in

s in

)

ϑ

∂

∂ϑ

ϑ ∂ψ

∂ϑ

1

2

2

2

r

r

sin

ϑ

∂ ψ

∂

8

2

2

π m

h

1

4

2

π ε

o

e

r

ψ

mee

32

h n

4

2

o

2

2 2

π ε

h

2

π

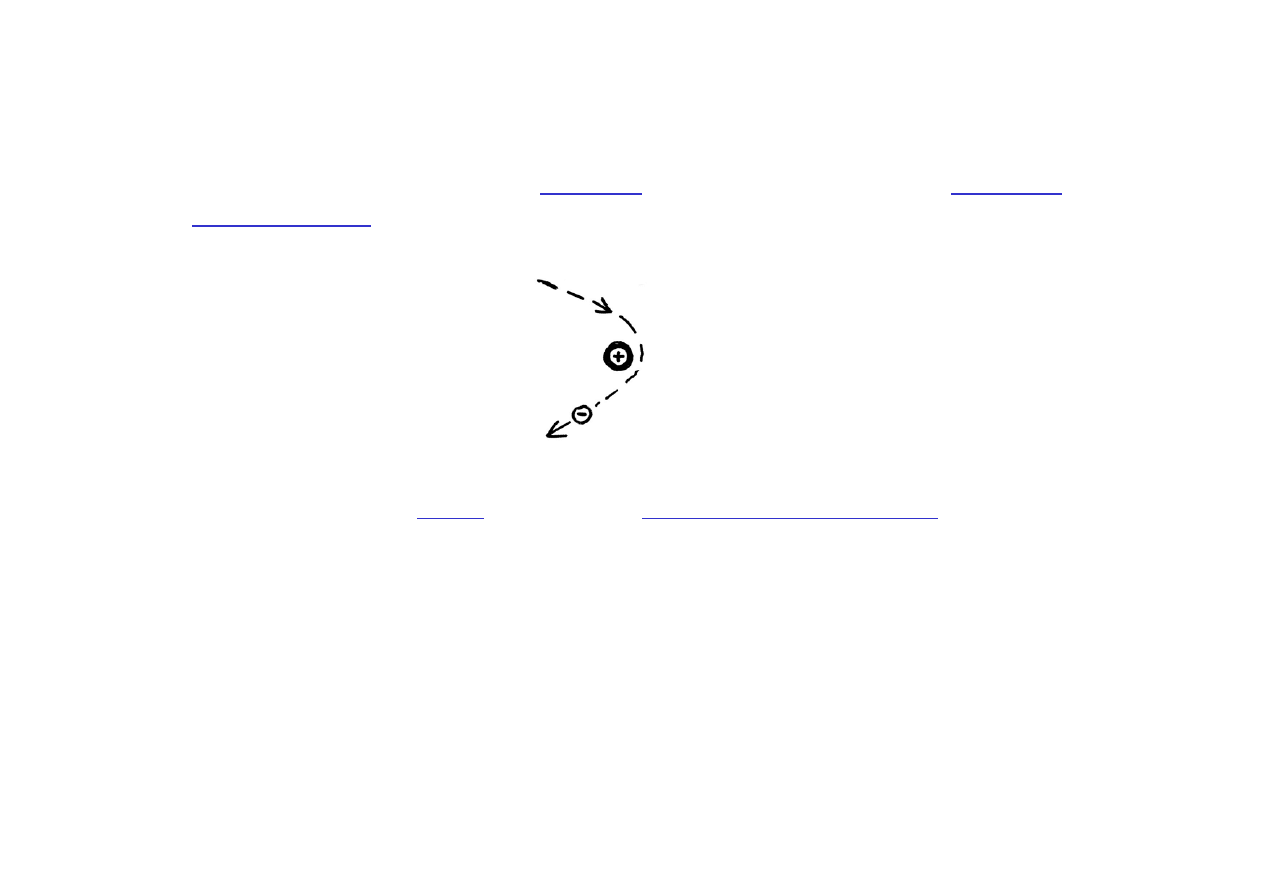
Przypadek 1), tzn. dla

E

> 0

, odpowiada sytuacji

elektronu

niezwiązanego

z jądrem (elektron obdarzony dużą energią kinetyczną

zbliża się do jądra dodatniego i ponownie oddala)

Przypadek 2), dla

E

< 0

, odpowiada

elektronowi związanemu

z jądrem;

wartości energii atomu wodoru E

n

wynikające z rozwiązania równania

Schrödingera są takie same jak uzyskane z modelu atomu Bohra (ale
Bohr musiał wprowadzić dodatkowe, sztuczne założenia).
W atomie wodoru liczba n, nazywana główną liczbą kwantową, określa
jednoznacznie wartość energii elektronu.

Dla atomów wieloelektronowych równanie Schrödingera jest bardziej
złożone, a rozwiązania tylko przybliżone.

Spośród nieskończonego szeregu rozwiązań równania Schrödingera
dla danego układu (atomu lub cząsteczki) wybieramy tylko te funkcje
falowe, które maleją szybko do zera ze wzrostem odległości od jąder,
bo odpowiadają one stanom związanym (prawdopodobnieństwo że
elektron jest daleko od jądra p =

= 0)

Odpowiadające im

wartości energii E wyznaczają dozwolone energie

atomu lub cząsteczki, a same

funkcje falowe nazywamy orbitalami

.

Kolejne odpowiednie funkcje falowe wyznaczające stany dozwolone
określone są przez podanie czterech liczb kwantowych :

n - główna liczba kwantowa (n = 1, 2, 3, ...)

l - orbitalna liczba kwantowa (l = 0, 1, 2, ,,,,, (n-1))

m

l

- magnetyczna orbitalna liczba kwantowa

(m

l

= - l, -(l-1), (l-1), l)

m

s

- magnetyczna spinowa liczba kwantowa

(m

s

= -

, + )

ψ

2

1

2

1

2

Liczba kwantowa n określa energię elektronu E w atomie wodoru;
w atomach wieloelektronowych energia elektronu zależy również od
liczby kwantowej l, która określa moment pędu elektronu L.
Magnetyczna liczba kwantowa m

l

określa rzut momentu pędu na

wyróżniony kierunek L

z

(np. wymuszony przez pole magnetyczne), a

m

s

- rzut spinu

σ

z

na wyróżniony kierunek.

Elektron atomu lub cząsteczki w danym stanie kwantowym nie
wypromieniowuje ani nie pochłania energii; nie zmienia wartości
momentu pędu, spinu ani ich orientacji przestrzennej.

Zakaz Pauliego

: W jakimkolwiek układzie wieloelektronowym stan

określony przez cztery liczby kwantowe n, l, m

l

, m

s

może być zajęty

tylko przez jeden elektron.
Orbitale są określone przez liczby kwantowe :
n określa wielkość, l - kształt, m

l

- orientację w przestrzeni orbitalu.

Odosobniony atom może być przedstawiony
jako jama potencjału, w której elektron może
zajmować jeden z szeregu dyskretnych stanów
energetycznych.

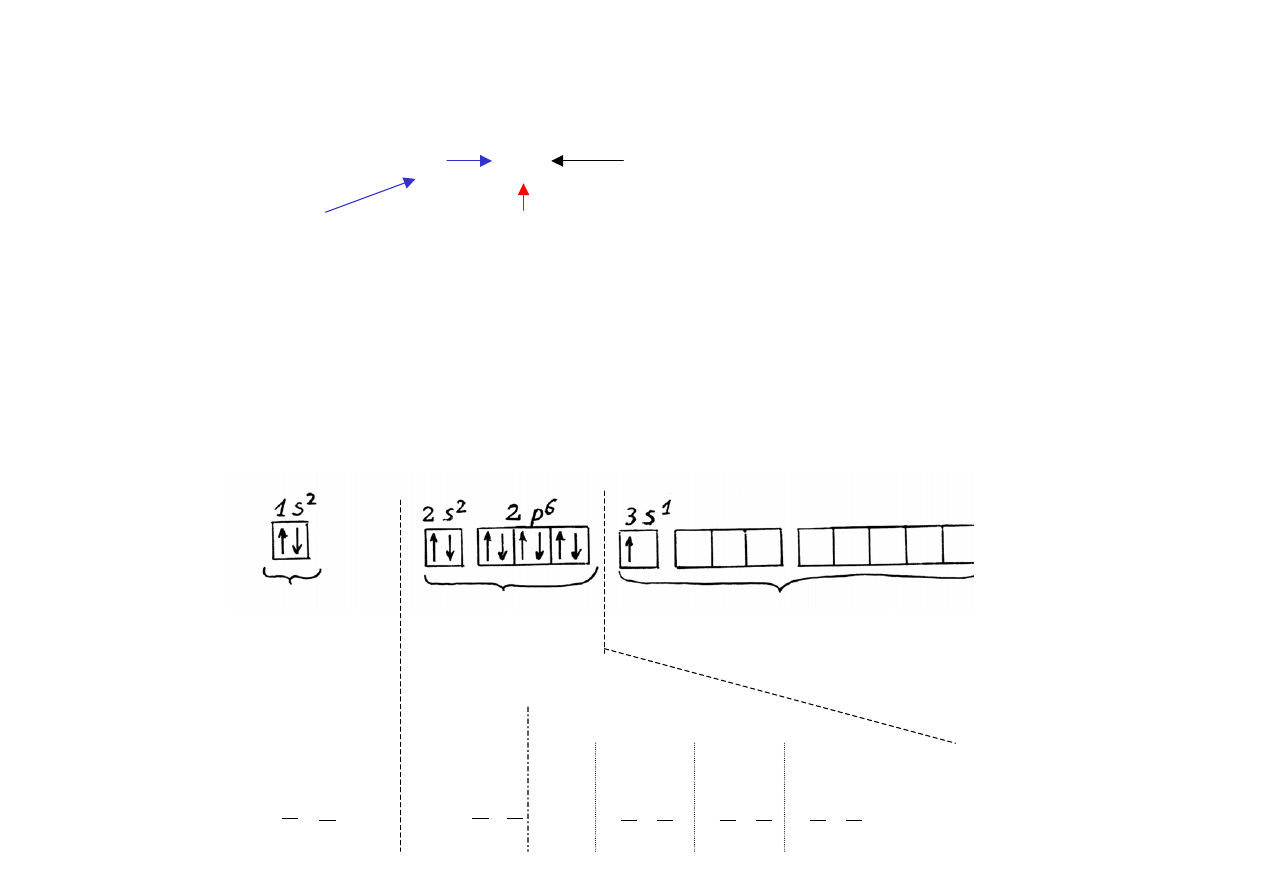
Konfigurację elektronową opisuje się podając (przykład):

wartość n

3

p

5

liczba elektronów w

w danej podpowłoce

(numer powłoki

literę określającą podpowłokę

elektronowej)

(litery s, p, d, f, g, h, .... odpo-
wiadają kolejnym wartościom

liczby kwantowej l)

Zapis ten nie uwzględnia sposobu rozmieszczenia elektronów w danej
podpowłoce na poszczególnych poziomach, ani orientacji rzutu ich
spinów. Można to przedstawić graficznie np. dla atomu sodu:

powłoka K

powłoka L

powłoka M (n = 3)

(n=1)

(n = 2)

1 podpowłoka s 2 podpowłoki:

(l =0) s (l= 0)

p (l=1)

m

l

= 0

m

l

= 0

m

i

= -1

0,

1

m

s

= - ,

m

s

= - , m

s

= -

,

-

,

-

,

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

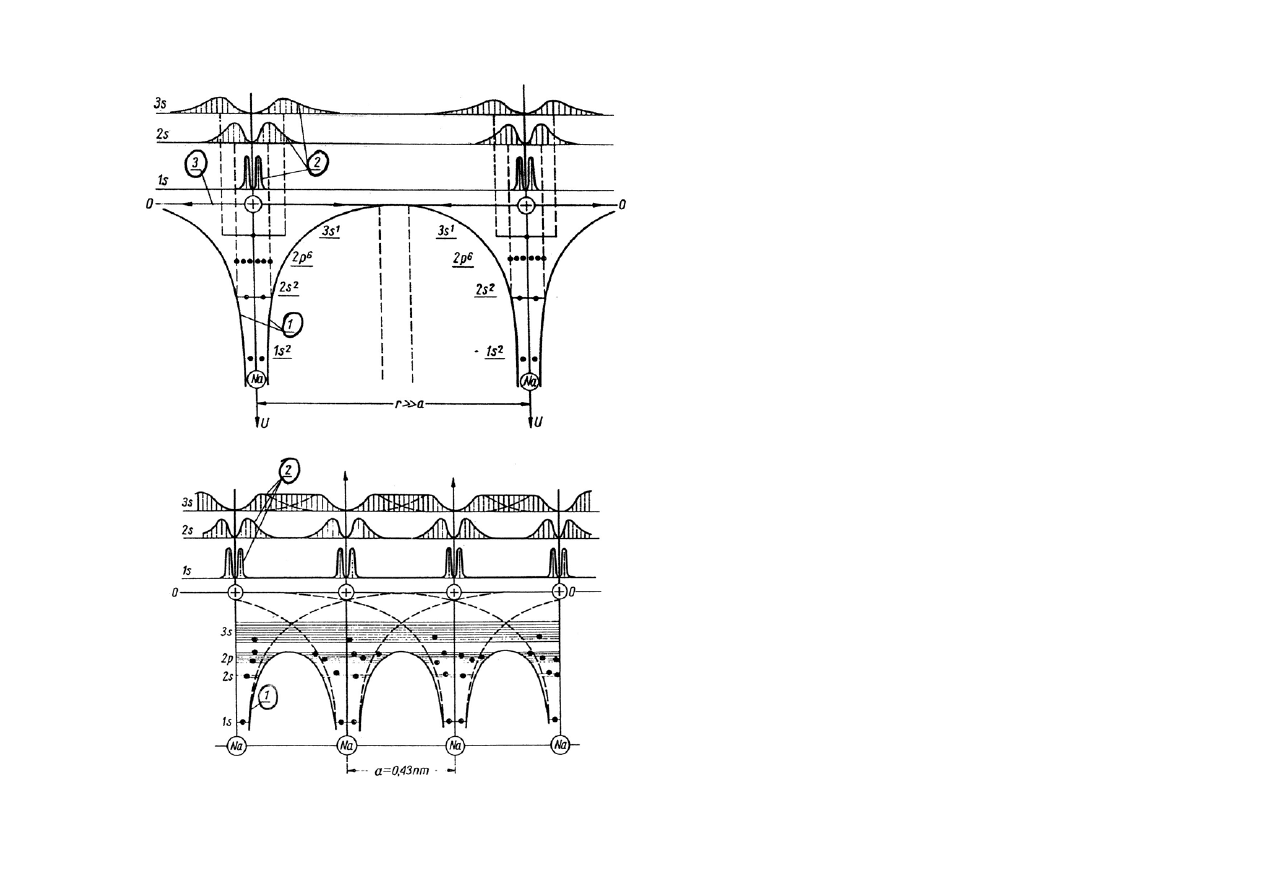
Jeżeli zbliżymy do siebie dwa atomy
tak, że jeszcze nie oddziałują na siebie,
to poziomy energetyczne elektronów i
kształt barier nie ulegną zmianie.

1 - kształt bariery
2 - rozkład prawdopodobieństwa
3 - zerowy poziom energii

Gdy odległość atomów zmniejszymy
poniżej ok. 10

-9

m (1nm) zaczną na

siebie oddziaływać.

Dla atomów sodu w krysztale minimum energii oddziaływania jest
osiągnięte dla stałej sieciowej a = 0,43 nm. Bariera potencjału 1 jest
niższa i węższa, jej szczyt jest poniżej poziomów energetycznych
elektronów walencyjnych 3s;

elektrony walencyjne mogą poruszać się

swobodnie w krysztale (gaz elektronowy).

W wyniku oddziaływań

poziomy energetyczne ulegają poszerzeniu i

rozszczepieniu w pasma

, zgodnie z zakazem Pauliego (można to

wyjaśnić na podstawie zasady nieoznaczoności Heisenberga dla
energii w postaci

∆E∆t ≥ h)

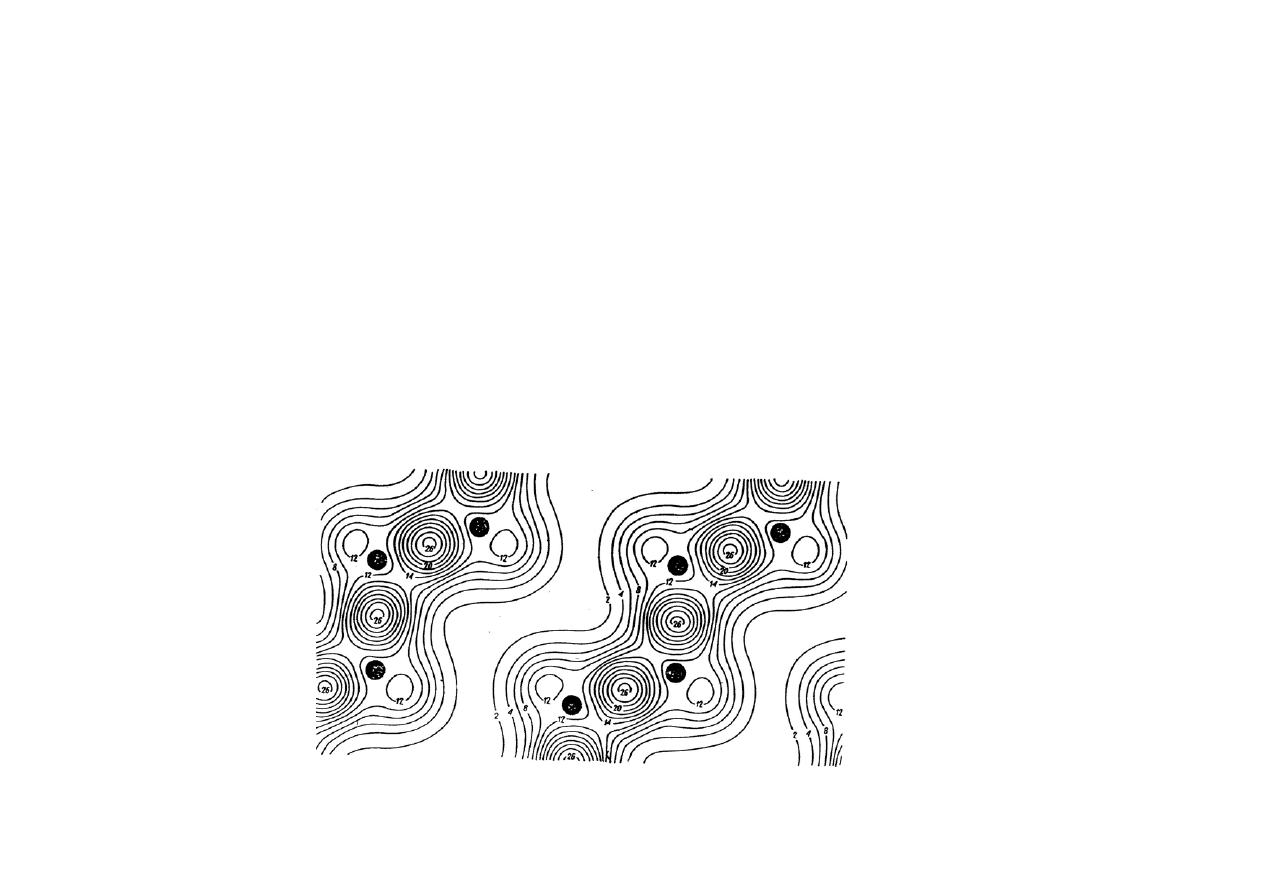
W kryształach kowalencyjnych elektrony walencyjne są skupione
pomiędzy rdzeniami atomów.

Np. w krysztale germanu o strukturze diamentu (pierwiastek
czterowartościowy), warstwice gęstości elektronów walencyjnych
ukazują maksima w połowie odległości między parami rdzeni Ge.
W kryształach metali, dzięki „swobodnym” elektronom możliwy jest
przepływ ładunku - przewodnictwo elektryczne. W kryształach jonowych
i kowalencyjnych również zewnętrzne elektrony są zlokalizowane, są
więc izolatorami.

Modele oddziaływania elektronów w krysztale

Układ jest bardzo skomplikowany - konieczność uproszczeń :

1. Kryształ jest układem złożonym z dwóch podukładów : prędkich
elektronów i nieruchomych jąder - elektrony wypełniają przestrzeń
między węzłami sieci krystalicznej. Przybliżenie to wynika z różnicy
mas jąder i elektronów i nosi nazwę

przybliżenia adiabatycznego

.

2. Pojedyńczy elektron porusza się w wypadkowym polu wytworzonym
przez pozostałe elektrony, co upraszcza równanie Schrödingera :

∇

2

ψ

+

[ E - U ]

ψ

= 0

gdzie : U - energia potencjalna elektronu w polu jonów i pozostałych
elektronów (pole to nie zależy od chwilowego położenia elektronu);
E - energia całkowita elektronu.
Jest to

przybliżenie jednoelektronowe

, stanowiące podstawę teorii

pasmowej ciała stałego.
Mimo tych uproszczeń, konieczne są modele przybliżone.

8

2

2

π m

h

a) Model elektronów swobodnych

Przybliżenie, że elektrony poruszają się swobodnie w całej objętości
kryształu, ładunek dodatni jest rozłożony równomiernie i wytwarza
pole o stałym potencjale (por. rysunek dolny na str. 24 - przybliżenie
to dotyczy obszaru pomiędzy jądrami, tzn. ok. 90% objętości
kryształu, przy założeniu że potencjał sieci jest słaby).

Kryształ jest

jamą potencjału o płaskim dnie

.

b) Model słabego wiązania elektronów.

Przybliżenie to również dotyczy obszaru pomiędzy jądrami, ale
potencjał pola wytworzonego przez jądra jest funkcją okresowemu
uporządkowaniu dodatnich jąder.

Kryształ jest jamą potencjału z falistym dnem.

c) Model silnego wiązania elektronów.

Założenie, że wpływ sąsiednich atomów na poziomy energetyczne
jest zaniedbywalny, są one takie jak w atomach swobodnych (por. str.
24 - dotyczy obszaru bliskiego jąder, gdzie pole jest silne i potencjał
zmienia się bardzo silnie).

W pojedyńczym atomie swobodnym, każdej parze liczb kwantowych
n, l odpowiada 2(2l + 1) stanów kwantowych zależnych od liczb
kwantowych m

l

i m

s

.

Jeśli w krysztale jest N atomów, to ze względu na zakaz Pauliego,
musi powstać N(2l +1) podpoziomów (na każdym mogą być po dwa
elektrony o różnej liczbie kwantowej m

s

, tzn. o przeciwnych spinach).

Np. z poziomu s tworzy się N podpoziomów mieszczących 2N
elektronów, z poziomu p - 3N podpoziomów mieszczących 6N
elektronów.

Z pojedyńczych poziomów energetycznych tworzą się pasma

.

Przykład

: W 1g kryształu, zawierającego N = 10

22

atomów, poziom s

rozszczepia się na N podpoziomów. Zakładając, że szerokość
utworzonego pasma wynosi 1 eV , odległość pomiędzy podpoziomami
wynosi 10

-22

eV. Podpoziomy tworzą więc praktycznie ciągłe pasmo,

które nazywa się pasmem dozwolonym.

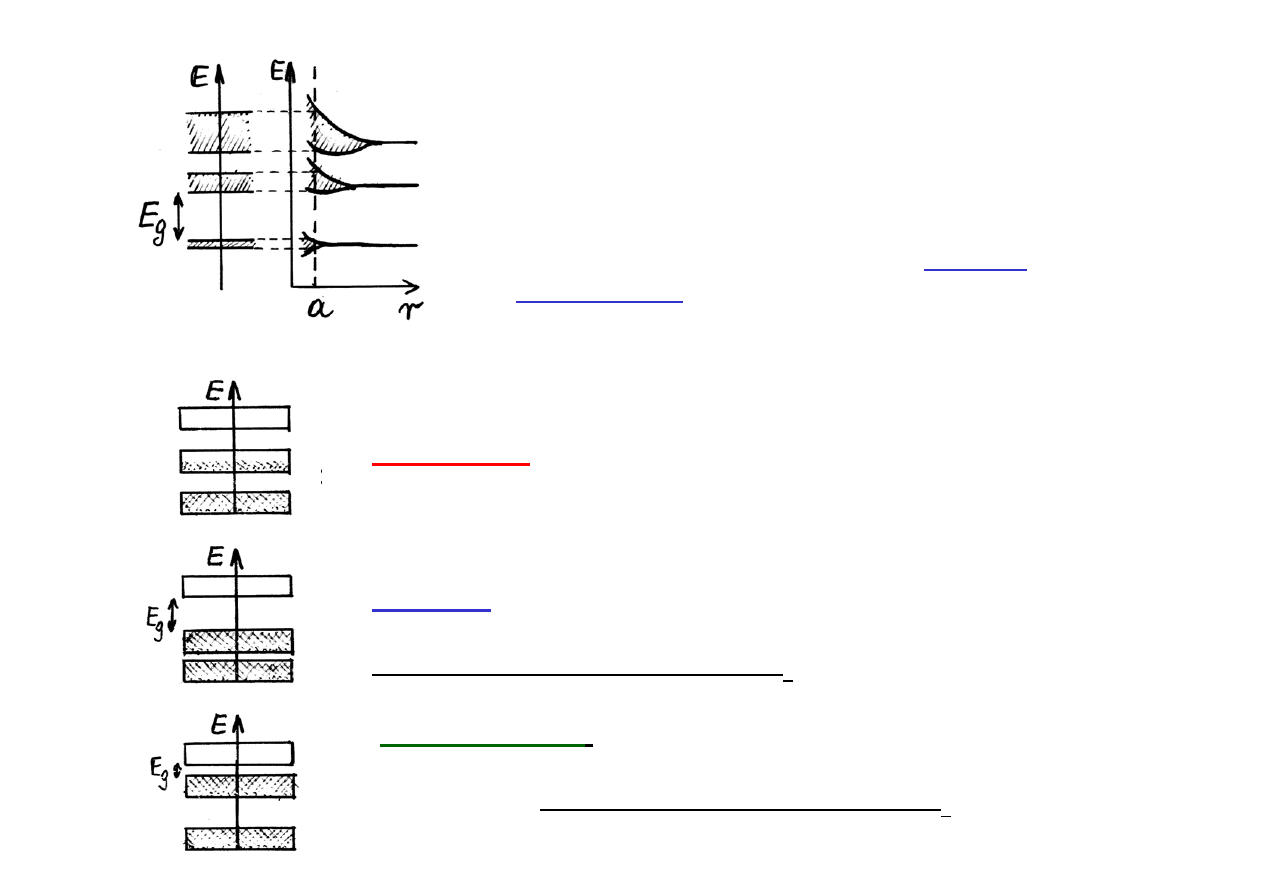
W każdym paśmie może się znajdować ograniczona liczba
elektronów (zakaz Pauliego). Zależnie od stopnia
wypełnienia pasm, kryształy dzielimy na :

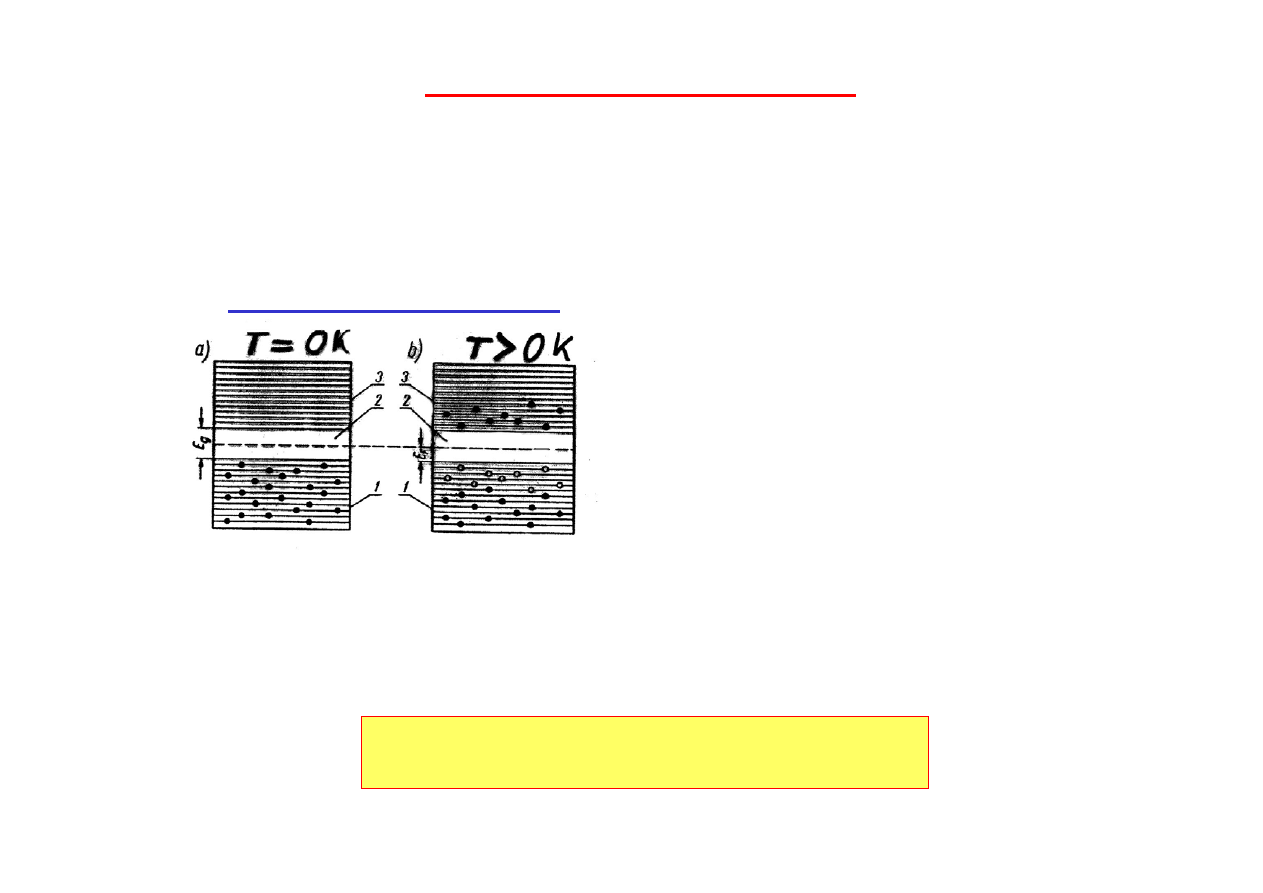
Tworzenie się pasm energetycznych w
krysztale (w wyniku zmniejszania się odległości
r pomiędzy swobodnymi atomami aż do
wartości a, będącej stałą sieci krysztalicznej).
Pasma dozwolone są rozdzielone

pasmem

wzbronionym o szerokości E

g

Przewodniki

. Nad całkowicie zapełnionym pasmem

walencyjnym leży częściowo zapełnione pasmo
przewodnictwa.

Izolatory.

Nad całkowicie zapełnionym pasmem

walencyjnym znajduje się puste pasmo, oddzielone
szerokim pasmem wzbronionym E

g

.

Półprzewodniki.

Wypełnienie pasm takie jak w

izolatorach, ale puste pasmo odzielone jest od
zapełnionego wąskim pasmem wzbronionym. E

g

Elementy fizyki statystycznej

Układy fizyczne często składają z olbrzymiej ilości cząstek; opisanie
zachowania się każdej cząstki indywidualnie jest niemożliwe. Nie
jest to jednak konieczne, aby móc opisać zachowanie się całego
układu - wystarczy określenie rozkładów cząstek w zależności od ich
energii, pędu lub prędkości.
Np. energetyczny rozkład cząstek jest określony przez

funkcję

rozkładu f (E);

wówczas f(E)dE określa liczbę cząstek układu o

energiach z przedziału (E, E+dE).

Znajomość funkcji rozkładu pozwala określić wartości średnie danej
wielkości fizycznej, np. energii, a na ich podstawie można wyliczyć
pewne parametry charakteryzujące układ makroskopowy, np.
ciśnienie gazu, przewodnictwo elektryczne i cieplne, temperaturę i
inne.

Cząstki podzielone są na trzy grupy podlegające różnym rozkładom :

Cząstki rozróżnialne

(np. atomy i cząsteczki) podlegają rozkładowi

Maxwella - Boltzmanna

.

Fermiony

(cząstki o spinie połówkowym, 1/2 h, 3/2 h, ...., np. elektrony,

protony, neutrony, neutrina) objęte są zakazem Pauliego (p. str. 23) i
podlegają rozkładowi

Fermiego - Diraca

Bozony

(cząstki o spinie całkowitym, 0, h, 2h, ...., np. fotony i jądra

składające się z parzystej liczby nukleonów) podlegają rozkładowi

Bosego - Einsteina

.

Zadaniem fizyki statycznej jest znalezienie najbardziej prawdopodobnego
rozkładu cząstek w zależności od ich energii, pędu lub prędkości, tzn.
znalezienie odpowiedniej funkcji rozkładu f(E), f(p) lub f( ).

Rozkład Maxwella - Botlzmanna.

Funkcja rozkładu obsadzenia stanów f

B

(E) dana jest wzorem :

f

B

(E) =

exp(

)

gdzie : n - liczba cząstek w jednostce objętości układu,

h - stała Plancka, s - spin, m - masa cząstki,
k - stała Boltzmanna, T - temperatura bezwzględna
E - energia cząstek

υ

n

s

h

mkT

(

)

(

)

/

2

1 2

2

3 2

+

π

−

E

kT

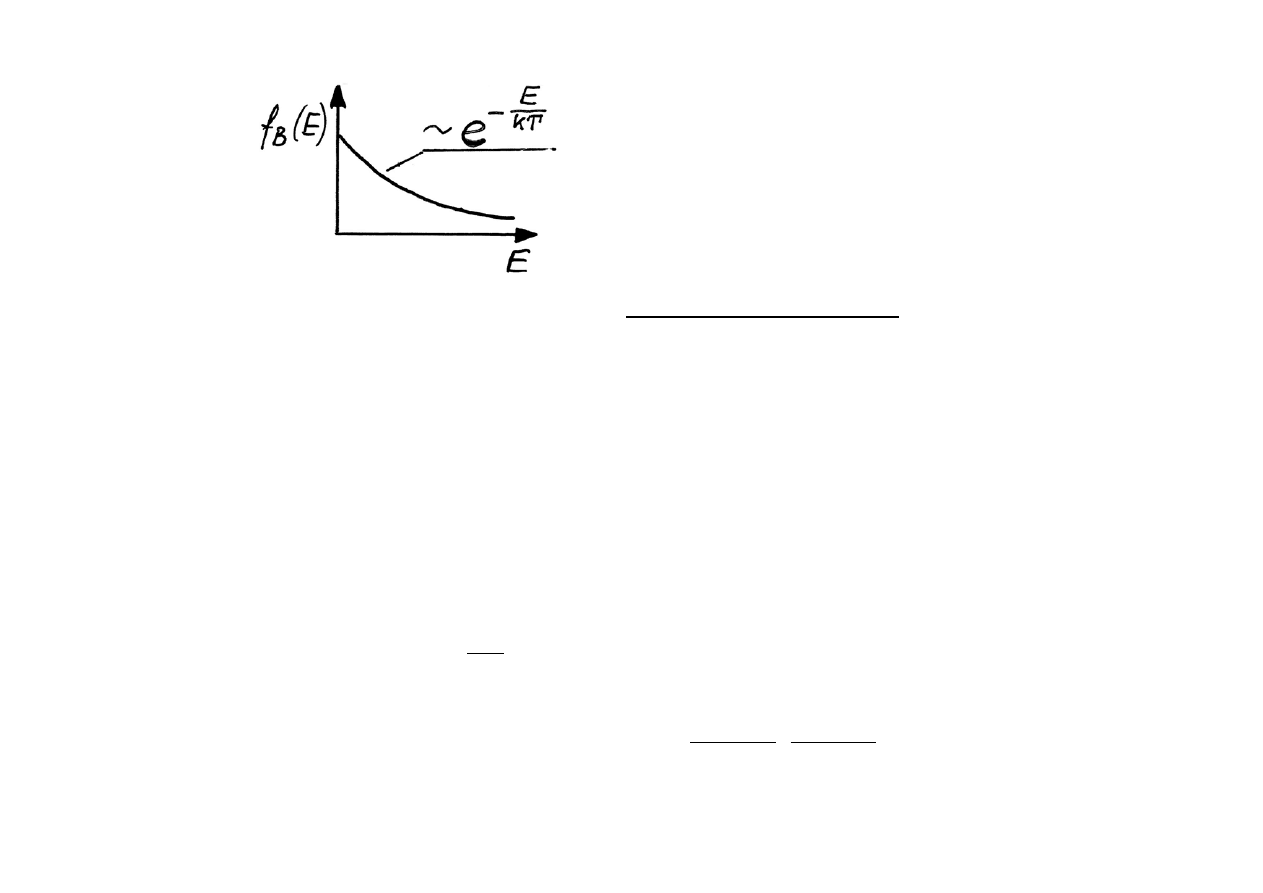
Wykres funkcji obsadzenia
stanów cząstkami dla rozkładu
Maxwella - Boltzmanna (M-B).

Rozkład M-B pozwala m.in. określić potencjał chemiczny

µ

.

Z pierwszej zasady termodynamiki :

dU = TdS - pdV +

µ

dN

gdzie : U - energia wewnętrzna, S - entropia, p - ciśnienie,
V - objętość,

µ

- potencjał chemiczny, N - liczba cząstek w układzie.

Zmiana energii wewnętrznej układu może zajść nie tylko przy wymianie
ciepła i pracy, ale również przy zmianie liczby cząstek w układzie
(każda cząstka wnosi lub wynosi z sobą pewną ilość energii). Pochodna
cząstkowa energii U względem liczby cząstek N określa potencjał
chemiczny

µ

:

µ

:

z rozkładu M - B wynika, że :

µ

= kT ln

∂

∂

U
N

S V









,

n

s

h

mkT

(

)

(

/

2

1 2

2

3 2

+

















π

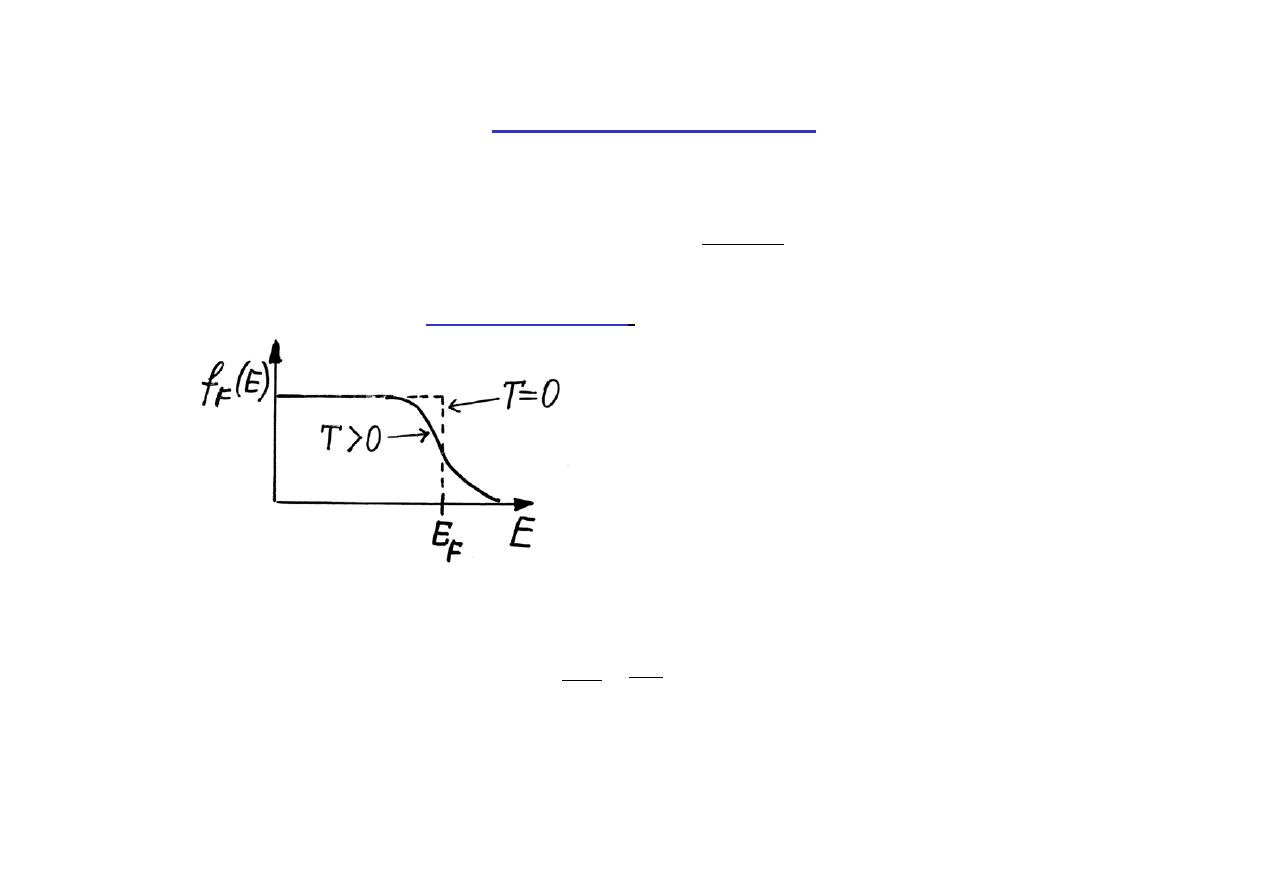
Rozkład Fermiego-Diraca

Dla fermionów (np. elektronów) funkcja rozkładu obsadzeń f

F

(E) dana jest

wzorem :

f

F

(E) =

gdzie

E

F

nosi nazwę

energii Fermiego

.

Wykres funkcji obsadzenia stanów
fermionami (rozkład Fermiego-Diraca (F-D))
w temp. T = 0 i T

> 0K.

Energię Fermiego E

F

można obliczyć z funkcji pełnego rozkładu energii F-D

otrzymując :

E

F

=

Potencjał chemiczny

µ

w temperaturze 0K osiąga wartość energii Fermiego E

F

.

Dla metali

µ ≈

E

F

aż do temperatur pokojowych.

1

1

+

−







−

e xp(

)

E E

kT

F

h

m

2

2

3
8

2 3

n

π









/

Metal

E

f

(eV)

v

F

(m/s)

Na 3,12

∼1,0 10

6

Cu 7,07

∼1,6 10

6

Ag 5,51

∼1,4 10

6

Wartość energii Fermiego
dla niektórych metali i
odpowiadające im prędkości
elektronów v

F

Elektrony swobodne w metalach mają olbrzymie prędkości w
temperaturze 0K, ponad 1000 km/s. Rozkład F-D istotnie różni się
od rozkładu klasycznego przewidującego, że energia kinetyczna
gazu doskonałego w temp. 0K wynosi zero.

Rozkład Bosego – Einsteina

Dla bozonów (cząstek o spinie całkowitym, np. fotonów) funkcja
rozkładu obsadzeń f

B

(E) dana jest wzorem :

f

B

(E) =

Rozkład B-E pozwala na obsadzenie dowolnego stanu dowolną
liczbą cząstek. Rozkład B-E stosuje się m.in. w teorii ciepła
właściwego ciał stałych.

e xp(

)

E

kT

−







−

1

1

Przewodnictwo metali

Wewnątrz częściowo zapełnionego pasma elektrony mogą
być

łatwo wzbudzane (przenoszone na wyższe poziomy

energetyczne). Zewnętrzne pole elektryczne wymusza wypadkowy
ruch elektronów zgodny z liniami sił pola. Dzięki temu elektrony
uzyskują wyższą energię, tzn. przechodzą na wyższy poziom
energetyczny w paśmie.
Przewodnictwo elektryczne dla metalu można wyprowadzić z rozkłądu
Fermiego-Diraca:wyrazić :

σ =

gdzie N - gęstość elektronów; e - ładunek elektronu;

u - średnia prędkość elektronów

Wzór ten został wyprowadzony przy omawianiu prawa Ohma.

Elektrony w krysztale ulegają rozproszeniu wskutek drgań sieci,
średnia droga swobodna skraca się ze wzrostem temperatury, gdy
drgania stają się intensywniejsze :

w =

(wynika z rozproszenia falide Broglie’a elektronu)

gdzie

ε

- moduł Younga, a - stała sieci, N - gęstość atomów

Ne w

mu

2

ε

π

a

NkT

Po podstawieniu do wzoru na przewodnictwo :

σ =

Tzn. że rezystywność (

ρ

T

=

):

ρ

T

∼

T

Tak jest dla idealnie czystego metalu. Obecność zanieczyszczeń, na
których także rozpraszają się elektrony (w sposób niezależny od
temperatury) sprawia, że występują tzw. rezystywność resztkowa,

ρ

r

niezależna od temperatury, wtedy :

ρ

=

ρ

r

+

ρ

T

=

ρ

r

+ A T

e

a

mu kT

2

ε

π

1

σ

Przewodnictwo półprzewodników

Elektrony w całkowicie zapełnionym paśmie nie mogą łatwo przejść

na wyższy poziom energetyczny. Zewnętrzne pole elektryczne nie
może więc nadać elektronom dodatkowej energii - elektrony nie
mogą się poruszać. Aby popłynął prąd, musi zwolnić się miejsce w
paśmie walencyjnym i/albo pojawić się elektron w paśmie pustym.

Półprzewodnik samoistny

W temperaturze zera bezwzglę-
dnego jest idealnym izolatorem.
W wyższych temperaturach, jeśli
przerwa energetyczna E

g

nie

jest zbyt szeroka, możliwe jest
termiczne wzbudzenie ele-
ktronów

do pustego pasma

przewodnictwa (elektrony mogą

być

również

wzbudzone

promieniowaniem, np. światłem). Gęstość elektronów n

n

w paśmie

przewodnictwa odpowiada gęstości dziur n

p

w paśmie walencyjnym -

prąd płynie zarówno dzięki ruchowi ujemnych elektronów jak i
dodatnich dziur :

σ

=

σ

n

+

σ

p

= e n

n

µ

n

+ e n

p

µ

p

= e n(

µ

n

+

µ

p

)

gdzie

µ

n

jest ruchliwością elektronów, a

µ

p

- dziur.

Ruchliwość jest współczynnikiem proporcjonalności między prędkością
przepływu ładunku v i polem elektrycznym E wywołującym przepływ :

v =

µ

E

czyli

µ

=

v

E

Podstawowe parametry samoistnych półprzewodników Ge i Si oraz

dwu typowych samoistnych związków półprzewodnikowych, PbS i InSb

Ge Si

PbS

InSb

σ (300 K)

µ

n

(300 K)

µ

p

(300 K)

E

g

(0 K)

n (300 K)

2,3 (Ωm)

-1

0,38 m

2

/Vs

0,18 m

2

/Vs

0,78 eV

2,5⋅10

19

/m

3

1,6⋅10

-3

(Ωm)

-1

0,17 m

2

/Vs

0,035 m

2

/Vs

1,21 eV

1,5⋅10

16

/m

3

30 (Ωm)

-1

0,06 m

2

/Vs

0,07 m

2

/Vs

0,37 eV

2⋅10

21

/m

3

2⋅10

4

(Ωm)

-1

7,7 m

2

/Vs

0,08 m

2

/Vs

0,24 eV

1,6⋅10

22

/m

3

Zależność przewodnictwa od temperatury określona jest przez
zależność od temperatury gęstości nośników ładunku i ruchliwości. Z
rozkładu

Fermiego-Diraca

można obliczyć gęstość nośników ładunku w

danej temperaturze :

(C - stała)

n

n

= CT

3/2

exp

n

p

= CT

3/2

exp

W półprzewodniku samoistnym n

n

= n

p

, więc z powyższych wzorów

wynika : E

F

= E

g

- E

F

⇒

E

F

=

tzn., że poziom Fermiego leży w

połowie przerwy energetycznej.

−







F

E
kT

−

−







g

F

E

E

kT

g

E

2

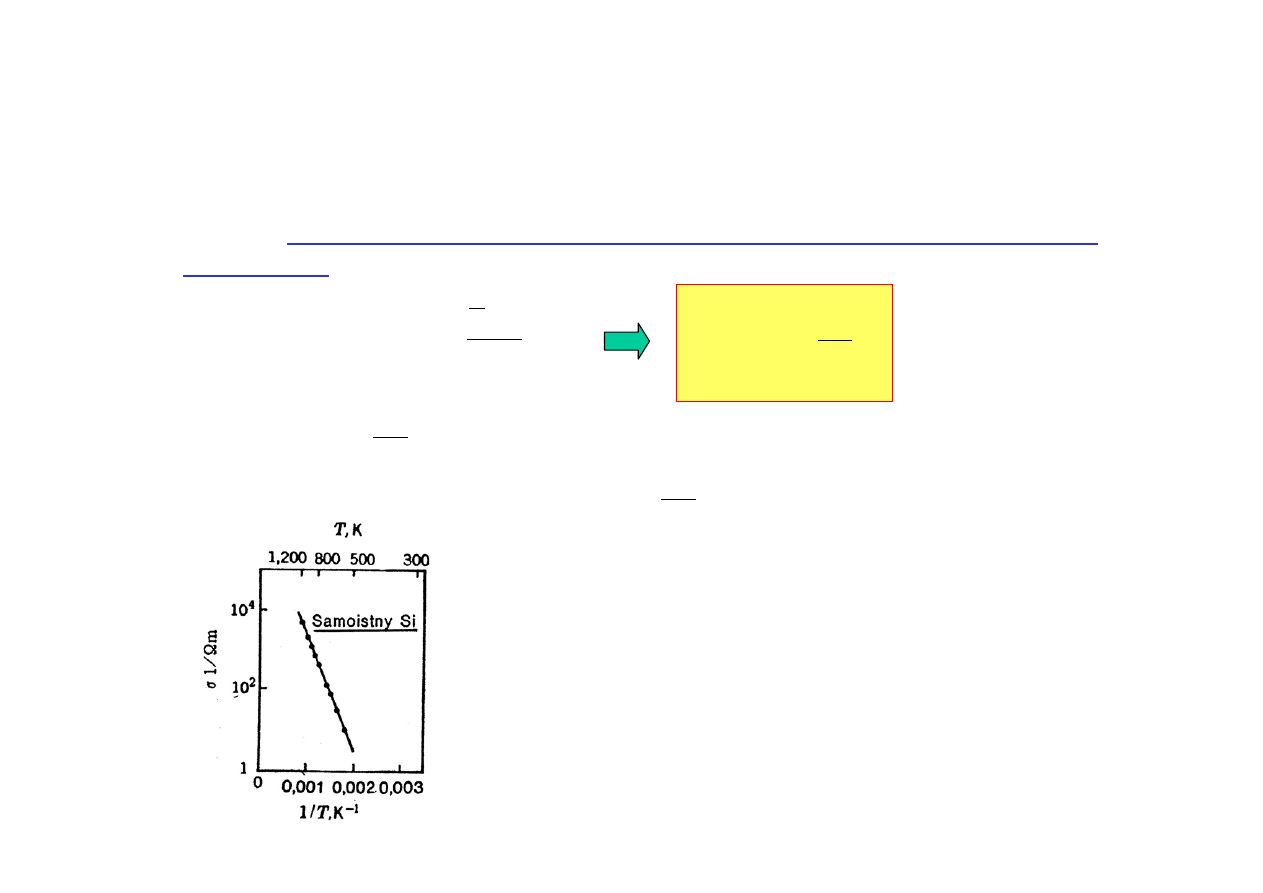
Ruchliwość w półprzewodniku zależy od rozpraszania nośników na
drganiach sieci krystalicznej (fononach) i maleje ze wzrostem temperatury w
przybliżeniu jak :

µ

n

∼

T

-3/2

; ta zależność jest słaba w porównaniu z

zależnością wykładniczą e

-E/kT

we wzorze dla n

n

na poprzedniej stronie,

zatem

dla półprzewodników samoistnych

przewodnictwo rośnie z

temperatura

:

σ

∼ exp

σ

∼ exp

Zatem : ln

σ

∼ -

tzn, że wykres zależności ln

σ

od 1/T powinien być

linią prostą o współczynniku nachylenia

.

Można więc wyznaczyć z pomiaru zależności
przewodnictwa od temperatury energię
Fermiego E

F

(równą w przybliżeniu

potencjałowi chemicznemu

µ

) oraz szerokość

przerwy energetycznej E

g

= 2 E

F

.

Np. dla samoistnego Si: E

F

= 0,6 eV; E

g

= 1,2 eV.

−





















1

2

g

E

kT

−







F

E
kT

F

E
kT

F

E

k

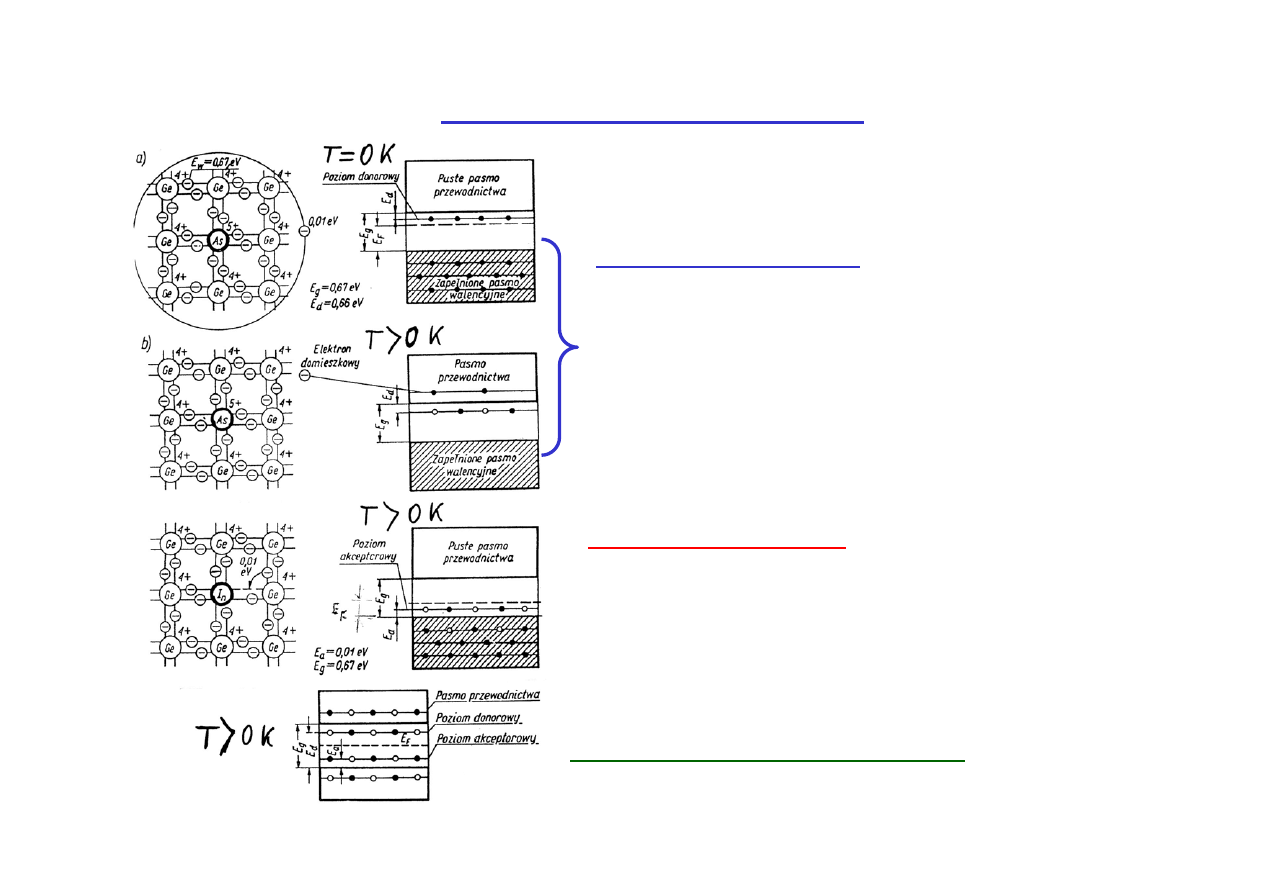
Półprzewodniki domieszkowe

Półprzewodniki typu n

Domieszka donora elektronów - pojawia się
nowy poziom w przerwie wzbronionej, z
którego łatwo można wzbudzić elektron do
pasma przewodnictwa

(przewodnictwo

elektronowe).

Półprzewodnik typu p

Domieszka akceptora elektronów. Po
przejściu elektronu z pasma walencyjnego
powstaje dodatnia dziura

(przewodnictwo

dziurowe).

Półprzewodnik typu mieszanego.

W półprzewodnikach domieszkowych położenie poziomu Fermiego
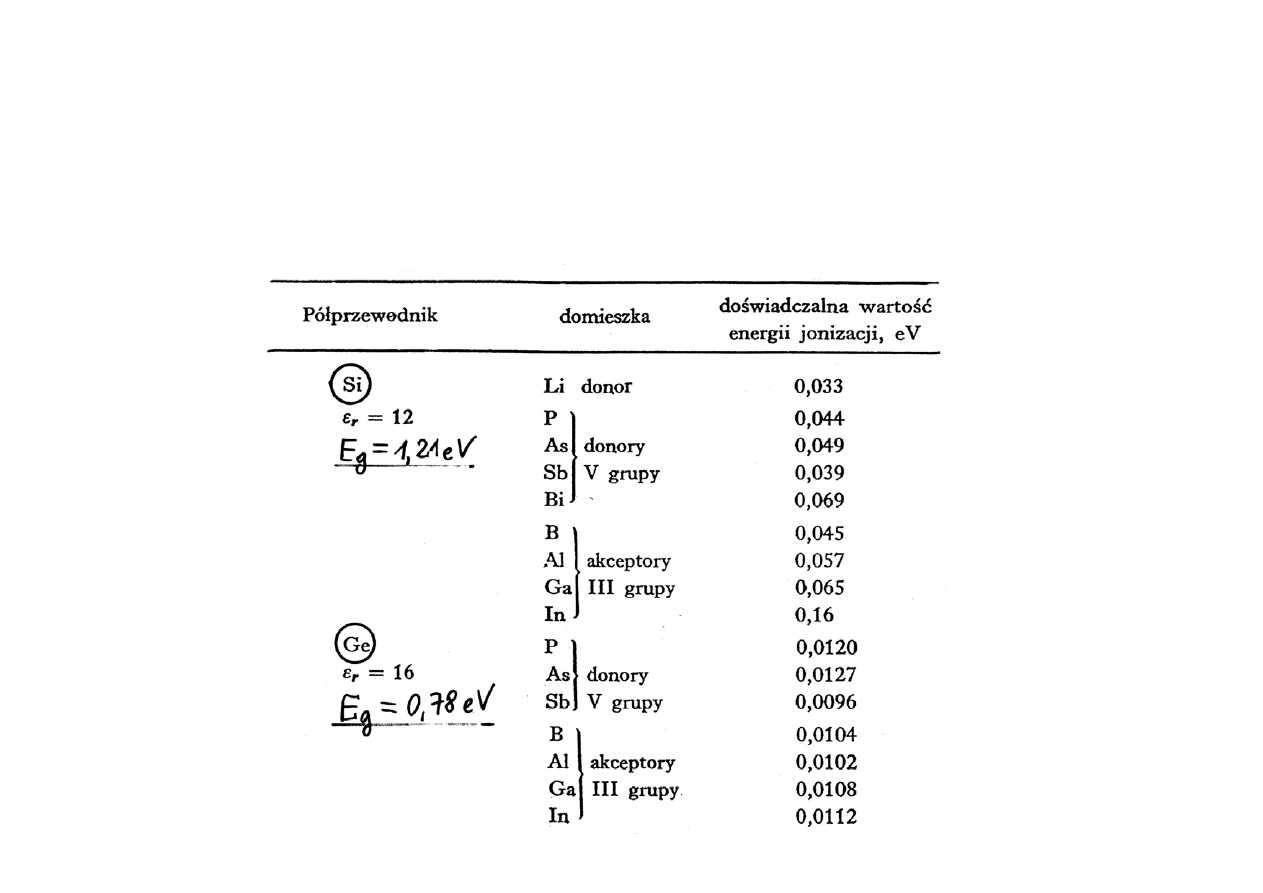
zależy od temperatury oraz od koncentracji domieszek donorowych i
akceptorowych i ich położenia na skali energii. Poziomy donorowe leżą
bardzo blisko pasma przewodnictwa, a poziomy akceptorowe blisko
pasma walencyjnego (por. wartości z poniższej tabeli z szerokością
przerwy energetycznej E

g

).

Z rozkładu Fermiego-Diraca można obliczyć, np. dla półprzewodnika
typu n gęstość elektronów n

n

w paśmie przewodnictwa powstałych

wskutek termicznej jonizacji donorów :

n

n

= AT

3/2

exp

−





















1

2

d

E

kT

Ze względu na znacznie słabszą zależność ruchliwości od temperatury
można ją zaniedbać, więc wyrażenie na zależność przewodnictwa od
temperatury ma postać:

σ ∼ exp (przewodnictwo

rośnie ze

wzrostem temperatury)

Analogicznie jak dla półprzewodnika samoistnego można wyznaczyć
wartość E

d

, tzn. poziom energetyczny donora, z zależności

przewodnictwa od temperatury wykreślonych w układzie współrzędnych
ln

σ

i 1/T.

Mówimy, że zależności gęstości nośników ładunku i przewodnictwa od
temperatury mają

charakter aktywacyjny

z energiami aktywacji równymi

1/2 E

g

(półprz. samoistny) lub 1/2 E

d

(półprz. domieszkowy typu n).

−





















1

2

d

E

kT

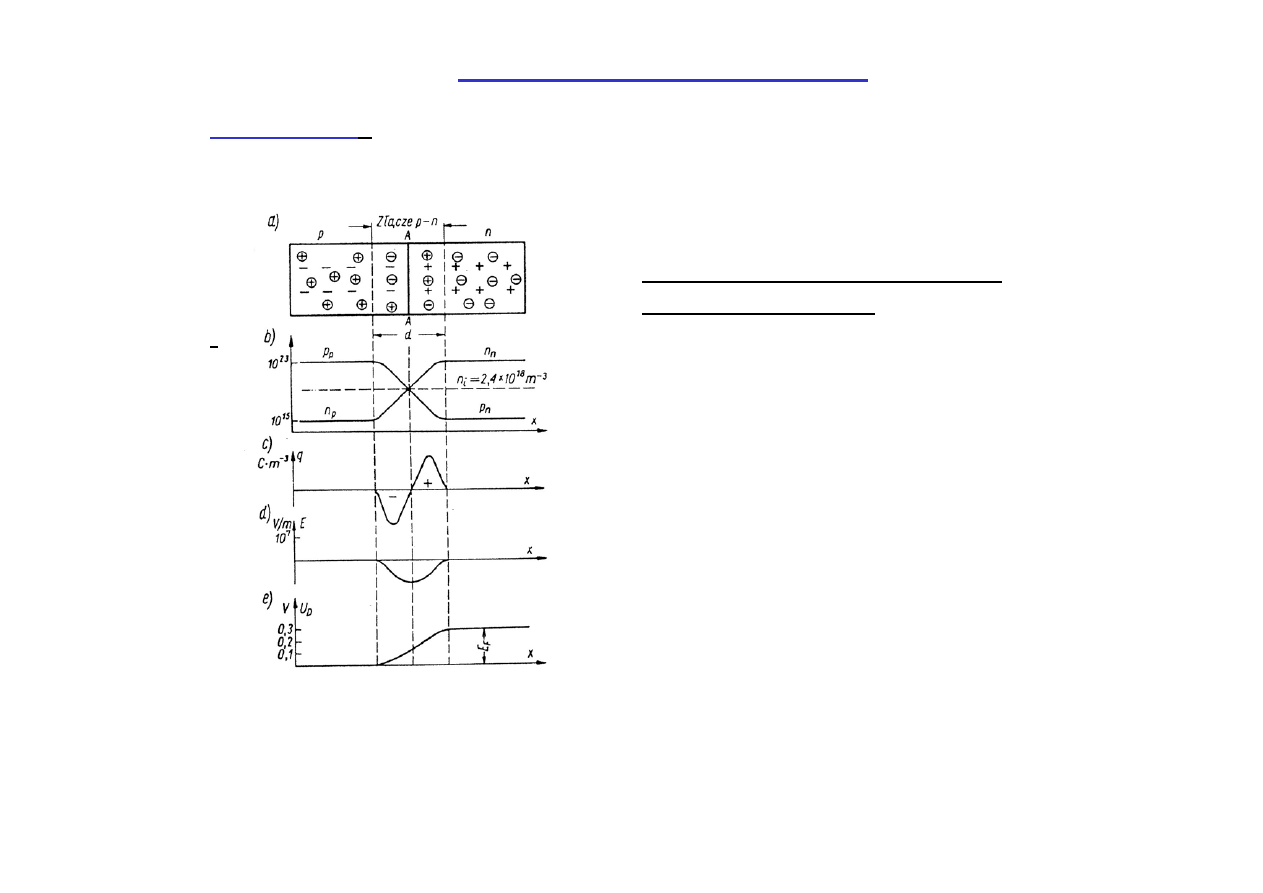
Elementy półprzewodnikowe

Złącze p -n

można uzyskać wprowadzając np. do kryształu germanu z

lewej strony domieszki indu (otrzymany półprzewodnik typu p), a z prawej
strony domieszki arsenu (otrzymany półprzewodnik typu n).

Złącze p-n bez zewnętrznego
pola elektrycznego.

Rozkłady gęstości nośników

Rozkład gęstości ładunku

Rozkład natężenia pola elektrycznego

Napięcie kontaktowe.

Różnica gęstości dziur i elektronów po obu stronach złącza spowoduje
dyfuzję dziur w prawo a elektronów w lewo, co wywoła powstanie pola
elektrycznego i różnicy potencjałów.
Dyfuzja będzie trwała, aż wyrównają się w obszarze złącza poziomy
Fermiego.

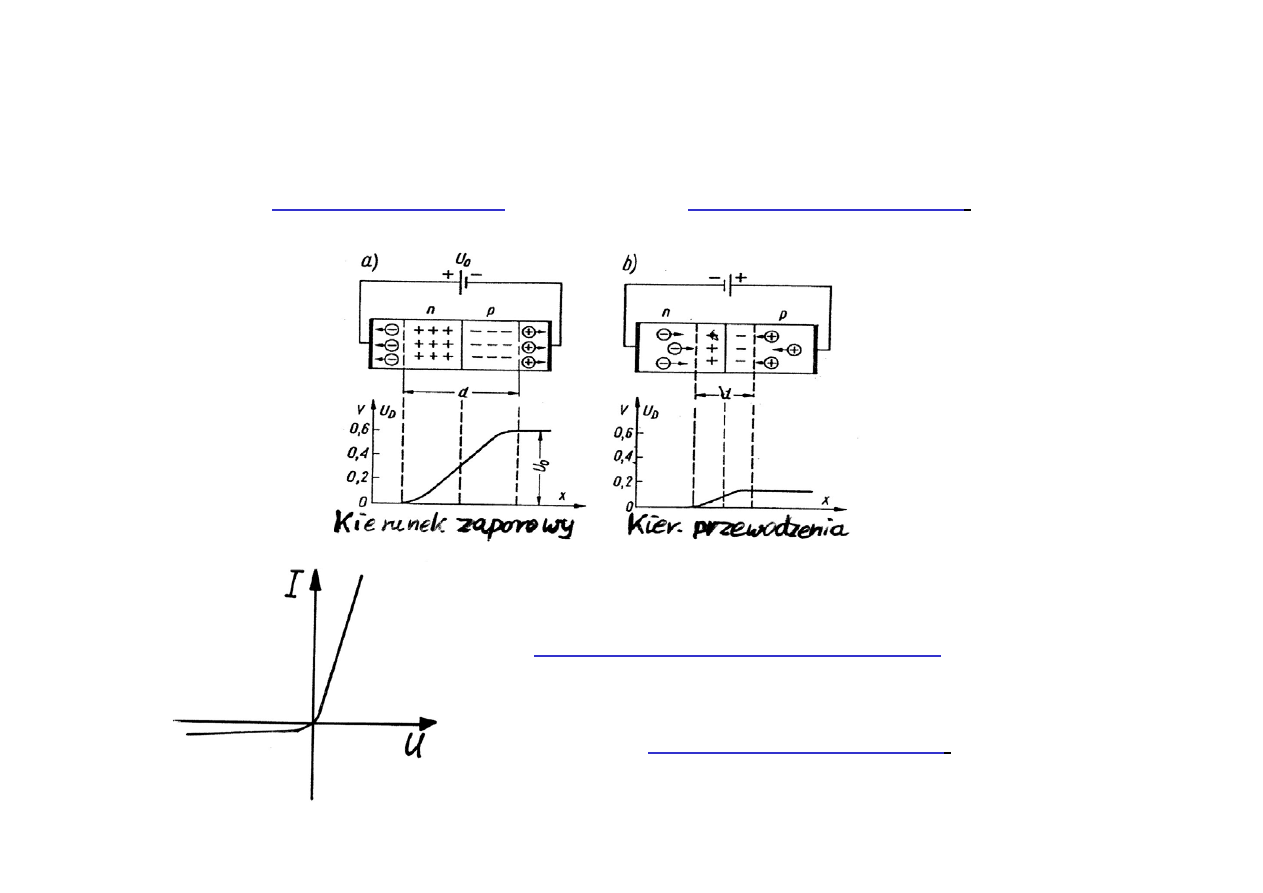
Przyłożenie napięcia
jak na

rys. a)

spowoduje

wzrost rezystancji złącza:

kierunek zaporowy.

Przyłożenie napięcia
odwrotnie

(rys.b)

spowoduje

obniżenie rezystancji złącza:

kierunek przewodzenia

.

Złącze p-n

działa

prostująco

, jak to

zilustrowano za pomocą

charakterystyki

prądowo-napięciowej. Ze złącza można
utworzyć

diodę półprzewodnikową

.

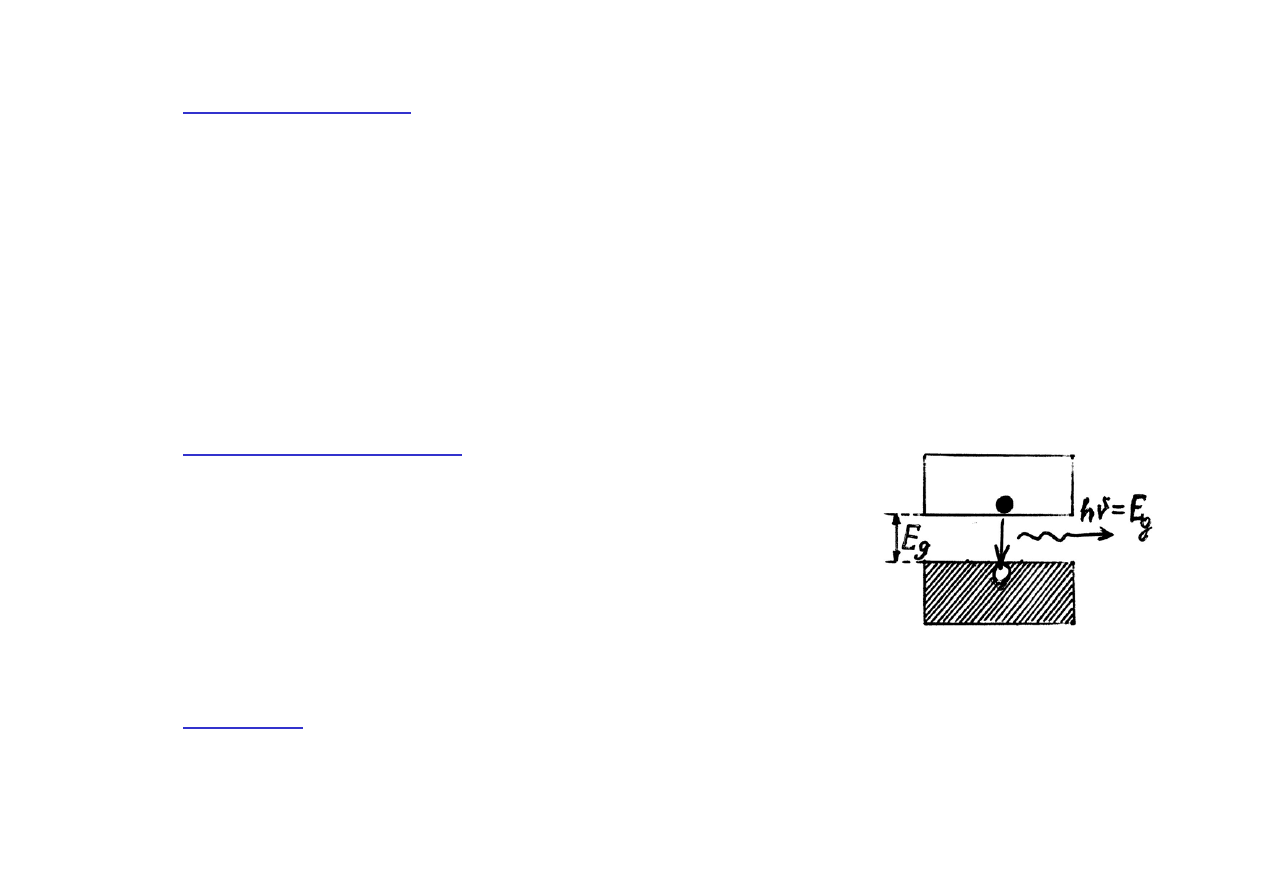
Baterie słoneczne

- przy oświetleniu złącza p-n światłem o takiej

częstotliwości

ν

, że energia fotonów E = h

ν

, jest większa od szerokości

przerwy energetycznej E

g

, każdy pochłonięty foton generuje parę elektron

- dziura. Powstałe dodatkowe dziury zostaną wciągnięte do obszaru typu
p, a dodatkowe elektrony do obszaru typu n (pod wpływem wewnętrznego
pola elektrycznego na złączu p-n).

Te dodatkowe swobodne nośniki ładunku mogą uczestniczyć w
przepływie prądu - tzn. że energia światła może być przemieniona
bezpośrednio na energię elektryczną.

Diody luminescencyjne

- wysokie napięcie w kierunku

przewodzenia może wywołać na tyle silny przepływ
elektronów przewodnictwa, że te w trakcie zderzeń
wytworzą pary elektron - dziura. Przy rekombinacji
każdej pary (elektron z pasma przewodnictwa „spada”
do dziury w paśmie walencyjnym) będzie emitowany
foton o częstotliwości danej wzorem Plancka :

ν

= E

g

/h

Fotodioda

- przyłożenie do baterii słonecznej (złącza p-n) napięcia

zaporowego sprawi, że mały prąd w kierunku zaporowym silnie wzrośnie
przy oświetleniu złącza (pojawią się nowe nośniki ładunku). Fotodioda jest
bardzo czuła na zmiany natężenia światła (fotokomórki itp.)

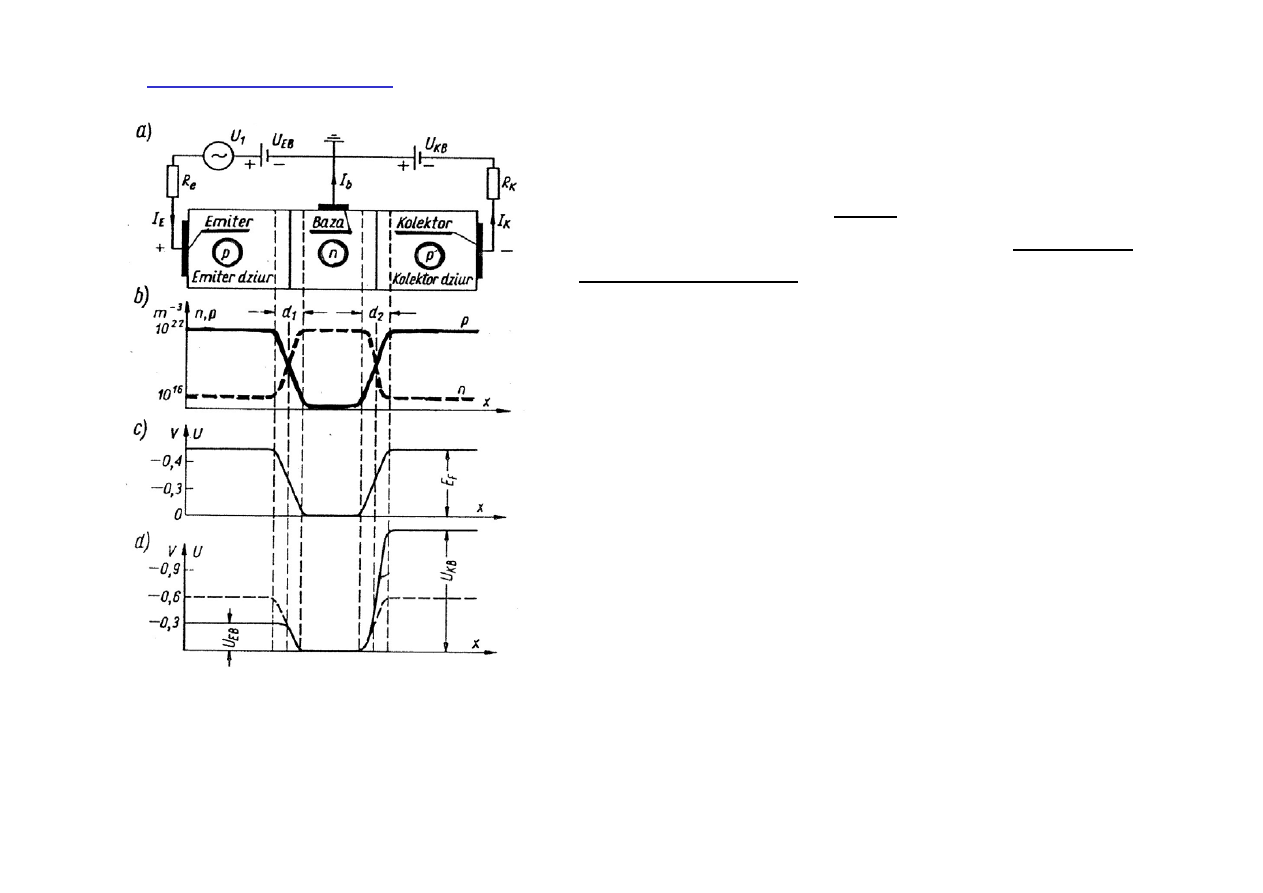
Tranzystor złączowy

jest połączeniem dwóch złączy półprzewodnikowych co może

dać strukturę p-n-p lub n-p-n.

Schemat tranzystora p-n-p i sposób
połączenia obwodu elektrycznego z emiterem,
bazą i kolektorem.

Wykres koncentracji nośników ładunku

Rozkład potencjału bez przepływu prądu

Rozkład potencjału przy przepływie prądu
przez tranzystor

Napięcie U

EB

przyłożone jest do złącza emiter - baza w kierunku przewodzenia. Dziury

dyfundują z emitera do obszaru bazy który jest tak cienki, że ok. 99% dziur dyfunduje dalej,
do obszaru kolektora (sprzyja temu napięcie U

KB

). Stosunek prądu kolektora, I

K

, do prądu

bazy I

B

, nazywamy współczynnikiem wzmocnienia :

β

≡ I

K

/I

B

. Jeśli I

B

jest słabym prądem, np.

odbieranym przez antenę radiową, to prąd I

K

będzie się tak samo zmieniał w czasie, ale

będzie 100 razy silniejszy. Tranzystor wzmacnia słaby sygnał.