Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

1

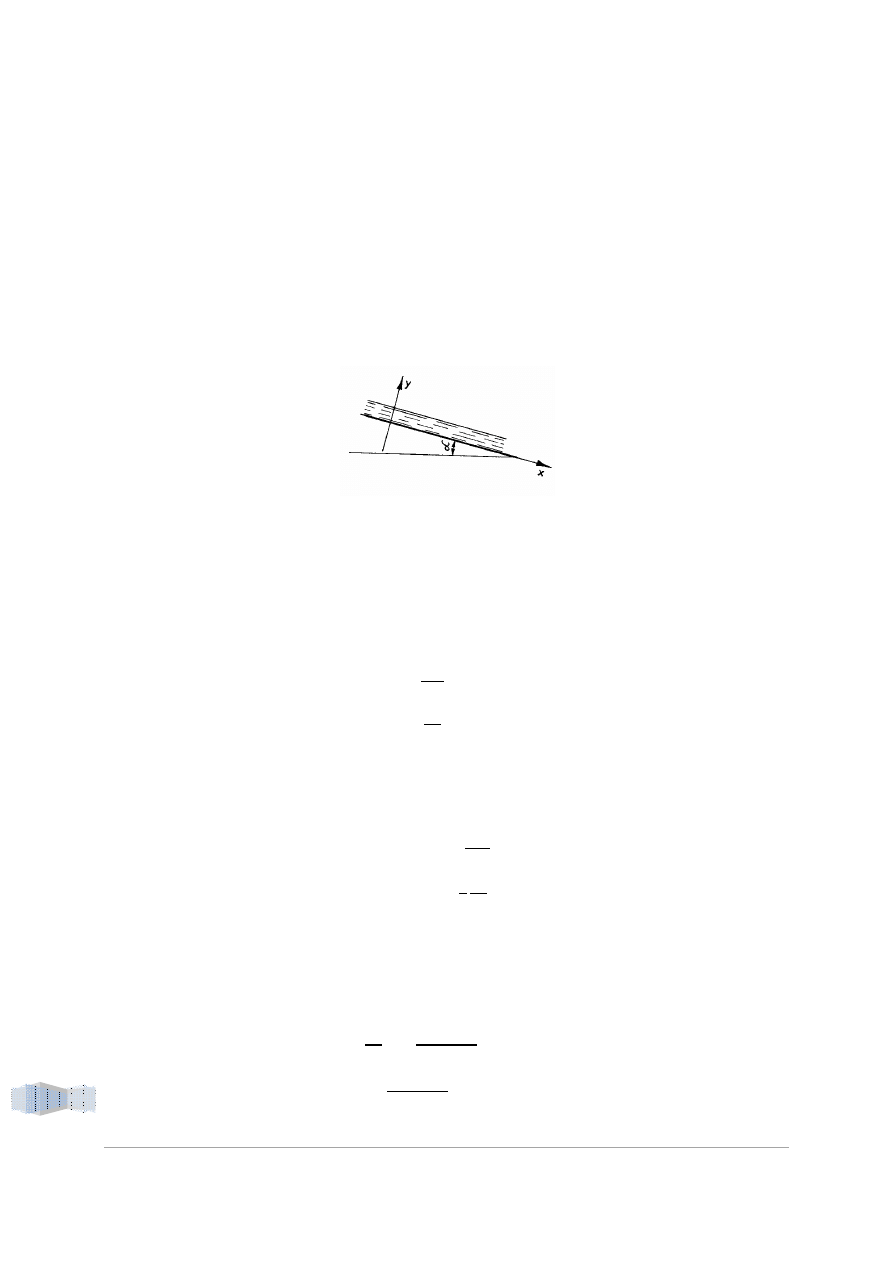
Zadanie 1

Warstwa cieczy o wysokości b = 3mm i lepkości

= 1,5 ∙ 10

/ płynie równomiernie pod

działaniem siły ciężkości po płaszczyźnie nachylonej do poziomu pod kątem

= 15°. Wyznaczyć:

a) Rozkład prędkości.

b) Prędkość maksymalną.

c) Prędkość średnią.

d) Stosunek prędkości średniej do maksymalnej.

e) Strumień objętości przez przekrój poprzeczny o szerokości L = 1m.

Naprężenia styczne na granicy fazy ciekłej i gazowej pominąć.

Rozwiązanie:

Przepływ ten można rozpatrywać, jako przepływ płaski. Po zorientowaniu układu współrzędnych w

sposób pokazany na rysunku powyżej, z warunków zadania wynika, że:

= 0

= 0 = (0)

= 0

= 0

=

∙ sin ( )

= − ∙ cos ( )

Równanie Naviera-Stokesa uprości się, zatem do postaci:

∙ sin( ) +

= 0

∙ cos( ) +

1

= 0

Po scałkowaniu drugiego równania dla warunków brzegowych p = p

0

gdy y = b, można wyznaczyć

rozkład ciśnienia w warstwie cieczy:

=

+

∙

∙ cos( ) ∙ ( − )

Po scałkowaniu pierwszego równania otrzymamy:

= −

∙ sin( )

∙ +

= −

∙ sin( )

2

∙

+

+

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

2

Po uwzględnieniu warunków brzegowych: v = 0 dla y = 0,

= 0 dla y = b (ponieważ na granicy fazy

ciekłej i gazowej

= 0).

=

∙ sin( )

2

∙

∙ (2 − )

Krzywa rozkładu prędkości jest parabolą. Maksymalna prędkość występuje na powierzchni cieczy

=

∙ sin( )

2

∙

= 7,6

Strumień objętości przez przekrój poprzeczny o szerokości L:

=

=

∙ sin( )

2

(2 − )

=

∙ sin( )

3

= 1,52

A średnia prędkość:

=

=

∙ sin( )

3

= 5,1

Stosunek prędkości średniej do maksymalnej:

= 2/3

Zadanie 2

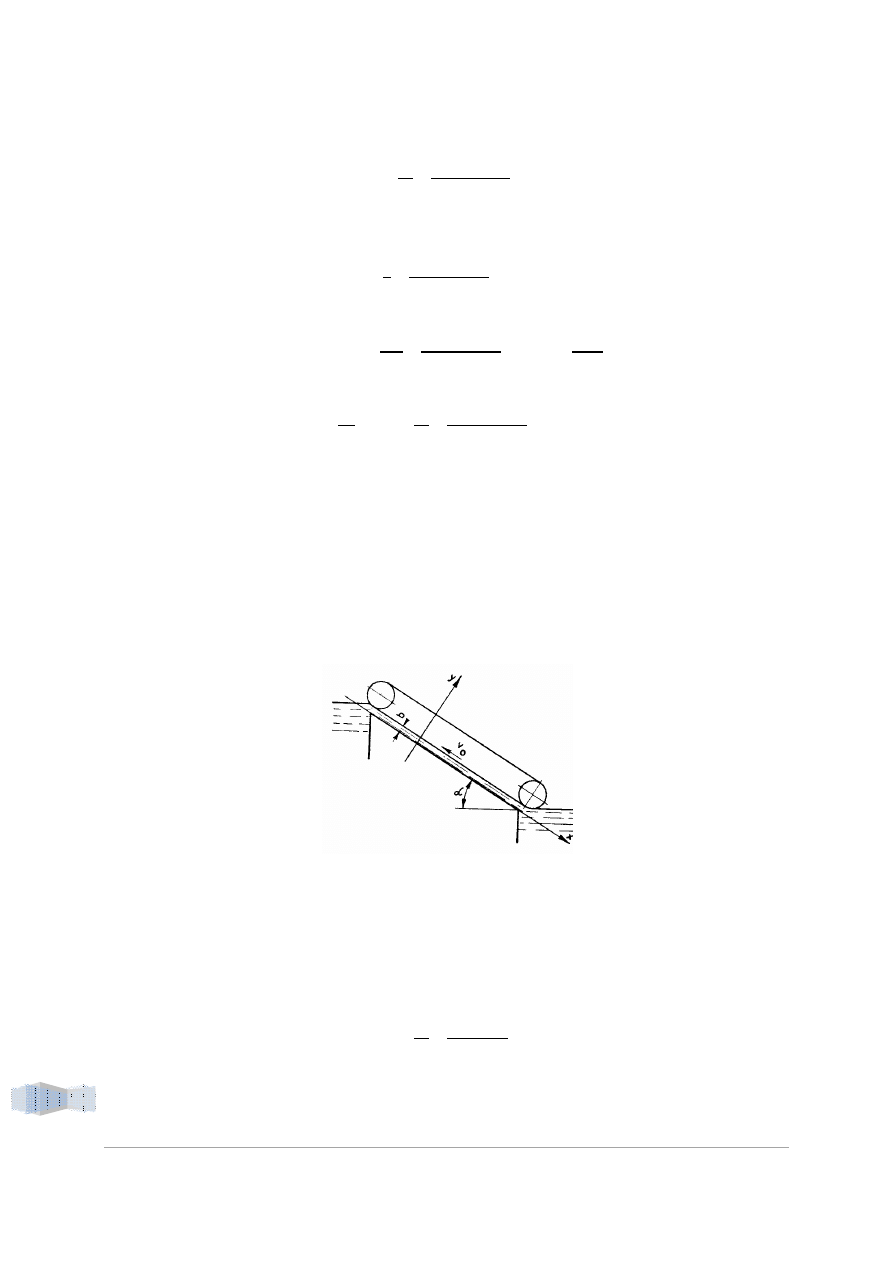
Ciecz znajduje się między dwiema równoległymi płytami, nachylonymi pod kątem do poziomu. Płyta

górna porusza się w kierunku zgodnym ze spadkiem płyt, ze stałą prędkością

. Wyznaczyć rozkład

prędkości i strumień objętości przypadający na jednostkę szerokości oraz naprężenie styczne na

ruchomej płycie, jeżeli:

= 0,2 / ,

= 15°,

= 0,5

, gęstość cieczy

= 900

, i lepkość

= 0,2

/

.

Rozwiązanie:

Rozwiązanie tego zadania różni się od rozwiązania zadania 1 tylko warunkami brzegowymi. Stałe

całkowania w całce ogólnej:

= −

∙

∙ sin( )
2

∙

+

+

Wyznaczamy dla warunków brzegowych:

= 0,

= 0,

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

3

=

,

= ,

skąd

=

+

∙

∙ sin( )
2

∙

= 0

Rozkład prędkości określony jest zależnością:

=

−

∙

∙ sin( )
2

∙ ( − )

Strumień objętości przypadający na jednostkę szerokości płyty:

=

=

2

−

∙

∙ sin( )

12

= 50,1

∙

Naprężenie styczne na ruchomej płycie obliczamy z zależności:

=

=

−

∙

∙ sin( )

2

= 79,4

Zadanie 3

Nad płytą, po której spływa warstwa cieczy, rozpięto pas transmisyjny. Obliczyć przy jakiej prędkości

przesuwu pasa strumień objętości między zbiornikami będzie równy zeru. Obliczenia przeprowadzić

dla:

= 4

,

= 30°, = 1,5 ∙ 10

/ .

Rozwiązanie:

Zadanie to różni się od poprzednich warunkami brzegowymi:

= 0,

= 0,

= − ,

= ,

skąd

= −

+

∙ sin( )

2

∙

= 0

Prędkość w dowolnym punkcie:

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

4

= −

+

∙ sin( )

2

∙ ( − )

Znając rozkład prędkości wyznaczamy strumień objętości:

=

= −

2

+

∙ sin( )

12

Warunki zadania wymagają, by Q = 0, a więc:

2

=

∙ sin( )

12

=

∙ sin( )

6

= 87,2

/

Zadanie 4

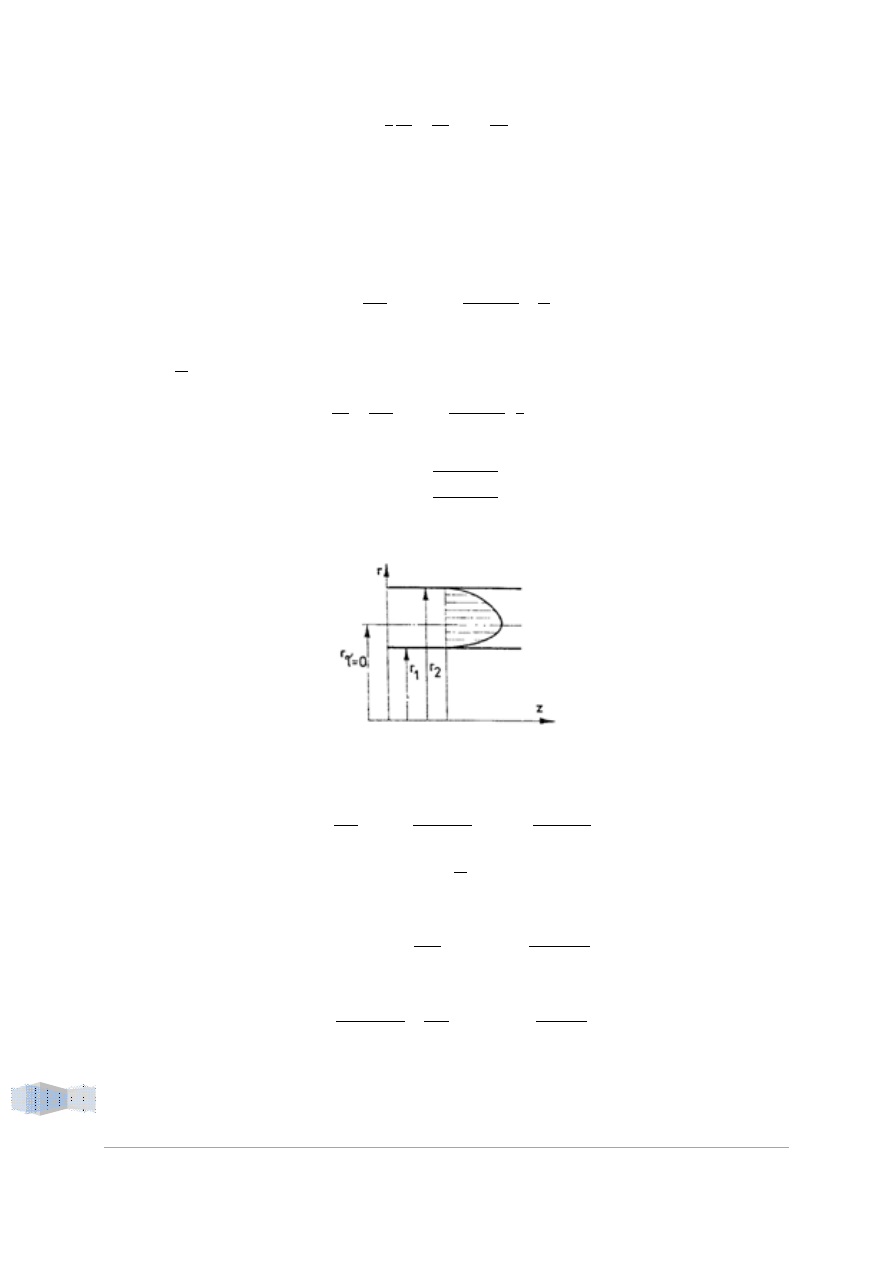
Ciecz o lepkości płynie w szczelinie pierścieniowej, utworzonej przez dwa współśrodkowe walce o

promieniach r

1

i r

2

, pod działaniem stałego gradientu ciśnienia dp/dz = -Δp/L. Wyznaczyć:

a) rozkład prędkości,

b) prędkość maksymalną,

c) prędkość średnią,

d) strumień objętości.

Rozwiązanie:

Rozpatrywany przepływ jest ustalonym przepływem osiowosymetrycznym w kierunku osi z (tzn.

=

= 0). Równania ruchu po pominięciu sił masowych sprowadzą się zatem do układu:

= 0

= −

1

+

+

1

= 0

Ponieważ

=

= ( ), a

= ( ), więc ruch cieczy opisany jest równaniem różniczkowym

zwyczajnym:

+

1

=

1

które można przedstawić w dogodniejszej postaci:

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

5

1

= −

∆

Rozwiązując powyższe równanie dla warunków brzegowych:

= 0,

=

,

= 0,

=

,

otrzymamy:

=

∆

4

−

+

−

ln ( / )

Prędkość osiąga maksymalną wartość w promieniu, na którym naprężenia styczne są równe zeru, tzn.

tam gdzie

= 0. Tak więc:

=

∆

4

−2 +

−

ln ( / )

∙

1

= 0

Skąd:

=

−

2ln ( / )

a po podstawieniu:

=

∆

4

1 −

1 −

2 (1/ )

∙ 1 −

1 −

2 (1/ )

=

Strumień objętości:

=

2

=

∆

8

1 −

−

(1 −

)

(1/ )

prędkość średnia:

=

(

−

)

=

∆

8

1 +

−

1 −

(1/ )

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

6

Zadanie 5

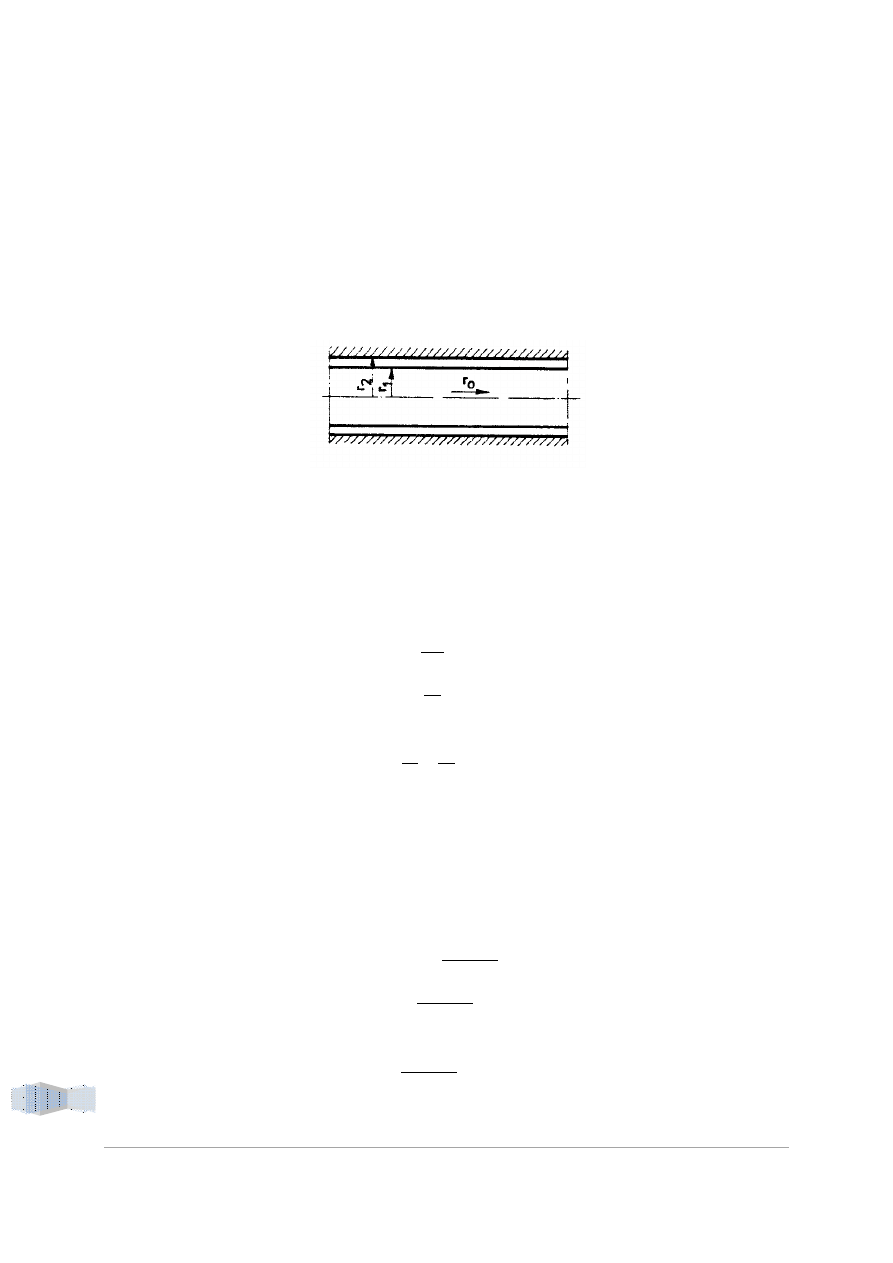
Pierścieniowa szczelina utworzona przez dwa walce o promieniach r

1

i r

2

jest zapełniona cieczą o

lepkości . Walec wewnątrz porusza się wzdłuż osi ze stałą prędkością

. Określić:

a) rozkład prędkości w szczelinie,

b) strumień objętości,

c) siłę tarcia na długości L wewnątrz walca

obliczenia strumienia objętości i siły tarcia wykonać dla danych:

= 20

,

= 32

,

= 0,2

/

,

= 0,5 / , = 1 .

Rozwiązanie:

Z warunków zadania wynika, że:

=

= 0

= 0

=

= ( )

= 0

= 0

Układ równań można zapisać następująco:

= 0

Po dwukrotnym scałkowaniu:

=

∙

+

Stałe całkowania wyznaczone z warunków brzegowych:

= 0,

=

,

=

,

=

,

wynoszą:

= −

ln ( / )

=

ln ( / )

∙

Rozkład prędkości jest więc określony zależnością:

=

ln ( / )

∙ ln ( / )

Strumień objętości:

Przepływy laminarne - zadania

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

7

=

2

=

2

ln ( / )

=

−

2ln ( / )

−

= 0,414

/

Siła tarcia:

= 2

Naprężenia styczne:

= −

=

r ∙ ln ( / )

Naprężenia styczne na promieniu r = r

1

:

=

r ∙ ln ( / )

a zatem siła tarcia na walcu wewnętrznym:

=

2

ln ( / )

= 1,34