Dynamika
1.Prawa Newtona
-

PIERWSZE

-

Punkt materialny, na który

nie działa żadna siła lub działające siły
się równoważą, pozostaje w spoczynku
lub porusza się ruchem jednostajnym po
linii prostej.

-

DRUGIE

- Przyśpieszenie punktu

materialnego jest proporcjonalne do siły
działającej na ten punkt i ma kierunek
siły. Jeżeli siłę działającą na punkt
materialny oznaczymy przez F, a jego
przyśpieszenie przez a, to drugie prawo
Newtona możemy przedstawid w
postaci równania wektorowego: ma=F
-

TRECIE

-Siły wzajemnego oddziaływania

dwóch punktów materialnych mają
jednakowe wartości, leżą na prostej
łączącej te punkty i są przeciwnie
skierowane.
Prawo to nosi nazwę prawa akcji i
reakcji. Ma ono charakter ogólny i nie
zależy od sposobu wywierania siły −
dotyczy zarówno ciał stykających się, jak
i ciał działających na siebie z odległości.
Jeżeli układ materialny składa się z
więcej niż dwóch punktów, to trzecie
prawo Newtona stosuje się do każdej
pary punktów materialnych.
-

CZWARTE

-Jeżeli na punkt materialny

działa jednocześnie kilka sił, to każda z
nich działa niezależnie od pozostałych, a
wszystkie razem działają jak jedna siła
równa wektorowej sumie danych sił.
Prawo to nosi nazwę zasady
superpozycji. Pozwala ono zastąpid kilka
sił działających na punkt materialny
jedną siłą.
-

PIĄTE

-Każde dwa punkty materialne o

masach m1 i m2 przyciągają się z siłą
wprost proporcjonalną do iloczynu ich
mas i odwrotnie proporcjonalną do
kwadratu odległości r między nimi.
Kierunek siły leży na prostej łączącej te
punkty.

prawo nosi nazwę prawa powszechnego
ciążenia lub prawa grawitacji, a
współczynnik proporcjonalności k jest
stałą grawitacji.

2. Zasada d’Alemberta
a)

Suma sił rzeczywistych i siły

bezwładności działających na punkt
materialny jest w każdej chwili równa
zeru. Z zasady tej wynika, że poprzez
formalne wprowadzenie siły
bezwładności zagadnienie dynamiczne
można sprowadzid do zagadnienia
statycznej równowagi sił.
F+P

b

=0

P

b

=-ma

b)

Suma sił zewnętrznych i sił

bezwładności dla danego układu
materialnego oraz sumy momentów
tych sił względem nieruchomego
bieguna redukcji w każdej chwili są
równe zeru.

3.Praca, moc, pęd, kręt

PRACĄ MECHANICZNĄ

nazywamy

energię dostarczoną z zewnątrz za
pomocą układu sił do rozpatrywanego
układu materialnego w czasie jego
ruchu. Celem ogólnego zdefiniowania
pracy rozpatrzymy ruch punktu
materialnego po torze krzywoliniowym
pod wpływem siły P. Punkt przyłożenia A
siły P jest opisany wektorem wodzącym
r.

Jednostką pracy w układzie SI jest dżul
równy pracy 1 niutona na przesunięciu 1
metra:

a) Pracę wykonuje jedynie składowa siły
styczna do toru, a praca składowej
normalnej jest równa zeru.
b) Wartośd pracy może byd zarówno
dodatnia, jak i ujemna
c) Jeżeli na punkt materialny działa układ
sił P

k

, których suma jest równa

wypadkowej , to praca tej siły na
przesunięciu elementarnym dr jest
równa sumie prac elementarnych
poszczególnych sił na tym przesunięciu

MOCĄ

chwilową nazywamy stosunek

pracy elementarnej dL do czasu dt.

Pędem punktu materialnego o masie m i
prędkości v nazywamy iloczyn masy
punktu i jego prędkości: p=mv

KRĘTEM

k

O

punktu materialnego o

masie m względem punktu O nazywamy
moment pędu p=mv tego punktu
materialnego względem punktu O.

powyższej definicji wynika, że kręt −
zdefiniowany podobnie jak moment siły
względem punktu − jest wektorem
prostopadłym do płaszczyzny
wyznaczonej przez punkt O i wektor
prędkości v.

4.Energia kinetyczna, potencjalna

ENERGIĄ KINETYCZNĄ

punktu

materialnego o masie m, poruszającego
się z prędkością v, nazywamy połowę
iloczynu masy punktu i kwadratu jego

prędkości:

Energia kinetyczna układu punktów
materialnych jest równa energii tegoż
układu w jego ruchu względem środka
masy oraz energii kinetycznej masy
całkowitej poruszającej się z prędkością
środka masy.

ENERGIA POTENCJALNA

jest to energia

jaką posiada element umieszczony w
polu potencjalnym. Energię potencjalną
zawsze definiuje się względem jakiegoś
poziomu zerowego. Podobnie jak pracę,
energię potencjalną mierzy się w
dżulach *J+. Energia potencjalna ciała
zależy od jego położenia względem
drugiego ciała, z którym oddziałuje. Gdy
położenie to ulega zmianie, zmienia się
również energia potencjalna ciała.
E

p

=mgh

5.Przemieszczenia wirtualne

-

WIĘZY IDEALNE

-bez luzów i tarcia

Istnieją dwie zasady prac wirtualnych
-zasada o pracy rzeczywistych obciążeo
na wirtualnych przemieszczeniach
-zasada o pracy wirtualnych obciążeo na
rzeczywistych przemieszczeniach

6. Drgania swobodne

drgania ciała wywołane wychyleniem z
położenia równowagi trwałej, kiedy na
ciało nie działają żadne siły, poza
określającymi położenie równowagi i
dążącymi do przywrócenia równowagi.
Amplituda drgao zależy od wielkości
początkowego wychylenia (energii
potencjalnej) oraz jego prędkości
początkowej (energii kinetycznej).
Szczególnym rodzajem drgao
swobodnych są drgania harmoniczne
swobodne zachodzące gdy siła
przywracająca równowagę jest
proporcjonalna do wychylenia.
Drgania swobodne są przeciwieostwem
drgao wymuszonych.
Ruch harmoniczny drgania opisane
funkcją harmoniczną (sinusoidalną), jest
to najprostszy w opisie matematycznym
rodzaj drgao.

-RUCH HARMONICZNY-

jest często

spotykanym rodzajem drgao, wiele
rodzajów jest w przybliżeniu
harmoniczna. Każde drganie można
przedstawid jako sumę drgao
harmonicznych. Przekształceniem
umożliwiającym rozkład ruchu
drgającego na drgania harmoniczne jest
transformacja Fouriera.

7.Drgania wymuszone harmoniczne,
zjawisko rezonansu

-

DRGANIA HARMONICZNE TŁUMIONE

-

występują dla wymuszonego oscylatora
harmonicznego tłumionego, czyli drgao
o jednym stopniu swobody, tłumionych i
wymuszonych. Przy tłumieniu i
wymuszaniu nie zmieniającym się w
czasie układ dochodzi do drgao z
częstotliwością wymuszającą i stałą
amplitudą. Taka sytuacja zwana jest
stanem stacjonarnym.

-

REZONANS

- zjawisko fizyczne

zachodzące dla drgao wymuszonych,
objawiające się pochłanianiem energii
poprzez wykonywanie drgao o dużej
amplitudzie przez układ drgający dla
określonych częstotliwości drgao.
-

DRGANIA HARMONICZNE

WYMUSZONE

- Dobrze wiemy, że aby

długo huśtad się na huśtawce tak, jak
dama na tym pięknym obrazie,
potrzebny jest ktoś, kto będzie
huśtawkę popychał w odpowiednich
momentach. W ogólności siłę
podtrzymującą drganie, zwaną też siłą
wymuszającą, przedstawiamy jako siłę
zależną sinusoidalnie od czasu. Na
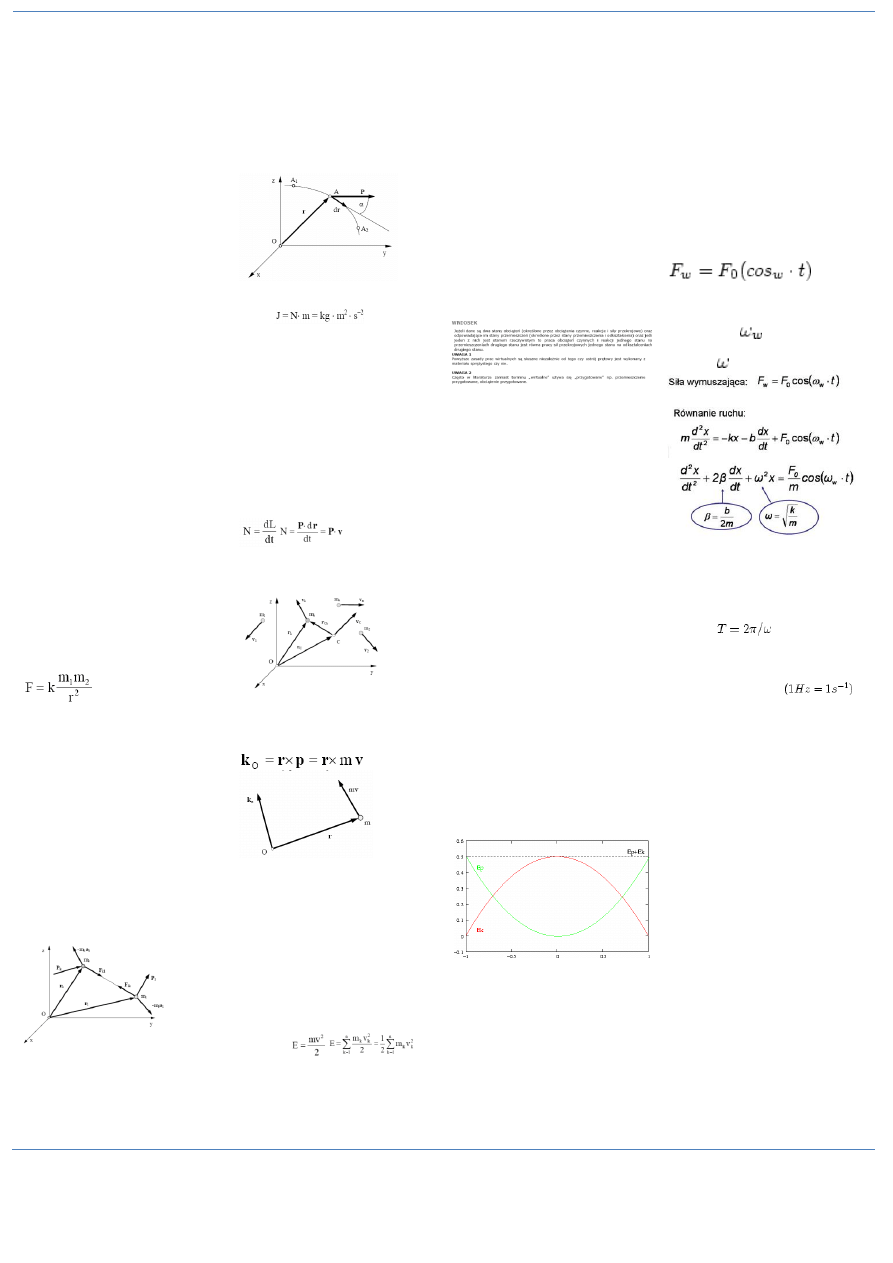
przykład może ona mied postad:

. Równanie

ruchu uwzględnia zarówno siłę
wymuszającą, jak i tłumiącą drgania.
Zwródmy uwagę, że częstośd siły
wymuszającej

jest w ogólnym

przypadku inna niż częstośd drgao
własnych

.

8.Okres i częstotliwośd

OKRESEM

nazywamy czas jednego

pełnego drgania. Po upływie okresu
drgające ciało jest znów w takiej samej
fazie. Okres powiązany jest z częstością
wzorem:

Odwrotnośd okresu, czyli liczbę drgao w
jednostce czasu nazywamy

CZĘSTOTLIWOŚCIĄ

. Jednostką

częstotliwości jest hertz