Opracował: dr in

ż

. Mariusz Leus 

- 1 - 

 

T: Wytrzymało

ść

 zło

ż

ona – zginanie i skr

ę

canie 

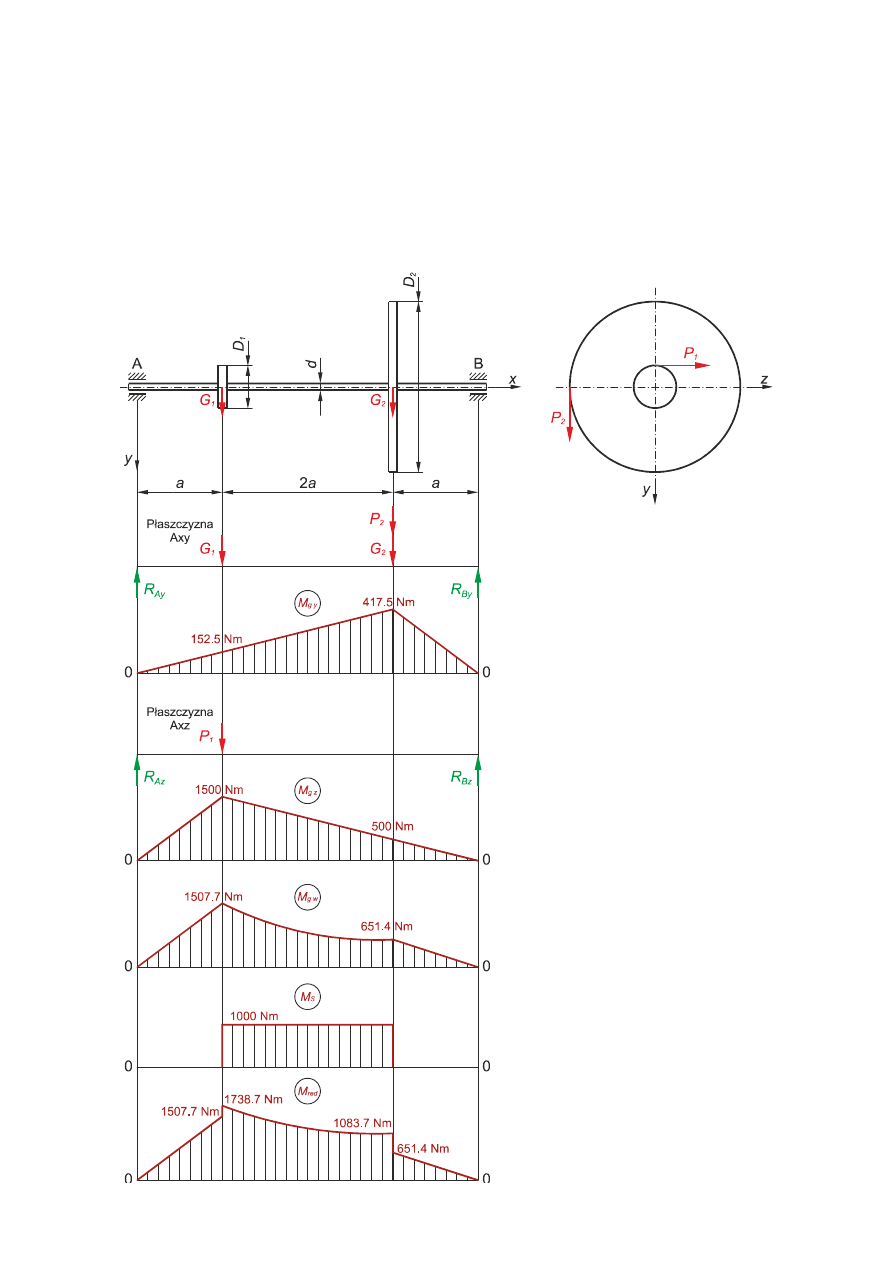
Zadanie 1. 

Wykorzystuj

ą

c hipotez

ę

 Hubera obliczy

ć

 

ś

rednic

ę

 d wału na którym osadzone s

ą

 dwa koła pasowe 

1 i 2  o 

ś

rednicy  D

1

 = 100 mm  i  D

2

 = 400 mm  oraz  ci

ęż

arze  G

1

 = 200 N  i  G

2

 = 500 N.  Wał  przenosi 

moc  N = 52.36 kW  przy  pr

ę

dko

ś

ci  n = 500 obr/min.  Wykona

ć

  wykresy  momentów  gn

ą

cych, 

skr

ę

caj

ą

cych i zredukowanych. Przyj

ąć

 k

z

 = 120 N/mm

2

. Rozmieszczenie sił przyj

ąć

 jak na rys.  

Dane: D

1

 = 100 mm, D

2

 = 400 mm, G

1

 = 200 N, G

2

 = 500 N, N = 52.36 kW, n = 500 obr/min, 

a = 0.1 m, k

z

 = 120 N/mm

2

 

Szukane: d = ? 

 

 

Opracował: dr in

ż

. Mariusz Leus 

- 2 - 

 

 

1. Moment skr

ę

caj

ą

cy M

S

 

 

n

N

M

S

⋅

=

3

,

9549

   

 

Nm

 

1000

500

36

.

52

3

,

9549

=

⋅

=

S

M

   

Nm

 

1000

=

S

M

  

2. Sił P

1

 i P

2

 na kole 1 i 2 

 

2

2

2

2

1

1

D

P

D

P

M

S

⋅

=

⋅

=

    

 

kN

 

20

N

 

20000

1

.

0

1000

2

2

1

1

=

=

⋅

=

=

D

M

P

S

   

kN

 

20

1

=

P

    

   

kN

 

5

N

 

5000

4

.

0

1000

2

2

2

2

=

=

⋅

=

=

D

M

P

S

     

kN

 

5

2

=

P

   

3. Zginanie w płaszczy

ź

nie Axy 

Reakcje w ło

ż

yskach A i B  w płaszczy

ź

nie Axy: 

 

a) 

∑

=

0

A

M

; 

(

)

0

4

3

2

2

1

=

⋅

−

⋅

+

+

⋅

a

R

a

G

P

a

G

By

  

 

 

(

)

(

)

4

.

0

3

.

0

500

5000

1

.

0

200

4

3

2

2

1

⋅

+

+

⋅

=

⋅

+

+

⋅

=

a

a

G

P

a

G

R

By

  

 

 

N

 

4175

=

By

R

  

 

 

b) 

∑

=

0

B

M

; 

(

)

0

3

4

2

2

1

=

⋅

+

−

⋅

−

⋅

a

G

P

a

G

a

R

Ay

  

 

 

(

)

(

)

4

.

0

1

.

0

500

5000

3

.

0

200

4

3

2

2

1

⋅

+

+

⋅

=

⋅

+

+

⋅

=

a

a

G

P

a

G

R

Ay

  

 

 

N

 

1525

=

Ay

R

  

Momenty gn

ą

ce w płaszczy

ź

nie Axy: 

 

Nm

 

0

 

=

A

y

g

M

    

 

Nm

 

5

.

152

1

0

1525

1

.

0

1

 

=

⋅

=

⋅

=

.

R

M

Ay

y

g

    

 

Nm

 

5

.

417

1

.

0

4175

1

.

0

2

 

=

⋅

=

⋅

=

By

y

g

R

M

    

 

Nm

 

0

 

=

B

y

g

M

    

4. Zginanie w płaszczy

ź

nie Axz 

Reakcje w ło

ż

yskach A i B  w płaszczy

ź

nie Axz: 

 

a) 

∑

=

0

A

M

; 

0

4

1

=

⋅

−

⋅

a

R

a

P

Bz

  

 

 

4

.

0

1

.

0

20000

4

1

⋅

=

⋅

=

a

a

P

R

Bz

  

 

 

N

 

5000

=

Bz

R

  

 

 

b) 

∑

=

0

B

M

; 

0

3

4

1

=

⋅

−

⋅

a

P

a

R

Az

  

 

 

4

.

0

3

.

0

20000

4

3

1

⋅

=

⋅

=

a

a

P

R

Az

  

 

 

N

 

15000

=

Az

R

  

 

Opracował: dr in

ż

. Mariusz Leus 

- 3 - 

 

 

Momenty gn

ą

ce w płaszczy

ź

nie Axz: 

 

Nm

 

0

 

=

A

z

g

M

    

 

Nm

  

1500

1

.

0

15000

1

.

0

1

 

=

⋅

=

⋅

=

Az

z

g

R

M

    

 

Nm

  

500

1

.

0

5000

1

.

0

2

 

=

⋅

=

⋅

=

Bz

z

g

R

M

    

 

Nm

 

0

 

=

B

z

g

M

    

5. Momenty gn

ą

ce wypadkowe

 

 

2

 

2

 

 

z

g

y

g

w

g

M

M

M

+

=

   

 

Nm

 

0

0

0

2

2

2

 

2

 

 

=

+

=

+

=

A

z

g

A

y

g

A

w

g

M

M

M

     

 

Nm

 

7

.

1507

1500

5

.

152

2

2

2

1

 

2

1

 

1

 

=

+

=

+

=

z

g

y

g

w

g

M

M

M

   

 

Nm

 

4

.

651

500

5

.

417

2

2

2

2

 

2

2

 

2

 

=

+

=

+

=

z

g

y

g

w

g

M

M

M

      

 

Nm

 

0

0

0

2

2

2

 

2

 

 

=

+

=

+

=

B

z

g

B

y

g

B

w

g

M

M

M

     

6. Momenty zredukowane

 

 

2

2

 

75

.

0

S

w

g

red

M

M

M

⋅

+

=

   

 

Nm

 

0

0

75

.

0

0

75

.

0

2

2

2

2

 

=

⋅

+

=

⋅

+

=

A

S

A

w

g

A

red

M

M

M

     

 

Nm

 

7

.

1507

0

75

.

0

7

.

1507

75

.

0

2

2

2

1

2

1

 

L

  

1

=

⋅

+

=

⋅

+

=

S

w

g

red

M

M

M

   

 

Nm

 

7

.

1738

1000

75

.

0

7

.

1507

75

.

0

2

2

2

1

2

1

 

P

  

1

=

⋅

+

=

⋅

+

=

S

w

g

red

M

M

M

   

 

Nm

 

7

.

1083

1000

75

.

0

4

.

651

75

.

0

2

2

2

2

2

2

 

L

  

2

=

⋅

+

=

⋅

+

=

S

w

g

red

M

M

M

      

 

Nm

 

4

.

651

0

75

.

0

4

.

651

75

.

0

2

2

2

2

2

2

 

P

  

2

=

⋅

+

=

⋅

+

=

S

w

g

red

M

M

M

      

 

Nm

 

0

0

75

.

0

0

75

.

0

2

2

2

2

 

=

⋅

+

=

⋅

+

=

B

S

B

w

g

B

red

M

M

M

     

7. 

Ś

rednica wału d

 

 

g

z

red

red

k

W

M

≤

=

max

σ

;        

32

3

d

W

z

⋅

=

π

;        

Nm

 

7

.

1738

max

=

red

M

   

 

g

red

red

k

d

M

≤

⋅

=

32

3

max

π

σ

     

      

mm

 

85

.

52

120

1000

7

.

1738

32

32

3

3

max

=

⋅

⋅

⋅

=

⋅

⋅

=

π

π

g

red

k

M

d

     

      

 

mm

 

85

.

52

=

d