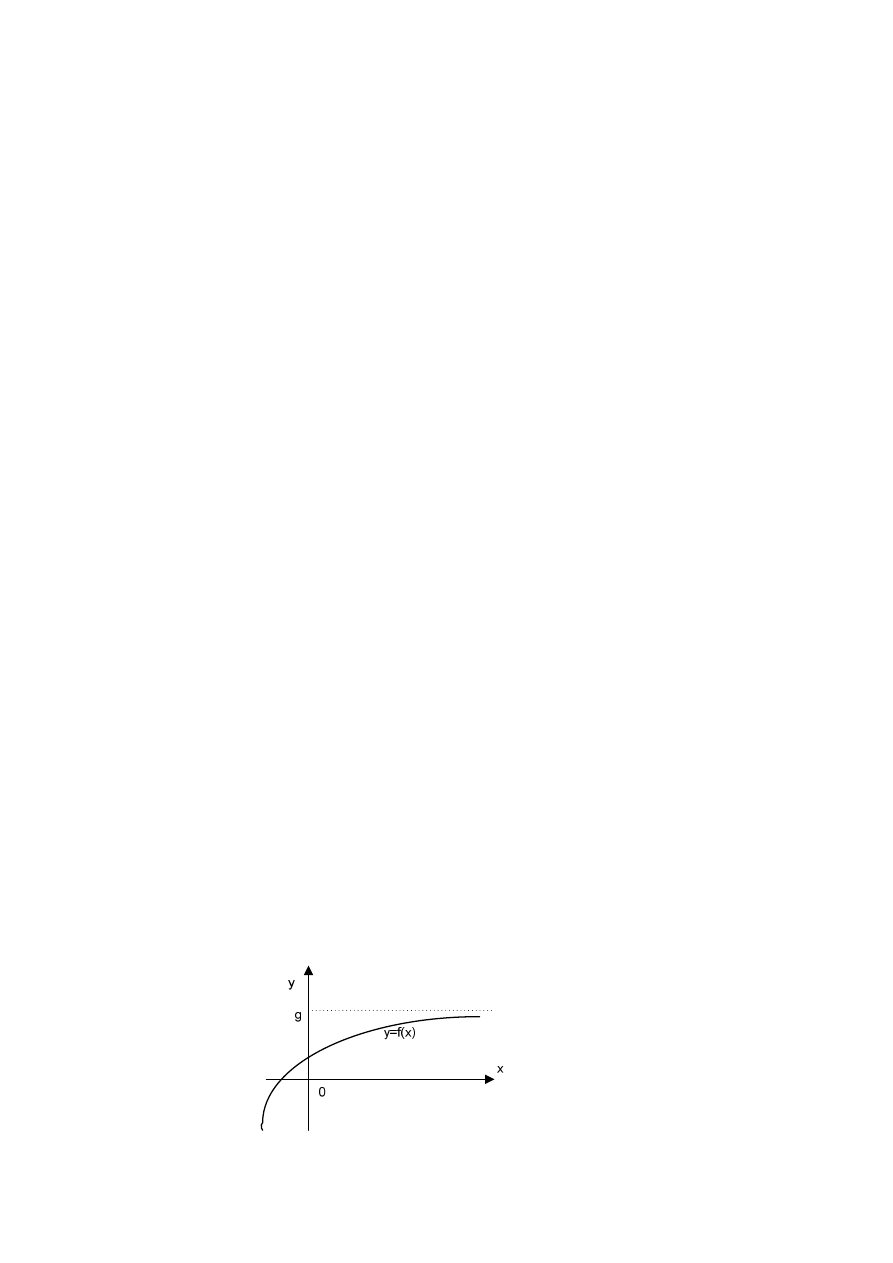
2.5. Granice jednostronne funkcji

Granice jednostronne

Może się zdarzyć, że nie wiemy, czy istnieje granica funkcji f w punkcie a, ale potrafimy

wskazać takie sąsiedztwo punktu a, że dla:

a)

argumentów większych od a tego sąsiedztwa ma już w punkcie a nieciągłość usuwal-

ną. Po usunięciu tej nieciągłości (czyli zdefiniowaniu funkcji ciągłej f*) wartość g

funkcji ciągłej f* w punkcie a nazywamy granicą prawostronną funkcji f w punkcie a i

piszemy g =

)

(

lim

x

f

a

x

+

→

.

b) argumentów mniejszych od a tego sąsiedztwa ma już w punkcie a nieciągłość usuwal-

ną. Po usunięciu tej nieciągłości (czyli zdefiniowaniu funkcji ciągłej f*) wartość g

funkcji ciągłej f* w punkcie a nazywamy granicą lewostronną funkcji f w punkcie a i

piszemy g =

)

(

lim

x

f

a

x

−

→

.

Twierdzenia

a)

Jeżeli g jest granicą funkcji f w punkcie a, to obie granice jednostronne tej funkcji w

punkcie a istnieją i są równe g.

b)

Jeżeli granice jednostronne funkcji f w punkcje a istnieją i są równe g, to funkcja f ma

granicę w punkcie a równą g.

c)

Jeżeli granice jednostronne funkcji f w punkcie a istnieją, ale są różne, to funkcja f nie

ma granicy w punkcie a.

Granice w nieskończoności

Definicje

a)

Niech funkcja ciągła f będzie określoną na przedziale (x

0, +

∞

). Jeśli dla coraz to więk-

szych argumentów x wartości f(x) funkcji f będą coraz to bliższe liczbie g, wówczas

mówimy, że g jest granicą funkcji f w plus nieskończoności. Piszemy g =

)

(

lim

x

f

x

+∞

→

.

b)

Analogicznie, niech funkcja ciągła f będzie określoną na przedziale (

-

∞

, x

0

). Jeśli dla

coraz to mniejszych argumentów x wartości f(x) funkcji f będą coraz to bliższe liczbie

g, wówczas mówimy, że g jest granicą funkcji f w minus nieskończoności. Piszemy

g =

)

(

lim

x

f

x

−∞

→

.

Granice niewłaściwe

Definicje

a)

Niech funkcja ciągła f będzie określoną na przedziale (a,

,

b). Jeśli dla argumentów co-

raz to bliższych a odpowiadające im wartości funkcji f będą coraz to większe, wów-

czas mówimy, że funkcja f ma w punkcie a granicę plus nieskończoność. Piszemy

)

(

lim

x

f

a

x

→

= +

∞

.

b)

Niech funkcja ciągła f będzie określoną na przedziale (a,

,

b). Jeśli dla argumentów co-

raz to bliższych a odpowiadające im wartości funkcji f będą coraz to mniejsze, wów-

czas mówimy, że funkcja f ma w punkcie a granicę minus nieskończoność. Pisze-

my

)

(

lim

x

f

a

x

→

= -

∞

.

Granice +

∞

i -

∞

nazywamy granicami niewłaściwymi.

Przykład

Dana jest funkcja określona wzorem f(x) =

x

1

. Jest ona funkcją ciągłą w swojej dziedzinie. Jej

wykres przedstawia rysunek.

Mamy: a)

x

x

1

lim

−∞

→

= 0, b)

x

x

1

lim

+∞

→

= 0, c)

x

x

1

lim

0

+

→

= +

∞

, d)

x

x

1

lim

0

−

→

= -

∞

.

W zerze funkcja ta nie ma granicy, bowiem granice jednostronne w 0 są różne.

Ćwiczenia

Zad. 1.

Dana jest funkcja określona wzorem f(x) = x

−

2

.

a) Naszkicuj jej wykres.

b) Oblicz jej granice w punkcie: -3, 5,

7

.

c) Oblicz jej granice jednostronne w zerze oraz granice w +

∞

i -

∞

.

Zad. 2

Wyznacz granicę prawostronną i lewostronną funkcji f w punkcie a, jeżeli:

a) f(x) =

2

5

−

x

, a = 2; b) f(x) =

2

3

4

−

−

x

x

, a = 2;

c) f(x) =

2

1

x

−

, a = 0; d) f(x) =

2

9

1

x

−

, a = 3; e) f(x) =

2

2

9

x

x

−

, a = 3;

f) f(x) =

2

1

3

x

−

−

, a = -1.

Zad. 3.

Wyznacz granice funkcji f w +

∞

i -

∞

, jeżeli:

a) f(x) =

2

3

−

−

x

; b) f(x) =

2

4

5

x

−

; c) f(x) =

2

1

3

x

−

−

.

Odpowiedzi

Zad.1.: b) kolejno:

9

1

,

25

1

,

7

1

. c) 0.

Zad.2.: prawostronne: a) +

∞

; b) +

∞

, c) -

∞

, d) -

∞

, e) -

∞

, f) +

∞

,

lewostronne: a) -

∞

; b) -

∞

, c) -

∞

, d)

∞

, e)

∞

, f) +

∞

.

Zad. 3.: w plus nieskończoności: a) -2, b) 5, c) 0,
w minus nieskończoności: a) -2, b)