Grupa przestrzenna
1
Grupa przestrzenna
Grupa przestrzenna – w matematyce, geometrii i krystalografii jest to grupa symetrii. W przestrzeni
trójwymiarowej zazwyczaj dzieli przestrzeń na powtarzalną grupę dyskretną.
W przestrzeni trójwymiarowej istnieje 219 różnych typów grup przestrzennych (230 uwzględniając chiralne). Grupy
przestrzenne są badane i występują także w przestrzeniach o różnej ilości wymiarów. Za przykład mogą posłużyć
grupy Bieberbacha
[]
.
W krystalografii spotyka się grupy określane mianem krystalograficznych grup przestrzennych lub grup Fiodorowa.
Przedstawiają i opisują symetrie kryształów
[]
.
Rys historyczny
Grupy przestrzenne w przestrzeni dwuwymiarowej były znane od bardzo dawna. Pierwsze grupy przestrzenne dla
przestrzeni trójwymiarowej wyliczono pod koniec XIX wieku. W 1891 roku dokonali tego niezależnie Fiodorow
(1853-1919) i Schonflies (1853-1928). W 1894 roku wyliczeń dokonał również Barlow (1845-1934). Pierwsza prace
zawierały błędy. Fiodorow i Schonflies korespondencyjnie wymienili się wyliczeniami. Rezultatem tego był w pełni
poprawna lista 230 grup przestrzennych
[][][]
.
Elementy grup przestrzennych
Grupy przestrzenne w trójwymiarowej przestrzeni powstały w wyniku połączenia 32 krystalograficznych grup
punktowych z 14 sieciami Bravais’go należących do jednego z 7 układów krystalograficznych. Z tego powodu grupy
przestrzenne uwzględniają kombinacje translacji komórki elementarnej i operacji wykonywanych na grupach
punktowych.
Notacje grup przestrzennych
Istnieje co najmniej dziewięć sposobów określania grup przestrzennych:
• numeryczna – Międzynarodowa Unia Krystalografii (IUCr) publikuje tabele wszystkich typów grup
przestrzennych i przypisuje każdej unikatowy numer od 1 do 230. Grupy przestrzenne tych samych układów
krystalograficznych i grup punktowych przydzielone mają kolejne numery.
• międzynarodowa (M, notacja Hermanna–Mauguina) – składa się z dużej litery oznaczającej typ sieci Bravais’go,
z liczb oznaczających osie symetrii zwykłe, inwersyjne lub śrubowe oraz z małych liter jako symboli płaszczyzn
symetrii i poślizgu. Znając reguły składania elementów symetrii możliwe jest przedstawienie rozmieszczenia
elementów symetrii w komórce elementarnej
[]
.
• notacja Halla
[]
• notacja Kreutza-Zaremby – za twórcze elementy symetrii przyjmuje się osie i środek symetrii. W symbolach klas
opuszcza się płaszczyzny symetrii, jeżeli wynikają one z iloczynu osi parzystokrotnych i środka symetrii.
• notacja Schonfliesa – składa się z dużej litery C, D, S, T, O określającej rodzaj grupy obrotowej oraz z dolnych
indeksów informujących o krotności głównej osi symetrii (n), rodzaju płaszczyzny symetrii (v, h, d) i o istnieniu
środka symetrii (i). Z takich symboli nie można określić typu sieci Bravais’go i wszystkich elementów symetrii
grupy
[]
.
•• symbol Shubnikova
• notacja orbifold dla dwuwymiarowej przestrzeni i notacja fibrifold dla trójwymiarowej przestrzeni – twory
matematyczne wprowadzone przez Conwaya i Thurstona. Niektórym grupom przestrzennym można
przyporządkować symbole orbifoldów i fibrifoldów
[]
.
Grupa przestrzenna
2
• notacja Coxetera – przestrzenna i punktowa grupa symetrii przedstawiona w postaci grup Coxetera.
Klasyfikacja grup przestrzennych
Istnieje co najmniej 10 różnych możliwości klasyfikowania grup przestrzennych w przestrzeni trójwymiarowej.
Skatalogowane są w tabeli od postaci najbardziej szerokiej, aż do wąskich klas na samym dole:
Krystalograficzne grupy przestrzenne (230 klas)
Afiniczne grupy przestrzenne (219 klas)
Arytmetyczne grupy przestrzenne (73 klasy)
Klasy krystalograficzne (32 klasy) Grupa punktowa sieci Bravais’go (14 klas)
Układ krystalograficzny (7 klas)
Sieć Bravais’go (7 klas)
Rodzina krystalograficzna (6 klas)
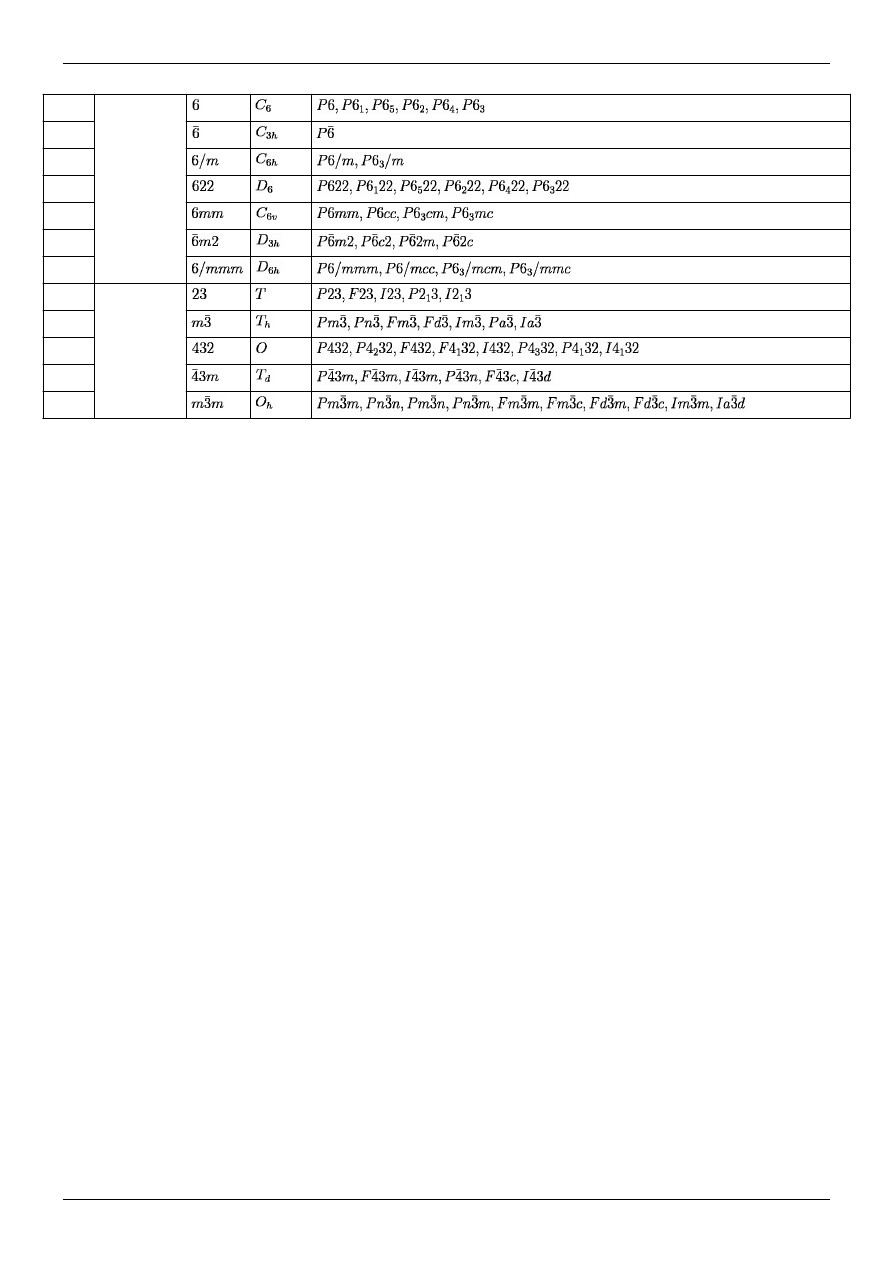
Grupa przestrzenna w 3 wymiarach
Układ
krystalograficzny
Grupy punktowe
Grupy przestrzenne
M
Schonflies
1
trójskośny (2)
2
3–5
jednoskośny
(13)
6–9
10–15
16–24
rombowy (59)
25–46
47–74
75–80
tetragonalny
(68)
81–82
83–88
89–98
99–110
111–122
123–142
143–146 trygonalny (25)
147–148
149–155
156–161
162–167
Grupa przestrzenna
3
168–173 heksagonalny
(27)
174
175–176
177–182
183–186
187–190
191–194
195–199 regularny (36)
200–206
207–214
215–220
221–230
Wprowadzenie przez IUCr pojęcia płaszczyzny poślizgu e spowodowało w 1996 roku zmianę symboli i rysunków
niektórych grup przestrzennych. Zmiana dotyczyła 7 grup w układzie rombowym oraz pięciu dla układów
tetragonalnego i regularnego. Rysunki wszystkich wymienionych grup zostały zmienione. Symbole grup zostały
zmienione tylko dla 5 przypadków w układzie rombowym (np. Abm2 na Aem2)
[]
.
Przypisy
Linki zewnętrzne
• Międzynarodowa Unia Krystalograficzna (UICr) (http:/
/
www.
iucr.
org)
(
ang.
)
• Grupy punktowe i sieci Bravais’go (http:/
/
neon.
mems.
cmu.
edu/
degraef/
pointgroups/
)
(
ang.
)
• Wyszukiwarka grup przestrzennych (http:/
/
cci.
lbl.
gov/
cctbx/
explore_symmetry.
html)
(
ang.
)
• Spis grup przestrzennych (http:/
/
cst-www.
nrl.
navy.
mil/
lattice/
spcgrp/
)
(
ang.
)
• Lista wszystkich grup przestrzennych (http:/
/
img.
chem.
ucl.
ac.
uk/
sgp/
mainmenu.
htm)
(
ang.
)
• Spis grup przestrzennych w 3D (http:/
/
www.
spacegroup.
info/
html/
space_groups.
html)
(
ang.
)
• Równania symetrii w przestrzeni dwuwymiarowej (http:/
/
www.
geom.
uiuc.
edu/
docs/
reference/
CRC-formulas/
node9.
html)
(
ang.
)
• Równania symetrii w przestrzeni trójwymiarowej (http:/
/
www.
geom.
uiuc.
edu/
docs/
reference/
CRC-formulas/
node45.
html)
(
ang.
)
Źródła i autorzy artykułu
4
Źródła i autorzy artykułu
Grupa przestrzenna Źródło: http://pl.wikipedia.org/w/index.php?oldid=35803077 Autorzy: Beno, Doomgiver
Licencja
Creative Commons Attribution-Share Alike 3.0 Unported
//creativecommons.org/licenses/by-sa/3.0/