Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
1
Zadanie 1
Rozważmy następującą, uproszczoną wersję gry w ,,wojnę’’. Talia składa się z 52 kart.
Dobrze potasowane karty rozdajemy dwóm graczom, każdemu po 26 i układamy w dwie
kupki. Gracze wykładają kolejno po jednej karcie z wierzchu swojej kupki i sprawdzają
wysokość obu kart. Jeśli obie wyłożone karty są równej wysokości (dwa asy lub dwa króle
itd.) to mówimy, że następuje wojna. Po sprawdzeniu, obie karty odkładamy na bok i nie
biorą już one udziału w dalszej grze. Powtarzamy tę procedurę 26 razy; gra kończy się, gdy
obaj gracze wyłożą wszystkie karty.
Oblicz wartość oczekiwaną liczby wojen.
(A)
17
26
(B)
17
52
(C) 4
(D)
10
11
12
13
4
49
50
51
52
4
⋅
⋅
⋅
⋅
⋅
⋅
⋅
(E)
40
1
41
2
...
50
11
51
12
52
13
+
+
+
+
+
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
2
Zadanie 2
Niech
3
2
1
,
,
W
W
W
będą niezależnymi zmiennymi losowymi o jednakowym rozkładzie
wykładniczym o gęstości
<
≥
=
−
.
0
0
;
0
)
(
w
dla
w
dla
e
w
f
w
λ
λ
Oblicz medianę zmiennej losowej
3
2
1
W
W
W
+
.
(A)
1
+
=
λ
λ
med
(B)
2
2
=
med
(C)
1
2
−
=
med
(D)
3
2
=
med
(E)
2
1
=
med
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
3
Zadanie 3
Załóżmy, że
K oznacza liczbę sukcesów w
n
próbach Bernoulliego z nieznanym
prawdopodobieństwem sukcesu
θ , czyli
k
n
k
k
n
k
K
−
−
=
=
)
1
(
)
Pr(
θ
θ
.
Rozważmy estymator parametru
θ postaci
n
b
K
a
+
+
=
θ
ˆ
.
Niech
16
=
n
.
Przypuśćmy, że
dodatnie liczby
a
i
b
dobrane zostały tak, że funkcja ryzyka
estymatora,
]
)
ˆ
[(
)
(
2
θ
θ
θ
θ
−
= E
R
jest funkcją stałą, czyli
R
R
=
)
(
θ
dla każdej wartości parametru
θ
.
Jeśli stwierdzisz, że
a
i
b
można tak dobrać, podaj liczbę R .
(A)
64
1
=
R
(B)
16
1
=
R
(C)
100
1
=
R
(D) nie istnieją takie liczby
a
i
b
dla których ryzyko jest stałe
(E)
4
1
=
R
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
4
Zadanie 4
Wiemy, że zmienne losowe
n
m
X
X
X
X
,...,
,...,
,
2
1
są niezależne i mają jednakowy rozkład
prawdopodobieństwa. Zakładamy, że
n
m
<
<
1
i znamy
2
)
(
σ
=
i
X
Var
. Niech
m
m
X
X
X
S
+
+
+
=
...
2
1
i.
n
m
n
X
X
X
X
S
+
+
+
+
+
=
...
...
2
1
.
Oblicz )
|
(
n
m
S
S
Var
E
.
(A)
2
)
|
(
σ
n
m
S
S
Var
E
n
m
=
(B)
2
1
)
|
(
σ
+
=
n
m
S
S
Var
E
n
m
(C) podane informacje nie wystarczają do obliczenia
)
|
(
n
m
S
S
Var
E
(D)
2
1
)
|
(
σ
n
n
m
S
S
Var
E
n
m
−
=
(E)
2
)
|
(
σ
n
m
n
m
S
S
Var
E
n
m
−
=
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
5
Zadanie 5
Załóżmy, że
Y
X , są zmiennymi losowymi o łącznym rozkładzie normalnym,
0
)
(
)
(
=
=
Y
E
X
E
, 1
)
(
)
(
=
=
Y
Var
X
Var
i
ρ
=
)
,
(
Y
X
Cov
.
Oblicz
)
(XY
Var
.
(A)
2
1
)
(
ρ
+
=
XY
Var
(B)
2
2
1
)
(
ρ
+
=
XY
Var
(C)
2
1
)
(
ρ
−
=
XY
Var
(D)
1
)
(
=
XY
Var
(E)
2
2
)
1
(
)
(
ρ
+
=
XY
Var
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
6
Zadanie 6
Załóżmy, że
4
1
,..., X
X
jest próbką z rozkładu normalnego
)
1
,
(
µ
N
, zaś
9
1
,...,Y
Y
jest próbką z
rozkładu normalnego
)
2
,
(
2
µ
N
. Niech
∑
=
=
4
1
4
1
i
i
X
X
będzie średnią z pierwszej próbki;
∑
=
=
9
1
9
1
i
i
Y
Y
będzie średnią z drugiej próbki.
(Wariancja jest dla obu próbek znana, zaś
µ
jest nieznane).
Znajdź takie liczby
r i
d
, żeby przedział
]
)
1
(
,
)
1
(
[
d
Y
r
X
r
d
Y
r
X
r
+
−
+
−
−
+
był przedziałem ufności dla
µ
na poziomie ufności
95
.
0
1
=
−
α
i przy tym długość tego
przedziału (
d
2
) była najmniejsza.
(A)
=
r 0.47,
=
d
0.980
(B)
=
r
0.69,
=
d
1.022
(C)
=
r
0.50,
=
d
0.888
(D)
=
r 0.53,
=
d
1.960
(E)
64
.
0
=
r
,
784
.
0
=
d
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
7
Zadanie 7
Niech
n
X
X
X
,...,
,
2
1
będzie próbką z rozkładu prawdopodobieństwa Pareto o dystrybuancie
<
≥
−
=
.
1
0
;
1
1
1
)
(
x
dla
x
dla
x
x
F
θ
θ
Przyjmując bayesowski punkt widzenia, przyjmujemy, że nieznany parametr
θ jest zmienną
losową o rozkładzie a priori wykładniczym, z gęstością
<
≥
=
−
.
0
0
;
0
)
(
θ
θ
λ
θ
π
θ
λ
dla
dla
e
Oblicz bayesowski estymator parametru
θ , czyli wartość oczekiwaną a posteriori:
)
,...,
|
(
ˆ
1
n
X
X
E
θ
θ
=
.
(A)
∑
+
+
=
λ
θ
i
X
n
ln
1
ˆ
(B)
n
X
i
∑
+
=
λ
θ
ln
ˆ
(C)
∑
+
+
=
λ
θ
i
X
n
1
ˆ
(D)
∑
+
+
=
i
X
n
ln
1
ˆ
λ
θ
(E)
∑
+
+
=
λ
λ
θ
i
X
n
ˆ
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
8
Zadanie 8
Niech )
(
2
1
.
0
n
χ
oznacza kwantyl rzędu 0.1 rozkładu chi-kwadrat z
n
stopniami swobody
(liczbę, od której zmienna losowa o rozkładzie chi-kwadrat jest mniejsza z prawdopodo-
bieństwem 0.1).
Oblicz
n
n
n
g
n
−
=
∞
→
)
(
lim
2
1
.
0
χ
.
(z dokładnością do 0.01).
(A)
81
.
1
=
g
(B)
28
.
1
−
=
g
(C)
81
.
1
−
=
g
(D)
56
.
2
−
=
g
(E) granica nie istnieje
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
9
Zadanie 9
Niech
10
1
,..., X
X
będzie próbką z rozkładu prawdopodobieństwa o gęstości
<
<
=
−
.
0
;
1
0
)
(
1
przypadku
przeciwnym
w
x
dla
x
x
f
θ
θ
θ
Rozważmy test jednostajnie najmocniejszy hipotezy
1
:
0
=
θ
H
przeciwko alternatywie
1
:
1
>
θ
H
na poziomie istotności
01
.
0
=
α
. Dla jakich wartości parametru
θ ten test ma moc
nie mniejszą, niż
99
.
0
?
(Podaj wynik z dokładnością do 0.01).
(A) moc
99
.
0
≥
wtedy i tylko wtedy, gdy
55
.
4
≥
θ
(B)
moc
99
.
0
≥
wtedy i tylko wtedy, gdy
07
.
9
≥
θ
(C)
nie istnieje takie
1
>
θ
, dla którego test ma moc
99
.
0
≥
(D)
moc
99
.
0
≥
wtedy i tylko wtedy, gdy
61
.
4
≥
θ
(E) moc
99
.
0
≥
wtedy i tylko wtedy, gdy
09
.
8
≥
θ
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
10
Zadanie 10
Rozważmy następujący schemat urnowy:
W każdej z 10 urn znajdują się 2 kule, oznaczone liczbami:
• W urnie 1 znajdują się 2 kule oznaczone liczbą 1,
• w urnie 2 znajdują się 2 kule oznaczone liczbą 2,
• ..................................................................
• w urnie 10 znajdują się 2 kule oznaczone liczbą 10.
Losujemy kulę z urny 1 i przekładamy ją do urny 2. Następnie (po wymieszaniu kul)
losujemy kulę z urny 2 i przekładamy do urny 3, itd., kulę wylosowaną z urny 9 przekładamy
do urny 10, wreszcie losujemy kulę z urny 10. Jakie jest prawdopodobieństwo, że ta ostatnia
wylosowana kula ma numer większy, niż 6 ?
(A)
10
7
(B)
81
80
(C)
11
7
(D)
243
241
(E)
81
77
Prawdopodobieństwo i statystyka
12.10.2002 r
.
___________________________________________________________________________
11
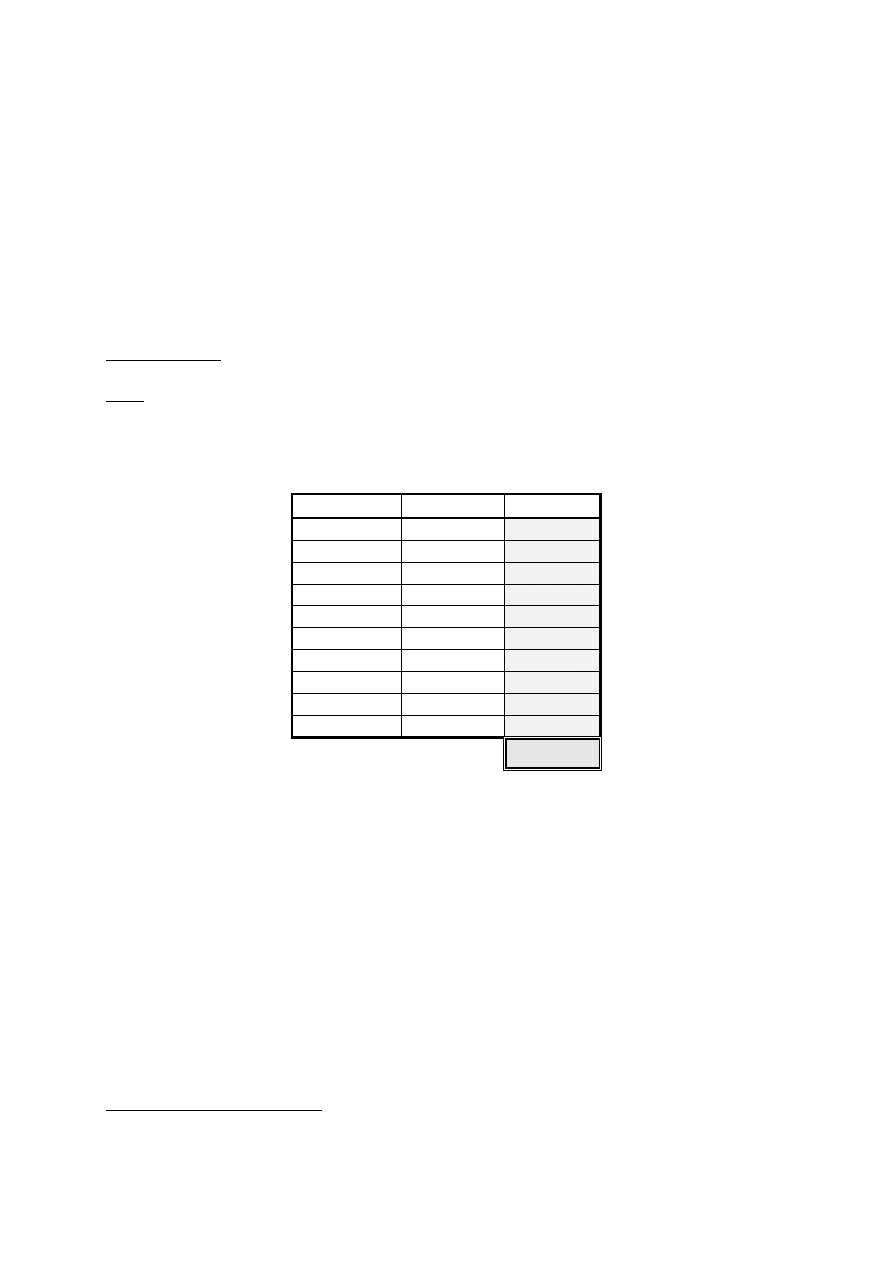
Egzamin dla Aktuariuszy z 12 października 2002 r.
Prawdopodobieństwo i Statystyka
Arkusz odpowiedzi
*
Imię i nazwisko .................... K L U C Z O D P O W I E D Z I .........................
Pesel ...........................................
Zadanie nr
Odpowiedź Punktacja
♦
1 A
2 C
3 C
4 E
5 A
6 E
7 A
8 C
9 A
10 B
*
Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.
♦
Wypełnia Komisja Egzaminacyjna.