Rozdział 3

Algorytm sympleks

3.1

Wprowadzenie

Stosowanie geometrycznej metody rozwiązywania ZPL jest możliwe właściwie tylko w przy-

padku zagadnień, w których sformułowaniu występują tylko dwie zmienne decyzyjne. Jeże-

li liczba zmiennych decyzyjnych jest równa 3, to możliwa jest geometryczna interpretacja

ograniczeń (wyznaczają one pewien wielokąt wypukły zawarty w pierwszym oktancie ukła-

du współrzędnych), ale, na ogół, trudne jest wykonanie dostatecznie dokładnego rysunku

ilustrującego wzajemne położenie zbioru rozwiązań dopuszczalnych i poziomic funkcji ce-

lu, które są płaszczyznami w R

3

. W przypadku większej liczby zmiennych decyzyjnych

praktycznie niemożliwe jest efektywne sporządzenie rysunków mogących ułatwić znalezie-

nie rozwiązania ZPL. Dodatkową trudność sprawia duża liczba dopuszczalnych rozwiązań

bazowych (czyli wierzchołków zbioru rozwiazań dopuszczalnych D), jakie należy wyliczyć,

aby poprawnie opisać wielościan D (np. dla ZPL z ośmioma zmiennymi bazowymi i za-

wierajacego cztery ograniczenia liczba takich wierzchołków może być równa 70). Rodzi się

więc pytanie, czy istnieje metoda rozwiązywania ZPL, która działa niezależnie od liczby

zmiennych decyzyjnych, jest efektywna i nie wymaga wyznaczania wsystkich dopuszczal-

nych rozwiązań bazowych. Na szczęście, odpowiedź na to pytanie jest twierdząca i brzmi:

algorytm sympleks. Jest to algorytm iteracyjny, który startuje od dowolnie ustalonego

dopuszcalnego rozwiązania bazowego i w każdym kroku zastępuje aktualne rozwiązanie no-

wym „sąsiednim” dopuszczalnym rozwiązaniem bazowym, dla którego wartość funkcji celu

jest bliższa wartości optymalnej, przy czym zmiana wartości funkcji celu przy przejściu

od „starego” do „nowego” rozwiązania jest największa z możliwych. Przez „rozwiązania

sąsiednie” rozumiemy tutaj dwa dopuszczalne rozwiązania bazowe, dla których zbiory ich

zmiennych bazowych różnią się jednym elementem. Rozwiązania takie odpowiadają końcom

łączącej je krawędzi w wielościanie D.

1

W poprzednim rozdziale pokazaliśmy, w jaki sposób przekształcić dowolne ZPL do

zagadnienia równoważnego zapisanego w bazowej postaci kanonicznej. W dalszym ciągu

omówimy stosowanie algorytmu sympleks właśnie dla takiej postaci ZPL. Istnieją modyfi-

kacje tego algorytmu, które działają przy nieco innych założeniach (np. nie wymaga się, aby

kanoniczna postać zagadnienia była bazowa), ale wydaje się, że opis algorytmu sympleks i

uzasadnienie jego poprawności są najłatwiejsze w postulowanej powyżej sytuacji.

3.2

Wskaźniki optymalności

Zacznijmy od przypomnienia ogólnych założeń. Dane jest ZPL:

f (x

1

, x

2

, . . . , x

n

) = c

1

x

1

+ c

2

x

2

+ . . . + c

n

x

n

→ max

(min)

a

11

x

1

+ a

12

x

2

+ . . . + a

1n

x

n

=

b

1

,

. . .

a

m1

x

1

+ a

m2

x

2

+ . . . + a

mn

x

n

=

b

m

,

x

1

­ 0, x

2

­ 0, . . . , x

n

­ 0.

(3.1)

gdzie współczynniki a

ij

oraz b

i

są ustalonymi liczbami rzeczywistymi, b

i

­ 0 dla każdego

i = 1, 2, . . . , m oraz m < n. Zbiór rozwiązań dopuszczalnych zadania (3.1), czyli zbiór

wszystkich punktów (x

1

, x

2

, . . . , x

n

) ∈ R

n

spełniających ograniczenia, będziemy oznaczać

symbolem D, tak jak to robiliśmy dotychczas. Zauważmy, że wymiar zbioru D jest równy

n − m i jest mniejszy od wymiaru przestrzeni R

n

, ale nadal jest to wielościan zawarty w

pierwszym ortancie układu współrzędnych przestrzeni R

n

, którego wierzchołki wyznaczone

są przez odpowiednie dopuszczalne rozwiązania bazowe układu równań











































a

11

x

1

+ a

12

x

2

+ . . . + a

1n

x

n

= b

1

,

a

21

x

1

+ a

22

x

2

+ . . . + a

2n

x

n

= b

2

,

..

.

a

m1

x

1

+ a

m2

x

2

+ . . . + a

mn

x

n

= b

m

.

(3.2)

Wobec uwagi poczynionej na końcu poprzedniego podrozdziału będziemy zakładać,

że układ równań tworzących ograniczenia w ZPL (3.1) zapisany jest w bazowej postaci

kanonicznej, a jego zmiennymi bazowymi są x

1

, x

2

, . . ., x

m

. Założenie to de facto nie

wprowadza żadnych dodatkowych warunków, lecz służy jedynie wygodzie zapisu. Przy

2

takim założeniu układ ograniczeń (3.2) można zapisać prościej w nastepującej postaci:











































x

1

+ a

1 m+1

x

m+1

+ a

1 m+2

x

m+2

+ . . . + a

1n

x

n

= b

1

,

x

2

+ a

2 m+1

x

m+1

+ a

2 m+2

x

m+2

+ . . . + a

2n

x

n

= b

2

,

..

.

x

m

+ a

m m+1

x

m+1

+ a

m m+2

x

m+2

+ . . . + a

mn

x

n

= b

m

.

(3.3)

Ze względu na założenie o znakach prawych stron ograniczeń, rozwiązanie bazowe

¯

X = (b

1

, b

2

, . . . , b

m

, 0, 0, . . . , 0)

układu równań (3.3) jest dopuszczalnym rozwiązaniem bazowym. Zbudowanie następnego

dopuszczalnego rozwiązania bazowego polega na zastąpieniu jednej ze zmiennych bazowych

(nazywanej dalej: zmienną wychodzacą z bazy) przez odpowiednią zmienną niebazo-

wą (czyli zmienną wchodzącą do bazy). Zmienną wychodzacą z bazy wybieramy tak,

aby w nowym rozwiązaniu bazowym wszystkie wartości zmiennych były nieujemne. W po-

przednim rozdziale został omówiony sposób, jak to zrobić: po ustaleniu, która zmienna

ma wejść do bazy, zmienną wychodzącą z bazy wyznacza się obliczając ilorazy wyjścia

dla wszystkich dodatnich zmiennych bazowych i wybierając tę zmienną, dla której iloraz

wyjścia jest najmniejszy. Pozostaje więc znaleźć kryterium pozwalające na optymalny wy-

bór zmiennej wchodzącej do bazy. W celu znalezienia tego kryterium należy przeprowadzić

pewne rozważania teoretyczne.

Rozważmy dowolne rozwiązanie dopuszczalne X = (x

1

, x

2

, . . . , x

n

) układu równań

(3.3). Wówczas

x

i

= b

i

−

n

X

s=m+1

a

is

x

s

dla

i = 1, 2, . . . , m,

Korzystając z tej równości możemy teraz obliczyć różnicę pomiędzy wartościami funkcji

celu f dla rozwiązań X i ¯

X (pamiętamy,że ¯

x

i

= b

i

dla i = 1, . . . , m:

f (X) − f ( ¯

X) =

m

X

i=1

c

i

x

i

+

n

X

s=m+1

c

s

x

s

−

m

X

i=1

c

i

b

i

=

=

m

X

i=1

c

i





b

i

−

n

X

s=m+1

a

is

x

s





+

n

X

s=m+1

c

s

x

s

−

m

X

i=1

c

i

b

i

=

=

n

X

s=m+1

m

X

i=1

a

is

c

i

− c

s

!

x

s

.

Ponieważ wszystkie wartości x

s

są nieujemne, znak różnicy f (x) − f (¯

x) zależy od znaków

wyrażeń w nawiasach w ostatniej sumie. Przyjmujemy następującą definicję.

3

Definicja 1. Przy wprowadzonych powyżej oznaczeniach, dla każdej zmiennej niebazowej

x

s

liczbę

∆

s

=

m

X

i=1

a

is

c

i

− c

s

nazywamy wskaźnikiem optymalności dla tej zmiennej.

Oczywiście, w praktyce zmienna niebazowa może mieć indeks mniejszy lub równy m.

Zakres zmienności dla tego indeksu, którym posługiwaliśmy się wyżej, był konsekwencją

przyjętego założenia mającego na celu uproszczenie notacji.

Posługując się oznaczeniem wskaźnika optymalności można powyżej otrzymaną równość

zapisać następująco:

f (X) = f ( ¯

X) −

n

X

s=m+1

∆

s

x

s

.

(3.4)

Załóżmy teraz, że rowiązywane ZPL polega na maksymalizacji funkcji celu. Jeżeli ∆

s

­ 0

dla s = m + 1, . . . , n, to z równości (3.4) wynika, że f (X) ¬ f ( ¯

X) dla każdego rozwią-

zania dopuszczalnego x, a więc ¯

X jest optymalnym rozwiązaniem rozważanego zadania.

Z drugiej strony, jeżeli istnieje taki wskaźnik s, że x

s

> 0 oraz ∆

s

< 0, to f (X) > f ( ¯

X

i, w konsekwencji, rozwiązanie bazowe ¯

X nie jest rozwiązaniem optymalnym. Podobne

rozumowanie przeprowadzone w przypadku ZPL(min) pokazuje, że wówczas ¯

X jest roz-

wiązaniem optymalnym, jeżeli wszystkie wskaźniki optymalności są niedodatnie. Zachodzi

więc twierdzenie:

Twierdzenie 1. Niech ¯

X będzie bazowym rozwiązaniem dopuszczalnym ZPL

f (x) → max

(min)

Ax = b,

x ­ 0,

zaś X będzie dowolnym rozwiązaniem dopuszczalnym tego zadania. Wówczas

1) jeżeli dla każdej zmiennej niebazowej odpowiadający jej wskażnik optymalności spełnia

warunek ∆

j

­ 0, to f (X) ¬ f ( ¯

X); w szczególności ¯

X jest rozwiązaniem ZPL(max),

2) jeżeli dla każdej zmiennej niebazowej odpowiadający jej wskażnik optymalności spełnia

warunek ∆

j

¬ 0, to f (X) ­ f ( ¯

X); w szczególności ¯

X jest rozwiązaniem ZPL(min).

Na koniec rozważań poświęconych wskaźnikom optymalności zajmiemy się problemem

wymiany zmiennej bazowej w nieoptymalnym bazowym rozwiazaniu dopuszczalnym. Ak-

tualnie rozważane rozwiązanie bazowe nie jest optymalne, gdy ∆

s

< 0 dla pewnego s w

przypadku ZPL(max) oraz gdy ∆

s

> 0 dla pewnego s w przypadku ZPL(min). W tym

4

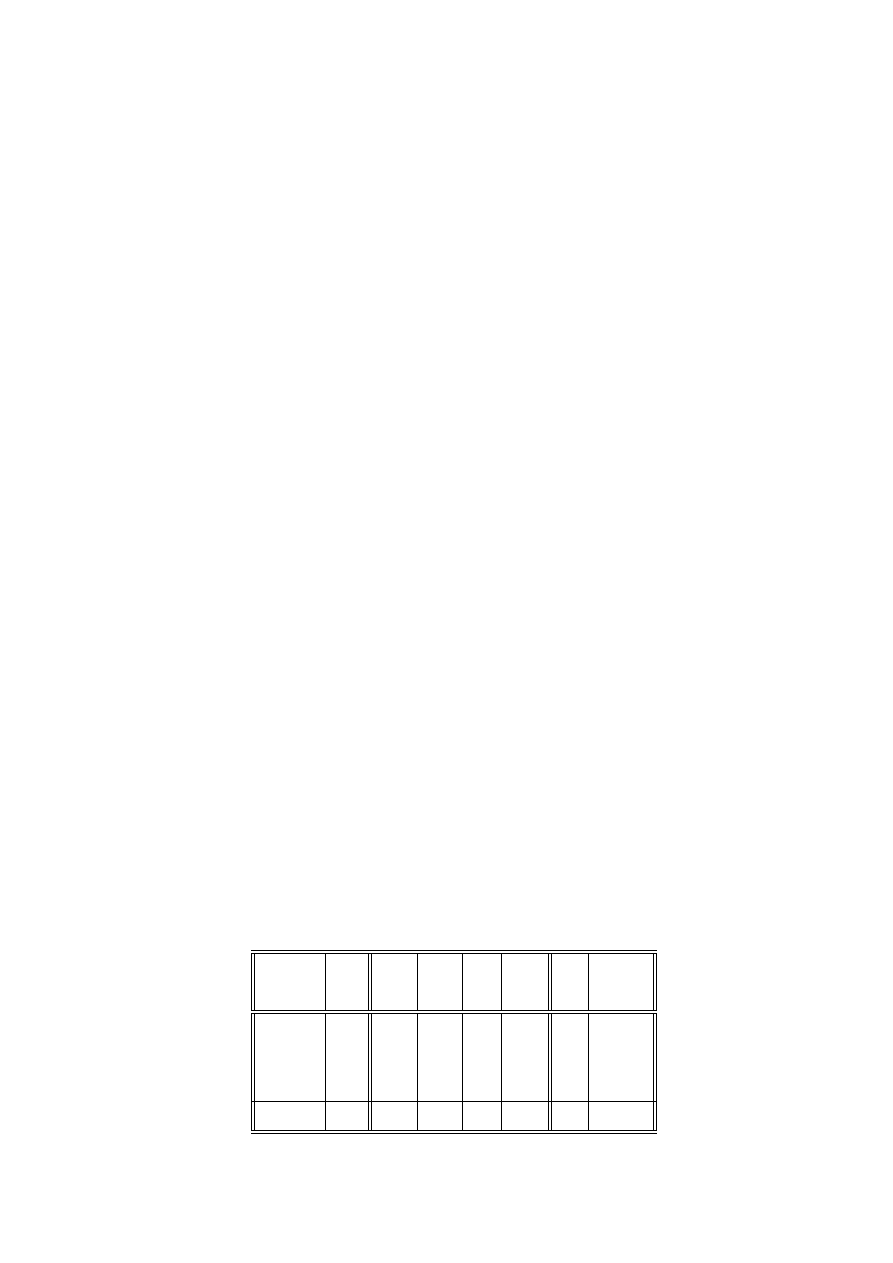
przypadku wzór (3.4) pozwala wybrać zmienną niebazową, która zostanie wprowadzona do

bazy w następnym rozwiązaniu. Wyboru tej zmiennej należy dokonać w taki sposób, aby w

przypadku ZPL(max) (odpowiednio: ZPL(min)) przyrost (odpowiednio: spadek) wartości

celu był jak największy. Można to zrobić podstawiając wartość 1 w miejsce sprawdzanej

zmiennych niebazowej i 0 w miejsce pozostałych zmiennych niebazowych, a następnie wy-

bierając tę zmienną niebazową, dla której wartość bezwzględna różnicy f (X) − f ( ¯

X) jest

największa. W przypadku ZPL(max) będzie to ta zmienna niebazowa x

s

, dla której ∆

s

ma

wartość najmniejszą, a w przypadku ZPL(min) — ta zmienna niebazowa x

s

, dla której ∆

s

ma wartość największą.

3.3

Opis algorytmu sympleks

Wnioski dotyczące wskaźników optymalności sformułowane w poprzednim podrozdziale

pozwalają na opisanie procedury iteracyjnej, w wyniku stosowania której albo zostanie

znalezione rozwiązanie optymalne ZPL, albo zostanie ustalone, że takie rozwiązanie opty-

malne nie istnieje.

Algorytm sympleks

Dane jest ZPL w bazowej postaci kanonicznej:

f (x

1

, x

2

, . . . , x

n

) = c

1

x

1

+ c

2

x

2

+ . . . + c

n

x

n

→ max

(min)

a

11

x

1

+ a

12

x

2

+ . . . + a

1n

x

n

=

b

1

,

. . .

a

m1

x

1

+ a

m2

x

2

+ . . . + a

mn

x

n

=

b

m

,

x

1

­ 0, x

2

­ 0, . . . , x

n

­ 0.

(3.5)

gdzie współczynniki a

ij

oraz b

i

są ustalonymi liczbami rzeczywistymi, b

i

­ 0 dla każdego

i = 1, 2, . . . , m oraz m < n, przy czym z kolumn macierzy A = [a

ij

] można wybrać m

kolumn tworzących pełny układ kolumn macierzy jednostkowej I

m

.

Krok 1. Tworzymy tablicę sympleksową:

zmienne

c

1

c

2

. . .

c

n

iloraz

bazowe

c

B

x

1

x

2

. . .

x

n

b

wyjścia

x

k

1

c

k

1

a

11

a

12

. . .

a

1n

b

1

..

.

..

.

..

.

..

.

..

.

..

.

x

k

m

c

k

m

a

m1

a

m2

. . .

a

mn

b

m

∆

j

.

5

Tablica ta zawiera w nagłówku środkowych kolumn nazwy wszystkich zmiennych decy-

zyjnych i współczynniki znajdujące się we wzorze funkcji celu przy tych zmiennych. Każda

z tych kolumn zawiera wyrazy z odpowiedniej kolumny macierzy współczynników układu

równań tworzących ograniczenia ZPL. W dwóch kolumnach z lewej strony tabeli wpisujemy

nazwy zmiennych bazowych i odpowiednie współczynniki c

j

w ten sposób, że na przecięciu

wiersza i kolumny zawierających zmienną x

j

znajduje się liczba 1. Dwiema kolumnami po

prawej stronie tabeli są: kolumna wyrazów wolnych kolejnych ograniczeń (kolumna ta ozna-

czona jest w nagłówku symbolem b) i kolumna, w której wpisywane bedą ilorazy wyjścia.

W ostatnim wierszu tabeli wpiszemy w każdej kolumnie zmiennej niebazowej obliczony dla

tej zmiennej wskaźnik optymalności.

Krok 2. Z tablicy sympleksowej odczytujemy dopuszczalne rozwiązanie bazowe X przy-

pisując każdej zmiennej bazowej x

k

i

odpowiednią wartość wyrazu wolnego b

i

znajdującego

się w tym samym wierszu. Zmiennym niebazowym przypisujemy wartość 0.

Krok 3. Dla każdej zmiennej niebazowej x

j

obliczamy wskaźnik optymalności

∆

j

=

m

X

i=1

c

k

i

a

ij

− c

j

i umieszczamy go w ostatnim wierszu tablicy w kolumnie zmiennej niebazowej x

j

.

Krok 4. Sprawdzamy, czy otrzymane rozwiązanie X jest optymalne. W przypadku ZPL(max)

rozwiązanie jest optymalne, jeżeli wszystkie wskaźniki optymalności są nieujemne: ∆

j

­ 0.

W przypadku ZPL(min) rozwiązanie jest optymalne, jeżeli wszystkie wskaźniki optymal-

ności są niedodatnie: ∆

j

¬ 0. Jeżeli rozwiązanie jest optymalne, to kończymy procedurę

sympleksową. W przeciwnym wypadku wykonujemy następny krok.

Krok 5. Ustalamy zmienną, która wejdzie do bazy w następnym dopuszczalnym rozwią-

zaniu bazowym. Czynimy to znajdując w przypadku ZPL(max) (odpowiednio: ZPL(min))

najmniejszy (odpowiednio: największy) ze wskaźników optymalności; jest on oczywiście

niedodatni (odpowiednio: nieujemny). Zmienna, w której kolumnie znajduje się znaleziony

wskaźnik optymalności, jest zmienną wchodzącą do bazy. Załóżmy, że jest to zmienna x

j

0

.

Krok 6. Ustalamy zmienną, która opuści bazę w następnym dopuszczalnym rozwiązaniu

bazowym. W tym celu dla wszystkich dodatnich wyrazów kolumny zmiennej x

j

0

obliczamy

ilorazy wyjścia:

b

i

a

ij

0

i = 1, . . . , m,

(o ile

a

ij

0

> 0).

Najmniejszy z obliczonych ilorazów wyjścia wyznacza zmienną wychodzącą z bazy.

Przyjmijmy, że zmienna ta znajduje się w wierszu o numerze i

0

, czyli zmienną wychodzącą

z bazy jest x

k

i0

.

6

Krok 7. Element stojący na skrzyżowaniu kolumny zawierającej zmienną wchodzącą do

bazy i wiersza zawierającego zmienną wychodzącą z bazy nazywamy elementem cen-

tralnym lub głównym. Korzystając z metody eliminacji Gaussa-Jordana przekształcamy

macierz












a

11

a

12

. . . a

1n

b

1

a

21

a

22

. . . a

2n

b

2

..

.

..

.

..

.

..

.

a

m1

a

m2

. . . a

mn

b

m












zawartą w tablicy sympleksowej w ten sposób, aby kolumna o numerze j

0

stała się ko-

lumną macierzy jednostkowej z elementem 1 w wierszu o numerze i

0

. Otrzymane współ-

czynniki zapisujemy w nowej tablicy sympleksowej, w której z lewej strony zastępujemy

nazwę zmiennej wychodzącej z bazy nazwą zmiennej wchodzącej do bazy i wpisujemy od-

powiadający jej współczynnik c

j

. Nazwy pozostałych zmiennych i odpowiednie wartości

współczynników pozostawiamy bez zmian. Dla tak otrzymanej nowej tablicy sympleksowej

powracamy do kroku 2.

7