Ćwiczenia do wykładu Synteza i właściwości nanostruktur

Zestaw 5

Zadanie 1 – mikroskop STM

Proszę rozważyć sytuację z jaka mamy do czynienia w mikroskopie tunelowym podczas obrazowania
próbki z metalu metalowym ostrzem (patrz rys. 1). Początek układu współrzędnych jest przyjęty na
granicy próbka bariera. Ostrze i próbka charakteryzują się odpowiednio pracami wyjścia ϕ

0

i ϕ

P

oraz

energiami poziomu Fermiego E

fo

oraz E

fp

. Napięcie V przyłożone jest tak, że próbka staje sie elektrodą

ujemną, a ostrze elektrodą dodatnią, a tunelujące z próbki do ostrza elektrony dysponują energią
z zakresu od E

fp

−|e|V do E

fp

. Taka polaryzacja przyłożonego napięcia powoduje, że obrazowane będą

tzw. stany pełne próbki. Odległość ostrza od próbki wynosi z. Przybliżając rzeczywistą barierę
potencjału barierą prostokątną oraz zakładając, że przyłożone napięcie jest małe w stosunku do
wysokości tej bariery wykaż, że prąd tunelowy można opisać przybliżonym wyrażeniem:

gdzie ρ(z,E

fp

) oznacza lokalną gęstość stanów elektronowych na poziomie Fermiego próbki

w odległości od powierzchni w jakiej znajduje sie ostrze mikroskopu.

Wskazówka 1: Skorzystaj z rozwiązania zadania tunelowania przez prostokątną barierę potencjału. Co
w naszym przykładzie będzie pełnić rolę wysokości bariery?
Wskazówka 2: Lokalna gęstość stanów jest zdefiniowana następująco:

gdzie Ψ

n

(x) są funkcjami falowymi stanów z przedziału energetycznego od E−ε do E.

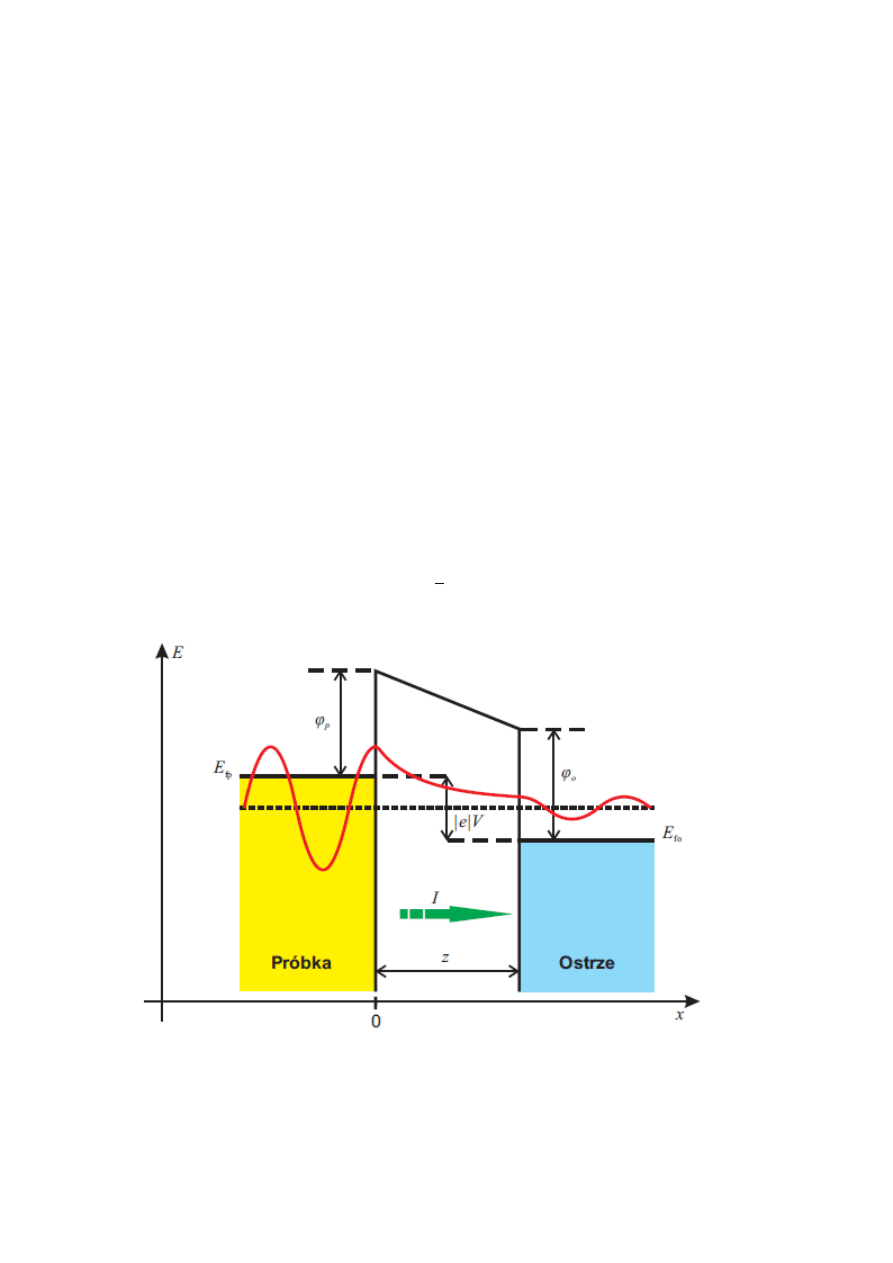
Rysunek 1: Schemat tunelowania w mikroskopie STM. E

fp

- energia Fermiego dla próbki, E

fo

- energia Fermiego

dla ostrza, V - przyłożona różnica potencjałów,

ϕ

p

- praca wyjścia materiału próbki,

ϕ

o

- praca wyjścia materiału

ostrza, z - odległość ostrze-próbka, I - prąd tunelowania, którego zwrot oznaczony jest zieloną strzałką.
Czerwona linia schematycznie przedstawia część przestrzenną przykładowej funkcji falowej tunelującego
elektronu.

Zadanie 2 - bezkontaktowy mikroskop sił atomowych (ncAFM)

W bezkontaktowej mikroskopii sił atomowych rolę skanującej sondy pełni drgająca belka zakończona
ostrzem. W trakcie oddziaływania atomów ostrza z atomami badanej próbki zmianie ulega częstość
drgań belki. Przyjmując uproszczony model, w którym zaniedbujemy efekty tłumienia drgań belki
oraz zakładamy małą amplitudę drgań i mały gradient siły wzdłuż kierunku z wykaż, że zmiana
częstości drgań belki w wyniku oddziaływania z podłożem wyniesie:

Jak wygląda wyrażenie na amplitudę w takim przypadku?

Wskazówka 1: Brak tłumienia oznacza, że belka drgająca w dużej odległości od powierzchni zachowuje się jak

jednowymiarowy oscylator swobodny o częstości

(k

0

oznacza stałą sprężystości belki, a m jej masę), a

blisko powierzchni jak oscylator wymuszony z siłą wymuszającą F(z) (znajomość jawnej postaci siły nie jest
konieczna w tych rozważaniach).

Wskazówka 2: W rozważanym przypadku wygodnie jest przyjąć rozwiązanie równania oscylatora swobodnego
w postaci z(t) = Asin(ω

0

t + ϕ), wyznaczając A i ϕ z warunków początkowych z(0) = a i z’(0) = v

0

. Takie same

warunki początkowe należy przyjąć w sytuacji, gdy mamy do czynienia z siłą wymuszającą.

Wskazówka 3: Założenie małych amplitud pozwala uprościć równanie z siłą wymuszającą, a założenie małych
gradientów konieczne jest, by otrzymać ostateczny wynik.

Zadanie 3 - mikroskopia sondy skanującej STM vs. ncAFM

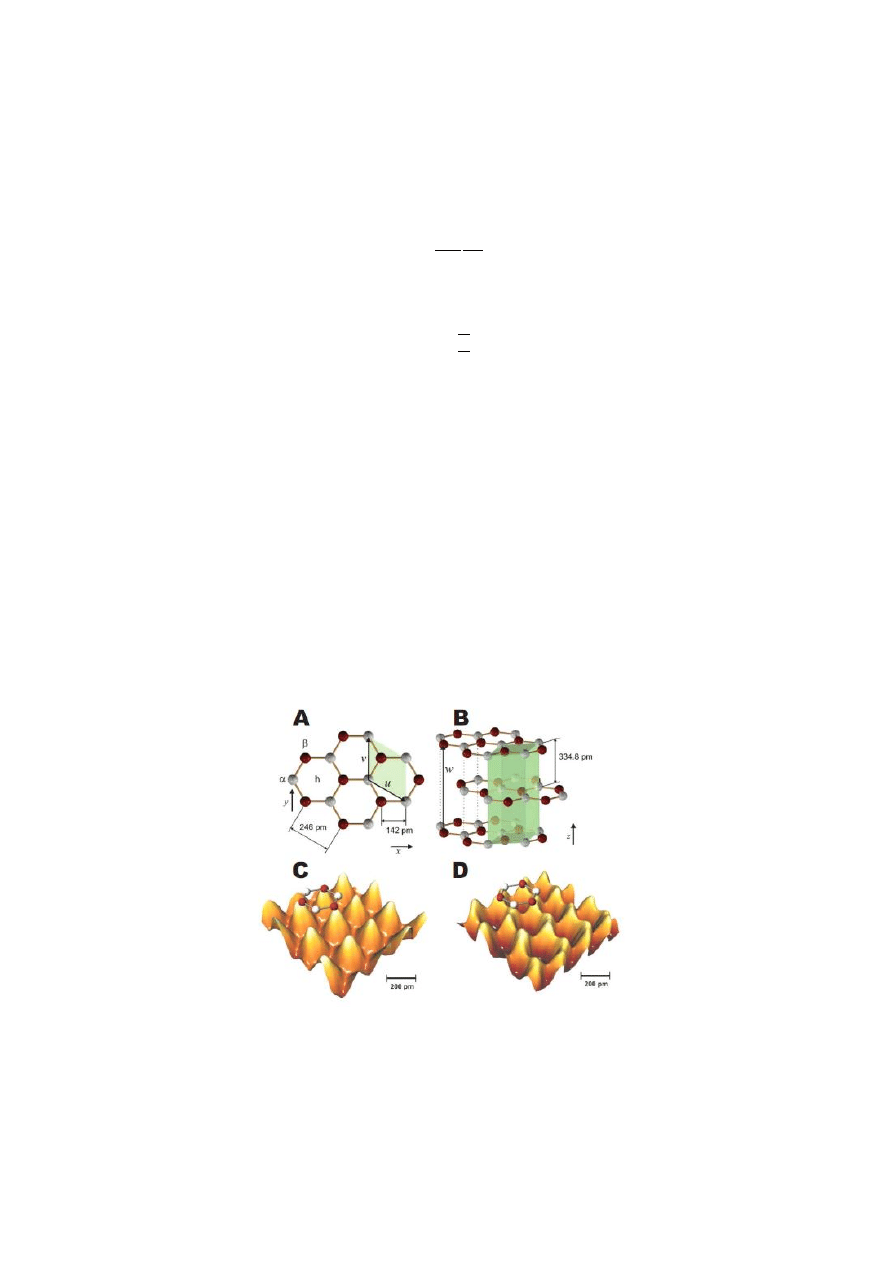
Na rysunku 2 przedstawiona jest struktura krystaliczna grafitu oraz wizualizacja 3D obrazów
powierzchni grafitu (HOPG - z ang. highly oriented pyrolytic graphite) otrzymanych mikroskopem
sondy skanującej pracującym w trybach STM i ncAFM. Proszę rozstrzygnąć, który z obrazów (C) czy
(D) został zebrany mikroskopem STM, a który ncAFM. Jaka jest przyczyna widocznej różnicy?

Wskazówka 1: Warto rozważyć konfigurację elektronową oraz hybrydyzację atomów węgla w graficie.

Wskazówka 2: Warto zajrzeć do pracy Hembacher et al., PNAS 100, 12541 (2003) - z komputerów w Instytucie
powinien być dostęp do czasopisma PNAS (Proceedings of the National Academy of Sciences).

Szymon Godlewski