Podstawy obliczeń
i rachunek współrzędnych

wykłady z przedmiotu
„Geodezja i kartografia”

Dr hab. inż. Andrzej Kobryń

Formy rachunkowe Hausbrandta



Podstawowym pojęciem w symbolice Hausbrandta jest

forma

rachunkowa prosta

(czteroelementowy zbiór liczb ujętych w

prostokątną tabelę:

Forma rachunkowa jest jedynie sposobem zapisu i nie określa
żadnych działań matematycznych.

Działania takie są możliwe jedynie po ustaleniu określonej funkcji
rachunkowej.



Forma rachunkowa złożona

składa się z dwóch lub większej ilości

form rachunkowych prostych zapisanych obok siebie np.:

d

c

b

a

f



.....

2

2

2

2

1

1

1

1

n

n

n

n

d

c

b

a

d

c

b

a

d

c

b

a

F



Funkcje form rachunkowych



Funkcja pierwsza (iloczyn wyznacznikowy) jest to suma
wyznaczników drugiego stopnia obliczonych z poszczególnych
form rachunkowych prostych:



Funkcja druga (iloczyn kolumnowy

) jest to suma iloczynów par

elementów znajdujących się w poszczególnych kolumnach formy
rachunkowej:



























i

i

i

i

n

n

n

n

c

b

d

a

c

b

d

a

c

b

d

a

c

b

d

a

F

...

2

2

2

2

1

1

1

1

1



























i

i

i

i

n

n

n

n

d

b

c

a

d

b

c

a

d

b

c

a

d

b

c

a

F

...

2

2

2

2

1

1

1

1

2

Funkcje form rachunkowych (c.d.)



Funkcja zerowa (

iloraz główny) jest to stosunek funkcji pierwszej

do drugiej:



Funkcje względne proste stanowią ilorazy funkcji pierwszej lub
drugiej przez sumę elementów dolnego lub górnego wiersza
formy rachunkowej.

W zależności od tego, który wiersz podlega sumowaniu, symbol
funkcji (1) lub (2) umieszcza się u dołu lub u góry symbolu formy:

2

1

0

F

F

F



)

(

;

)

(

;

)

(

;

)

(

2

(2)

1

)

1

(

2

)

2

(

1

)

1

(

i

i

i

i

i

i

i

i

b

a

F

F

b

a

F

F

d

c

F

F

d

c

F

F

























Funkcje form rachunkowych (c.d.)



Funkcje względne kwadratowe są ilorazami funkcji pierwszej lub
drugiej przez sumę kwadratów elementów dolnego lub górnego
wiersza formy.

Podobnie jak poprzednio w zależności od tego, czy sumujemy
kwadraty elementów dolnego, czy górnego wiersza, odpowiedni
symbol funkcji

– jedynkę lub dwójkę w nawiasie kwadratowym lub

małym kwadracie – umieszczamy u dołu lub u góry symbolu
formy:

)

(

;

)

(

;

)

(

;

)

(

2

2

2

[2]

2

2

1

]

1

[

2

2

2

]

2

[

2

2

1

]

1

[

i

i

i

i

i

i

i

i

b

a

F

F

b

a

F

F

d

c

F

F

d

c

F

F

























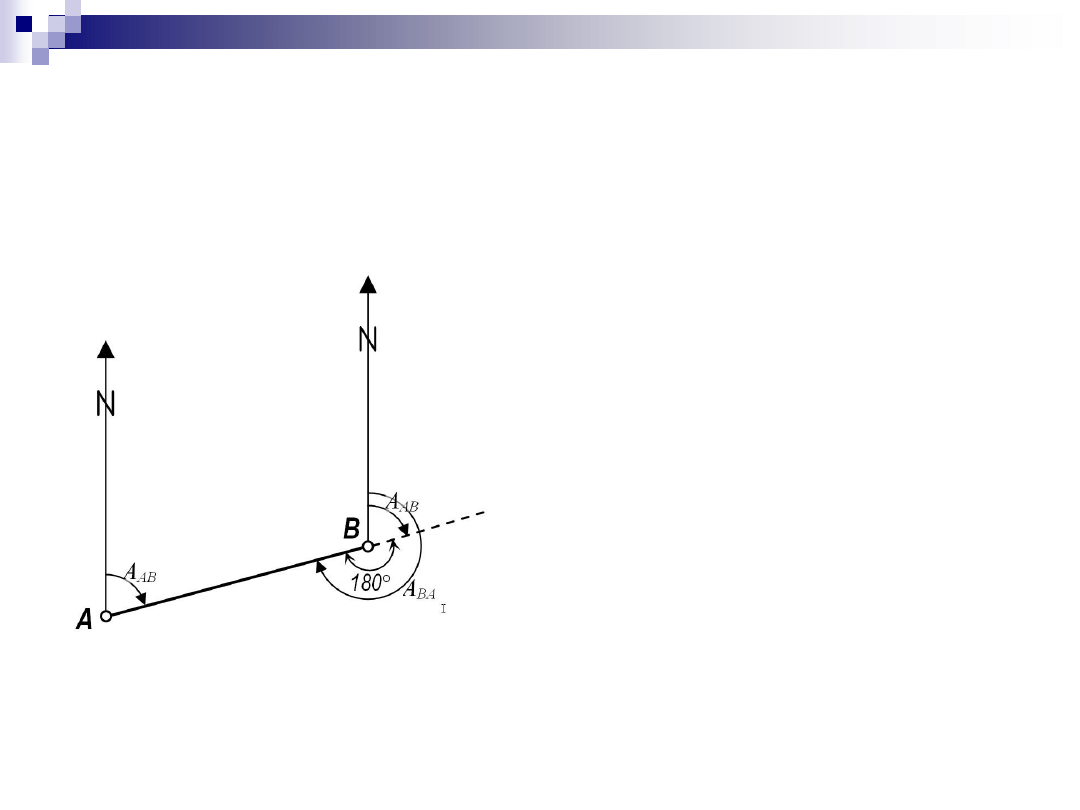
Orientacja pomiarów geodezyjnych



Azymut A

AB

boku AB:

kąt poziomy, zawarty w
przedziale od 0 do 400

g

,

pomiędzy kierunkiem północy

wychodzącym z punktu A a
danym bokiem AB, liczony od

kierunku północy w prawo,
czyli zgodnie z ruchem

wskazówek zegara



wyróżnia się kierunki północy:



geograficznej,



topograficznej



magnetycznej

g

AB

BA

A

A

200





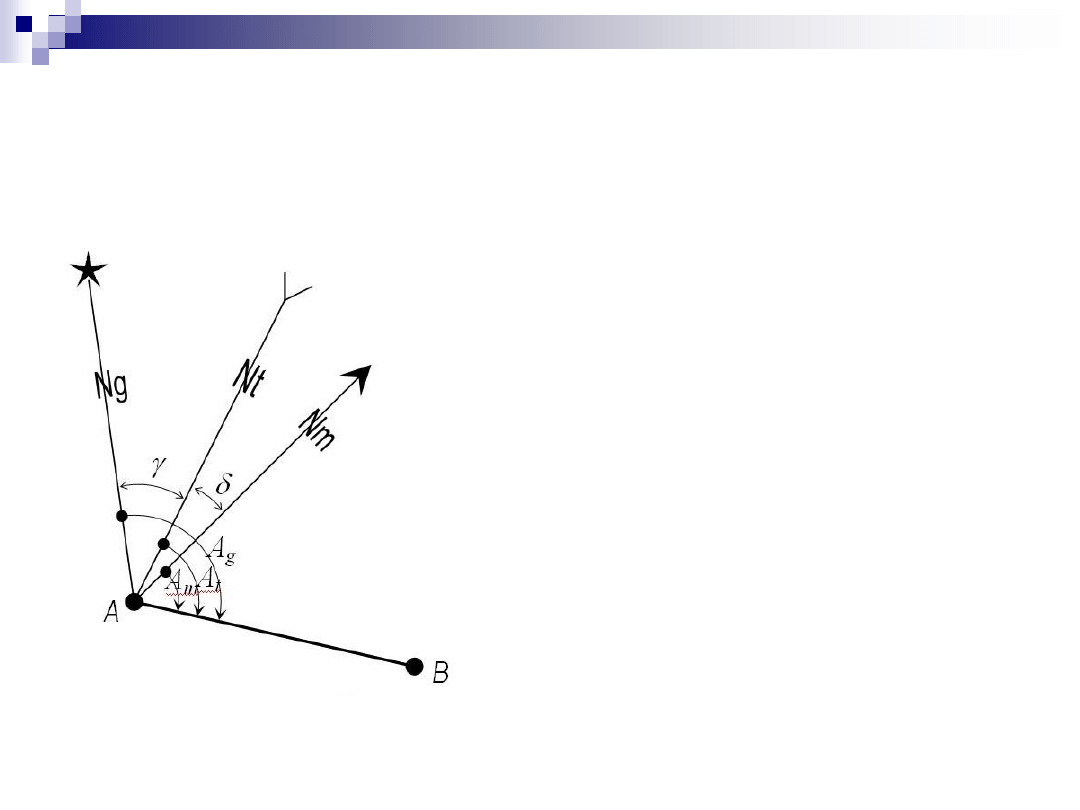
Definicje kierunków północy



geograficzna

(

kierunek północnej części południka

geograficznego, łączącego ten punkt z

geograficznym biegunem północnym
Ziemi)

Wyznaczenie kierunku północy
geograficznej i azymutu przedmiotu

ziemskiego stanowią jedno z

ważniejszych zadań astronomii
geodezyjnej.

Dość dokładnie kierunek ten wskazuje
Gwiazda Polarna (



-Ursae Minoris

)

w

gwiazdozbiorze Małej Niedźwiedzicy.

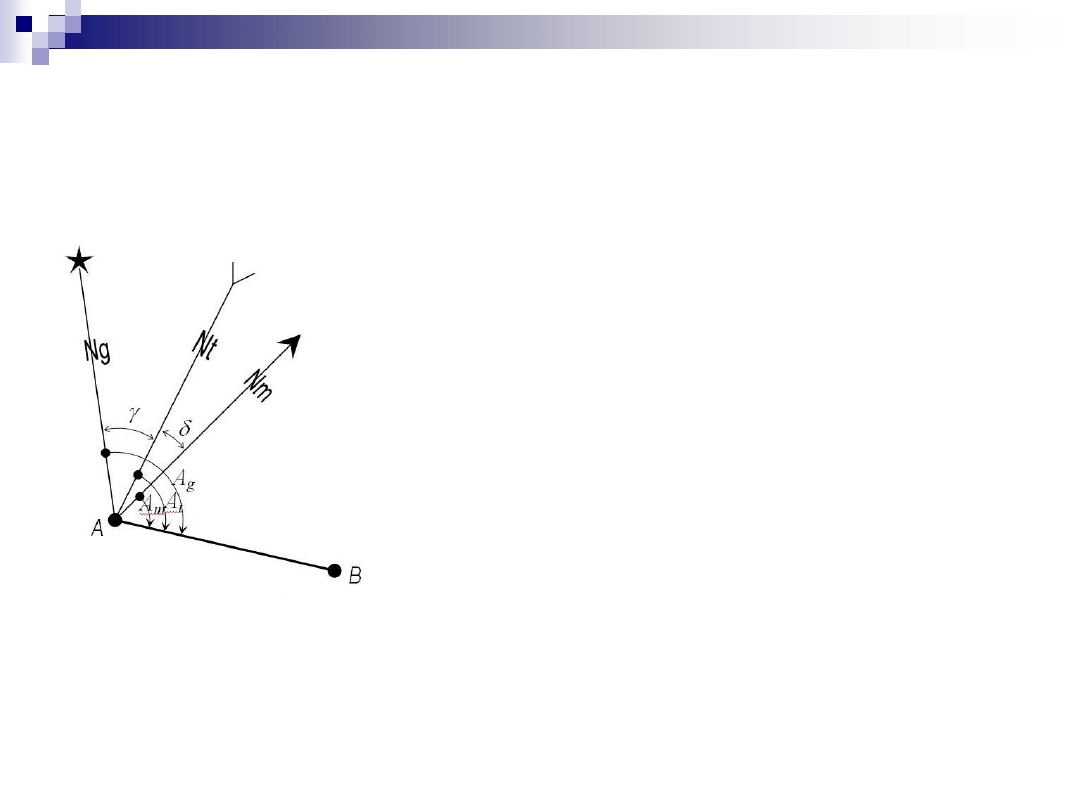
Definicje kierunków północy



topograficzna (kartograficzna)

(ściśle związana z przyjętym odwzorowaniem

kartograficznym oraz z zależnym od niego układem

współrzędnych prostokątnych)

Dodatni kierunek osi x

układu pokrywa się

przeważnie z kierunkiem północy geograficznej

(południka geograficznego).

Dla punktów znajdujących się poza osią x, kierunek

północy topograficznej stanowi prostą równoległą

do półosi +x.

Południki wyznaczające północ geograficzną w

różnych punktach terenowych nie są jednak

równoległe, lecz zbiegają się w punkcie N –

biegunie północnym Ziemi.

Dlatego odchylenie kierunku północy topograficznej
danego punktu A

od północy geograficznej tego

punktu jest równe kątowi

g

, zwanemu

zbieżnością

południków (rys. 8.2). Dodając kąt

g

do azymutu

topograficznego At, otrzymamy azymut
geograficzny

.



magnetyczna

(

kierunek jest wskazywany przez igłę magnetyczną

busoli, umieszczonej w punkcie początkowym A)

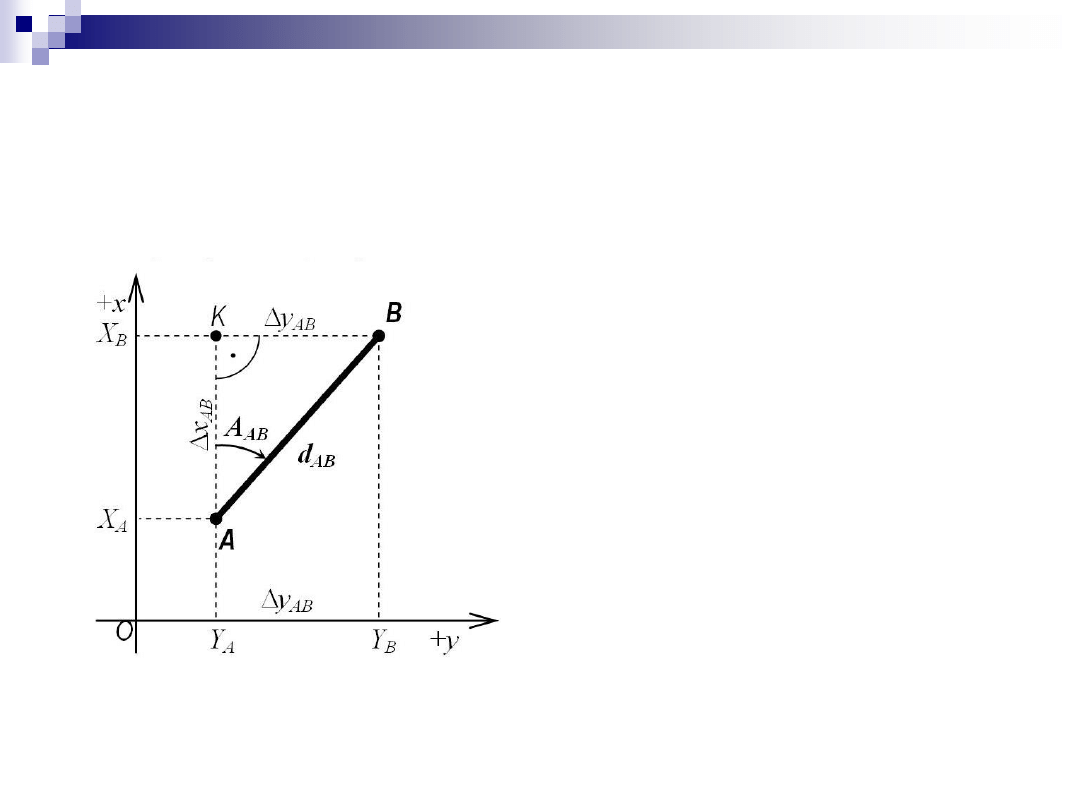
Podstawowe związki

Przyrosty współrzędnych:

czyli:

Współrzędne końca linii:

A

B

AB

A

B

AB

Y

Y

y

X

X

x

Δ

Δ









AB

A

B

AB

A

B

y

Y

Y

x

X

X

Δ

Δ









BA

AB

BA

AB

y

x

x













Δy

Δ

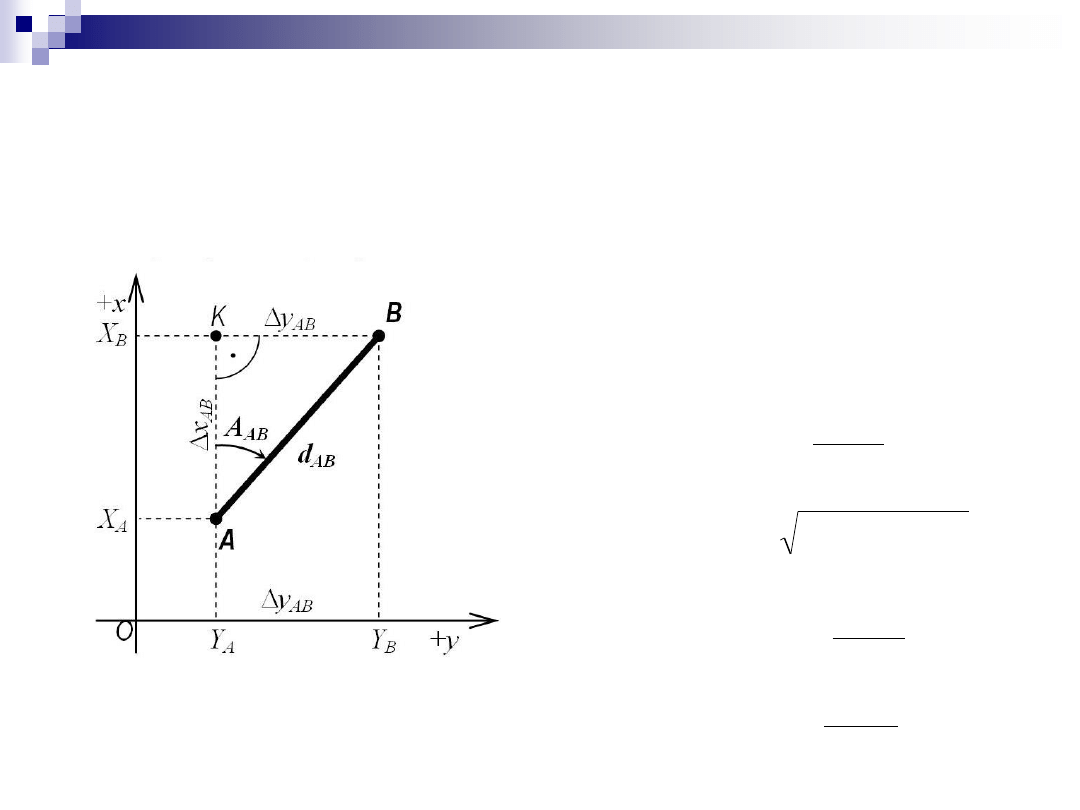
Podstawowe związki (c.d.)



przyrosty współrzędnych



zależności pomocnicze

oraz:

AB

AB

AB

x

y

A







tg

AB

AB

AB

AB

AB

AB

A

d

y

A

d

x

sin

Δ

cos

Δ









AB

AB

AB

AB

AB

AB

d

y

A

d

x

A

Δ

sin

Δ

cos





2

2

AB

AB

AB

y

x

d









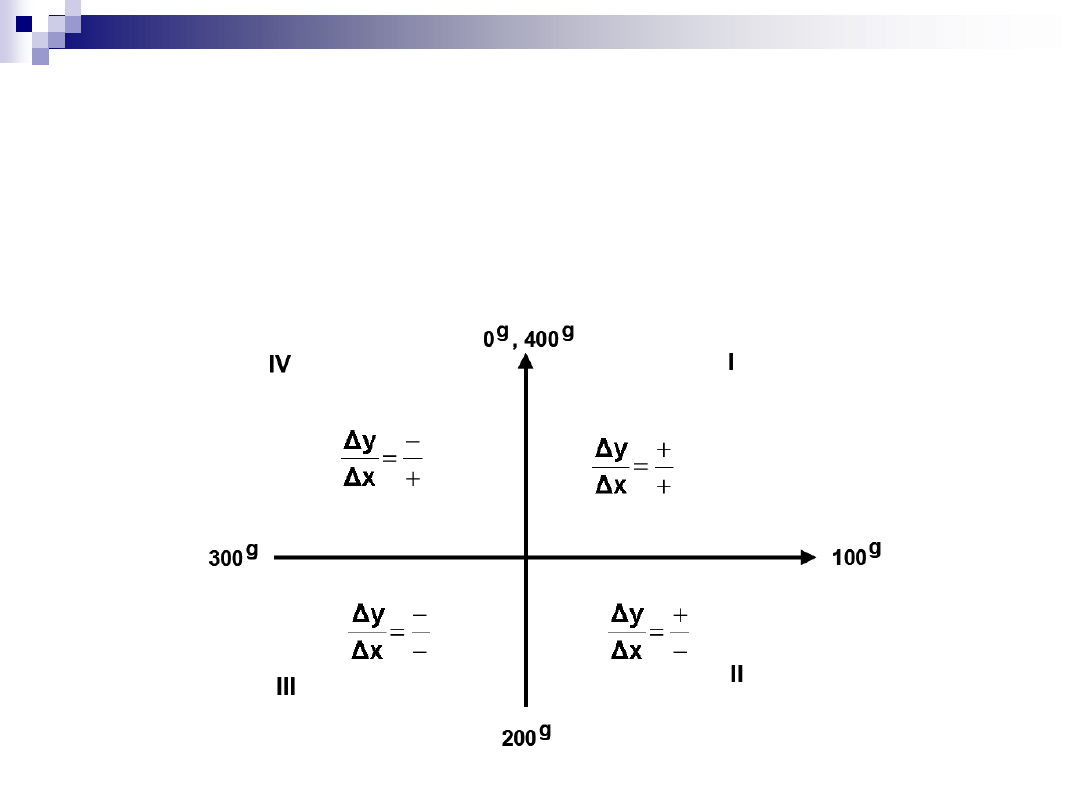
Znaki przyrostów współrzędnych



znaki przyrostów współrzędnych są zależne od położenia końca linii
względem lokalnego układu współrzędnych z początkiem
znajdującym się w punkcie początkowym linii

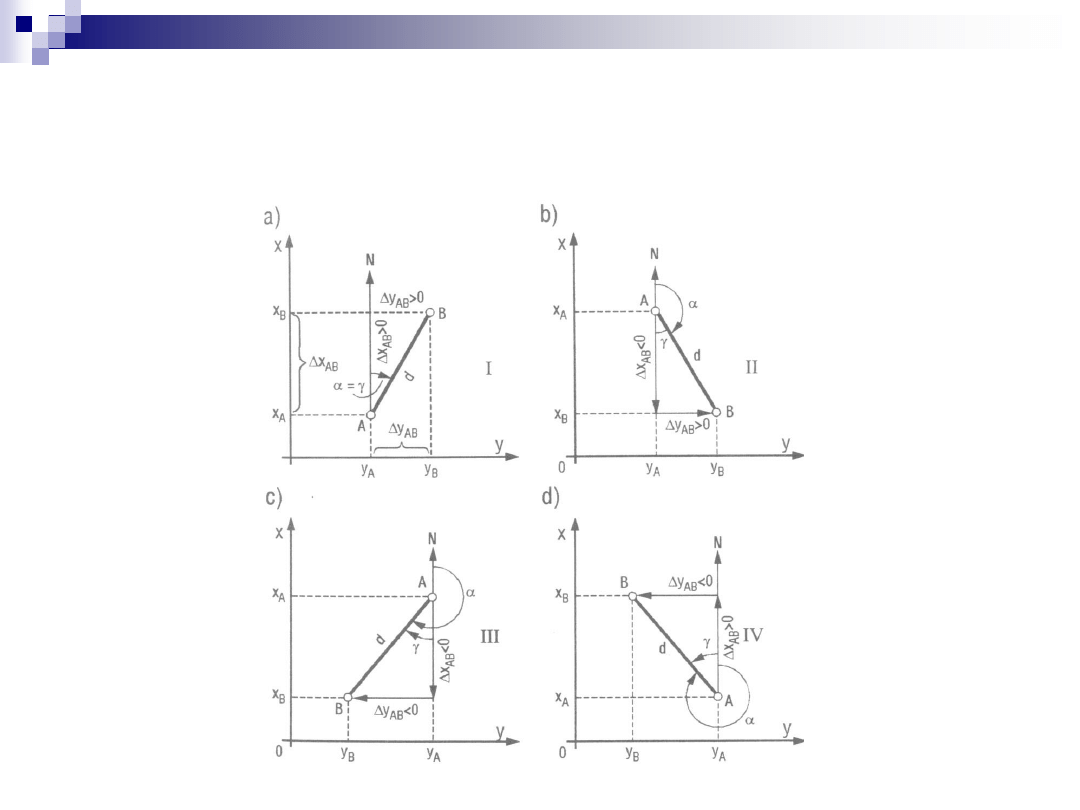
Znaki przyrostów współrzędnych (c.d.)

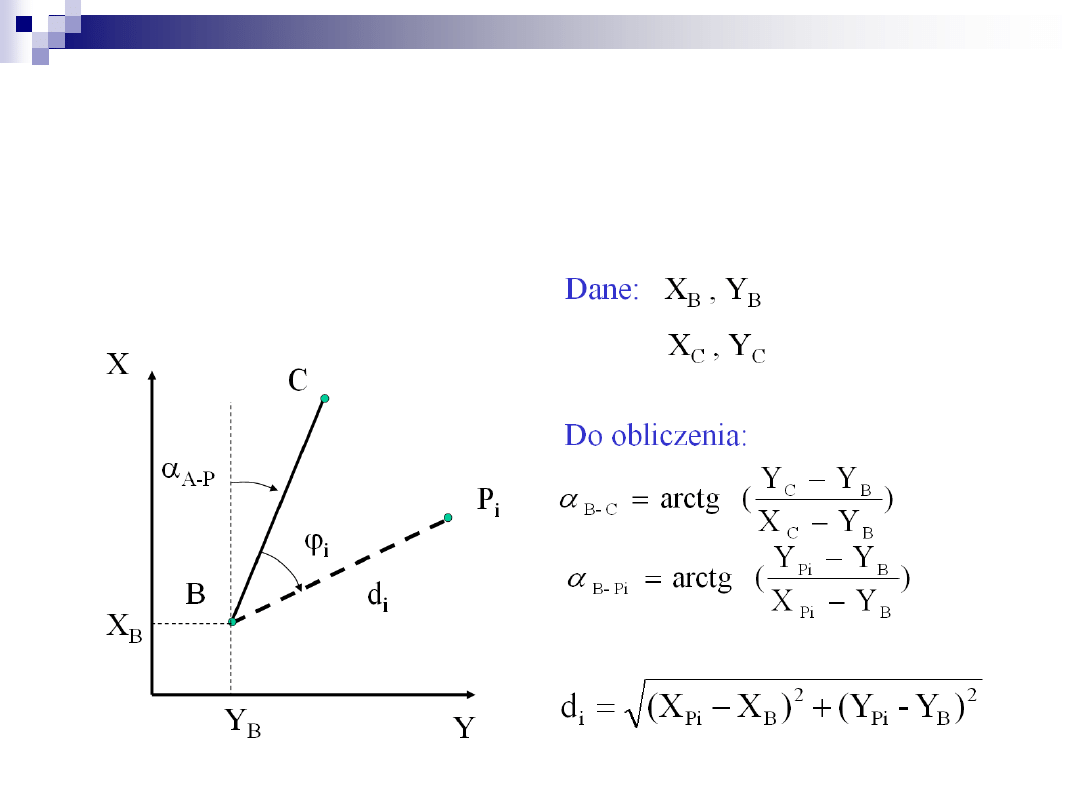
Obliczenie azymutu i długości linii
ze współrzędnych

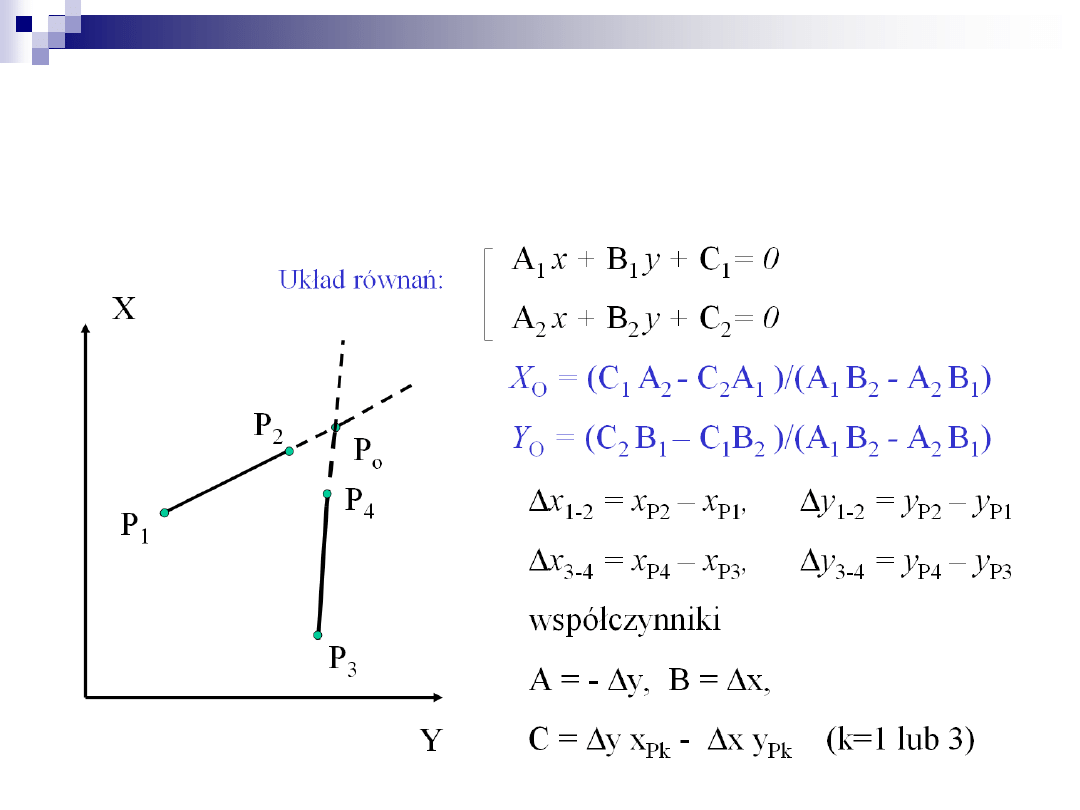
Obliczenie punktu przecięcia dwóch
prostych

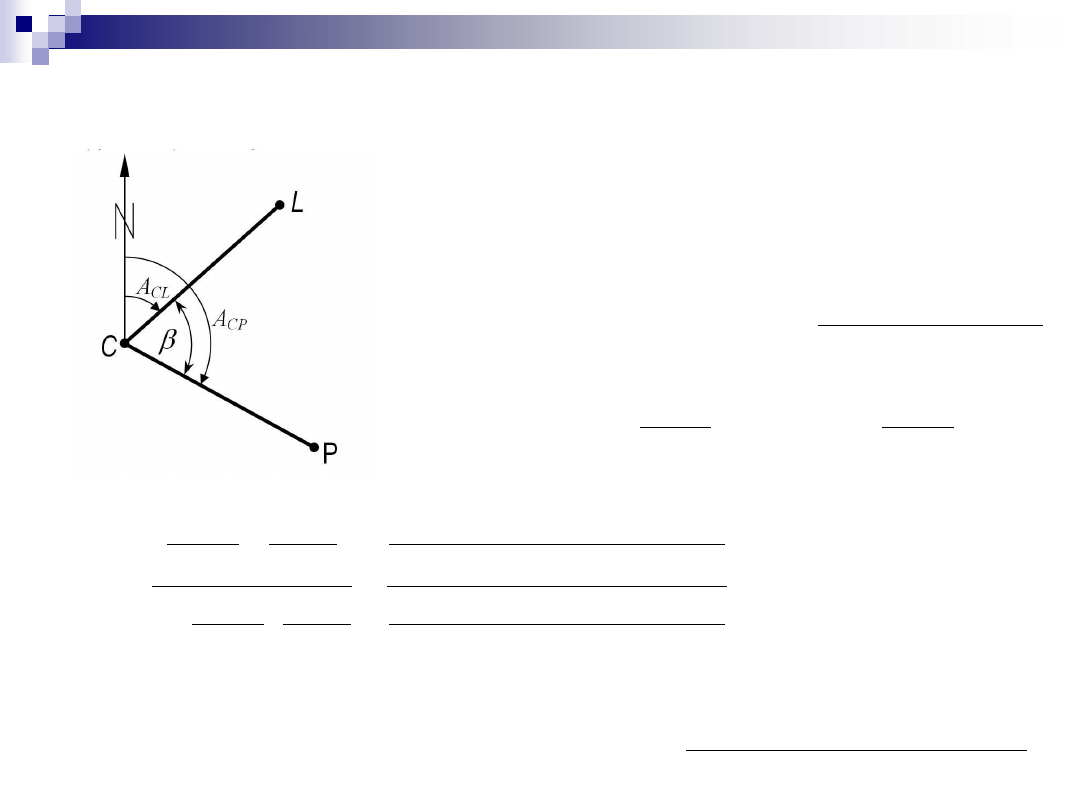
Obliczenie kąta ze współrzędnych



I sposób



II sposób

czyli:

CL

CP

A

A











tg

tg

1

tg

tg

tg

tg

CL

CP

CL

CP

CL

CP

A

A

A

A

A

A















CP

CP

CP

CP

CL

CL

x

y

A

x

y

A













tg

;

tg

CP

CL

CP

CL

CP

CL

CP

CL

CP

CL

CP

CL

CL

CL

CP

CP

CL

CL

CP

CP

x

x

y

y

x

x

x

x

x

y

y

x

x

y

x

y

x

y

x

y



































































1

tg



CP

CL

CP

CL

CL

CP

CP

CL

y

y

x

x

y

x

y

x

































tg

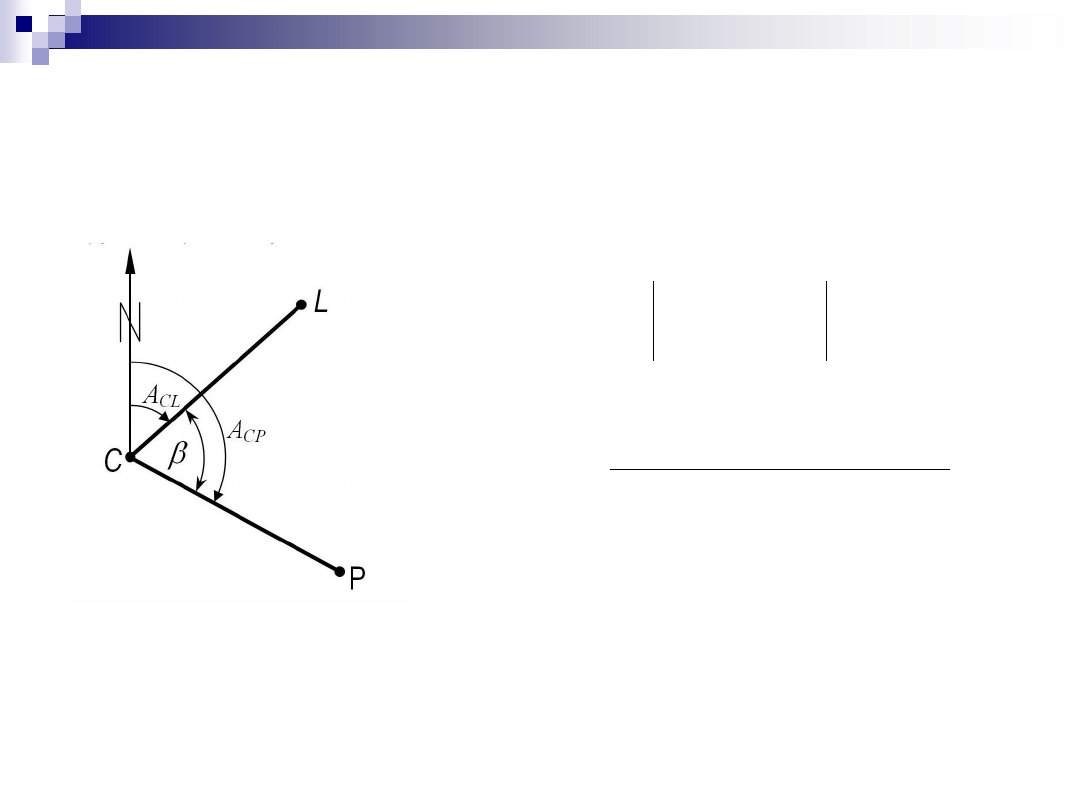
Obliczenie kąta ze współrzędnych
z użyciem form Hausbrandta



wzory obliczeniowe

czyli:

CP

CL

CP

CL

CL

CP

CP

CL

y

y

x

x

y

x

y

x

































tg

0

tg

CP

CP

CL

CL

y

x

y

x













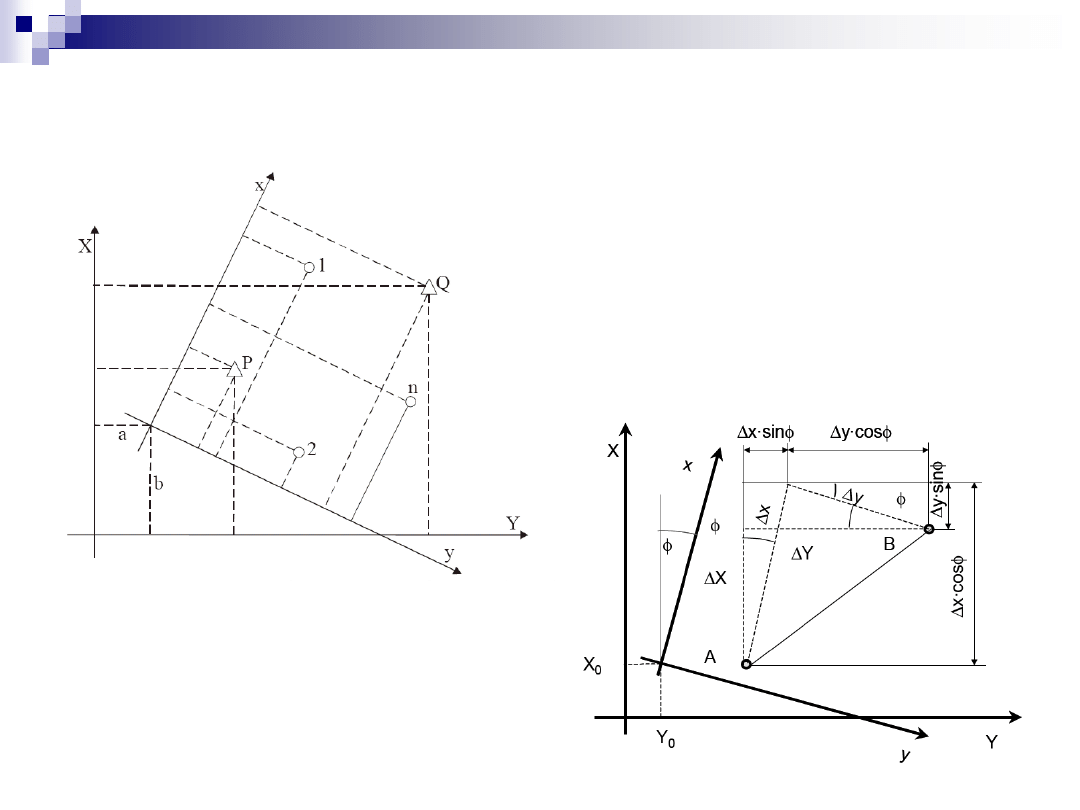
Transformacja współrzędnych

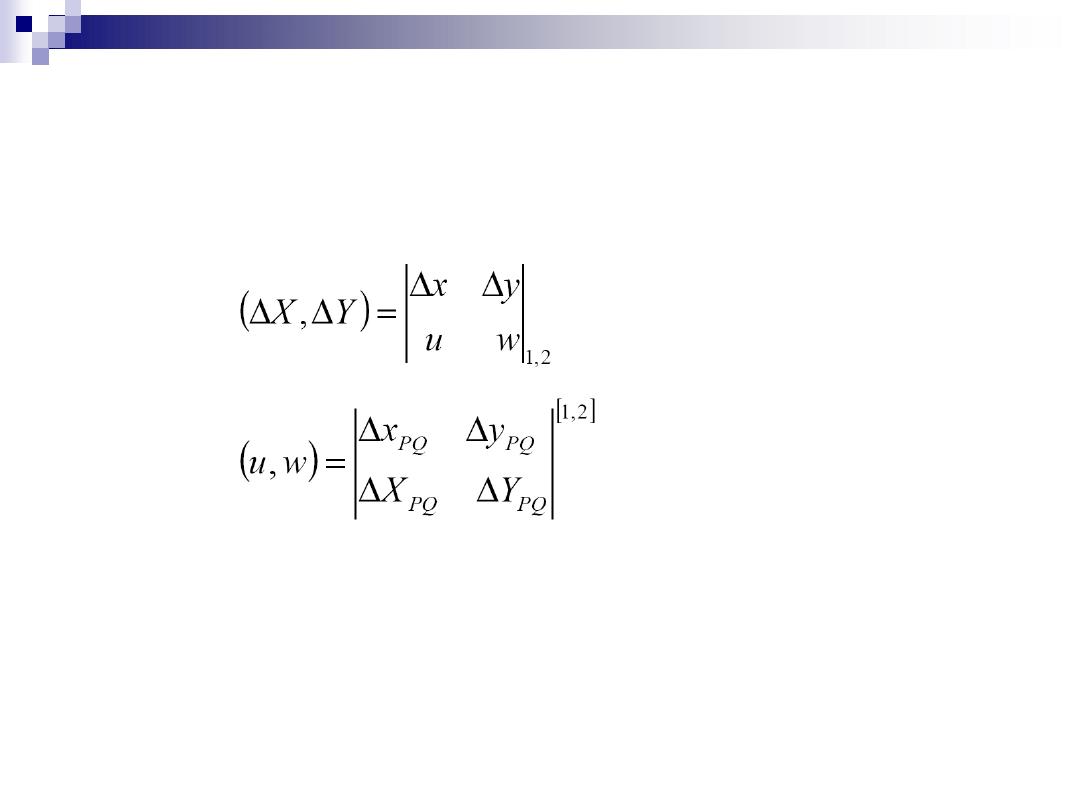
Transformacja współrzędnych (c.d.)



wzory transformacyjne (w ujęciu Hausbrandta)



kontrola obliczeń – za pomocą pierwszego wzoru dla różnic
współrzędnych między punktami dostosowania P i Q

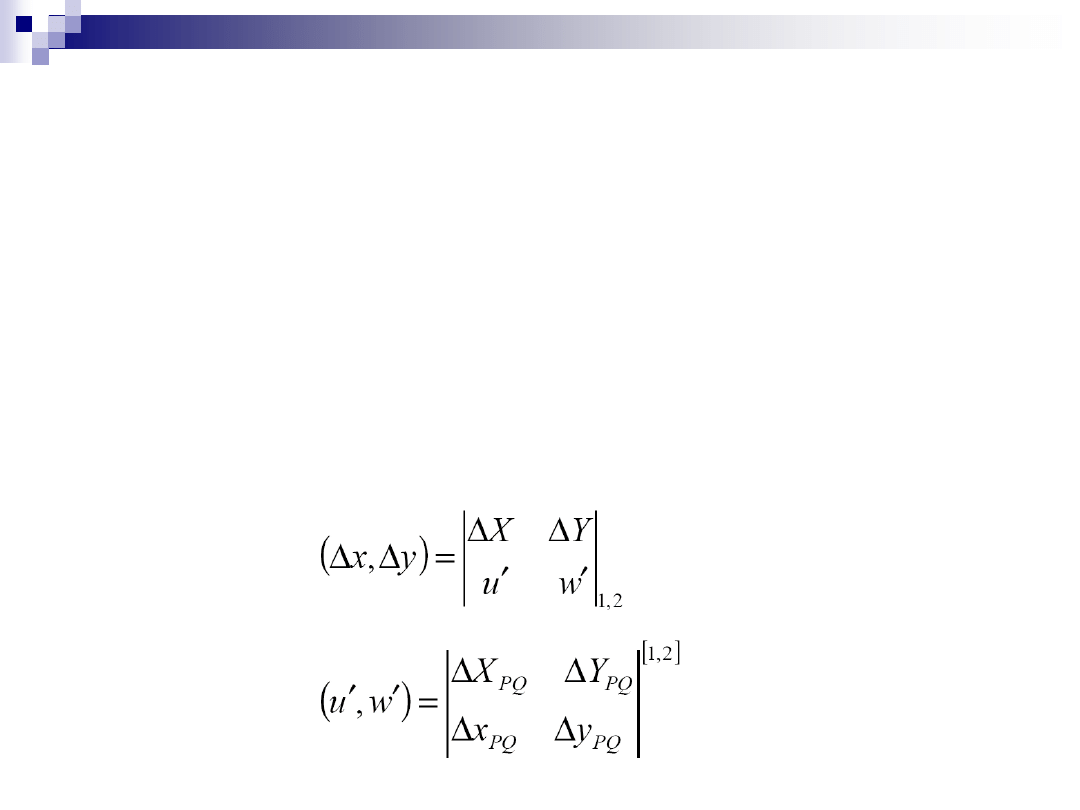
Transformacja współrzędnych (c.d.)

Tok obliczeń:



obliczenie współczynników u oraz v



przeliczenie współrzędnych



x i



y na



X i



Y



obliczenie współrzędnych wszystkich punktów w układzie XY

(za pomocą metody poligonowej)



kontrola obliczeń



m.in. przez transformację z układu wtórnego na układ pierwotny

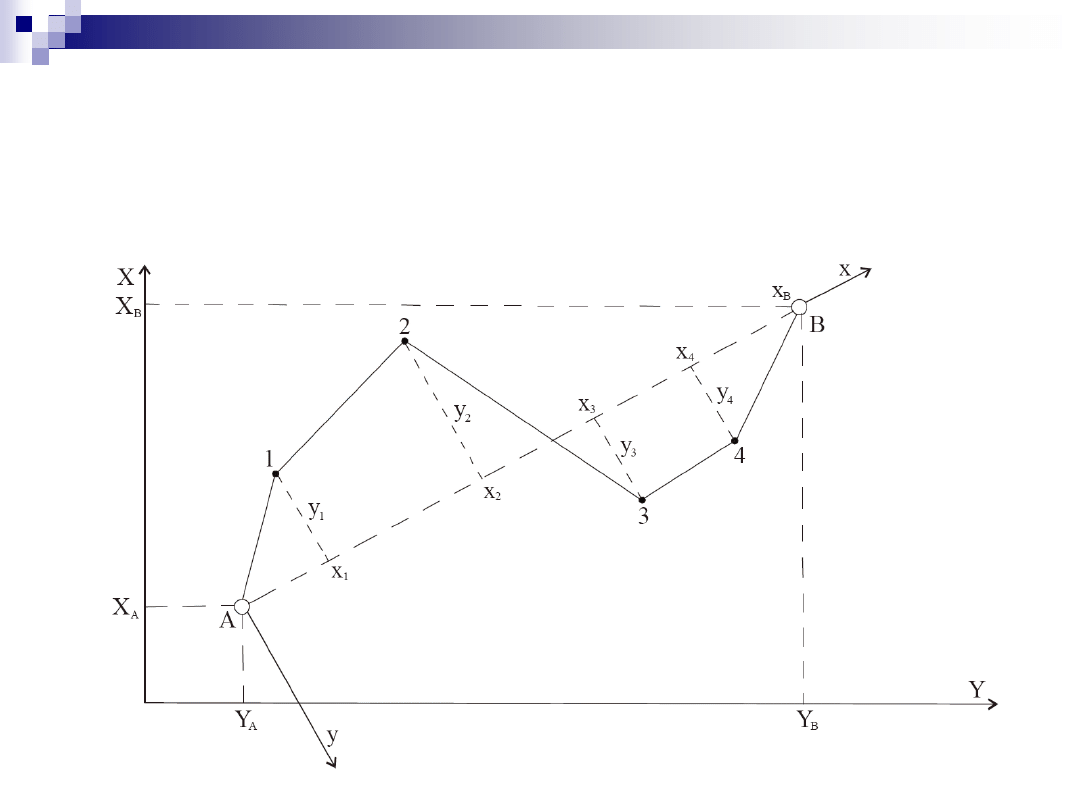
Transformacja współrzędnych (c.d.)



poligon wyznaczający kolejność obliczeń transformowanych
współrzędnych punktów

Transformacja z wykorzystaniem
wzoru macierzowego

Transformacja z wykorzystaniem
wzoru macierzowego (c.d.)



współczynnik

zmiany

skali



kąt skrętu

Transformacja sposobem Helmerta



tzw. transformacja 4-parametrowa



ma zastosowanie, jeśli liczba punktów

dostosowania jest większa od 2



polega na wyrównaniu metoda najmniejszych

kwadratów różnic v

x

i v

y

między znanymi

współrzędnymi punktów dostosowania (X, Y) a

ich współrzędnymi po transformacji (X

t

, Y

t

)



warunek



v

p

2

=



(v

x

2

+v

y

2

) = minimum

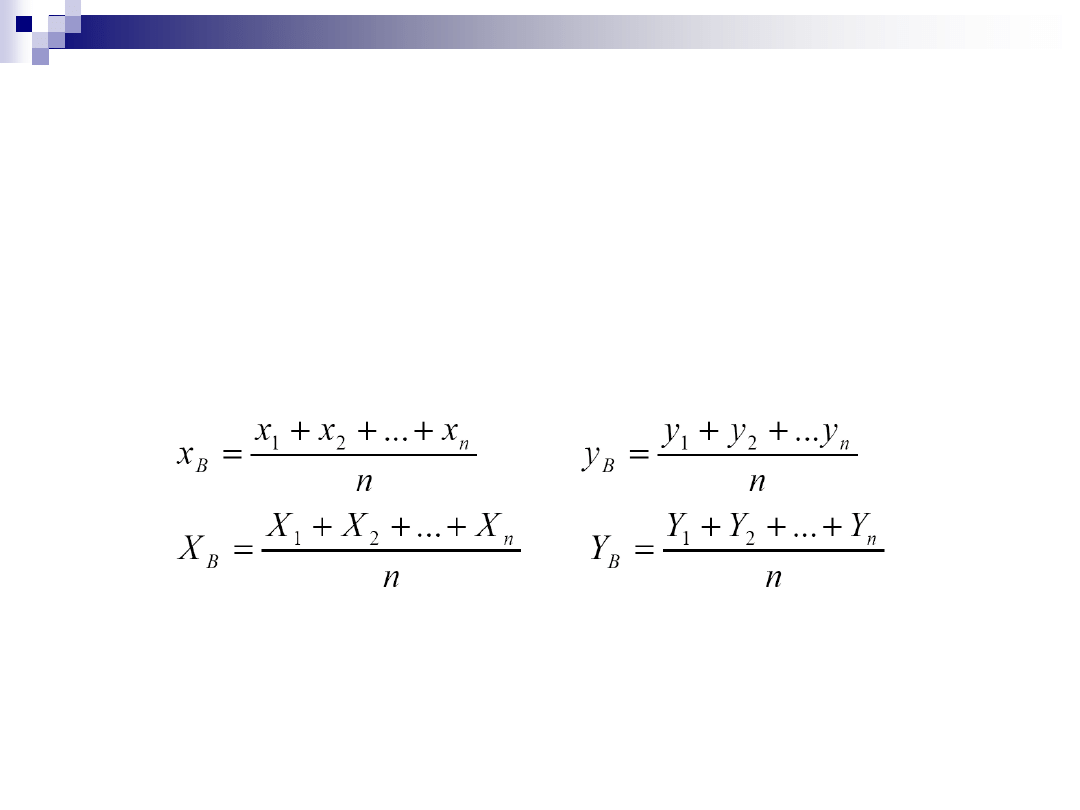
Transformacja sposobem Helmerta
– procedura obliczeniowa



obliczenie współrzędnych bieguna B przekształcenia

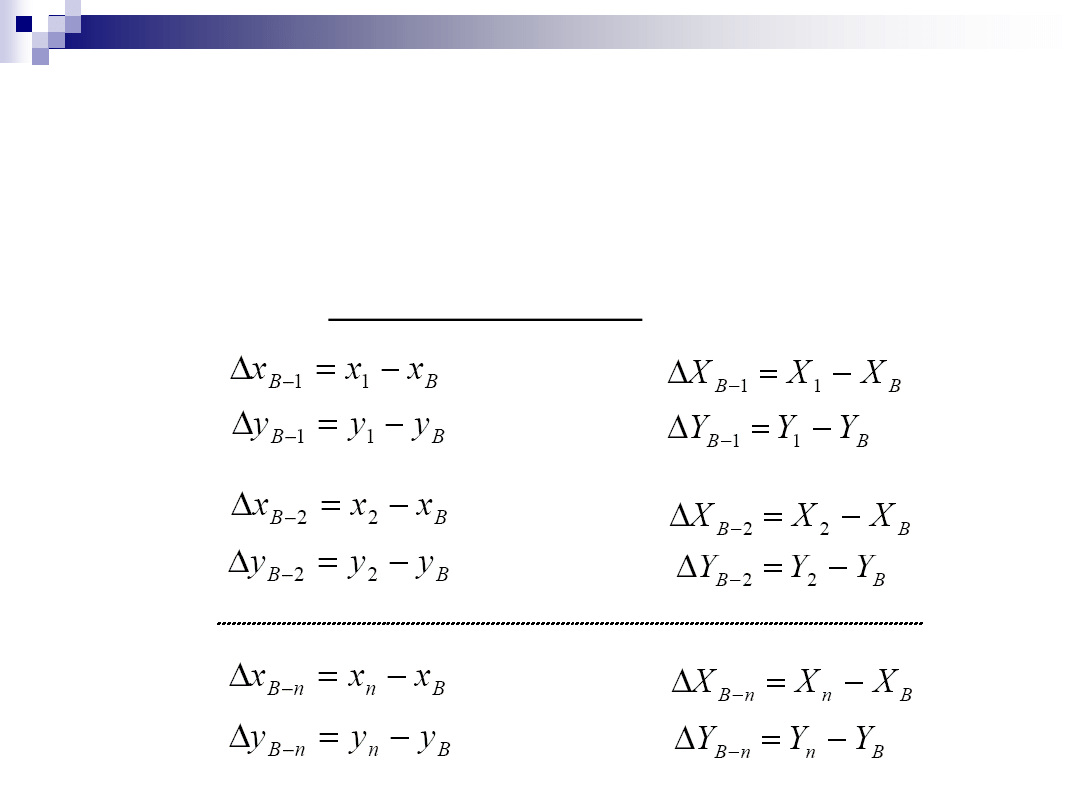
Transformacja sposobem Helmerta
– procedura obliczeniowa (c.d.)



obliczenie w obu układach przyrostów współrzędnych między

poszczególnymi punktami dostosowania a biegunem

Transformacja sposobem Helmerta
– procedura obliczeniowa (c.d.)



zestawienie formy rachunkowej i obliczenie współczynników

przekształcenia



obliczenie

w układzie pierwotnym przyrostów między

poszczególnymi parami sąsiednich punktów (rozpoczynając i

kończąc na biegunie) => suma przyrostów = 0

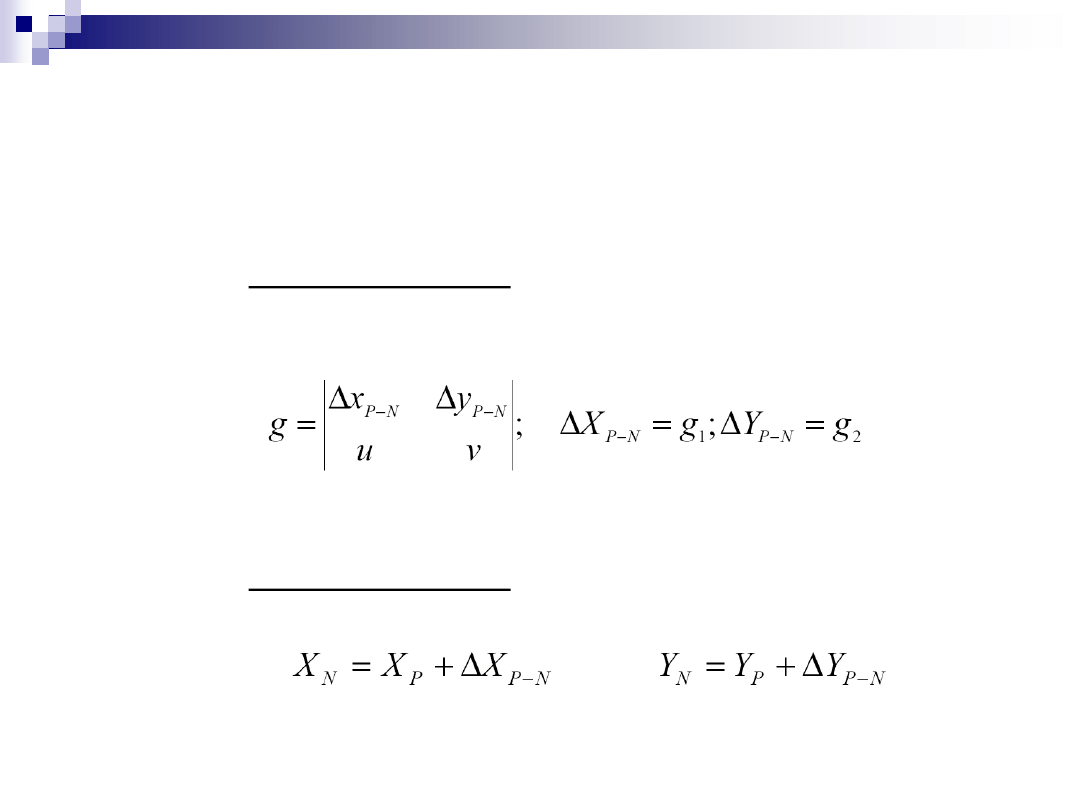
Transformacja sposobem Helmerta
– procedura obliczeniowa (c.d.)



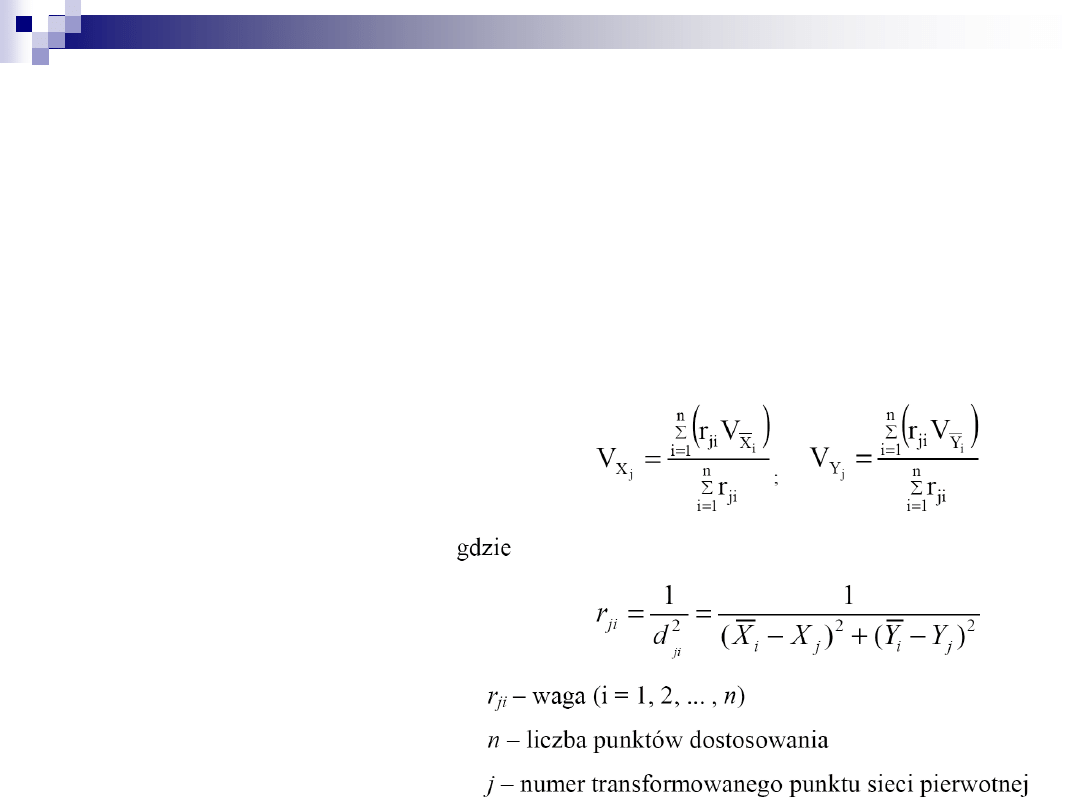
obliczenie

w układzie wtórnym przyrostów między poszczególnymi

parami sąsiednich punktów (ciąg rozpoczynający się i kończący na

biegunie) => suma przyrostów = 0



obliczenie

w układzie wtórnym współrzędnych wszystkich punktów

Transformacja sposobem Helmerta

– inne kwestie



problem wyboru współrzędnych punktów dostosowania (podwójne

wartości – przed i po transformacji)



zwykle pozostawia się współrzędne pierwotne



skutek -

deformacja sieci przetransformowanych punktów



w celu minimalizacji tych deformacji

– tzw. poprawki Hausbrandta

do współrzędnych pierwotnych wszystkich punktów (z wyjątkiem

punktów dostosowania)

Transformacja sposobem Helmerta

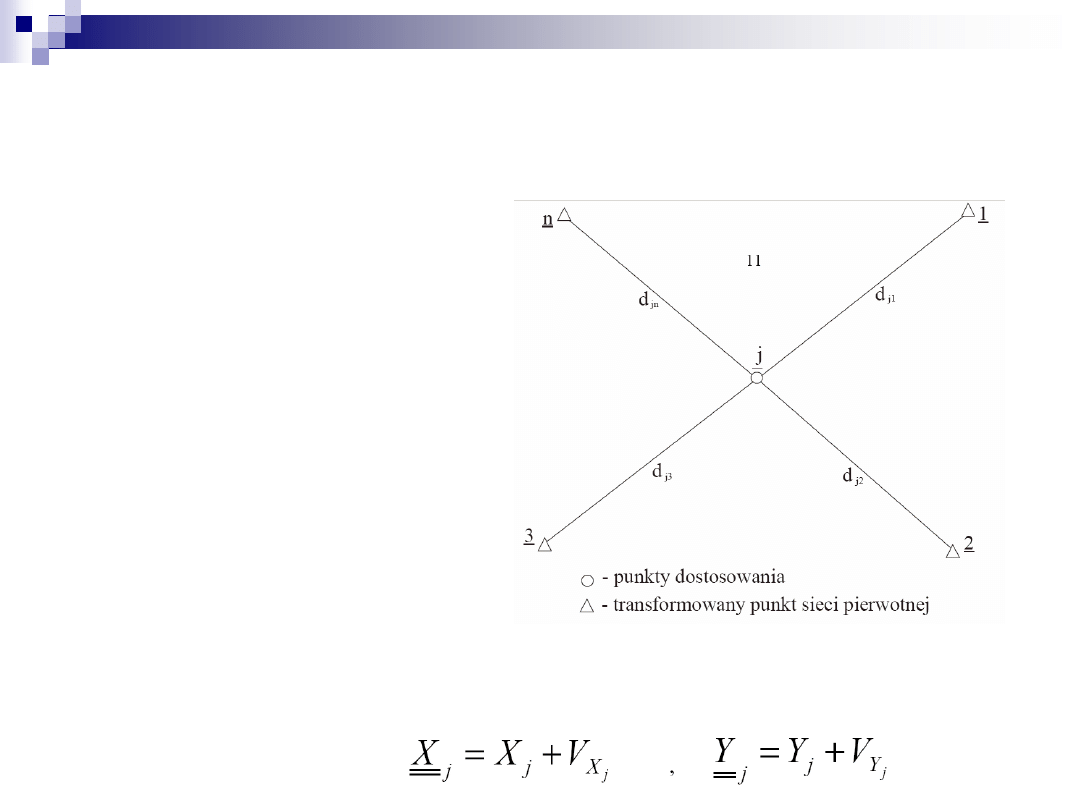
– inne kwestie (c.d.)



ilustracja obliczania wag



ostateczne wartości współrzędnych transformowanych punktów

sieci pierwotnej (z pominięciem punktów dostosowania)