38

Joule’s 1845 Experiment

The total energy of the universe is constant; the total entropy is continually
increasing. (Rudolf Clausius)

I know that most men, including those at ease with problems of the highest
complexity, can seldom accept even the simplest and most obvious truth if
it be such as would oblige them to admit the falsity of conclusions which
they have delighted in explaining to colleagues, which they have proudly
taught to others, and which they have woven, thread by thread, into the
fabric of their lives. (Tolstoy)

38.1 The Experiment

For illustration, we recall Joule’s experiment [105] from 1845 with a gas
initially at rest with temperature T = 1 at a certain pressure in a certain
volume immersed into a container of water, see Fig. 38.1. At initial time a
valve was opened and the gas was allowed to expand into the double volume
while the temperature change in the water was carefully measured by Joule.
To the great surprise of both Joule and the scientific community, no change
in the temperature of the water could be detected, in contradiction with the
expectation that the gas would cool off under expansion. Moreover, the ex-
pansion was impossible to reverse; the gas had no inclination to contract back
to the original volume.

We now simulate Joule’s experiment using an EG2 model where the two

volumes are connected by a small channel which is opened at t = 0. At initial
time t = 0 the gas is at rest with density ρ = 1 in the left container and
ρ = 0.1 in the right container, and the temperature T = 1 in both containers.
The difference in density causes the gas to flow from the left to the right
container for t > 0.

Results from the EG2 computation are displayed in Fig. 38.1–38.3, where

we discover the following scenario: The mean temperature in the left container
drops below 1 as the gas expands into the right container with increasing

352

38 Joule’s 1845 Experiment

velocity, and shocks/turbulence appearing which heat the gas in the right
container, increasing the mean temperature in the right container. The total
energy is, of course, conserved by the 1st Law, and in the final state with the
gas at rest in the two containers, corresponding to zero kinetic energy, the
temperature is back to T = 1. We can also understand that the rapidity of
the expansion process makes it difficult to detect any temperature drop in the
water in the initial phase.

Altogether, using EG2 we can first simulate and then understand Joule’s

experiment, and we thus see no reason to be surprised. We shall see below
as a consequence of the 2nd Law that reversal of the process with the gas
contracting back to the original small volume, is impossible because the only
way the gas can be put into motion is by expansion, and thus contraction is
impossible.

Fig. 38.1. The Joule-Thomson experiment

We now compare with an analysis of the experiment using classical ther-

modynamics based on statistical mechanics. We then recall that classical ther-
modynamics only considers systems in equilibrium, that is we start with the
gas at rest in the initial volume and we end up with the gas at rest in the
double volume. By energy conservation, we understand that the temperature
cannot change, so Joule’s observation is after all not surprising even with a
classical perspective. But how can we explain the irreversibility? Well, the
basic idea of classical thermodynamics is to say that there is something, the
entropy, which has increased from initial to final state. Boltzmann would say
that because the volume of the final state is larger, the final state is “less or-
dered” or “more probable”, and this would make the reverse process with the
gas contracting back to the initial small volume, if not completely impossible,
so at least very improbable. Of course, from a scientific point of view this is

38.1 The Experiment

353

Fig. 38.2. EG2 simulation of the Joule-Thomson experiment: snapshots of density
(upper 2 figures) and temperature (lower 2 figures) at 2 different time instants.

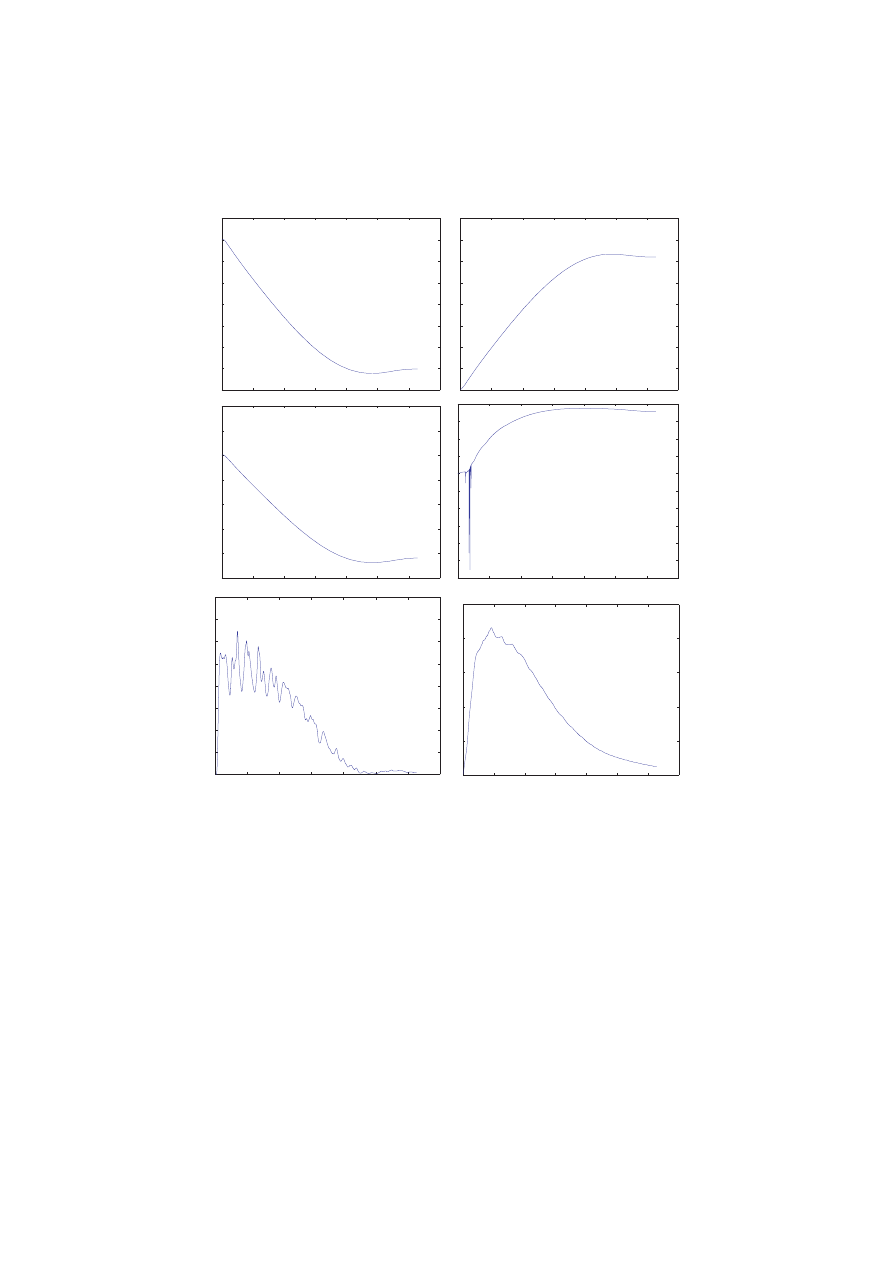
354

38 Joule’s 1845 Experiment

0

5

10

15

20

25

30

35

0.65

0.7

0.75

0.8

0.85

0.9

0.95

1

1.05

0

5

10

15

20

25

30

35

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0

5

10

15

20

25

30

35

0.75

0.8

0.85

0.9

0.95

1

1.05

1.1

0

5

10

15

20

25

30

35

0.4

0.5

0.6

0.7

0.8

0.9

1

1.1

1.2

1.3

1.4

0

5

10

15

20

25

30

35

0

1

2

3

4

5

6

7

8

x 10

4

0

5

10

15

20

25

30

35

0

0.005

0.01

0.015

0.02

0.025

Fig. 38.3. The Joule-Thomson experiment: mean density (upper), mean tempera-
ture (middle) and mean kinetic energy (lower), for the left (left) and right chamber
(right) in the initial phase of the EG2 simulation in Fig. 38.1.

not easy to make sense of, and we would still wonder why the gas would be
willing to expand but not contract. To say that expansion is “more probable”
does not explain anything, as far as we can see at least.

Another attempt of classical explanation would be to say that there is

something like the “total amount of temperature”, which has increased from
initial to final state with the increase in volume under constant temperature,
but again the physical significance would be unclear. We are thus led to the
impression that classical thermodynamics lacks a solid scientific foundation,

38.1 The Experiment

355

which is also reflected by the well-know difficulty to learn and teach this
subject.

In contrast, taking the true dynamics of the process into account includ-

ing in particular the heat generation from shocks and/or turbulence, we can
easily intuitively understand the observation of constant temperature and ir-
reversibility in a deterministic fashion without using any concept of entropy
ultimately based on statistics.