1 

STOCHASTYCZNY MODEL STACJI PALIW PŁYNNYCH 

FUNKCJONUJĄCEJ W SYSTEMIE POJAZDÓW  

TRANSPORTU ZBIOROWEGO  

Adam KADZIŃSKI, Bartosz MAJEWSKI 

Politechnika Poznańska 

Instytut Silników Spalinowych i Transportu 

 ul. Piotrowo 3, 60-965 Poznań 

e–mail: adam.kadzinski@put.poznan.pl, bartosz.majewski@op.pl  

 

STRESZCZENIE 

Przedstawiono  system  pojazdów  operatora  transportu  zbiorowego  z  usytuowaną  w  nim  stacją  paliw 

płynnych.  Stację  paliw  płynnych  potraktowano  jako  system  z  losowym  zapotrzebowaniem  na  zasoby 
generowanym w systemie pojazdów. Zaproponowano opis matematyczny procesów zachodzących na styku obu 
systemów.  Zbudowany  model  matematyczny  oprogramowano  i  stworzono  komputerowy  model  symulacyjny. 
Zaprezentowano możliwości aplikacyjne modeli.  

1.  WPROWADZENIE 

Przemieszczanie zbiorowe (masowe) osób lub ładunków wykonywane jest przeważnie 

przez  wyspecjalizowane  przedsiębiorstwa,  wyposażone  w  odpowiedni  tabor  oraz  niezbędną 
bazę  obsługową.  Wymienione  tu  elementy  integrowane  są  w  systemach  transportu 
zbiorowego. 

Badania  takich  systemów  w  warunkach  ich  rzeczywistej  eksploatacji  są  z  reguły 

pracochłonne  i  czasochłonne.  Podejmując  takie  badania,  należy  gruntownie  przeanalizować 
ich  niezbędność,  celowość  i  zakres.  Często  więc  eksperymentowanie  na  rzeczywistych 
systemach zastępuje się badaniami metodami modelowania i symulacji. 

Celem  niniejszej  pracy  jest  budowa  i  prezentacja  modeli  stacji  paliw  płynnych 

znajdujących się w strukturach systemów pojazdów transportu zbiorowego. 

2.  MIEJSCE STACJI PALIW W STRUKTURACH SYSTEMÓW  

LOGISTYCZNYCH 

Niech  system  logistyczny  to  „celowo  zorganizowane  i  zintegrowane – w  obrębie 

danego układu gospodarczego – przepływy materiałów i produktów oraz odpowiadających im 

POLITECHNIKA WARSZAWSKA 

Wydział Transportu 

Polska Akademia Nauk 

Komitet Transportu 

2 

informacji, umożliwiających optymalizację w zarządzaniu łańcuchami dostaw (…) [1]”. Tak 
rozumiany system logistyczny ma swoją  strukturę, którą tworzą podsystemy i ich elementy 
realizujące  postawione  cele.  Podsystemy  systemu  logistycznego  można  wyróżnić  stosując 
m.in. podziały fazowy i funkcjonalny.  

Fazowe  rozgraniczenie  podsystemów  opiera  się  na  kolejnych  etapach  przepływu 

materiałów i występujących tam problemach decyzyjnych [7]. Klasyfikacja fazowa pozwala – 
w  poszczególnych  fazach  przepływu  towaru  –  na  wyodrębnienie  osobnych  ośrodków 
decyzyjnych.  Można  zatem  przyjąć  podział  fazowy  jako  odpowiedni  dla  systemu 
logistycznego  paliw  płynnych,  gdzie  odpowiedzialność  za  poszczególne  etapy  przepływu 
materiałów i decyzji ponoszą konkretne  centra logistyczne, niekoniecznie związane ze sobą 
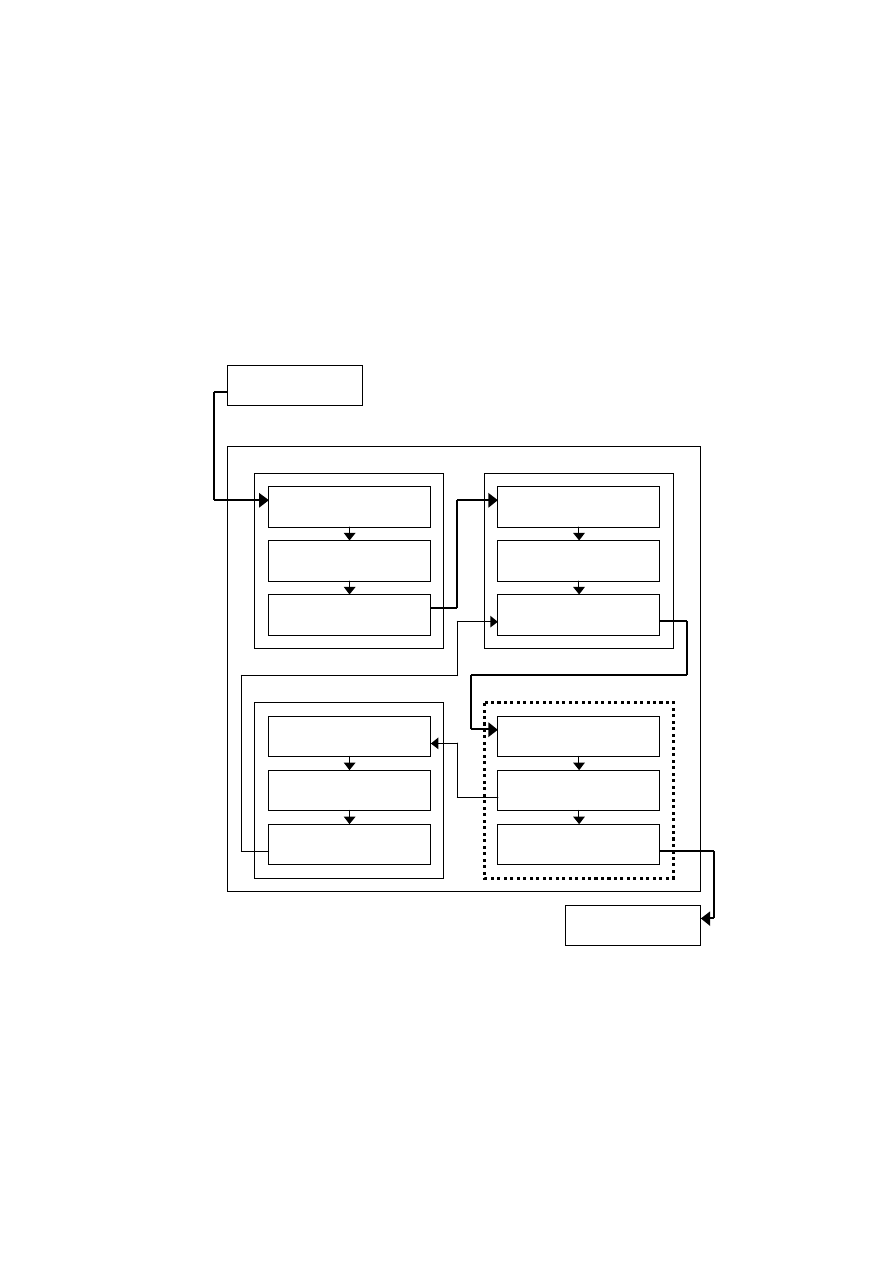
kapitałowo (rys. 1).  

 

Rys. 1.  Ogólny schemat systemu logistycznego paliw płynnych według podziału fazowego, gdzie:  

TK – transport kolejowy, TR – transport rurociągowy, TS – transport samochodowy,  

TM – transport morski (opracowanie własne) 

Funkcjonalne  rozgraniczenie  podsystemów  systemu  logistycznego  skupia  się  na 

funkcjach  spełnianych  przez  poszczególne  podsystemy  w  procesie  przepływu  towarów 
i stosuje  się  je  do  wyróżnienia  elementów  systemu  logistycznego  pojedynczego 
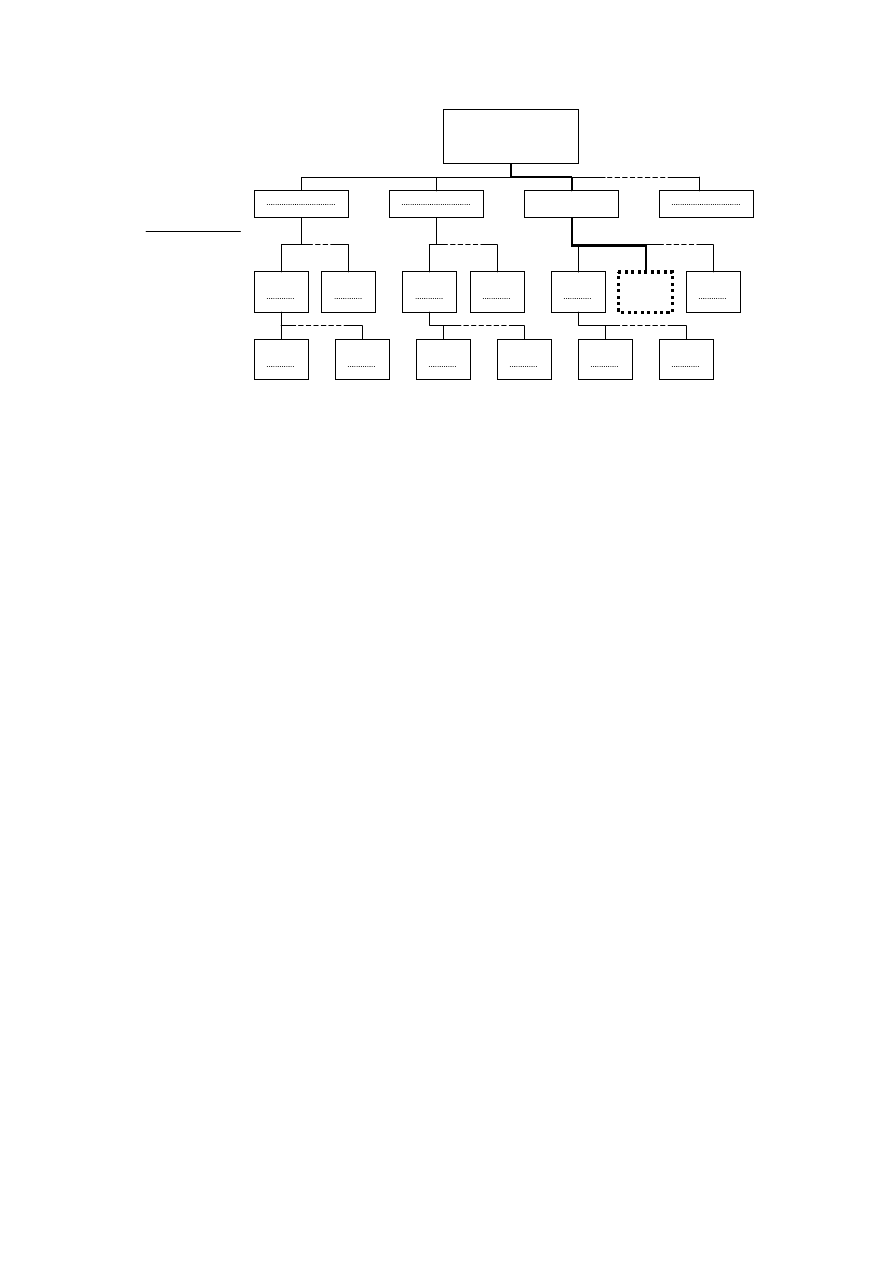
przedsiębiorstwa  [7].  Miejsca  stacji  paliw  płynnych  w  strukturach  systemów  transportu 
zbiorowego, według podziału funkcjonalnego jego podsystemów i elementów, przedstawiono 
na rys. 2. 

PRODUCENT PALIW 

Rozładunek i magazyno-

wanie ropy naftowej 

Przetwarzanie ropy naftowej, 

produkcja paliw płynnych 

Magazynowanie i załadunek 

paliw 

Rozładunek paliw 

Magazynowanie 

Załadunek paliw 

Określenie 

zapotrzebowania 

Analiza danych 

Decyzja o wielkości i czasie 

dostawy 

Rozładunek paliw 

Magazynowanie 

Wydawanie paliw 

BAZA PALIW 

DYSPOZYTORNIA 

STACJA PALIW 

SYSTEM LOGISTYCZNY PALIW PŁYNNYCH 

Zamówienie 

Infor-
macja 

o sta-

nie za-

pasów 

TK 
TR 

TK, TS 

Pojazdy  

Przemysł 

wydobywczy 

TK 
TR 

TM 

3 

 

Rys. 2. Ogólna prezentacja miejsca stacji paliw płynnych w strukturach logistycznych  systemów transportu 

zbiorowego (opracowanie własne) 

Głównym  zadaniem  stacji  paliw  płynnych  w  strukturach  systemów  transportu 

zbiorowego  jest  przechowywanie  i  dystrybucja  paliw  płynnych.  Niezbędne  do  tego  są 
odpowiednie  instalacje  i  urządzenia.  Problematyce  konstrukcji  oraz  eksploatacji  instalacji 
i urządzeń stosowanych na stacjach paliw poświęcona jest m.in. praca [6]. 

Do dalszych analiz wybrano stacje paliw płynnych o następujących cechach (rys. 3): 

– 

stacja  paliw  usytuowana  jest  w  systemie  transportu  zbiorowego  realizującego  zadania 
transportu pasażerów z miast i terenów wiejskich;  

– 

stacja paliw jest związana z systemem transportu zbiorowego, w którym eksploatowane 
są grupy pojazdów generujących zapotrzebowanie na paliwa płynne; 

– 

na  stacjach  paliw  prowadzi  się  ciągłą  kontrolę  stanu  zapasów  paliw  w  zbiornikach 
magazynowych  a  po  osiągnięciu  ustalonego  poziomu  paliwa  zamawiana  jest  jego 
dostawa; 

– 

gdy na stacjach paliw występuje potrzeba uzupełnienia zapasów magazynowych paliwa, 
zbierane są informacje o aktualnie obowiązujących cenach paliw u różnych oferentów 
i na tej podstawie dokonuje się wyboru dostawcy. 
 

 

SYSTEM 

TRANSPORTU 

ZBIOROWEGO 

Infrastruktura 

Stacja 

paliw 

Podsystemy 

Elementy 

podsystemów 

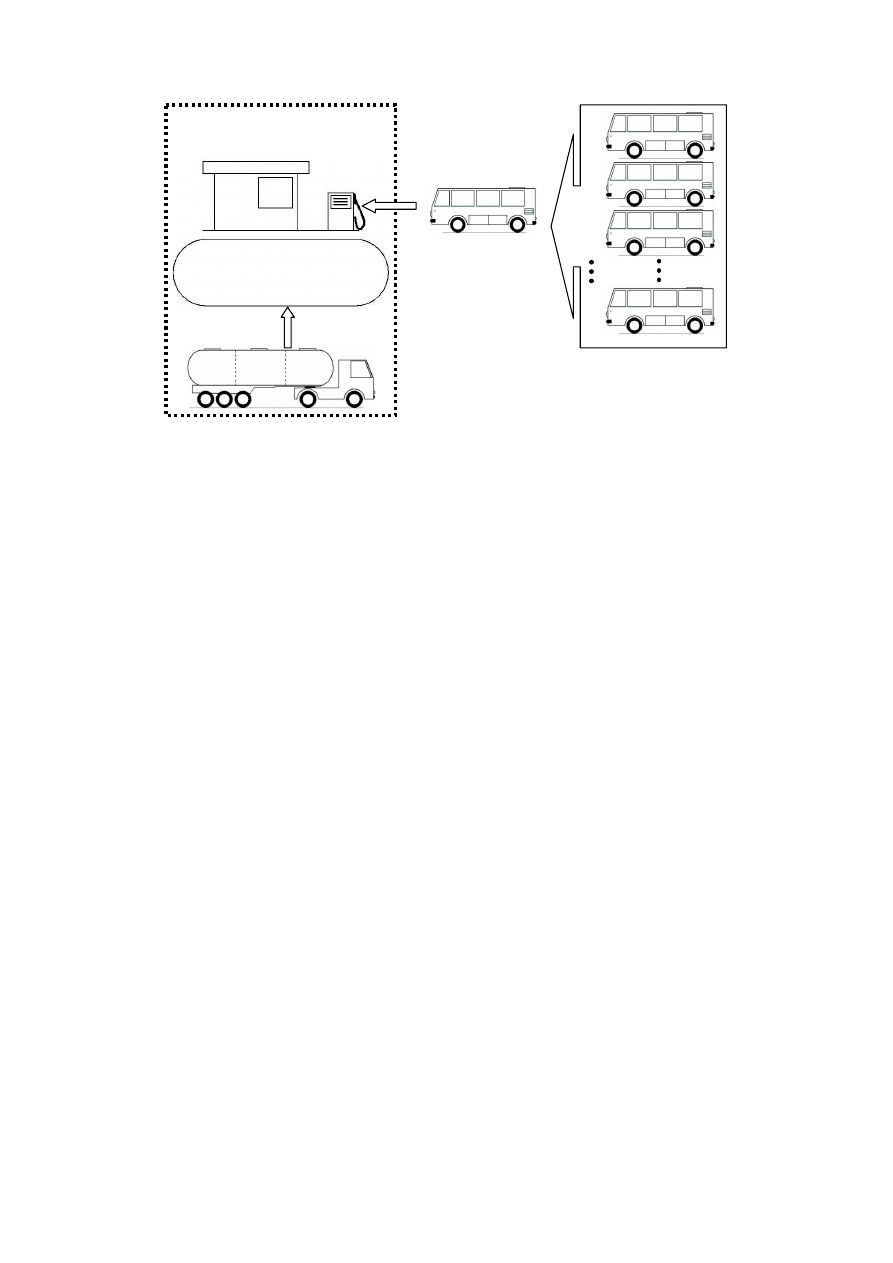
4 

Rys. 3. Schemat ideowy stacji paliw płynnych w systemie pojazdów transportu zbiorowego  

(opracowanie własne) 

3.  MODEL MATEMATYCZNY STACJI PALIW PŁYNNYCH W SYSTEMIE  

POJAZDÓW TRANSPORTU ZBIOROWEGO 

PRZYJĘTE WYBRANE OZNACZENIA 
L 

–  liczba  pojazdów  eksploatowanych  w  systemie  transportu  zbiorowego 

(rys. 4), 

V

zbior

 

–  łączna  pojemność  zbiorników  do  magazynowania  wybranego  asortymentu 

paliwa w stacji paliw (rys. 4), 

kT 

–  chwila  czasowa  końca  k-tego  (k=0,1,2,…,M)  okresu  funkcjonowania 

systemu pojazdów (rys. 5), 

V(kT–0) 

–  stan  zasobów  wybranego  asortymentu  paliwa  w  zbiornikach  stacji  paliw 

bezpośrednio przed chwilą czasową kT (rys. 4), 

V(kT+0) 

–  stan  zasobów  wybranego  asortymentu  paliwa  w  zbiornikach  stacji  paliw 

bezpośrednio po chwili czasowej kT (rys. 4), 

L

v

(kT

–

0) 

−  liczba pojazdów, w których uzupełnia się zasoby paliwa w przedziale czasu 

<(k–1)T, kT), 

v

l

(kT–0) 

–  zapotrzebowanie  l-tego  pojazdu  na  paliwo  w  przedziale  czasu  <(k–1)T, kT) 

(rys. 4), 

ΔV

popyt

(kT–0)  –  łączne zapotrzebowanie na paliwo w systemie pojazdów w przedziale czasu 

<(k–1)T, kT) (rys. 4), 

V

u

 

–  poziom  uzupełniania  zasobów  paliwa  w  zbiornikach  magazynowych  stacji 

paliw  (objętość  wybranego  asortymentu  paliwa  w  zbiornikach,  przy  której 
składa się zamówienie na uzupełnienie zasobów paliwa) (rys. 4), 

ΔV(kT) 

–  wielkość  (objętość)  partii  dostawczej  zwiększającej  zasoby  paliwa 

w zbiornikach magazynowych stacji paliw w chwili czasowej kT (rys. 4), 

V

0

= V(0T+0)  –  początkowa  objętość  wybranego  asortymentu  paliwa  w  zbiornikach 

magazynowych stacji paliw (rys. 5), 

 

 

 

 

 

 

1 

2 

 

Uzupełnianie 

zasobów paliwa 

L 

3 

 

STACJA PALIW 

Zbiorniki do 

magazynowania 

paliw płynnych 

Strumień popytu 

na paliwo 

Pojazdy eksploatowane w systemie transportu 

zbiorowego

 

5 

V

c

 

–  pojemność jednej komory zbiornika naczepy cysternowej (rys. 4 i 5), 

l

c

 

–  liczba komór zbiornika naczepy cysternowej (rys. 4 i 5). 

ZAŁOŻENIA 
1. 

W  systemie  transportu  zbiorowego,  w  przedziale  czasu  <0, MT),  eksploatowana  jest 
stała liczba L pojazdów. 

2. 

Stacja paliw usytuowana w systemie obsługuje tylko pojazdy należące do rozważanego 
systemu transportu zbiorowego. 

3. 

Czas  w  jakim  obserwowany  jest  system  transportu  zbiorowego  podzielony  jest  na 
okresy o jednakowej długości T, a jeden okres odpowiada jednemu dniu funkcjonowania 
systemu. 

4. 

U

l

(kT–0) (l=1,2,..L, k=1,2,…,M)  są  niezależnymi  zmiennymi  losowymi  o  określonym 

rozkładzie prawdopodobieństwa przyjmującymi wartości ze zbioru W={0,1}. 

5. 

v

l

(kT–0) (l=1,2,..L

v

(kT–0), k=1,2,…,M)  są  niezależnymi  zmiennymi  losowymi  

o określonym rozkładzie prawdopodobieństwa typu ciągłego. 

6. 

Zakłada się, że: 

– 

koszt nabycia jednostki objętości paliwa wynosi c

n

, 

– 

jednostkowy  koszt  dodatkowej  specjalnej  dostawy  paliwa  do  systemu  –  w 
związku z brakiem paliwa potrzebnego do zaspokojenia potrzeb wynikających z 
realizacji wszystkich zadań transportowych – wynosi c

b

, 

– 

jednostkowy  koszt  „zamrożonych”  w  zasobach  paliwa  środków  finansowych  na 
początku każdego okresu pracy systemu wynosi c

z

. 

 
 

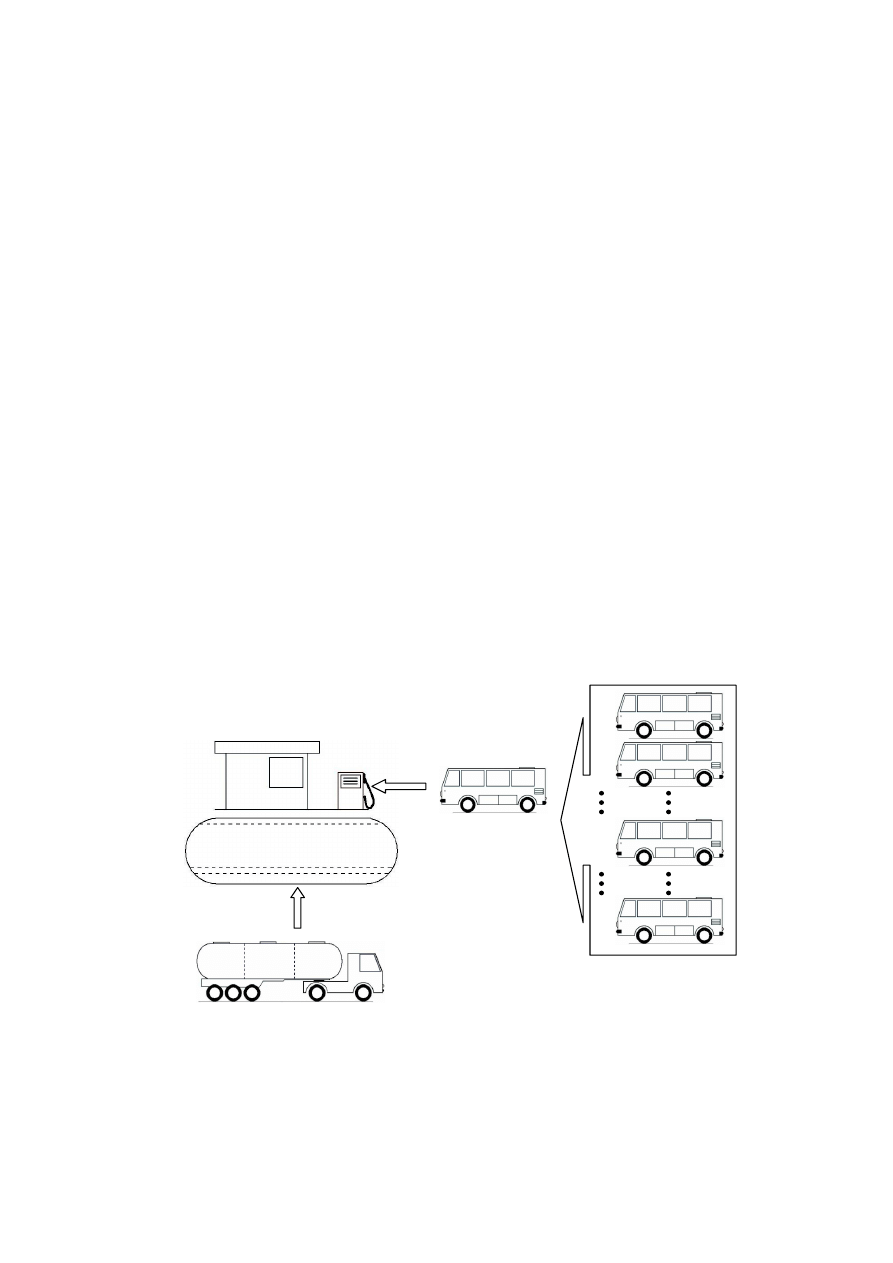
Rys. 4. Schemat oznaczeń stosowanych w modelu matematycznym stacji paliw płynnych funkcjonującej 

w systemie pojazdów transportu zbiorowego – objaśnienie oznaczeń w tekście (opracowanie własne) 

 

 

 

 

 

 

 

 

1 

2 

 

ΔV(kT) 

L 

V

c

 

V

c

 

V

c

 

l 

 

ΔV

popyt

(kT–0) 

V

zbior 

V

u 

V(kT–0)

 

V(kT+0)

 

v

l

(kT–0), l=1,2…L

v 

U

l

(kT–0), l=1,2…L

v

 

l

c

 

6 

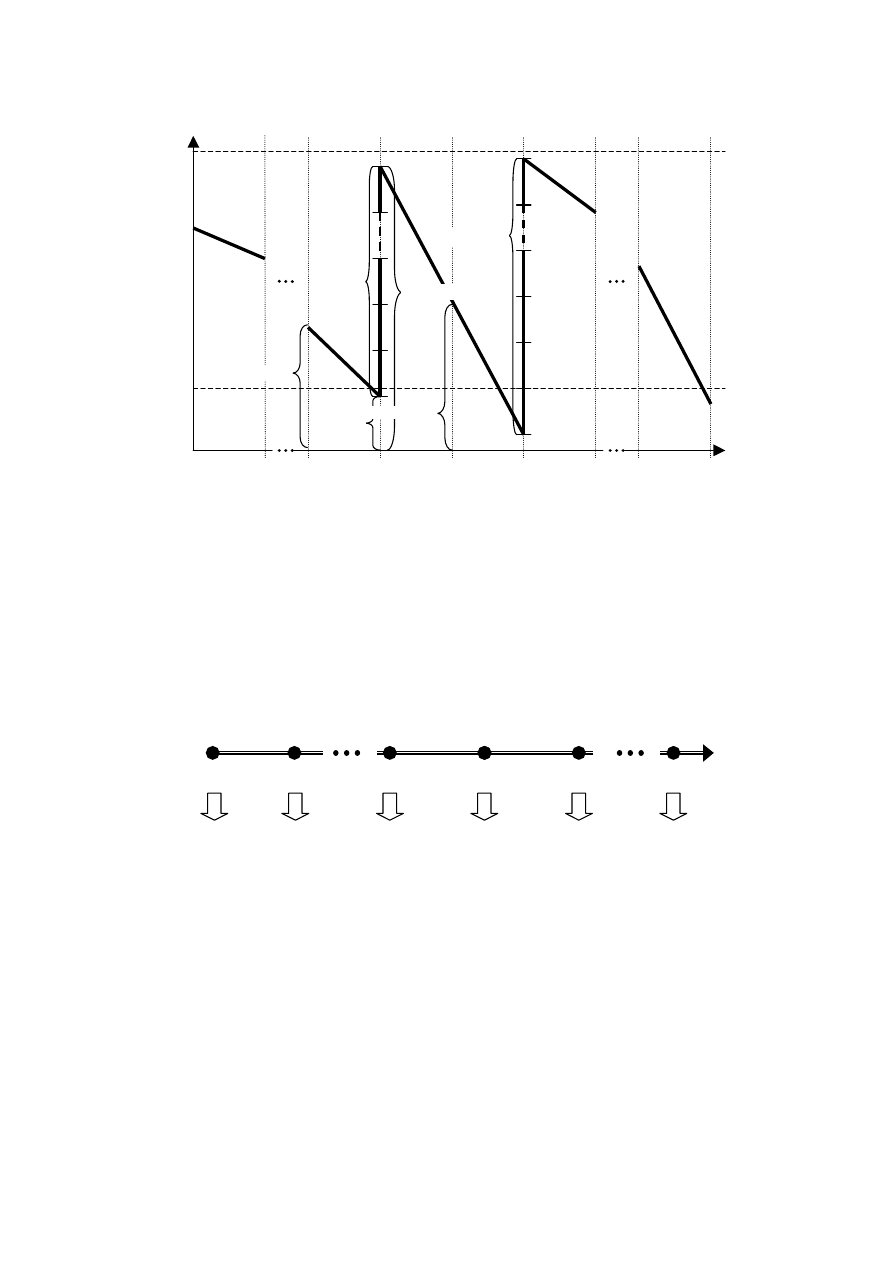
Rys. 5. Ilustracja graficzna zmian zasobów paliwa w stacji paliw płynnych oraz objaśnienie oznaczeń 

stosowanych w jej modelu matematycznym (opracowanie własne) 

MODEL MATEMATYCZNY 
1. 

W systemie transportu zbiorowego jest stała liczba L pojazdów. Czas, w jakim działa 
system podzielono na okresy czasu o jednakowej długości T (wykorzystując koncepcję 
przyjętą  w  pracy [4]).  Okres  czasu  T  odpowiada  jednemu  dniu  roboczemu 
funkcjonowania  systemu  pojazdów  transportu  zbiorowego  z  działającą  w  jego 
strukturach  stacją  paliw.  Okres  T  jest  to  więc  przedział  czasu  <(k–1)T, kT),  gdzie 
k=1,2,…,M (rys. 6).  

 

 

 

Rys. 6. Schemat ideowy upływu czasu w modelu matematycznym i wybrane zmienne  

z nim związane – objaśnienie oznaczeń w tekście (opracowanie własne) 

2. 

Zmiany  stanu  systemu  zasobów  paliwa  dokonywane  są  w  chwili  czasowej  kT.  Stan 
systemu określa  się bezpośrednio przed (czyli w  chwili (kT–0)) oraz bezpośrednio po 
zmianie (czyli w chwili (kT+0)). 

3. 

Wśród  L  pojazdów  funkcjonujących  w  systemie  jest  L

v

(kT–0)

 

pojazdów,  które 

wymagają uzupełnienia paliwa w okresie <(k–1)T, kT), bo pojazdy te realizowały w tym 
okresie zadania transportowe. Liczba L

v

(kT–0) wyznaczana jest na podstawie zmiennej 

U

l

 (l=1,2,...,L) 

o 

znanym 

dwupunktowym 

rozkładzie 

prawdopodobieństwa 

0T 

1T 

(k–1)T 

(k+1)T 

kT 

MT 

V(kT–0) 

V

popyt

(kT–0) 

ΔV(kT) 

V(kT+0) 
C(kT–0) 

C

śr

(kT–0) 

V

0

 

 

ΔV(0T) 

V(0T+0) 

 

V(1T–0) 

V

popyt

(1T–0) 

ΔV(1T) 

V(1T+0) 
C(1T–0) 

C

śr

(1T–0) 

V((k–1)T–0) 

V

popyt

((k–1)T–0) 

ΔV((k–1)T) 

V((k–1)T+0) 
C((k–1)T–0) 

C

śr

((k–1)T–0) 

V((k+1)T–0) 

V

popyt

((k+1)T–0) 

ΔV((k+1)T) 

V((k+1)T+0) 
C((k+1)T–0) 

C

śr

((k+1)T–0) 

V(MT–0) 

V

popyt

(MT–0) 

ΔV(MT) 

V(MT+0) 
C(MT–0) 

C

śr

(MT–0) 

V 

ΔV(kT) 

V

zbior

 

V

c

 

V

c

 

V

c

 

V

c

 

V

c

 

V

c

 

V

c

 

V

c

 

(k+1)T 

kT 

(k–1)T 

0T 

V

u

 

ΔV((k+2)T) 

V

0

 

V(kT–0) 

(k+2)T 

(k+3)T  (M–1)T 

MT 

1T 

V((k+1)T–0) 

V(kT+0) 

V

c

 

V((k–1)T+0) 

7 

wskazującym  potrzebę  (lub  jej  brak)  uzupełnienia  paliwa  w  pojeździe  –  według 
zależności: 

 

)

0

(

)

0

(

1

!

=

!

"

=

kT

U

kT

L

L

l

l

#

. 

(1) 

4. 

Każdy pojazd, który w okresie <(k–1)T, kT) realizował zadania transportowe, wykazuje 
potrzebę  uzupełnienia  paliwa  w  objętości  wyrażonej  zmienną  losową  v

l

 (l=1,2,...,L

v

), 

o znanym  rozkładzie  prawdopodobieństwa.  Łączne  zapotrzebowanie  na  paliwo  dla 
L

v

(kT–0)  pojazdów  składa  się  na  objętość  paliwa  (ΔV

popyt

),  o  którą  zmniejszają  się 

zasoby paliwa w systemie stacji paliw, a wyraża to zależność: 

 

(

)

!

"

=

"

=

"

#

0

1

)

0

(

)

0

(

kT

L

l

l

popyt

kT

v

kT

V

$

. 

(2) 

5. 

Stan  zasobów  paliwa  w  systemie  stacji  paliw  na  końcu  okresu  <(k–1)T, kT)  wskazuje 
zależność: 

 

V(kT–0) = V((k–1)T+0) – ΔV

popyt

(kT–0). 

(3) 

6. 

Istnieje poziom V

u

 (rys. 4 i 5) zasobów paliwa, który wskazuje na potrzebę wdrożenia 

procedury  uzupełnienia  zasobów  w  systemie  stacji  paliw. Procedura  ta  wdrażana  jest, 
gdy: 

 

V(kT–0) ≤ V

u

. 

(4) 

7. 

Zakłada  się,  że  gdy  spełniony  jest  warunek (4),  dostawa  uzupełniająca  zasoby  paliwa 
w stacji  paliw  realizowana  jest  na  początku  okresu  <kT, (k+1)T),  tj.  w  chwili 
czasowej kT (rys. 5). 

8. 

Zakłada  się  także,  że  paliwo  dostarczane  jest  do  systemu  stacji  paliw  pojazdami 
wyposażonymi  w  cysterny  podzielone  na  komory  o  jednakowych  pojemnościach  V

c

, 

a wielkość  partii  dostawczej  paliwa  odpowiada  wielokrotności  V

c

  i  wyznaczana  jest 

z zależności:  

 

c

c

zbior

V

V

kT

V

V

kT

V

!

"

#

"

$

%

$

&

&

=

'

)

0

(

)

(

. 

(5) 

9. 

Jeżeli warunek (4) nie jest spełniony, tzn. jeżeli:  

 

V(kT–0) > V

u

,  

(6) 

to 

ΔV(kT) = 0. 

(7) 

10.  Stan  zasobów  paliwa  w  systemie  stacji  paliw  na  początku  okresu  <kT, (k+1)T), 

bezpośrednio po ewentualnym uzupełnieniu jego zasobów, wskazuje zależność: 

 

V(kT+0) = V(kT–0) + ΔV(kT). 

(8) 

11.  W warunkach losowej liczby obsługiwanych pojazdów L

v

 i losowego zapotrzebowania 

na paliwo przez pojedynczy pojazd v

l

, w przedziale czasu <(k–1)T, kT) system ponosi 

całkowite koszty C(kT–0) (rys. 6) utrzymania zasobów paliwa. Koszty te przedstawiają 
następujące modele matematyczne: 
– 

jeżeli V((k–1)T–0) > V

u

, to 

 

)

0

)

1

((

)

0

(

+

!

"

=

!

T

k

V

c

kT

C

z

, 

(9) 

– 

jeżeli V((k–1)T–0) ≤ V

u

, to 

 

)

0

)

1

((

)

)

1

((

)

0

(

+

!

"

+

!

#

"

=

!

T

k

V

c

T

k

V

c

kT

C

z

n

, 

(10) 

– 

jeżeli V(kT–0) < 0, to 

 

b

z

n

c

T

k

V

c

T

k

V

c

kT

C

+

+

!

"

+

!

#

"

=

!

)

0

)

1

((

)

1

((

)

0

(

. 

(11) 

8 

12.  Rozpatrując  funkcjonowanie  systemu  zasobów  wybranego  asortymentu  paliwa 

w długim okresie czasu, który jest wielokrotnością M okresów o długości T, to model 
matematyczny  średnich  kosztów  ponoszonych  przez  system  na  utrzymanie  w  nim 
zasobów paliwa – w okresie o długości T – można przedstawić w następujący sposób 
(rys. 6): 

 

!

=

"

#

=

"

M

k

œr

kT

C

M

MT

C

1

)

0

(

1

)

0

(

. 

(12) 

4.  SYMULATOR KOMPUTEROWY STACJI PALIW PŁYNNYCH W SYSTEMIE  

POJAZDÓW TRANSPORTU ZBIOROWEGO 

Model matematyczny, opisujący funkcjonowanie stacji paliw (systemu zasobów paliwa) 

znajdującej  się  strukturze  systemu  pojazdów  transportu  zbiorowego,  odwzorowano 
w symulatorze  komputerowym  Sym_Stacji_Paliw.xls.  Do  stworzenia  tego  symulatora 
komputerowego wykorzystano koncepcję i procedury symulatorów przedstawionych m.in. w pracach 
[2, 3].  Symulator  Sym_Stacji_Paliw.xls  oprogramowano  w  formacie  programu  Microsoft 
Excel  wykorzystując  m.in.  język  makr  MS4.  Podstawą  symulatora  cyfrowego  jest  arkusz 
szablonu.  Na  jego  podstawie  tworzone  są  arkusze  robocze,  w  których  przeprowadza  się 
eksperymenty  symulacyjne.  Widok  ekranu  zasadniczej  części  przykładowego  arkusza 
roboczego symulatora, pokazano na rysunku 7. 

9 

Rys. 7. Widok ekranu symulatora Sym_Stacji_Paliw.xls z przykładowymi wynikami eksperymentu 

symulacyjnego

 

 
Arkusze  robocze  symulatora  zawierają  formularz  do  wprowadzania  danych,  które 

opisują  model  i  warunki  eksperymentu  symulacyjnego.  W  formularzu  deklaruje  się 
następujące parametry: 
− 

liczba doświadczeń M eksperymentu symulacyjnego, 

− 

liczba pojazdów L w systemie, 

− 

całkowita pojemność V

zbior

 zbiorników magazynowych paliw, 

− 

objętość  paliwa  V

0

  w  zbiorniku  magazynowym  na  początku  eksperymentu 

symulacyjnego, 

− 

poziom uzupełniania V

u

 zasobów paliwa w zbiornikach magazynowych stacji paliw, 

− 

maksymalna liczba komór l

c

 zbiornika cysterny, którą może być dostarczane paliwo na 

stację paliw, 

− 

pojemność V

c

 pojedynczej komory zbiornika cysterny, 

− 

jednostkowe  koszty  c

n

,  c

b

  oraz  c

z

  ponoszone  w  związku  z  funkcjonowaniem  systemu 

zasobów paliwa, 

− 

parametr  dwupunktowego  rozkładu  prawdopodobieństwa  wskazującego  potrzebę 
uzupełnienia paliwa przez pojedynczy pojazd, 

− 

identyfikator  typu  i  parametry  rozkładu  prawdopodobieństwa  zmiennej  losowej 
wyrażającej wielkość uzupełnienia paliwa w pojedynczym pojeździe. 
Wyniki  symulacji  po  kolejnych  doświadczeniach  eksperymentu  symulacyjnego 

zapisywane  i  zapamiętywane  są  w  bazie  danych  w  układzie  kolumnowym  (rys. 7). 
W kolejnych kolumnach tabeli rejestrowane lub obliczane są następujące wielkości: 
− 

numer doświadczenia eksperymentu symulacyjnego odpowiadający w modelu okresowi 
czasu o długości T, 

10 

− 

liczba  komór  cystern  wykorzystanych  w  k-tym  doświadczeniu  eksperymentu 
symulacyjnego do uzupełnienia paliwa w zbiornikach stacji paliw, 

− 

wielkość  partii  dostawczej  paliwa  na  początku  w  k-tego  doświadczeniu  eksperymentu 
symulacyjnego, obliczona wg zależności: 

 

!

"

!

#

$

%

&

&

'

(

)

(

*

+

*

&

&

&

>

&

&

=

&

,

u

c

c

zbior

u

V

T

k

V

V

V

T

k

V

V

V

T

k

V

T

k

V

)

0

)

1

((

gdy

)

0

)

1

((

)

0

)

1

((

gdy

0

)

)

1

((

. 

(13) 

− 

objętość  paliwa  w  zbiornikach  magazynowych  stacji  paliw  na  początku  k-tego 
doświadczeniu eksperymentu symulacyjnego, obliczona wg zależności:  

 

)

)

1

((

)

0

)

1

((

)

0

)

1

((

T

k

V

T

k

V

T

k

V

!

"

+

!

!

=

+

!

. 

(14) 

− 

liczba pojazdów, które uzupełniały zużyte (na realizację zadań transportowych) paliwo 
w k-tym doświadczeniu eksperymentu symulacyjnego, obliczona wg zależności (1), 

− 

łączne uzupełnienia zużytego w systemie (na realizację zadań transportowych) paliwa 
(popyt na paliwo) w k-tym doświadczeniu eksperymentu symulacyjnego, obliczone wg 
zależności (2), 

− 

objętość  paliwa  w  zbiornikach  magazynowych  stacji  paliw  na  końcu  k-tego 
doświadczenia eksperymentu symulacyjnego, obliczona wg zależności (3), 

− 

wielkość  niezaspokojonego  popytu  na  paliwo  w  k-tym  doświadczeniu  eksperymentu 
symulacyjnego, 

− 

koszty  utrzymania  zasobów  paliwa  w  systemie  w  k-tym  doświadczeniu  eksperymentu 
symulacyjnego, obliczone wg zależności (9) lub (10) lub (11), 

− 

średnie  koszty  utrzymania  zasobów  paliwa  w  systemie,  obliczone  na  podstawie 
k doświadczeń eksperymentu symulacyjnego, wg zależności: 

 

!

=

"

#

=

"

k

i

œr

iT

C

k

kT

C

1

)

0

(

1

)

0

(

. 

(15) 

Użytkownik  symulatora  Sym_Stacji_Paliw.xls  ma  do  dyspozycji  szereg  przycisków, 

które  pozwalają  w  wygodny  sposób  przeprowadzać  eksperymenty  symulacyjne.  Do 
przycisków przypisano procedury operacyjne (rys. 7), których znaczenie opisano w [2, 3]. 

5.  PODSUMOWANIE 

Głównym  zadaniem  stacji  paliw  płynnych  zlokalizowanych  w  strukturach  systemów 

transportu  zbiorowego  jest  przechowywanie  i  dystrybucja  paliw  płynnych  dla  potrzeb 
związanych  z  realizacją  zadań  transportowych.  Odpowiednie  funkcjonowanie  stacji  paliw 
jako  systemu  pewnych  zasobów  jest  jednym  z  warunków  efektywnego  funkcjonowania 
systemów  pojazdów  transportu  zbiorowego.  Do  badania  efektywności  stacji  paliw 
zaproponowano  metodę  modelowania  i  symulacji.  W  tym  celu  zbudowano  model 
matematyczny  stacji  paliw  płynnych  zlokalizowanej  w  strukturach  systemów  pojazdów 
transportu zbiorowego oraz odwzorowano go w postaci symulatora komputerowego.  

Stworzone modele można wykorzystać m.in. do: 

− 

wyznaczenia  średnich  kosztów  ponoszonych  przez  system  na  utrzymanie  w  nim 
zasobów  paliwa  przy  określonych  parametrach  systemu  pojazdów  i  określonych 

11 

parametrach  i  zasadach  charakteryzujących  współdziałający  z  nim  logistyczny  system 
paliw płynnych, 

− 

optymalizacja poziomu uzupełniania V

u

 zasobów paliwa w zbiornikach magazynowych 

i  całkowitej  pojemności  V

zbior

  zbiorników  magazynowych  paliw,  przy  określonych 

parametrach systemu pojazdów i przy określonych pozostałych parametrach i zasadach 
charakteryzujących współdziałający z nim logistyczny system paliw płynnych, według 
określonej funkcji celu (np. minimalizacja średnich kosztów ponoszonych przez system 
na utrzymanie w nim zasobów paliwa w okresie czasu T), 

− 

racjonalizacja  doboru  parametrów  (V

c

, l

c

)  zbiornika  cysterny  wykorzystywanej 

w procesie uzupełniania zasobów paliwa w zbiorniku magazynowym, przy określonych 
parametrach systemu pojazdów i przy określonych pozostałych parametrach i zasadach 
charakteryzujących współdziałający z nim logistyczny system paliw płynnych, według 
określonej funkcji celu. 
Pewne możliwości wykorzystania opisanych w niniejszej pracy modeli przedstawiono 

m.in. w [5]. 

LITERATURA 

[1]  Abt S.: Systemy  logistyczne  w  gospodarowaniu:  teoria  i  praktyka  logistyki.  Wyd.  Akademii 

Ekonomicznej, Poznań, 1997. 

[2]  Kadziński A., Andrzejczak K.: Modele  i  badania  symulacyjne  popytu  na  wybrany  asortyment 

zasobów  dla  systemu  jednorodnych  pojazdów  szynowych.  Pojazdy  Szynowe,  kwartalnik,  2004, 
nr 3–4, s. 78÷82. 

[3]  Kadziński A., Kwaśnikowski J.: Modele i badania symulacyjne kosztów funkcjonowania systemu 

lokomotyw  przeznaczonego  do  realizacji  losowej  liczby  zadań.  Pojazdy  Szynowe,  kwartalnik, 
2001, nr 2, s. 47÷51. 

[4]  Kadziński A., Woźniak A.: Model 

systemu 

obsługiwania 

wagonów 

towarowych 

w wagonowniach  z  potokową  linią  obsługową.  Zagadnienia  Eksploatacji  Maszyn,  kwartalnik 
PAN, zeszyt 2/1992, s. 305÷323. 

[5]  Majewski B.: Stacje  paliw  płynnych  w  systemach  transportu  zbiorowego.  Politechnika 

Poznańska,  Wydział  Maszyn  Roboczych  i  Transportu,  praca  dyplomowa,  2005,  promotor 
A. Kadziński, niepublikowane. 

[6]  Nowa Encyklopedia Stacji Paliw. Praca zbiorowa pod red. K. Apanasiewicza, Wyd. Polskiej Izby 

Paliw Płynnych, Warszawa, 2004. 

[7]  Pfohl H. C.: Systemy logistyczne. Wyd. Instytutu Logistyki i Magazynowania, Poznań, 2001. 

STOCHASTIC MODEL OF FUEL STATION FUNCTIONING IN A SYSTEM OF VEHICLES  

OF COLLECTIVE TRANSPORT  

ABSTRACT 

A system of vehicles of collective transport operator including a fuel station has been presented. The fuel 

station has been  treated as a system with a random demand for resources generated in a system of vehicles. A 
mathematical  model  of  processes  occurring  on  the  verge  of  both  systems  has  been  proposed.  For  the  model 
which  had  been  created  appropriate  software  and  computer  simulation  model  have  been  worked  out.  
Capabilities of the practical application of those models have been also discussed.