Laboratorium z przedmiotu „Sztuczna inteligencja”

Temat: Sieci Bayesa, Wnioskowanie probabilistyczne, GeNIe

Laboratorium nr 1

Sied Bayesowska służy do przedstawiania zależności pomiędzy zdarzeniami bazując na rachunku
prawdopodobieostwa. Klasycznym przykładem jest reprezentowanie zależności pomiędzy symptomami a
chorobą. Sied Bayesa to skooczony, acykliczny graf skierowany, zbudowany na podstawie
prawdopodobieostw warunkowych (które są zawarte w zbiorze CP).

Sied Bayesa to trójka: B = <N, E, Cp>

Gdzie: N – zbiór wierzchołków grafu, E – zbiór krawędzi grafu, Cp – zbiór prawdopodobieostw warunkowych.

Wierzchołkami grafu są stwierdzenia lub hipotezy. Krawędzie grafu to relacje określające przejście od
wierzchołka do wierzchołka z prawdopodobieostwem określającym to przejście.

1. Jeśli nie istnieje połączenie pomiędzy węzłami sieci, oznacza to, że zdarzenia reprezentowane przez te

węzły są niezależne. Na przykład, w poniższej sieci zdarzenia A i D są od siebie niezależne.

2. Prawdopodobieństwo danego węzła zależy od wartości węzłów rodzicielskich, które „zasłaniają”

poprzedzające węzły. Na przykład, dla przedstawionej poniżej sieci mamy:

3. W powyższej sieci prawdopodobieństwo p(E|A) można wyznaczyć wg następującego wzoru:

przy czym

Inny przykład:

4. Reguła łańcuchowa i wykorzystanie niezależności warunkowych:

5. Prawdopodobieństwo łączne wybranych zdarzeń, np.

Ćw. 1. Zbuduj Sied Bayesa dla określonego zbioru Cp:

P = {P(a), P(b|a), P(c|b), P(d|b), P(G|c), P(G|d), P(e|a), P(F|e), P(F|c)}

Rozwiązanie:

Taki graf pozwala na prowadzenie wnioskowania w oparciu o prawdopodobieostwo i wzór Bayesa.

Małe litery stwierdzenia lub zaobserwowane fakty. Wielkie litery hipotezy.

Koocową hipotezą może byd G lub F.

Zadania do wykonania samodzielnie:

Zadanie 1.

Proszę korzystając z programu GeNIe stworzyd sied Bayesa na wymyślony przez Paostwa temat (każdy inny) i
przeprowadzid wnioskowanie

Zadanie 2

W podanym niżej tekście występują pewne zależności przyczynowo skutkowe opisane liczbowo
prawdopodobieństwami warunkowymi. Proszę podać zbiór CP takich prawdopodobieństwa warunkowych
oraz narysować graf przyczynowo–skutkowy.

Prawdopodobieństwo wystąpienia anginy w przypadku objawów takich jak ból gardła i gorączka
jest wysokie i wynosić może 0.8. Jednak wystąpienie gorączki i bólu głowy może świadczyć o
grypie, co jest hipoteza prawdopodobna na 0.6. W przypadku gdy pacjent cierpiący na grypę nie
wyleczył się całkowicie może dojść do zapalenia oskrzeli z prawdopodobieństwem 0.4. Zapalenie
oskrzeli może spowodować ból gardła z prawdopodobieństwem 0.3.

Zadanie 3

W podanym niżej tekście występują pewne zależności przyczynowo skutkowe opisane liczbowo
prawdopodobieństwami warunkowymi. Proszę podać zbiór CP takich prawdopodobieństw warunkowych
oraz narysować graf przyczynowo–skutkowy.

Prawdopodobieństwo awarii suportu roweru z powodu zawilgocenia wynosi 0.4, zabrudzenia 0.1,
natomiast z powodu zużycia 0.3. Awaria suportu na pewno spowoduje większe opory w czasie
jazdy. Awaria suportu może na30% spowodować uszkodzenie mufy suportowej, to z kolei na 85%
spowoduje konieczność zakupu nowej ramy. Zabrudzenie na pewno wpłynie na nieprecyzyjną pracę
przerzutek a także na 5% może spowodować wzrost oporów w czasie jazdy. Wzrost oporów w
czasie jazdy może spowodować z prawdopodobieństwem 0.35 awarię suportu.

Zadanie 4

W podanym niżej tekście występują pewne zależności przyczynowo skutkowe opisane liczbowo
prawdopodobieństwami warunkowymi. Proszę podać zbiór CP takich prawdopodobieństw warunkowych
oraz narysować graf przyczynowo–skutkowy.

Prawdopodobieństwo awarii tylniej przerzutki z powodu zawilgocenia wynosi 0.3, zabrudzenia 0.6,
natomiast z powodu zużycia 0.7. Awaria tylniej przerzutki uniemożliwi jazdę na 40%. Zawilgocenie
i zabrudzenie na 70% spowodują przedwczesne wytarcie się klocków hamulcowych. Wytarte klocki
na 20% uniemożliwią jadę. Prawdopodobieństwo awarii suportu roweru z powodu zawilgocenia
wynosi 0.6 a zabrudzenia 0.3. Awaria suportu na pewno uniemożliwi jazdę. Brak możliwości jazdy
na rowerze na 40% spowoduje spadek zainteresowania jego stanem technicznym, a to na pewno
negatywnie wpłynie na jego czystość – czyli na jego zabrudzenie.

Laboratorium nr 1 (dodatek)

Prawdopodobieostwo łączne (całkowite)

Jeśli zbiór



podzielimy na zbiory B, ~B takie, że B



~B =



,

B



~B = ø i P(B) > 0 oraz P(~B) > 0, to dla dowolnego zdarzenia A





prawdziwy jest wzór:

P(A



B) = P(A|B)*P(B) + P(A|~B)*P(~B)

gdzie:

P(B) – prawdopodobieostwo zajścia zdarzenia B

P(~B) – prawdopodobieostwo zajścia zdarzenia przeciwnego do B

P(A|B) – prawdopodobieostwo (warunkowe) zajścia zdarzenia A pod warunkiem zajścia zdarzenia B.

Uwaga !: Jeśli zdarzenia A i B są niezależne wówczas prawdopodobieostwo łączne liczone jest ze wzoru:

P(A



B) =P(A)*P(B)

Prawdopodobieostwo warunkowe (twierdzenie Bayesa)

Przykład I: Rozważmy następującą sied:

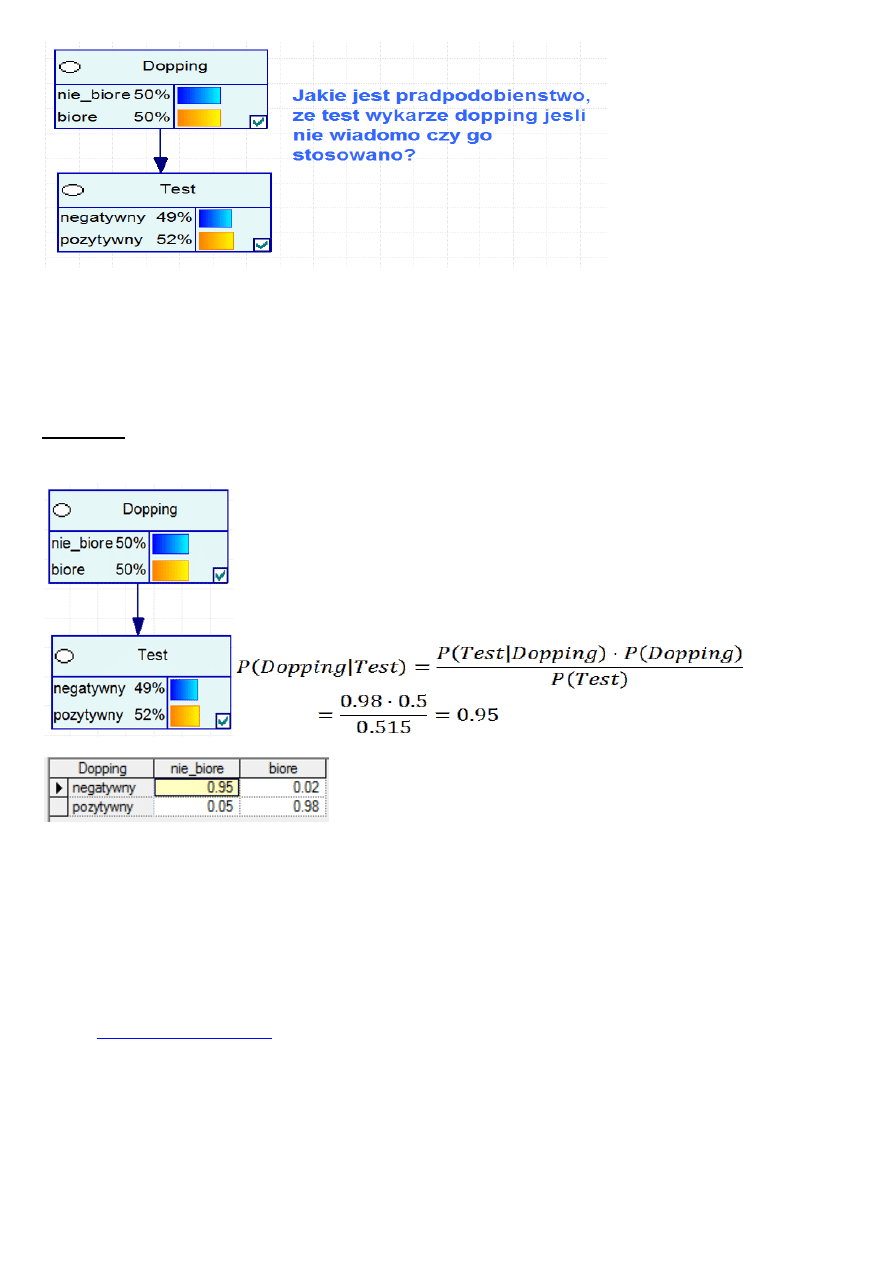
Wiadomo, że test w 95% daje wynik negatywny jak dopingu nie brano. W 5% daje wynik pozytywny jeśli
doping stosowano.

P(Test) = P(Test| Dopping)*P(Dopping) + P(Test| ~Dopping)*P~(~Dopping) = 0.98*0.5 + 0.05*0.5 = 0.49 +
0.025 = 0.515 ~= 0.52

Przykład II: Albo odwrotnie – jeśli wiemy, że test dał wynik pozytywny to jakie jest podobieostwo, że używam
doppingu?

Wiadomo, że test w 95% daje wynik negatywny jak dopingu nie brano. W 5% daje wynik pozytywny jeśli
doping stosowano.

Laboratorium nr 2 i 3

GeNIe narzędziem pozwalającym na budowę I analizę Sieci Bayesa

 Do modelowania i wnioskowania w sieciach Bayesa można wykorzystad oprogramowanie GeNIe:

http://genie.sis.pitt.edu

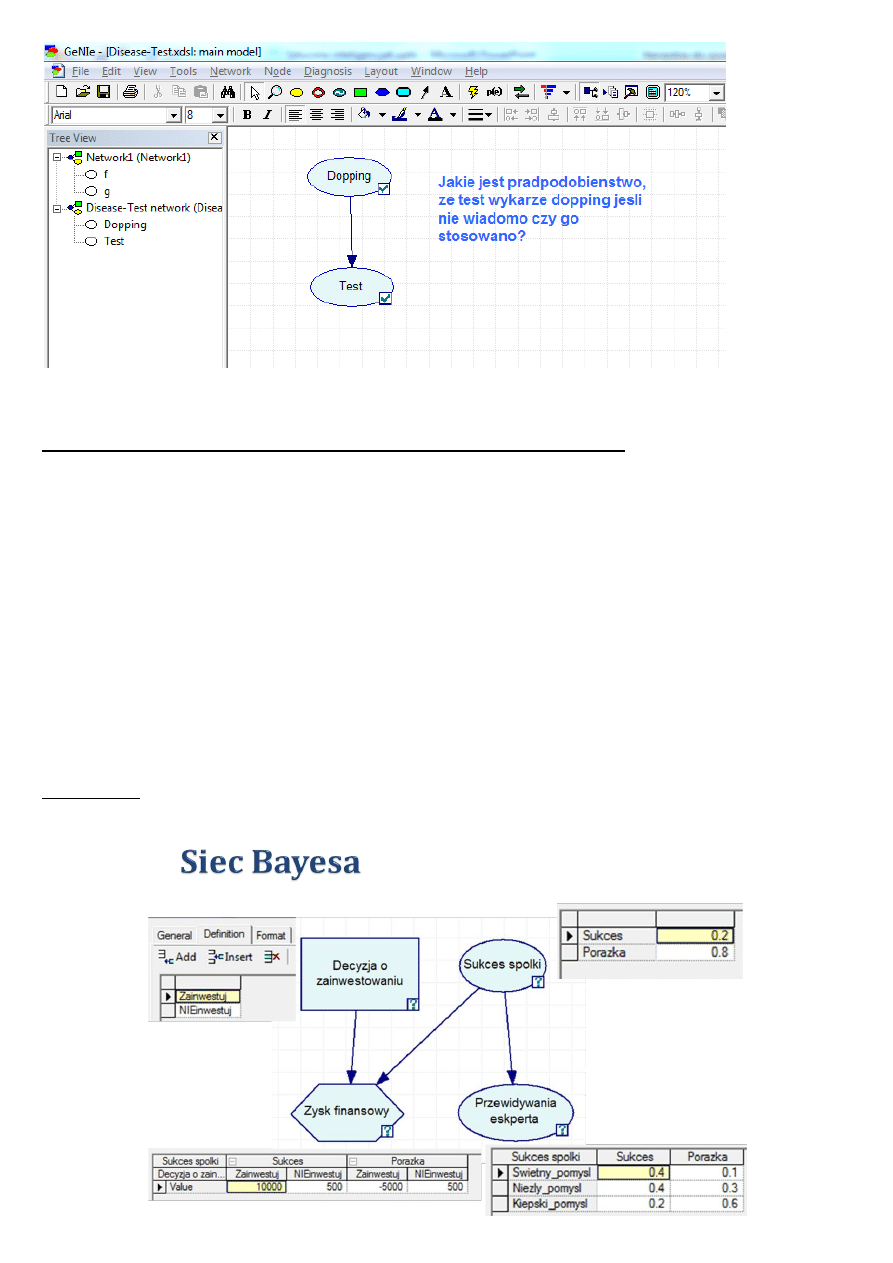
Ćwiczenie do rozpoznania i później w domu do wykonania (zadanie domowe).

Wyobraźmy sobie, że inwestor zastanawia się nad ryzykiem zainwestowania w nowo powstałą firmę. Źródłem
niepewności jest tutaj sukces tej firmy. Inwestor jest świadom faktu, że tylko ok. 20% wszystkich
nowopowstałych firm osiąga sukces. Tą niepewnośd można zmniejszyd pytając o zdanie eksperta.
Przewidywania eksperta jednak nie zawsze się sprawdzają. Ekspert ocenia, że ze wszystkich firm które osiągają
sukces 40% ma dobry pomysł na rozwój działalności, 40% ma średni pomysł, a 20% ma kiepski pomysł.
Spośród wszystkich firm którym się nie udaje, ekspert wyznaczył, że 10% ma świetny pomysł, 30% ma niezły
pomysł, a 60% ma kiepski pomysł.

Załóżmy, że inwestor chce włożyd kwotę $5,000 w przedsięwzięcie. Wie on, że jeśli firma osiągnie sukces to
zarobi na tym $10,000. Jeśli firma upadnie to straci on swój wkład $5,000, ale jeśli w ogóle nie zainwestuje,
zyska $500 na bezpiecznej lokacie w banku.

Co zrobid? Inwestowad czy nie?

Rozwiązanie:

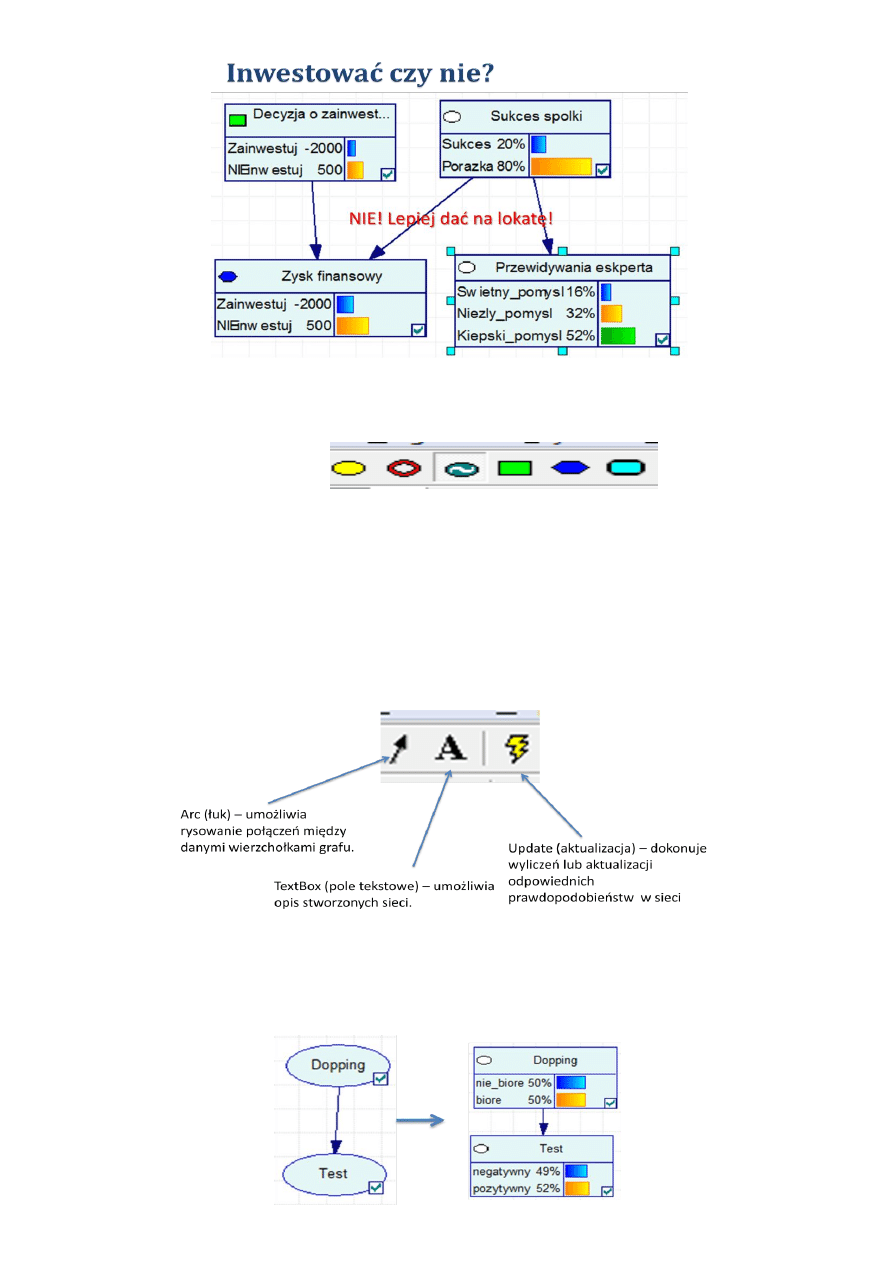
GeNIe – podstawy

Podstawowe elementy w pasku menu:

 Chance (szansa) – przyjmują wartości dyskretne.
 Deterministic (deterministyczne) – przyjmują wartości stałe, bądź wartośd nominalną określoną przez

użytkownika ze skooczonego zbioru wartości.

 Equation (równanie) – wyraża bardziej skomplikowane zależności miedzy zmiennymi, które należy

poddad ocenie.

 Decision (decyzja) – modeluje możliwe do podjęcia przez użytkownika decyzje.
 Value (wartość) – modelują wartości powiązane z każdą możliwą do wykonania decyzją użytkownika.
 Submodel – oznacza konceptualnie powiązaną grupę zmiennych.

Menu Node / View as umożliwia zmianę sposobu wyświetlania zaznaczonych węzłów sieci.

Menu Node / Set Evidence określenie które zdarzenie miało miejsce.

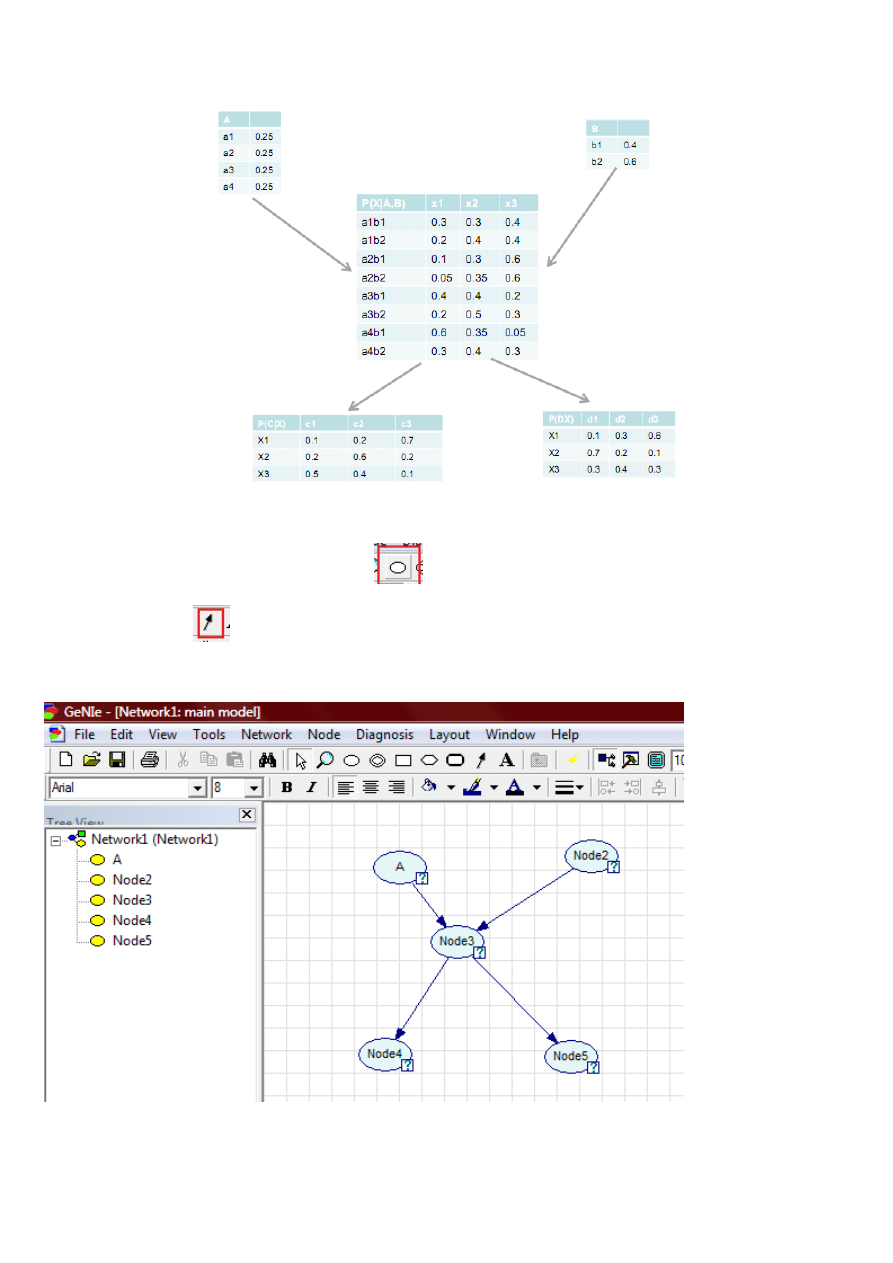
GeNIe – budujemy sieć Bayesa krok po kroku

Zbudujemy następującą sied Bayesa:

Użyjemy do tego narzędzia GeNIe.

Do budowy węzłów sieci używamy komponentu:

Do budowy krawędzi:

Definiujemy każdy węzeł w sieci. Klikając dwukrotnie w dany węzeł, otwieramy okno z właściwościami.

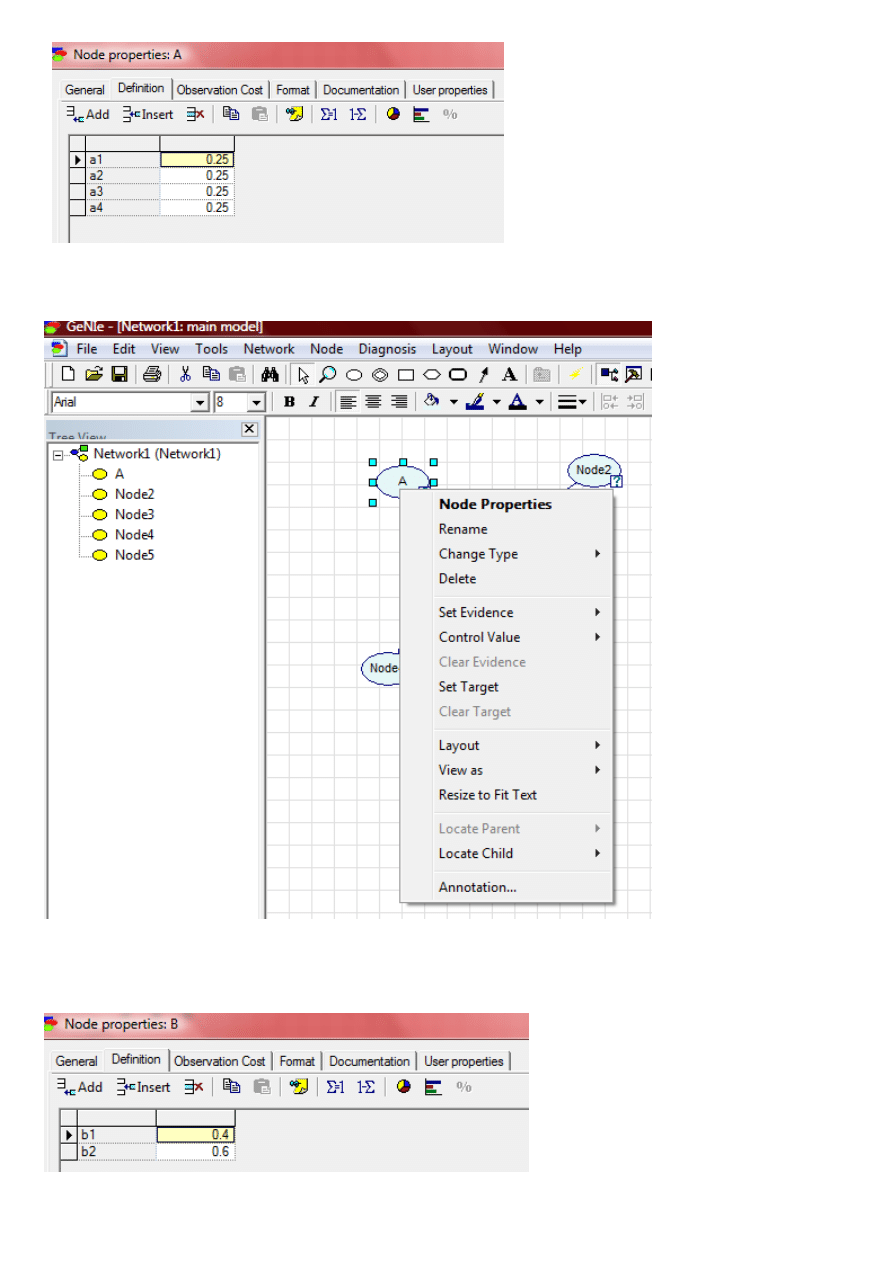
Również klikając prawym przyciskiem myszy w dany węzeł pokaże się menu podręczne. Klikając opcję *Node Properties+
otworzy się to samo okno *Node Properties. Node 1+

Pamiętając, że definicja sieci jest następująca:

Definiujemy poszczególne węzły:

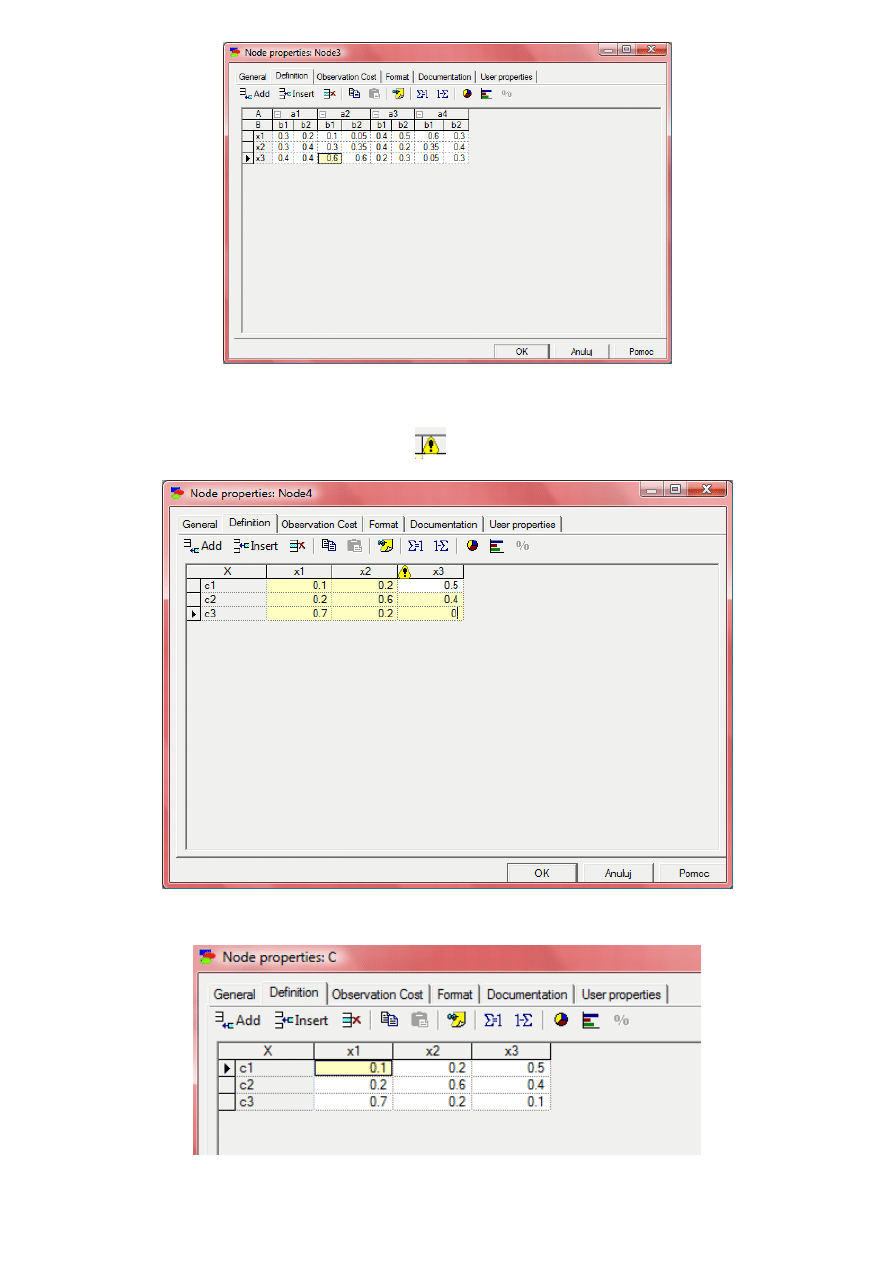
Warto zauważyd, że GeNIe cały czas nadzoruje czy wartości prawdopodobieostw spełniają podstawowe założenia, o
sumowaniu się do wartości 1. Gdy dla danego węzła (patrz rysunek poniżej) nie uzupełniono wartości w ostatniej

kolumnie i wierszu, GeNIe sygnalizuje błąd rysunkiem

.

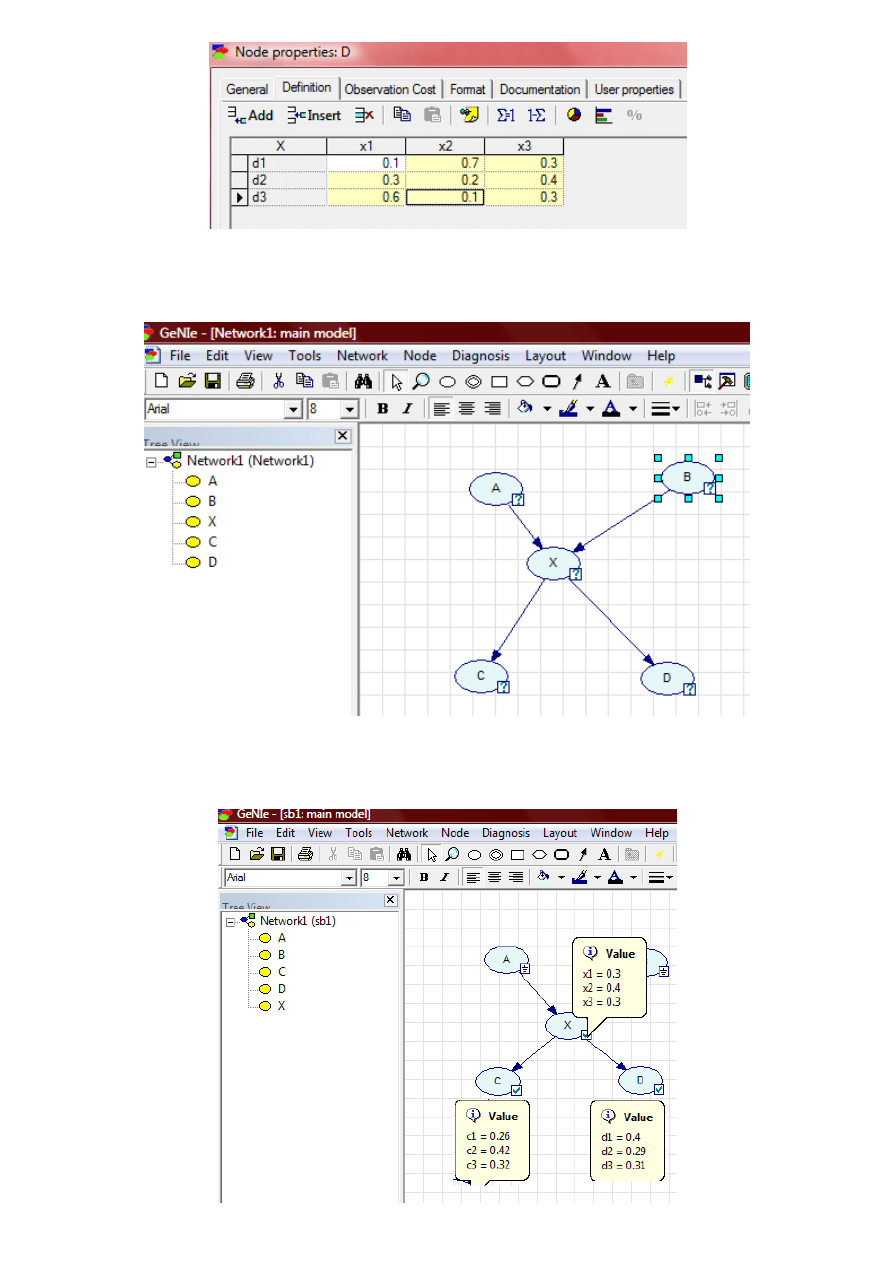
Teraz cała sied jest już zdefiniowana:

Obliczamy prawdopodobieostwa różnych zdarzeo:

Gdy a=a4 i b=b2, wtedy

Gdy zaś chcemy wyznaczyd prawdopodobieostwo zdarzenia, że

P(c=c2|x=x3,a=a4,b=b2) = p(c=c2|x=x3)*p(X=x3|a=a4,b=b2)*p(A=a4)*p(B=b2) = 0.4 *
0.3 * 0.25 * 0.6 = 0.018

Proszę obliczyd prawdopodobieostwa zdarzeo:

1. P(c=c2|x=x3,a=a3,b=b1) = ?
2. P(c=c3|x=x3,a=a4,b=b2) = ?
3. P(d=d2|x=x3,a=a4,b=b2) = ?
4. P(X=x2|a=a4,b=b2) = ?
5. P(X=x2|a=a1,b=b1) = ?