W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

Cel ćwiczenia

: Celem ćwiczenia jest zapoznanie ćwiczących z analogowymi sygnałami zmiennymi, ich

podstawowymi parametrami czasowymi i amplitudowymi oraz sposobem obliczeniowym jak i pomiarowym
wyznaczania wartości tych parametrów. Dodatkowo realizacja ćwiczenia pozwala na ugruntowanie
umiejętności posługiwania się oscyloskopem analogowym jako narzędziem pomiarowym.

Program ćwiczenia

W celu realizacji ćwiczenia należy:
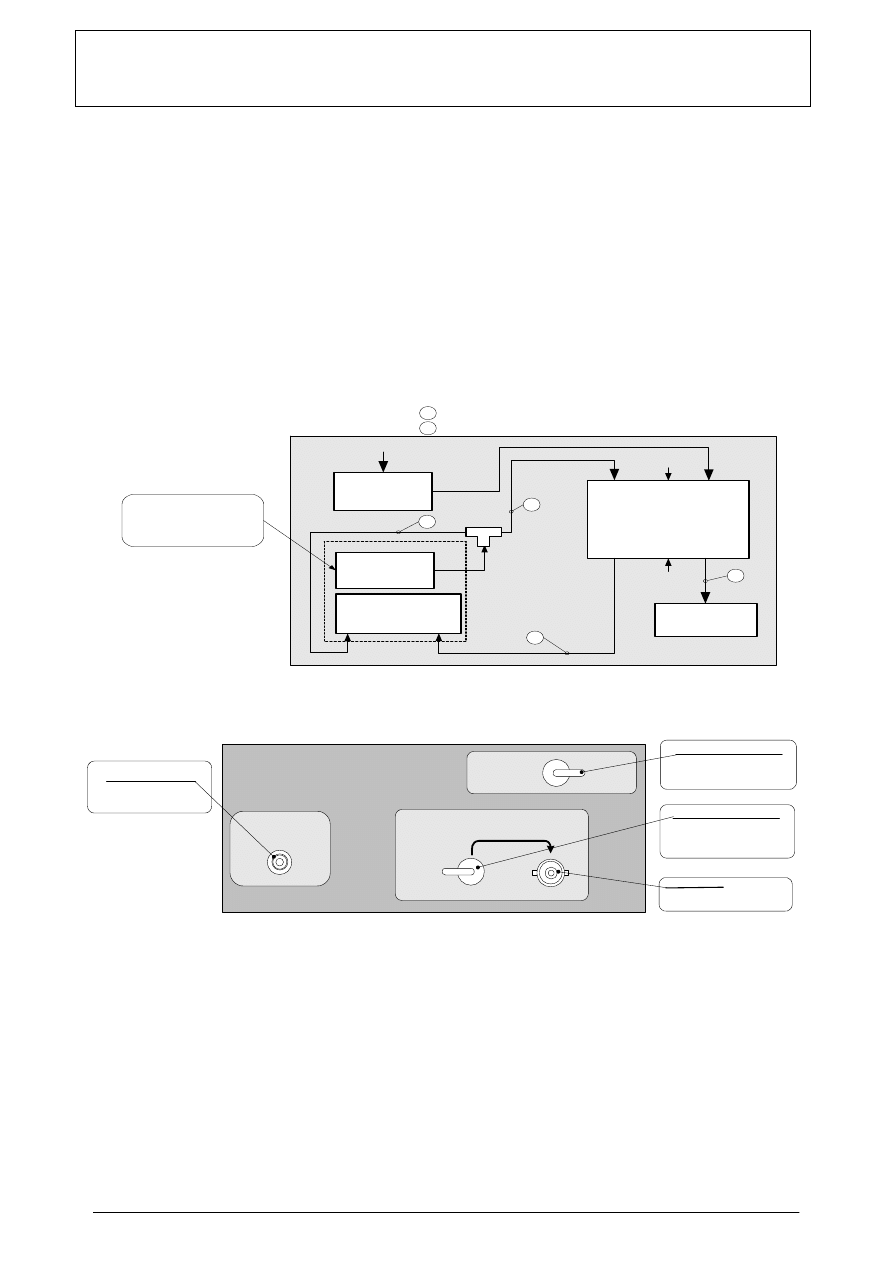
1. Zmontować układ pomiarowy jak na schemacie 1.
2. W celu uruchomienia makiety podłączyć wyjście transformatora zasilającego (wtyk współosiowy na

kablu transformatora) do gniazda na płycie tylniej makiety MD-1 (rysunek 1). Przełącznik
dwupozycyjny, umożliwiający wybór zasilania, przełączyć w pozycję „Detektory” (dźwignia
przełącznika dwupozycyjnego ustawiona w „prawo” – pozycja „1”). Włączyć transformator do sieci
zasilającej 230V/50Hz. Kontrolka na płycie czołowej makiety MD-1 świeci światłem o zielonej barwie.

P rz y rz ą d a n a lo g o w y

"M E T E X "

W e jś c ie s y g n a łu Z a s ila n ie

b a d a n e g o

M a k ie ta d y d a k ty c z n a

M D -1

w y jś c ie w y jś c ie
o s c y lo s k o p M E T E X

T ra n s fo rm a to r

z a s ila ją c y

S ie ć 2 3 0 V / 5 0 H z

T ró jn ik B N C

P ły ta c z o ło w a

m a k ie ty

P ły ta ty ln ia

m a k ie ty

1 5 V -2 2 V /0 .5 A

/5 0 H z

G e n e ra to r

fu n k c y jn y

O s c y lo s k o p

Y

1

Y

2

M o ż e to b y ć g e n e ra to r

a u to n o m ic z n y lu b

g e n e ra to r w b u d o w a n y

d o o s c y lo s k o p u

k a b e l k o n c e n try c z n y w ty k B N C - w ty k B N C (s z tu k 3 )

1

1

1

1

2

2

k a b e l w ty k "ra d io w y "- w ty k "ra d io w y " (s z tu k 2 )

Schemat 1. Sposób połączenia urządzeń na stanowisku pomiarowym

Przełącznik dwupozycyjny

Zasilanie

1. zasilanie układu "detektory"
2. zasilanie układu "tabilizator"

1

2

Detektory

Stabilizator

Gniazdo BNC do podłączenia
sygnału z generatora
funkcyjnego (sygnał mierzony)

Przełącznik dwupozycyjny

Wybór rodzaju wejścia

1. Wejście zmiennoprądowe
2. Wejście stałoprądowe

2

1

( = )

( ~ )

Wejście

sygnału z generatora

Gniazdo współosiowe

do podłączenia

transformatora zasilającego

ZASILANIE

MAKIETY
20V/50Hz

Rys 1. Przełączniki i gniazda na płycie tylniej makiety MD-1

3. Wprowadzić nastawy na generatorze sygnałowym takie, aby dostarczany przez niego sygnał miał

następujące parametry; kształt sinusoidalny, częstotliwość

f = (1

±0,05)kHz, amplitudę

A

d

= A

u

= (1

±0,05)V, podpolaryzowanie sygnałem stałym U

d c

= 0V, przy ustawianiu wymaganych

parametrów posługiwać się obrazem sygnału na ekranie lampy oscyloskopowej. Sygnał z generatora
doprowadzić (rysunek 1) do gniazda BNC umieszczonego na płycie tylniej makiety MD-1.
Przełącznikiem dwupozycyjnym na polu „Wejście sygnału z generatora” ustawić rodzaj wejścia –
1-zmiennoprądowe, jeżeli przedmiotem pomiaru są parametry amplitudowe sygnału bez składowej stałej,
2-stałoprądowe, jeżeli przedmiotem pomiaru są parametry sygnału zmiennoprądowego nałożonego na
sygnał stałoprądowy. Po ustawieniu sygnał z generatora dołączyć również do wejścia Y

1

oscyloskopu.

4. Na płycie czołowej urządzenia „

MAKIETA MD-1

” (rysunek 2) przełącznik dwupozycyjny na polu

„

SYGNAŁ BADANY

” ustawić w pozycji w lewo, a przełącznik obrotowy (czteropozycyjny) w pozycji

Strona 1 z 5

W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

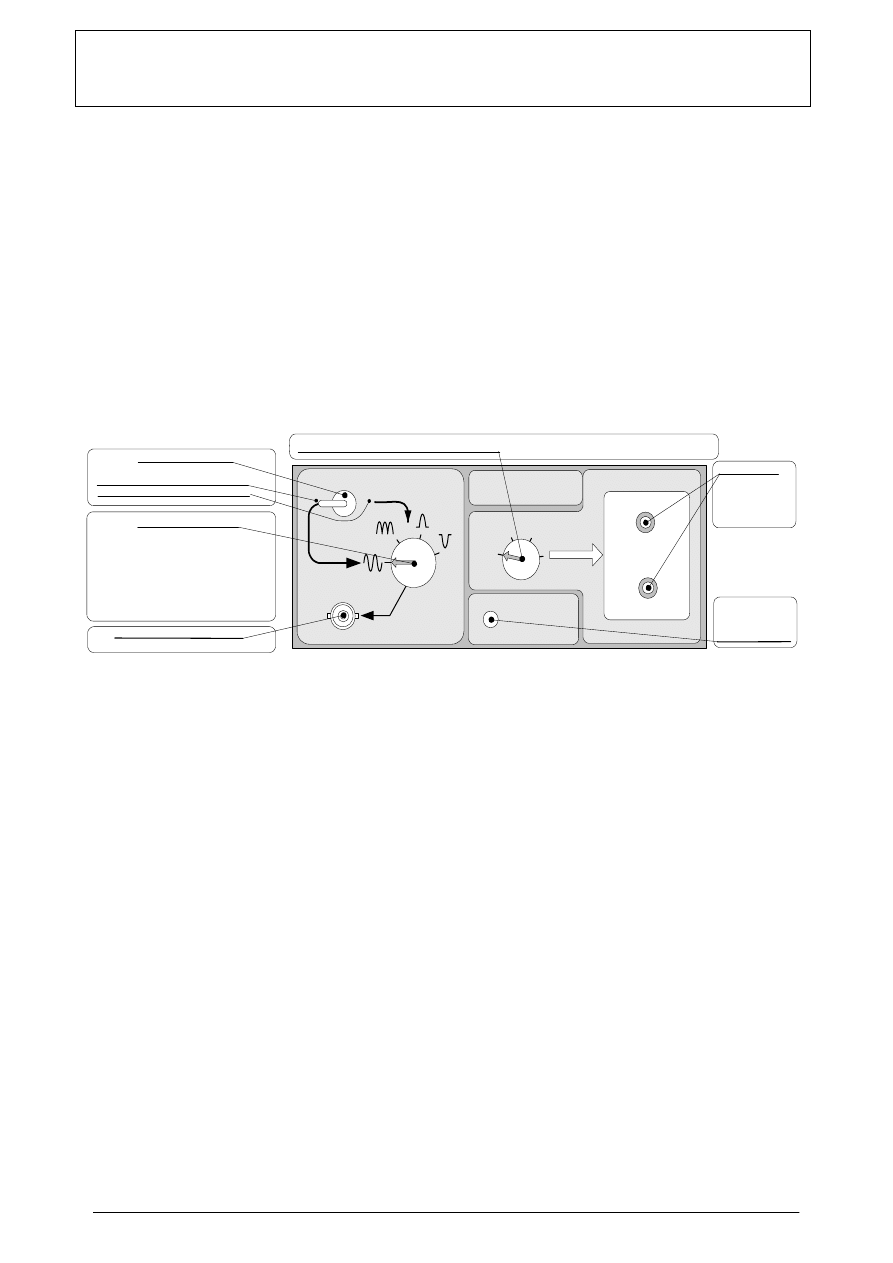
„1”. Przy takich ustawieniach przełączników na polu „

SYGNAŁ BADANY

” przełączać przełącznik

„

WARTOŚĆ MIERZONA

” kolejno od pozycji „1”do pozycji „4” odczytując za każdym ustawieniem tego

przełącznika wartość napięcia stałego wskazywaną przez multimetr cyfrowy „

METEX

”. Jednocześnie

należy rejestrować (odrysować) kształt sygnału obserwowanego w kanale 2 oscyloskopu. Odrysowując
kształt sygnału należy na szkicu zaznaczyć wszystkie istotne wartości wymiarów obrazu, jak również
nastawy ustawione pokrętłami oscyloskopu. Należy pamiętać, o ustawieniu pokręteł regulatorów
„płynnej regulacji czułości odchylania pionowego”, jak również płynnej regulacji „szybkości podstawy
czasu”, w pozycji „kalibrowane”! W przeciwnym razie wyznaczone na podstawie wymiarów obrazu
wartości amplitud bądź czasów analizowanego sygnału, będą błędne. Odczytywane z multimetru
cyfrowego wartości napięcia są równe, co do wartości odpowiednim parametrom amplitudowym sygnału
mierzonego (kształt tego sygnału, którego dany parametr jest mierzony, jest jednocześnie za każdym
razem pokazywany na ekranie lampy oscyloskopowej jako obraz sygnału w kanale 2 oscyloskopu) – w
tym etapie ćwiczenia mierzone są parametry amplitudowe sygnału nie poddanego detekcji lub inaczej
sygnału nie poddanego procesowi prostowania.

Do toru Y

2

oscyloskopu

SYGNAŁ BADANY

1

2

3

4

1

2

3

4

WARTOŚĆ MIERZONA

MAKIETA MD-1

Przełącznik dwupozycyjny

Selekcja -

sygnał bez prostowania (dźwignia w lewo)
sygnał po prostowaniu ( dźwignia w prawo)

Przełącznik czteropozycyjny

Selekcja rodzaju prostowania

1 - sygnał bez prostowania
(ważne tylko przy dźwidni przeł. dwupoz. w lewo)
2, 3, 4 - sygnał z prostowaniem
(ważne tylko przy dźwigni przeł. dwupoz. w prawo)
Prostowanie 2- dwupołówkowe

3- jedno[połowkopwe (dodatnie)
4- jednopołówkowe (ujemne)

Gniazdo BNC na którym występuje
sygnał przetwarzany (do obserwacji)

Czteropozycyjny przełącznik rodzaju wartości mierzonej (1-skuteczna, 2-średnia , 3-szczytowa, 4-międzyszczytowa)

Zaciski sygnału
napięcia stałego
o wartości równej
wartości mierzonego
parametru

+

-

Sygnalizator zasilania

Ma świecić na
zielono!!

Rys 2. Pokrętła na płycie czołowej makiety MD-1 i ich funkcje

5. W kolejnym etapie ćwiczenia przełącznik przechylny na polu „

SYGNAŁ BADANY

” przełączyć w prawo.

Przełącznik obrotowy w pozycję 2 (prostowanie dwupołówkowe). Dla takiego ustawienia przełączników
na polu „

SYGNAŁ BADANY

” przełączać kolejno przełącznik „

WARTOŚĆ MIERZONA

” od pozycji „1”

do pozycji „4” odczytując za każdym razem wskazania multimetru cyfrowego oraz rejestrując kształt
sygnału (obraz w kanale 2 oscyloskopu).

6. Po wykonaniu pomiarów dla sygnału prostowanego dwupołówkowo, przełącznik obrotowy na polu

„

SYGNAŁ BADANY

” ustawić w pozycji „3” (prostowanie jednopołówkowe – dodatnia część fali

sygnału). Ponownie zmierzyć wartości parametrów amplitudowych sygnału oraz rejestrować kształt
sygnału.

7. Te same pomiary powtórzyć dla sygnału wyprostowanego jednopołówkowo, ale przy prostowaniu

ujemnej części fali sygnału (przełącznik obrotowy na polu „

SYGNAŁ BADANY

” w pozycji „4”).

8. Zmienić kształt sygnału z sinusoidalnego na prostokątny (pozostałe parametry sygnału pozostają bez

zmian) i powtórzyć całą procedurę pomiarową od punktu 4 do punktu 7 programu ćwiczenia.

9. Zmienić kształt sygnału z prostokątnego na trójkątny (pozostałe parametry sygnału pozostają bez zmian)

i powtórzyć całą procedurę pomiarową od punktu 4 do punktu 7 programu ćwiczenia.

10. Wyniki pomiarów zestawić w formie tabeli. W sprawozdaniu wyliczyć wartości odpowiednich

parametrów amplitudowych dla sygnałów wskazanych przez prowadzącego i porównać wyliczone
wartości z wartościami zmierzonymi w czasie ćwiczenia. Wyliczyć wartości odpowiednich
współczynników szczytu i kształtu na podstawie wyników pomiarów i porównać z współczynnikami
wynikającymi z obliczeń teoretycznych. Przy porównywaniu wykazać jak duży wpływ ma dokładność
pomiaru multimetru cyfrowego oraz dokładność wyznaczenia wartości sygnału z obrazu widzianego na
ekranie oscyloskopu. Określić, jaki jest wpływ składowej stałej sygnału zmiennego na wartości
wyznaczanych współczynników amplitudowych sygnału zmiennego? Odpowiedź uzasadnić Wyniki
analizy przedstawić w sprawozdaniu w punkcie „uwagi i wnioski końcowe”.

Strona 2 z 5

W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

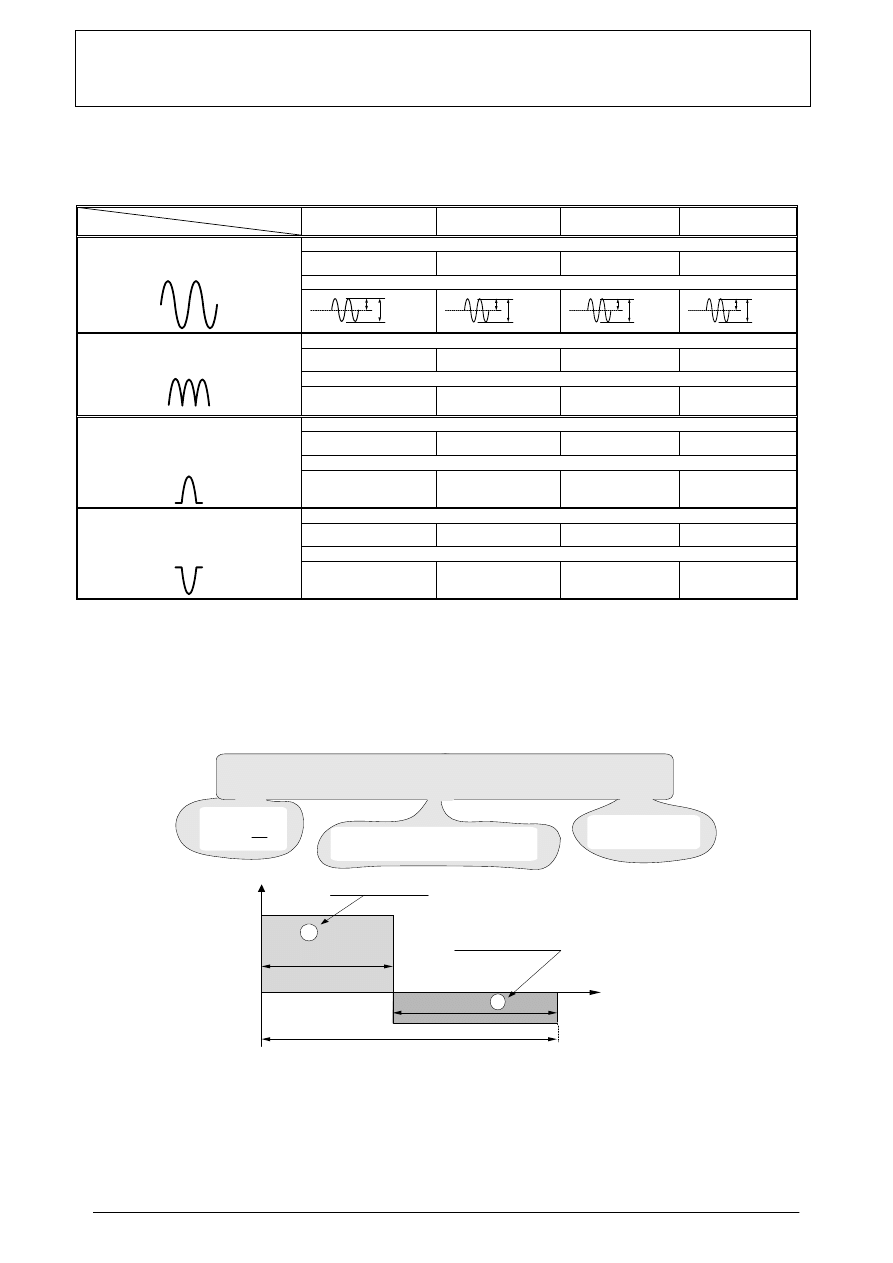
Przykładowe tabele pomiarowe

Kształt sygnału: sinusoida, (prostokąt ?, trójkąt ?)

częstotliwość: 1kHz,

A

d

= A

u

= 1 [V]

Parametr amplitudowy

Detekcja sygnału

U

sk

[V]

U

śr

[V]

U

szczyt

[V]

U

pp

[V]

Wartości napięć stałych zmierzonych multimetrem cyfrowym

0,718 0,003

1,003

1,999

Kształt sygnału obserwowanego na ekranie oscyloskopu (kanał 2)

Sygnał bez detekcji

4 dz / S

y

=0,5[V/dz]

2 dz

0 [V]

4 dz / S

y

=0,5[V/dz]

2 dz

0 [V]

4 dz / S

y

=0,5[V/dz]

2 dz

0 [V]

4 dz / S

y

=0,5[V/dz]

2 dz

0 [V]

Wartości napięć stałych zmierzonych multimetrem cyfrowym

? ?

?

?

Kształt sygnału obserwowanego na ekranie oscyloskopu (kanał 2)

Sygnał wyprostowany
Detekcja dwupołówkowa

? ?

?

?

Wartości napięć stałych zmierzonych multimetrem cyfrowym

? ?

?

?

Kształt sygnału obserwowanego na ekranie oscyloskopu (kanał 2)

Sygnał wyprostowany
Detekcja jednopołówkowa
Dodatnia połówka sygnału

? ?

?

?

Wartości napięć stałych zmierzonych multimetrem cyfrowym

? ?

?

?

Kształt sygnału obserwowanego na ekranie oscyloskopu (kanał 2)

Sygnał wyprostowany
Detekcja jednopołówkowa
Ujemna połówka sygnału

? ?

?

?

Wprowadzenie

Zachodzącą w czasie zmianę wielkości fizycznych, jakimi są prąd i napięcie nazywamy sygnałem
elektrycznym. Najczęściej spotykane sygnały elektryczne należą do grupy tak zwanych sygnałów
analogowych (ciągłych w czasie). Tym sygnałom poświęcone jest niniejsze ćwiczenie. Z sygnałem
analogowym bezpośrednio związane są jego parametry czasowe (rysunek 3) i amplitudowe (rysunek 4).

Okres sygnału

periodycznego

f

1

T

=

Faza początkowa

sygnału

Parametry czasowe analogowego sygnału

elektrycznego

Pole dodatnie S

0

u(t)

t

1

Pole ujemne S

2

t

u

t

d

+

-

T= t

d

+ t

u

Czas trwania
sygnału

ujemnej części

Czas trwania

sygnału

dodatniej części

Rys 3. Zestawienie podstawowych parametrów czasowych sygnału zmiennego i ich interpretacja fizyczna na przykładzie sygnału
prostokątnego o różnych czasach trwania dodatniej i ujemnej części sygnału.

Omawiany sygnał ma kształt fali prostokątnej, niesymetrycznej względem osi czasu, jak również o różnych
czasach trwania dodatniej (

τ

) i ujemnej części ( T –

τ

) fali. W podanym przykładzie ( T -

τ

) >

τ

. Łatwo

zauważyć, że zarówno dodatnia jak i ujemna część fali mają swoją wartość maksymalną; A

d

i A

u

. Wartość A

d

nazywana jest amplitudą dodatnią lub dodatnią wartością szczytową sygnału, a wartość A

u

amplitudą ujemną

Strona 3 z 5

W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

lub ujemną wartością szczytową. Zatem w przypadku sygnału zmiennego w czasie, jedną z wielkości
opisujących ten sygnał są jego wartości maksymalne, czyli amplitudy lub inaczej wartości szczytowe.
Suma wartości bezwzględnych amplitud, dodatniej A

d

i ujemnej A

u

przebiegu przemiennego, jest równa

wartości wielkości oznaczonej symbolem A

ss

, nazywanej inaczej wartością międzyszczytową (wartość

szczyt – szczyt). Obie wielkości tj. wartości amplitud A

d

, A

u

, jak i wartość międzyszczytowa A

ss

sygnałów

przemiennych, są proste w interpretacji (patrz rysunek 4).
Oprócz wyżej wymienionych, zmienny w czasie sygnał u(t), charakteryzują jeszcze trzy kolejne wielkości.
Nazywamy je odpowiednio:

Wartość skuteczna sygnału - nazwana w niniejszym opracowaniu jako A

sk

(w nazewnictwie

angielskojęzycznym oznaczana symbolem A

eff

). Reprezentuje ona wartość sygnału zmiennego, który może

wykonać taką samą pracę jak sygnał stałoprądowy spełniający następujący warunek A

DC

= A

sk

(gdzie A

DC

jest

wartością napięcia lub prądu stałego).

Wartość średnia z modułu wartości funkcji - wartość |u(t)|. Jest ona równa wartości średniej przebiegu

przemiennego u(t) po prostowaniu jego dodatniej i ujemnej części i w niniejszym opracowaniu oznaczana
jest symbolem A

śrb

. Taki sposób przemiany sygnału nosi nazwę prostowania pełno-okresowego lub

prostowania dwu-połówkowego. Na rysunku 4 wartość średnia z |u(t)| odpowiada wartości średniej
wyliczonej z sumy wartości pól dodatniej S

1

i ujemnej S

2

części sygnału. Jest to wartość (S

1

+S

2

) rozłożona

równomiernie na odcinku równym, co do długości, okresowi T sygnału.

Wartość średnia sygnału u(t), jest wartością wyliczaną za jeden okres dla sygnału nie poddanego

procesowi prostowania (detekcji). Na rysunku 4 omawiana wartość średnia sygnału, odpowiada wartości
średniej sumy pola powierzchni dodatniej S

1

i ujemnej S

2

części sygnału zsumowanych z przynależnymi

znakami (S

1

– S

2

). Wartość ta jest też rozłożona równomiernie na odcinku równym okresowi sygnału. W

opracowaniu ta wartość średnia jest oznaczana symbolem A

śr

.

Łatwo zauważyć, że pomiędzy wartościami wyżej wymienionych wielkości charakterystycznych dla sygnału
u(t), o kształcie jak na rysunku 4 słuszne są relacje:

A

ss

> A

d

> A

sk

> A

śrb

> A

śr

(1)

W przypadku sygnałów o kształcie innym niż pokazany na rysunku 4, podane w zależności (1)
relacje mogą być inne. Wartość każdej z wyżej omówionych wielkości charakterystycznych dla
przebiegów zmiennych, może być przedmiotem pomiaru.

Dla każdego sygnału okresowego, można wyznaczyć wartość liczbową określającą stosunek wartości
skutecznej (A

sk

) tego przebiegu do jego wartości średniej bezwzględnej (A

śrb

).

śrb

sk

A

A

K

=

(2)

Wyznaczony według wzoru (2) współczynnik K nosi nazwę współczynnika kształtu.
Podobnie można wyznaczyć stosunek wartości maksymalnej sygnału (A

d

lub A

u

) do jego wartości skutecznej

A

sk

, czyli:

.

sk

A

A

F

=

(3)

gdzie: A jest przyjętą do obliczeń bezwzględną wartością maksymalną. Dla przebiegu symetrycznego słuszne jest, że |A

d

|

= |A

u

|

= A.

Wyliczony według równania (3) współczynnik F nosi nazwę współczynnika szczytu. Między
współczynnikami szczytu i kształtu słuszne są relacje K

≥1, F ≥1, F ≥ K.

Z podanych powyżej uwag łatwo wywnioskować, że tak zdefiniowane współczynniki kształtu i szczytu są
różne dla sygnałów o różnych kształtach. Dla sygnałów o identycznych kształtach, niezależnie od
częstotliwości tych sygnałów ich amplitudy i fazy początkowej, współczynniki K i F mają tą samą wartość.
Wartości współczynników K i F, dla kilku podstawowych kształtów sygnałów elektrycznych zestawiono w
tabeli 1.
Oporność (w ogólnym przypadku impedancja) wewnętrzna źródła sygnału zmienno-prądowego jest jednym
z elementów określających wydajność energetyczną źródła. Idealne źródło napięciowe ma oporność
(impedancję) wewnętrzną o wartości równej zero (R

źr

= 0). Oznacza to, że napięcie na zaciskach źródła ma

stałą wartość równą wartości SEM (SEM-siła elektromotoryczna) tego źródła. Wartość napięcia

Strona 4 z 5

W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

wyjściowego jest niezależna od wartości oporności obciążenia dołączonego do zacisków idealnego źródła
napięcia a więc nie zależy od wartości prądu pobieranego ze źródła.

W a rto ś ć ś re d n ia

s yg n a łu A

śr

.

W a rto ś ć s k u te c z n a
s yg n a łu A

s k

.

.

W a rto ś ć ś re d n ia

z m o d u łu fu n k c ji

A

ś rb

∫

=

T

0

śr

d t

)

t

(

u

T

1

A

∫

=

T

0

2

sk

d t

)

t

(

u

T

1

A

∫

=

T

0

śrb

d t

)

t

(

u

T

1

A

M a k s ym a ln a w a rto ś ć

d o d a tn ia (a m p litu d a

d o d a tn ia ) A d .

M a k s ym a ln a w a rto ś ć

u je m n a (a m p litu d a
u je m n a )

A u .

W a rto ś ć

m ię d z ys z c z yto w a

A

s s

=

|A

d

| + |A

u

|

s yg n a łu e le k tryc z n e g o

P a ra m e try a m p litu d o w e a n a lo g o w e g o

c za s t

u (t)

A

d

A

ss

A

u

A

śrb

A

śr

A

sk

0

T

τ

P o le d o d a tn ie S

1

P o le d o d a tn ie S

1

P o le u je m n e S

2

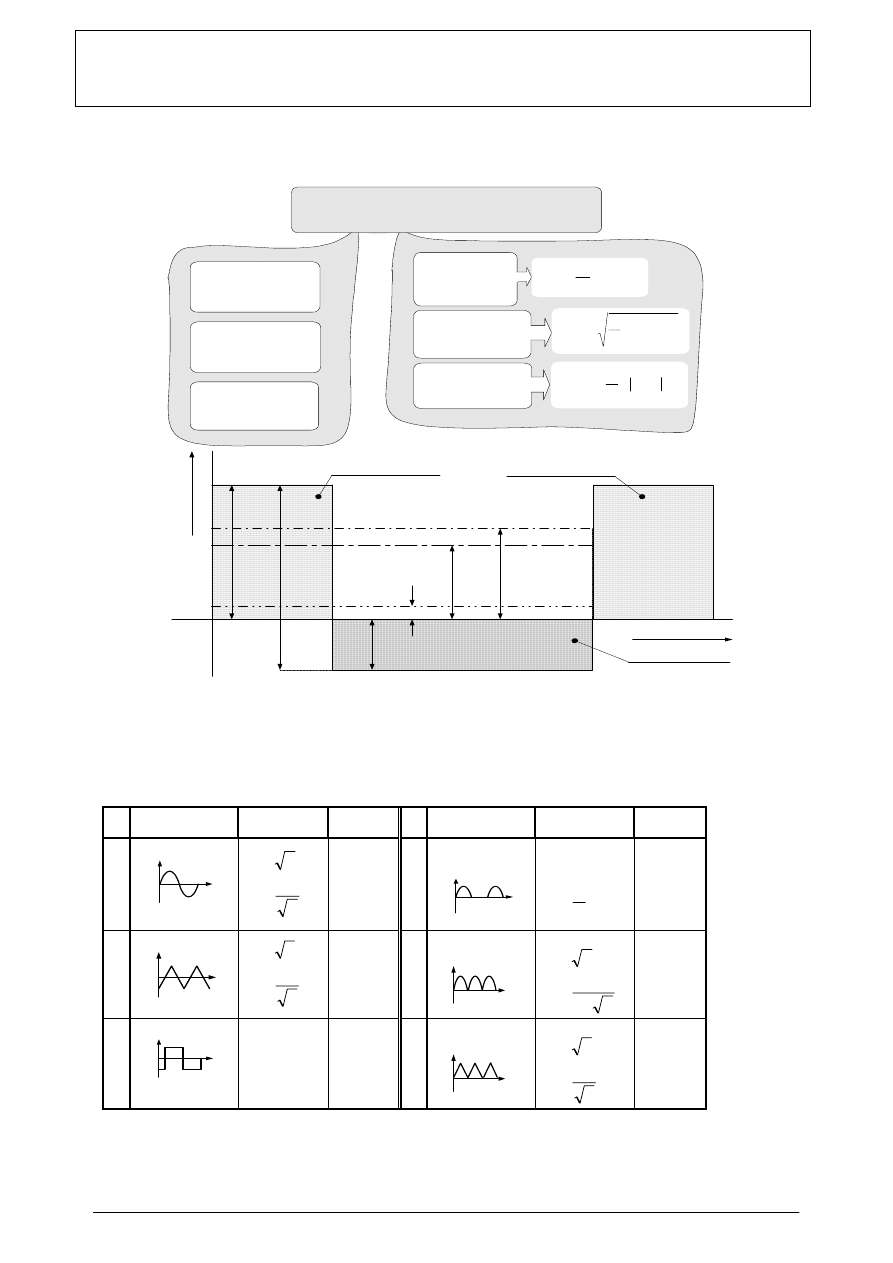
Rys 4. Zestawienie podstawowych parametrów amplitudowych sygnałów zmiennych, opisujące je zależności matematyczne,
przykład ilustrujący fizyczne znaczenie podstawowych parametrów amplitudowych (na przykładzie sygnału prostokątnego
niesymetrycznych amplitudach dodatniej i ujemnej oraz różnych czasach ich trwania).

Tabela 1. Zestawienie współczynników szczytu i kształtu dla wybranych sygnałów zmiennych.

Lp.

Kształt sygnału

Wzory

określające

współczynniki

Wartość

liczbowa

Lp.

Kształt sygnału

Wzory

określające

współczynniki

Wartość

liczbowa

1

Sinus

u(t)

t

2

F

=

8

K

π

=

F = 1.414

K = 1.111

4

Połowa sinusoidy,

prostowanie

jednopołówkowe

t

u(t)

2

F

=

2

K

π

=

F= 2
K = 1,571

2

Trójkąt

t

u(t)

3

F

=

3

2

K

=

F = 1.732

K = 1.155

5

Wyprostowana
sinusoida

u(t)

t

2

F

=

2

2

K

⋅

=

π

F= 1,414
K= 1,111

3

Prostokąt

t

u(t)

K = F = 1

6

Wyprostowany
trójkąt

u(t)

t

3

F

=

3

2

K

=

F = 1,732
K= 1,155

Rzeczywiste źródło napięciowe ma oporność wewnętrzną większą od zera (

R

źr

>0). Dołączenie do

rzeczywistego źródła oporności obciążenia

R

ob

powoduje zamknięcie obwodu i inicjuje w tym obwodzie

przepływ prądu (prąd obciążenia). Wartość prądu wyznaczamy z prawa Ohma znając wartość SEM źródła
oraz wartość sumy oporności występujących w obwodzie przepływu prądu. W najprostszym przypadku jest

Strona 5 z 5

W

YDZIAŁ

PPT

L

ABORATORIUM Z

E

LEKTROTECHNIKI I

E

LEKTRONIKI

Ćwiczenie nr 6. Okresowe sygnały elektryczne, parametry amplitudowe

D-1

to suma wartości szeregowo połączonych oporności

R

źr

i

R

ob

. Praktycznie, każdy bardziej złożony obwód

obciążający źródło, można sprowadzić do tego najprostszego przypadku. Prąd obciążenia, przepływając
przez oporność wewnętrzną źródła powoduje, powstanie spadku napięcia na tej oporności (prawo Ohma).
Wiemy, że suma spadków napięć w zamkniętym oczku jest równa zeru (prawo Kirchhoffa). Zatem można
bez problemów wyznaczyć wartość napięcia występującego na zaciskach rzeczywistego źródła
napięciowego. Z wyliczeń wynika, że wartość napięcia na zaciskach wyjściowych rzeczywistego źródła
napięcia jest tym mniejsza od wartości SEM źródła im większa jest wartość oporności wewnętrznej źródła
oraz im większa jest wartość prądu pobieranego ze źródła. Spadek napięcia występujący na oporności
wewnętrznej źródła oznacza stratę energii. Wartość tej energii jest wprost proporcjonalna do wartości
oporności wewnętrznej źródła napięcia oraz kwadratu wartości skutecznej prądu płynącego przez tą
oporność.
Idealne źródło prądowe ma oporność wewnętrzną nieskończenie dużą (

R

źr

=

∞). Oznacza to, że idealne źródło

prądu dostarcza do obciążenia stałej wartości prądu niezależnej od wartości oporności obciążenia
dołączonego do tego źródła.

Zadania kontrolne (minima programowe do przygotowania)

Minimalny zakres wiadomości teoretycznych studenta przystępującego realizacji do ćwiczenia
laboratoryjnego „sygnały zmiennoprądowe” dotyczy zagadnień takich jak:

pojęcie sygnału elektrycznego

zmiennego i stałego, jednostki napięcia i prądu (wielokrotności i pod-wielokrotności tych jednostek),
znajomość i umiejętność interpretacji znaczenia pojęć parametry czasowe sygnału oraz parametry
amplitudowe sygnału, znajomość sposobu obliczeniowego i doświadczalnego (na podstawie obrazu sygnału
na ekranie lampy oscyloskopowej) wyznaczania wartości niektórych parametrów czasowych i
amplitudowych sygnałów analogowych (w szczególności dla sygnałów o kształcie sinusoidy, prostokąta i
trójkąta), rozumienie procesu prostowania (detekcji) sygnału. Wskazane są również wiadomości z zakresu;
oporność wewnętrzna źródła sygnału zmienno-prądowego, oporność wewnętrzna idealnego źródła napięcia i
idealnego źródła prądu, proste schematy zastępcze źródeł idealnych i rzeczywistych, wpływ wartości
oporności wewnętrznej źródła na wartość sygnału występującego na jego zaciskach, prawo Ohma, prawa
Kirchhoffa, pojęcie impedancji (część rzeczywista i urojona impedancji, zasady łączenia oporności
(połączenie szeregowe i równoległe).
Wykonanie ćwiczenia wymaga wcześniejszego opanowania w stopniu, co najmniej dostatecznym;
umiejętności praktycznej obsługi oscyloskopu, prostego generatora funkcyjnego (np. zabudowanego we
wspólnej obudowie z oscyloskopem) oraz multimetru cyfrowego.

Literatura

1. A. Jellonek, Z. Karkowski.: Miernictwo radiotechniczne. Wyd. III, WNT, Warszawa 1972r.
2. Praca zbiorowa.: Elektrotechnika i elektronika dla nieelektryków. WNT, Warszawa 1971r.
3. S. Bolkowski.: Teoria obwodów elektrycznych. WNT, Warszawa 1995r.
4. Materiał z wykładu „Podstawy Elektrotechniki i Elektroniki”

Zestaw przyrządów pomiarowych

1.

Oscyloskop analogowy, dwukanałowy

szt1.

2.

Generator funkcyjny G-432 lub wbudowany w oscyloskop

szt1.

3.

Multimetr cyfrowy typu METEX

szt1.

4.

Makieta

dydaktyczna

MD-1

szt1.

5.

Transformator zasilający

15-20V/0,5A/50Hz

szt1.

6.

Trójnik

BNC

szt1.

7.

Kabel koncentryczny „wtyk BNC-wtyk

BNC”

szt3.

8.

Kabel „wtyk radiowy-wtyk radiowy”

szt2.

Opracował: Piotr Ruszel

Instytut Inżynierii Biomedycznej i Pomiarowej Wydziału PPT Politechniki Wrocławskiej

Strona 6 z 5