Przestrzeń wektorowa

1. Pojęcia podstawowe

Wektor

Przyjmujemy, że

V

k

jest zbiorem ciągów k wyrazowych [x

1

, x

2

, … , x

k

]; ciągi te

nazywamy wektorami i oznaczamy symbolicznie

→

u

,

→

v

…..

Wektory równe

Przyjmujemy, że wektory są równe, gdy mają te same współrzędne, czyli

→

u

=

→

v

wtedy i tylko wtedy, gdy u

1

= v

1

, u

2

= v

2

, , … , u

k

=

v

k

.

Suma wektorów. Iloczyn wektora przez liczbę

W zbiorze wektorów (ciągów ) definiujemy dodawanie i mnożenie wektora przez

liczbę następująco:

a) jeżeli

→

u

= [u

1

, u

2

, … , u

k

] oraz

→

v

= [v

1

, v

2

, … , v

k

] ,

to

→

u

+

→

v

= [u

1

+ v

1

, u

2

+ v

2

, … , u

k

+ v

k

];

b)

α

→

u

= [

α

u

1

,

α

u

2

, … ,

α

u

k

], dla

α

∈

R.

Składowe wektora

Jeżeli

→

u

= [u

1

, u

2

, … , u

k

] jest wektorem przestrzeni V

k

, to liczby u

1

, u

2

, … , u

k

nazywamy składowymi wektora

→

u

.

Wektor zerowy. Wektory przeciwne

a) Wektor [ 0, 0, …, 0] =

→

0

o zerowych składowych nazywamy wektorem zerowym.

b) Wektor -1

→

u

= -

→

u

= [- u

1

, - u

2

, … , - u

k

] nazywamy wektorem przeciwnym do

wektora

→

u

.

Wektorowa interpretacja różnych sytuacji

Zestaw zakupów: 4 bułki, 1 piwo, 0,3kg cytryn, 3 czekolady, 5 lodów można opisać

wykorzystując pojęcie wektora jako [ 4; 1; 0,3; 3; 5 ].

Podobnie kurs walut (kupno):

USD/PLN 2.8905 , EUR/PLN 4.2150 , CHF/PLN 2.7909 , EUR/USD 1.4570 opisuje wek-

tor [2.8905 , 4.2150 , 2.7909 , 1.4570].

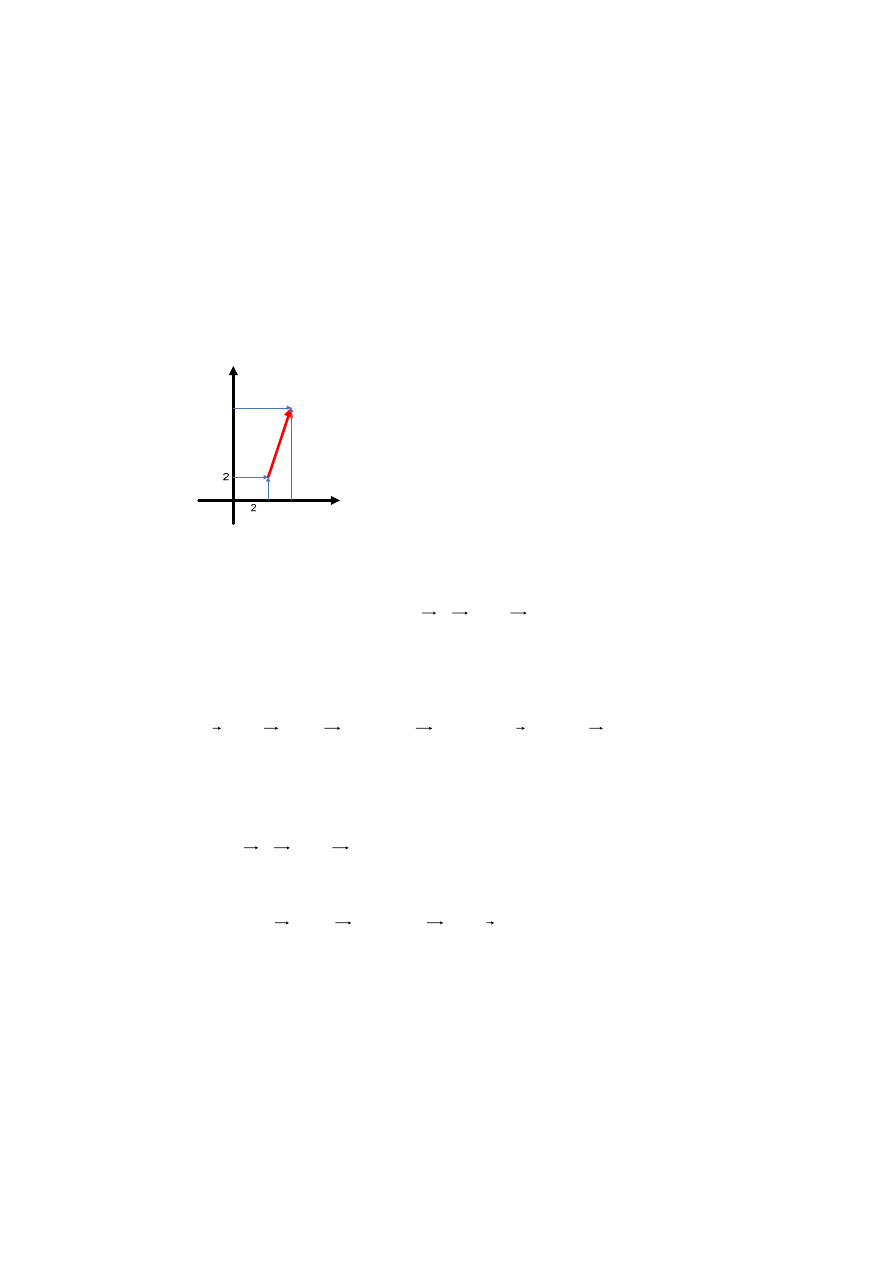
Geometrycznie: wektor [2, 6] przestrzeni V

2

w układzie współrzędnych na płasz-

czyźnie reprezentuje strzałka (rys., kolor czerwony).

Kombinacja liniowa wektorów

Kombinacją liniową n - wektorów

1

x

,

2

x

, … ,

n

x

przestrzeni

V

k

(każdy z

wektorów ma więc k składowych) o współczynnikach

α

1

,

α

2

, … ,

α

n

nazywamy

wektor

x =

α

1

1

x

+

α

2

2

x

+ …+

α

n

n

x

, inaczej x =

∑

=

n

i

i

i

x

1

α

.

Zależność, niezależność układu wektorów

Wektory

1

x

,

2

x

, … ,

n

x

są liniowo niezależne, gdy dla dowolnych

współczynników

α

1

,

α

2

, … ,

α

n

zachodzi warunek:

α

1

1

x

+

α

2

2

x

+ …+

α

n

n

x

= 0

c

c

c

c

α

1

=

α

2

= … =

α

n

= 0

W przeciwnym przypadku mówimy, że wektory te są liniowo zależne.

Twierdzenie

Wektory

1

x

,

2

x

, … ,

n

x

są liniowo zależne, gdy istnieją liczby

α

1

,

α

2

, … ,

α

n

nie

wszystkie równe 0 oraz takie, że

α

1

1

x

+

α

2

2

x

+ …+

α

n

n

x

= 0 .

2. Przykłady

Przykład 1.

Pokaż, że każdy wektor [p, q] jest kombinacją liniową wektorów [1, -2], [2, 3].

Udowodnimy ten fakt, gdy wskażemy takie liczby

α

1

,

α

2 ,

aby

α

1

[1, -2] +

α

2

[2, 3] = [p, q].

To równanie prowadzi do układu równań







=

+

−

=

+

q

p

2

1

2

1

3

2

2

α

α

α

α

Ten układ ma zawsze rozwiązanie. Jest nim para liczb

(

α

1

,

α

2

) = (

7

2

3

q

p

−

,

7

2

q

p

+

).

Zatem każdy wektor [p, q] jest kombinacją liniową wektorów [1, -2], [2, 3].

Przykład 2.

Pokaż, że wektory

1

x

= [1, -2],

2

x

= [ 2, 3] są liniowo niezależne.

Niech a, b będą liczbami rzeczywistymi i takimi, że a

1

x

+ b

2

x

= 0 .

Czyli

a [1, -2] + b [ 2, 3] = [0, 0]

Z definicji iloczynu wektora przez liczbę mamy

[1a, -2a] + [ 2b, 3b] = [0, 0]

Z definicji sumy wektorów

[1a + 2b, -2a+ 3b] = [0, 0]

Z definicji równości wektorów otrzymujemy układ równań

a + 2b = 0 i -2a+ 3b = 0

Jedynym rozwiązaniem tego układu jest para liczb (a, b) = (0, 0).

Pokazaliśmy, że

a [1, -2] + b [ 2, 3] = [0, 0]

⇔

a = 0 i b = 0. Zgodnie z podanym twierdze-

niem układ wektorów [1, -2], [ 2, 3] jest układem liniowo niezależnym.

3. Baza przestrzeni wektorowej

Definicja

Wymiarem liniowej przestrzeni wektorowej nazywamy największą liczbę liniowo

niezależnych wektorów tej przestrzeni.

Oznaczamy tę liczbę symbolem dimV.

Twierdzenie

dim R

n

= n, czyli wymiar przestrzeni wektorów o n składowych wynosi n.

Definicja

dim {

→

0

} = 0, czyli wymiar przestrzeni utworzonej z jednego wektora zerowego jest 0.

Definicja

Każdy układ n liniowo niezależnych wektorów przestrzeni n - wymiarowej nazywamy

bazą tej przestrzeni.

Przykład 3.

Pokaż, że układ wektorów

→

1

u

= [1, 0, 0],

→

2

u

= [2,1,0],

→

3

u

= [3,2,1] jest bazą

przestrzeni

R

3

.

Wystarczy sprawdzić, że wektory

→

1

u

,

→

2

u

,

→

3

u

tworzą układ liniowo niezależny,

czyli pokazać, że jedynym rozwiązaniem równania:

α

1

[1, 0, 0] +

α

2

[2, 1, 0] +

α

3

[3, 2, 1] = [0, 0, 0] jest trójka liczb

(

α

1

,

α

2

,

α

3

, ) = (0, 0, 0).

Rzeczywiście tak jest, zatem układ wektorów:

[1, 0, 0], [2, 1, 0], [3, 2, 1] jest bazą przestrzeni R

3

.

Twierdzenie

Każdy wektor przestrzeni wektorowej n - wymiarowej

jest kombinacją liniową

wektorów bazy tej przestrzeni.

Inaczej:

Jeżeli

→

1

b

,

→

2

b

, … ,

→

n

b

jest bazą przestrzeni

V

n

oraz

→

x

jest dowolnym

wektorem

→

x

∈

V

n

to istnieją takie liczby x

1

, x

2

, …, x

n

, że

→

x

= x

1

→

1

b

+ x

2

→

2

b

+ … + x

n

→

n

b

.

Taki rozkład wektora

→

x

jest jednoznaczny. Liczby x

1

, x

2

, …, x

n

nazywamy

współrzędnymi wektora

→

x

w bazie

→

1

b

,

→

2

b

, … ,

→

n

b

.

Definicja

Bazę

→

1

b

= [1, 0, 0 … 0],

→

2

b

= [0, 1, … 0] ,

→

n

b

= [ 0, 0, …, 1] przestrzeni R

n

nazywamy

bazą standardową (podstawową) przestrzeni R

n

.

Przykład 4.

Wyznacz współrzędne wektora

→

x

= [1,4] w bazie

a)

[1,-1], [2, 3],

b)

standardowej.

a) Współrzędnymi wektora

→

x

= [1,4] w bazie

[1,-1], [2, 3], są takie liczby c

1

, c

2

, które spełniają równanie:

c

1

[1,-1] + c

2

[2, 3] = [1,4], czyli [ c

1

+ 2c

2

, - c

1

+ 3 c

2

] = [1, 4].

Skoro wektory są równe, więc ich odpowiednie składowe są równe, zatem mamy

układ równań:

c

1

+ 2c

2

= 1

i - c

1

+3c

2

= 4

Jego rozwiązaniem jest para liczb (c

1

, c

2

)

= (-1, 1).

Zatem

→

x

= [-1,1] w bazie [1,-1], [2, 3].

b) W bazie standardowej współrzędnymi wektora

→

x

są liczby: 1 (pierwsza), 4 (druga);

zatem

→

x

= [1,4] .

Ćwiczenia

1. a) Dobierz tak liczby x, y, by każdy z wektorów:

[ 2x , -3y], [2x – y, 4x – 2y], [ -4x + 3y -2, x – y +5] był równy wektorowi [-3, 4].

b) Przedstaw te wektory w układzie współrzędnych.

2. W banku Och-Ach ulokowały swoje oszczędności osoby A: 230 zł, B: 85 zł; C: 100 zł. Za-

rząd banku postanowił zwiększyć ich wkłady o 20%. Jednak urzędnik zmniejszył o 20%.

zamiast je zwiększyć. Gdy pomyłka wyszła na jaw, postanowił każdą z otrzymanych po

zmniejszeniu kwot zwiększyć o 20%. Jak sądzisz, czy klienci banku dostrzegli skutki tych

operacji bankowych. Opisz tę sytuację w języku wektorów.

3. W ciągu jednego dnia kurs walut USD/PLN: 2.89 , EUR/PLN: 4.21 , CHF/PLN: 2.79 ,

EUR/USD: 1.45 zmienił się następująco: USD/PLN: 0,01

↑

, EUR/PLN: 0,02

↓

,

CHF/PLN: 0,03

↓

, EUR/USD: 0,02

↑

. Opisz tę sytuację w języku wektorów.

4. Stan wód w zbiornikach A, B, C, D, E opisuje wektor [ 4, -3, 0, 5, 1]. Po ostatnich opadach

stan wód w tych zbiornikach opisuje wektor [ 3, 3, 5, 4, -2]. Scharakteryzuj zaszłe zmia-

ny. Opisz tę sytuację w języku wektorów.

5. Paragon zakupów przedstawia ile produktów kupiono, ceny jednostkowe tych produktów,

kwotę płaconą za dany produkt oraz pobierany podatek VAT w procentach. Wybierz kilka

produktów i ułóż paragon zakupów. Opisz tę sytuację w języku wektorów.

6. Przedstaw wektor [ -3, 2, 0] jako kombinację liniową wektorów:

a) [ -2, 1, 0], [ 0, 2, -1], [ 0, 1, 1] , b) [ -2, 0, 0], [ 0, 0, -1], [ 0, 3, 0] .

7. Zinterpretuj geometrycznie w układzie współrzędnych:

a) sumę wektorów [ -2, 1], [ 2, 6],

b) iloczyn wektora [ -2, 1] przez liczbę 3; wektora [ 2, 6] przez liczbę -2; wektora [ -2, 1]

przez liczbę 0; wektora [ 2, 6] przez liczbę -1.

8. Pokaż, że układ wektorów [ -2, 1, 3], [ -4, 2, 6], [ 6, -3, -9] jest układem liniowo zależ-

nym.

9. Pokaż, że układ wektorów [ -2, 1], [ 2, 6] jest układem liniowo niezależnym. Zinterpretuj

ten fakt geometrycznie w układzie współrzędnych.

10. Wskaż kilka baz przestrzeni: a) R

2

, b) R

4

.