Spis treści

DZIAŁ DODATKOWY...................................................................................... 2

Dodatkowe, powtórzeniowe zadania z rozwiązaniami...........................................2

Wielomiany i funkcje wymierne................................................................. 2

DZIAŁ DODATKOWY

Dodatkowe, powtórzeniowe zadania z rozwiązaniami.

Wielomiany i funkcje wymierne.

Zadanie I

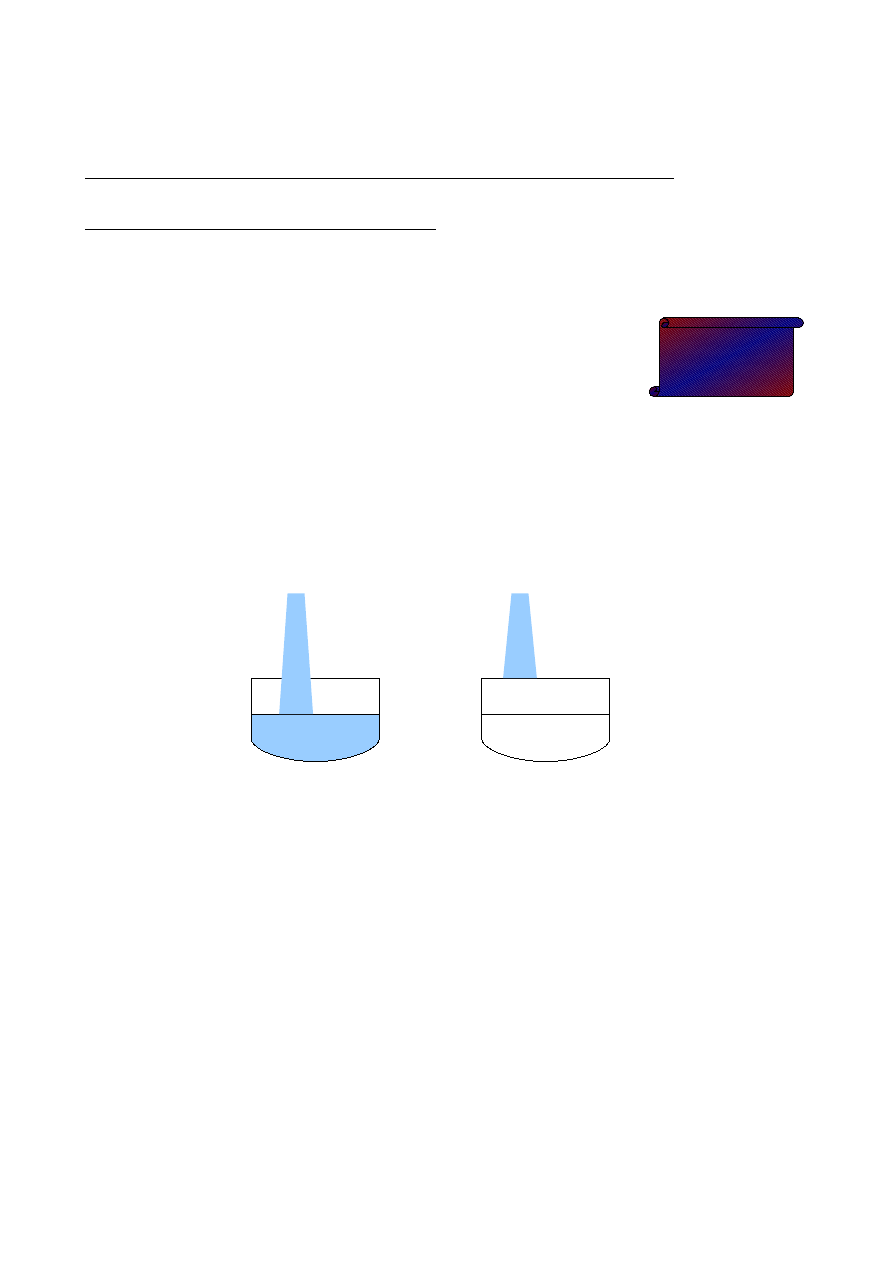
Do dwóch basenów nalewana jest woda. Do pierwszego z szybkością 100 l/h,
do drugiego 150 l/h. W pierwszym było początkowo 500 l, natomiast drugi był
pusty. Nalewanie rozpoczęto w tym samym momencie. Po jakim czasie w
basenach będzie taka sama ilość wody? Oblicz tę ilość.

Rysunek

Rozwiązanie.
Oznaczenia:

t

- czas w godzinach

a

1

=

0,1

- szybkość nalewania wody do pierwszego basenu (w tysiącach litrów

na godzinę)

a

2

=

0,15

- szybkość nalewania wody do drugiego basenu (w tysiącach litrów

na godzinę)

b

1

=

0,5

- początkowa ilość wody w pierwszym basenie (w tysiącach litrów)

b

2

=

0

- początkowa ilość wody w drugim basenie

L

1



t 

- ilość wody w pierwszym basenie w zależności od czasu

ZADANIE

Basen 1

Basen 2

100 l/h

150 l/h

500 l

0 l

L

2



t

- ilość wody w drugim basenie w zależności od czasu

Określamy funkcje

L

1



t 

oraz

L

2



t

.

L

1



t =a

1

⋅

tb

1

t≥0

L

1



t =0,1⋅t0,5

t≥0

L

2



t=a

2

⋅

tb

2

t≥0

L

2



t=0,15⋅t

t≥0

Szukamy takiej wartości

t

, dla której

L

1



t =L

2



t

.

L

1



t =L

2



t

0,1⋅t0,5=0,15⋅t

0,05⋅t=0,5

t=10

Po dziesięciu godzinach od momentu rozpoczęcia wypełniania basenów ilość
wody w obydwu z nich będzie sobie równa.

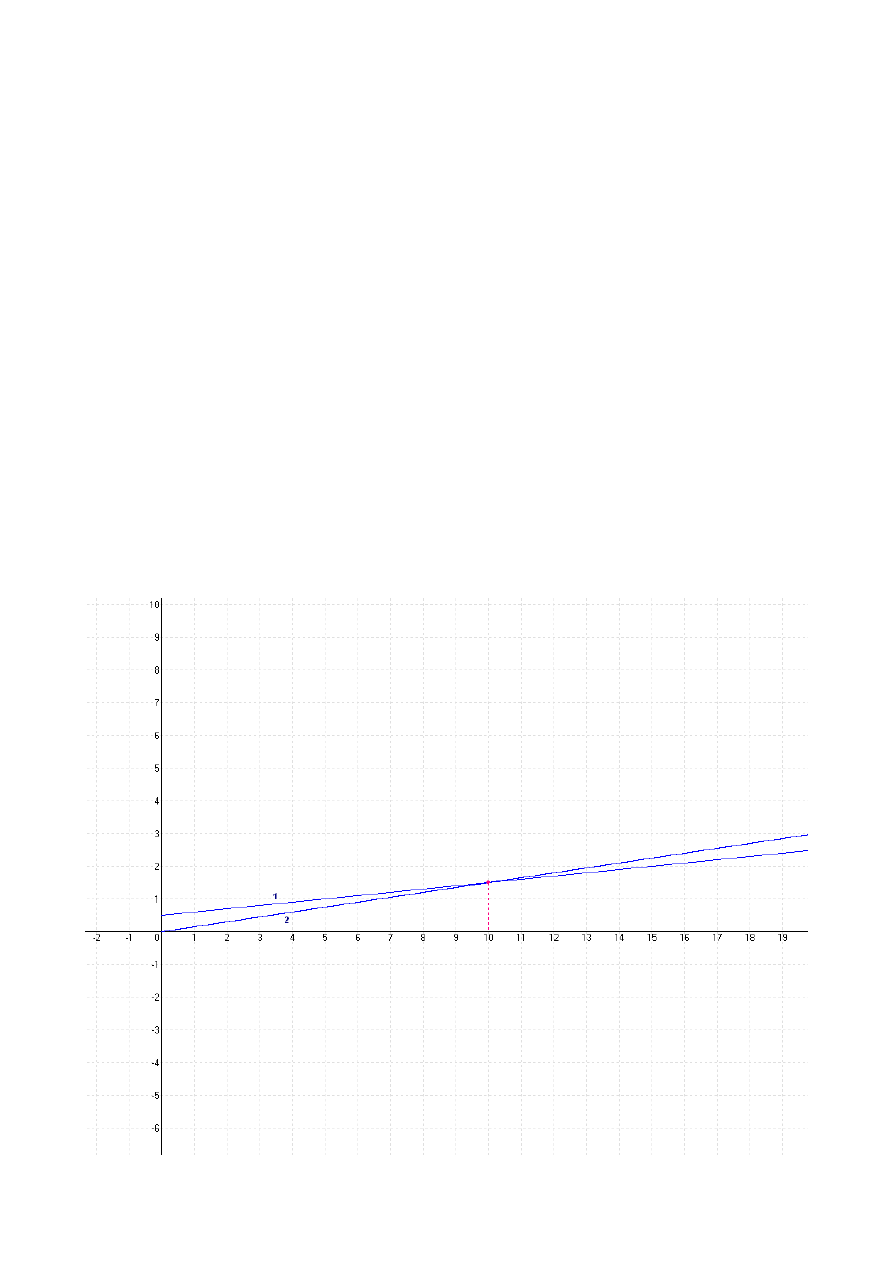
Zadanie to mogliśmy także rozwiązać graficznie. Narysujmy układ
współrzędnych, w którym oś OX odpowiada za czas (w godzinach), natomiast
oś OY za ilość wody (w tysiącach litrów).

Nanieśliśmy na wykres dwie funkcje liniowe:
1:

L

1



t =0,1⋅t0,5

2:

L

2



t=0,15⋅t

Zauważmy, że

t≥0

.

Funkcje te przecinają się w punkcie odpowiadającemu argumentowi

t=10

.

Obliczamy ilość wody po czasie 10 h.

L

1



10=0,1⋅100,5=1,5

Odpowiedź: Po czasie 10 godzin w obu basenach będzie ta sama ilość wody
równa 1500 l.

Zadanie II

Dana jest funkcja kwadratowa

f  x =

1
8

x

2



1
4

x−

35

8

. Narysuj wykres oraz

znajdź:

1. dziedzinę oraz przeciwdziedzinę funkcji,
2. miejsca zerowe (o ile istnieją),
3. przedziały monotoniczności,
4. najmniejszą i największą wartość funkcji w przedziale

< 1 ;5 >

,

5. najmniejszą i największą wartość funkcji,
6. zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie,

ujemne, niedodatnie, nieujemne.

Rozwiązanie.
Przekształcamy wzór funkcji do postaci iloczynowej.

f  x =

1
8

x

2



1
4

x−

35

8

f  x =

1
8

⋅

x

2



2 x−35

f  x =

1
8

⋅

x7⋅ x−5

ZADANIE

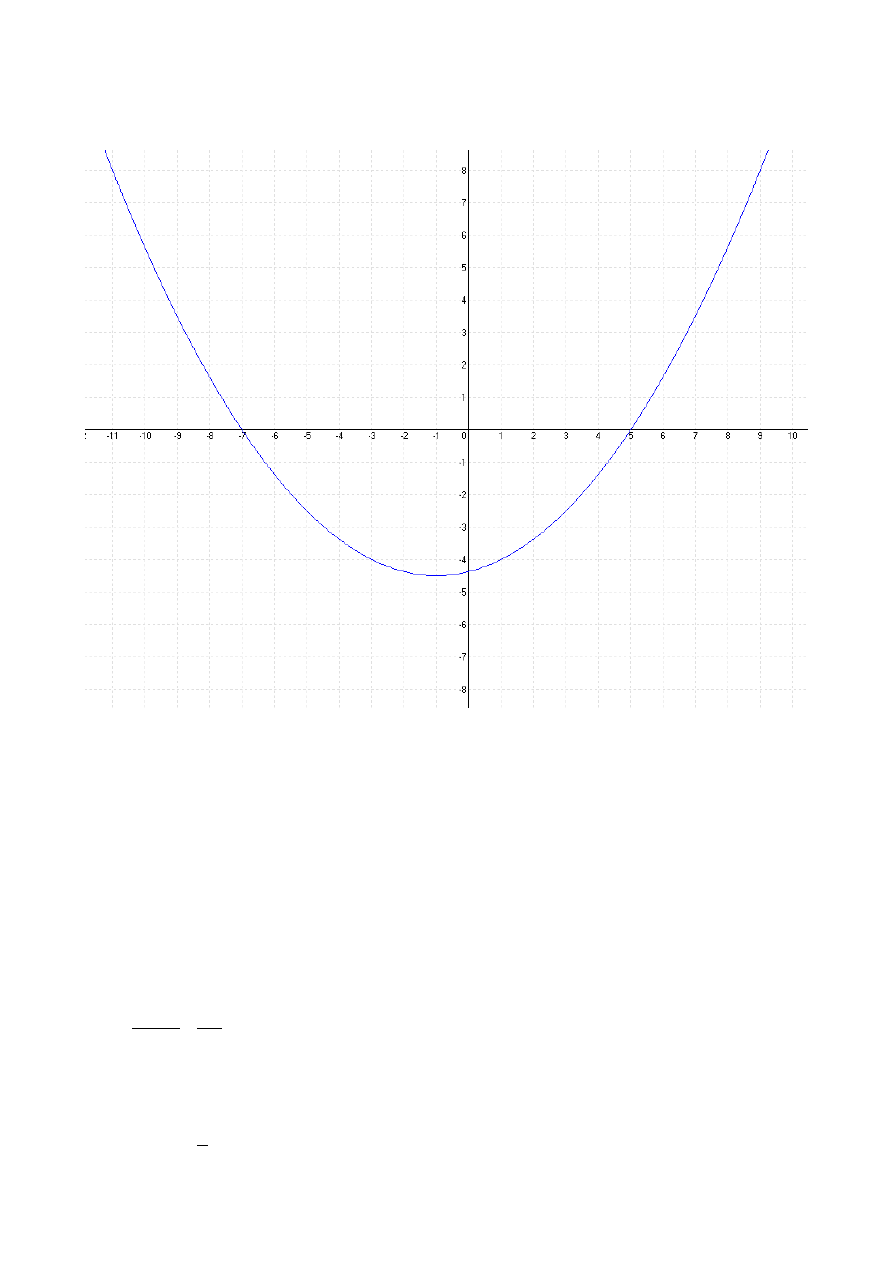
Rysujemy wykres funkcji.

1. Wyznaczamy dziedzinę oraz przeciwdziedzinę.

Dziedziną każdej funkcji kwadratowej jest zbiór liczb rzeczywistych.

D

f

=

R

Aby wyznaczyć przeciwdziedzinę musimy znać wartość w wierzchołku
wykresu funkcji. Z własności funkcji kwadratowych wynika, że wierzchołek
ma współrzędną x równą średniej arytmetycznej pierwiastków (jeśli je
posiada).

x

w

- współrzędna x wierzchołka wykresu funkcji

x

w

=

−

75

2

=

−

2

2

=−

1

Wyznaczamy współrzędną y wierzchołka.

y

w

- współrzędna y wierzchołka wykresu funkcji

y

w

=

f −1=

1
8

⋅−

17⋅−1−5

y

w

=

f −1=

1
8

⋅

6⋅−6

y

w

=

f −1=−

36

8

=−

4

1
2

y

w

=−

4

1
2

Przeciwdziedzina funkcji:

D

f

−

1

=

<−4

1
2

;∞ )

2. Wyznaczamy miejsca zerowe funkcji.

Miejsca zerowe wyznaczamy bezpośrednio z postaci iloczynowej:

f  x =

1
8

⋅

x7⋅ x−5

x

0

=−

7

oraz

x

0

=

5

3. Wyznaczamy przedziały monotoniczności.

Funkcja jest malejąca w przedziale

(−∞ ;−1 >

.

Funkcja jest rosnąca w przedziale

<−1 ;∞ )

.

4. Wyznaczamy największą i najmniejszą wartość funkcji w przedziale

< 1 ;5 >

.

Funkcja jest w tym przedziale rosnąca więc najmniejszą wartość przyjmuje dla

x=1

, natomiast największą dla

x=5

.

f

min < 1; 5 >

=

f 1=

1
8

⋅

17⋅1−5

f 1=

1
8

⋅

8⋅−4=−4

f

min < 1; 5 >

=−

4

f

max <1 ; 5 >

=

f 5=

1
8

⋅

57⋅5−5

f 5=0

f

max <1 ; 5 >

=

0

5. Wyznaczamy najmniejszą i największą wartość funkcji.

Najmniejsza wartość funkcji jest równa

−

4

1
2

.

Funkcja nie posiada największej wartości.

6. Wyznaczamy zbiór argumentów, dla których funkcja przyjmuje wartości

dodatnie, ujemne, niedodatnie, nieujemne.

Funkcja przyjmuje wartości dodatnie dla

x ∈(−∞ ;−7 )∪(5 ;∞ )

.

Funkcja przyjmuje wartości ujemne dla

x ∈(−7 ;5 )

.

Funkcja przyjmuje wartości nieujemne dla

x ∈(−∞ ;−7 >∪< 5 ;∞ )

.

Funkcja przyjmuje wartości niedodatnie dla

x ∈<−7 ;5 >

.

Zadanie III

Rozwiąż układ równań:

y=x

2



2x

y=−x

2



3x6

Rozwiązanie.
Można rozwiązać układ równań na dwa sposoby: analitycznie i graficznie.

Rozwiązywanie analityczne:

y=x

2



2x

y=−x

2



3x6

x

2



2x=−x

2



3x6

2x

2

−

x−6=0

Δ=−1

2

−

4⋅2⋅−6=148=49



Δ=



49=7

ZADANIE

x

1

=

1−



Δ

4

=

1−7

4

=

−

6

4

=−

3

2

x

2

=

1



Δ

4

=

17

4

=

8
4

=

2

Dla

x

1

wyznaczamy

y

1

. Podstawiamy

x

1

do równania

y=x

2



2x

.

y

1

=

x

1

2



2x

1

y

1

=



−

3
2



2



2⋅



−

3
2



y

1

=

9
4

−

3=−

3
4

Dla

x

2

wyznaczamy

y

2

. Podstawiamy

x

2

do równania

y=x

2



2x

.

y

2

=

x

2

2



2x

2

y

2

=

2

2



2⋅2=44=8

Rozwiązania:

1:

x=−

3
2

∧

y=−

3
4

2:

x=2 ∧ y=8

Rozwiązanie graficzne.
Rysujemy wykresy dwóch funkcji:

y=x

2



2x

y=−x

2



3x6

w jednym układzie współrzędnych.

Punkty przecięcia się wykresów są rozwiązaniami układu równań. Możemy
porównać wynik z rozwiązaniem analitycznym.

Wykres:

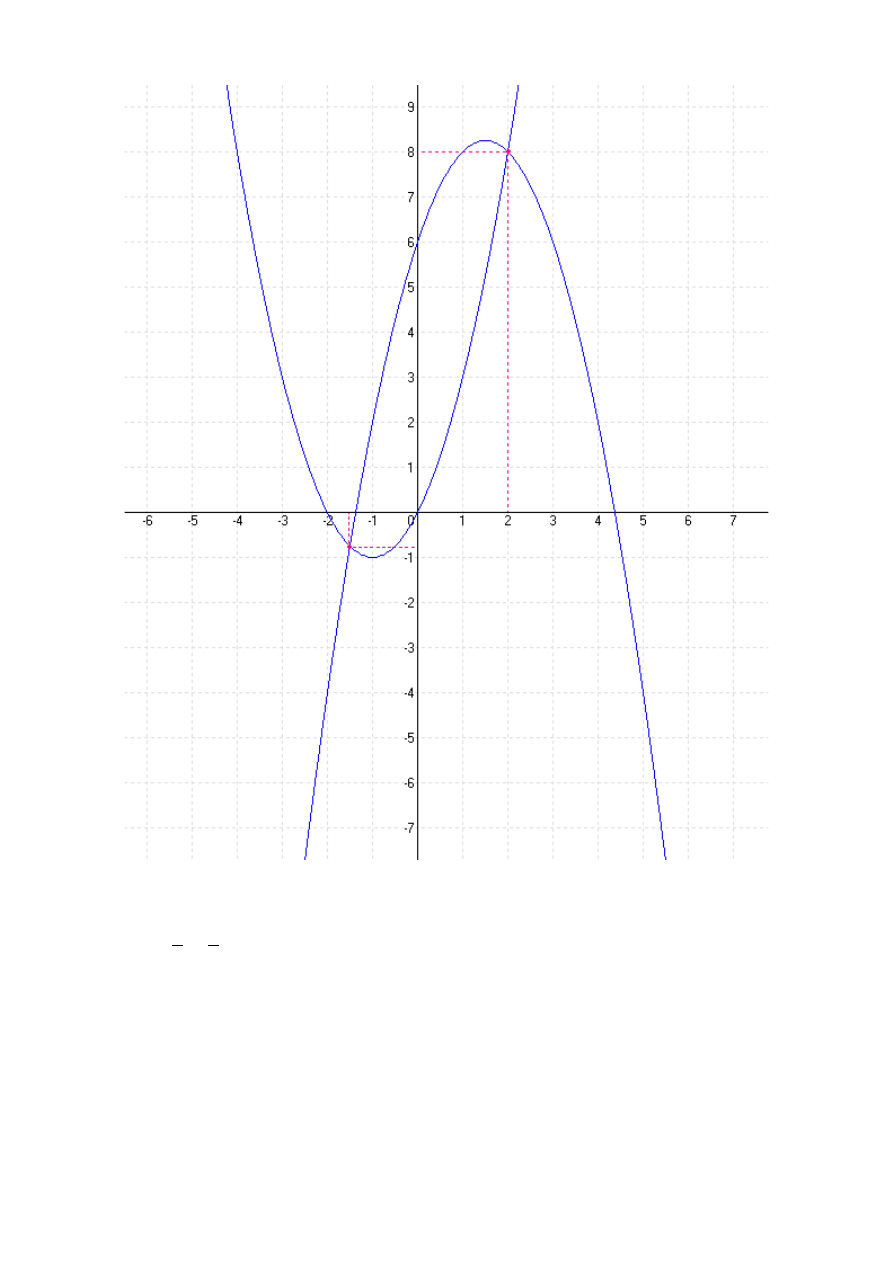
Punkty przecięcia:

1:

−

3
2

,−

3
4



2:



2 ,8

Uzyskaliśmy identyczne rozwiązania układu równań.

Zadanie IV

Dane są liczby n i k takie, że



n
k



=



n

15



,

k ≠15

oraz



15

k



=

15

.

Rozwiązanie.

Równość



n
k



=



n

15



informuje nas o tym, że

k =15

lub

k =n−15

.

Drugi warunek

k ≠15

.

Równość



16

k



=

16

stawia nowy warunek:

k =1

lub

k =15

.

Zbieramy wszystkie warunki:

[

k =15∨k =n−15]∧k ≠15∧[k =1∨k =15]

[

k =n−15]∧[k =1]

Otrzymaliśmy, że

k =1

oraz

k =n−15

, więc:

k =n−15

1=n−15

n=16

Sprawdzamy warunki dla

n=16

oraz

k =1

:



n
k



=



n

15



⇔



16

1



=



16
15



=

16

k ≠15



15

k



=

15

⇔



15

1



=

15

Odpowiedź:

k =1

,

n=16

.

Zadanie V

Dane jest funkcja

y=

2x4
5x1

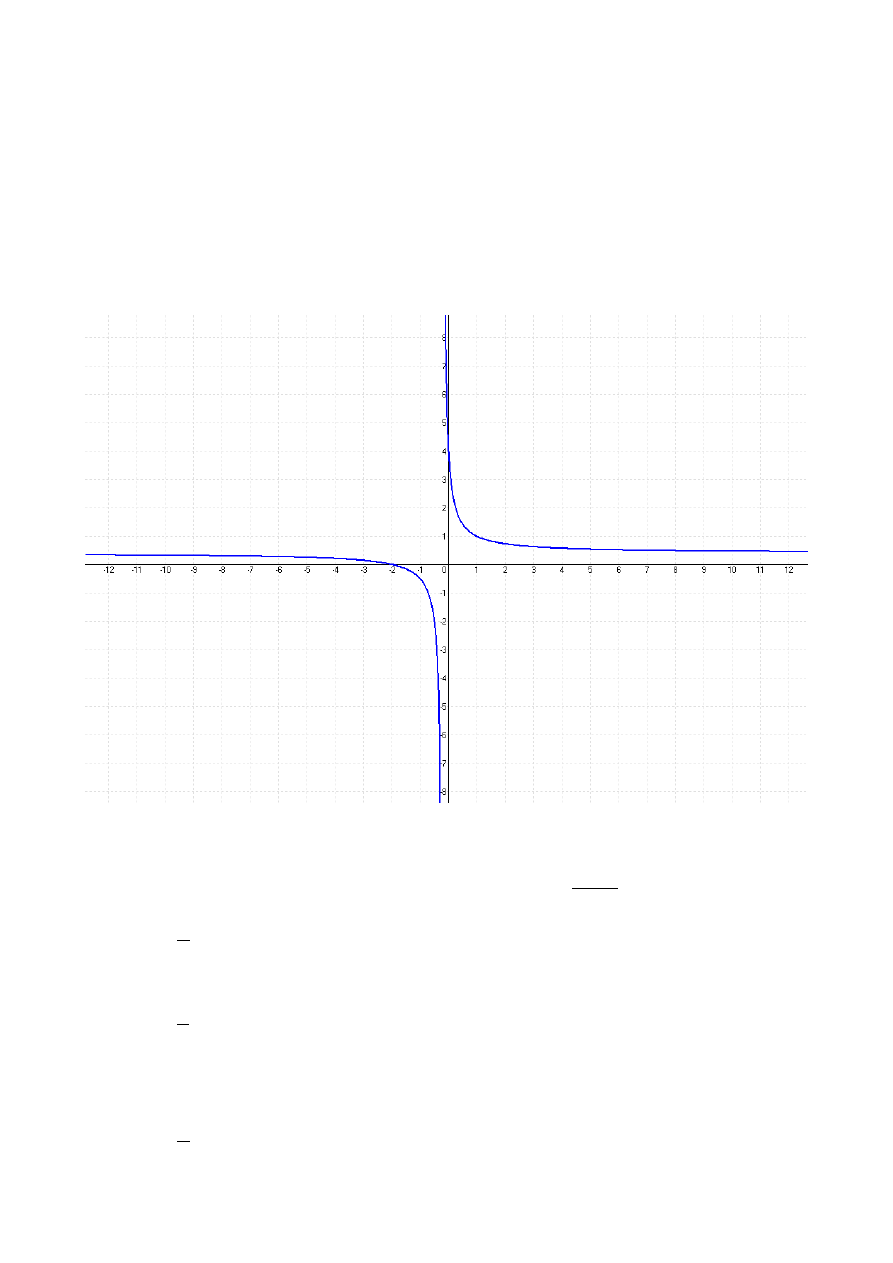
. Naszkicuj wykres funkcji.

ZADANIE

ZADANIE

Wyznacz:

1. dziedzinę i przeciwdziedzinę,
2. miejsce zerowe,
3. przedziały monotoniczności.

Rozwiązanie.
Wykres funkcji:

1. Wyznaczamy dziedzinę oraz przeciwdziedzinę funkcji.

Pamiętamy, że dziedzina funkcji homograficznej

y=

axb

cxd

jest następująca:

D=R∖ {−

d

c

}

Przeciwdziedzina ma natomiast postać:

D

−

1

=

R ∖{

a

c

}

Obliczamy dziedzinę funkcji.

D=R∖ {−

d

c

}

D=R∖ {−

1
5

}

Obliczamy przeciwdziedzinę funkcji.

D

−

1

=

R ∖{

a

c

}

D

−

1

=

R ∖ {

2
5

}

2. Wyznaczamy miejsce zerowe.

y=0
2x4
5x1

=

0

2x4=0 ∧ 5x1≠0

x=−2 ∧ x≠−

1
5

x=−2

3. Wyznaczamy przedziały monotoniczności.

Funkcja jest malejąca w całej dziedzinie, tzn. dla:

x ∈R∖ {−

1
5

}

Zadanie VI

Narysuj wykresy funkcji:

1.

f  x =−x

2

−

x−1

2.

f  x =3x

2

−

4x1

3.

f  x =−

1

2

x

2

−

1
4

x4

4.

f  x =

1

10

⋅

3x−4⋅5x12

ZADANIE

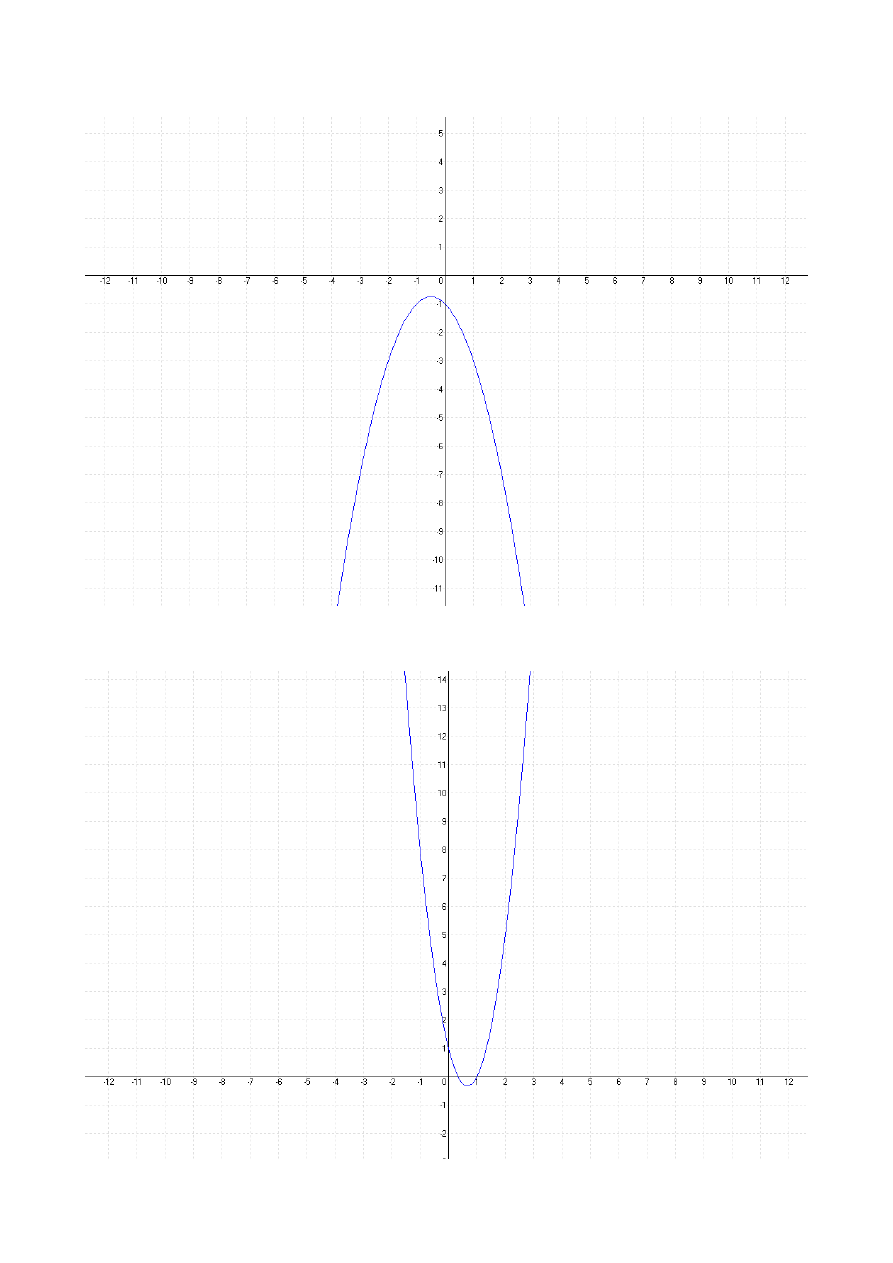
Wykres funkcji

f  x =−x

2

−

x−1

.

Wykres funkcji

f  x =3x

2

−

4x1

.

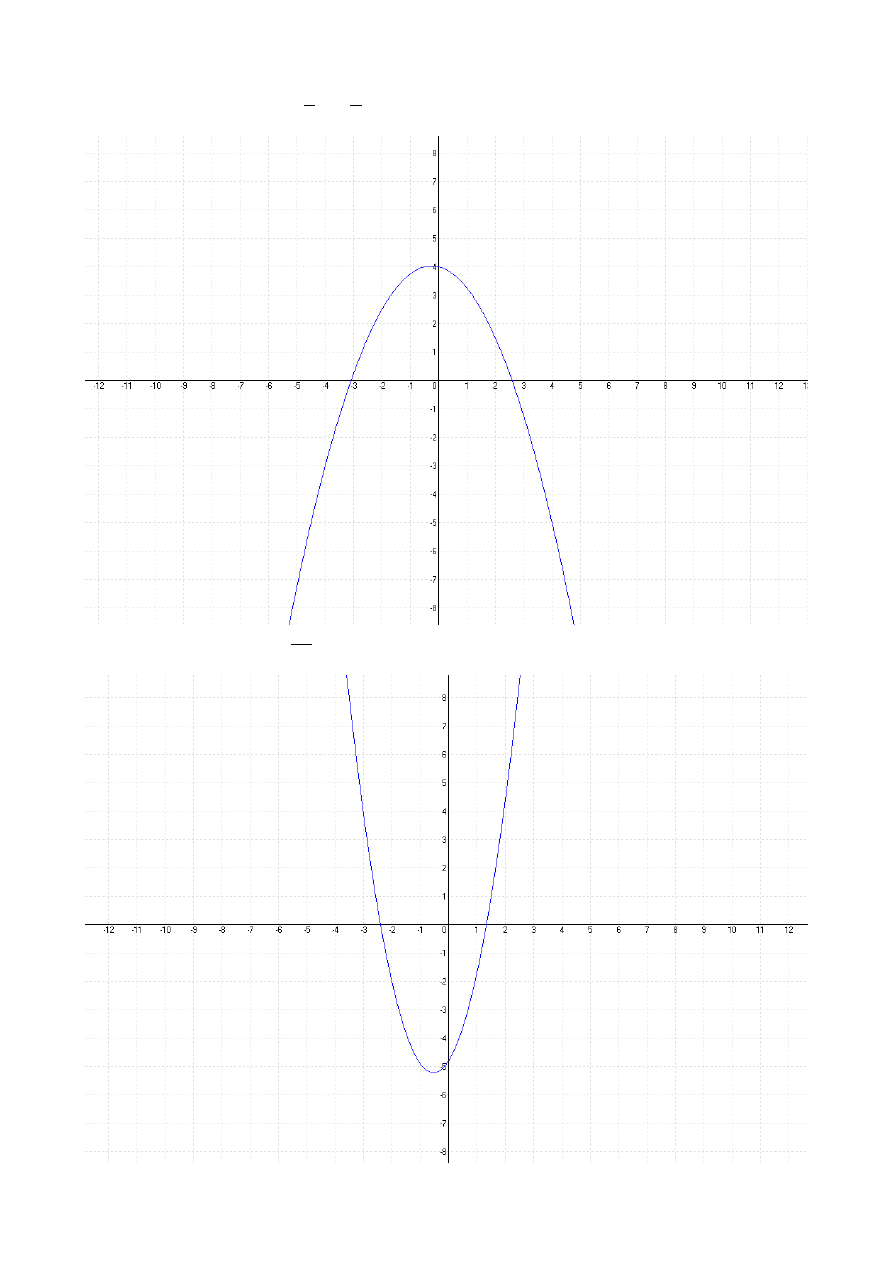
Wykres funkcji

f  x =−

1

2

x

2

−

1
4

x4

.

Wykres funkcji

f  x =

1

10

⋅

3x−4⋅5x12

.