Gliwice 2010

Całkowanie numeryczne

Metody całkowania numerycznego



Kwadratury interpolacyjne:

- metoda prostokątów

- metoda trapezów

- metoda Simpsona

Gliwice 2010



Wzory Cotesa



Kwadratury Gaussa



Kubatury Gaussa (całki podwójne)



Metoda Monte Carlo

Całkowanie numeryczne

Gliwice 2010

Kwadratury interpolacyjne

Gliwice 2010

Rozpatrujemy funkcję

f (x)

ciągłą i ograniczoną w przedziale

domkniętym

[a, b]

.

Kwadratury interpolacyjne

Przedział

[a, b]

dzielimy na skończoną liczbę podprzedziałów,

wyróżniając na osi

x

zbiór punktów

0

1

2

1

i

i

n

a

x

x

x

x

x

x

b





 



 







Punkty

x

i

,

i = 0, 1, … n

tworzą siatkę o stałym kroku (z reguły)

1

const

i

i

h

x

x





 

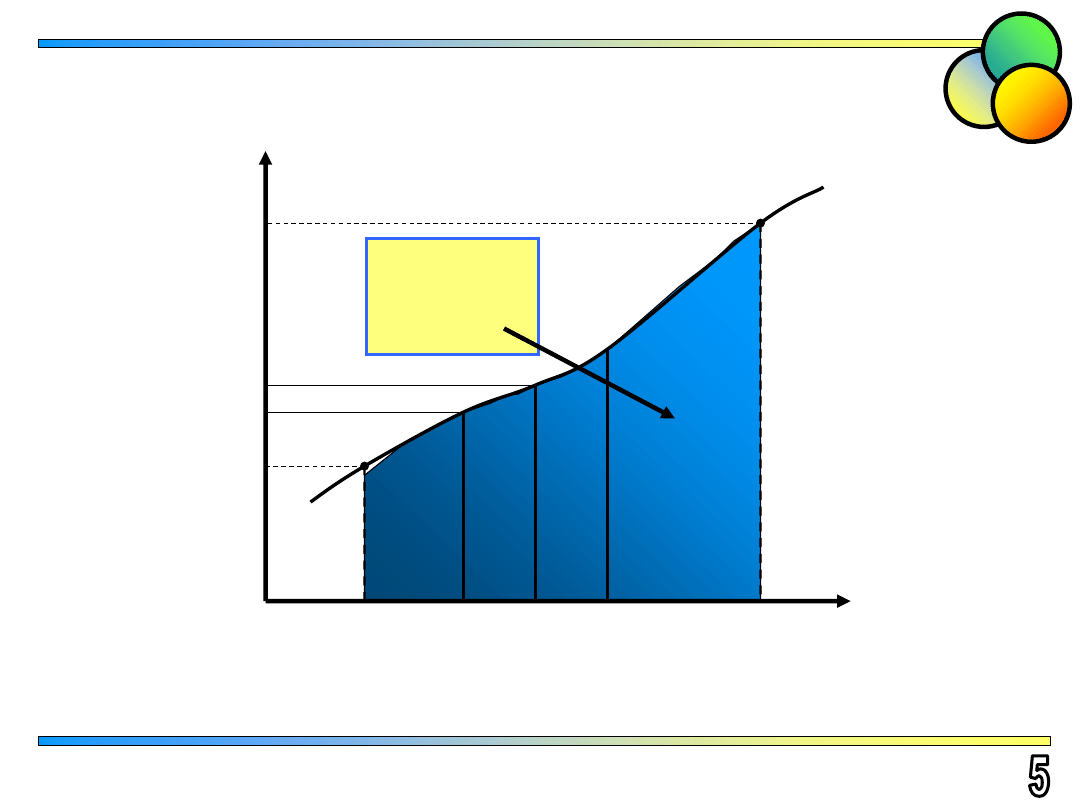
Gliwice 2010

Kwadratury interpolacyjne

Kwadratury interpolacyjne

a = x

0

x

n

= b

x

i

x

i +1

x

i +2

y

i

y

i +1

x

f (x)

σ

i

σ

i +1

y

n

= f(b)

y

0

= f(a)

0

( ) d

n

x

b

x

a

f x

x







Gliwice 2010

Kwadratury interpolacyjne

Z własności całki oznaczonej wynika, że

1

0

1

0

( ) d

( ) d

i

n

i

x

x

b

n

i

x

a

x

f x

x

f x

x



















Oznaczenie

1

( ) d

i

i

x

i

x

f x

x









Gliwice 2010

Kwadratury interpolacyjne

Istota metody kwadratur interpolacyjnych

przybliżenie funkcji podcałkowej

f (x)

w przedziale

[x

i

, x

i+1

]

lub przedziale odpowiednio poszerzonym wzorem interpolacyjnym

1

1

( ) d

( ) d

i

i

i

i

x

x

i

x

x

f x

x

W x

x















W (x)

- wielomian interpolacyjny

Gliwice 2010

Kwadratury interpolacyjne

Wyprowadzenie wzorów przybliżających wartość

całki w przedziale

[a, b]

wielomian interpolacyjny

I wzór Newtona

2

(

1)

( )

2!

i

i

i

q q

W x

y

q y

y



   





gdzie

i

x

x

q

h





Gliwice 2010

Metoda prostokątów

Gliwice 2010

Metoda prostokątów

Niech

Oznacza to:

f (x)

w przedziale

[x

i

, x

i+1

]

jest przybliżona wielomianem

interpolacyjnym ograniczonym do pierwszego składnika

( )

i

W x

y



1

[

,

]

i

i

x

x

x





f (x)

na odcinku

[x

i

, x

i+1

]

zastępujemy linią poziomą

1

1

( ) d

d

i

i

i

i

x

x

i

i

x

x

f x

x

y x















Gliwice 2010

Metoda prostokątów

Wprowadzamy podstawienie

Otrzymujemy

1

1

,

d

d ,

0,

1

i

i

i

x

x

q

q

x

x

x

q

x

x

q

h

h









  



 

1

1

0

d

d

i

i

x

i

i

i

i

x

y x

h y q

h y















1

1

0

0

( ) d

b

n

n

i

i

i

i

a

f x

x

h

y





















czyli

Gliwice 2010

Metoda prostokątów

Wzór prostokątów:

1

0

( ) d

b

n

i

i

a

f x

x h

y











Gliwice 2010

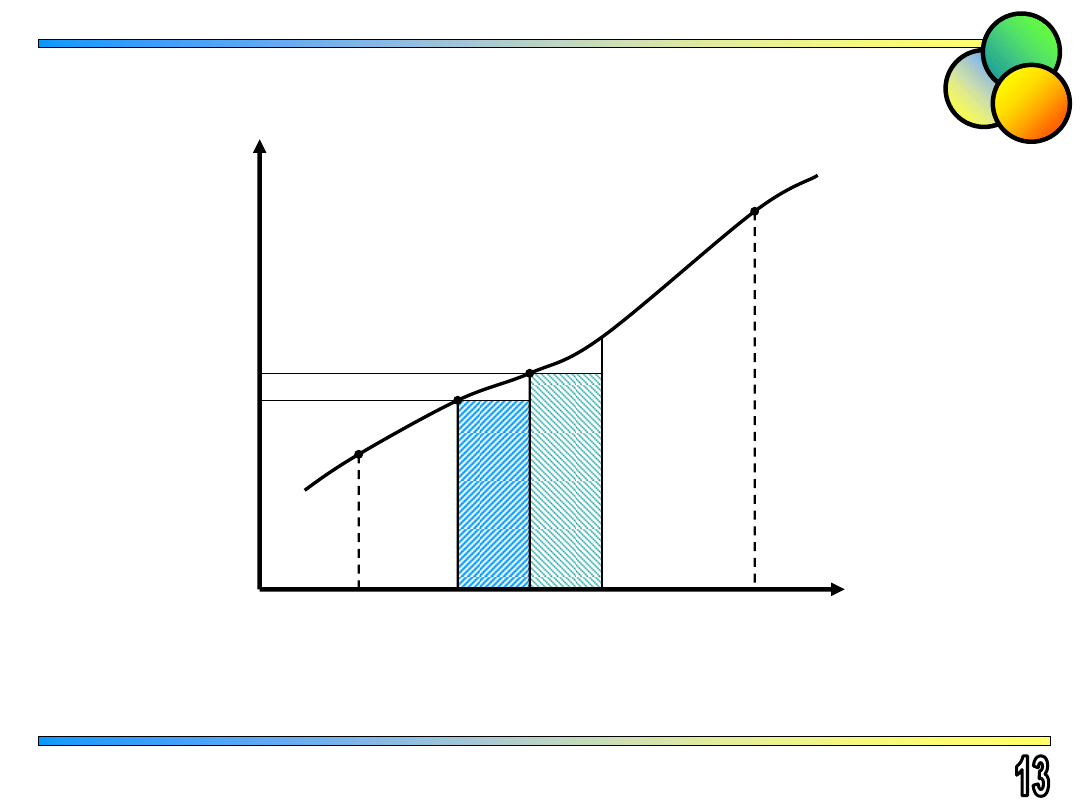
Metoda prostokątów

Metoda prostokątów

a = x

0

x

n

= b

x

i

x

i+1

x

i+2

y

i

y

i+1

x

f(x)

σ

i+1

σ

i

Gliwice 2010

Metoda trapezów

Gliwice 2010

Metoda trapezów

Niech

Oznacza to:

f (x)

w przedziale

[x

i

, x

i + 1

]

jest przybliżona wielomianem

interpolacyjnym

ograniczonym

do

dwóch

pierwszych

składników

( )

i

i

W x

y

q y

  

1

[

,

]

i

i

x

x

x





1

1

( ) d

(

) d

i

i

i

i

x

x

i

i

i

x

x

f x

x

y

q

y

x











 





Gliwice 2010

Metoda trapezów

Wykorzystujemy podstawienia jak przy metodzie prostokątów

1

1

1

0

0

( ) d

2

b

n

n

i

i

i

i

i

a

y

y

f x

x

h









































1

1

0

1

(

) d

2

i

i

i

i

i

h

y

q

y

q

h y

y







 







Gliwice 2010

Metoda trapezów

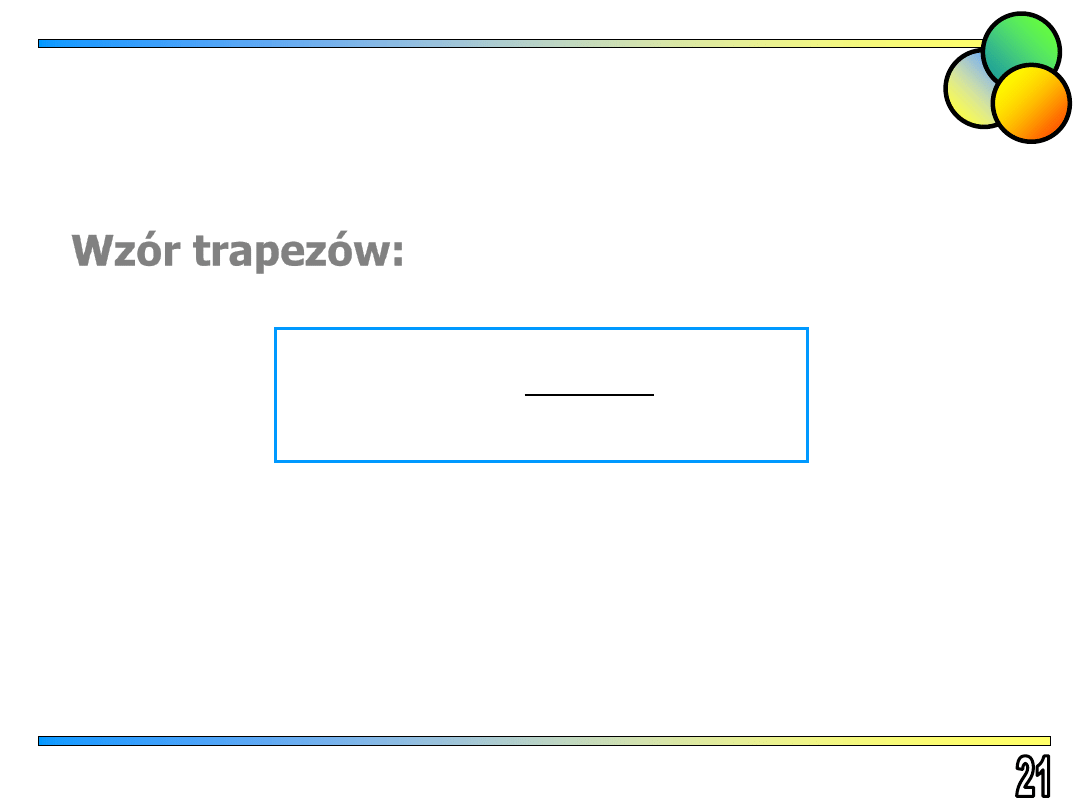
Wzór trapezów:

1

0

1

( ) d

2

b

n

n

i

i

a

y

y

f x

x h

y



























Gliwice 2010

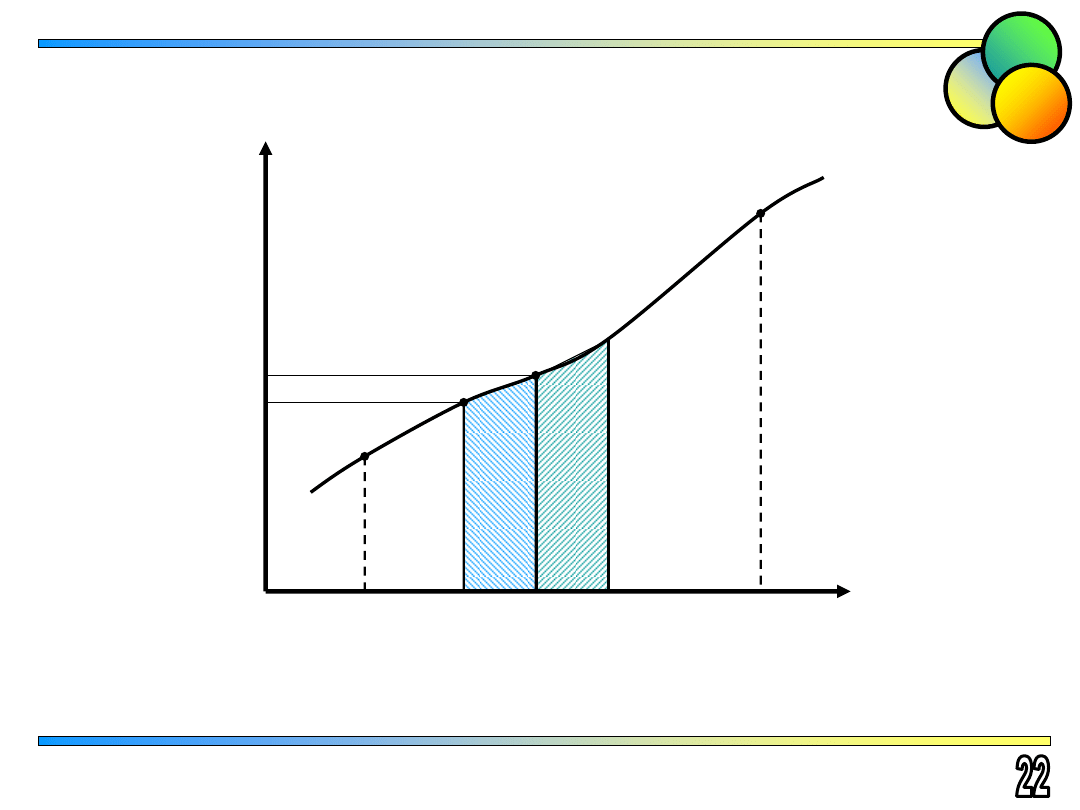
Metoda trapezów

Metoda trapezów

a = x

0

x

n

= b

x

i

x

i+1

x

i+2

y

i

y

i+1

x

f(x)

σ

i+1

σ

i

Gliwice 2010

Wzór Simpsona

Gliwice 2010

Wzór Simpsona

Niech

Oznacza to:

f (x)

w przedziale

[x

i

, x

i + 1

]

jest przybliżona wielomianem

interpolacyjnym

ograniczonym

do

trzech

pierwszych

składników





2

1

( )

,

2!

i

i

i

q q

W x

y

q y

y



   



1

[

,

]

i

i

x

x

x





Przedział

[a, b]

dzieli się parzystą ilość podprzedziałów.

Pole pojedynczego trapezu krzywoliniowego:









2

0

2

0

0

0

0

0

1

2

1

(

) d

4

2!

3

x

x

q q

h

y

q

y

y

x

y

y

y







  











Gliwice 2010

Wzór Simpsona

Wzór Simpsona:





0

1

2

3

2

1

( ) d

4

2

4

... 2

4

3

b

n

n

n

a

h

f x

x

y

y

y

y

y

y

y













 







Gliwice 2010

Kwadratury Gaussa

Gliwice 2010

Rozpatrujemy funkcję

f (x)

ciągłą i ograniczoną w przedziale

domkniętym

[a, b]

.

Kwadratury Gaussa

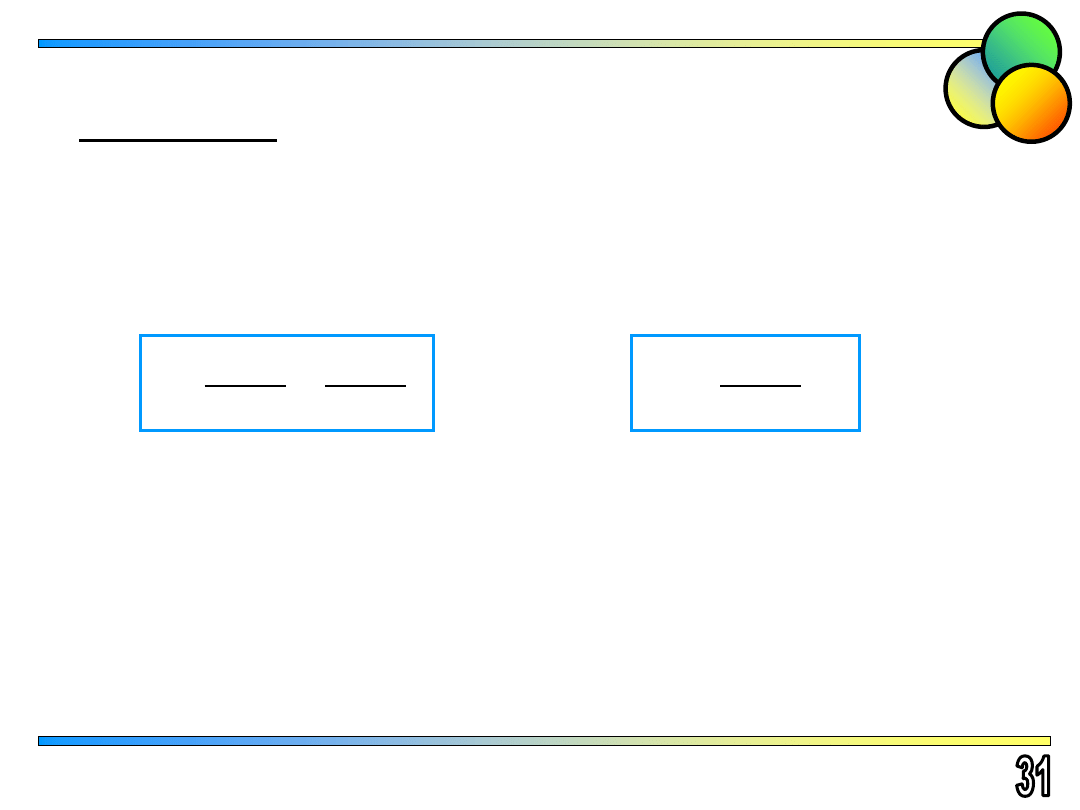
Pierwszy krok:

Sprowadzenie całki

( ) d

b

a

f x

x



do postaci znormalizowanej

1

1

(ξ) dξ

F





Dokonano zmiany granic całkowania

 





,

1, 1

a b





Gliwice 2010

Normalizacja

Kwadratury Gaussa

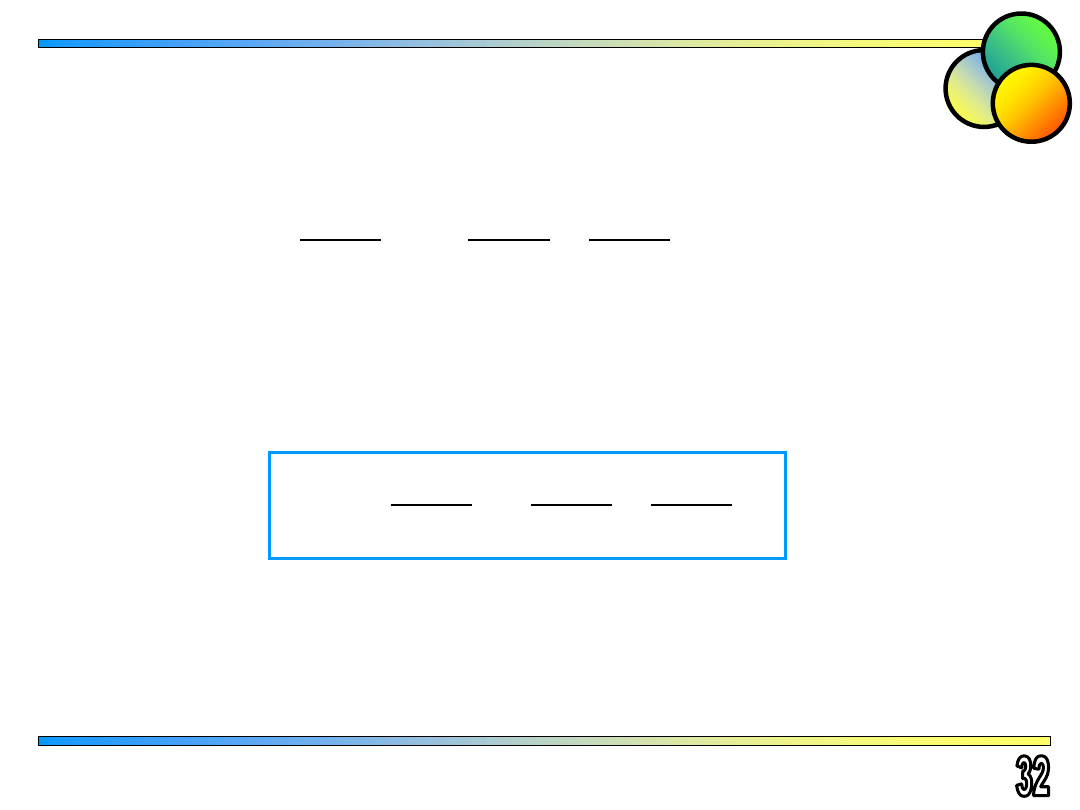
Podstawienia

ξ

2

2

a b

b a

x









d

d ξ

2

b a

x





ξ

1

x

a

   

ξ 1

x

b

  

Gliwice 2010

Czyli otrzymujemy

Kwadratury Gaussa

1

1

1

1

( ) d

ξ dξ

(ξ) dξ

2

2

2

b

a

b a

a b

b a

f x

x

f

F



































Funkcja

F( )

ma postać

ξ

(ξ)

ξ

2

2

2

b a

a b

b a

F

f























Gliwice 2010

Znormalizowaną funkcję podcałkową

F ( )

w przedziale

[-1, 1]

przybliża się wielomianem stopnia

2n



1

Kwadratury Gaussa

Następnie obliczamy wartość przybliżoną całki oznaczonej

ξ

2

2

1

0

1

2

2

1

(ξ)

ξ

ξ

...

ξ

n

n

F

a

a

a

a











 

1

1

1

(ξ) dξ

(ξ )

n

i

i

i

F

F

w











gdzie:

n

- liczba punktów Gaussa,

- odcięte tzw. punktów Gaussa,

w

i

- wagi punktów Gaussa.

ξ

i





ξ

1, 1

i

 

Gliwice 2010

Kwadratury Gaussa

Wagi i odcięte punktów Gaussa dla różnych wartości

n

n

ξ

i

i

w

2

4



0.57735

0.57735



0.86113



0.33998

0.33998
0.86113

1.00000
1.00000

0.34785
0.65214
0.65214
0.34785

Gliwice 2010