Metody Numeryczne, semestr letni 2013/2014
Wykład 8: Całkowanie numeryczne, cz.1
Kwadratury Newtona-Cotesa.
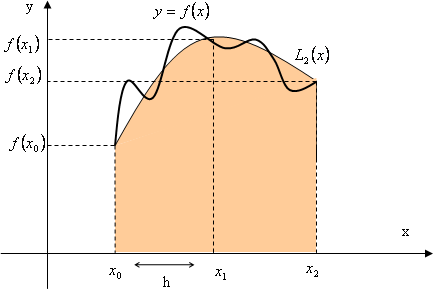
Zajmiemy się zagadnieniem przybliżonego obliczania całki oznaczonej funkcji jednej zmiennej rzeczywistej. W wielu przypadkach nie można wyrazić funkcji pierwotnej za pomocą funkcji ele-mentarnych lub wyrażenie takie jest bardzo skomplikowane. Ponadto, gdy funkcja podcałkowa jest dana tabelarycznie, to pojęcie funkcji pierwotnej traci sens.
Metody przybliżonego obliczania całek sprowadzają się do obliczania wartości całki jako kombinacji liniowej wartości funkcji podcałkowej w wybranych punktach. Tak więc zastępujemy daną funkcję f w rozpatrywanym przedziale [ a, b] funkcją interpolującą lub aproksymującą.
b
Do przybliżonego obliczania całki S( f ) = R p( x) f ( x) dx będziemy stosować wzór postaci a
n
Q( f ) = X Akf ( xk) , xk ∈ [ a, b] ,
(1)
k=0
przy czym współczynniki Ak nie zależą od funkcji f . Wzór (1) nazywamy kwadraturą, a xk - wę-
złami kwadratury. Funkcję p nazywamy funkcją wagową. Kwadratury z węzłami równoodległy-mi noszą nazwę kwadratur Newtona-Cotesa. Największe znaczenie praktyczne mają wzory, w których końce przedziału są węzłami i waga p( x) ≡ 1, zwane kwadraturami zamkniętymi.
Na wykładzie ograniczymy się tylko do takiego przypadku.
Jeden z możliwych sposobów konstrukcji kwadratur jest następujący: wybieramy węzły xk, budujemy wielomian interpolacyjny oparty na tych węzłach, a następnie całkujemy go. Są to tzw. kwadratury interpolacyjne.
Załóżmy, że przedział całkowania [ a, b] jest skończony, węzły xk = a+ b−a ·k, k = 0 , 1 , 2 . . . , n.
n
Zastosujemy wzór interpolacyjny Lagrange’a:
n
L
X
n( x) =
f ( xk)Φ k( x) ,
k=0
gdzie
( x − x
Φ
0)( x − x 1) . . . ( x − xk− 1)( x − xk+1) . . . ( x − xn) k ( x) =
.
( xk − x 0)( xk − x 1) . . . ( xk − xk− 1)( xk − xk+1) . . . ( xk − xn) Otrzymujemy
b
b
n
n
b
n
Z
Z
Z
Q( f ) =
L
X
X
X
n( x) dx =
f ( xk)Φ k( x) dx =
f ( xk)
Φ k( x) dx =
f ( xk) Ak
a
a k=0
k=0
a
k=0
dla
b
Z
( x − x
A
0)( x − x 1) . . . ( x − xk− 1)( x − xk+1) . . . ( x − xn) k ( x) =
dx.
( xk − x 0)( xk − x 1) . . . ( xk − xk− 1)( xk − xk+1) . . . ( xk − xn) a
Ponieważ węzły są w równej odległości, więc oznaczając b − a
h =
n
1
zapisujemy współczynniki Ak, k = 0 , 1 . . . , n w postaci b
Z
( x − x
A
0)( x − x 1) . . . ( x − xk− 1)( x − xk+1) . . . ( x − xn) k
=
dx
( xk − x 0)( xk − x 1) . . . ( xk − xk− 1)( xk − xk+1) . . . ( xk − xn) a
b
( − 1) n−k
Z
=
( x − a)( x − a − h) . . . ( x − a − ( k − 1) h)( x − a − ( k + 1) h) . . . ( x − a − nh) dx hnk!( n − k)! a
x = a + th
dx = h dt
=
=
x
a
b
t
0
n
n
( − 1) n−kh Z
=
th( th − h) . . . ( th − ( k − 1) h)( th − ( k + 1) h) . . . ( th − nh) dt hnk!( n − k)! 0
n
( − 1) n−khn+1 Z
=
t( t − 1) . . . ( t − ( k − 1))( t − ( k + 1)) . . . ( t − n) dt hnk!( n − k)! 0
n
( − 1) n−kh Z t( t − 1) . . . ( t − n)
=
dt
k!( n − k)!
t − k
0
Rozważmy przypadki n = 1, n = 2, n = 3.
1) Dla n = 1 mamy h = b − a oraz 1
"
#1
Z
t 2
h
k = 0 :
A 0 = −h ( t − 1) dt = −h
− t
=
2
2
0
0
1
Z
h
k = 1 :
A 1 = h
t dt =
,
2
0
czyli
h
Q( f ) = A 0 f ( x 0) + A 1 f ( x 1) =
f ( x
.
(2)
2
0) + f ( x 1)
Jest to wzór trapezów.
Wyznaczymy błąd wzoru trapezów. Na podstawie wzoru na błąd przybliżenia funkcji f wielo-mianem L 1( x) otrzymujemy
b
b
Z
Z
1
E( f ) =
f ( x) − L 1( x) dx =
ω
2 2( x) f ′′( ξ) dx,
ξ ∈ ( a, b) .
a
a
2
Stąd
x = a + th
b
1
M
Z
dx = h dt
M
Z
|E( f ) | ¬
2
|( x − a)( x − b) | dx =
2
=
h
|( a + th − a)( a + th − b) | dx 2
x
a
b
2
a
0
t
0
1
1
1
M
"
#1
Z
M
Z
M
t 3
t 2
M
=
2 h 3 |t( t − 1) | dx = − 2 h 3 t( t − 1) dx = − 2 h 3
−
=
2 h 3 ,
2
2
2
3
2
12
0
0
0
gdzie
M 2 = max |f ′′( x) |.
x∈[ a,b]
2) Dla n = 2 otrzymujemy
b − a
h =
2
2
h
"
#2
Z
h t 3
3 t 2
h
k = 0 :
A 0 =
( t − 1)( t − 2) dt =
−
+ 2 t
=
2
2
3
2
3
0
0
2
"
#2
Z
t 3
4 h
k = 1 :
A 1 = −h
t( t − 2) dt = −h
− t 2
=
3
3
0
0
2
h
"
#2
Z
h t 3
t 2
h
k = 2 :
A 2 =
t( t − 1) dt =
−
=
2
2
3
2
3
0
0
czyli
h
Q( f ) = A 0 f ( x 0) + A 1 f ( x 1) + A 2 f ( x 2) =
f ( x
.
(3)
3
0) + 4 f ( x 1) + f ( x 2) Jest to wzór parabol lub inaczej wzór Simpsona.
Na oszacowanie błędu uzyskujemy wzór
M
|E( f ) | ¬
4 h 5 ,
(4)
90
gdzie
M 4 = max |f (4)( x) |.
x∈[ a,b]
3
3) Dla n = 3 dostajemy wzór 3/8
3 h
b − a
Q( f ) =
f ( x
,
h =
,
(5)
8
0) + 3 f ( x 1) + 3 f ( x 2) + f ( x 3) 3
oraz
3 M
|E( f ) | ¬
4 h 5 ,
M
|f (4)( x) |.
80
4 = max
x∈[ a,b]
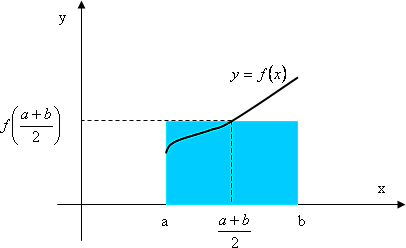
Możemy jeszcze wyprowadzić inny wzór na całkowanie numeryczne, tzw. wzór prostoką-
tów:
a + b!
( b − a)3 M
Q( f ) = ( b − a) f
,
|E( f ) | ¬
2
(6)
2
24
W przypadku dużej ilości węzłów odpowiednie współczynniki są bardzo skomplikowane i pojawia się trudność oszacowania błędu. W związku z tym przedział całkowania dzieli się na dostatecznie dużą ilość małych przedziałów, a następnie w każdym z nich stosuje się wzór Newtona-Cotesa z małą ilością węzłów. W ten sposób otrzymuje się wzory o prostej strukturze, przy czym ich dokładność może być dowolnie duża. Kwadraturę, która jest sumą kwadratur na podprzedziałach, nazywamy kwadraturą złożoną.
Złożone kwadratury Newtona-Cotesa
Złożony wzór trapezów
Przedział całkowania [ a, b] dzielimy na n równych części o długości h = b−a. W każdym prze-n
dziale stosujemy wzór trapezów i wyniki sumujemy. Otrzymujemy h
Q( f ) =
f ( x
,
(7)
2
0) + 2 f ( x 1) + 2 f ( x 2) + . . . + 2 f ( xn− 1) + f ( xn) oraz oszacowanie błędu
( b − a)3
|E( f ) | ¬
M
|f ′′( x) |.
(8)
12 n 2
2 ,
M 2 = max
x∈[ a,b]
Złożony wzór parabol
Przedział całkowania [ a, b] dzielimy na n równych części o długości h = b−a, przy czym n
4
n jest parzyste. W przedziałach [ a, a + 2 h] , . . . [ a + ( n − 2) h, b] o długości 2 h stosujemy wzór parabol i wyniki sumujemy. Dostajemy
h n
Q( f ) =
f ( x
f ( x
(9)
3
0) + f ( xn) + 2
2) + f ( x 4) + . . . + f ( xn− 2)
o
+4 f ( x 1) + f( x 3) + . . . + f( xn
,
(10)
− 1)
oraz oszacowanie błędu
( b − a)5
|E( f ) | ¬
M
|f (4)( x) |.
180 n 4
4 ,
M 4 = max
x∈[ a,b]
Złożony wzór 3/8
Przedział całkowania [ a, b] dzielimy na n równych części o długości h = b−a, przy czym n
n jest podzielne przez 3, ( n = 3 m): 3 h n
Q( f ) =
f ( x
f ( x
(11)
8
0) + f ( x 3 m) + 3
1) + f ( x 4) + . . . + f ( x 3 m− 2)
+3 f ( x 2) + f( x 5) + . . . + f( x 3 m (12)
− 1)
o
+2 f ( x 3) + f( x 6) + . . . + f( x 3 m
,
(13)
− 3)
oraz
3( b − a)5
|E( f ) | ¬
M
|f (4)( x) |.
80 n 4
4 ,
M 4 = max
x∈[ a,b]
Złożony wzór prostokątów
(
h !
3 h!
(2 n − 1) h!)
Q( f ) = h f a +
+ f a +
+ . . . + f a +
,
(14)
2
2
2
b − a
h =
,
(15)
n
oraz
( b − a)3
|E( f ) | ¬
M
|f ′′( x) |.
24 n 2
2 ,
M 2 = max
x∈[ a,b]
3
Przykład 1 Obliczyć całkę R dx metodą złożonego wzoru trapezów z błędem mniejszym niż log x
2
ε = 1 · 10 − 2.
2
W celu wyznaczenia liczby przedziałów na jaką podzielimy przedział całkowania [2 , 3] obli-czamy
1
f ( x) = log x
ln 10
f ′( x) = − x ln2 x
(2 + ln x) ln 10
f ′′( x) =
x 2 ln3 x
(6 + 6 ln x + 2 ln2 x) ln 10
f ′′′( x) = −
.
x 3 ln4 x
5
Ponieważ w przedziale [2 , 3] funkcja f ′′′( x) jest ujemna, więc f ′′( x) jest malejąca. Ponadto w przedziale [2 , 3] druga pochodna f ′′( x) przyjmuje tylko wartości dodatnie. Stąd M 2 = f′′(2) ≈ 4 , 7.
Ze wzoru (8) mamy
( b − a)3 M
12 n 2
2 < ε
(3 − 2)3
1
4 , 7 <
· 10 − 2
12 n 2
2
470 < n 2
6
n > 8 , 9 .
Przyjmujemy zatem n = 9 i wyznaczamy h = 1 , x
, i = 0 , 1 , . . . , 9.
9
i = 2 + i
9
Obliczamy zgodnie ze wzorem (7):
h
Q( f ) =
f ( x
≈ 2 . 576733462 .
2
0) + 2 f ( x 1) + . . . + 2 f ( x 8) + f ( x 9) 6
Wyszukiwarka
Podobne podstrony:
Wykład 9- Całkowanie numeryczne.Kwadratury Gaussa
kwadratury newtona cotesa
Calkowanie numeryczne, WIP AIR, SEM 1, TEINF, TEINF, Teinf projekty
całkowanie numeryczne
Calkowanie numeryczne
Działania na potęgach o wykładniku całkowitym, Matematyka, Konspekty
1 Metody całkowania numerycznego 1 1
matematyka, POTĘGI O WYKŁADNIKU CAŁKOWITYM, POTĘGI O WYKŁADNIKU CAŁKOWITYM
matematyka, funkcje potęgi, POTĘGI O WYKŁADNIKU CAŁKOWITYM
Metody numeryczne wykres Newton
Całkowanie numeryczne
Calkowanie numeryczne pdf
calkowanie numeryczne
sciaga malek 24-25, Algorytmy wielokrotnego całkowania numeryczne
Całkowanie numeryczne, Studia, ZiIP, SEMESTR III, Metody numeryczne
Całkowanie numeryczne metoda trapezów mini, Studia, ZiIP, SEMESTR III, Metody numeryczne
Całkowanie numeryczne
całkowanie numeryczne
więcej podobnych podstron