Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 1

Całkowanie numeryczne

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 2

Plan zajęć

1. Całkowanie przybliżone funkcji jednej zmiennej z użyciem

wbudowanych funkcji Scilaba

integrate(), inttrap(),

intsplin()

2. Całkowanie funkcji 2 zmiennych

•

wykorzystanie wbudowanej funkcji

int2d()

•

użycie metody Monte Carlo

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 3

Ćwiczenie 1

Utwórz skrypt (zapisując go jako

~/calki.sce

) zawierający instrukcje wykonujące

następujące czynności:

●

zdefiniowanie funkcji użytkownika

●

narysowanie wykresu funkcji na przedziale [-1,1]

●

przy użyciu funkcji Scilaba

integrate()

obliczenie wartość całki

2

1

)

(

x

x

f

−

=

)

4

(

)

(

1

0

π

=

∫

dx

x

f

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 4

Ćwiczenie 1

Utwórz skrypt (zapisując go jako

~/calki.sce

) zawierający instrukcje wykonujące

następujące czynności:

●

zdefiniowanie funkcji użytkownika

●

narysowanie wykresu funkcji na przedziale [-1,1]

●

przy użyciu funkcji Scilaba

integrate()

obliczenie wartość całki

2

1

)

(

x

x

f

−

=

)

4

(

)

(

1

0

π

=

∫

dx

x

f

// zdefiniowanie funkcji f(x), narysowanie wykresu

deff('[y]=f(x)','y=sqrt(1-x^2)')
xp = -1:0.05:1
plot2d (xp, f(xp), [2])

// obliczenie całki

w =

integrate

('f(x)','x',0,1)

w =

0.7853982

-1.0

-0.8

-0.6

-0.4

-0.2

0.0

0.2

0.4

0.6

0.8

1.0

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 5

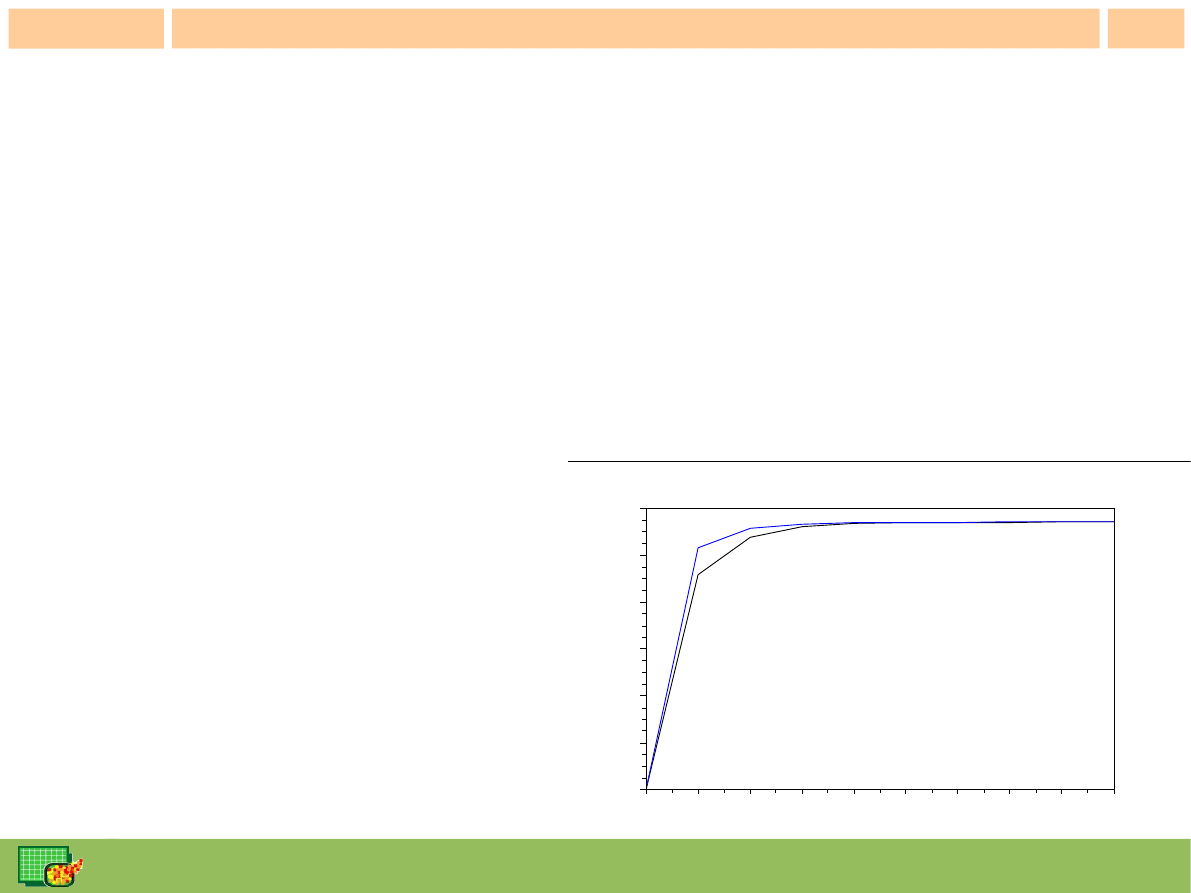
Ćwiczenie 1 - cd

obliczenie wartości całki przy użyciu funkcji

inttrap(), intsplin():

●

otrzymując wyniki przybliżonych wartości całki dla każdej z funkcji dokonując
podziału przedziału całkowania na 2

k

części (k=1,2,...,10). Wyniki zapisz w

dwóch wektorach

wt[1:10], ws[1:10]

●

otrzymane wyniki przedstaw na wykresie w zależności od zmiennej
k=1,2,...,10.

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 6

Ćwiczenie 1 - cd

obliczenie wartości całki przy użyciu funkcji

inttrap(), intsplin():

●

otrzymując wyniki przybliżonych wartości całki dla każdej z funkcji dokonując
podziału przedziału całkowania na 2

k

części (k=1,2,...,10). Wyniki zapisz w

dwóch wektorach

wt[1:10], ws[1:10]

●

otrzymane wyniki przedstaw na wykresie w zależności od zmiennej
k=1,2,...,10.

// obliczenie całki przy użyciu funkcji inttrap(), intsplin()

for i=1:10

x=

linspace

(0,1,2^i)

wt(i)=

inttrap

(x,f(x))

ws(i)=

intsplin

(x,f(x))

end

// narysowanie wykresu

k=1:10, plot2d(k, [wt(k) ws(k)])

1

2

3

4

5

6

7

8

9

1 0

0 .5 0

0 .5 5

0 .6 0

0 .6 5

0 .7 0

0 .7 5

0 .8 0

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 7

Ćwiczenie 1 - cd

●

otrzymane wyniki zapisz do sformatowanego pliku tekstowego

~/w-calki.txt

zapisując w 3 kolumnach

(podając wartości całek z dokładnością do 6 miejsc po przecinku)

:

●

k,

●

wynik otrzymany za pomocą

inttrap(),

●

wynik otrzymany za pomocą

intsplin().

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 8

Ćwiczenie 1 - cd

●

otrzymane wyniki zapisz do sformatowanego pliku tekstowego

~/w-calki.txt

zapisując w 3 kolumnach

(podając wartości całek z dokładnością do 6 miejsc po przecinku)

:

●

k,

●

wynik otrzymany za pomocą

inttrap(),

●

wynik otrzymany za pomocą

intsplin().

// zapisanie wyników do pliku tekstowego

u1 =

file

('open','~/w-calki.txt','new')

for k=1:10

write

(u1,[k, wt(k), ws(k)],'(f3.0,2X,f9.6,2X,f9.6)')

end

file

('close',u1);

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 9

Ćwiczenie 2

W otwartym skrypcie dopisz instrukcje służące do obliczenia,

korzystając z funkcji

int2d()

wartości przybliżone całek dla :

gdzie

●

z(x,y)=1, S=[0,2]x[0,4]

(wartość dokładna = 8)

●

f(x,y)=xy

2

, S=[0,2]x[0,4]

(wartość dokładna = 42,666)

●

f(x,y)=xy

2

, H= jest obszarem pomiędzy prostą y=2x a parabolą y=x

2

(wartość dokładna = 32/5)

funkcja

I = int2d(X,Y,f)

oblicza całkę po obszarze podzielonym na trójkąty

●

X

macierz prostokątna wymiaru 3 x N - każda kolumna przedstawia
współrzędne X-owe jednego trójkąta

●

Y

macierz prostokątna wymiaru 3 x N - każda kolumna przedstawia
współrzędne Y-owe jednego trójkąta

●

f

zdefiniowana funkcja podcałkowa

∫

S

fdS

∫

H

fdH

∫

S

zdS

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 10

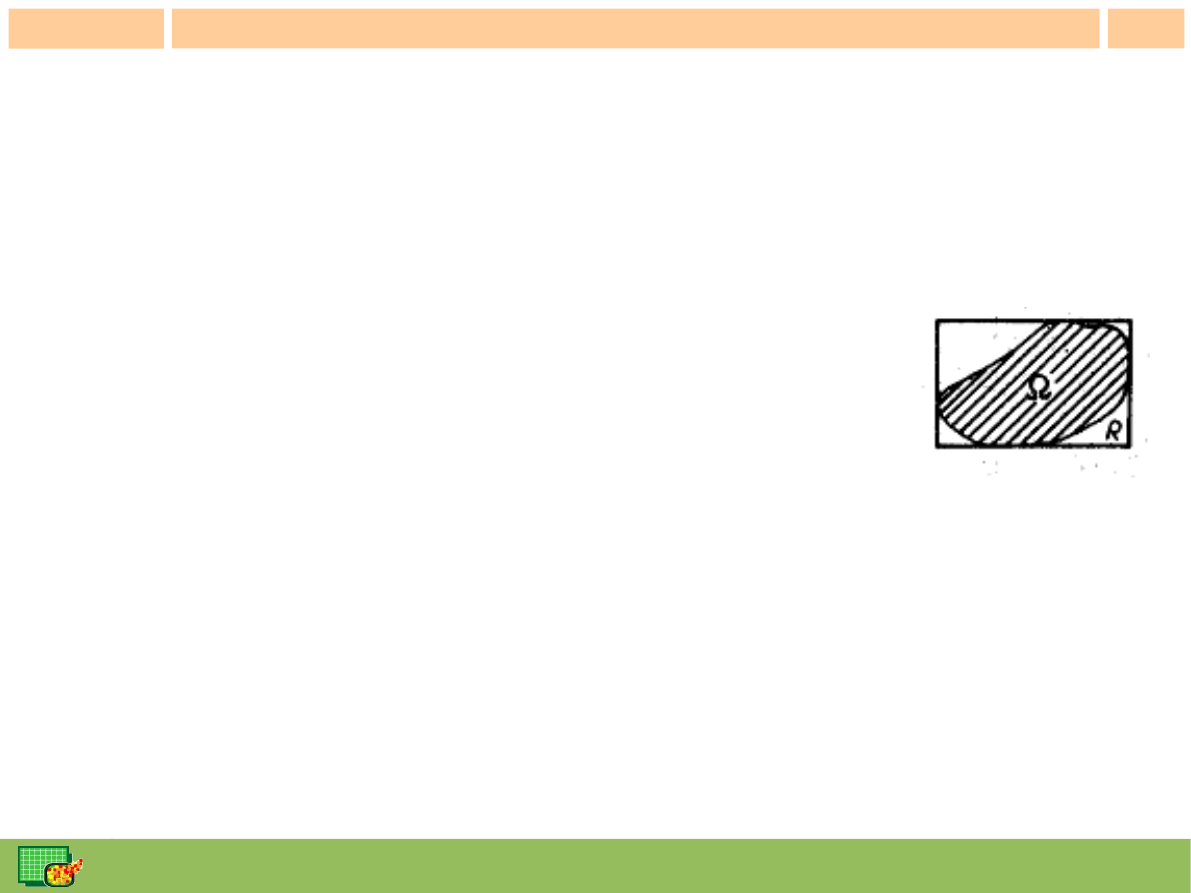
Ćwiczenie 2 - cd

●

Dla z(x,y)=1, S=[0,2]x[0,4] - dokonując podziału obszaru całkowania na

2 trójkąty

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 11

Ćwiczenie 2 - cd

// podział obszaru całkowania [0,2]x[0,4] na 2
trójkąty

X=[0,0;2,0;2,2];
Y=[0,0;0,4;4,4];

// zdefiniowanie funkcji podcałkowej

deff('zp=z(x,y)','zp=1')

// obliczenie całki

I=int2d(X,Y,z)
disp(I)

> 8.

●

Dla z(x,y)=1, S=[0,2]x[0,4] - dokonując podziału obszaru całkowania na

2 trójkąty

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 12

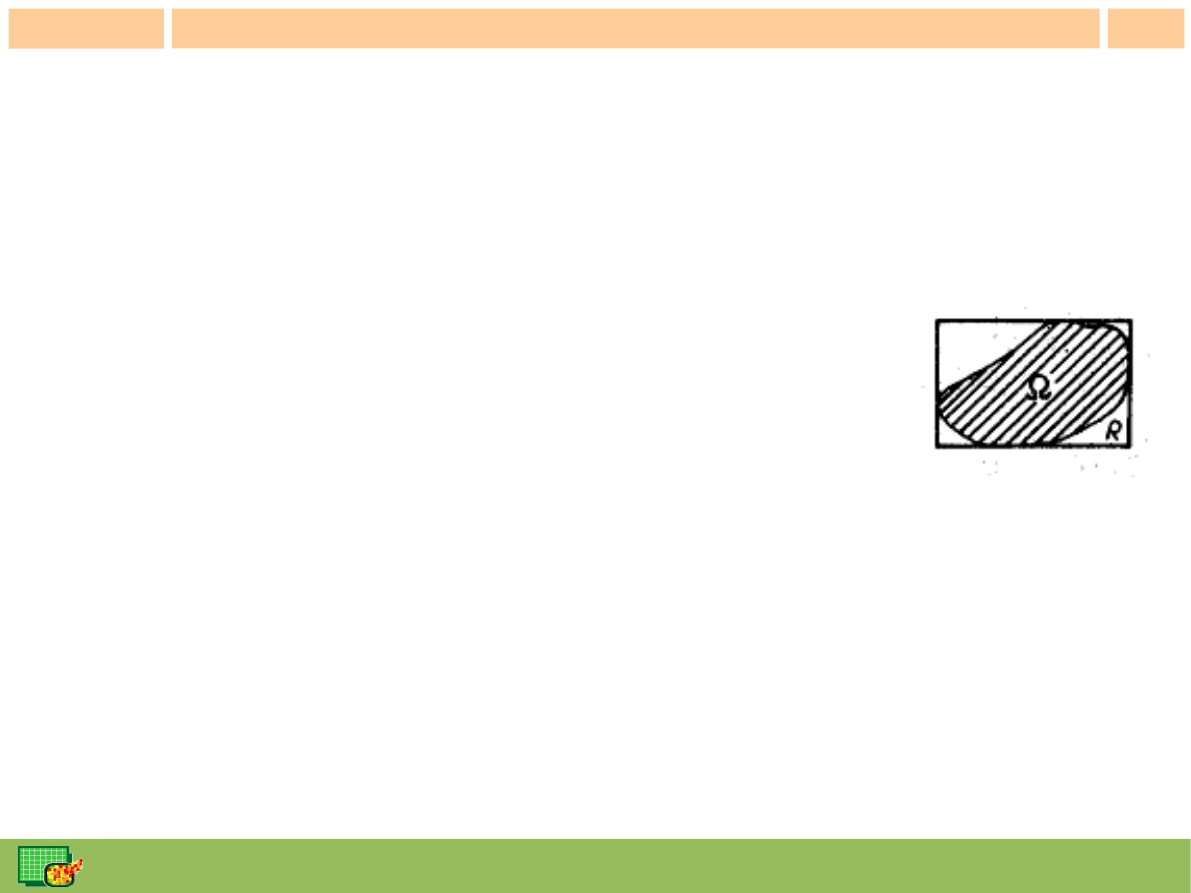
Ćwiczenie 2 - cd

●

Dla f(x,y)=xy

2

, S=[0,2]x[0,4], wykorzystując już utworzony podział

●

Dla obszaru całkowania pomiędzy prostą y=2x a parabolą y=x

2

wpisując obszar w

prostokąt [0,2]x[0,4], definiując nową funkcję podcałkową i wykorzystując już

utworzony podział

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 13

Ćwiczenie 2 - cd

●

Dla z(x,y)=xy

2

, S=[0,2]x[0,4], wykorzystując już utworzony podział

●

Dla obszaru całkowania pomiędzy prostą y=2x a parabolą y=x

2

wpisując obszar w

prostokąt [0,2]x[0,4], definiując nową funkcję podcałkową i wykorzystując już

utworzony podział

// zdefiniowanie funkcji podcałkowej

deff('z=f(x,y)','z=x*y^2')

I=

int2d

(X,Y,f)

// obliczenie całki

disp(I)

> 42.666667

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 14

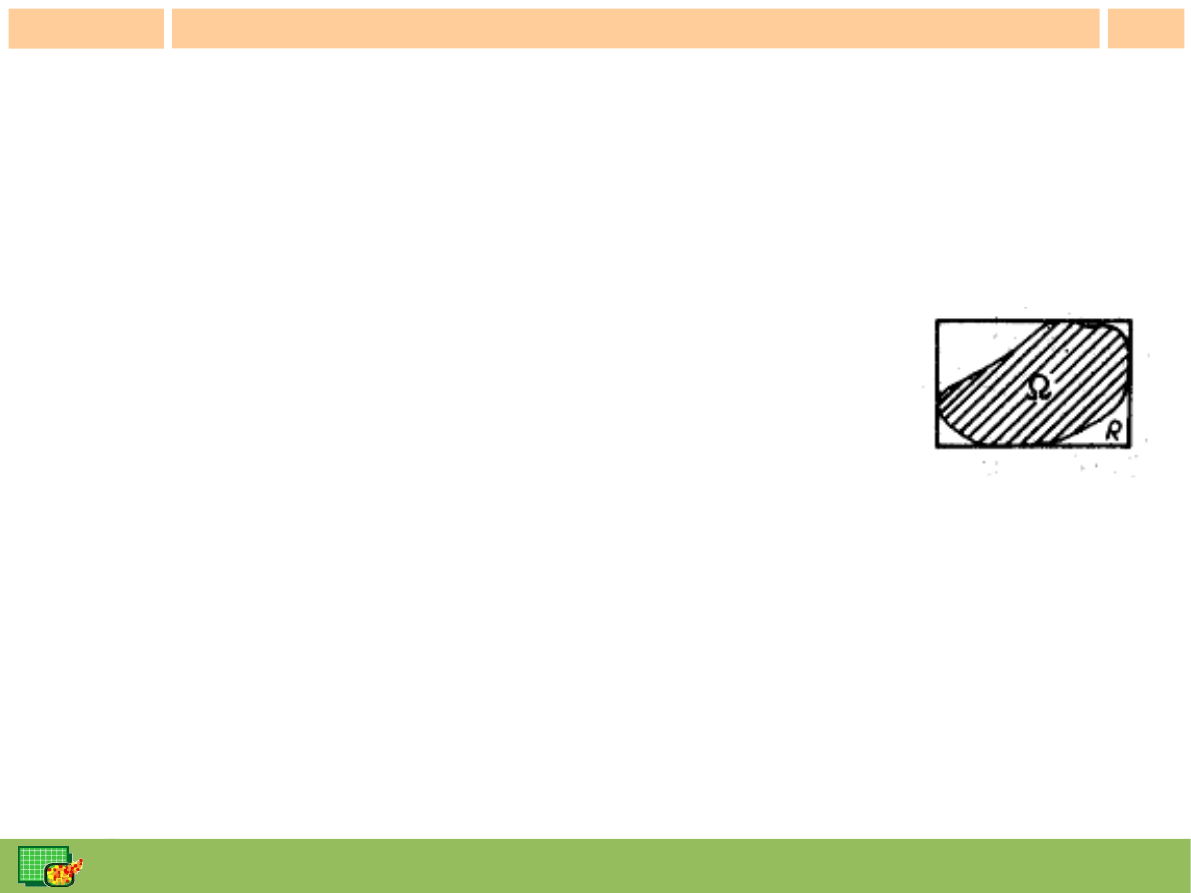
Ćwiczenie 2 - cd

●

Dla z(x,y)=xy

2

, S=[0,2]x[0,4], wykorzystując już utworzony podział

●

Dla obszaru całkowania pomiędzy prostą y=2x a parabolą y=x

2

wpisując obszar w

prostokąt [0,2]x[0,4], definiując nową funkcję podcałkową i wykorzystując już

utworzony podział

// zdefiniowanie funkcji podcałkowej

deff('z=f(x,y)','z=x*y^2')

I=

int2d

(X,Y,f)

// obliczenie całki

disp(I)

> 42.666667

function [z]=fn(x,y)
z=0
if (y<=2*x)&(y>=x^2) then
z=f(x,y)
end
endfunction

I=

int2d

(X,Y,fn)

// obliczenie całki

disp(I)

> 4.8634489

(wartość dokładna 32/5 = 6.4)

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 15

Ćwiczenie 2 - cd

●

Dla obszaru całkowania pomiędzy prostą y=2x a parabolą y=x

2

wpisując obszar w

prostokąt [0,2]x[0,4], dzieląc prostokąt na trójkąty prostokątne o
przyprostokątnych = 1

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 16

Ćwiczenie 2 - cd

●

Dla obszaru całkowania pomiędzy prostą y=2x a parabolą y=x

2

wpisując obszar w

prostokąt [0,2]x[0,4], dzieląc prostokąt na trójkąty prostokątne o
przyprostokątnych = 1

// podział obszaru [0,2]x[0,4] na trójkąty prostokątne o boku =1

for i=1:2

for j=1:4

k=2*i-1+4*(j-1)
X(1,k)=i-1,

X(2,k)=i,

X(3,k)=i

Y(1,k)=j-1,

Y(2,k)=j-1,

Y(3,k)=j

k=2*i + 4*(j-1)
X(1,k)=i-1,

X(2,k)=i-1,

X(3,k)=i

Y(1,k)=j-1,

Y(2,k)=j,

Y(3,k)=j

end

end
I=

int2d

(X,Y,fn), disp(I)

> 6.5729887

(wartość dokładna 32/5 = 6.4)

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 17

Ćwiczenie 2 - cd

Oszacować przy użyciu Metody Monte Carlo, korzystając z generatora

liczb losowych wartość całki

dla funkcji :

z(x,y)=xy

2

, S jest obszarem pomiędzy prostą y=2x a parabolą y=x

2

(wartość dokładna = 32/5)

●

znajdując N

0

=10000 punktów losowych w obszarze S

0

= obszar prostokątny [0,2] x [0,4]

∫

S

zdS

// wygenerowanie punktów losowych z obszaru [0,2] x [0,4]

N_0=1000
xy =rand(2,N_0)
xy(1,:)=2*xy(1,:), xy(2,:)=4*xy(2,:)

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 18

Ćwiczenie 2 - cd

●

Obliczając N - liczbę punktów losowych leżących w obszarze S i korzystając z formuły

przybliżyć wartość całki (suma we wzorze obliczana jest tylko dla punktów leżących w
obszarze całkowania

S

)

∑

∑

∑

∫

=

=

=

=

⋅

≈

≈

N

i

i

i

N

i

i

i

N

i

i

i

S

y

x

z

N

S

y

x

z

N

N

N

S

y

x

z

N

S

zdS

1

0

0

1

0

0

1

)

,

(

)

,

(

1

)

,

(

1

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 19

Ćwiczenie 2 - cd

●

Obliczając N - liczbę punktów losowych leżących w obszarze S i korzystając z formuły

przybliżyć wartość całki (suma we wzorze obliczana jest tylko dla punktów leżących w
obszarze całkowania

S

)

∑

∑

∑

∫

=

=

=

=

⋅

≈

≈

N

i

i

i

N

i

i

i

N

i

i

i

S

y

x

z

N

S

y

x

z

N

N

N

S

y

x

z

N

S

zdS

1

0

0

1

0

0

1

)

,

(

)

,

(

1

)

,

(

1

N=0, sumka = 0, S0 = 8
for i=1:N_0
x= xy(1,i), y= xy(2,i)

// sprawdzenie czy losowy punkt należy do obszaru S

if (y<=2*x)&(y>=x^2) then
sumka = sumka + f(x,y)
N = N+1
end
end
calka = S0 * sumka/N_0
disp(calka), disp(N),

> 6.2687125

(wartość całki - dokładna 6.4)

> 172

Instytut K onstrukcji Budowlanych

Metody Obliczeniowe

Zakład K omputerowego W spomagania Projektowania

Semestr II.

27 styczeń 2009

SciLab w obliczeniach numerycznych - część 4

Slajd 20

Funkcje SciLaba

Funkcje przybliżonego całkowania:

●

int2d()

–

obliczenie całki z funkcji 2 zmiennych po obszarze opisanym siatką

trójkątów

●

int3d()

–

obliczenie całki z funkcji 3 zmiennych, obszar całkowania opisany

siatką czworościanów

●

integrate(), intg()

–

obliczenie całki z funkcji jednej zmiennej metodą

kwadratur

●

intsplin()

– obliczenie całki z funkcji sklejanej (jednej zmiennej) interpolującej

zbiór punktów

●

inttrap()

– obliczenie całki z funkcji (jednej zmiennej) interpolującej zbiór

punktów – wzór trapezów