Metody numeryczne

całkowania

Ewa Skubalska-Rafajłowicz

Wrocław 2009

Definicja całki oznaczonej Riemanna:

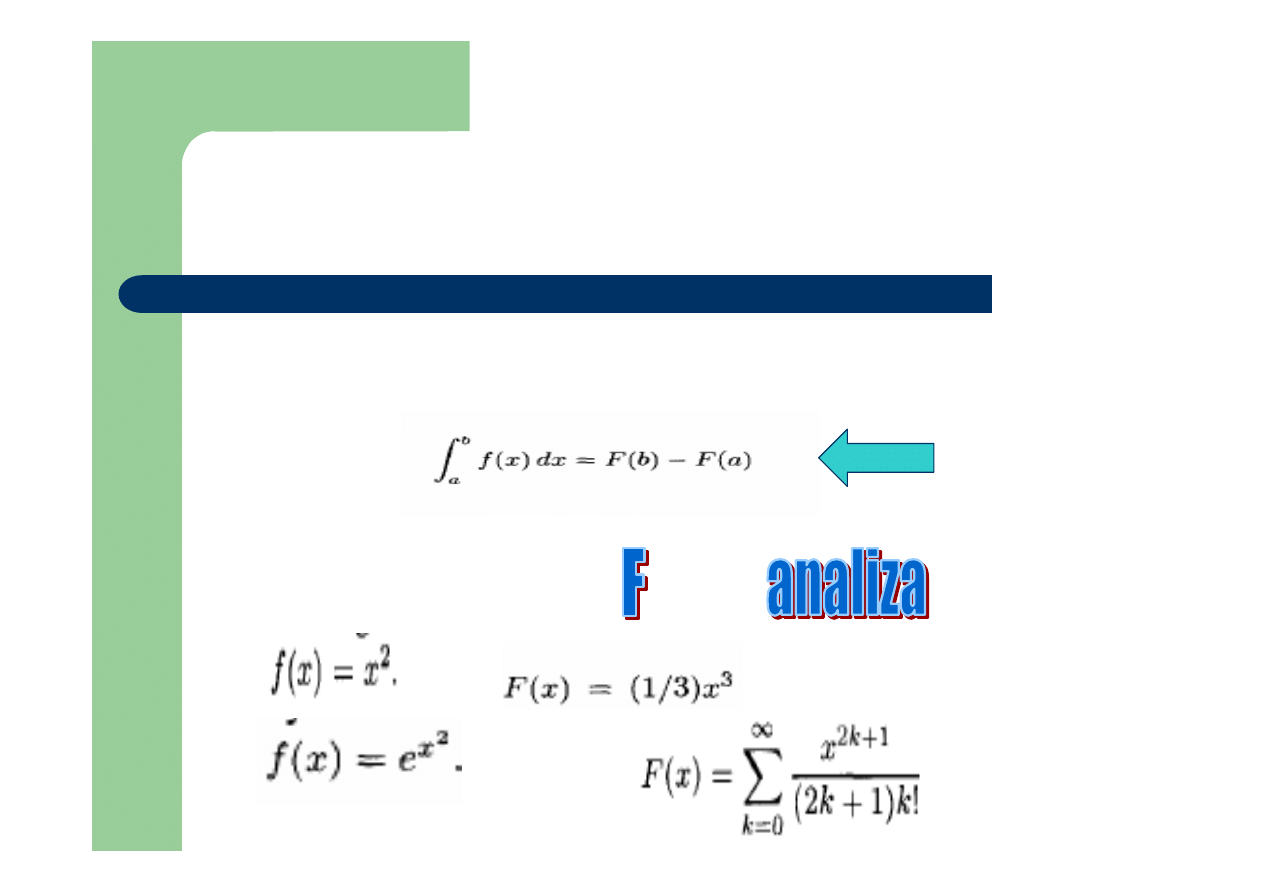
Na podstawie funkcji pierwotnej

Kwadratury interpolacyjne

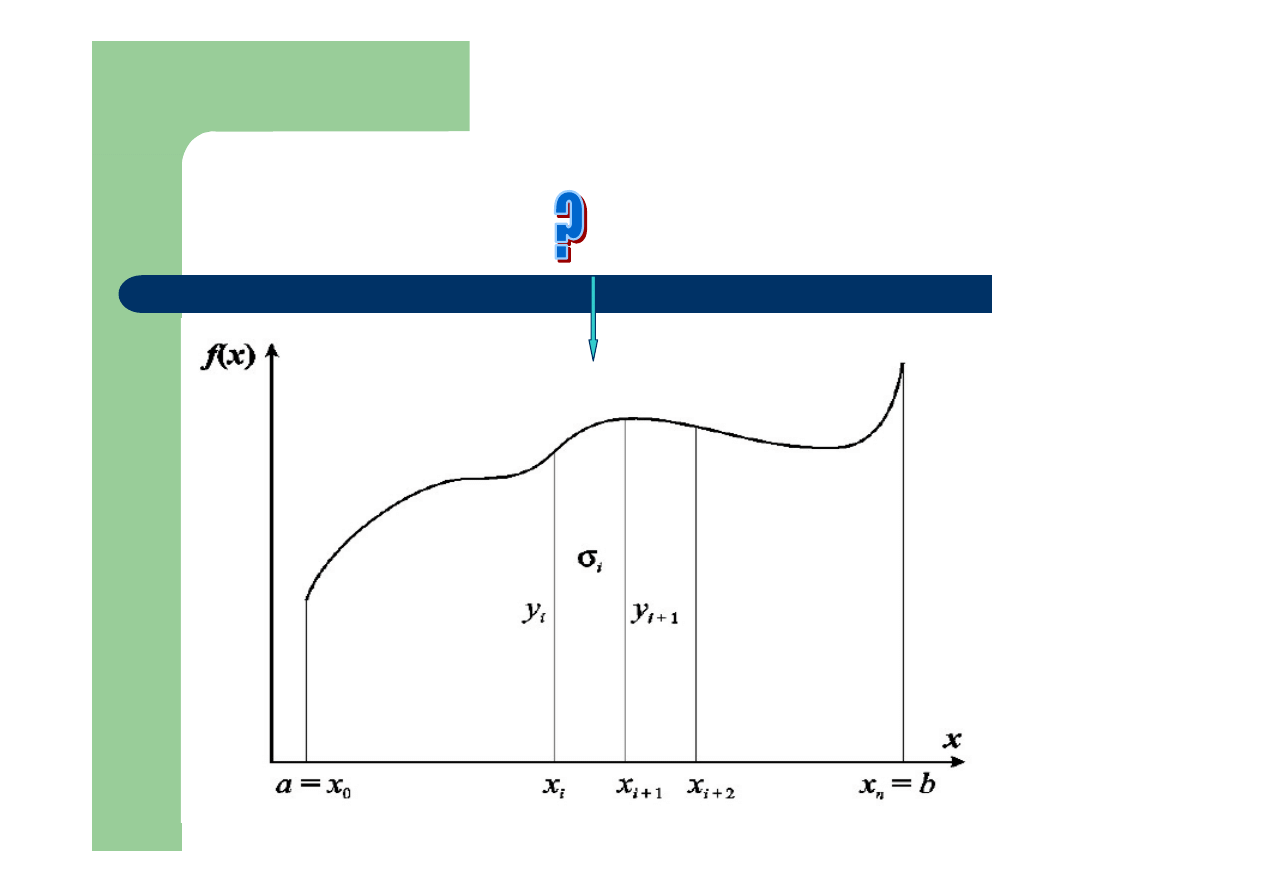
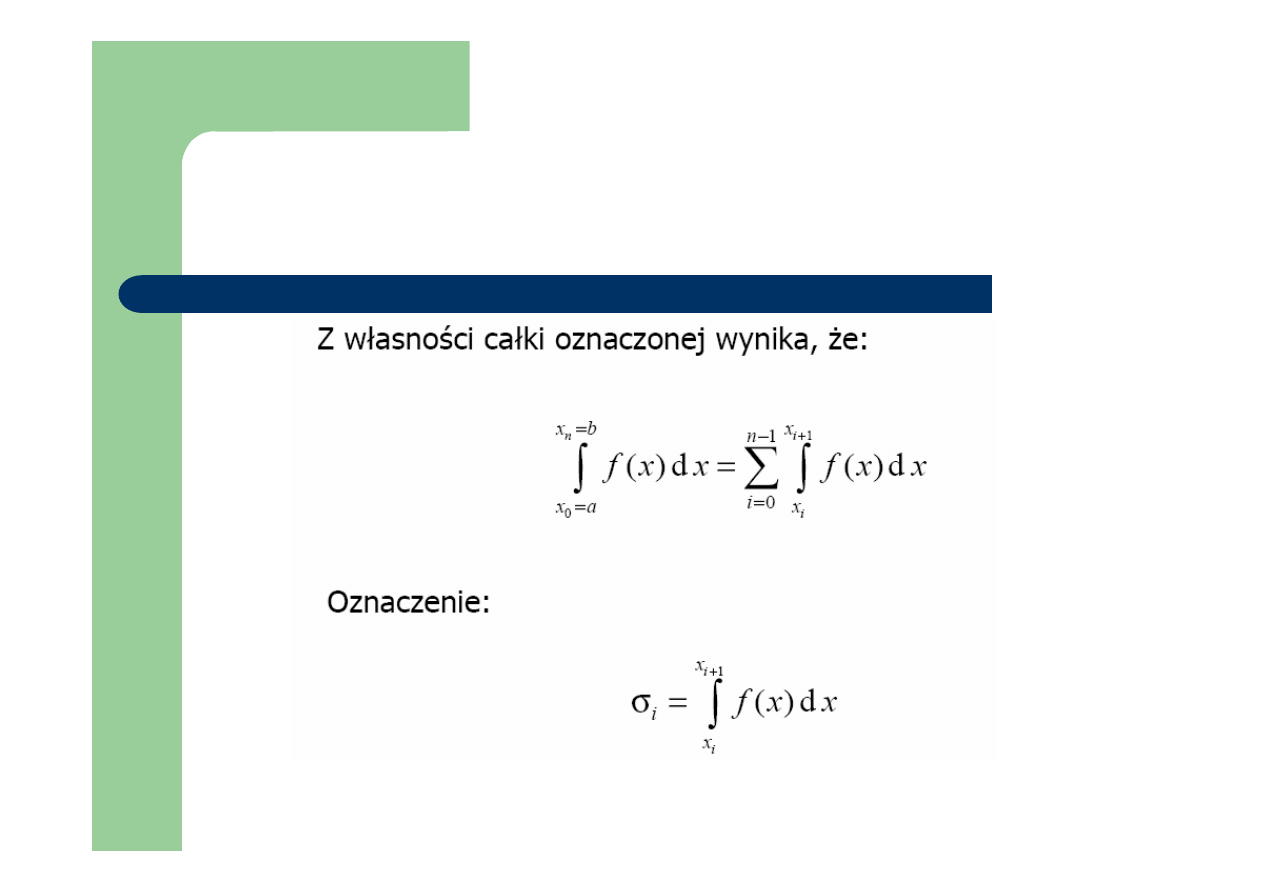
Idea kwadratur interpolacyjnych

Metoda prostokątów

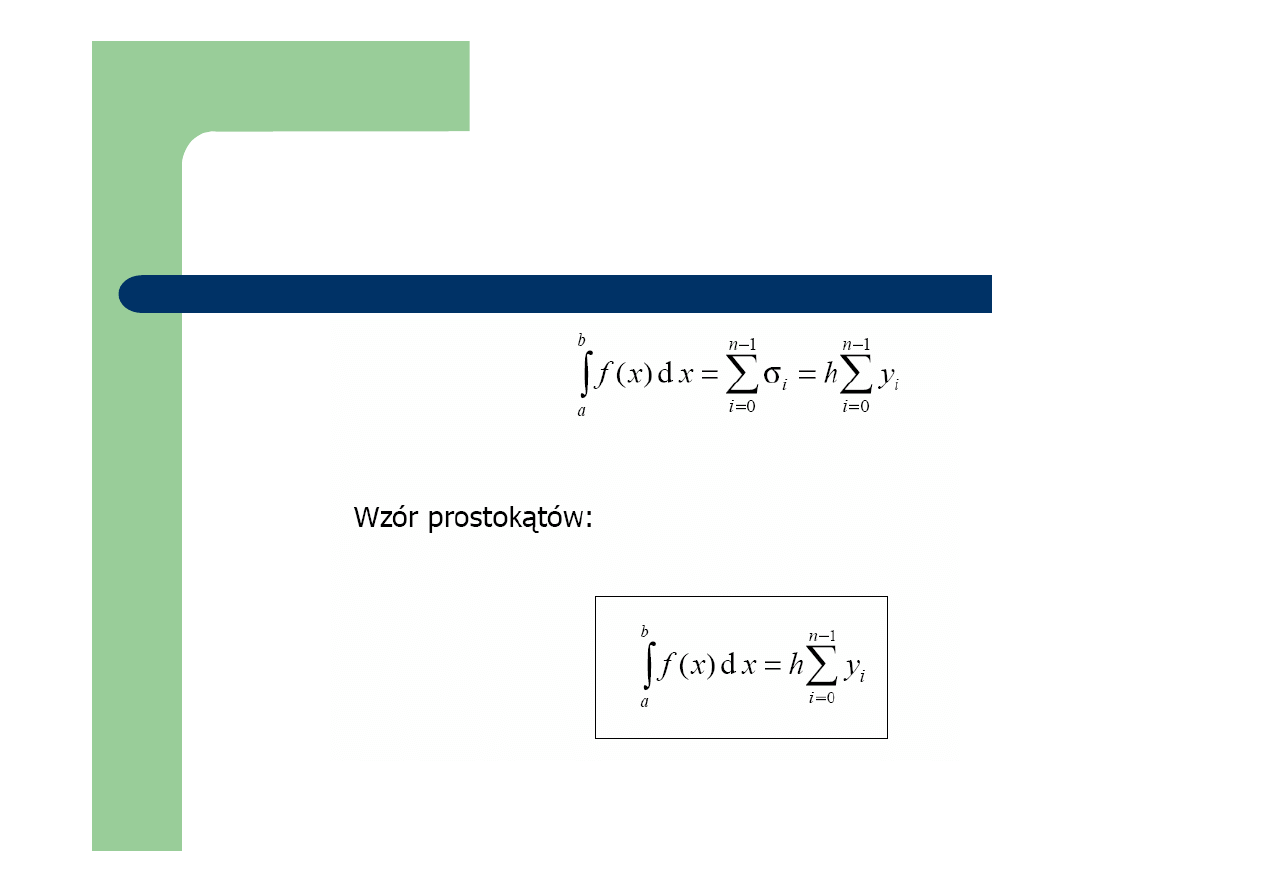
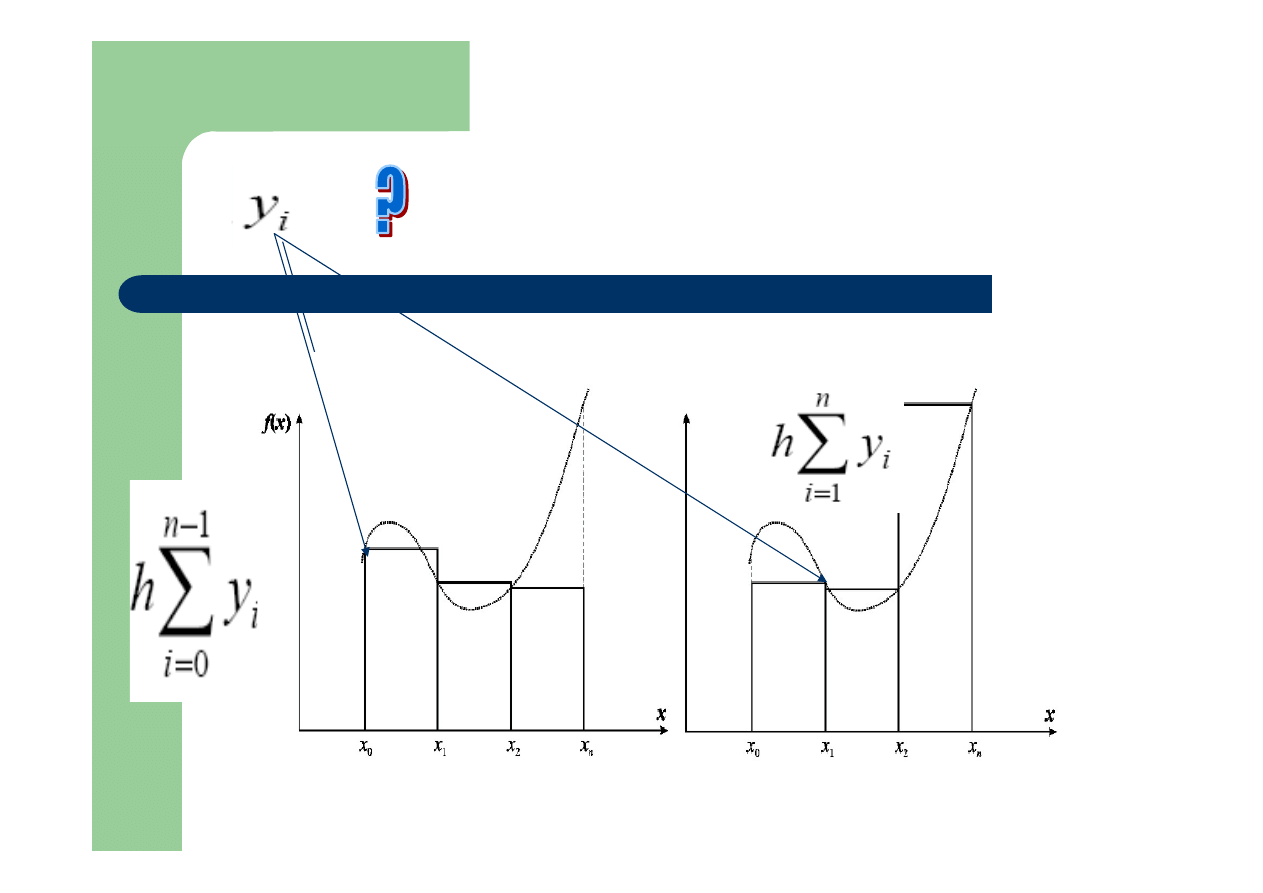
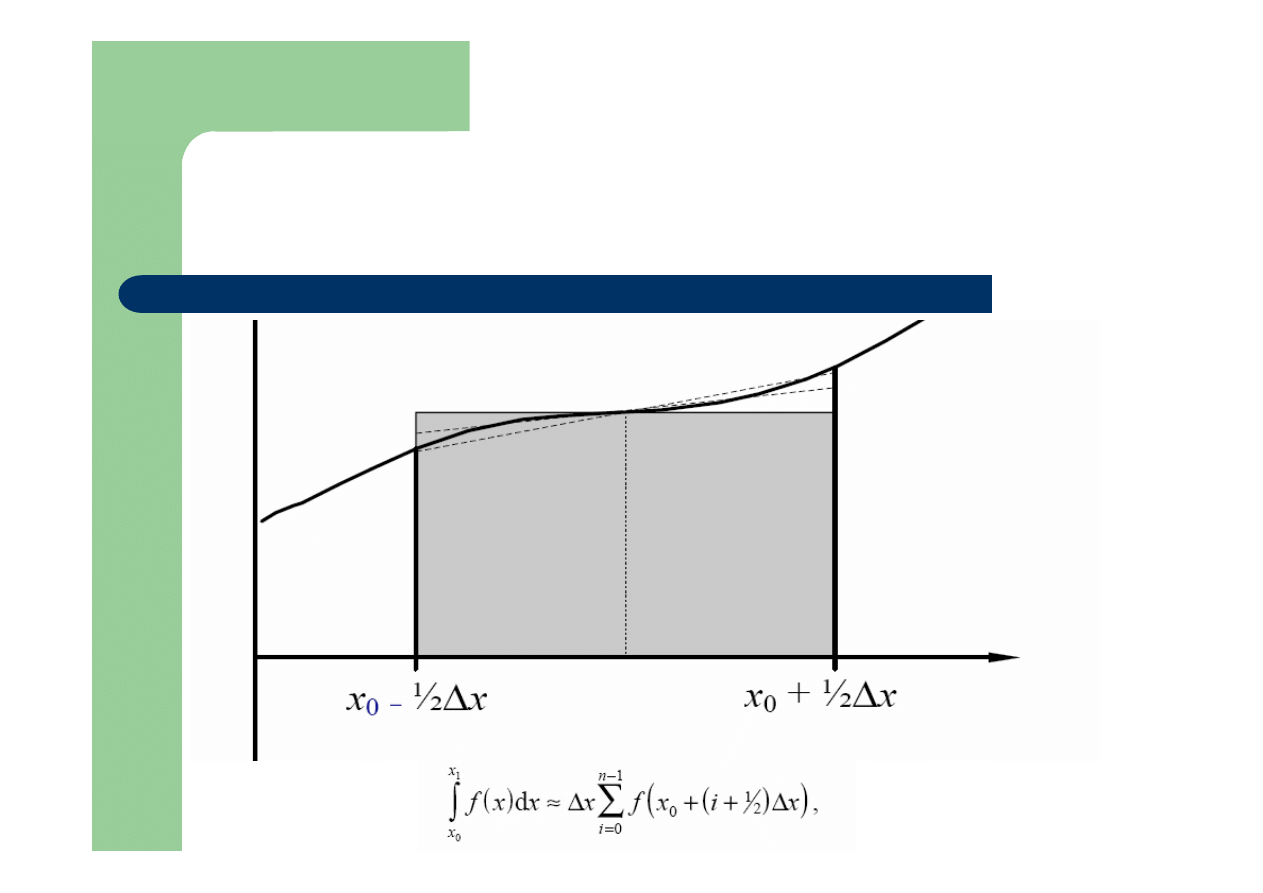
Metoda punktu środkowego

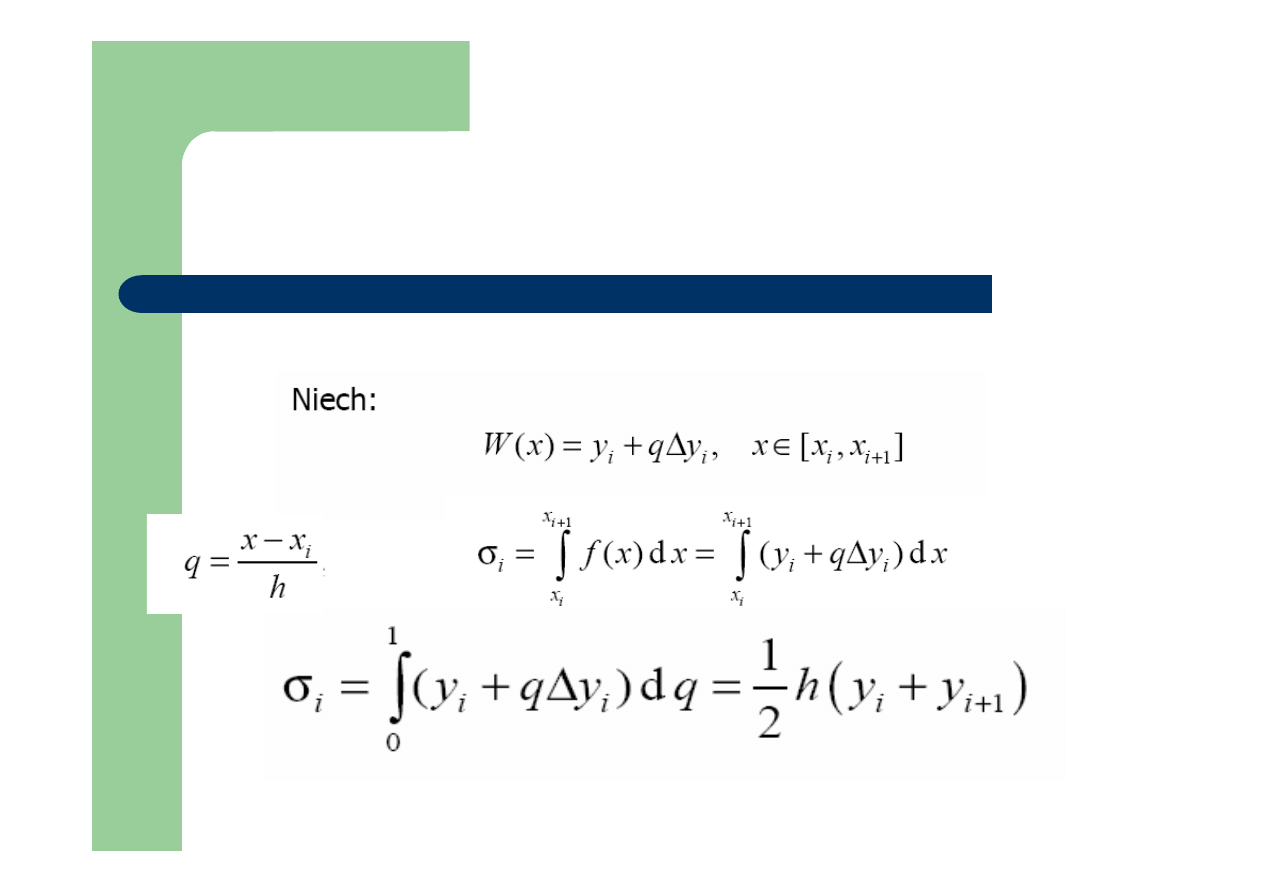
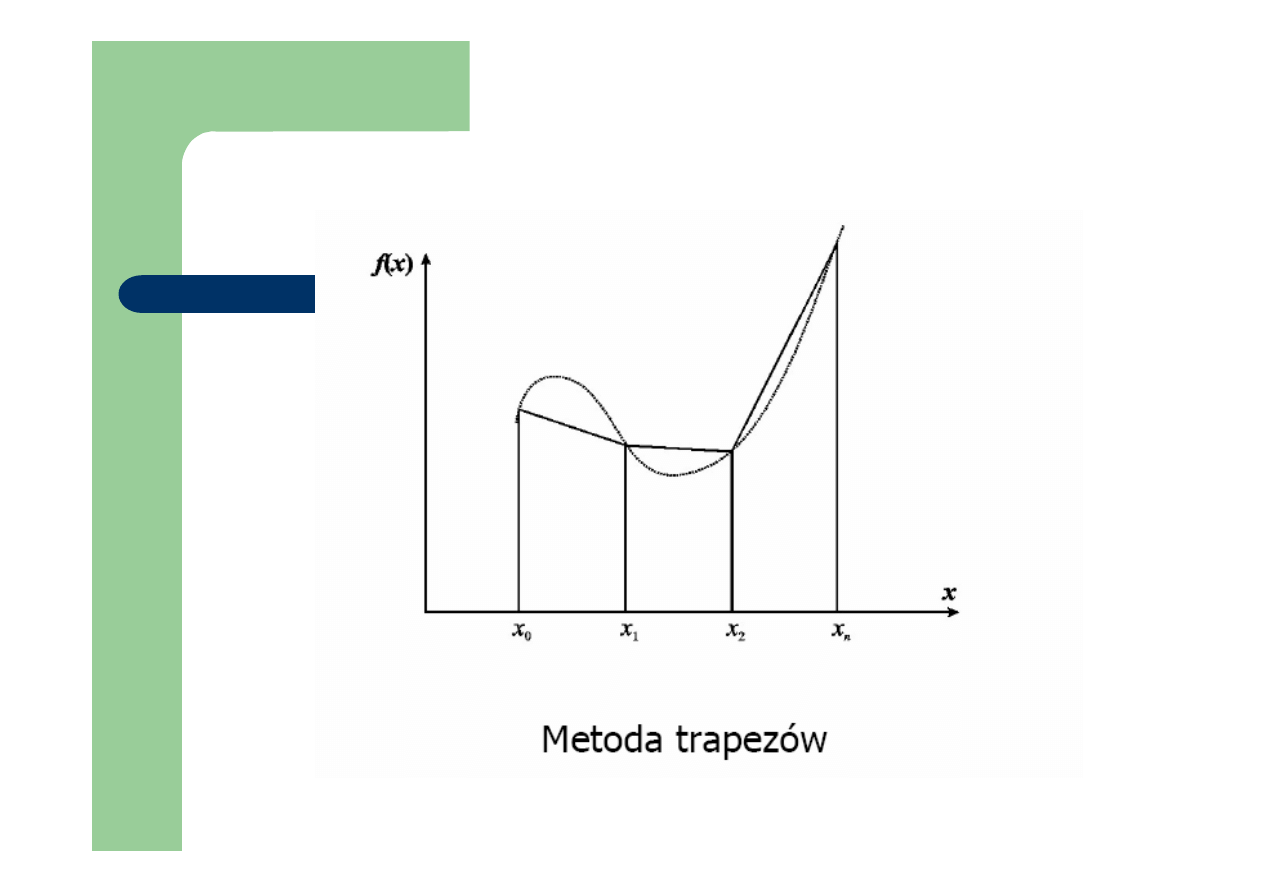
Metoda trapezów

Metoda Simpsona

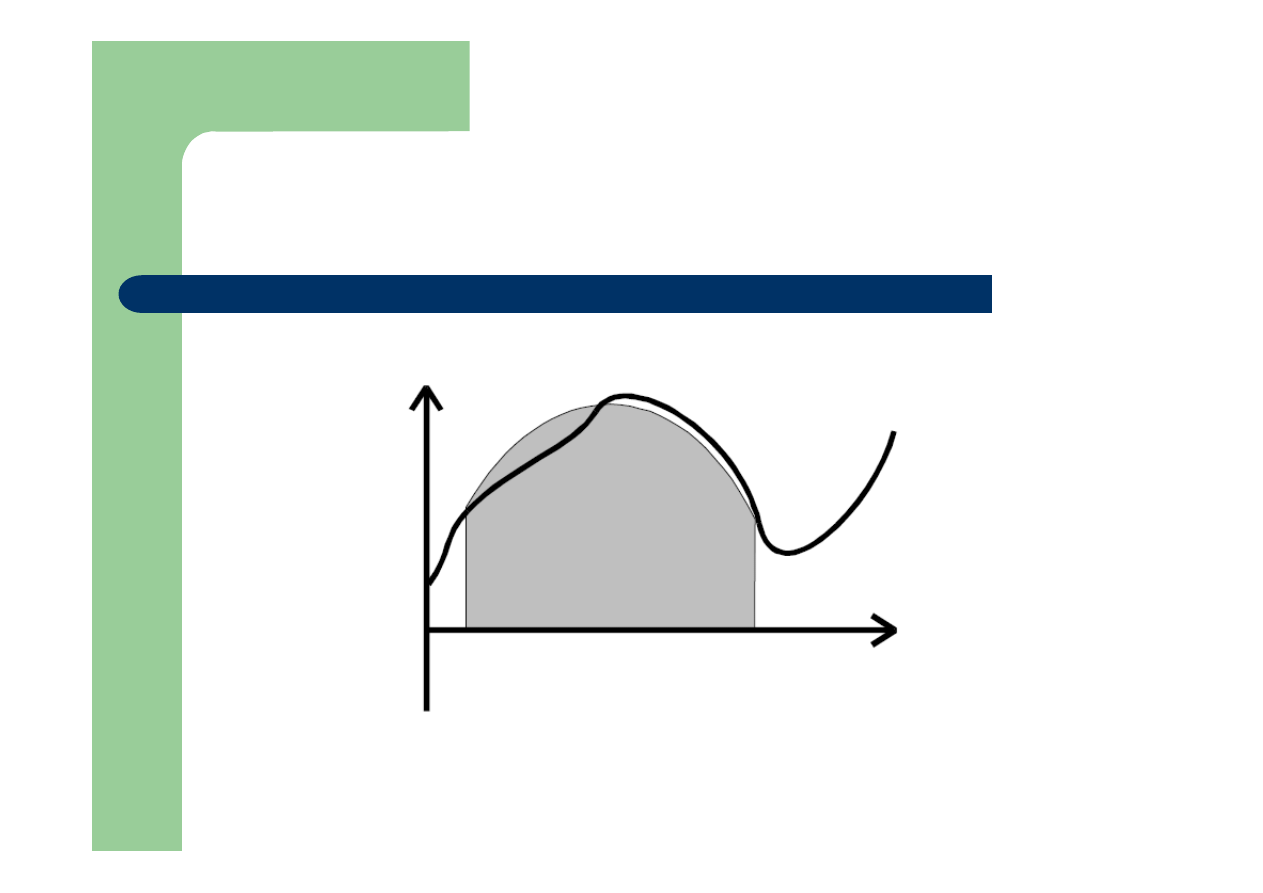
Interpolacja funkcją kwadratową

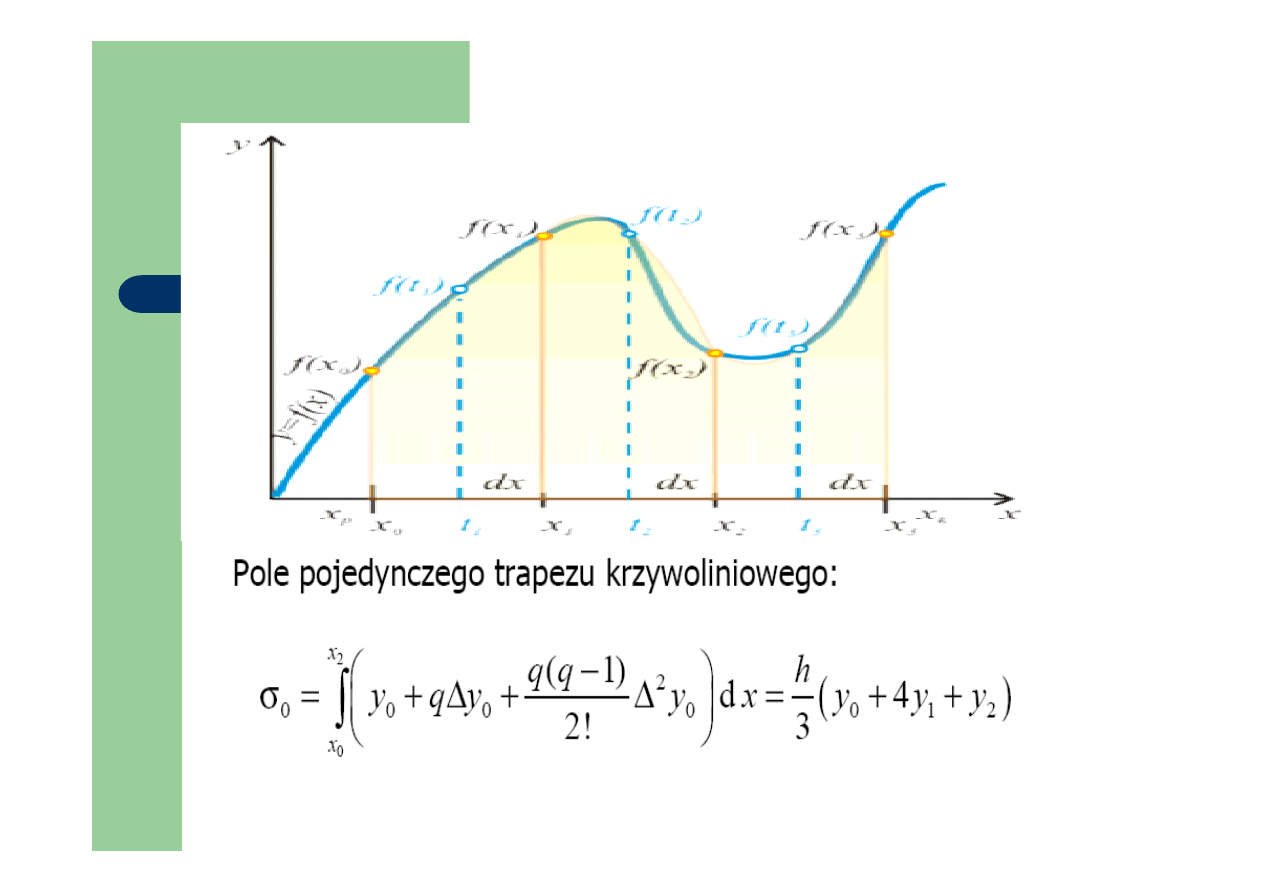
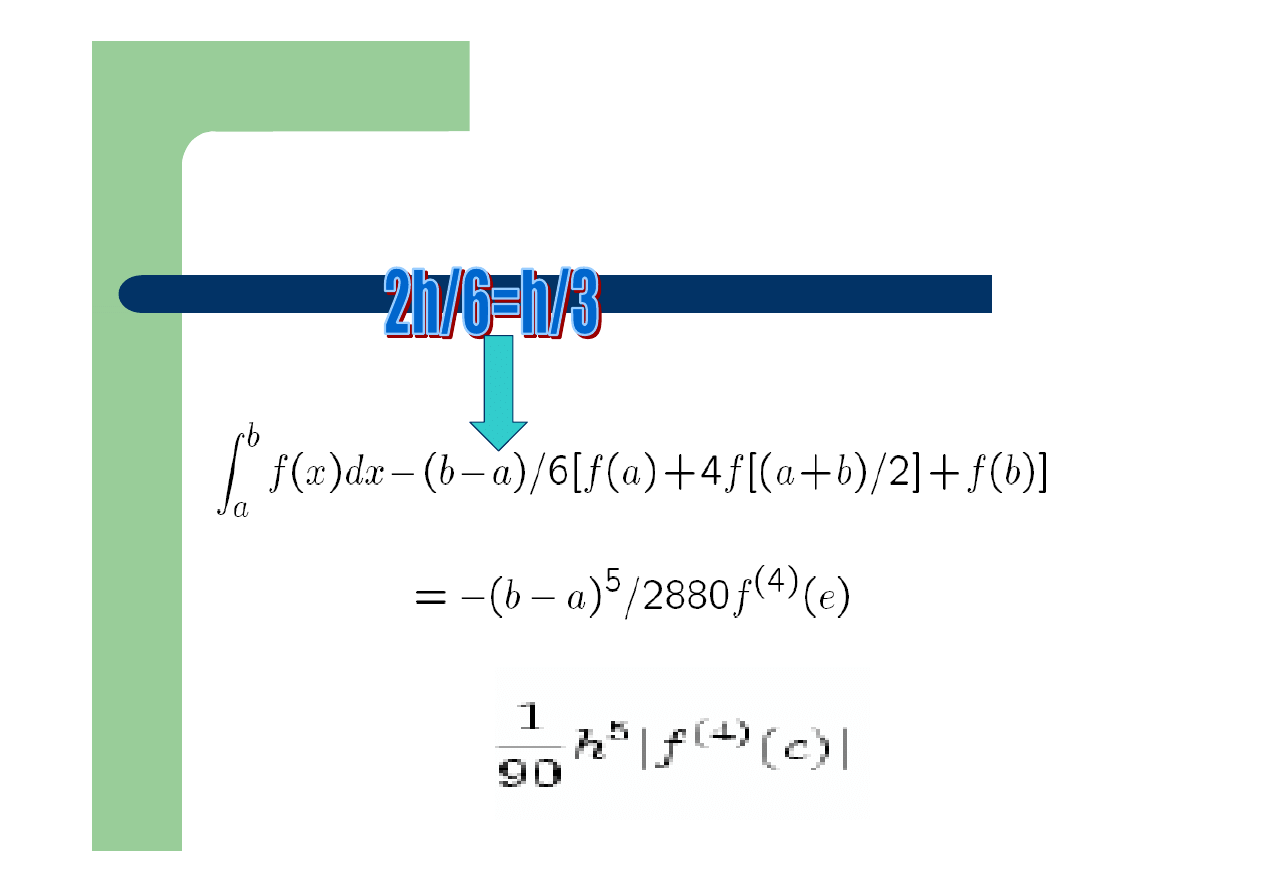
Dokładność metody Simpsona

Wzór Simpsona

h=(b-a)/n

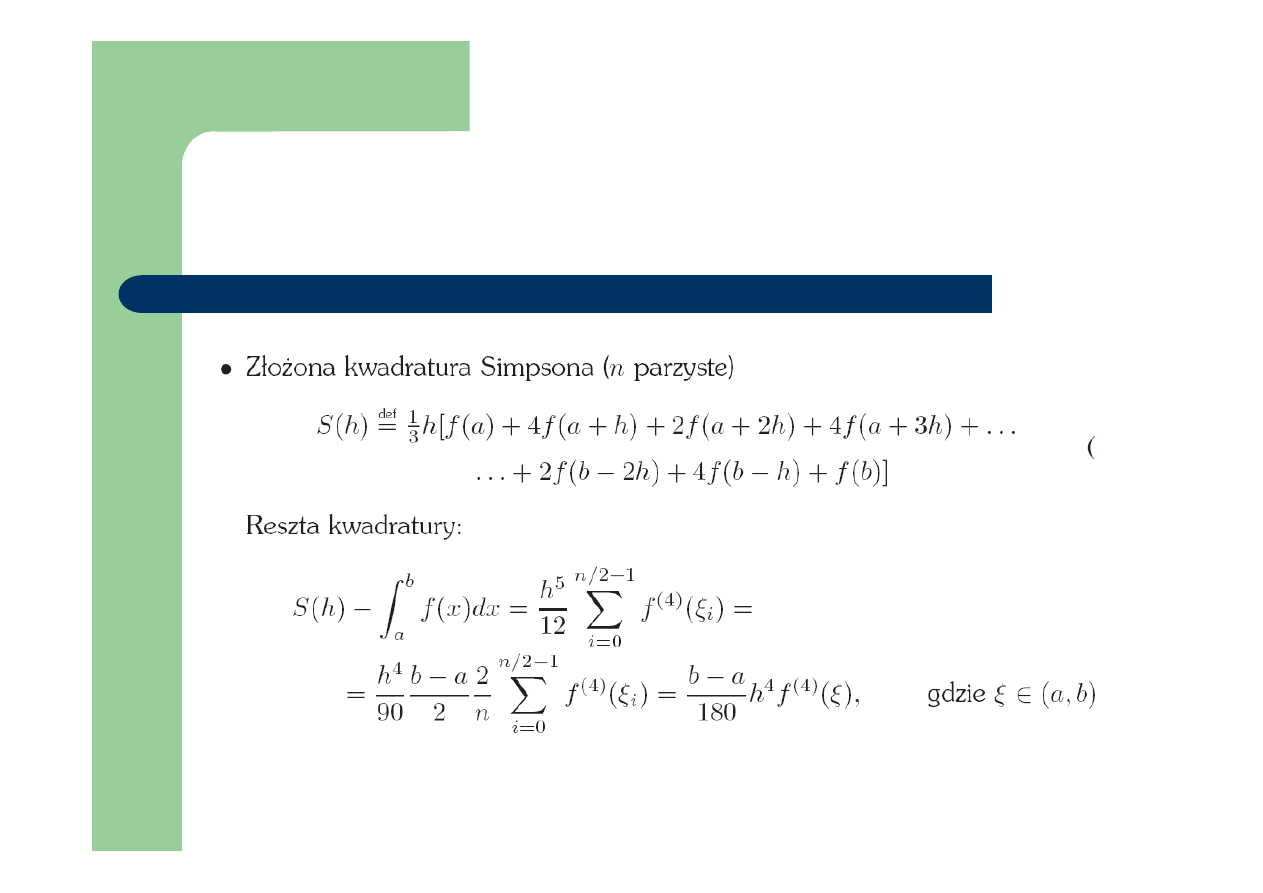
Dokładność:

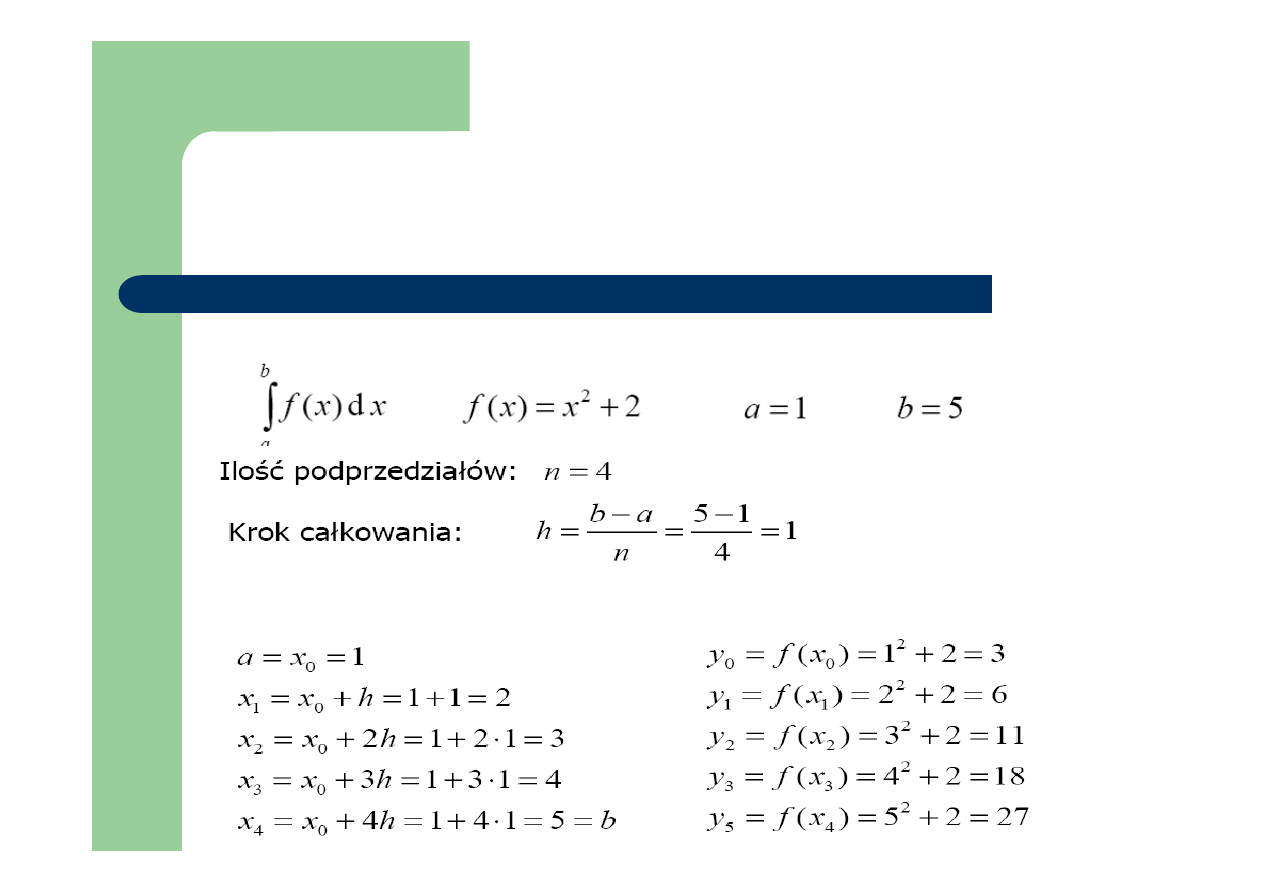
Przykład:

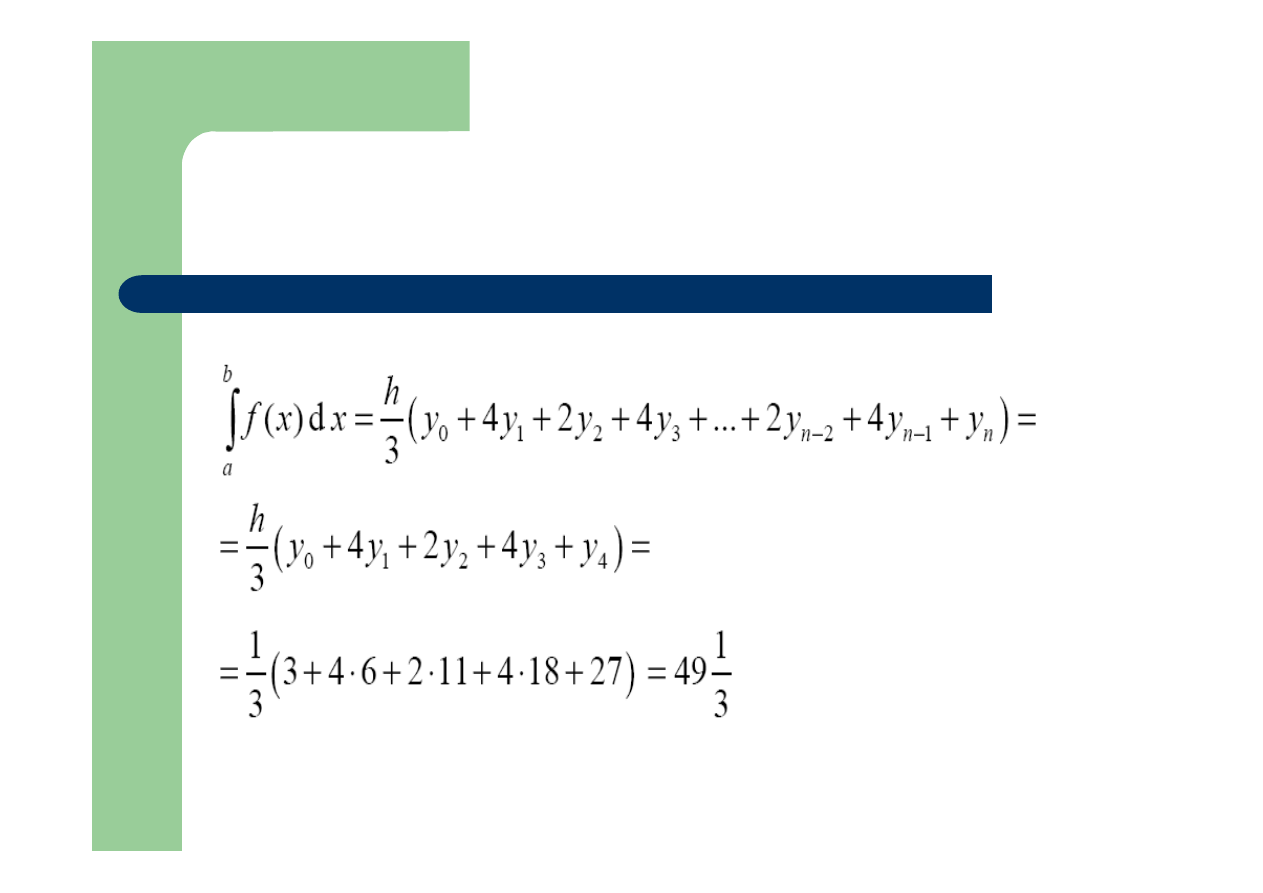
Przykład cd.

Wzory Newtona-Cotesa

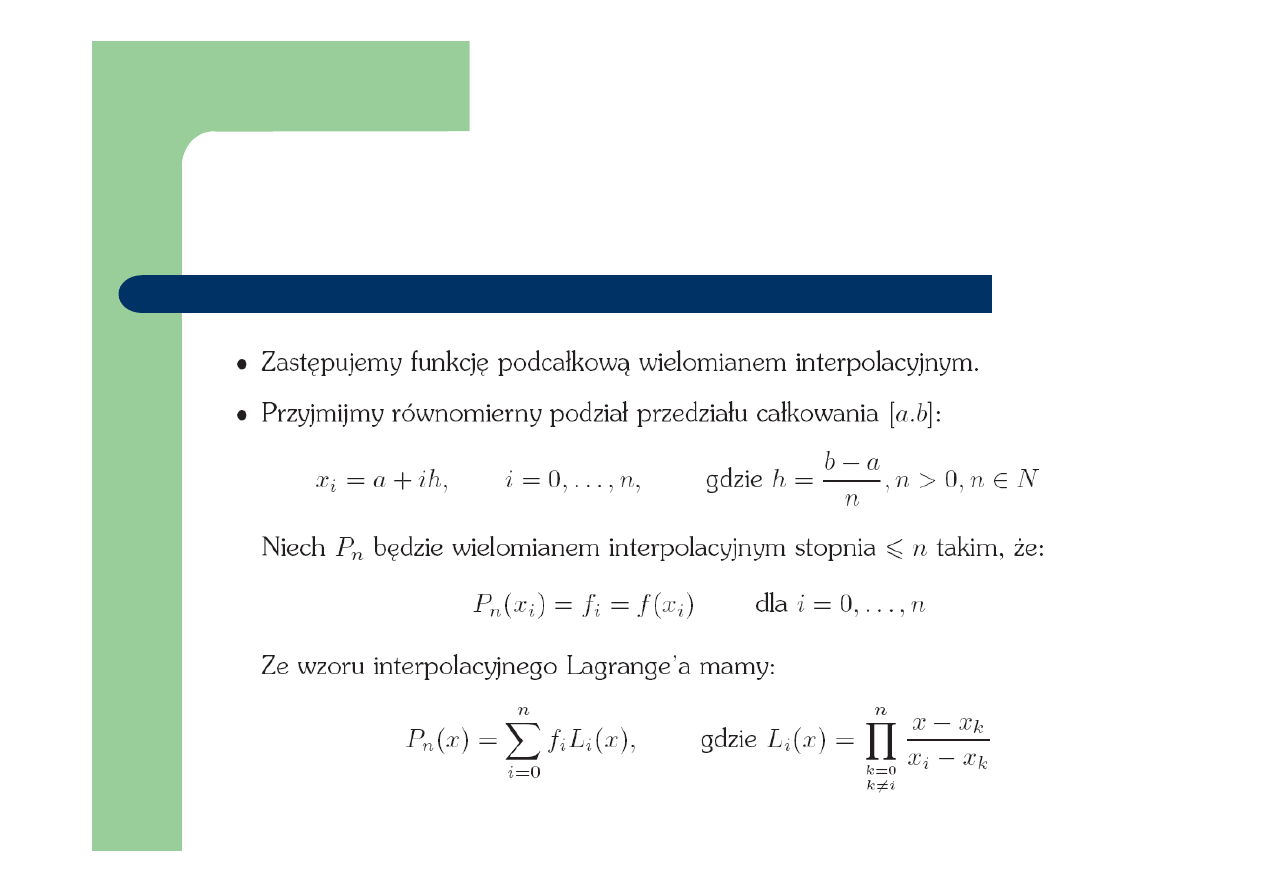
Wzory Newtona-Cotesa

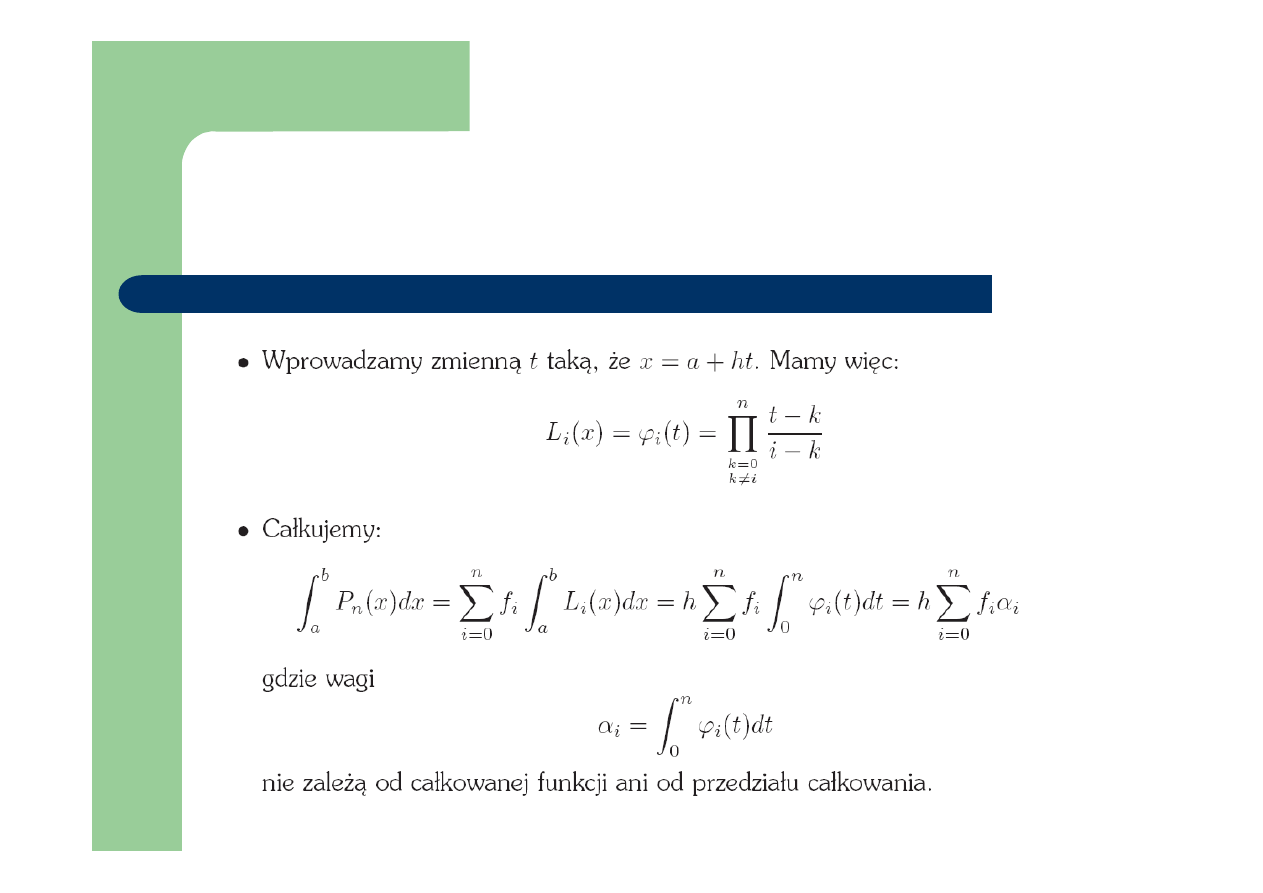
Wzory Newtona-Cotesa

Wzór Simpsona:

Wzory Newtona-Cotes (zamknięte)

Wzory Newtona-Cotes (otwarte)

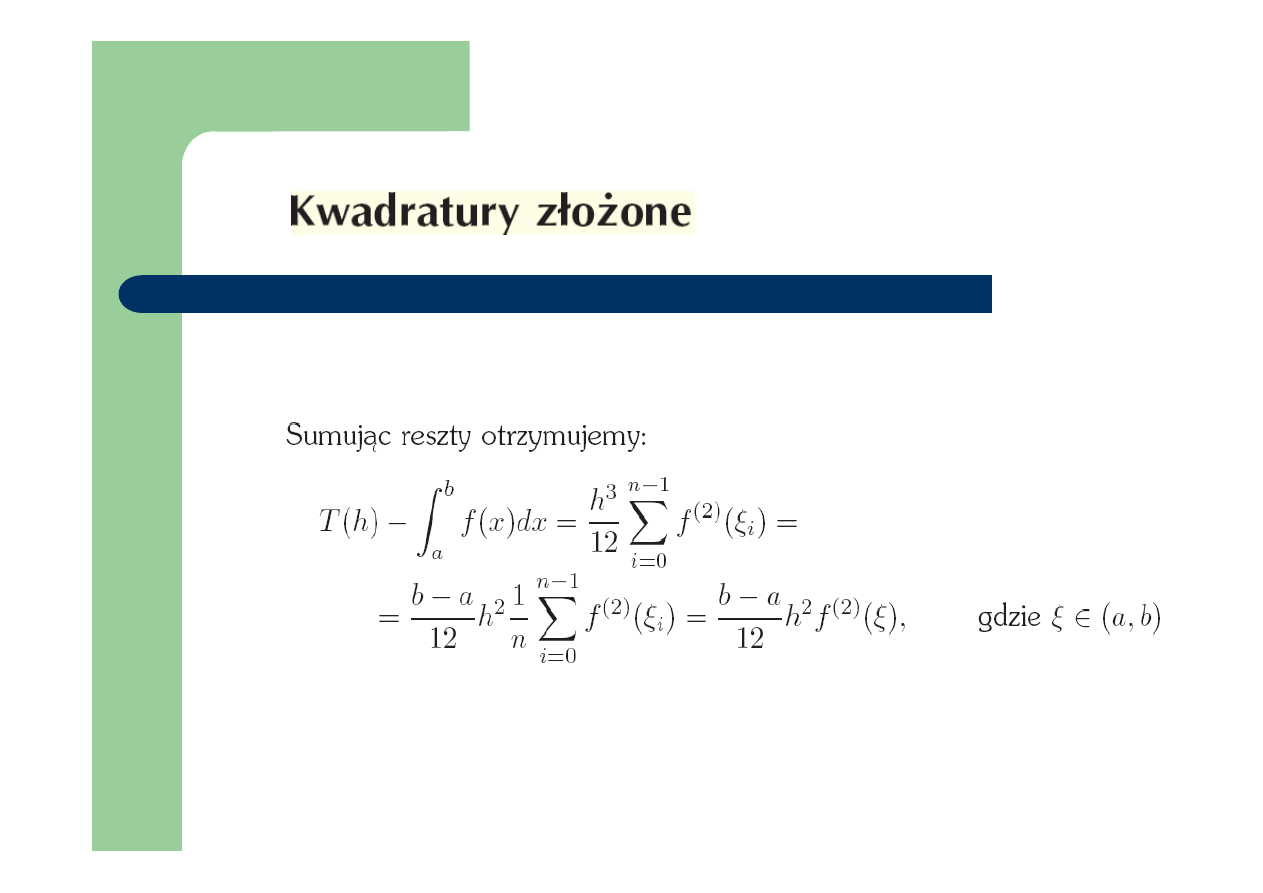
Kwadratury złożone-dokładność

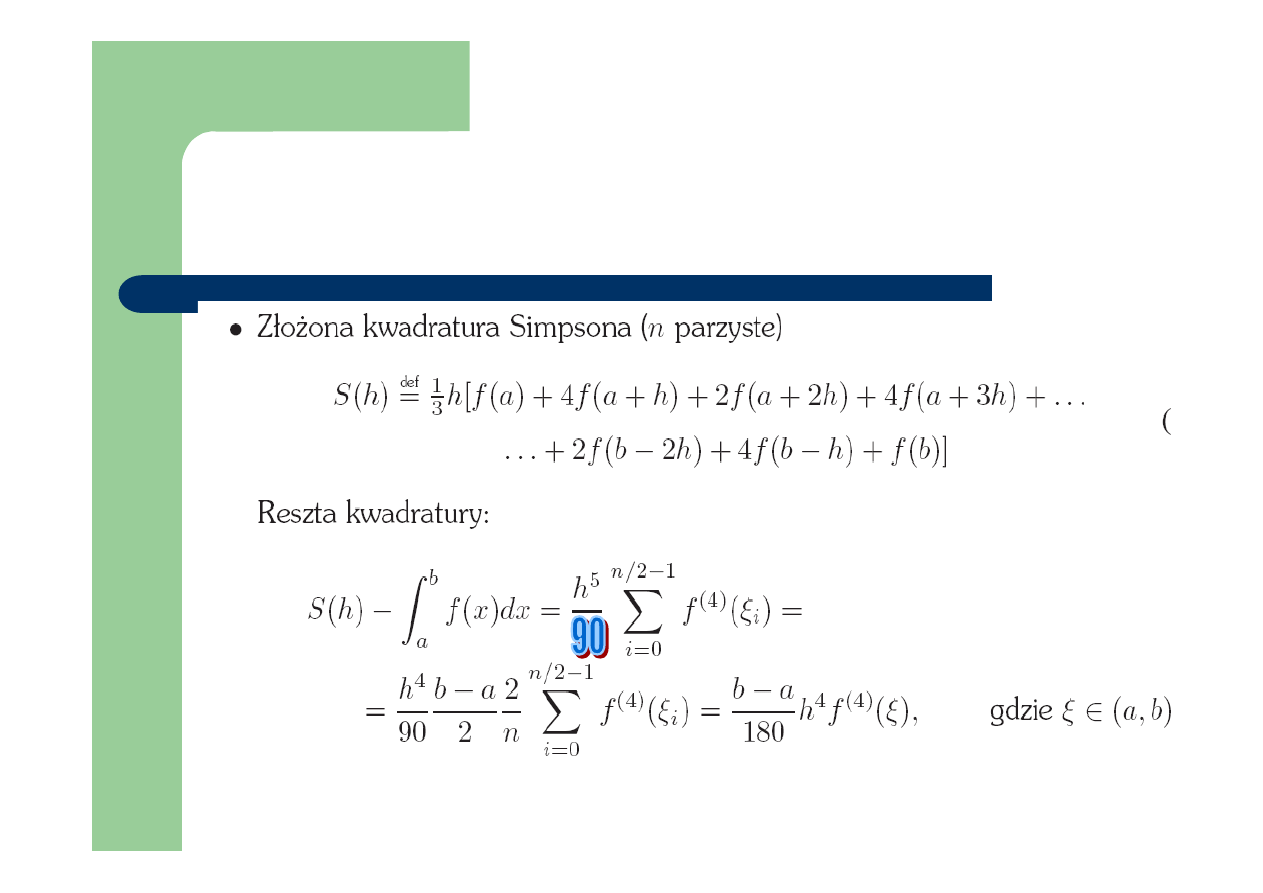
Dokładność kwadratury złożonej

Simpsona:

Kwadratury Gaussa

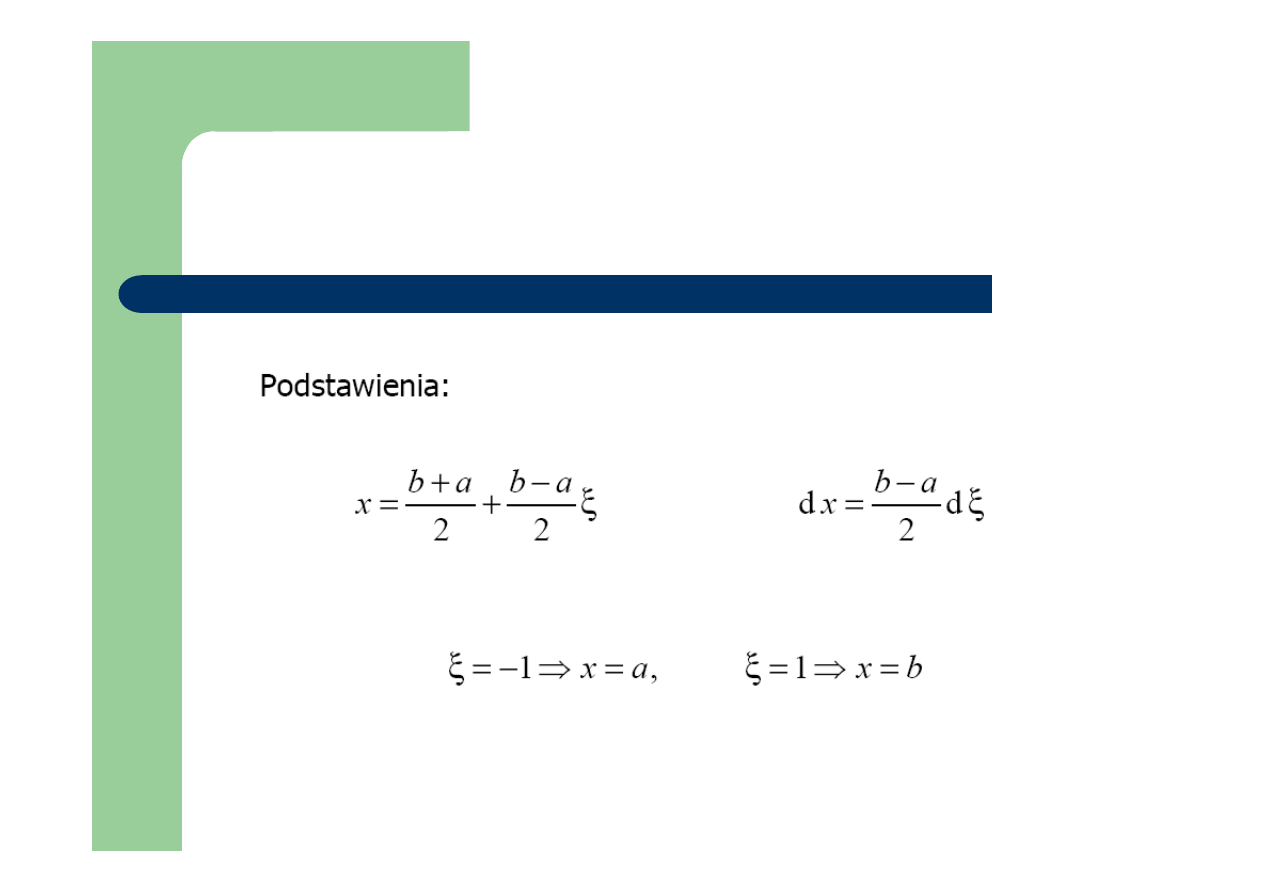
Normalizacja:

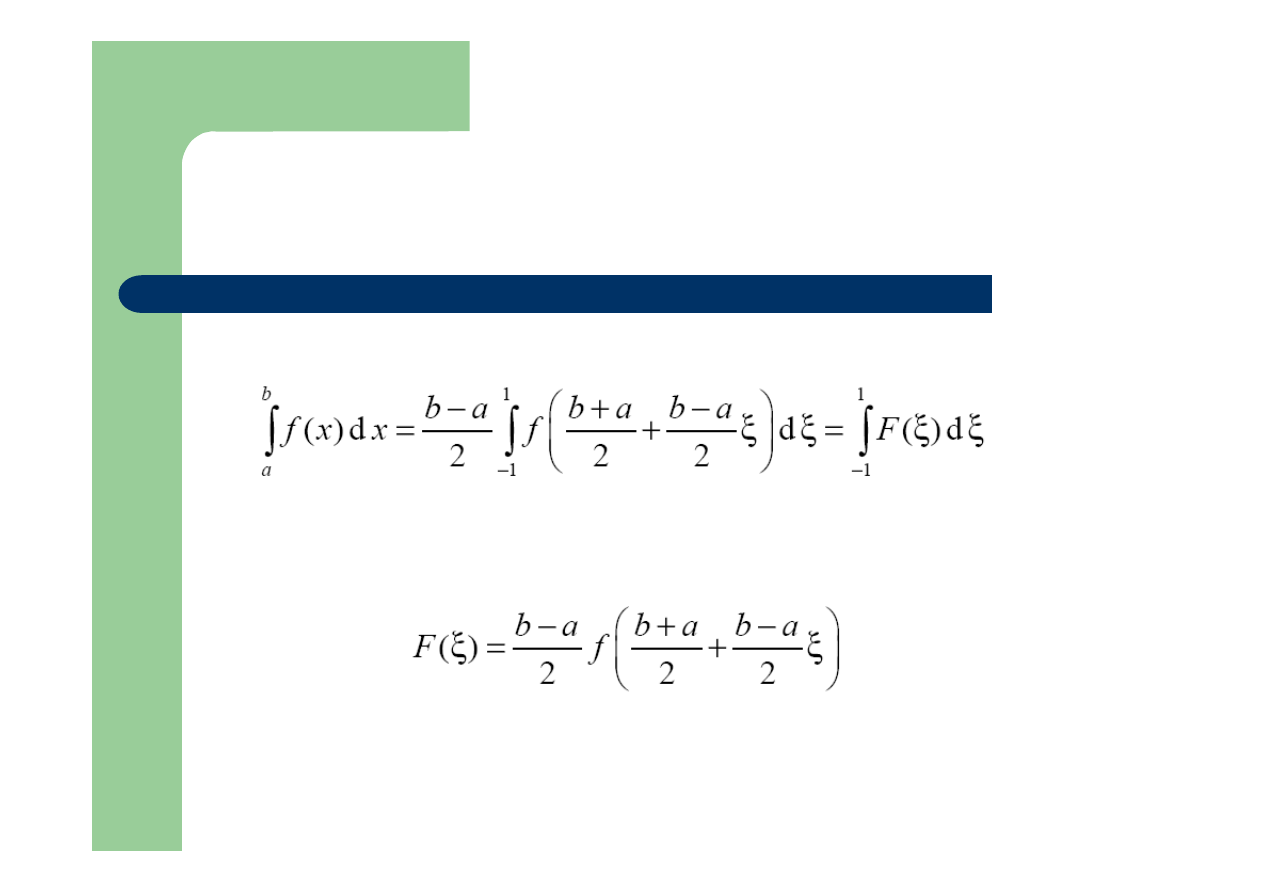
Czyli:

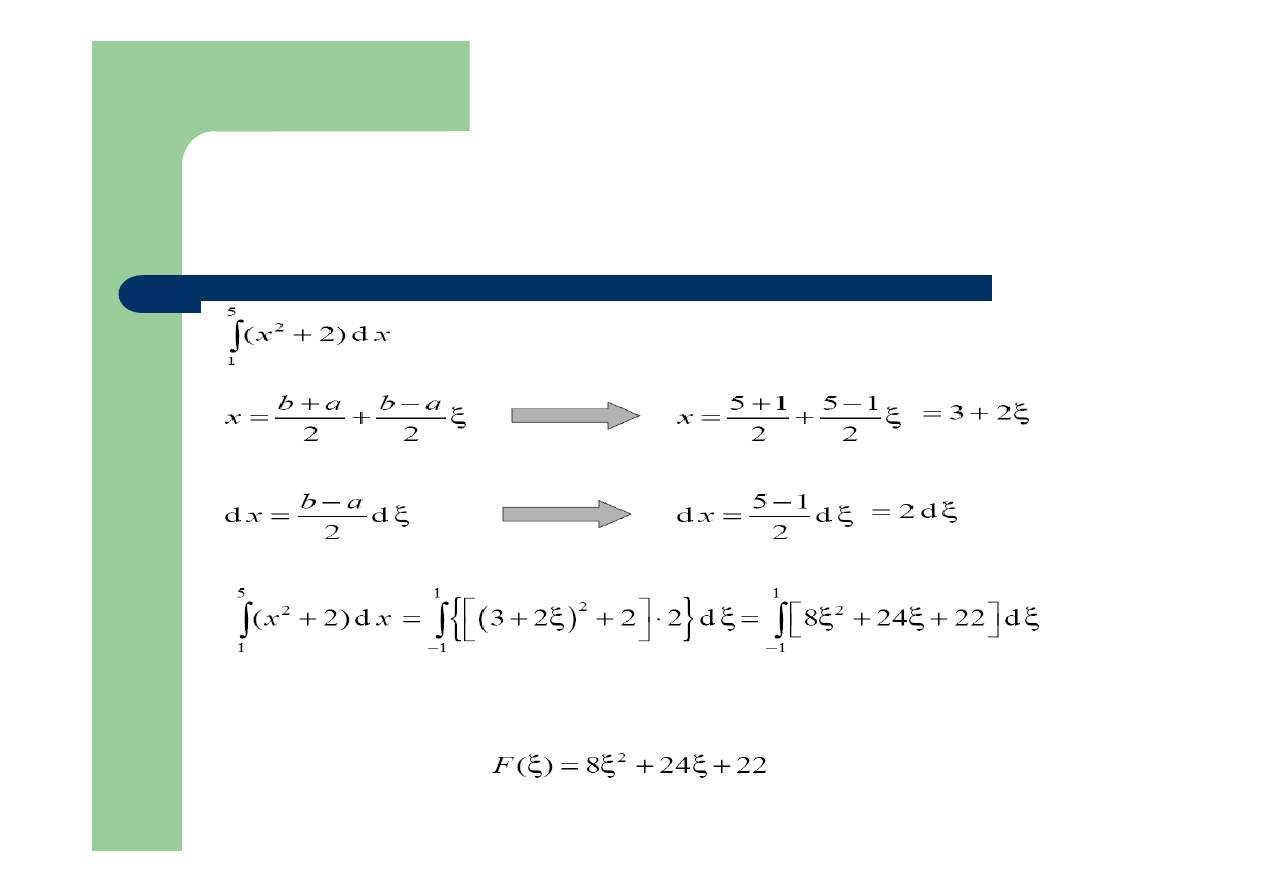
Przykład:

Kwadratury Gaussa:

Uwagi:

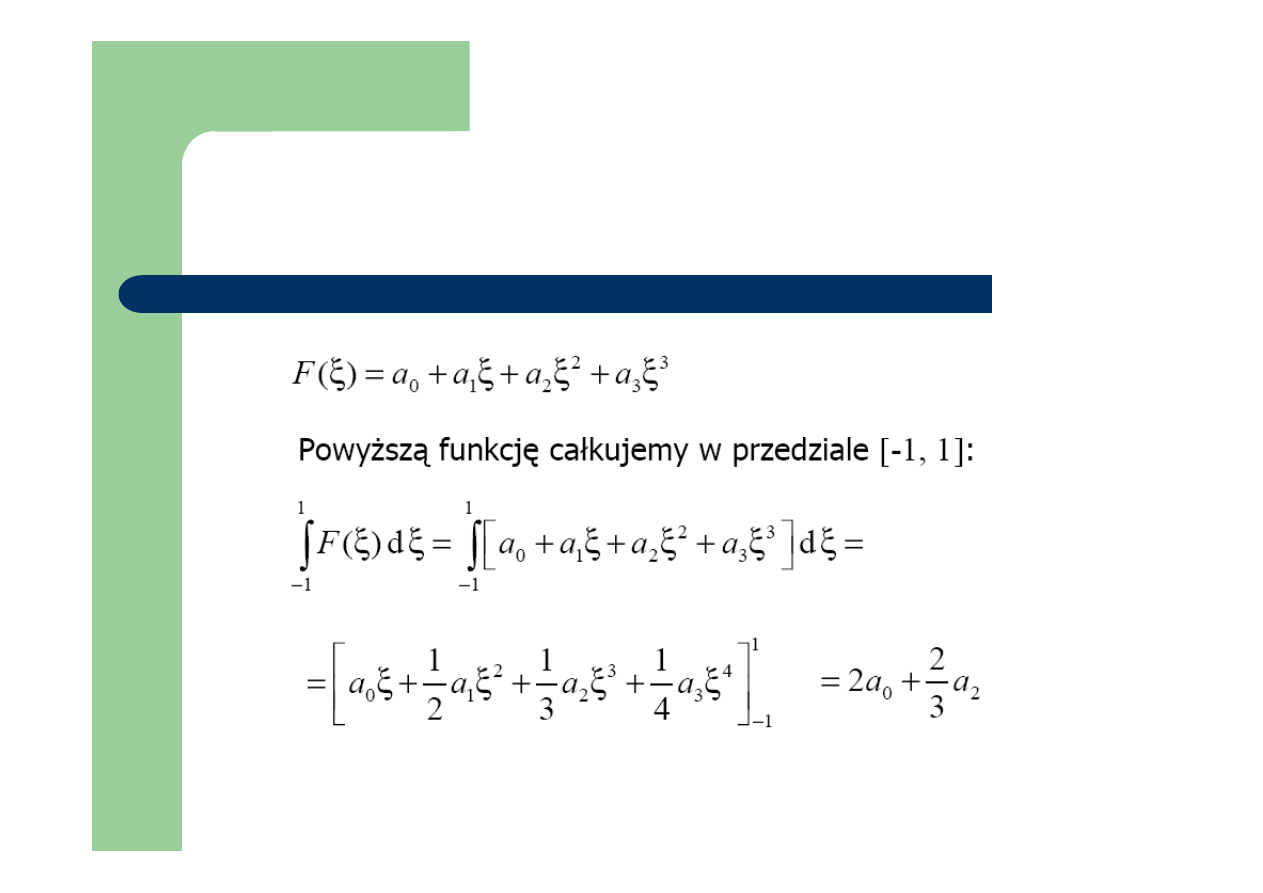
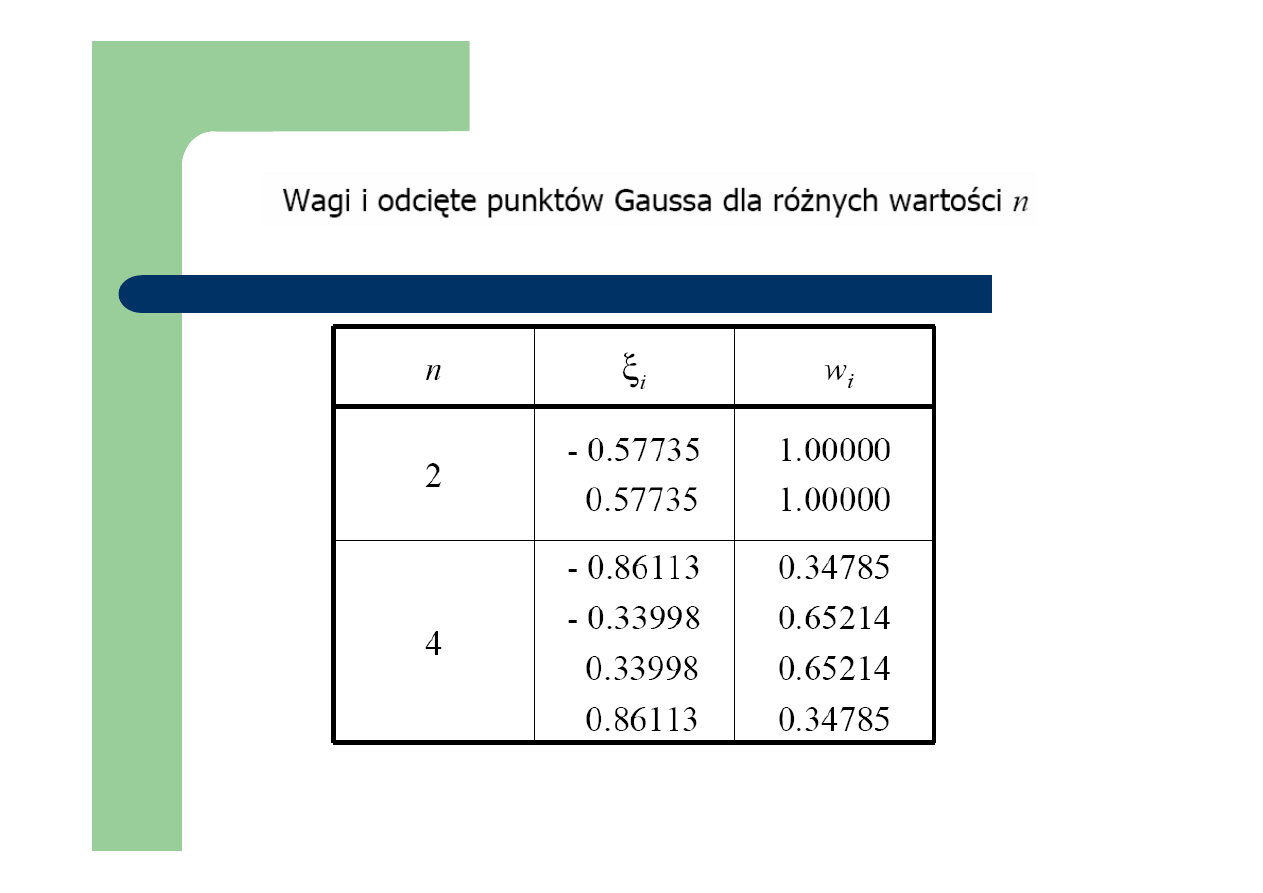
Kwadratura Gaussa dla n=2

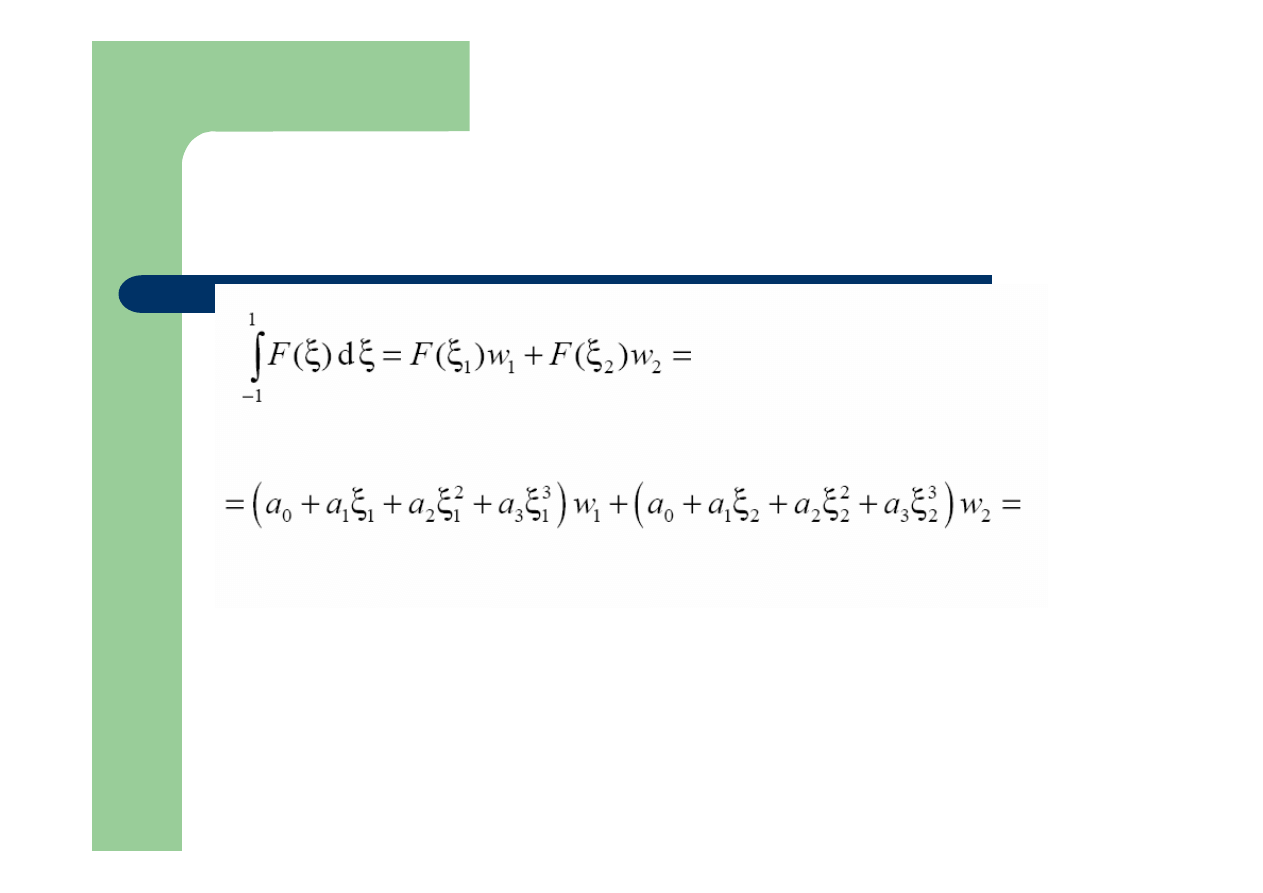
Równocześnie:

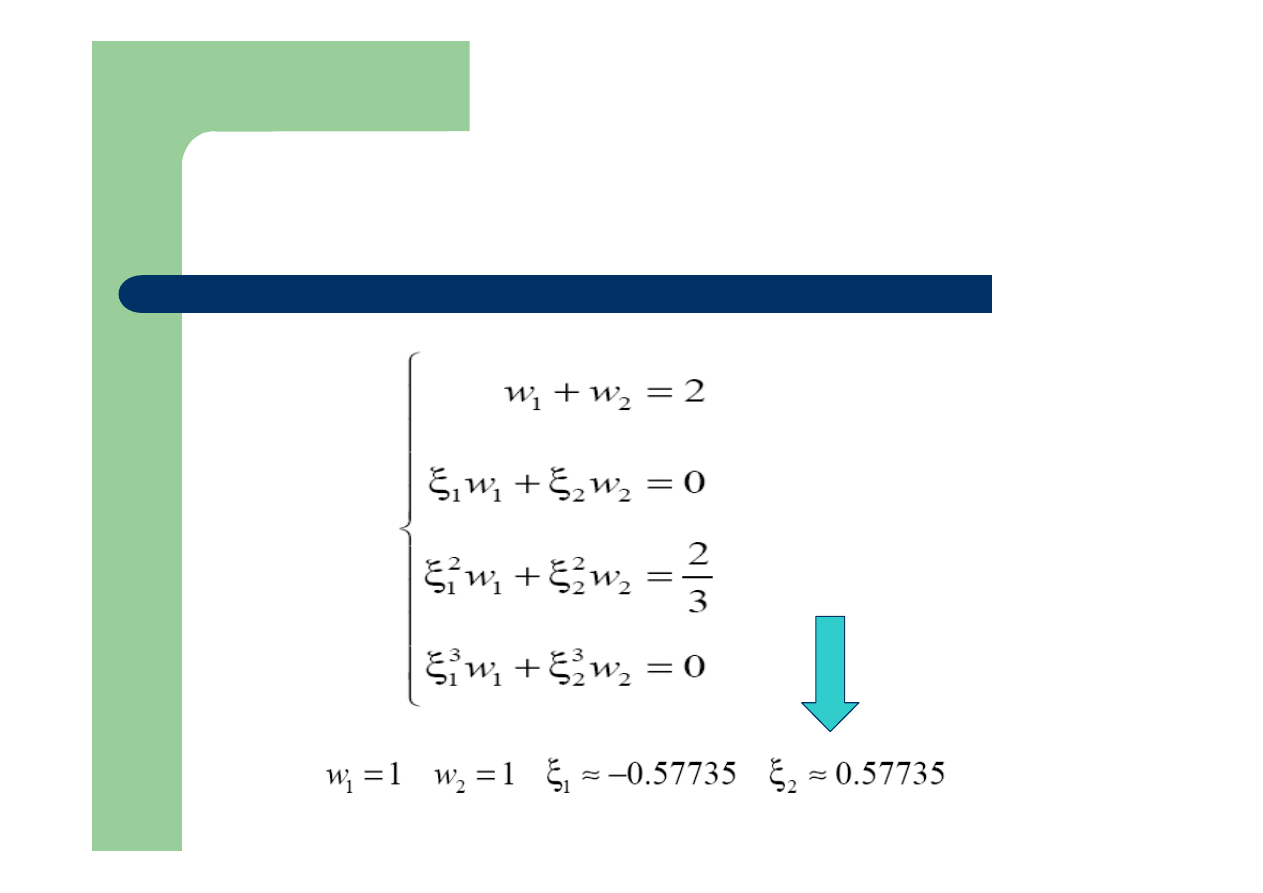
Stąd:

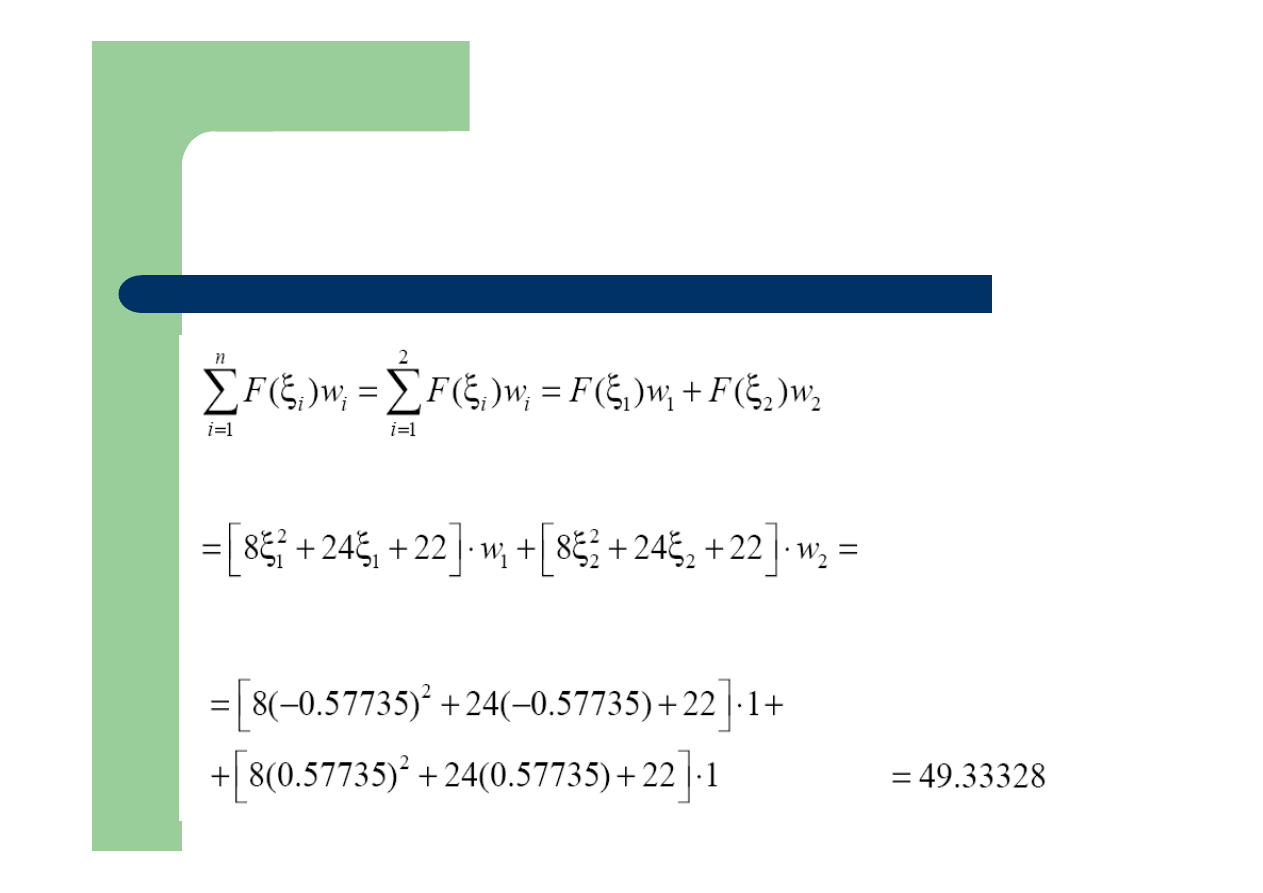
Dla naszego przykładu i n=2

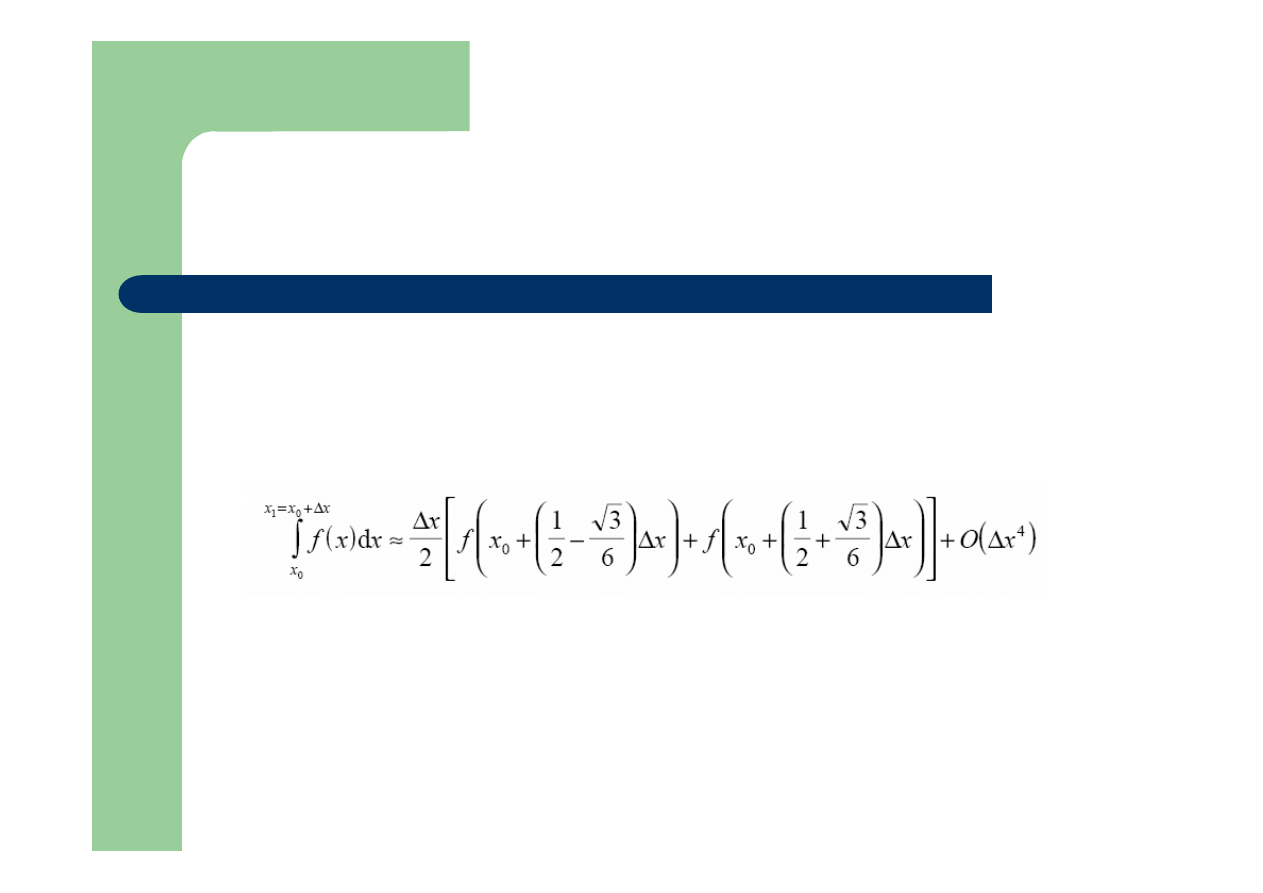
Dwupunktowa kwadratura Gaussa

przeliczona do przedziału [0,1]

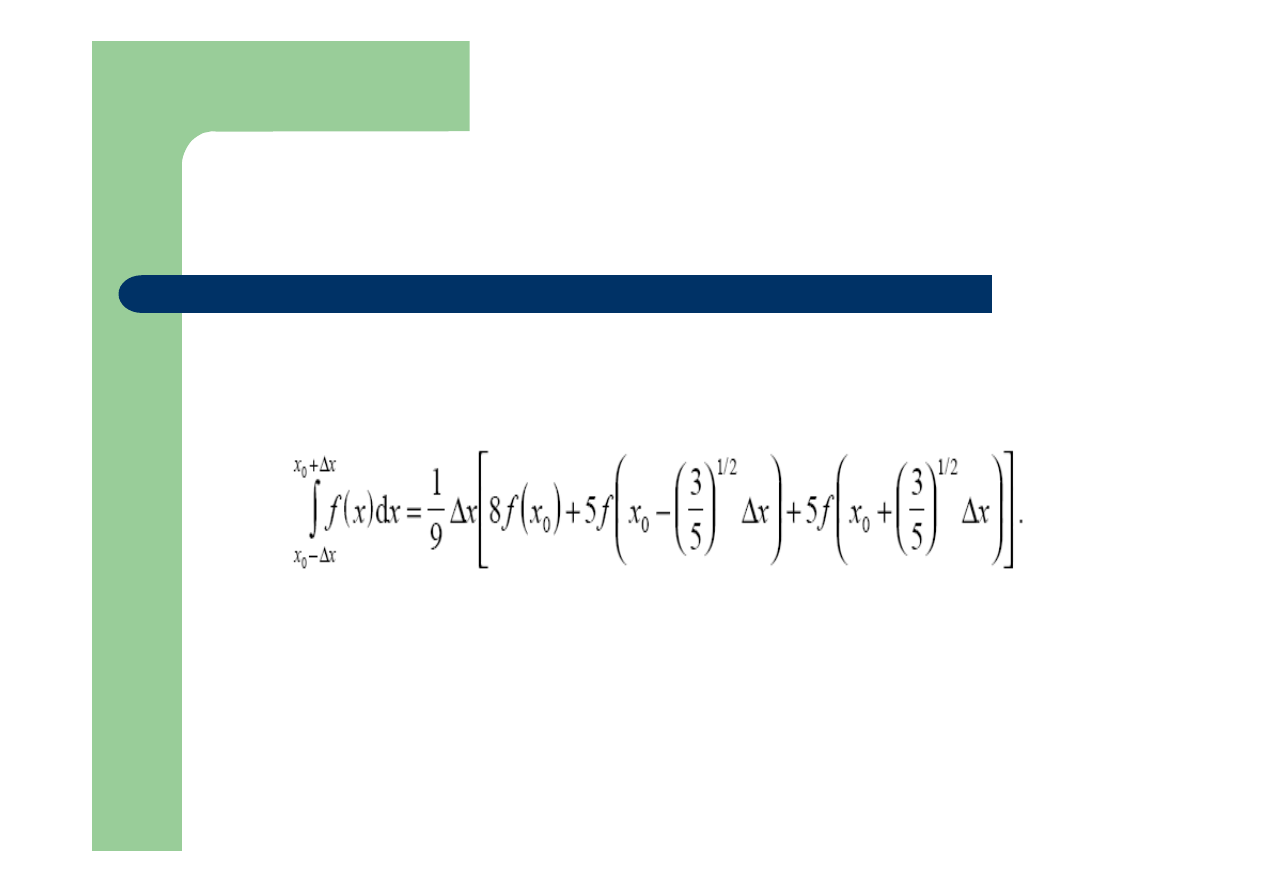
Dla trzech punktów:

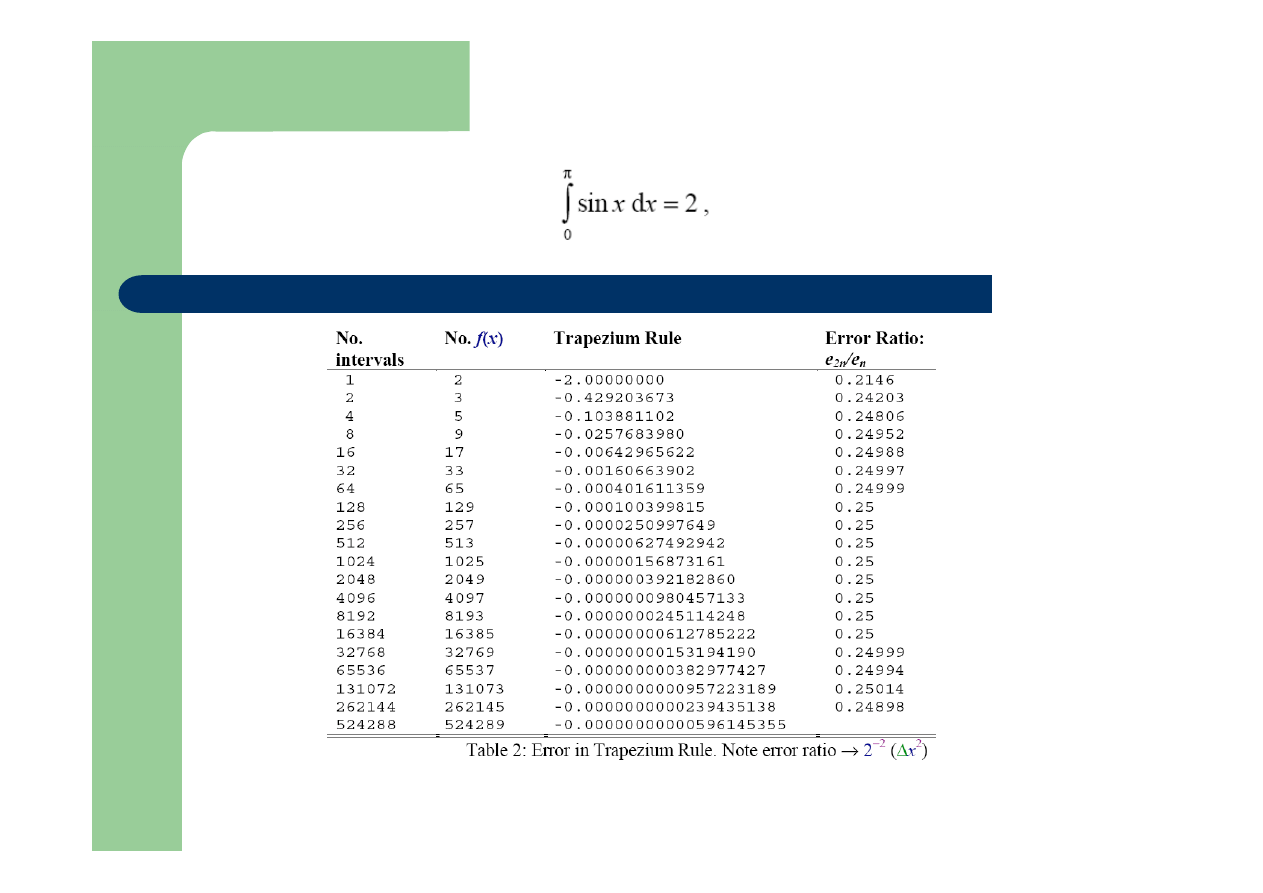
Przykład :

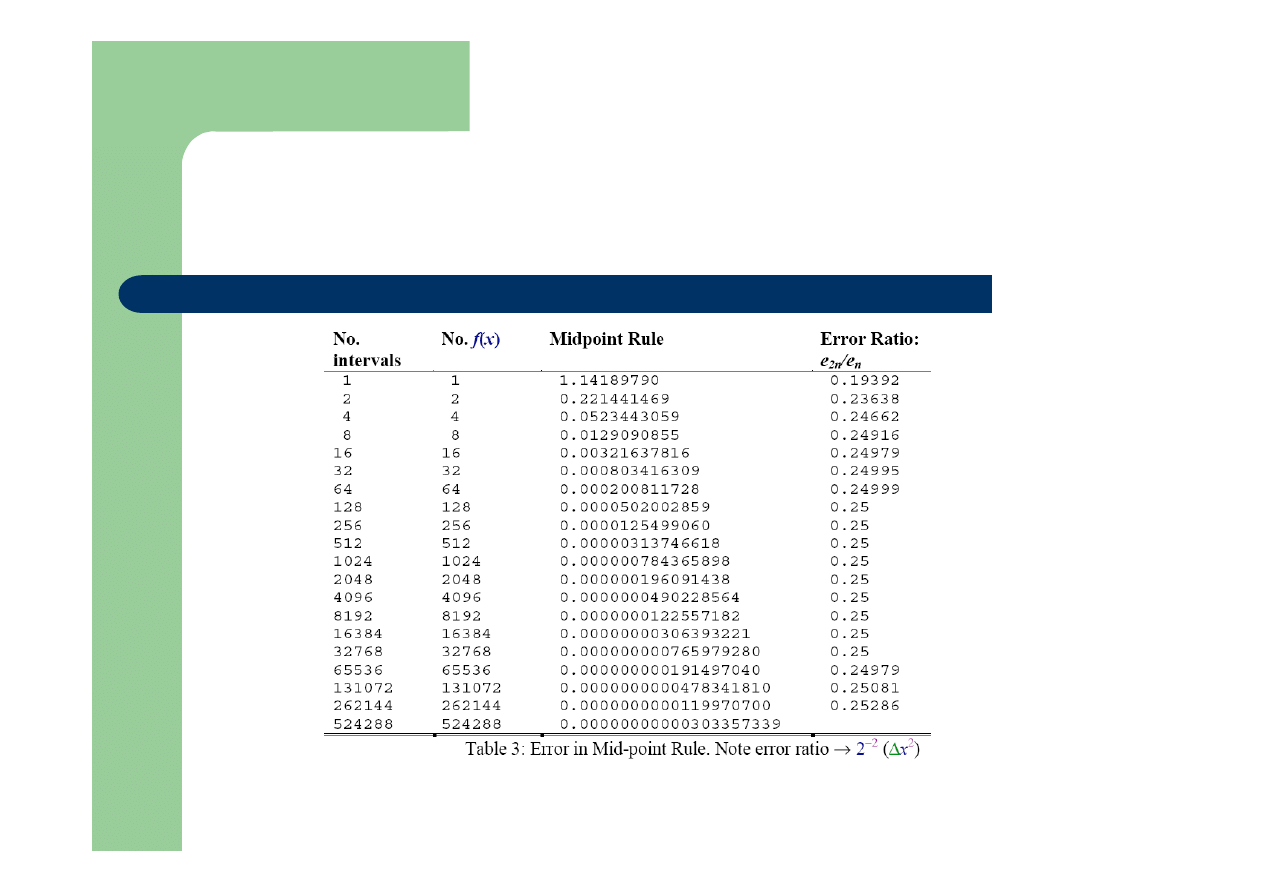
cd.

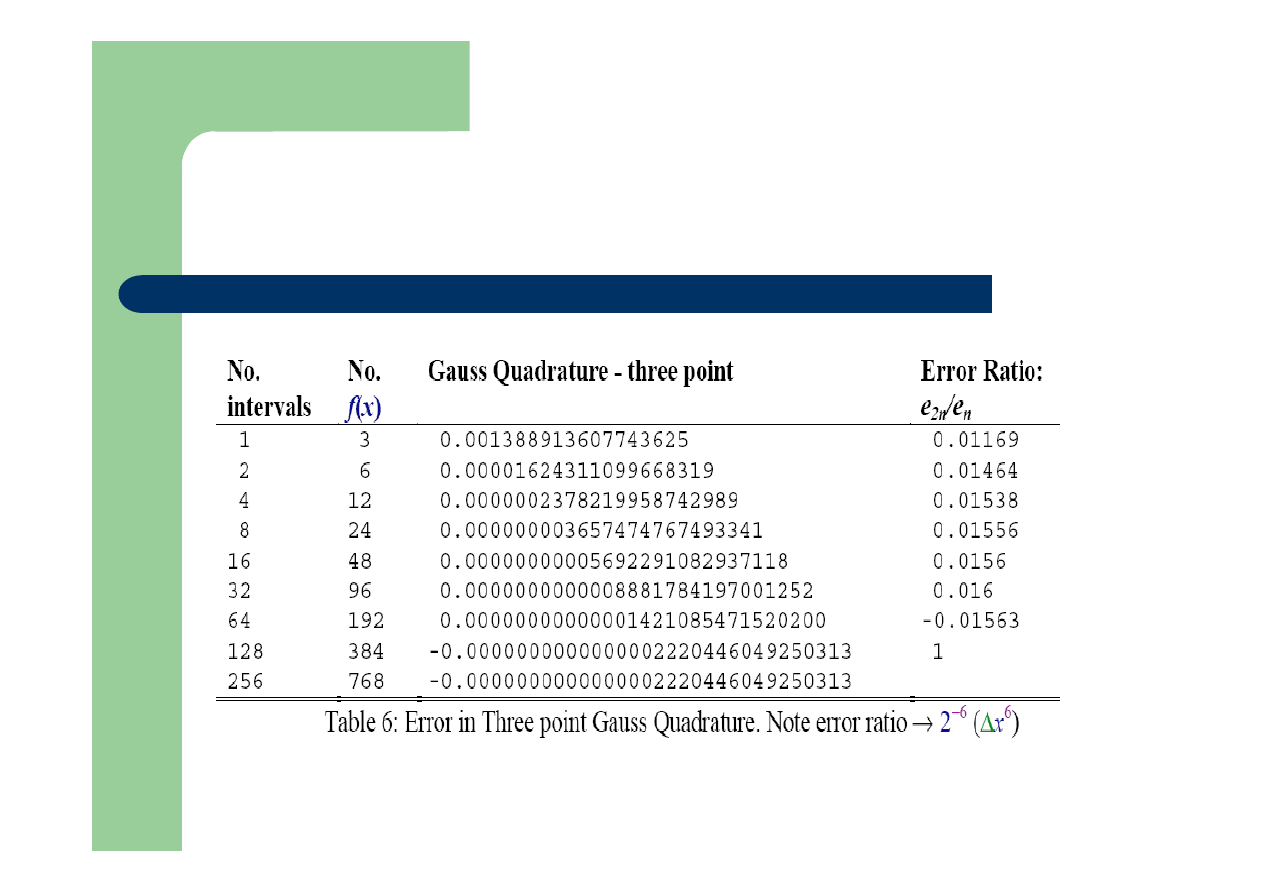
Złożona dwupunktowa