Tablica 1.2

x	m		błąd
	2	1.4142136	9.7E-17
	3	1.2599210	2.6E-17
	4	1.1892071	4.0E-17
	5	1.1486984	9.1E-17
2	6	1.1224620	3.6E-17
	7	1.1040895	8.7E-17
	8	1.0905077	2.5E-17
	9	1.0800597	6.1E-17
	10	1.0717735	3.3E-17
	2	1.7320508	1.0E-16
	3	1.4422496	8.1E-17
	4	1.3160740	8.3E-17
	5	1.2457309	7.1E-17
3	6	1.2009370	1.4E-17
	7	1.1699308	4.7E-17
	8	1.1472027	1.5E-17
	9	1.1298310	1.6E-17
	10	1.1161232	5.9E-17
	3	1.5874011	1.1E-16
	4	1.4142136	9.7E-17
	5	1.3195079	6.0E-17
4	6	1.2599210	2.6E-17
	7	1.2190137	5.8E-17
	8	1.1892071	4.0E-17
	9	1.1665290	4.8E-17
	10	1.1486984	9.1E-17

Ćwiczenia

1.1. Należy obliczyć wartość funkcji

z dokładnością do dwóch cyfr dziesiętnych po przecinku. Przyjmując jako przybliżone wartości zmiennych x i y równe, odpowiednio, 15.2 i 57° wyznaczyć błąd bez-względny obu tych wielkości.

1.2. Dany jest wielomian Należy opracować program do obliczania wartości tego wielomianu przy wykorzystaniu schematu Hornera dla oraz wyznaczania numeru największej z tych wartości.

1.3. Należy ułożyć program do obliczania wszystkich pochodnych zadanego wielomianu dla stosując algorytm schematu Hornera.

1.4. Zmodyfikować program 1.2 dodając w nim obliczanie kolejnych pierwiastków: , , , ... z ich rozwinięć w ułamki łańcuchowe.

1.5. Przedstawić funkcję zawierającą wyrazy do włącznie w postaci funkcji wymiernej

i następnie rozwinąć ją w ułamek łańcuchowy.

6. Napisać program przeznaczony do obliczania funkcji z jej rozwinięcia w ułamek łańcuchowy

1.7. Dane są liczby rzeczywiste p, q, r i Należy ułożyć program, w którym obliczana jest suma szeregu o wyrazach:

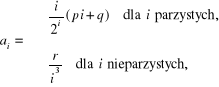
przerywając sumowanie w momencie, gdy

gdzie

1.8. Zmodyfikować program 1.4 dodając w nim obliczanie wartości funkcji si x i 
z ich rozwinięć w szeregi potęgowe (1.36) - (1.37) oraz (1.40) - (1.41).

1.9. Napisać program, analogiczny do programu 1.4, w którym obliczane są wartości funkcji ln x i arctg x w przedziale dla z ich rozwinięć w szeregi potęgowe:

1.10. Napisać program, analogiczny do programu 1.5, przeznaczony do obliczania wartości funkcji

metodą Newtona, po zapisaniu funkcji (1.42) w postaci

42 1. Wprowadzenie do metod numerycznych

Ćwiczenia 43

---