Dla układu równań z pięciodiagonalną macierzą blokową

(2.108)

uogólniając wzory (2.97) i (2.98), wyznaczamy najpierw macierze:

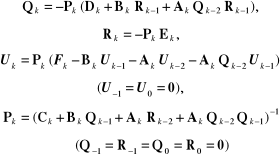
dla k = 1, 2, ..., n, a następnie obliczamy wektory niewiadomych:

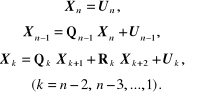
(2.109)

2.6. Stacjonarne metody iteracyjne

Omawianie metod iteracyjnych rozpoczniemy od przedstawienia macierzy wyjściowego układu równań

(2.110)

w postaci sumy

(2.111)

macierzy trójkątnej dolnej S o zerowych elementach diagonalnych, macierzy diagonalnej oraz macierzy trójkątnej górnej T o zerowych elementach diagonalnych. Rozwiązywany układ równań (2.110) możemy więc zapisać następująco

(2.112)

Jeśli macierz D jest nieosobliwa możemy przejść do postaci

(2.113)

gdzie

i utworzyć ciąg kolejnych przybliżeń (2.40)

(2.114)

gdzie:

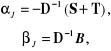
określający najprostszą metodę iteracyjną zwaną metodą Jacobiego lub też metodą iteracji prostej. Łatwo można sprawdzić, że zachodzi następująca zależność po-między współrzędnymi kolejnych przybliżeń

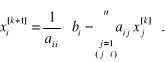
(2.115)

Metoda Gaussa i Seidela jest modyfikacją metody Jacobiego, w której przy obliczaniu przybliżenia wyższego niewiadomej wykorzystywane są znane już wartości każdego wyższego przybliżenia niewiadomych Metodę Ga-ussa i Seidela określa zatem zmodyfikowany układ równań (2.115), w którym czyni się użytek z wyższego przybliżenia natychmiast po jego obliczeniu

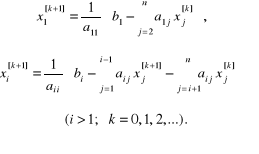
(2.116)

Korzystając z przedstawienia (2.113) układu równań (2.110) możemy te zależności zapisać w następującej postaci macierzowej

(2.117)

gdzie:

Przepisując zależności (2.116) w postaci

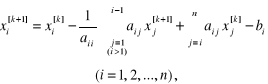
po pomnożeniu poprawek obliczanych niewiadomych , , ...,  przez odpowiednio dobraną liczbę: ω ∈ (0, 2), otrzymujemy ciągi kolejnych przybliżeń:

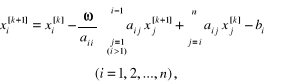
(2.118)

określające metody relaksacyjne. Liczba ω oznacza tzw. parametr relaksacji.
W przypadku

(2.119)

metoda nosi nazwę metody kolejnych nadrelaksacji (w skrócie SOR, od ang. successive overrelaxation), w przypadku

(2.120)

mówimy o podrelaksacji; dla ω = 1 wzór (2.118) redukuje się do wzorów (2.116).

Przekształcone równania (2.118)

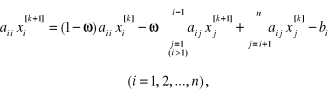
możemy łatwo zapisać w postaci macierzowej

skąd wynika zapis macierzowy metod relaksacyjnych

(2.121)

gdzie:

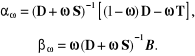
Mnożąc obydwie strony równania (2.110) przez parametr p i dodając do nich wektor X dostajemy zależność

(2.122)

która pozwala na utworzenie ciągu kolejnych przybliżeń metody iteracyjnej, nazywanej metodą Richardsona

(2.123)

gdzie:

*

Podstawowymi własnościami każdej metody iteracyjnej, decydującymi o ich wa-lorach użytkowych są zbieżność i szybkość zbieżności.

Wprowadzając błąd k-tej iteracji jako różnicę

(2.124)

między przybliżonym rozwiązaniem układu (2.110) i jego rozwiązaniem dokładnym, warunek zbieżności (2.41) możemy przepisać w postaci

(2.125)

Odejmując stronami równanie (2.39) od równania (2.40) otrzymujemy zależność między błędami kolejnych iteracji

(2.126)

zważywszy, że itd. Stąd i z własności norm dostajemy oszacowanie

z którego wynika, że warunek zbieżności (2.125) dowolnej metody iteracyjnej sprowadza się do nierówności

(2.127)

Dla zbieżności ciągu zdefiniowanego wzorem (2.40) wystarcza zatem, aby dowolna norma macierzy zdefiniowana wzorami (2.31) - (2.34) była mniejsza od jedności, przy czym wielkość normy decyduje o szybkości zbieżności metody iteracyjnej [2]

(2.128)

Układami równań liniowych nie wymagającymi spełnienia dodatkowego warunku zbieżności (2.127) są układy normalne. Układ równań liniowych (2.110) nazywamy normalnym, jeśli macierz A jego współczynników jest symetryczna i dodatnio określona. Układem normalnym jest układ równań powstały przez lewostronne pomnożenie równania (2.110) przez macierz transponowaną

(2.129)

Symetryczność macierzy (2.27) wynika z własności operacji transponowania macierzy, a dla wykazania jej dodatniej określoności należy zbadać od-powiadającą jej formę kwadratową (2.10)

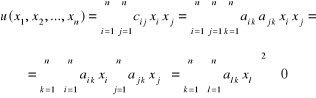
i uwzględnić fakt, że przy założeniu układ jednorodny ma tylko rozwiązanie zerowe.

Ważną klasę układów równań spełniających warunek (2.127) są układy z diagonalnie dominującymi macierzami współczynników. Macierz A nazywamy diagonalnie silnie dominującą, jeżeli moduły elementów na diagonali są większe od sumy modułów pozostałych elementów występujących w tym samym wierszu

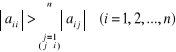
lub jeśli moduły elementów na diagonali są większe od sumy modułów pozostałych elementów należących do tej samej kolumny

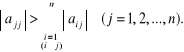
Ważną wielkością charakteryzującą metody iteracyjne jest promień spektralny macierzy - decydujący nie tylko o zbieżności metody iteracyjnej (norma spektralna), ale także o szybkości zbieżności konstruowanego ciągu (2.40), gdyż dla dowolnego > 0 i dla dostatecznie dużych k prawdziwe jest oszacowanie [6]

a ponadto zachodzą równości [12]:

dla macierzy A (2.111) zgodnie uporządkowanych tzn. takich, że wartości własne macierzy

są niezależne od dla

Dodatkowo przy stosowaniu czterech rozważanych metod iteracyjnych należy wziąć pod uwagę ich różne szczególne własności i uwarunkowania:

1. Metody Jacobiego i Gaussa-Seidela wymagają ustalenia takiej kolejności rów-nań, aby na diagonali występowały elementy niezerowe. Na ogół metoda Gaussa-Seidela jest szybciej zbieżna niż metoda Jacobiego, jednak w ogólnym przypadku nie ma takiej zależności - istnieją bowiem przykłady, że metoda Gaussa-Seidela jest rozbieżna, a metoda Jacobiego zbieżna i odwrotnie.

2. W metodach relaksacyjnych optymalna wartość jest większa od jedności, a więc występuje przy nadrelaksacji. Dla macierzy A (2.111) zgodnie uporządkowanej [6, 12]

(2.130)

gdzie jest największą co do modułu wartością własną macierzy promień spektralny macierzy jest wtedy równy

Charakter zależności promienia spektralnego od wartości ilustruje rysunek 2.1. Widać z niego, że gdy nie znamy wartości parametr relaksacji należy raczej przyjmować z niewielkim nadmiarem niż niedomiarem.

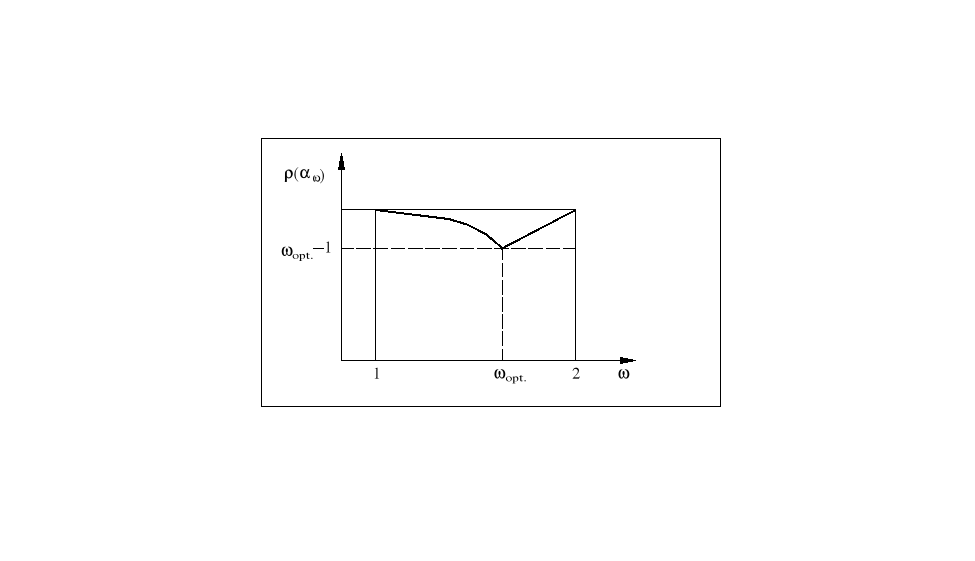
Rys. 2.1

3. W metodzie Richardsona dla macierzy A symetrycznych i dodatnio określonych można wyrazić w postaci [6]

Podobnie więc jak w metodach relaksacyjnych wielkość wskaźnika uwarunkowania układu nie tylko charakteryzuje jego wrażliwość na zaburzenia danych, ale również decyduje o szybkości zbieżności.

Na zakończenie tego podrozdiału przytoczymy jeszcze porównanie szybkości zbieżności omawianych metod dla układów równań o macierzach symetrycznych, dodatnio określonych i zgodnie uporządkowanych - zaczerpnięte z [6]. W tablicy 2.1 podano wielkości promienia spektralnego oraz liczbę k, będącą minimalną liczbą iteracji niezbędnych dla dziesięciokrotnej redukcji błędu przybliżenia początkowego

Tablica 2.1

cond (A)	Metody Jacobiego i Richardsona			Metoda Gaussa-Seidela			Metoda SOR
		k		k		k
10 100 10000	0.8182 0.9801 0.9998	12 116 11509	0.6694 0.9606 0.9996	6 58 5755	0.2699 0.6694 0.9608	6 18 233

Przy przyjętych założeniach najefektywniejsze okazało się użycie metody SOR, która jest szczególnie przydatna przy rozwiązywaniu zadań o dużym wskaźniku uwarunkowania.

*

{Program 2.3}

uses Crt;

type wym=1..20;

var

i,j,k,n,iter,licz: Integer;

bl,eps,om,sp,xn: Real;

A,AT,C: array[wym,wym] of Real;

B,D,X: array[wym] of Real;

norm: Boolean;

plik: Text;

zn: Char;

label omin,powt;

begin

Assign(plik,'Pr_2_3.dan');

Reset(plik);

Readln(plik,n,eps,iter);

for i:=1 to n do begin

for j:=1 to n do

Read(plik,A[i,j]);

Read(plik,B[i]);

end;

Close(plik);

ClrScr;

Writeln('PROGRAM 2.3');

Writeln('Rozwiazywanie ukladu rownan liniowych.');

Writeln('Metoda relaksacji.'); Writeln;

Write('Parametr relaksacji - om = '); Readln(om);

Write('Uklad w postaci normalnej: (t/n)? ');

zn:=ReadKey; Writeln;

if zn='t' then norm:=True else norm:=False;

Assign(plik,'Pr_2_3.wyn');

Rewrite(plik);

Writeln(plik,'PROGRAM 2.3');

Writeln(plik,'Rozwiazywanie ukladu rownan liniowych.');

Writeln(plik,'Metoda relaksacji.');

Writeln(plik);

Writeln(plik,'Liczba rownan ukladu - n = ',n:2);

Writeln(plik,'Parametr relaksacji - om = ',om:6:3);

Writeln(plik,'Zadana liczba iteracji - iter = ',iter:4);

Writeln(plik,'Zadana dokladnosc obliczen - eps = ',eps:13);

if norm=True then

Writeln(plik,'Uklad sprowadzono do postaci normalnej.');

Writeln(plik);

Writeln(plik,'Macierz wspolczynnikow:');

for i:=1 to n do begin

Writeln(plik,' wiersz nr ',i:2);

k:=0; Write(plik,' ');

for j:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',A[i,j]:13);

end;

Writeln(plik);

end;

Writeln(plik); k:=0;

Writeln(plik,'Wektor prawych stron:');

Write(plik,' ');

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0; Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',B[i]:13);

end;

Writeln(plik);

if not norm then goto omin;

{Sprowadzanie ukladu rownan do postaci normalnej}

for i:=1 to n do

for j:=1 to n do

AT[i,j]:=A[j,i];

for i:=1 to n do

for j:=1 to n do begin

sp:=0;

for k:=1 to n do

sp:=sp+AT[i,k]*A[k,j];

C[i,j]:=sp;

end;

for i:=1 to n do begin

sp:=0;

for k:=1 to n do

sp:=sp+AT[i,k]*B[k];

D[i]:=sp;

end;

for i:=1 to n do begin

B[i]:=D[i];

for j:=1 to n do

A[i,j]:=C[i,j];

end;

omin:

{Rozwiazywanie ukladu rownan}

licz:=0; Writeln;

for i:=1 to n do

X[i]:=B[i];

powt:

licz:=licz+1; bl:=0;

for i:=1 to n do begin

sp:=0;

for j:=1 to n do

sp:=sp+A[i,j]*X[j];

if Abs(A[i,i])<1e-10 then Halt(1);

xn:=X[i]-om*(sp-B[i])/A[i,i];

if Abs(xn-X[i])>bl then bl:=Abs(xn-X[i]);

X[i]:=xn;

end;

Write('Iteracja nr ',licz:3);

Writeln(' Norma bledu: ',bl:13);

if (licz<iter) and (bl>eps) then goto powt;

Writeln(plik);

Writeln(plik,'Liczba wykonanych iteracji: ',licz:3);

Writeln(plik);

Writeln(plik,'Rozwiazanie ukladu rownan:');

Write(plik,' '); k:=0;

for i:=1 to n do begin

k:=k+1;

if k=5 then begin

k:=0;

Writeln(plik);

Write(plik,' ');

end;

Write(plik,' ',X[i]:13);

end;

Writeln(plik);

Close(plik);

end.

Zadaniem programu 2.3 jest rozwiązywanie układu równań liniowych metodą relaksacji z możliwością sprowadzania zadanego układu do postaci normalnej dla przybliżenia początkowego wektora niewiadomych równego wektorowi prawych stron. Dane do programu wczytywane z pliku Pr_2_3.dan składają się z następujących elementów:

n - liczba równań,

A[1..n,1..n] - tablica zawierająca współczynniki układu równań,

B[1..n] - tablica zawierająca prawe strony układu równań,

eps - zadana dokładność obliczeń,

iter - zadana liczba iteracji;

ponadto po wczytaniu z klawiatury litery 't' lub litery 'n' następuje wybór alternatywy obliczeń; w przypadku wczytania zn ='t' układ jest sprowadzany do postaci normalnej.

Porównując tabulogramy programów 2.1, 2.2 i 2.3 możemy stwierdzić, że metody iteracyjne są bardzo ekonomiczne pod względem wykorzystania pamięci maszyny cyfrowej. Metody iteracyjne są więc wygodne w stosowaniu dla bardzo dużych macierzy, chociaż dla większości macierzy A wymagają one dłuższych obliczeń dla uzyskania żądanej dokładności, niż metody dokładne.

Tabulogramy wyników uzyskanych po wczytaniu danych określających układ równań (2.59) dla trzech wartości parametru relaksacyjnego: ω = 0.9, 1.3 i 1.5 są następujące:

PROGRAM 2.3

Rozwiazywanie ukladu rownan liniowych.

Metoda relaksacji.

Liczba rownan ukladu - n = 3

Parametr relaksacji - om = 0.900

Zadana liczba iteracji - iter = 50

Zadana dokladnosc obliczen - eps = 1.000000E-06

Uklad sprowadzono do postaci normalnej.

Macierz wspolczynnikow:

wiersz nr 1

1.000000E+00 -1.000000E+00 2.000000E+00

wiersz nr 2

2.000000E+00 1.000000E+00 -1.000000E+00

wiersz nr 3

1.000000E+00 3.000000E+00 -1.000000E+00

Wektor prawych stron:

5.000000E+00 1.000000E+00 4.000000E+00

Liczba wykonanych iteracji: 44

Rozwiazanie ukladu rownan:

9.999984E-01 2.000002E+00 3.000002E+00

PROGRAM 2.3

Rozwiazywanie ukladu rownan liniowych.

Metoda relaksacji.

Liczba rownan ukladu - n = 3

Parametr relaksacji - om = 1.300

Zadana liczba iteracji - iter = 50

Zadana dokladnosc obliczen - eps = 1.000000E-06

Uklad sprowadzono do postaci normalnej.

Macierz wspolczynnikow:

wiersz nr 1

1.000000E+00 -1.000000E+00 2.000000E+00

wiersz nr 2

2.000000E+00 1.000000E+00 -1.000000E+00

wiersz nr 3

1.000000E+00 3.000000E+00 -1.000000E+00

Wektor prawych stron:

5.000000E+00 1.000000E+00 4.000000E+00

Liczba wykonanych iteracji: 16

Rozwiazanie ukladu rownan:

1.000000E+00 2.000000E+00 3.000000E+00

PROGRAM 2.3

Rozwiazywanie ukladu rownan liniowych.

Metoda relaksacji.

Liczba rownan ukladu - n = 3

Parametr relaksacji - om = 1.500

Zadana liczba iteracji - iter = 50

Zadana dokladnosc obliczen - eps = 1.000000E-06

Uklad sprowadzono do postaci normalnej.

Macierz wspolczynnikow:

wiersz nr 1

1.000000E+00 -1.000000E+00 2.000000E+00

wiersz nr 2

2.000000E+00 1.000000E+00 -1.000000E+00

wiersz nr 3

1.000000E+00 3.000000E+00 -1.000000E+00

Wektor prawych stron:

5.000000E+00 1.000000E+00 4.000000E+00

Liczba wykonanych iteracji: 26

Rozwiazanie ukladu rownan:

9.999994E-01 2.000000E+00 3.000000E+00

Tabulogramy wyników uzyskanych po wczytaniu danych określających układ równań równoważny układowi (2.59) - powstały przez przyjęcie innej kolejności równań:

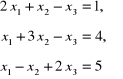
dla trzech wartości parametru relaksacyjnego ω = 0.9, 1.2, 1.4 mają postać:

PROGRAM 2.3

Rozwiazywanie ukladu rownan liniowych.

Metoda relaksacji.

Liczba rownan ukladu - n = 3

Parametr relaksacji - om = 0.900

Zadana liczba iteracji - iter = 50

Zadana dokladnosc obliczen - eps = 1.000000E-06

Macierz wspolczynnikow:

wiersz nr 1

2.000000E+00 1.000000E+00 -1.000000E+00

wiersz nr 2

1.000000E+00 3.000000E+00 -1.000000E+00

wiersz nr 3

1.000000E+00 -1.000000E+00 2.000000E+00

Wektor prawych stron:

1.000000E+00 4.000000E+00 5.000000E+00

Liczba wykonanych iteracji: 16

Rozwiazanie ukladu rownan:

9.999999E-01 2.000000E+00 3.000000E+00

PROGRAM 2.3

Rozwiazywanie ukladu rownan liniowych.

Metoda relaksacji.

Liczba rownan ukladu - n = 3

Parametr relaksacji - om = 1.200

Zadana liczba iteracji - iter = 50

Zadana dokladnosc obliczen - eps = 1.000000E-06

Macierz wspolczynnikow:

wiersz nr 1

2.000000E+00 1.000000E+00 -1.000000E+00

wiersz nr 2

1.000000E+00 3.000000E+00 -1.000000E+00

wiersz nr 3

1.000000E+00 -1.000000E+00 2.000000E+00

Wektor prawych stron:

1.000000E+00 4.000000E+00 5.000000E+00

Liczba wykonanych iteracji: 41

98 2. Układy równań liniowych

2.6. Stacjonarne metody iteracyjne 93

---