PROGRAM 1.1.

Schemat Hornera.

Stopień wielomianu - n = 5

Współczynniki wielomianu Pn(x):

a[5] = 4.000000000E+0000

a[4] = 1.000000000E+0000

a[3] = 0.000000000E+0000

a[2] = -3.000000000E+0000

a[1] = 2.000000000E+0000

a[0] = -1.000000000E+0000

Argument - ksi = 3.0000

Pn(ksi) = 1.0310000E+0003

Współczynniki wielomianu Qn-1(x):

b[0] = 4.0000000E+0000

b[1] = 1.3000000E+0001

b[2] = 3.9000000E+0001

b[3] = 1.1400000E+0002

b[4] = 3.4400000E+0002

Rys. 1.2

1.5. Ułamki łańcuchowe

Ułamkiem łańcuchowym nazywamy wyrażenie postaci

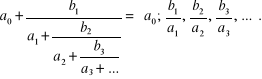
(1.14)

Elementy ułamka łańcuchowego: mogą być liczbami rzeczywistymi lub zespolonymi, jak również funkcjami jednej lub kilku zmiennych niezależnych. Ułamki: nazywają się ogniwami ułamka łańcuchowego (odpowiednio zerowym, pierwszym itd.), a liczby bądź też funkcje
i - elementami k-tego ogniwa.

Ułamek łańcuchowy (1.14) zawierający skończoną liczbę ogniw

(1.15)

nazywa się skończonym ułamkiem łańcuchowym. Jego wartość można łatwo obliczyć korzystając ze schematu Hornera dla dzielenia:

(1.16)

Rozkładanie liczb w ułamki łańcuchowe (1.15) - (1.16) wykorzystamy do obliczania wartości trzech pierwiastków: i

W przypadku kolejno wyznaczamy:

i ostatecznie mamy

(1.17)

W podobny sposób rozkładamy

(1.18)

oraz

(1.19)

Ułamki łańcuchowe (1.17) ÷ (1.19) są zbieżne [2], gdyż wszystkie ich elementy są dodatnie oraz i

Obliczenia i opisaną metodą rozkładania w ułamki łańcuchowe są realizowane w programie 1.2. Tabulogram modułu Obliczenia tego programu jest następujący:

{Program 1.2}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;

. . . . . . . . . . . . . . . . . . . . . .

var

Form3: TForm3;

a: array [0..30] of Real;

bl,c,eps,sn,sp: Real;

k,n,m: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

begin

Form2.Show;

AssignFile(plik,Edit2.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 1.2.');

Writeln(plik,'Obliczanie pierwiastka kwadratowego.');

Writeln(plik,'Przedstawianie w postaci ułamka łańcuchowego.');

Writeln(plik,'');

if RadioButton1.Checked then m:=3;

if RadioButton2.Checked then m:=5;

if RadioButton3.Checked then m:=7;

Writeln(plik,'Pierwiastek(m) - m = ',m);

eps:=StrToFloat(Edit1.Text);

Writeln(plik,'Dokładność obliczeń - eps = ',eps:4);

if m=3 then a[0]:=1 else a[0]:=2;

for k:=1 to 30 do begin

case m of

3: if (k div 2) = k/2 then a[k]:=2 else a[k]:=1;

5: a[k]:=4;

7: if (k div 4) = k/4 then a[k]:=4 else a[k]:=1;

end;

end;

n:=1; sp:=a[0];

repeat

c:=1/a[n];

for k:=1 to n do begin

sn:=a[n-k]+c;

c:=1/sn;

end;

bl:=Abs(sn-sp);

n:=n+1; sp:=sn;

until bl<eps;

Writeln(plik,''); bl:=sn-Sqrt(m);

Writeln(plik,'Wartość pierwiastka: ',sn:18);

Writeln(plik,'Błąd pierwiastka: ',bl:11);

Writeln(plik,'Liczba ogniw ułamka: ',n);

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit2.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Uzyskane za pomocą programu 1.2 wyniki obliczeń zawierają dwie następujące kopie wydruków ukazujących się na ekranie monitora oraz zapisywanych do pliku Pr_1_2.wyn:

PROGRAM 1.2.

Obliczanie pierwiastka kwadratowego.

Przedstawianie w postaci ułamka łańcuchowego.

Pierwiastek(m) - m = 3

Dokładność obliczeń - eps = 1.0E-0010

Wartość pierwiastka: 1.732050808E+0000

Błąd pierwiastka: 1.38E-0011

Liczba ogniw ułamka: 20

20 1. Wprowadzenie do metod numerycznych

1.5. Ułamki łańcuchowe 21

---