1. Założenia do projektu:

Wysokość budynku :

H

15.0m

:=

Szerokość budynku :

B

25.0m

:=

Ilość przęseł płatwi:

n

9

:=

Rozstaw wiązarów

Lp

7.0m

:=

Długość budynku:

L

n Lp

⋅

63 m

=

:=

Typ wiązara:

A

Lokalizacja:

Zielona Góra

Strefa śniegowa:

1

Strefa obciążęnia wiatrem: 1

Spadek połaci dachowej: 10%

Gatunek stali:

S235

Granica plastyczność

fy

235 MPa

⋅

:=

Moduł sprężystości stali:

E

210GPa

:=

1.1. Wstępne określenie geometrii wiązara.

h

1

8

1

12

÷













B

=

h

1

10

B

2.5 m

=

:=

przyjeto:

h

2.5 m

=

1.2. Rozstaw słupków w kratownicy:

a

B

10

2.5 m

=

:=

przyjeto:

a

2.5 m

=

1.4. Pochylenie połaci dachowej:

Przyjęto pochylenie 10%

α

10%

5.73 deg

⋅

=

:=

2. Zestawianie obciążęń.

2.1. Obciążenie stałe (od pokrycia dachu).

Płyta warstwowa Ruukki SP2C PU gr 140/100 mm

Masa płyty:

mp

12.0

kg

m

2

⋅

:=

Ciężar płyty:

g

mp

m

s

2

⋅

10

⋅

0.120000

kN

m

2

⋅

=

:=

g

0.120

kN

m

2

⋅

:=

gd

0.162

kN

m

2

⋅

:=

gd

1.35 g

⋅

0.162000

kN

m

2

⋅

=

:=

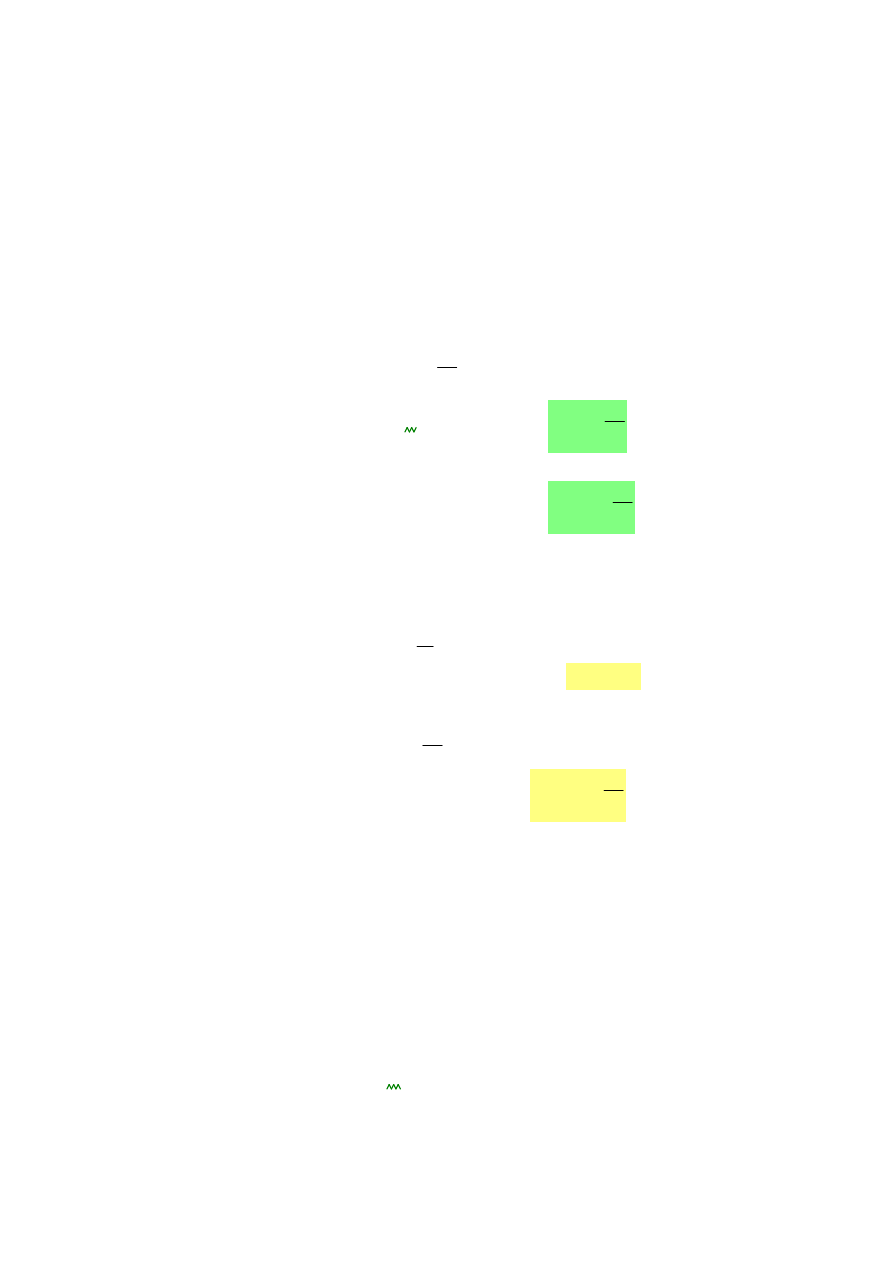
2.2. Obciążenie śniegiem (wg PN-EN 1991-1-3).

Obciążenie charakterystyczne śniegiem:

s

μi Ce

⋅

Ct

⋅

sk

⋅

=

Współczynnik kształtu dachu:

μi

0.8

:=

Współczynnik ekspozycji:

Ce

1.0

:=

Współczynnik termiczny:

Ct

1.0

:=

Wartość c harak terys tyczna obciążenia
śniegiem gruntu:

sk

0.7

kN

m

2

⋅

:=

Obciążenie charakterystyczne śniegiem:

s

μi Ce

⋅

Ct

⋅

sk

⋅

:=

s

0.56

kN

m

2

⋅

=

Obciążenie obliczeniowe śniegiem:

γf

1.5

:=

sd

s

γf

⋅

:=

sd 0.84

kN

m

2

⋅

=

2.3. Obciążenie wiatrem (wg PN-EN 1991-1-4).

Wysokość nad poziomem gruntu:

z

15

:=

Współczynnik ekspozycji:

Przyjęto teren kategorii III

ce

1.9

z

10













0.26

:=

ce 2.111

=

Średnia wysokość n.p.m. dla Zielona Góra:

115mnpm

Bazowa prędkość wiatru:

qb

0.3

kN

m

2

⋅

:=

Szczytowe ciśnienie prędkości:

qp

ce qb

⋅

:=

qp 0.633

kN

m

2

⋅

=

Współczynnik obliczeniowy dla obc. wiatrem:

γf 1.5

=

2.3.1. Ciśnienie wiatru działające na węzeły wiązara (wiatr z boku hali):

współczynniki ciśnienia zewnętrznego dla dachów dwuspadowych:

cpe10G

1.2

−

:=

cpe10H

0.6

−

:=

cpe10I

0.6

−

:=

cpe10J

0.6

−

:=

Cpe.10F

1.7

−

:=

wysokość hali:

H

15 m

=

wymiar prostopadły do kierunku wiatru:

b

L

63 m

=

:=

odległość od krawędzi:

e

min b 2H

,

(

)

30 m

=

:=

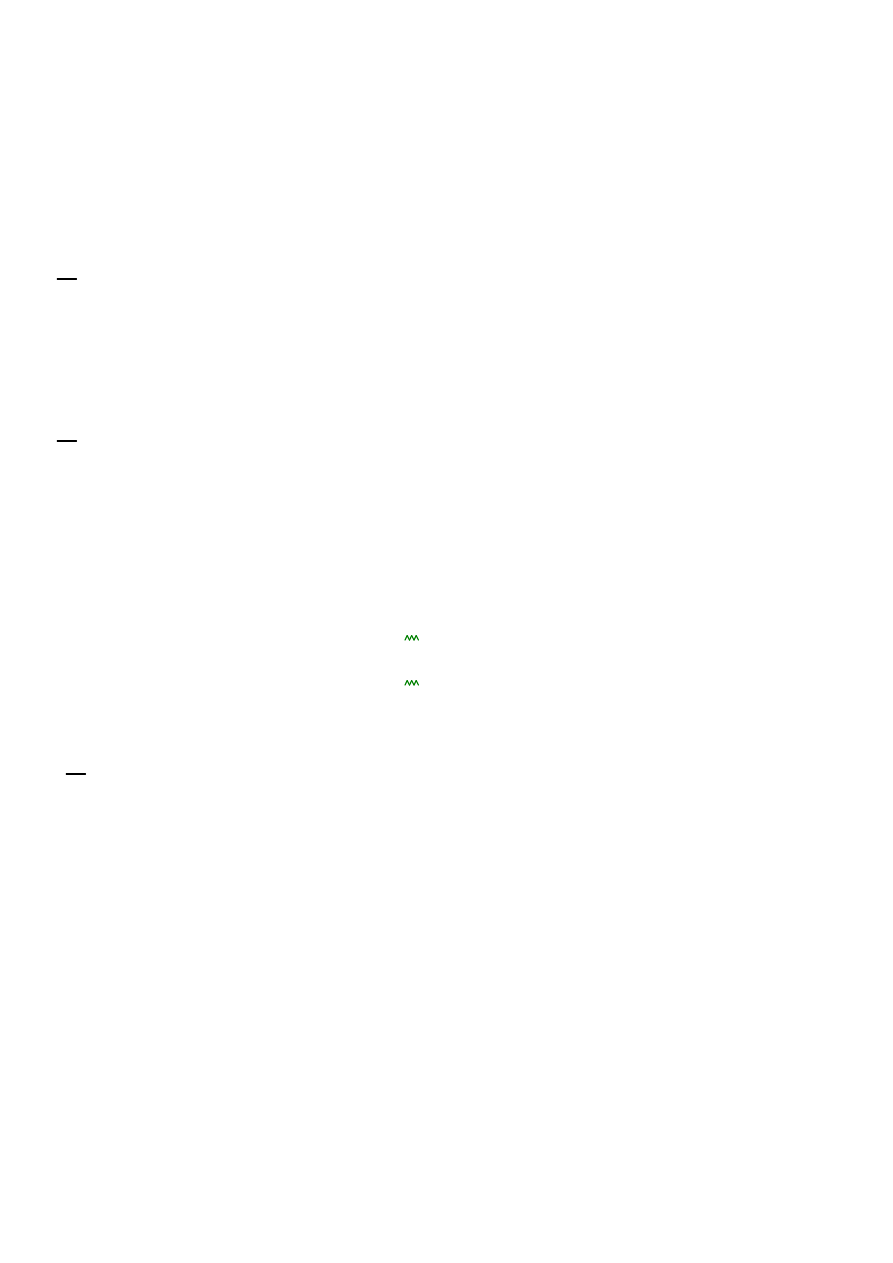
w1

qp 1.250m 4

⋅

m

(

) Cpe.10F

⋅

1.250m 3

⋅

m

(

) cpe10G

⋅

+





⋅

8.234

−

kN

⋅

=

:=

w2

qp 1.750m 4

⋅

m

(

) Cpe.10F

⋅

1.750m 3

⋅

m

(

) cpe10G

⋅

+

0.750m 7

⋅

m

(

) cpe10H

⋅

+





13.522

−

kN

⋅

=

:=

w3

qp 2.500m 7

⋅

m

(

) cpe10H

⋅





6.65

−

kN

⋅

=

:=

w3

2

3.325

−

kN

⋅

=

w4

qp 1.250m 7

⋅

m

(

) cpe10J

⋅





3.325

−

kN

⋅

=

:=

w5

qp 1.750m 7

⋅

m

(

) cpe10J

⋅

0.750m 7

⋅

m

(

) cpe10I

⋅

+





⋅

6.65

−

kN

⋅

=

:=

w6

qp 2.500m 7

⋅

m

(

) cpe10I

⋅





6.65

−

kN

⋅

=

:=

w6

2

3.325

−

kN

⋅

=

2.3.2. Ciśnienie wiatru działające na węzeły wiązara (wiatr wzdłuż hali):

współczynniki ciśnienia zewnętrznego dla dachów dwuspadowych:

Cpe.10F'

1.6

−

:=

cpe.10G'

1.3

−

:=

cpe.10H'

0.700

−

:=

cpe.10I'

0.600

−

:=

wysokość hali:

H

15 m

=

wymiar prostopadły do kierunku wiatru:

b

B

25 m

=

:=

odległość od krawędzi:

e

min b 2H

,

(

)

25 m

=

:=

w7

qp 2.500m 7

⋅

m cpe.10H'

⋅

(

)

(

)

7.759

−

kN

⋅

=

:=

w7

2

3.879

−

kN

⋅

=

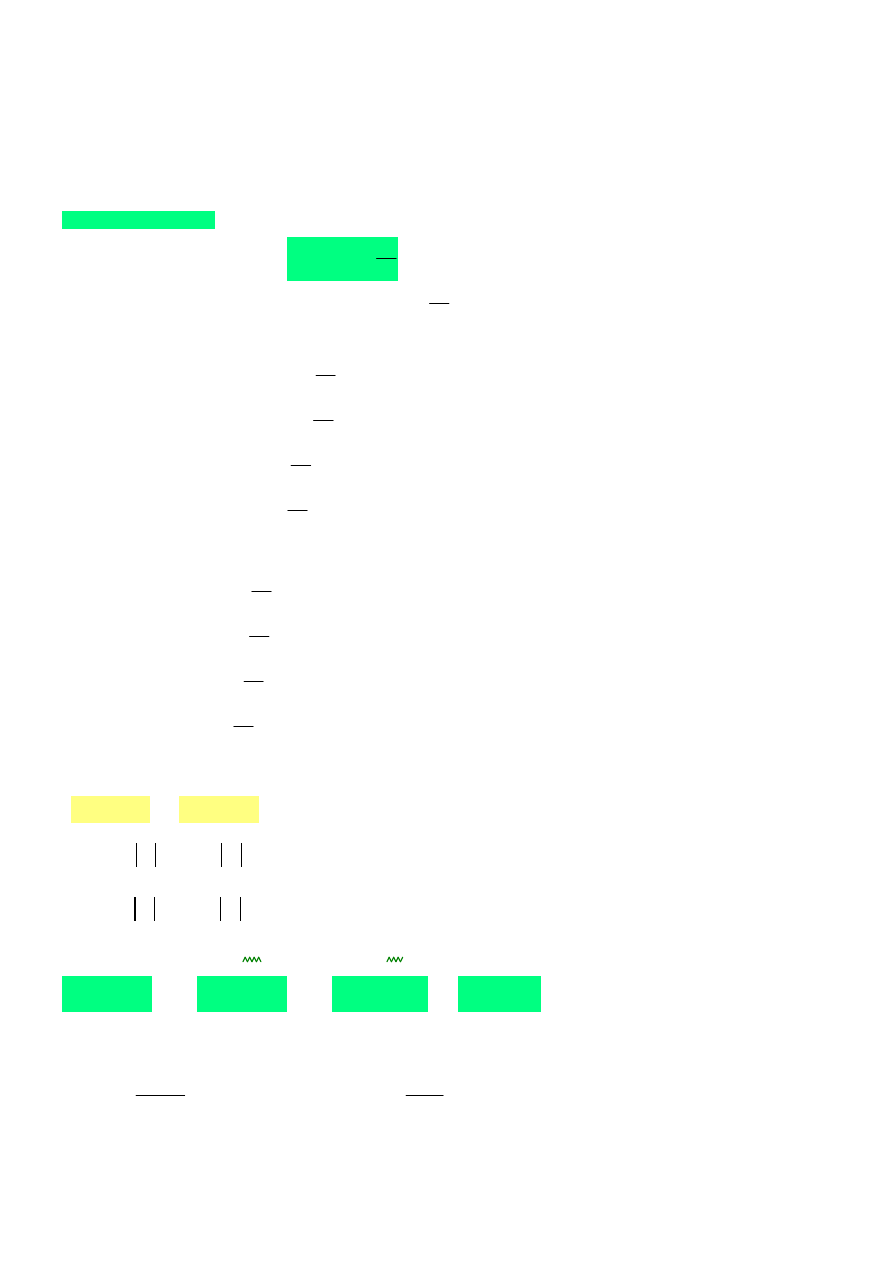
3. Wymiarowanie płatwii dachowej - przyjęto IPE180

3.1 Równania do wyliczenia maksymalnych obciążeń:

rozstaw płatwii IPE 180

a

2.5 m

=

ciężar charakterystyczny płatwii

gIPE

0.188

kN

m

:=

ciężar obliczeniowy płatwii

gd.IPE

1.35 gIPE

⋅

0.254

kN

m

⋅

=

:=

kąt nachylenia połaci

α

5.73 deg

⋅

=

gdy.pl

gd a

⋅

gd.IPE

+

(

)

cos

α

( )

⋅

0.656

kN

m

⋅

=

:=

gdz.pl

gd a

⋅

gd.IPE

+

(

)

sin

α

( )

⋅

0.066

kN

m

⋅

=

:=

gy.pl

g a

⋅

gIPE

+

(

)

cos

α

( )

⋅

0.486

kN

m

⋅

=

:=

gz.pl

g a

⋅

gIPE

+

(

)

sin

α

( )

⋅

0.049

kN

m

⋅

=

:=

qdy.pl

sd a

⋅

(

)

cos

α

( )

⋅

2.09

kN

m

⋅

=

:=

qdz.pl

sd a

⋅

(

)

sin

α

( )

⋅

0.21

kN

m

⋅

=

:=

qy.pl

s a

⋅

(

) cos

α

( )

⋅

1.393

kN

m

⋅

=

:=

qz.pl

s a

⋅

(

) sin

α

( )

⋅

0.14

kN

m

⋅

=

:=

3.2 Obliczenie maksymalnego momentu gnącego:

kg

0.105

−

:=

kq

0.119

−

:=

My.Ed

kg gdy.pl

⋅

kq qdy.pl

⋅

+

(

)

Lp

2

⋅

15.557 kN m

⋅

⋅

=

:=

Mz.Ed

kg gdz.pl

⋅

kq qdz.pl

⋅

+

(

)

Lp

2

⋅

1.561 kN m

⋅

⋅

=

:=

γmo

1.0

:=

γm1

1.0

:=

fy

235MPa

:=

E

210GPa

:=

Sy

83.2cm

3

:=

Iy

1320cm

4

:=

Wz

22.2cm

3

:=

Iz

101cm

4

:=

Wply

2 Sy

⋅

166.400 cm

3

⋅

=

:=

My.bRd

Wply fy

⋅

γmo

39.104 kN m

⋅

⋅

=

:=

Mz.bRd

Wz fy

⋅

γmo

5.217 kN m

⋅

⋅

=

:=

Warunek nośności:

dla IPE 160 warunek wynosi 92% ale ugięcia
przekraczają 100%

My.Ed

My.bRd

Mz.Ed

Mz.bRd

+

69.701 %

⋅

=

3.3 Obliczenie maksymalnej siły ścinającej:

Maksymalna siła tnąca:

współczynnik Winklera:

kV

1.218

:=

rozstaw wiązarów:

Lp 7 m

=

VEd

kV gdy.pl qdy.pl

+

(

)

⋅

Lp

⋅

23.404 kN

⋅

=

:=

Ścinanie:

hIPE

180mm

:=

RIPE

9mm

:=

tf.IPE

8.0mm

:=

tw.IPE

5.3mm

:=

γM0

1.0

:=

Av

hIPE tw.IPE

⋅

9.54 cm

2

⋅

=

:=

Vpl.Rd

Av fy

3

÷

(

)

⋅

γM0

129.436 kN

⋅

=

:=

Warunek nośności:

VEd

Vpl.Rd

0.181

=

3.4 Obliczenie maksymalnego ugięcia :

kg.1

0.00657

:=

kq.1

0.00973

:=

kg.2

0.00152

:=

kq.2

0.00725

:=

kg.3

0.00315

:=

kq.3

0.00809

:=

fy1

kg.1 gy.pl

⋅

kq.1 qy.pl

⋅

+

(

)

Lp

4

⋅

E Iy

⋅

1.45 cm

⋅

=

:=

fz1

kg.1 gz.pl

⋅

kq.1 qz.pl

⋅

+

(

)

Lp

4

⋅

E Iz

⋅

1.902 cm

⋅

=

:=

fy2

kg.2 gy.pl

⋅

kq.2 qy.pl

⋅

+

(

)

Lp

4

⋅

E Iy

⋅

0.939 cm

⋅

=

:=

fz2

kg.2 gz.pl

⋅

kq.2 qz.pl

⋅

+

(

)

Lp

4

⋅

E Iz

⋅

1.231 cm

⋅

=

:=

fy3

kg.3 gy.pl

⋅

kq.3 qy.pl

⋅

+

(

)

Lp

4

⋅

E Iy

⋅

1.109 cm

⋅

=

:=

fz3

kg.3 gz.pl

⋅

kq.3 qz.pl

⋅

+

(

)

Lp

4

⋅

E Iz

⋅

1.454 cm

⋅

=

:=

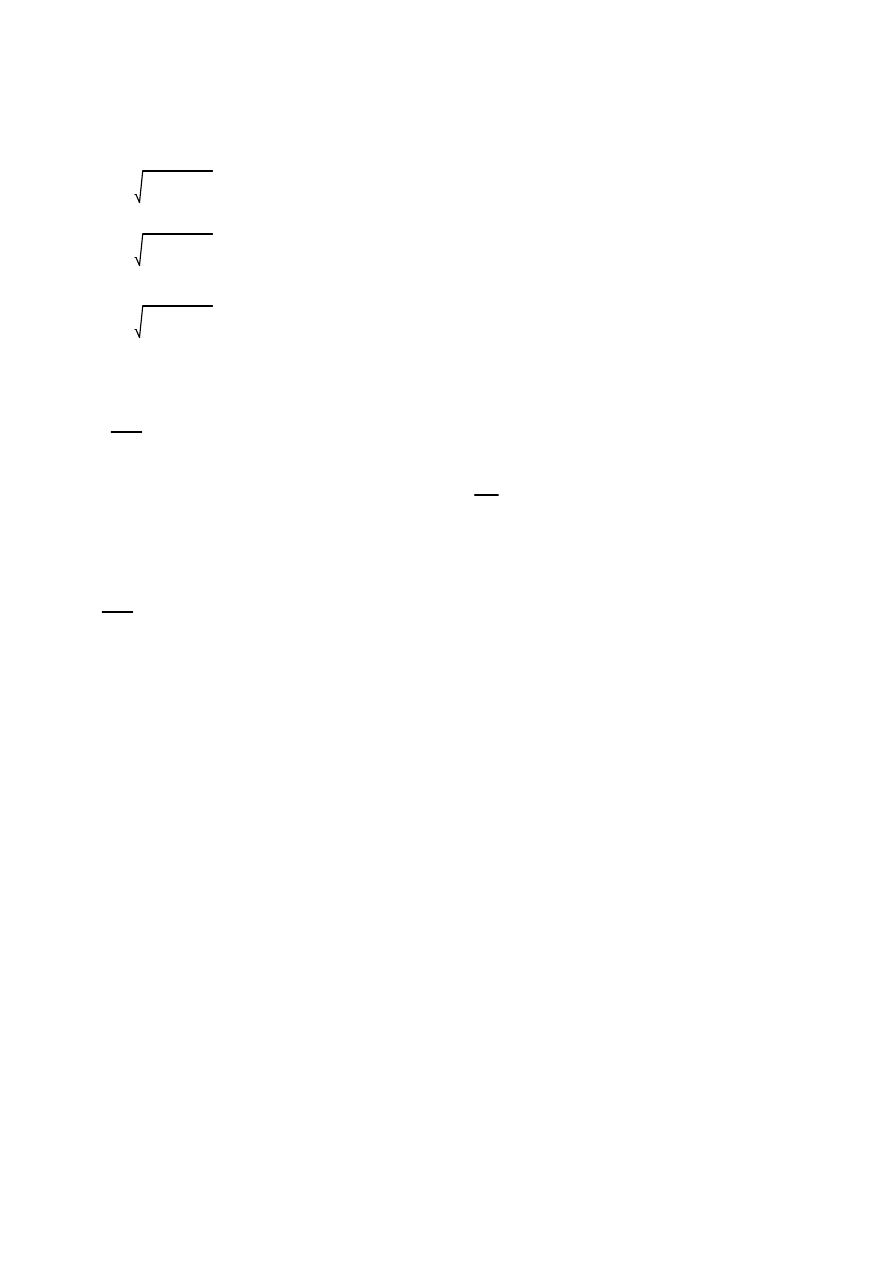
f1

fy1

2

fz1

2

+

2.392 cm

⋅

=

:=

f2

fy2

2

fz2

2

+

1.548 cm

⋅

=

:=

f3

fy3

2

fz3

2

+

1.828 cm

⋅

=

:=

warunek ugięcia:

fmax

fdop

< 1

ugięcia dopuszczalne:

fdop

Lp

200

3.5 cm

⋅

=

:=

fmax

max f1 f2

,

f2

,

(

)

2.392 cm

⋅

=

:=

dla IPE 160 warunek wynosi 101% czyli nie jest
spełniony warunek ugięć

fmax

fdop

68.334 %

⋅

=

4. Zestawienie obciążeń na wiązar dachowy

A - obciążenie stałe pokrycia dachu

P1

gd Lp a

⋅

(

)

⋅

gIPE Lp

⋅

+

4.151 kN

⋅

=

:=

P2

0.5P1 2.075 kN

⋅

=

:=

P3

sd a

⋅

Lp

⋅

14.7 kN

⋅

=

:=

B - obciążenie śniegiem

P4

0.5P3 7.35 kN

⋅

=

:=

5. Wymiarowanie

5.1 Wymiarowanie Pasa górnego RK 120x120x5 :

Sprawdzenie klasy przekroju:

Wymiary przekroju:

h

120mm

:=

t

5mm

:=

R

5mm

:=

ε

235MPa

fy

1

=

:=

c

h

2t

−

2R

−

100 mm

⋅

=

:=

t

5 mm

⋅

=

c

t

20

=

<

33

ε

⋅

33

=

klasa 1

Całość klasa 1

Pole przekroju poprzecznego:

A

22.7cm

2

:=

Współczynnik częściowy:

γM0

1

:=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rd

A fy

⋅

γM0

533.45 kN

⋅

=

:=

Smukłość porównawcza:

λ1

π

E

fy

⋅

93.913

=

:=

Współczynnik długości wyboczeniowej:

μ

1

:=

Długość elementu:

L

2.512 m

⋅

:=

Długość wyboczeniowa (ta sama w obu płaszczyznach):

Lcr

μ L

⋅

2.512 m

=

:=

Promień bezwładności przekroju:

i

4.68cm

:=

Smukłość względna przy wyboczeniu giętnym:

λwzgl

Lcr

i

λ1

⋅

0.572

=

:=

Parametr imperfekcji:

α

0.21

:=

(krzywa a)

Parametr krzywej niestateczności:

Φ

0.5 1

α λwzgl 0.2

−

(

)

⋅

+

λwzgl

2

+









⋅

0.702

=

:=

Współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λwzgl

2

−

+

0.9

=

:=

γM1

1

:=

Nośność elementu z uwzględnieniem wyboczenia:

Nb.Rd

χ Nc.Rd

⋅

γM1

480.353 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

425.292kN

:=

pręty 14 i 17

Warunek nośności:

NEd

Nb.Rd

0.885

=

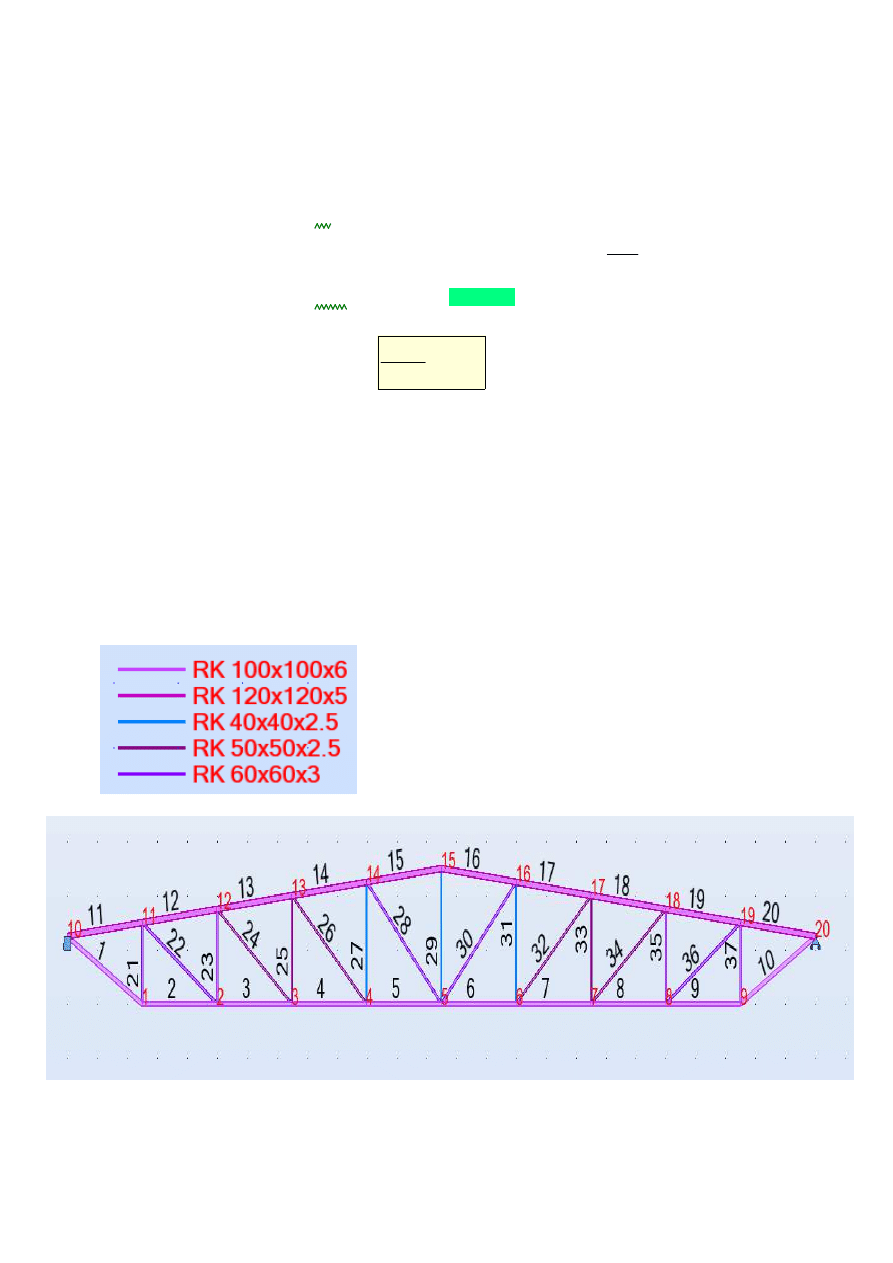
5.2 Wymiarowanie Pasa dolnego RK 100x100x6 :

Pole przekroju poprzecznego:

A

22.2cm

2

:=

Obliczeniowa nośność przekroju przy równomiernym rozciąganiu:

Npl.Rd

A fy

⋅

γM0

521.7 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

422.959 kN

⋅

:=

pręty 5 i 6

Warunek nośności:

NEd

Npl.Rd

0.811

=

5.3 Wymiarowanie Prętów skratowania :

Pręty skratowania podzielono na trzy grupy:

*Grupa 1 - pręty słabo obciążone (27/31, 29)

*Grupa 2 - pręty mocno obciążone (21/37, 22/36, 23/35, 28/30)

*Grupa 3 - pręty średnio obciążone (24/34, 25/33, 26/32)

5.3.1 Wymiarowanie Prętów skratowania - Grupa 1

5.3.1.1 Słupki - RK 40x40x2.5

Sprawdzenie klasy przekroju:

Wymiary przekroju:

h

40mm

:=

t

2.5mm

:=

R

2.5mm

:=

c

h

2t

−

2R

−

30 mm

⋅

=

:=

t

2.5 mm

⋅

=

ε

235MPa

fy

1

=

:=

c

t

12

=

<

33

ε

⋅

33

=

klasa 1

Całość klasa 1

Pole przekroju poprzecznego:

A

3.68 cm

2

⋅

:=

Współczynnik częściowy:

γM0

1

:=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rd

A fy

⋅

γM0

86.48 kN

⋅

=

:=

Smukłość porównawcza:

λ1

π

E

fy

⋅

93.913

=

:=

Współczynnik długości wyboczeniowej:

μ

1

:=

Długość elementu:

L

2.250 m

⋅

:=

Długość wyboczeniowa (ta sama w obu płaszczyznach):

Lcr

μ L

⋅

2.25 m

=

:=

Promień bezwładności przekroju:

i

1.52cm

:=

Smukłość względna przy wyboczeniu giętnym:

λwzgl

Lcr

i

λ1

⋅

1.576

=

:=

Parametr imperfekcji:

α

0.21

:=

(krzywa a)

Parametr krzywej niestateczności:

Φ

0.5 1

α λwzgl 0.2

−

(

)

⋅

+

λwzgl

2

+









⋅

1.887

=

:=

Współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λwzgl

2

−

+

0.342

=

:=

Nośność elementu z uwzględnieniem wyboczenia:

Nb.Rd

χ Nc.Rd

⋅

γM1

29.579 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

19.001 kN

⋅

:=

pręty 27 i 31

rura 30x30x3
nie spełnia
warunku
nośności

Warunek nośności:

NEd

Nb.Rd

0.642

=

5.3.1.2 Słupki - RK 40x40x2.5

Pole przekroju poprzecznego:

A

3.68cm

2

:=

Obliczeniowa nośność przekroju przy równomiernym rozciąganiu:

Npl.Rd

A fy

⋅

γM0

86.48 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

31.739 kN

⋅

:=

pręt 29

Warunek nośności:

NEd

Npl.Rd

0.367

=

5.3.2 Wymiarowanie Prętów skratowania - Grupa 2

5.3.2.1 Słupki - RK 60x60x3

Sprawdzenie klasy przekroju:

Wymiary przekroju:

h

60mm

:=

t

3mm

:=

R

3mm

:=

ε

235MPa

fy

1

=

:=

c

h

2t

−

2R

−

48 mm

⋅

=

:=

t

3 mm

⋅

=

c

t

16

=

<

33

ε

⋅

33

=

klasa 1

Całość klasa 1

Pole przekroju poprzecznego:

A

6.74cm

2

:=

Współczynnik częściowy:

γM0

1

:=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rd

A fy

⋅

γM0

158.39 kN

⋅

=

:=

Smukłość porównawcza:

λ1

π

E

fy

⋅

93.913

=

:=

Współczynnik długości wyboczeniowej:

μ

1

:=

Długość elementu:

L

1.5m

:=

Długość wyboczeniowa (ta sama w obu płaszczyznach):

Lcr

μ L

⋅

1.5 m

=

:=

Promień bezwładności przekroju:

i

2.32cm

:=

Smukłość względna przy wyboczeniu giętnym:

λwzgl

Lcr

i

λ1

⋅

0.688

=

:=

Parametr imperfekcji:

α

0.21

:=

(krzywa a)

Parametr krzywej niestateczności:

Φ

0.5 1

α λwzgl 0.2

−

(

)

⋅

+

λwzgl

2

+









⋅

0.788

=

:=

Współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λwzgl

2

−

+

0.853

=

:=

Nośność elementu z uwzględnieniem wyboczenia:

Nb.Rd

χ Nc.Rd

⋅

γM1

135.121 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

113.779 kN

⋅

:=

pręty 21 i 37

Warunek nośności:

NEd

Nb.Rd

0.842

=

5.3.2.2 Krzyżulce - RK 60x60x3

Sprawdzenie klasy przekroju:

Wymiary przekroju:

h

60mm

:=

t

3mm

:=

R

3mm

:=

ε

235MPa

fy

1

=

:=

c

h

2t

−

2R

−

48 mm

⋅

=

:=

t

3 mm

⋅

=

c

t

16

=

<

33

ε

⋅

33

=

klasa 1

Całość klasa 1

Pole przekroju poprzecznego:

A

6.74cm

2

:=

Współczynnik częściowy:

γM0

1

:=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rd

A fy

⋅

γM0

158.39 kN

⋅

=

:=

Smukłość porównawcza:

λ1

π

E

fy

⋅

93.913

=

:=

Współczynnik długości wyboczeniowej:

μ

1

:=

Długość elementu:

L

3.363m

:=

Długość wyboczeniowa (ta sama w obu płaszczyznach):

Lcr

μ L

⋅

3.363 m

=

:=

Promień bezwładności przekroju:

i

2.32cm

:=

Smukłość względna przy wyboczeniu giętnym:

λwzgl

Lcr

i

λ1

⋅

1.544

=

:=

Parametr imperfekcji:

α

0.21

:=

(krzywa a)

Parametr krzywej niestateczności:

Φ

0.5 1

α λwzgl 0.2

−

(

)

⋅

+

λwzgl

2

+









⋅

1.832

=

:=

Współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λwzgl

2

−

+

0.355

=

:=

Nośność elementu z uwzględnieniem wyboczenia:

Nb.Rd

χ Nc.Rd

⋅

γM1

56.174 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

47.897 kN

⋅

:=

pręty 28 i 30

Warunek nośności:

NEd

Nb.Rd

0.853

=

5.3.2.3 Krzyżulce - RK 60x60x3

Pole przekroju poprzecznego:

A

6.74cm

2

:=

Obliczeniowa nośność przekroju przy równomiernym rozciąganiu:

Npl.Rd

A fy

⋅

γM0

158.39 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

143.825 kN

⋅

:=

pręty 22 i 36

Warunek nośności:

NEd

Npl.Rd

0.908

=

5.3.3 Wymiarowanie Prętów skratowania - Grupa 3

5.3.3.1 Słupki - RK 50x50x2.5

Sprawdzenie klasy przekroju:

Wymiary przekroju:

h

50mm

:=

t

2.5mm

:=

R

2.5mm

:=

c

h

2t

−

2R

−

40 mm

⋅

=

:=

t

2.5 mm

⋅

=

ε

235MPa

fy

1

=

:=

c

t

16

=

<

33

ε

⋅

33

=

klasa 1

Całość klasa 1

Pole przekroju poprzecznego:

A

4.68cm

2

:=

Współczynnik częściowy:

γM0

1

:=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rd

A fy

⋅

γM0

109.98 kN

⋅

=

:=

Smukłość porównawcza:

λ1

π

E

fy

⋅

93.913

=

:=

Współczynnik długości wyboczeniowej:

μ

1

:=

Długość elementu:

L

2.0m

:=

Długość wyboczeniowa (ta sama w obu płaszczyznach):

Lcr

μ L

⋅

2 m

=

:=

Promień bezwładności przekroju:

i

1.93cm

:=

Smukłość względna przy wyboczeniu giętnym:

λwzgl

Lcr

i

λ1

⋅

1.103

=

:=

Parametr imperfekcji:

α

0.21

:=

(krzywa a)

Parametr krzywej niestateczności:

Φ

0.5 1

α λwzgl 0.2

−

(

)

⋅

+

λwzgl

2

+









⋅

1.204

=

:=

Współczynnik wyboczeniowy:

χ

1

Φ

Φ

2

λwzgl

2

−

+

0.594

=

:=

Nośność elementu z uwzględnieniem wyboczenia:

Nb.Rd

χ Nc.Rd

⋅

γM1

65.29 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

39.598 kN

⋅

:=

pręty 25 i 33

Warunek nośności:

NEd

Nb.Rd

0.606

=

5.3.3.3 Krzyżulce - RK 50x50x2.5

Pole przekroju poprzecznego:

A

4.68cm

2

:=

Obliczeniowa nośność przekroju przy równomiernym rozciąganiu:

Npl.Rd

A fy

⋅

γM0

109.98 kN

⋅

=

:=

Obliczeniowa siła podłużna:

NEd

70.089 kN

⋅

:=

pręty 24 i 34

Warunek nośności:

NEd

Npl.Rd

0.637

=

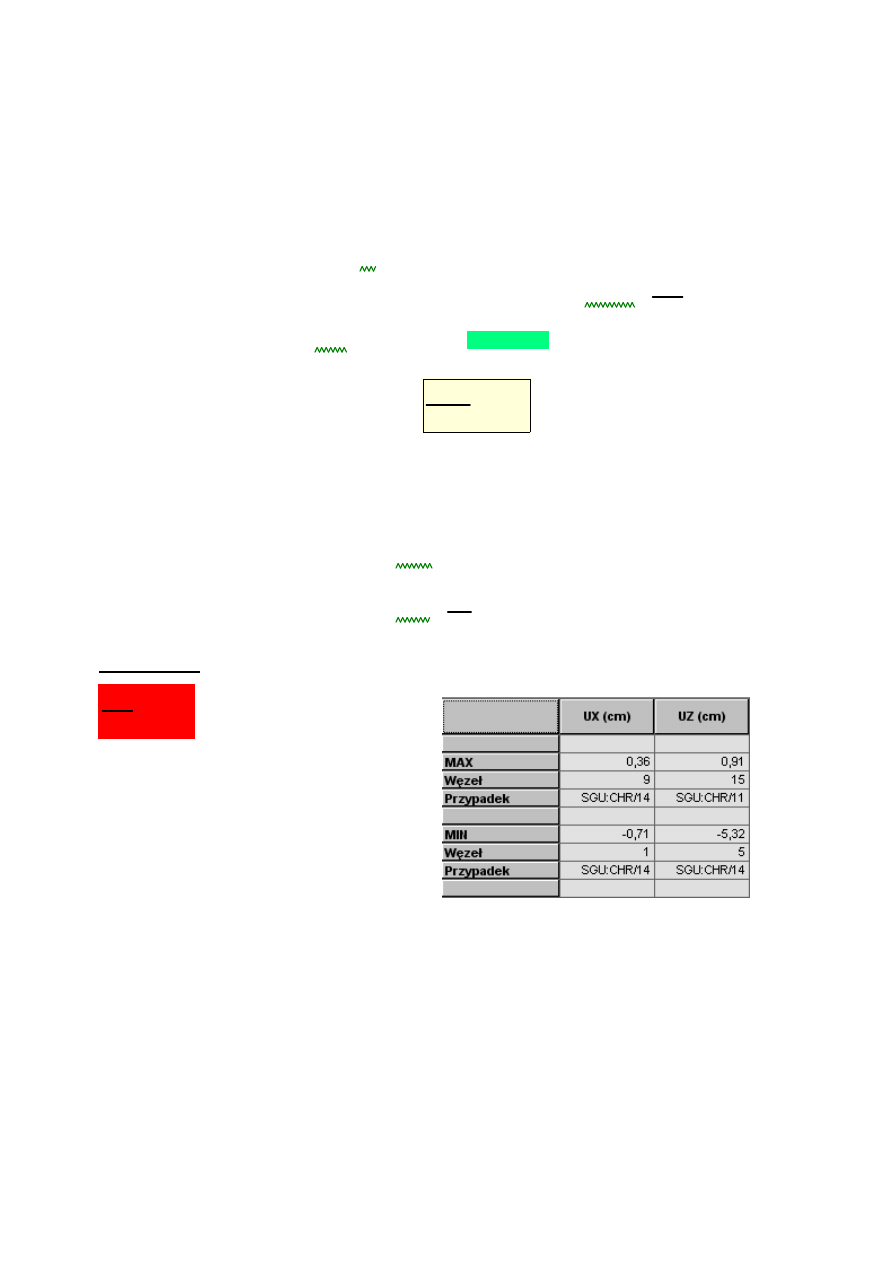
5.4. Sprawdzenie SGU

Rozpiętość wiązara:

B

25 m

=

Maksymalne przemieszczenie (węzeł 5):

fmax

5.32cm

:=

Ugięcie dopuszczalne:

fdop

B

250

10 cm

⋅

=

:=

Warunek SGU:

fmax

fdop

53.2 %

⋅

=

6. Połączenie doczołowe pasa dolnego wiązara

6.1. Dobór grubości blachy czołowej

Zastosowano śruby

M16 kl. 10.9

średnica śruby:

•

wytrzymałość na rozciąganie:

•

pole przekroju czynnego śruby:

•

minimalna średnica nakrętki lub śruby:

•

maksymalna średnica nakrętki lub śruby:

•

średnia średnica łba śruby lub nakrętki:

•

d

16mm

:=

fub

1000MPa

:=

As

1.61cm

2

:=

ss

23.67mm

:=

es

26.75mm

:=

dm

0.5 ss es

+

(

)

⋅

25.21 mm

⋅

=

:=

Wytrzymałość na rozciąganie blachy czołowej:

fu

360MPa

:=

fu.

fu

MPa

:=

Minimalna grubość blachy czołowej:

tp.min

d

3

fu.

1000

⋅

11 mm

⋅

=

:=

przyjęto:

tp

14mm

:=

6.2. Nośność połączenia na rozciąganie

współczynnik uwzględniający rodzaj łba śruby:

k2

0.9

:=

częściowy współczynnik bezpieczeństwa:

γM2

1.25

:=

Ft.Rd

k2 fub

⋅

As

⋅

γM2

115.92 kN

⋅

=

:=

6.3. Nośność połączenia na przeciągnięcie łba

Bp.Rd

0.6

π

⋅

dm

⋅

tp

⋅

fu

⋅

γM2

191.6 kN

⋅

=

:=

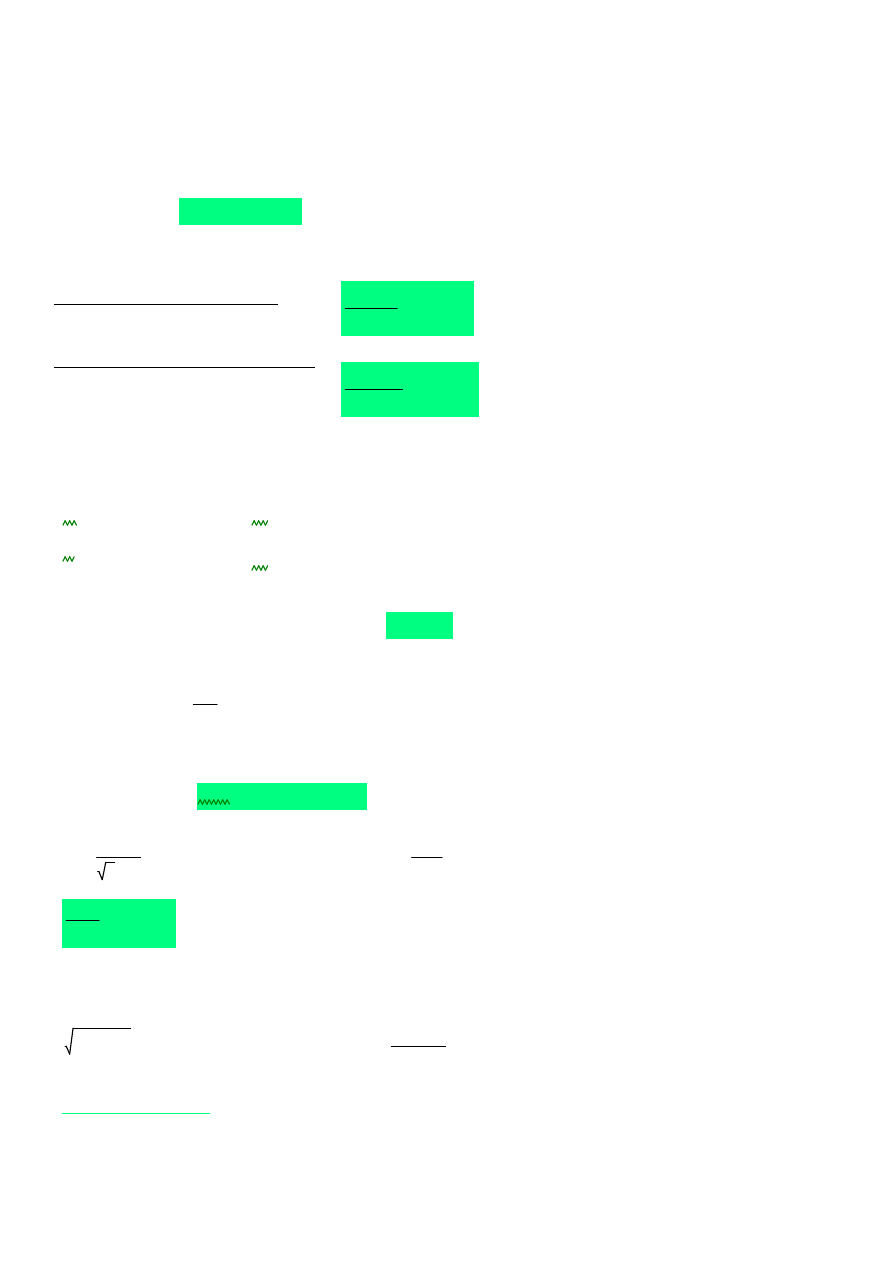
6.4. Sprawdzenie warunków nośności śrub

siła rozciągająca:

Ft.Ed

422.959kN

:=

ilość śrub:

ns

4

:=

Warunek nośności na rozciąganie:

Ft.Ed

ns Ft.Rd

⋅

91.218 %

⋅

=

Warunek nośności na przeciągnięcie łba

Ft.Ed

ns Bp.Rd

⋅

55.188 %

⋅

=

6.5. Sprawdzenie warunku nośności spoin

Wymiary przekroju pasa dolnego:

RK 100x100x6

b

100 mm

⋅

:=

R

6 mm

⋅

:=

t

6 mm

⋅

:=

A

22.2 cm

2

⋅

:=

Grubość spoiny:

as.max

t

6 mm

⋅

=

:=

przyjęto:

as

5mm

:=

Pole przekroju spoiny:

Aw

4 b

2 t

⋅

−

90

360

2

⋅

π

⋅

R

⋅













+













⋅

as

⋅

19.485 cm

2

⋅

=

:=

Naprężenia w spoinie:

siła rozciągająca:

NEd

Ft.Ed 422.959 kN

⋅

=

:=

σ

NEd

2 Aw

⋅

153.491 MPa

⋅

=

:=

<

σdop

0.9

fu

γM2

⋅

259.2 MPa

⋅

=

:=

τ

σ

:=

σ

σdop

59.217 %

⋅

=

współczynnik korelacji:

βw

0.8

:=

σ

2

3

τ

2

+

307 MPa

⋅

=

<

σmax

fu

βw γM2

⋅

360 MPa

⋅

=

:=

σ

2

3

τ

2

+

σmax

85.273 %

⋅

=

7. Połączenia spawane prętów skratowania z pasami wiązara

7.1. Pręty skratowania Grupa 1

Wymiary przekroju Grupy 1:

RK 40x40x2.5

b

40 mm

⋅

:=

R

2.5 mm

⋅

:=

t

2.5 mm

⋅

:=

A

3.68 cm

2

⋅

:=

Pręt obciążony największą siłą rozciągającą:

Nr 29

Siła rozciągająca:

NEd

31.739kN

:=

Kąt nachylenia:

α29

90deg

:=

Wymiar przekroju przy uwzględnieniu kąta nachylenia:

b'

b

cos 90deg

α29

−

(

)

40 mm

⋅

=

:=

Grubość spoiny:

as.max

t

2.5 mm

⋅

=

:=

przyjęto:

as

2mm

:=

Pole przekroju spoiny:

Aw

2 b

b'

+

(

)

⋅

as

⋅

3.2 cm

2

⋅

=

:=

Naprężenia w spoinie:

SIŁY:

prostopadła

•

NEd.Γ

NEd 31.739 kN

⋅

=

:=

σΓ

NEd.Γ

2 Aw

⋅

70.134 MPa

⋅

=

:=

<

σdop

0.9

fu

γM2

⋅

259.2 MPa

⋅

=

:=

τΓ

σΓ

:=

σΓ

σdop

27.058 %

⋅

=

współczynnik korelacji:

βw 0.8

=

σΓ

2

3

τΓ

( )

2

⋅

+

140.3 MPa

⋅

=

<

σmax

fu

βw γM2

⋅

360 MPa

⋅

=

:=

σΓ

2

3

τΓ

( )

2

⋅

+

σmax

38.963 %

⋅

=

7.2. Pręty skratowania Grupa 2

Wymiary przekroju Grupy 2:

RK 60x60x3.0

b

60 mm

⋅

:=

R

3 mm

⋅

:=

t

3 mm

⋅

:=

A

6.74 cm

2

⋅

:=

Pręt obciążony największą siłą rozciągającą:

Nr 22/36

Siła rozciągająca:

NEd

143.825kN

:=

Kąt nachylenia:

α22

31deg

:=

Wymiar przekroju przy uwzględnieniu kąta nachylenia:

b'

b

cos 90deg

α22

−

(

)

116 mm

⋅

=

:=

Grubość spoiny:

as.max

t

3 mm

⋅

=

:=

przyjęto:

as

3mm

:=

Pole przekroju spoiny:

Aw

2 b

b'

+

(

)

⋅

as

⋅

10.59 cm

2

⋅

=

:=

Naprężenia w spoinie:

SIŁY:

prostopadła

•

równoległa

•

NEd.Γ

NEd sin α22

(

)

⋅

74.075 kN

⋅

=

:=

NEd.II

NEd cos α22

(

)

⋅

123.282 kN

⋅

=

:=

σΓ

NEd.Γ

2 Aw

⋅

49.462 MPa

⋅

=

:=

<

σdop

0.9

fu

γM2

⋅

259.2 MPa

⋅

=

:=

τΓ

σΓ

:=

σΓ

σdop

19.083 %

⋅

=

τII

NEd.II

Aw

116.416 MPa

⋅

=

:=

współczynnik korelacji:

βw 0.8

=

σΓ

2

3

τΓ τII

+

(

)

2

⋅

+

291.5 MPa

⋅

=

<

σmax

fu

βw γM2

⋅

360 MPa

⋅

=

:=

σΓ

2

3

τΓ τII

+

(

)

2

⋅

+

σmax

80.982 %

⋅

=

7.3. Pręty skratowania Grupa 3

Wymiary przekroju Grupy 3:

RK 50x50x2.5

b

50 mm

⋅

:=

R

2.5 mm

⋅

:=

t

2.5 mm

⋅

:=

A

4.68 cm

2

⋅

:=

Pręt obciążony największą siłą rozciągającą:

Nr 24/34

Siła rozciągająca:

NEd

70.089kN

:=

Kąt nachylenia:

α24

35deg

:=

Wymiar przekroju przy uwzględnieniu kąta nachylenia:

b'

b

cos 90deg

α24

−

(

)

87 mm

⋅

=

:=

Grubość spoiny:

as.max

t

2.5 mm

⋅

=

:=

przyjęto:

as

2mm

:=

Pole przekroju spoiny:

Aw

2 b

b'

+

(

)

⋅

as

⋅

5.487 cm

2

⋅

=

:=

Naprężenia w spoinie:

SIŁY:

prostopadła

•

równoległa

•

NEd.Γ

NEd sin α24

(

)

⋅

40.201 kN

⋅

=

:=

NEd.II

NEd cos α24

(

)

⋅

57.414 kN

⋅

=

:=

σΓ

NEd.Γ

2 Aw

⋅

51.808 MPa

⋅

=

:=

<

σdop

0.9

fu

γM2

⋅

259.2 MPa

⋅

=

:=

τΓ

σΓ

:=

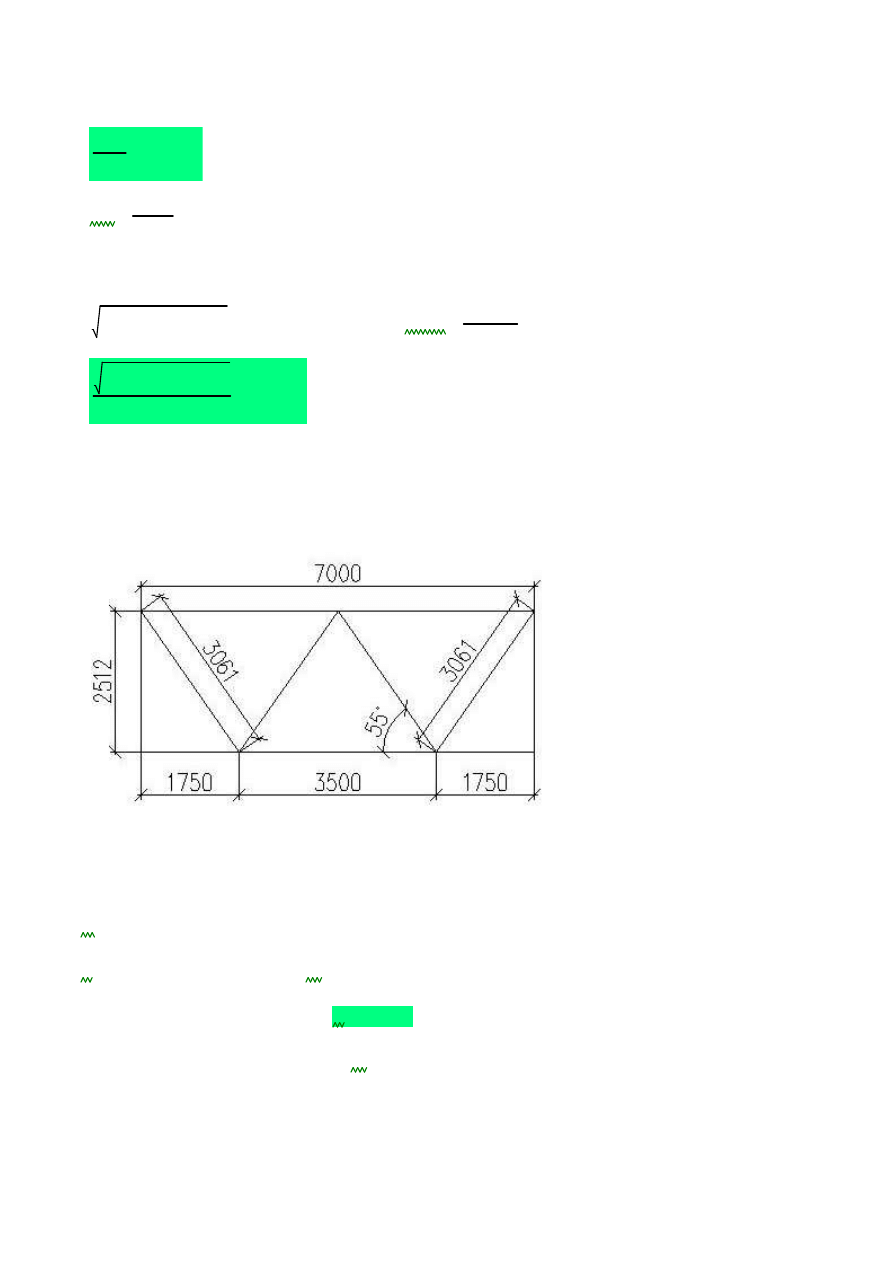
σΓ

σdop

19.988 %

⋅

=

τII

NEd.II

Aw

104.638 MPa

⋅

=

:=

współczynnik korelacji:

βw 0.8

=

σΓ

2

3

τΓ τII

+

(

)

2

⋅

+

275.9 MPa

⋅

=

<

σmax

fu

βw γM2

⋅

360 MPa

⋅

=

:=

σΓ

2

3

τΓ τII

+

(

)

2

⋅

+

σmax

76.634 %

⋅

=

8. Stężenia

8.1. Stężenia połaciowe

Dobrany profil:

RK 50x50x2.5

Wymiary przekroju:

b

50mm

:=

ARK

4.68cm

2

:=

Ix.y

17.5cm

4

:=

t

2.5mm

:=

R

2.5mm

:=

ix.y

1.93cm

:=

Długość elementu:

l

3061mm

:=

Współczynnik wyboczeniowy:

μ

1

:=

Smukłość elementu:

λ

μ l

⋅

ix.y

158.601

=

:=

Warunek smukłości:

λ

200

79.301 %

⋅

=

Połączenie śrubowe zakładkowe stężeń z płatwiami.

Zastosowano śruby

M16 kl. 5.6

średnica śruby:

•

średnica otworu:

•

wytrzymałość na rozciąganie:

•

pole przekroju trzpienia śruby:

•

d

16mm

:=

d0

d

2mm

+

18 mm

⋅

=

:=

fub

500MPa

:=

A

π d

2

⋅

4

2.011 cm

2

⋅

=

:=

Wytrzymałość blachy na rozciąganie:

fu

360MPa

:=

Grubość blachy:

tp 14 mm

⋅

=

Siła rozciągająca w ściągu:

Ft.Ed

0.5

ARK fy

⋅

γM0

⋅

54.99 kN

⋅

=

:=

Sprawdzenie warunku nośności śrub na ścinanie.

Współczynnik:

αv

0.6

:=

Nośność śruby na ścinanie:

Fv.Rd

αv fub

⋅

A

⋅

γM2

48.255 kN

⋅

=

:=

Ilość śrub:

ns

ceil

Ft.Ed

Fv.Rd













2

=

:=

Warunek nośności na ścinanie:

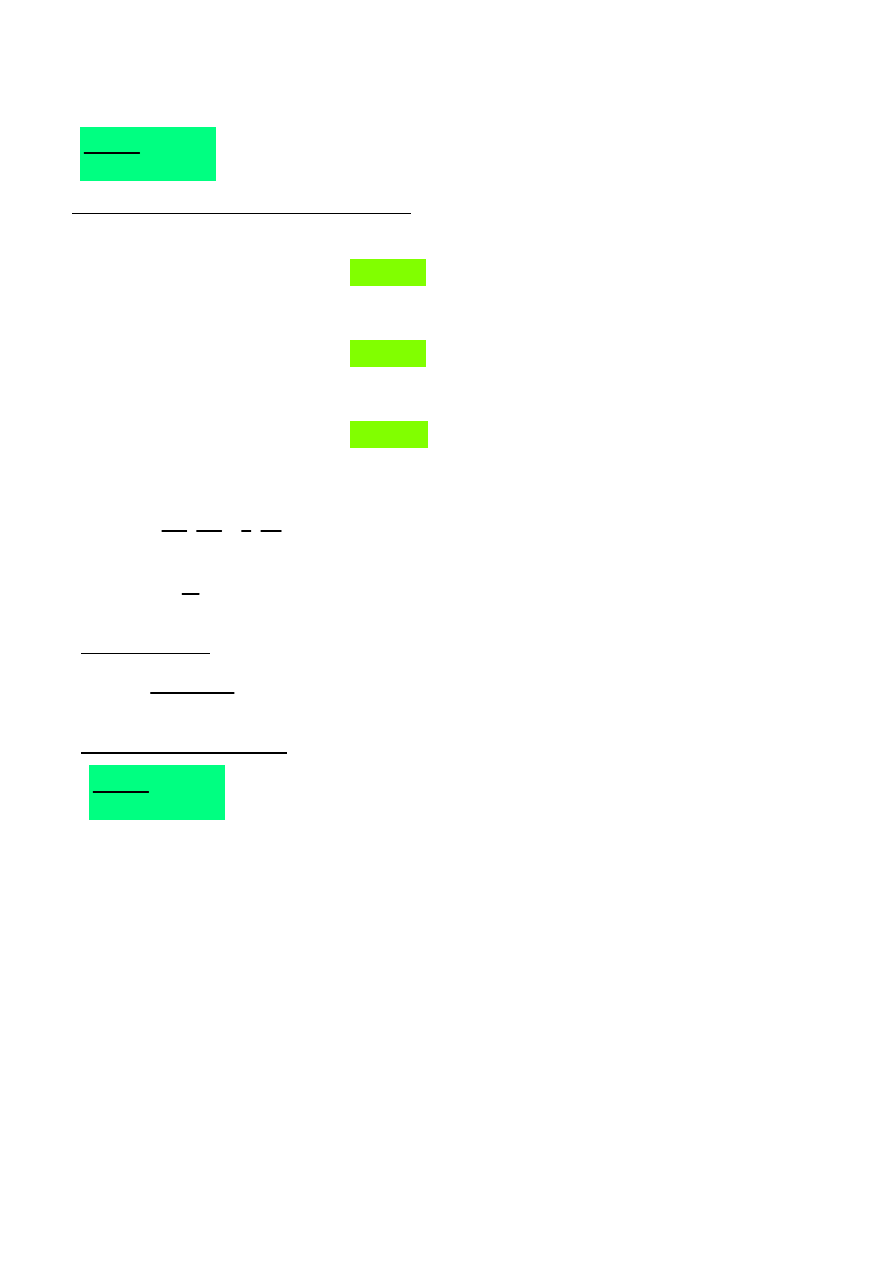
Ft.Ed

ns Fv.Rd

⋅

56.979 %

⋅

=

Sprawdzenie warunku nośności na docisk.

odległość osi łącznika od krawędzi, mierzona w kierunku obciążenia:

e1.min

1.2 d0

⋅

21.6 mm

⋅

=

:=

<

e1

25mm

:=

<

e1.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

odległość osi łącznika od krawędzi, mierzona w kierunku prostopadłym do obciążenia:

e2.min

1.2 d0

⋅

21.6 mm

⋅

=

:=

<

e2

25mm

:=

<

e2.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

osiowy rozstaw łączników w szeregu równoległym do kierunku obciążenia:

p1.min

2.2 d0

⋅

39.6 mm

⋅

=

:=

<

p1

45mm

:=

<

p1.max

14 tp

⋅

196 mm

⋅

=

:=

Współczynniki:

αb

min

e1

3d0

p1

3d0

1

4

−

,

fub

fu

,

1.0

,













0.463

=

:=

k1

min 2.8

e2

d0

⋅

1.7

−

2.5

,













2.189

=

:=

Nośność na docisk:

Fb.Rd

k1 αb

⋅

fu

⋅

d

⋅

tp

⋅

γM2

65.375 kN

⋅

=

:=

Warunek nośności na docisk:

Ft.Ed

ns Fb.Rd

⋅

42.057 %

⋅

=

8.2. Stężenia wewnętrzne i kalenicowe

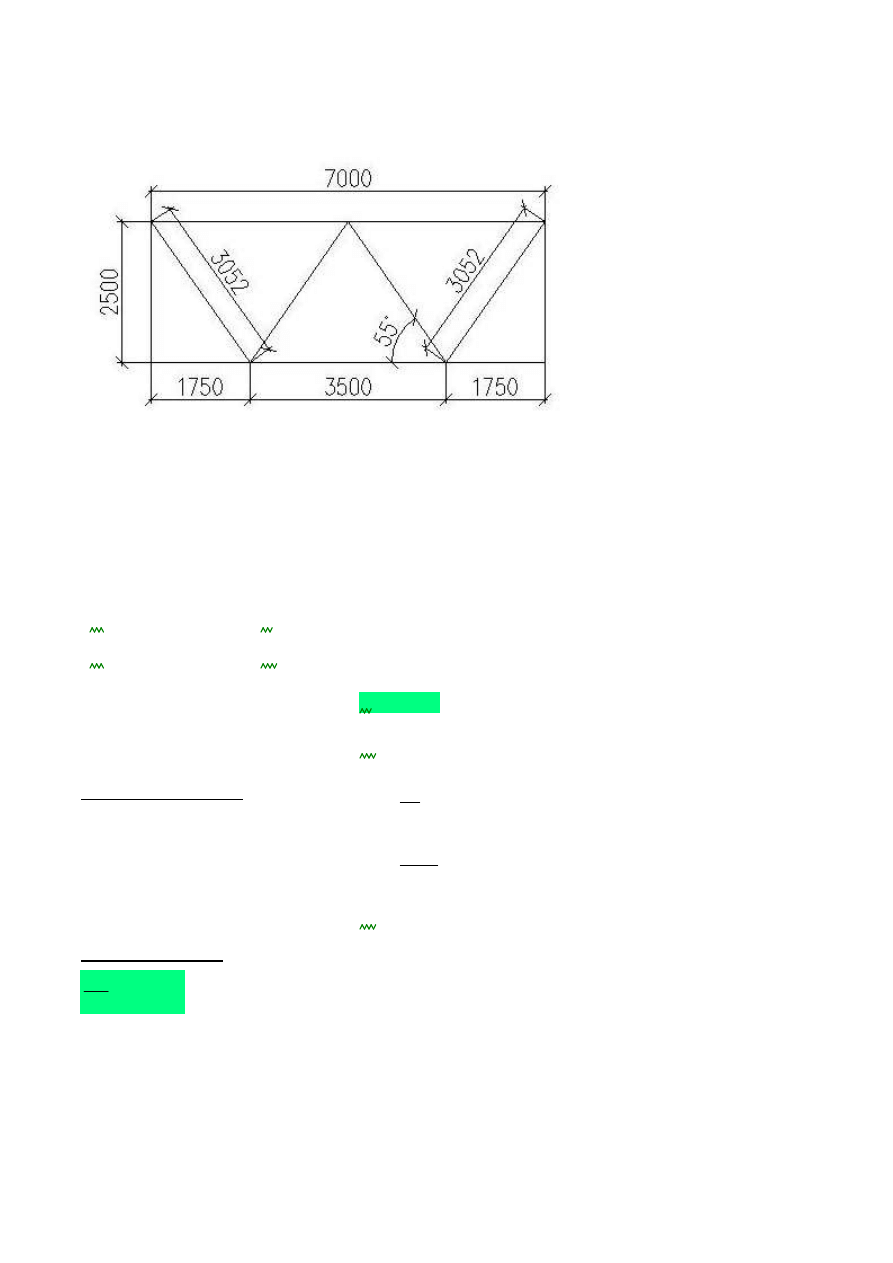
8.2.1. Stężenia kalenicowe

Dobrany profil:

RP 100x60x4

Wymiary przekroju:

h

100mm

:=

t

4mm

:=

ARP

12.0cm

2

:=

iy

2.43cm

:=

b

60mm

:=

R

4mm

:=

ix

3.63cm

:=

Długość elementu:

l

7000mm

:=

Współczynnik wyboczeniowy:

μ

1

:=

Smukłość elementu:

λx

μ l

⋅

ix

192.837

=

:=

λy

μ 0.5

⋅

l

iy

144.033

=

:=

λ

max

λx λy

,

(

)

192.837

=

:=

Warunek smukłości:

λ

200

96.419 %

⋅

=

Połączenie śrubowe zakładkowe

Zastosowano śruby

M20 kl. 5.6

średnica śruby:

•

średnica otworu:

•

wytrzymałość na rozciąganie:

•

pole przekroju trzpienia śruby:

•

d

20mm

:=

d0

d

2mm

+

22 mm

⋅

=

:=

fub

500MPa

:=

A

π d

2

⋅

4

3.142 cm

2

⋅

=

:=

Wytrzymałość blachy na rozciąganie:

fu

360MPa

:=

Grubość blachy:

tp 14 mm

⋅

=

Siła rozciągająca w sciągu:

Ft.Ed

0.5

ARP fy

⋅

γM0

⋅

141 kN

⋅

=

:=

Sprawdzenie warunku nośności śrub na ścinanie.

Współczynnik:

αv

0.6

:=

Nośność śruby na ścinanie:

Fv.Rd

αv fub

⋅

A

⋅

γM2

75.398 kN

⋅

=

:=

Ilość śrub:

ns

ceil

Ft.Ed

Fv.Rd













2

=

:=

Warunek nośności na ścinanie:

Ft.Ed

ns Fv.Rd

⋅

93.504 %

⋅

=

Sprawdzenie warunku nośności na docisk.

odległość osi łącznika od krawędzi, mierzona w kierunku obciążenia:

e1.min

1.2 d0

⋅

26.4 mm

⋅

=

:=

<

e1

30mm

:=

<

e1.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

odległość osi łącznika od krawędzi, mierzona w kierunku prostopadłym do obciążenia:

e2.min

1.2 d0

⋅

26.4 mm

⋅

=

:=

<

e2

30mm

:=

<

e2.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

osiowy rozstaw łączników w szeregu równoległym do kierunku obciążenia:

p1.min

2.2 d0

⋅

48.4 mm

⋅

=

:=

<

p1

50mm

:=

<

p1.max

14 tp

⋅

196 mm

⋅

=

:=

Współczynniki:

αb

min

e1

3d0

p1

3d0

1

4

−

,

fub

fu

,

1.0

,













0.455

=

:=

k1

min 2.8

e2
d0

⋅

1.7

−

2.5

,













2.118

=

:=

Nośność na docisk:

Fb.Rd

k1 αb

⋅

fu

⋅

d

⋅

tp

⋅

γM2

77.641 kN

⋅

=

:=

Warunek nośności na docisk:

Ft.Ed

ns Fb.Rd

⋅

90.803 %

⋅

=

8.2.2. Stężenia wewnętrzne

Dobrany profil:

RK 50x50x2.5

Wymiary przekroju:

b

50mm

:=

ARK

4.68cm

2

:=

Ix.y

17.5cm

4

:=

t

2.5mm

:=

R

2.5mm

:=

ix.y

1.93cm

:=

Długość elementu:

l

3052mm

:=

Współczynnik wyboczeniowy:

μ

1

:=

Smukłość elementu:

λ

μ l

⋅

ix.y

158.135

=

:=

Warunek smukłości:

λ

200

79.067 %

⋅

=

Połączenie śrubowe zakładkowe stężeń

Zastosowano śruby

M16 kl. 5.6

średnica śruby:

•

średnica otworu:

•

wytrzymałość na rozciąganie:

•

pole przekroju trzpienia śruby:

•

d

16mm

:=

d0

d

2mm

+

18 mm

⋅

=

:=

fub

500MPa

:=

A

π d

2

⋅

4

2.011 cm

2

⋅

=

:=

Wytrzymałość blachy na rozciąganie:

fu

360MPa

:=

Grubość blachy:

tp 14 mm

⋅

=

Siła rozciągająca w sciągu:

Ft.Ed

0.5

ARK fy

⋅

γM0

⋅

54.99 kN

⋅

=

:=

Sprawdzenie warunku nośności śrub na ścinanie.

Współczynnik:

αv

0.6

:=

Nośność śruby na ścinanie:

Fv.Rd

αv fub

⋅

A

⋅

γM2

48.255 kN

⋅

=

:=

Ilość śrub:

ns

ceil

Ft.Ed

Fv.Rd













2

=

:=

Warunek nośności na ścinanie:

Ft.Ed

ns Fv.Rd

⋅

56.979 %

⋅

=

Sprawdzenie warunku nośności na docisk.

odległość osi łącznika od krawędzi, mierzona w kierunku obciążenia:

e1.min

1.2 d0

⋅

21.6 mm

⋅

=

:=

<

e1

25mm

:=

<

e1.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

odległość osi łącznika od krawędzi, mierzona w kierunku prostopadłym do obciążenia:

e2.min

1.2 d0

⋅

21.6 mm

⋅

=

:=

<

e2

25mm

:=

<

e2.max

4 tp

⋅

40mm

+

96 mm

⋅

=

:=

osiowy rozstaw łączników w szeregu równoległym do kierunku obciążenia:

p1.min

2.2 d0

⋅

39.6 mm

⋅

=

:=

<

p1

45mm

:=

<

p1.max

14 tp

⋅

196 mm

⋅

=

:=

Współczynniki:

αb

min

e1

3d0

p1

3d0

1

4

−

,

fub

fu

,

1.0

,













0.463

=

:=

k1

min 2.8

e2

d0

⋅

1.7

−

2.5

,













2.189

=

:=

Nośność na docisk:

Fb.Rd

k1 αb

⋅

fu

⋅

d

⋅

tp

⋅

γM2

65.375 kN

⋅

=

:=

Warunek nośności na docisk:

Ft.Ed

ns Fb.Rd

⋅

42.057 %

⋅

=