D

rg

a

n

ia

i

f

a

le

5

S

K

*

A

D

A

N

IE

D

R

G

A

+

H

A

R

M

O

N

IC

Z

N

Y

C

H

R

u

ch

y

h

ar

m

o

n

ic

zn

e

s$

c

z

!s

to

r

u

ch

am

i

z

"o

#o

n

y

m

i

z

k

il

k

u

l

u

b

n

aw

et

zn

ac

zn

ej

l

ic

zb

y

r

u

ch

ó

w

h

ar

m

o

n

ic

zn

y

ch

.

O

g

ra

n

ic

zy

m

y

s

i!

d

o

a

n

al

iz

y

z

"o

#e

)

d

w

ó

ch

d

rg

a

).

S

k

"a

d

an

ie

d

rg

a

)

ró

w

n

o

le

g

"y

ch

M

am

y

d

w

a

d

rg

an

ia

s

k

"a

d

o

w

e:

(

(

(

(

(

(

co

s(

)

co

s

x

A

t

A

ω

δ

ϕ

=

+

=

2

2

2

2

2

2

co

s(

)

co

s

x

A

t

A

ω

δ

ϕ

=

+

=

Z

a

"o

#y

m

y

,

#e

(

0

A

>

i

2

0

A

>

.

Je

&l

i

ta

k

n

ie

j

es

t

to

z

n

ak

(

−

)

m

o

#n

a

u

w

zg

l!

d

n

i%

w

faza

ch

(

δ

i

2

δ

,

n

p

.

cos

(

)

cos

(

)

A

t

A

t

ω

δ

ω

δ

π

−

+

=

+

+

.

D

rg

an

ie

w

y

p

ad

k

o

w

e

d

an

e

je

st

r

ó

w

n

an

ie

m

[

]

(

2

(

(

2

2

(

)

(

)

(

)

co

s

co

s

(

)c

o

s

(

)

x

t

x

t

x

t

A

A

A

t

t

ϕ

ϕ

ϕ

=

+

=

+

=

Z

"o

#e

n

ie

d

w

ó

ch

d

rg

a

)

ró

w

n

o

le

g

"y

ch

o

d

o

w

o

ln

y

ch

a

m

p

li

tu

d

ac

h

m

o

#n

a

an

al

iz

o

w

a

%

u

#y

w

aj

$c

m

et

o

d

y

w

ek

to

ro

w

ej

l

u

b

m

et

o

d

y

w

sk

a

zó

w

.

D

ia

g

ra

m

w

ek

to

ro

w

y

Z

t

w

ie

rd

ze

n

ia

k

o

si

n

u

só

w

2

2

(

2

(

2

2

2

(

2

(

2

2

(

2

co

s

2

co

s(

)

A

A

A

A

A

A

A

A

A

α

ϕ

ϕ

=

+

−

=

+

+

−

(

(

2

2

(

(

2

2

si

n

si

n

tg

co

s

co

s

A

A

A

A

ϕ

ϕ

ϕ

ϕ

ϕ

+

=

+

m

ax

(

2

A

A

A

=

+

,

m

in

(

2

A

A

A

=

−

Je

&l

i

(

ϕ

i

/l

u

b

2

ϕ

s

$

fu

n

k

cj

am

i

cz

as

u

t

o

z

ar

ó

w

n

o

a

m

p

li

tu

d

a

A

j

ak

i

f

az

a

ϕ

s$

f

u

n

k

cj

am

i

cz

as

u

.

W

y

st

!p

u

je

m

o

d

u

la

cj

a

a

m

p

li

tu

d

y

i

f

az

y

(

b

$d

'

cz

!s

to

&c

i)

.

D

rg

a

n

ia

i

f

a

le

6

D

o

d

aw

an

ie

d

rg

a

)

p

ro

st

o

p

ad

"y

ch

W

e

'm

y

p

o

d

u

w

ag

!

d

rg

an

ie

p

u

n

k

tu

m

at

er

ia

ln

eg

o

b

!d

$c

e

w

y

n

ik

ie

m

n

a

"o

#e

n

ia

s

i!

d

w

ó

ch

d

rg

a

)

h

ar

m

o

n

ic

zn

y

ch

o

d

p

o

w

ie

d

n

io

w

zd

"u

#

o

si

x

i

y

.

co

s(

)

co

s(

)

x

x

x

y

y

y

x

A

t

y

A

t

ω

ϕ

ω

ϕ

=

+

 

=

+



-

r

ó

w

n

an

ie

t

o

ru

w

p

o

st

ac

i

p

ar

am

et

ry

cz

n

ej

P

o

"o

#e

n

ie

p

u

n

k

tu

m

o

#e

b

y

%

o

p

is

an

e

w

ek

to

re

m

(

)

(

)

(

)

x

y

r

t

x

t

e

y

t

e

=

+

!

!

!

N

ie

k

tó

re

s

zc

ze

g

ó

ln

e

p

rz

y

p

ad

k

i,

g

d

y

x

y

ω

ω

ω

=

=

,

0

x

ϕ

=

,

y

ϕ

ϕ

=

∆

co

s(

)

x

x

A

t

ω

=

co

s(

)

y

y

A

t

ω

ϕ

=

+

∆

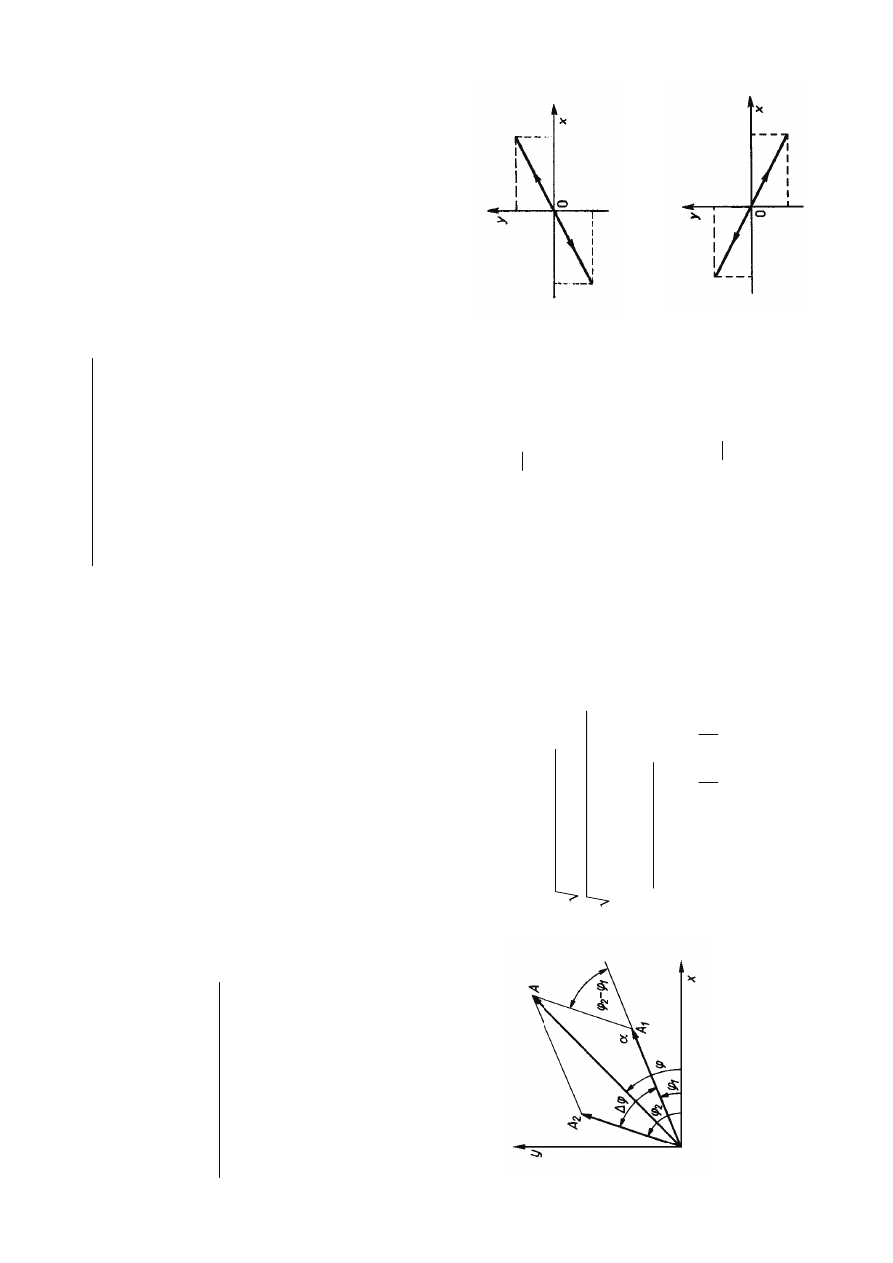
(a

)

2

,

0

,

(,

2

,.

..

n

n

ϕ

π

∆

=

=

±

±

y

x

A

y

x

A

→

=

(b

)

(2

()

,

0

,

(,

2

,.

..

n

n

ϕ

π

∆

=

+

=

±

±

y

x

A

y

x

A

→

=

−

D

rg

a

n

ia

i

f

a

le

7

D

o

d

aw

an

ie

d

rg

a

)

p

ro

st

o

p

ad

"y

ch

,

cd

.

2

a)

(2

()

,

0

,

(,

2

,.

..

2

x

y

n

n

A

A

A

π

ϕ

∆

=

+

=

±

±

=

=

2

2

2

x

y

A

+

=

ró

w

n

an

ie

o

k

r!

g

u

2

b

)

(2

()

,

0

,

(,

2

,.

..

2

x

y

n

n

A

A

π

ϕ

∆

=

+

=

±

±

≠

2

2

2

2

(

x

y

x

y

A

A

+

=

ró

w

n

an

ie

e

li

p

sy

P

rz

y

p

ad

ek

o

g

ó

ln

y

:

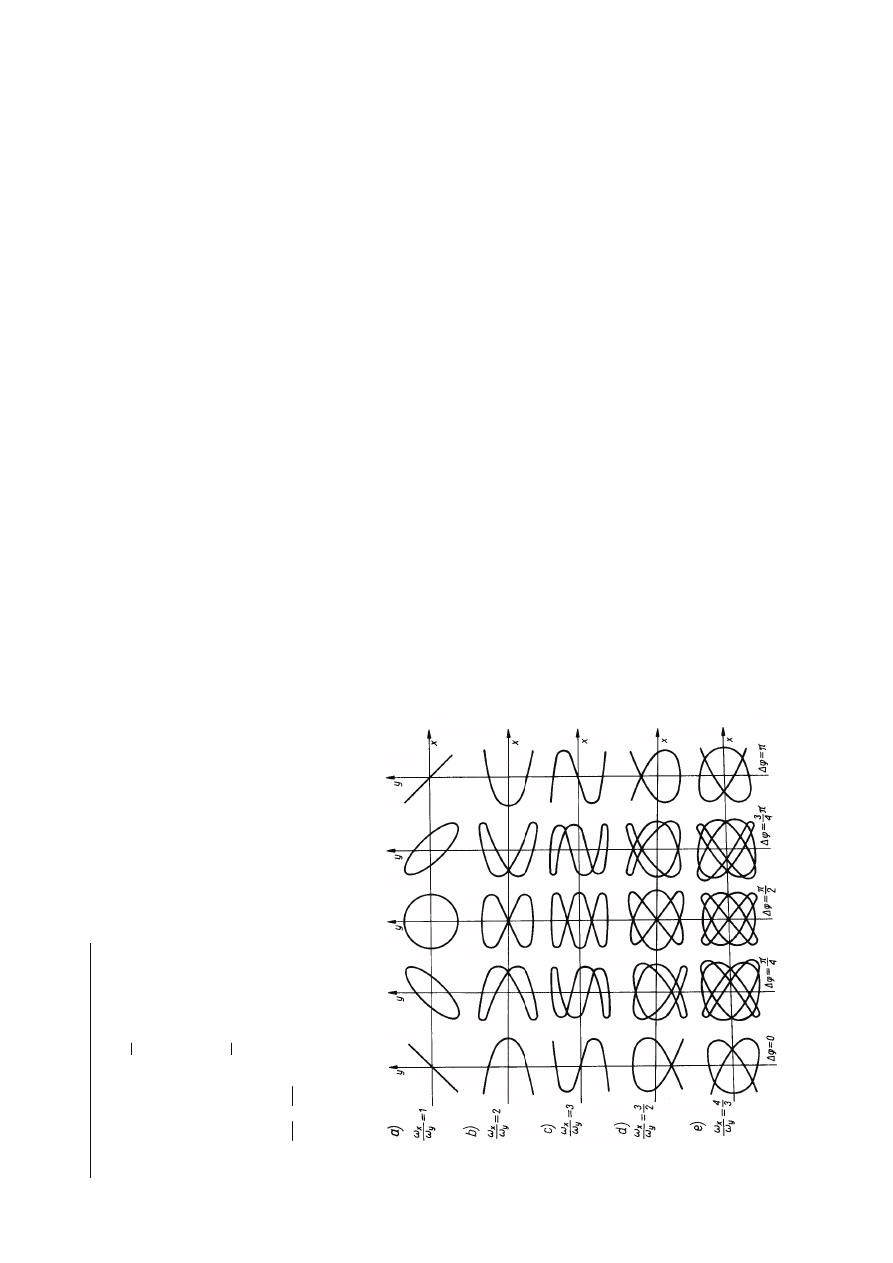
k

rz

y

w

e

L

is

sa

jo

u

s