WPROWADZENIE
DO SZTUCZNEJ INTELIGENCJI
POLITECHNIKA WARSZAWSKA
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
MEL
MEL
NS 586
Dr in
Ŝ
. Franciszek Dul
© F.A. Dul 2007
WPROWADZENIE
DO SZTUCZNEJ INTELIGENCJI
POLITECHNIKA WARSZAWSKA
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
MEL
MEL
NS 586
Dr in
Ŝ
. Franciszek Dul
© F.A. Dul 2007
15. WNIOSKOWANIE
PROBABILISTYCZNE
EWOLUCYJNE
EWOLUCYJNE
© F.A. Dul 2007
Wnioskowanie probabilistyczne ewolucyjne
Poka
Ŝ
emy,
Ŝ
e agent wnioskuj
ą
cy
probabilistycznie mo
Ŝ
e mimo
niepewno
ś
ci zrozumie
ć
, co działo si
ę
w przeszło
ś
ci, wła
ś
ciwie zinterpretowa
ć
w przeszło
ś
ci, wła
ś
ciwie zinterpretowa
ć
tera
ź
niejszo
ść
, a nawet przewidzie
ć
przyszło
ść
.
© F.A. Dul 2007
• Niepewno
ść
i czas
• Wnioskowanie w modelach czasowych
• Ukryte modele Markowa
• Filtracja Kalmana
• Dynamiczne sieci Bayesa
•
Zastosowanie - Rozpoznawanie mowy
Plan rozdziału
© F.A. Dul 2007
15.1. Niepewno
ść
i czas
Ś
wiat jest niepewny i zmienia si
ę
w czasie.
Opis probabilistyczny zjawisk zmieniaj
ą
cych si
ę
w czasie
polega na wyznaczeniu w ka
Ŝ
dej chwili czasu zmiennych
losowych, z których pewne s
ą
obserwowalne, a inne – nie:
• X
t
–
zmienne stanu
, nieobserwowane,
• E
t
–
zmienne obserwowanle
(evidence variables).
Zbiór warto
ś
ci
E
t
= e
t
w chwili
t
okre
ś
la zmienne obserwowalne.
Procesy stacjonarne
© F.A. Dul 2007
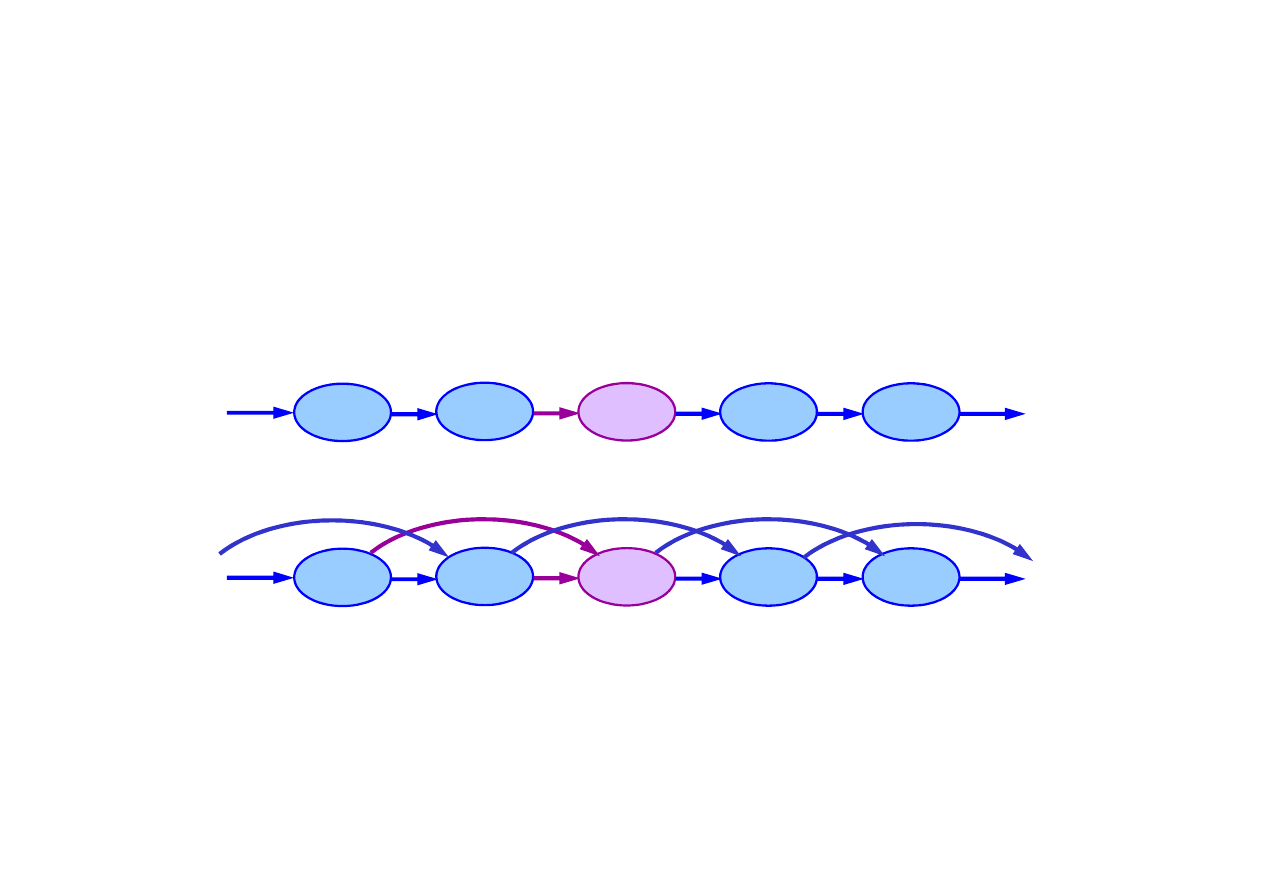
Procesy stacjonarne
Procesy stacjonarne
to takie, w których rozkłady g
ę
sto
ś
ci
prawdopodobie
ń
stwa zmiennych losowych
X
nie zmieniaj
ą
si
ę
wraz z czasem.
Parametry procesu stacjonarnego, takie jak warto
ść
ś
rednia
m
X
i wariancja
W
X
nie zale
Ŝą
od czasu.
x(t)
t
m
X
= 0
W
X
= const
15.1. Niepewno
ść
i czas
Procesy Markowa
Zało
Ŝ
enie Markowa
– stan bie
Ŝą
cy zale
Ŝ
y tylko od sko
ń
czonej
liczby stanów poprzednich.
Proces (ła
ń
cuch) Markowa
pierwszego rz
ę
du – taki w którym
stan bie
Ŝą
cy zale
Ŝ
y tylko od stanu poprzedniego i nie zale
Ŝ
y
od innych stanów wcze
ś
niejszych.
Sie
ć
Bayesa dla procesu Markowa pierwszego rz
ę
du
X
t-1
X
t
X
t+1
X
t+2
X
t-2
© F.A. Dul 2007
)
|
(
)
|
(
1
1
:
0
−
−
=
∀
t
t
t
t
t
X
X
P
X
X
P
Ewolucja stanu w procesie Markowa jest opisana całkowicie
rozkładem warunkowym
P
(
X
t
|
X
t-1
), który jest nazywany
modelem przej
ś
cia
.
Sie
ć
Bayesa dla procesu Markowa drugiego rz
ę
du
X
t-1
X
t
X
t+1
X
t+2
X
t-2
Prawdopodobie
ń
stwo warunkowe dla ła
ń
cucha Markowa
15.1. Niepewno
ść
i czas
)
|
(
)
,
|
(
1
:
0
:
0
t
t
t
t
t
X
E
P
E
X
E
P
=
−
Rozkład warunkowy
P
(
E
t
|
X
t
) nazywany jest
modelem
czujników
lub
modelem obserwacji
.
Zało
Ŝ
enie dla procesu Markowa: zmienne zaobserwowane
E
t
zale
Ŝą
tylko od stanu bie
Ŝą
cego
Rozkład ł
ą
czny prawdopodobie
ń
stwa zmiennych stanu
i obserwowalnych przy zało
Ŝ
eniu,
Ŝ
e proces jest procesem
Markowa pierwszego rz
ę
du
© F.A. Dul 2007
Markowa pierwszego rz
ę
du
∏
=
−
=
t
i
i
i
i
i
t
t
1
1
1
0
1
0
)
|
(
)
|
(
)
,...,
,
,
,...,
,
(
X
E
P
X
X
P
E
E
E
X
X
X
P
Proces Markowa pierwszego rz
ę
du jest jedynie przybli
Ŝ
eniem
procesów rzeczywistych.
Lepsze przybli
Ŝ
enia uzyskuje si
ę
stosuj
ą
c procesy Markowa
wy
Ŝ
szych rz
ę
dów, ale ich analiza jest bardziej zło
Ŝ
ona.
15.2. Wnioskowanie w modelach czasowych
Główne zadania wnioskowania probabilistycznego w czasie:
• Filtracja
(monitorowanie)
Wyznaczenie stanu wiarygodnego - rozkładu a posteriori
stanu bie
Ŝą
cego
na podstawie wszystkich obserwacji
do chwili bie
Ŝą
cej,
P
(
X
t
|
e
1:t
).
• Predykcja
(prognozowanie)
Wyznaczenie rozkładu a posteriori
stanu przyszłego
na podstawie wszystkich obserwacji do chwili bie
Ŝą
cej,
© F.A. Dul 2007
na podstawie wszystkich obserwacji do chwili bie
Ŝą
cej,
P
(
X
t+k
|
e
1:t
),
k > 0
.
• Wygładzanie
Wyznaczenie rozkładu a posteriori
stanu przeszłego
na podstawie wszystkich obserwacji do chwili bie
Ŝą
cej,
P
(
X
k
|
e
1:t
),
1
≤
k < t
.
• Najbardziej wiarygodne wyja
ś
nienie
Wyznaczenie stanów najbardziej wiarygodne generuj
ą
cych
dane obserwacje,
.
)
|
(
max
arg
:
1
:
1
:
1
t
t
t
e
x
P
x
15.2. Wnioskowanie w modelach czasowych
Filtracja
Je
Ŝ
eli znane s
ą
wyniki filtracji do chwili
t - 1,
to rozkład
prawdopodobie
ń
stwa zmiennej
X
t
mo
Ŝ
na wyznaczy
ć
na podstawie obserwacji
e
t
, za pomoc
ą
estymacji
∑
−
−
−
−
=
1
)
|
(
)
|
(
)
|
(
)
|
(
1
:
1
1
1
:
1
t
t
t
t
t
t
t
t
t
P
x
e
x
x
X
P
X
e
P
e
X
P
α
Funkcja
f
1:t
=
P
(
X
t
|
e
1:t
) opisuje propagacj
ę
informacji –
„wiadomo
ść
” – wzdłu
Ŝ
ci
ą
gu zmiennych stanu i obserwacji.
© F.A. Dul 2007
)
|
(
1
:
1
:
1
t
t
t
e
f
f
−
=
Forward
α
„wiadomo
ść
” – wzdłu
Ŝ
ci
ą
gu zmiennych stanu i obserwacji.
Rozkład prawdopodobie
ń
stwa zmiennej stanu przy danych
obserwacjach mo
Ŝ
na zapisa
ć
w postaci rekurencyjnej
15.2. Wnioskowanie w modelach czasowych
Predykcja
Predykcja mo
Ŝ
e by
ć
uwa
Ŝ
ana za filtracj
ę
w której pomini
ę
to
k ostatnich obserwacji,
e
t-k:t.
Rozkłady prawdopodobie
ń
stw zmiennych
X
t+k+1
mo
Ŝ
na
wyznaczy
ć
na podstawie obserwacji
e
t
, za pomoc
ą
estymacji
∑
+
+
+
+
+
+
+
=
k
t
t
k
t
k
t
k
t
t
k
t
P
x
e
x
x
X
P
e
X
P
)
|
(
)
|
(
)
|
(
:
1
1
:
1
1
Wiarygodno
ść
© F.A. Dul 2007
∑
=
=
t
t
t
t
t
P
L
x
x
e
)
(
)
(
:
1
:
1
:
1
l
Wiarygodno
ść
Wiarygodno
ść
ci
ą
gu obserwacji
P(e
1:t
)
jest wielko
ś
ci
ą
u
Ŝ
yteczn
ą
w wielu zastosowaniach.
Funkcja
ℓ
l
1:t
=
P
(
X
t
,
e
1:t
) opisuj
ą
ca „wiadomo
ść
” – propagacj
ę
wiarygodno
ś
ci mo
Ŝ
e by
ć
przedstawione w postaci
rekurencyjnej
)
|
(
1
:
1
1
:
1
+
+
=
t
t
t
e
l
l
Forward
α
Wiarygodno
ść
wyra
Ŝ
a si
ę
wzorem
15.2. Wnioskowanie w modelach czasowych
Wygładzanie
Wygładzanie polega na wyznaczeniu rozkładu a posteriori
stanów przeszłych
1
≤
k < t
na podstawie wszystkich
obserwacji do chwili bie
Ŝą
cej,
P
(
X
k
|
e
1:t
),.
X
1
X
k
X
t
X
0
E
1
E
k
E
t
. . .
. . .
© F.A. Dul 2007
t
k
k
t
k
:
1
:
1
:
1
)
|
(
+
=
b
f
e
X
P
α
1
b
e
b
b
=
=
+
+
+
+
t
t
t
k
t
k
t
k
:
1
:
1
:
2
:
1
,
)
,
(
Backward
oraz
wstecz
, od k+1 do t
Rozkłady prawdopodobie
ń
stw wygładzanych zmiennych
X
k
dane s
ą
wzorem rekurencyjnym
Wygładzanie przebiega w dwu etapach:
w przód
od 1 do k
)
|
(
1
:
1
:
1
k
k
k
e
f
f
−
=
Forward
15.2. Wnioskowanie w modelach czasowych
Najbardziej wiarygodne wyja
ś
nienie
Rozkłady prawdopodobie
ń
stw kolejnych obserwacji pozwalaj
ą
wyznaczy
ć
wiarygodno
ść
kolejnych stanów.
Jednak wiarygodno
ść
ci
ą
gu stanów nie jest równa wiarygod-
no
ś
ci stanów oddzielnych, gdy
Ŝ
s
ą
one na ogół zale
Ŝ
ne.
Wiarygodno
ść
ci
ą
gu stanów polega na wyznaczeniu ł
ą
cznego
rozkładu prawdopodobie
ń
stwa dla wszystkich chwil
k = 1,...,t
.
Istnieje zale
Ŝ
no
ść
rekurencyjna pomi
ę
dzy najbardziej
wiarygodnymi
ś
cie
Ŝ
kami do stanów
x
t+1
i
x
t
© F.A. Dul 2007
)
)
|
,
...
(
max
)
|
(
(
max
)
|
(
:
1
1
1
...
1
1
1
1
1
t
t
t
t
t
t
t
P
t
t
e
x
x
x
x
X
P
X
e
P
x
x
x
−
+
+
+
−
=
α
Zale
Ŝ
no
ść
ta jest identyczna z zale
Ŝ
no
ś
ci
ą
dla filtracji
po zast
ą
pieniu funkcji
f
1:t
=
P
(
X
t
|
e
1:t
) funkcja
Wyznaczenie najbardziej wiarygodnego ci
ą
gu stanów przy
pomocy
algorytmu Viterbiego
przebiega tak, jak przy filtracji.
wiarygodnymi
ś
cie
Ŝ
kami do stanów
x
t+1
i
x
t
=
+
+
)
|
,
...
(
max
1
:
1
1
1
...
1
t
t
t
t
e
X
x
x
P
x
x
)
|
,
...
(
max
:
1
1
1
...
:
1
1
1
t
t
t
t
t
e
X
x
x
P
m
x
x
−
−
=
Przykład
Stra
Ŝ
nik tajnych instalacji ukrytych pod ziemi
ą
mo
Ŝ
e
wnioskowa
ć
o pogodzie wył
ą
cznie na podstawie obserwacji
czy szef przychodzi rano z parasolem, czy te
Ŝ
bez.
Dla ka
Ŝ
dego dnia
t
zbiór zmiennych obserwowalnych
E
t
zawiera jedn
ą
zmienn
ą
U
t
okre
ś
laj
ą
c
ą
obserwacj
ę
parasola,
za
ś
zbiór zmiennych stanu
X
t
zawiera jedn
ą
zmienn
ą
R
t
okre
ś
laj
ą
c
ą
, czy pada deszcz.
15.2. Wnioskowanie w modelach czasowych
Sie
ć
Bayesa oraz rozkład prawdopodobie
ń
stw warunkowych
© F.A. Dul 2007
Deszcz
t
Deszcz
t+1
Deszcz
t-1
R
t
P(U
t
)
t
f
0.90
0.20
Parasol
t
Parasol
t+1
Parasol
t-1
R
t-1
P(U
t
)
t
f
0.70
0.30
Sie
ć
Bayesa oraz rozkład prawdopodobie
ń
stw warunkowych
15.3. Ukryte modele Markowa
Ukryte modele Markowa
(Hidden Markov Models, HMM)
s
ą
to modele probabilistyczne w których stan procesu opisuje
pojedy
ń
cza
dyskretna zmienna losowa
X
t
.
Ukryty model Markowa posiada proste reprezentacje modeli
przej
ś
cia, obserwacji oraz funkcji propagacji informacji.
Je
Ŝ
eli zmienna stanu
X
t
ma S warto
ś
ci, to model przej
ś
cia
T = P
(
X
t
|
X
t 1
) ma posta
ć
macierzy S
×
S której elementy
)
|
(
1
i
X
j
X
P
t
t
ij
=
=
=
−
T
© F.A. Dul 2007
1
t
t
ij
−
opisuj
ą
prawdopodobie
ń
stwo przej
ś
cia ze stanu i do stanu j.
Model obserwacji ma posta
ć
macierzy diagonalnej
O
t
której
elementy s
ą
równe
)
|
(
i
X
e
P
t
t
ii
=
=
O
Funkcje propagacji informacji w przód i wstecz maj
ą
postacie
wektorów
,
:
1
1
1
:
1
t
T
t
t
f
T
O
f
+
+
=
α
t
k
k
t
k
:
2
2
:
1
+
+
+
=
b
O
T
b
Ukryte modele Markowa umo
Ŝ
liwiaj
ą
zbudowanie efektywnych
algorytmów filtracji i wygładzania, w tym równie
Ŝ
on-line.
15.4. Filtracja Kalmana
W technice cz
ę
sto spotyka si
ę
zagadnienia dynamiczne
obarczone niepewno
ś
ci
ą
modelu lub obserwacji, np:
– wyznaczanie trajektorii ciał niebieskich
na podstawie niedokładnych obserwacji;
–
ś
ledzenie ruchu obiektów przy silnie
zakłóconych obserwacjach;
– nawigacja pojazdami
Program “Apollo” - lot na Ksi
ęŜ
yc!
Rudolph E. Kalman
© F.A. Dul 2007
S
ą
to problemy estymacji stanu obiektów (poło
Ŝ
enia i pr
ę
dko-
ś
ci) na podstawie zakłóconych (zaszumionch) obserwacji.
Do analizy takich dynamicznych zagadnie
ń
stochastycznych
u
Ŝ
ywa si
ę
powszechnie
filtracji Kalmana
.
Filtracja Kalmana jest to wnioskowanie w probabilistycznym
modelu dynamicznym zło
Ŝ
onym z losowego modelu zjawiska
fizycznego i losowego modelu obserwacji (pomiarów).
Filtracja Kalmana jest szczególnie przydatna w mechanice.
15.4. Filtracja Kalmana
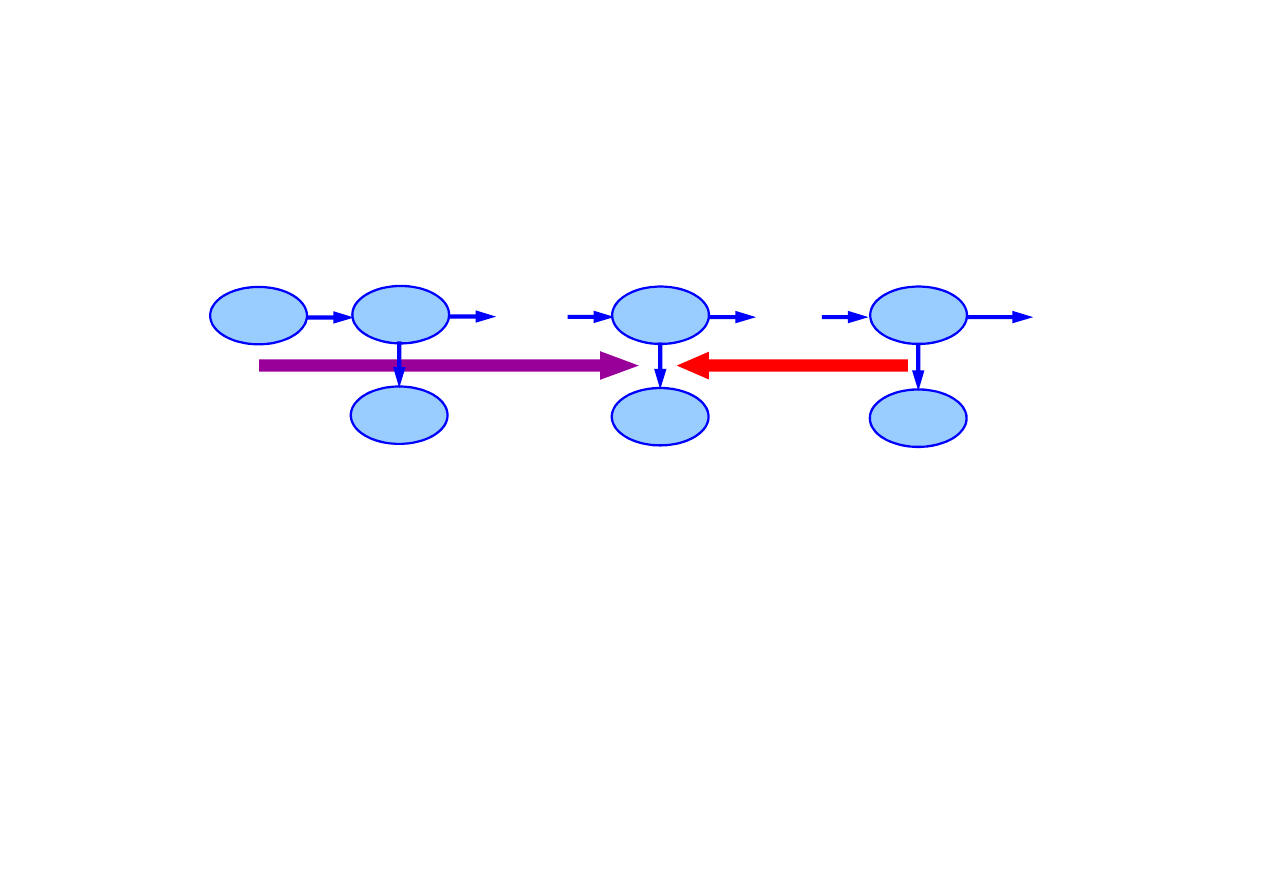
Idea filtracji Kalmana
Filtracja Kalmana ma na celu oszacowanie przyszłego stanu
układu x(t
)
na podstawie modelu układu, znanego stanu
poprzedniego x(t–
∆
t
)
oraz aktualnej obserwacji z(t
)
.
Filtracja Kalmana ma posta
ć
liniowej kombinacji wa
Ŝ
onej:
• predykcji stanu x(t
)
na podstawie (zaszumionego) modelu
i stanu poprzedniego x(t–
∆
t
)
,
• niepewnej (zaszumionej) obserwacji z(t),
)
(
)
(
~
)
(
t
a
t
t
a
t
z
x
x
+
∆
−
© F.A. Dul 2007
• Je
Ŝ
eli obserwacje s
ą
niepewne (du
Ŝ
e warto
ś
ci wariancji
obserwacji), to estymacja stanu przyszłego zawiera
wi
ę
cej stanu, a
x
> a
z
.
• Je
Ŝ
eli predykcja stanu jest bardziej niepewna (du
Ŝ
e
warto
ś
ci wariancji zmiennej stanu), to estymacja stanu
przyszłego zawiera wi
ę
cej obserwacji, a
z
> a
x
;
Filtracja Kalmana pozwala ponadto wyznaczy
ć
wariancje
zmiennych stanu i obserwacji.
)
(
)
(
~
)
(
t
a
t
t
a
t
z
x
z
x
x
+
∆
−
15.4. Filtracja Kalmana
,
)
(
)
(
t
t
t
∆
−
=
x
F
x
Rozkład prawdopodobie
ń
stwa warunkowego dla stanu
w chwili t jest równy
]
))
(
)
((
exp[
)
)(
,
(
1
2
1
µ
x
Q
µ
x
x
Q
µ
−
−
−
=
−
T
N
α
µµµµ
- wektor warto
ś
ci
ś
rednich, Q - macierz kowariancji białego szumu.
Filtracja Kalmana opiera si
ę
na dwóch zało
Ŝ
eniach:
• model obiektu jest liniowy,
• zakłócenia modelu i pomiarów maj
ą
rozkład normalny,
© F.A. Dul 2007
Liniowo
ść
modelu gwarantuje,
Ŝ
e estymacje stanu w kolejnych
chwilach czasu maj
ą
rozkład
normalny.
)
(
)
),
(
(
)
)
(
)
(
|
)
(
)
(
(
t
t
t
N
t
t
t
t
t
t
P
x
Fx
x
X
x
X
σ
∆
−
=
∆
−
=
∆
−
=
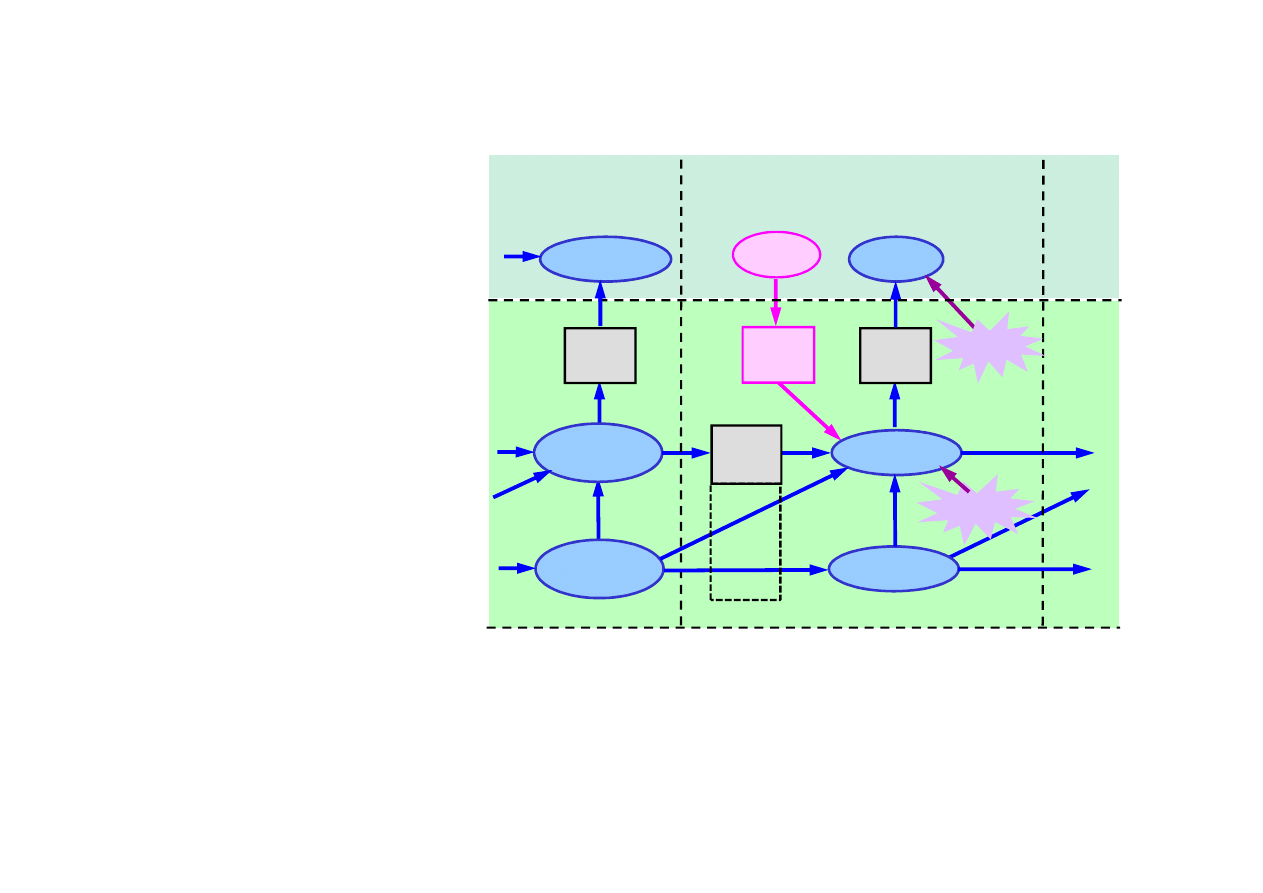
w chwili t jest równy
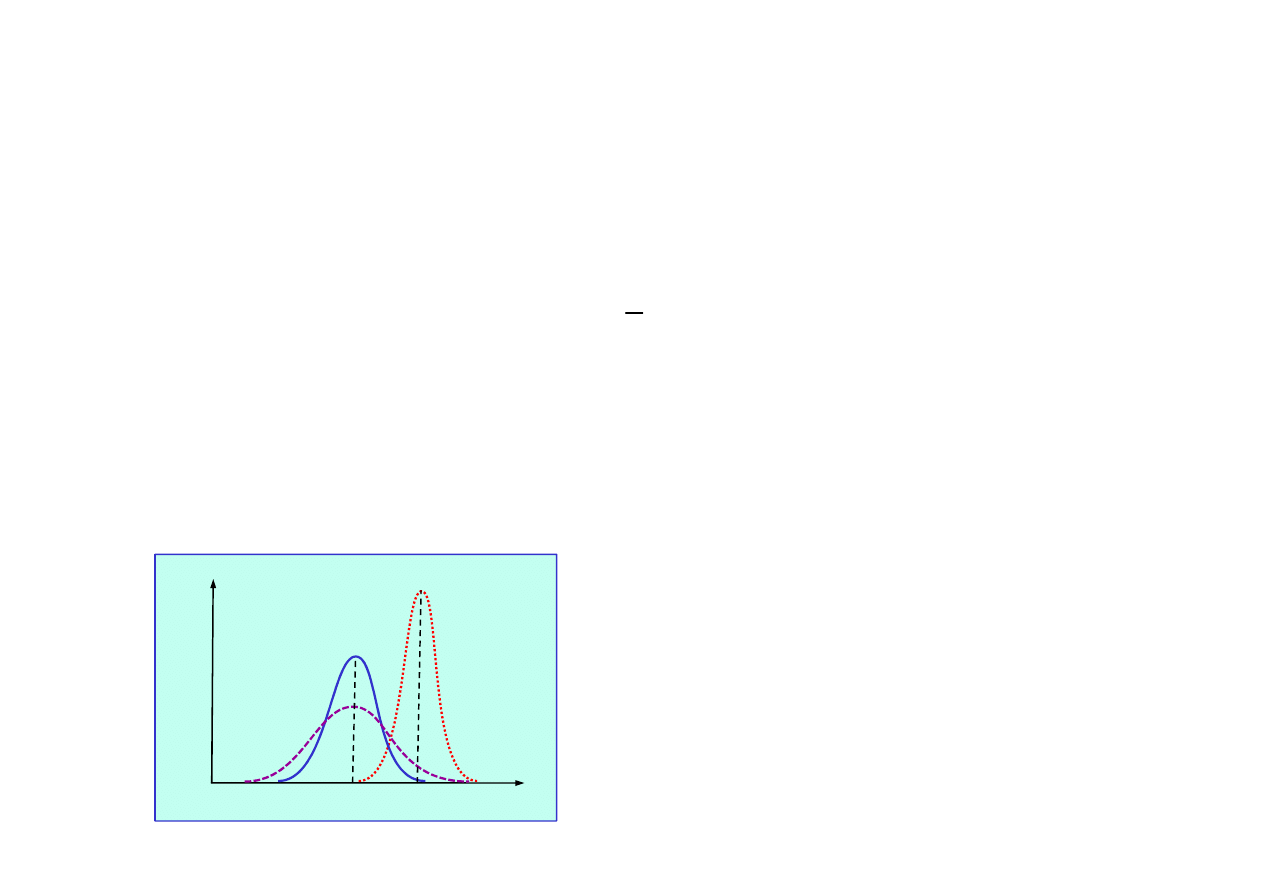
Kolejne predykcje stanu s
ą
spłaszczane przez szumy
pomiarów i modelu.
P(x
0
|z
1
=2,5)
P(x
0
)
P(x
1
)
-5 -2.5 0 2.5 x
5.0
0
0
.2
0
.4
0
.6
P
(x
)
15.4. Filtracja Kalmana
Sie
ć
Bayesa dla filtru Kalmana
Cz
ęść
widoczna:
B
)
(t
U
Cz
ęść
ukryta:
)
(
t
t
∆
−
X
)
(t
X
F
H
)
(t
Z
t -
∆
t
(k – 1)
t +
∆
t
(k+1)
t
(k)
)
(
t
R
w
)
(
t
t
∆
−
Z
H
• obserwacje Z(t),
• sterowanie U(t).
• stan X(t),
• zakłócenia
© F.A. Dul 2007
Modele układu i obserwacji maj
ą
posta
ć
)
(
)
(
)
(
t
t
t
t
Q
n
Fx
x
+
∆
−
=
)
(
)
(
)
(
t
t
t
R
w
Hx
z
+
=
+ Bu(t)
)
(
t
t
∆
−
X
)
(t
X
)
(
t
Q
n
F
)
(t
X
&
)
(
t
t
∆
−
X
&
• zakłócenia
stanu n(Q
t
),
• zakłócenia
obserwacji w(R
t
).
15.4. Filtracja Kalmana
Dla filtracja Kalmana ze stałym krokiem czasowym
t
k
t
k
∆
=
)
(
k
k
k
R
w
Hx
z
+
=
Zakłócenia stanu i pomiarów s
ą
opisane rozkładami
normalnymi Gaussa
1
x
Q
x
x
Q
0
Q
n
−
−
=
=
T
α
modele układu i obserwacji maj
ą
posta
ć
k
k
k
k
Bu
Q
n
Fx
x
+
+
=
−
)
(
1
© F.A. Dul 2007
k
k |
ˆx
Filtr Kalmana u
Ŝ
ywa nast
ę
puj
ą
cych zmiennych roboczych:
- estymacja stanu w chwili k.
k
k |
P
- estymacja macierzy kowariancji bł
ę
du stanu,
]
)
(
exp[
)
)(
,
(
)
(
1
2
1
x
Q
x
x
Q
0
Q
n
−
−
=
=
k
T
n
k
k
N
α
]
)
(
exp[
)
)(
,
(
)
(
1
2
1
x
R
x
x
R
0
R
w
−
−
=
=
k
T
w
k
k
N
α
k
k|
S
- estymacja macierzy kowariancji bł
ę
du pomiaru,
k
K
- macierz wzmocnienia optymalnego.
15.4. Filtracja Kalmana
Filtr Kalmana wyznacza estymacje stanu minimalizuj
ą
ce
warto
ść
oczekiwan
ą
E kwadratu bł
ę
du
min
]
)
ˆ
[(
2
|
→
−
k
k
k
E
x
x
Jest to równowa
Ŝ
ne minimalizacji
ś
ladu macierzy kowariancji
bł
ę
du P
k|k
wzgl
ę
dem macierzy wzmocnienia optymalnego K
k
0
2
)
(
2
)
(
tr
1
|
|
=
+
−
=
∂
∂
−
k
k
T
k
k
k
k
k
S
K
P
H
P
1
1
|
−
−
=
k
T
k
k
k
k
S
H
P
K
T
k
k
k
T
k
T
k
k
k
k
k
k
k
k
k
k
k
K
S
K
K
H
P
P
H
K
P
P
+
−
−
=
−
−
−
1
|
1
|
1
|
|
© F.A. Dul 2007
0
2
)
(
2
1
|
=
+
−
=
∂
−
k
k
k
k
k
k
S
K
P
H
K
1
|
−
=
k
k
k
k
k
S
H
P
K
Własno
ś
ci estymat otrzymanych za pomoc
ą
filtru Kalmana
0
]
ˆ
[
]
ˆ
[
1
|
|
=
−
=
−
−
k
k
k
k
k
k
E
E
x
x
x
x
0
]
[
=
k
E e
)
ˆ
cov(
|
|
k
k
k
k
k
x
x
P
−
=
)
ˆ
cov(
1
|
1
|
−
−
−
=
k
k
k
k
k
x
x
P
)
cov(
k
k
e
S
=
15.4. Filtracja Kalmana
k
T
k
k
k
k
k
k
Q
F
P
F
P
+
=
−
−
−
1
|
1
1
|
k
k
k
k
k
k
k
u
B
x
F
x
+
=
−
−
−
1
|
1
1
|
ˆ
ˆ
(predykcja stanu)
(predykcja macierzy kowariancji)
Filtracja Kalmana składa si
ę
z dwóch faz:
• predykcji
, która polega na wyznaczeniu estymat stanu
i macierzy kowariancji bł
ę
du na podstawie ich warto
ś
ci
w chwili poprzedniej.
• aktualizacji
, w której wykorzystuje si
ę
pomiary w chwili
bie
Ŝą
cej do poprawienia estymat uzyskanych w predykcji
© F.A. Dul 2007
k
T
k
k
k
k
k
R
H
P
H
S
+
=
−
1
|
1
|
ˆ
−
−
=
k
k
k
k
k
x
H
z
e
1
|
|
)
(
−
−
=
k
k
k
k
k
k
P
H
K
I
P
k
k
k
k
k
k
e
K
x
x
+
=
−
1
|
|
ˆ
ˆ
(aktualizacja bł
ę
du pomiaru)
(aktualizacja kowariancji bł
ę
du pomiaru)
(aktualizacja estymacji stanu)
(aktualizacja kowariancji bł
ę
du stanu)
1
1
|
−
−
=
k
T
k
k
k
k
S
H
P
K
(macierz wzmocnienia optymalnego)
bie
Ŝą
cej do poprawienia estymat uzyskanych w predykcji
w celu otrzymania dokładniejszych warto
ś
ci stanu
i macierzy kowariancji bł
ę
du.
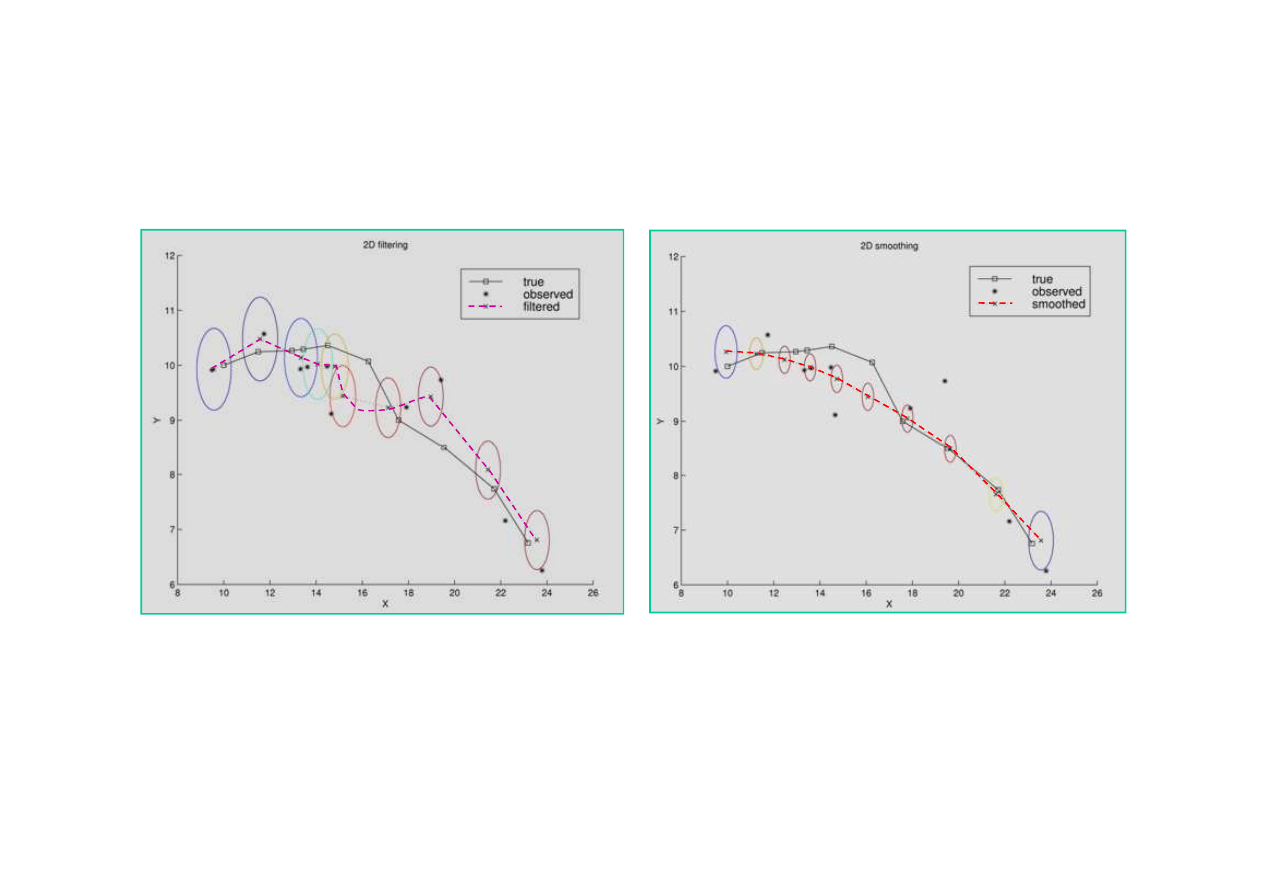
15.4. Filtracja Kalmana
Przykład
Zastosowanie filtracji Kalmana do
ś
ledzenia ruchu obiektu
w płaszczy
ź
nie X-Y. Stan obiektu - X(t) = [ X, Y, V
X
,V
Y
]
T
.
© F.A. Dul 2007
Wygładzanie
Filtracja
Filtracja Kalmana zapewnia
poprawne
ś
ledzenie ruchu.
Wariancja bł
ę
dów pomiaru
szybko si
ę
stabilizuje.
Filtracja Kalmana zapewnia
wygładzenie toru i znaczn
ą
redukcj
ę
wariancji bł
ę
dów
pomiaru.
15.4. Filtracja Kalmana
Przykład filtracji Kalmana
Sterowanie pojazdem
(Dan Simon,
www.embedded.com
)
k
k
k
k
dt
dt
dt
n
u
x
x
+
+
=
−
2
2
1
1
1
0
1
[
]
k
k
k
w
x
z
+
=
0
1
Nale
Ŝ
y wyznaczy
ć
estymacje poło
Ŝ
enia i pr
ę
dko
ś
ci pojazdu
opisanego modelem
© F.A. Dul 2007
Poło
Ŝ
enie pojazdu jest mierzone 10 razy na sekund
ę
, dt = 0.1,
z dokładno
ś
ci
ą
σ
z
= 3 m.
Przy
ś
pieszenie sterowania jest stałe i równe a = 0.33 m/s
2
.
Szum przy
ś
pieszenia wynosi
σ
a
= 0.07 m/s
2
.
Ze wzgl
ę
du na du
Ŝ
y szum pomiarowy u
Ŝ
ycie filtru Kalmana
powinno znacznie poprawi
ć
estymacj
ę
poło
Ŝ
enia w stosunku
do warto
ś
ci zmierzonych.
gdzie:
x(t) = [x,v]
T
– stan pojazdu,
u(t) = [a]
– sterowanie (stałe przy
ś
pieszenie).
15.4. Filtracja Kalmana
k
k
k
k
n
u
x
x
+
+
=
−
1
.
0
005
.
0
1
0
1
.
0
1
1
Model ruchu pojazdu dla przyj
ę
tych warto
ś
ci
Macierz kowariancji bł
ę
du stanu jest równa
[
]
=
=
=
=
]
[
]
[
]
[
2
2
v
v
v
v
v
x
x
x
E
x
x
E
E
T
k
xx
Q
=
⋅
⋅
⋅
⋅
=
2
2
1
2
2
2
2
1
)
)
((
)
(
)
(
a
a
a
dt
dt
dt
σ
σ
σ
© F.A. Dul 2007
=
⋅
⋅
⋅
⋅
=
2
2
2
2
1
)
(
)
(
)
)
((
a
a
a
dt
dt
dt
σ
σ
σ
[ ] [ ]
[ ]
9
3
]
[
2
2
=
=
=
=
z
T
k
E
σ
zz
R
Macierz kowariancji bł
ę
du obserwacji jest równa
=
⋅
⋅
⋅
⋅
⋅
⋅
=
2
2
2
2
2
2
)
07
.
0
(
)
1
.
0
(
)
07
.
0
(
)
1
.
0
(
)
005
.
0
(
)
07
.
0
(
)
1
.
0
(
)
005
.
0
(
)
07
.
0
(
)
005
.
0
(
⋅
⋅
⋅
⋅
=
−
−
−
−
5
6
6
7
10
90
.
4
10
45
.
2
10
45
.
2
10
225
.
1
P
o
ło
Ŝ
e
n
ie
(f
t)
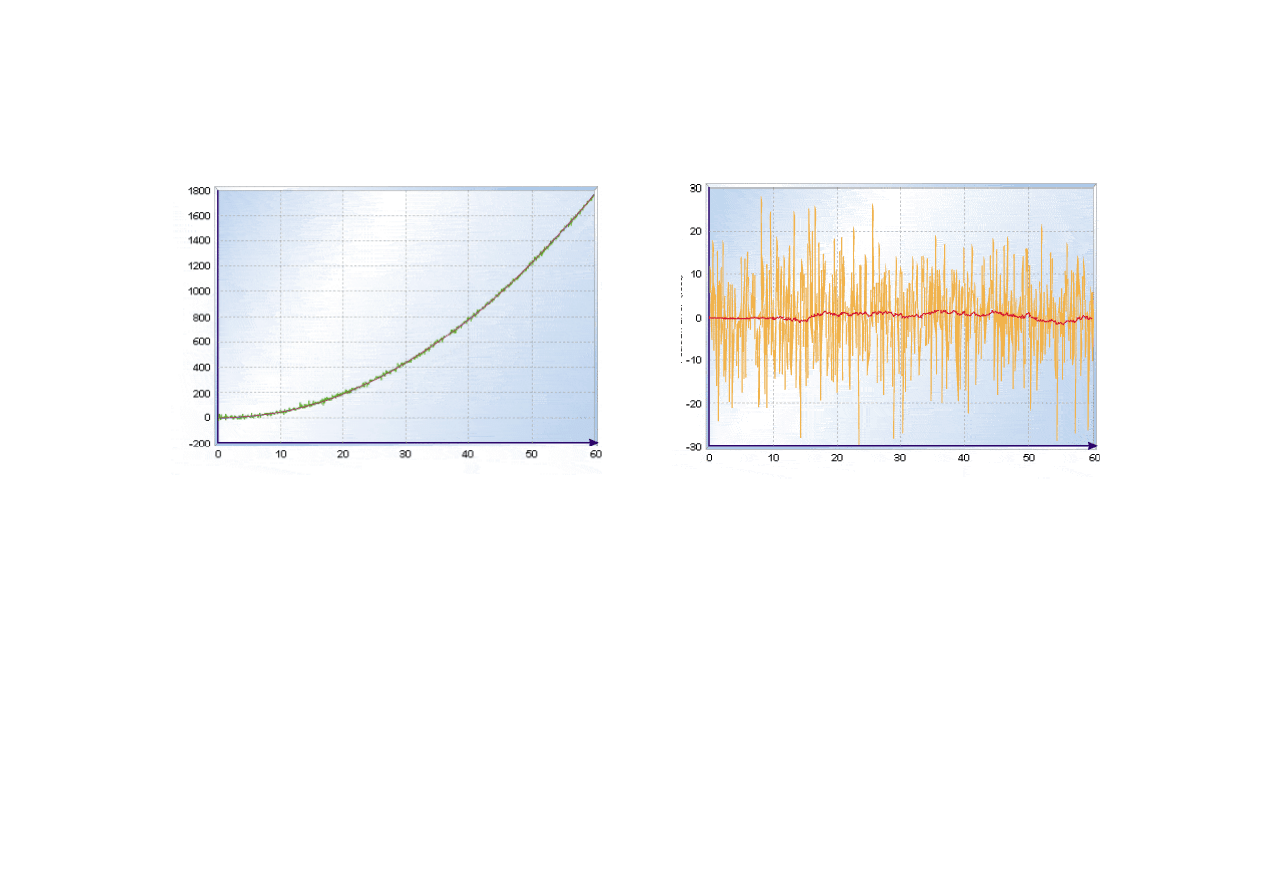
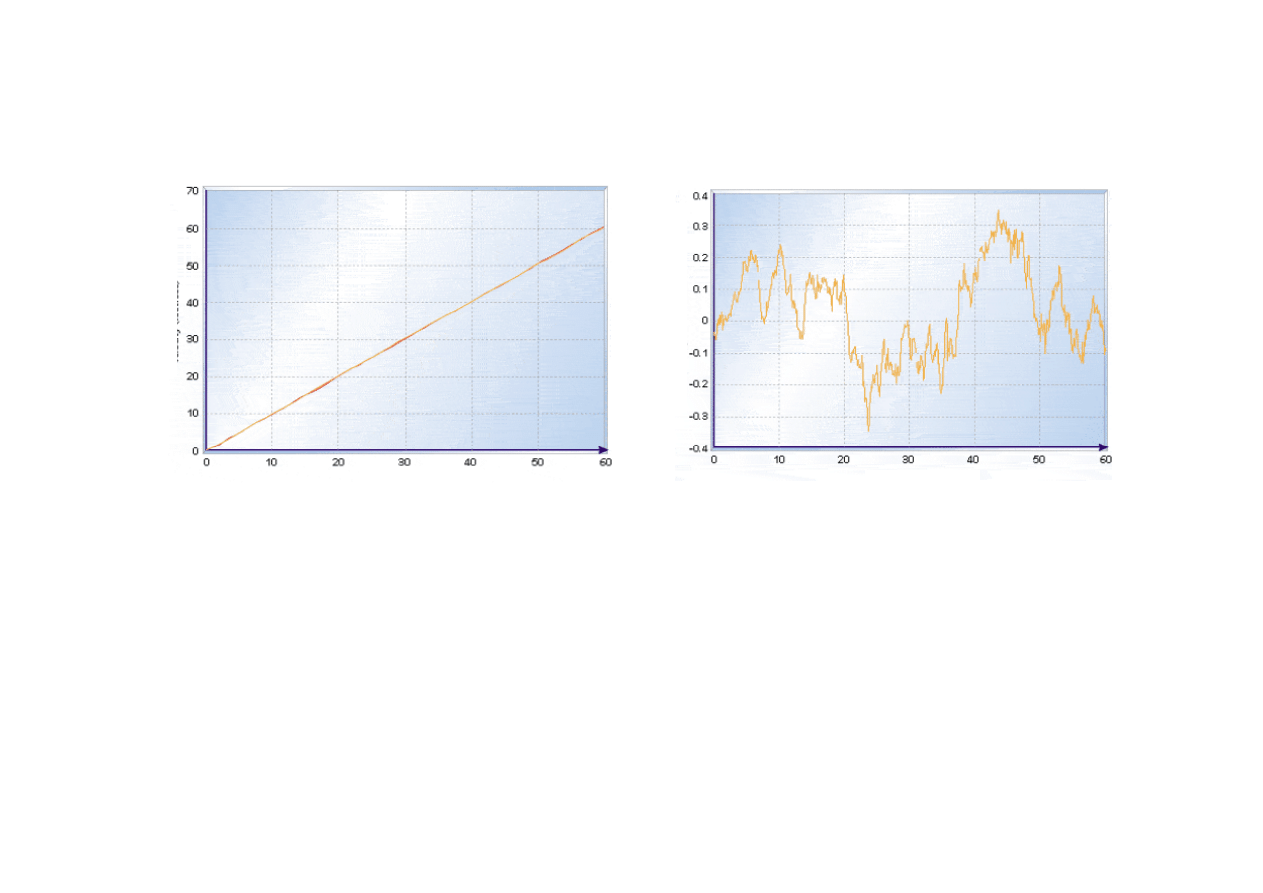
15.4. Filtracja Kalmana
Poło
Ŝ
enie dokładne, zmierzone i estymacja poło
Ŝ
enia
B
ł
ą
d
p
o
ło
Ŝ
e
n
ia
(
ft
)
Czas (s)
© F.A. Dul 2007
Poło
Ŝ
enie dokładne i jego
estymacja
s
ą
bardzo bliskie.
Poło
Ŝ
enie
zmierzone
jest silnie
zaszumione.
Czas (s)
U
Ŝ
ycie filtru Kalmana znacznie (~10 razy) poprawiło
estymacj
ę
poło
Ŝ
enia w stosunku do warto
ś
ci zmierzonych.
Odchylenie standardowe
bł
ę
du
estymacji
poło
Ŝ
enia ~0.7 m.
Odchylenie standardowe
bł
ę
du
pomiaru
poło
Ŝ
enia ~3
÷
10 m.
15.4. Filtracja Kalmana
Pr
ę
dko
ść
dokładna i jej estymacja
P
r
ę
d
k
o
ś
ć
(
ft
/s
)
B
ł
ą
d
p
r
ę
d
k
o
ś
c
i
(f
t/
s
)
© F.A. Dul 2007
Pr
ę
dko
ść
dokładna
oraz jej
estymacja
s
ą
bardzo bliskie
Czas (s)
Wida
ć
tutaj dodatkow
ą
zalet
ę
filtru Kalmana - pozwala on
uzyska
ć
poprawn
ą
estymat
ę
pr
ę
dko
ś
ci
bez konieczno
ś
ci
pomiaru samej pr
ę
dko
ś
ci
.
Czas (s)
Odchylenie standardowe
bł
ę
du pomiaru
pr
ę
dko
ś
ci
~0.35 m/s.
• model obiektu musi by
ć
liniowy,
• bł
ę
dy modelu i pomiarów musz
ą
mie
ć
rozkład normalny
Gaussa.
15.4. Filtracja Kalmana
Ograniczenia klasycznej filtracji Kalmana
Mimo swoich niezaprzeczalnych zalet klasyczny filtr Kalmana
ma dwa powa
Ŝ
ne ograniczenia:
Liniowo
ść
układu i gaussowski rozkład bł
ę
dów s
ą
w praktyce
ograniczeniami istotnymi.
Przykład
Wła
ś
ciwa estymacja poło
Ŝ
enia powinna
umo
Ŝ
liwi
ć
omini
ę
cie drzewa.
© F.A. Dul 2007
Przykład
Estymacja poło
Ŝ
enia lec
ą
cego ptaka przy
zało
Ŝ
eniu rozkładu Gaussa dla bł
ę
dów
modelu lotu sugeruje lot wprost na drzewo.
Wymaga to jednak u
Ŝ
ycia modelu nieliniowego.
Rozszerzony filtr Kalmana
(extended
Kalman filter) pozwala analizowa
ć
modele
nieliniowe o ile nieliniowo
ś
ci nie s
ą
zbyt silne.
• Nawigacja kosmiczna, lotnicza, l
ą
dowa i morska.
• Systemy nawigacji satelitarnej.
• Systemy naprowadzania bezwładno
ś
ciowego.
• Systemy autopilotów.
• Układy
ś
ledzenia radarowego i sonarowego.
• Wyznaczanie trajektorii cz
ą
stek elementarnych.
• Numeryczne prognozowanie pogody.
• Modelowanie cyrkulacji oceanów i atmosfery na podstawie
obrazów satelitarnych.
15.4. Filtracja Kalmana
Zastosowania filtracji Kalmana
obrazów satelitarnych.
• Równoczesna lokalizacja i tworzenie mapy (eksploracja
przez roboty nieznanego
ś
rodowiska).
• Sterowanie procesami produkcyjnymi.
• Nadzór elektrowni atomowych.
• Modelowanie demografii.
• Detekcja radioaktywno
ś
ci ziemskiej.
• Uczenie w logice rozmytej i sieciach neuronowych.
• Ekonomia, w szczególno
ś
ci makroekonomia, ekonometria.
• Rozpoznawanie obrazów.
© F.A. Dul 2007
Filtry Kalmana
Znaczenie filtru Kalmana jest trudne do przecenienia.
Filtr Kalmana umo
Ŝ
liwił realizacj
ę
lotów na Ksi
ęŜ
yc
i jest powszechnie u
Ŝ
ywany w nawigacji, sterowaniu
oraz wielu innych dziedzinach.
Wynalezienie filtru Kalmana przyczyniło si
ę
w stopniu
zasadniczym do rozwoju powy
Ŝ
szych dziedzin.
©
F.A. Dul 2007
Chocia
Ŝ
filtr Kalmana posiada ograniczenia, to jest
w dalszym ci
ą
gu podstawowym narz
ę
dziem
stochastycznego wnioskowania dynamicznego.
Ograniczenia filtracji Kalmana mo
Ŝ
na omin
ąć
stosuj
ą
c bardziej ogólne
dynamiczne sieci Bayesa
.
15.5. Dynamiczne sieci Bayesa
Dynamiczna sie
ć
Bayesa
(dynamic Bayesian network, DBN)
słu
Ŝ
y do reprezentacji dowolnych dynamicznych modeli
probabilistycznych.
Ka
Ŝ
dy ukryty model Markowa mo
Ŝ
e by
ć
reprezentowany
przez dynamiczn
ą
sie
ć
Bayesa, za
ś
ka
Ŝ
dy HMM mo
Ŝ
e by
ć
przekształcony do postaci DBN.
Ka
Ŝ
dy filtr Kalmana mo
Ŝ
e by
ć
reprezentowany przez
dynamiczn
ą
sie
ć
Bayesa, ale nie an odwrót.
© F.A. Dul 2007
dynamiczn
ą
sie
ć
Bayesa, ale nie an odwrót.
Dynamiczna sie
ć
Bayesa mo
Ŝ
e reprezentowa
ć
zmienne
losowe z wieloma maksimami lokalnymi, czego nie mo
Ŝ
na
osi
ą
gn
ąć
przy pomocy rozkładu Gaussa.
Dynamczne sieci Bayesa
Ukryte modele Markowa
Filtr Kalmana
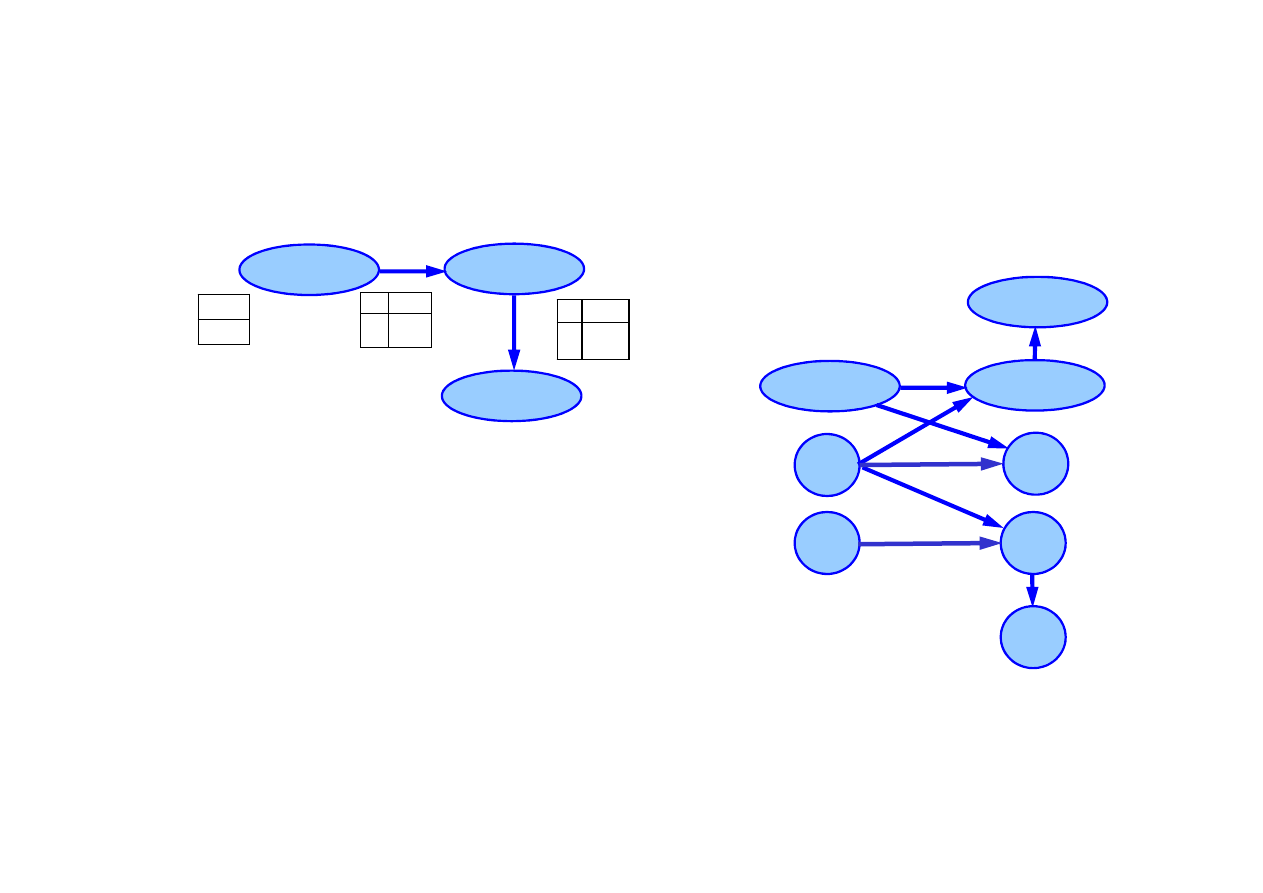
15.5. Dynamiczne sieci Bayesa
Przykłady dynamicznych sieci Bayesa
DBN dla zadania z parasolem
DBN dla ruchu robota
w płaszczy
ź
nie X-Y
Deszcz
1
Deszcz
0
R
1
P(U
1
)
t
f
0.90
0.20
Parasol
1
R
-0
P(R
0
)
t
f
0.70
0.30
P(R
0
)
0.70
Bateria
1
Bateria
0
MiernikB
1
© F.A. Dul 2007
V
0
V
1
Z
1
X
0
X
1
Do budowy DBN potrzebne s
ą
:
• rozkład prawdopodobie
ń
stwa
pocz
ą
tkowego zmiennej stanu
P
(
X
0
),
• model przej
ś
cia
P
(
X
t
|
X
t-1
),
• model obserwacji
P
(
E
t
|
X
t
),
• topologia sieci.
15.5. Dynamiczne sieci Bayesa
Wnioskowane
ś
cisłe w dynamicznych sieciach Bayesa
Wnioskowanie w DBN mo
Ŝ
e by
ć
przeprowadzone tak, jak
w zwykłej sieci Bayesa.
Nale
Ŝ
y w tym celu rozwin
ąć
sie
ć
powielaj
ą
c wielokrotnie
warstw
ę
pocz
ą
tkow
ą
(unrolling)
Deszcz
1
Deszcz
0
R
-0
P(R
0
)
t
f
0.70
0.30
P(R
0
)
0.70
Deszcz
2
R
-0
P(R
0
)
t
f
0.70
0.30
Deszcz
3
R
-0
P(R
0
)
t
f
0.70
0.30
. . .
© F.A. Dul 2007
R
1
P(U
1
)
t
f
0.90
0.20
Parasol
1
R
1
P(U
1
)
t
f
0.90
0.20
Parasol
2
R
1
P(U
1
)
t
f
0.90
0.20
Parasol
3
Rozwini
ę
ta DBN umo
Ŝ
liwia reprezentowanie nawet bardzo
zło
Ŝ
onych procesów w zwi
ę
zły sposób.
Wnioskowanie
ś
cisłe w sieci rozwini
ę
tej jest jednak bardzo
kosztowne, co praktycznie uniemo
Ŝ
liwia u
Ŝ
ycie metod
stosowanych w zwykłych sieciach Bayesa.
15.5. Dynamiczne sieci Bayesa
Wnioskowane przybli
Ŝ
one w dynamicznych sieciach
Bayesa
Wnioskowanie przybli
Ŝ
one w dynamicznych sieciach Bayesa
polega na zastosowaniu ogólnej zasady filtracji oddzielnie
dla ka
Ŝ
dej warstwy czasowej bez rozwijania sieci.
Tak wyznaczone zmienne stanu stanowi
ą
reprezentacj
ę
przybli
Ŝ
on
ą
rzeczywistego (
ś
cisłego) rozkładu stanu.
Do wnioskowania przybli
Ŝ
onego słu
Ŝą
do tego
algorytmy
filtrowania cz
ą
stkowego
.
• Na podstawie rozkładu P(X ) tworzy si
ę
zbiór N próbek
© F.A. Dul 2007
• Na podstawie rozkładu P(X
0
) tworzy si
ę
zbiór N próbek
X
0
(i), i = 1,...N.
• Za pomoc
ą
modelu przej
ś
cia
P(X
t+1
|X
t
) d
la ka
Ŝ
dej próbki
wyznaczany jest stan nast
ę
pny.
• Ka
Ŝ
da próbka jest wa
Ŝ
ona za pomoc
ą
wiarygodno
ś
ci
okre
ś
laj
ą
cej jej wkład do nowych obserwacji P(e
t+1
|x
t+1
).
• Nowa populacja próbek jest generowana za pomoc
ą
modelu przej
ś
cia z uwzgl
ę
dnieniem wag próbek.
Przy wystarczaj
ą
cej liczbie N próbek wnioskowanie przybli
Ŝ
one
prowadzi do wyników
ś
cisłych, N(x
t
|e
1:t
)/N = P(x
t
|e
1:t
).
15.6. Rozpoznawanie mowy
Rozpoznawanie mowy
pozwala komputerowi wyposa
Ŝ
onemu
w urz
ą
dzenie do rejestracji d
ź
wi
ę
ku (mikrofon) interpretowa
ć
mow
ę
ludzk
ą
.
Rozpoznawanie mowy pełni wa
Ŝ
n
ą
rol
ę
w wielu dziedzinach:
• interakcja człowieka z systemami komputerowymi,
• obsługa urz
ą
dze
ń
gospodarstwa domowego,
• sterowanie pojazdami – samochodami, samolotami,
statkami kosmicznymi,...
© F.A. Dul 2007
statkami kosmicznymi,...
• automatyczne notowanie.
Rozpoznawanie mowy polega na identyfikacji ci
ą
gu słów
wypowiedzianych przez mówc
ę
na podstawie zarejestrowane-
go sygnału akustycznego.
Zrozumienie
wypowiedzi jest krokiem nast
ę
pnym.
Zadaniem komplementarnym jest
synteza mowy
.
Jest to zadanie du
Ŝ
o łatwiejsze ni
Ŝ
rozpoznawanie mowy
(podobnie jak rysowanie obiektów jest znacznie łatwiejsze
ni
Ŝ
ich rozpoznawanie).
Mowa naturalna jest bardzo trudna do analizy, gdy
Ŝ
:
15.6. Rozpoznawanie mowy
• ten sam mówca mo
Ŝ
e ró
Ŝ
nie wypowiada
ć
to samo słowo,
• ró
Ŝ
ne słowa mog
ą
brzmie
ć
podobnie,
• ró
Ŝ
ni mówcy mog
ą
wymawia
ć
słowo w ró
Ŝ
ny sposób,
• tempo, intonacja i gło
ś
no
ść
mog
ą
zmienia
ć
si
ę
nawet w tej
samej wypowiedzi,
• gdy mówi wiele osób pojawiaj
ą
si
ę
interferencje słów,
• w płynnej wypowiedzi słowa zlewaj
ą
si
ę
,
• mowa mo
Ŝ
e by
ć
zaszumiona, zniekształcona.
© F.A. Dul 2007
• mowa mo
Ŝ
e by
ć
zaszumiona, zniekształcona.
Rozpoznawanie mowy jest wi
ę
c zadaniem wnioskowania
probabilistycznego.
Rozpoznawanie mowy jest najwa
Ŝ
niejszym zastosowaniem
czasowych modeli probabilistycznych.
Sformułowanie zadania rozpoznawania mowy
Words
– zmienna losowa opisuj
ą
ca wszystkie mo
Ŝ
liwe słowa.
signal
– obserwowany ci
ą
g sygnałów akustycznych.
Najbardziej prawdopodobn
ą
interpretacj
ą
wypowiedzi jest
warto
ść
zmiennej
Words
maksymalizuj
ą
ca
P(words | signal).
Z reguły Bayesa
15.6. Rozpoznawanie mowy
)
(
)
|
(
)
|
(
Words
P
Words
signal
P
signal
Words
P
α
=
P(signal |Words)
okre
ś
la
model akustyczny
opisuj
ą
cy
© F.A. Dul 2007
P(signal |Words)
okre
ś
la
model akustyczny
opisuj
ą
cy
brzmienie słów.
P(Words)
okre
ś
la
model j
ę
zyka
– prawdopodobie
ń
stwo
ka
Ŝ
dej wypowiedzi.
Modele j
ę
zyka okre
ś
laj
ą
prawdopodobie
ń
stwa wyst
ą
pienia
ci
ą
gu słów:
- bigram: prawdopodobie
ń
stwa dwóch kolejnych słów.
- trigram: prawdopodobie
ń
stwa trzech kolejnych słów, itd.
Np.:
P(”It is”) = 0.96, P(”It this”) = 0.001.
Fonem (phoneme) jest najmniejsz
ą
jednostk
ą
mowy
rozró
Ŝ
nian
ą
przez u
Ŝ
ytkowników danego j
ę
zyka.
Alfabet j
ę
zyka liczy zwykle 40-50 fonemów, np. International
Phonetic Alphabet (IPA), czy ARPAbet (American English):
[t] –
t
en, [ow] – b
oa
t, [m] –
m
et, [aa] – c
o
t, ...
Słowo „
tomato”
ma reprezentacj
ę
fonetyczn
ą
[t ow m aa t ow ].
Fonemy umo
Ŝ
liwiaj
ą
podział modelu akustycznego na
model
wymowy
oraz
model fonemów
.
Model wymowy okre
ś
la rozkład prawdopodobie
ń
stwa
15.6. Rozpoznawanie mowy
© F.A. Dul 2007
Model wymowy okre
ś
la rozkład prawdopodobie
ń
stwa
ka
Ŝ
dego słowa wzgl
ę
dem zbioru wszystkich fonemów.
Zmienna X
t
okre
ś
la fonem wypowiedziany w chwili t.
Model fonemów okre
ś
la sposób realizacji fonemów jako
sygnałów akustycznych.
Zmienna ukrytego modelu Markowa E
t
okre
ś
la własno
ś
ci
sygnału w chwili t.
Model fonemów okre
ś
la prawdopodobie
ń
stwo
P(E
t
|X
t
)
pojawienia si
ę
w chwili t własno
ś
ci E
t
w sygnale je
Ŝ
eli
wypowiedziany został fonem X
t
.
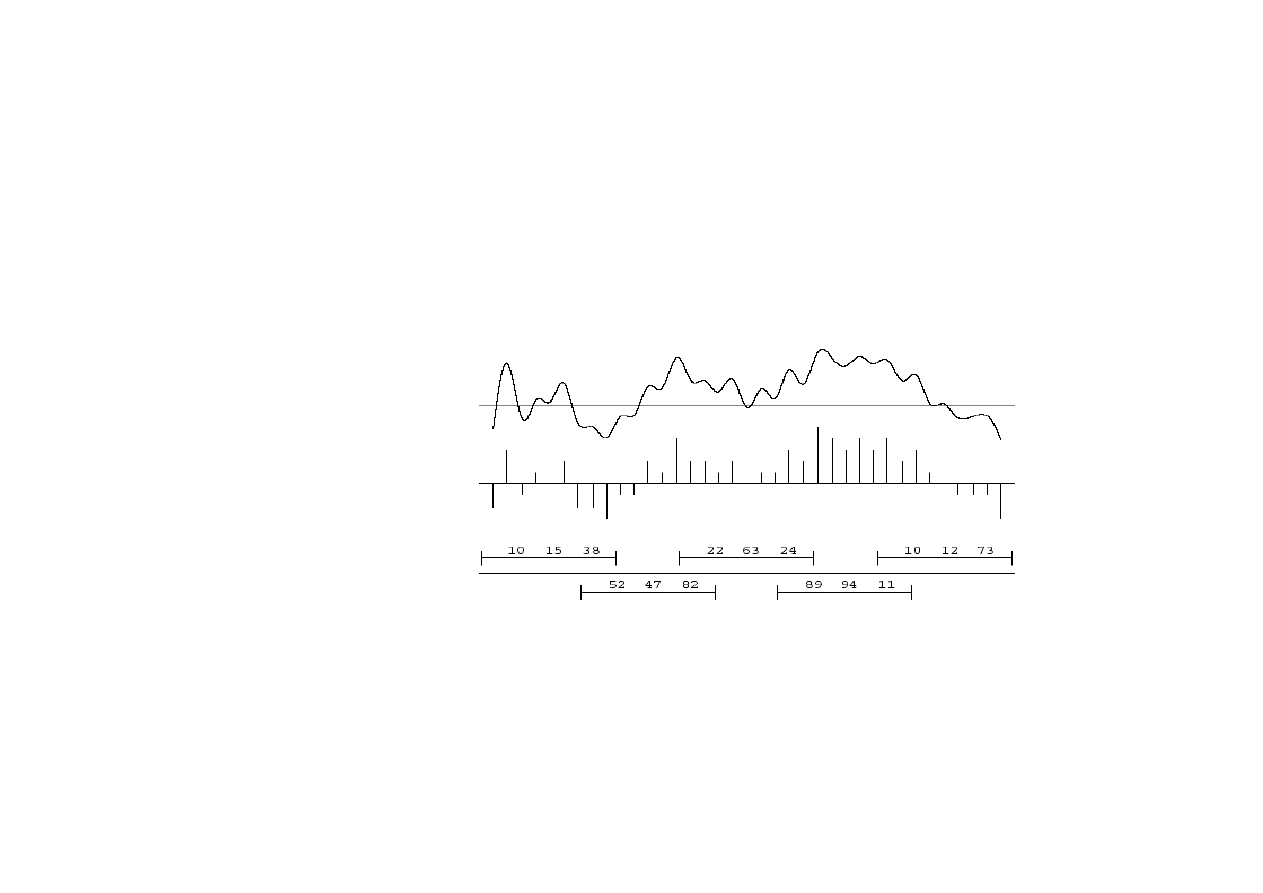
Reprezentacja sygnału mowy
Próbkowanie sygnału odbywa si
ę
z cz
ę
stotliwo
ś
ci
ą
8-16 kHz.
Sygnał rejestrowany jest z rozdzielczo
ś
ci
ą
8-12 bitów.
Wymagana pami
ęć
jest du
Ŝ
a – 1 MBajt / minut
ę
wypowiedzi,
wi
ę
c wyznaczenie
P(signal | phone)
nie jest praktyczne.
15.6. Rozpoznawanie mowy
Sygnał analogowy
© F.A. Dul 2007
Sygnał próbkowany
dyskretny
Ramki z własno
ś
ciami
Mowa reprezentowana jest wi
ę
c poprzez
ramki
(frames)
opisuj
ą
ce
n
własno
ś
ci
sygnału (features) w małych
przedziałach czasu (~50-100 próbek).
Własno
ś
ciami mog
ą
by
ć
np. energie d
ź
wi
ę
ku, formanty, itp.
Własno
ś
ci w ramkach s
ą
reprezentowane w zwartej postaci
za pomoc
ą
:
15.6. Rozpoznawanie mowy
• kwantyzacji wektorowej VC (obecnie rzadziej u
Ŝ
ywana),
• mieszanek Gaussa.
Mieszanka Gaussa to zbiór
k
rozkładów Gaussa z ró
Ŝ
nymi
warto
ś
ciami
ś
rednimi i wariancjami dobranymi tak, aby jak
najlepiej reprezentowały rozkład prawdopodobie
ń
stwa
P(features | phone)
w obszarze ramki.
Struktura czasowa fonemu opisywana jest
modelem
© F.A. Dul 2007
Struktura czasowa fonemu opisywana jest
modelem
trójstanowym
: ka
Ŝ
dy fonem składa si
ę
z trzech faz: Pocz
ą
tek,
Ś
rodek, Koniec (Onset, Mid, End).
Kontekst w którym pojawia si
ę
fonem opisywany jest
modelem trójfonemowym
: model akustyczny fonemu
uwzgl
ę
dnia trójk
ę
fonemów: poprzedni, bie
Ŝą
cy i nast
ę
pny.
Kombinacja modeli trójstanowego i trójfonemowego pozwala
zwi
ę
kszy
ć
liczb
ę
mo
Ŝ
liwych stanów z
n
do
3n
3
, co znacznie
poprawia dokładno
ść
reprezentacji sygnału akustycznego.
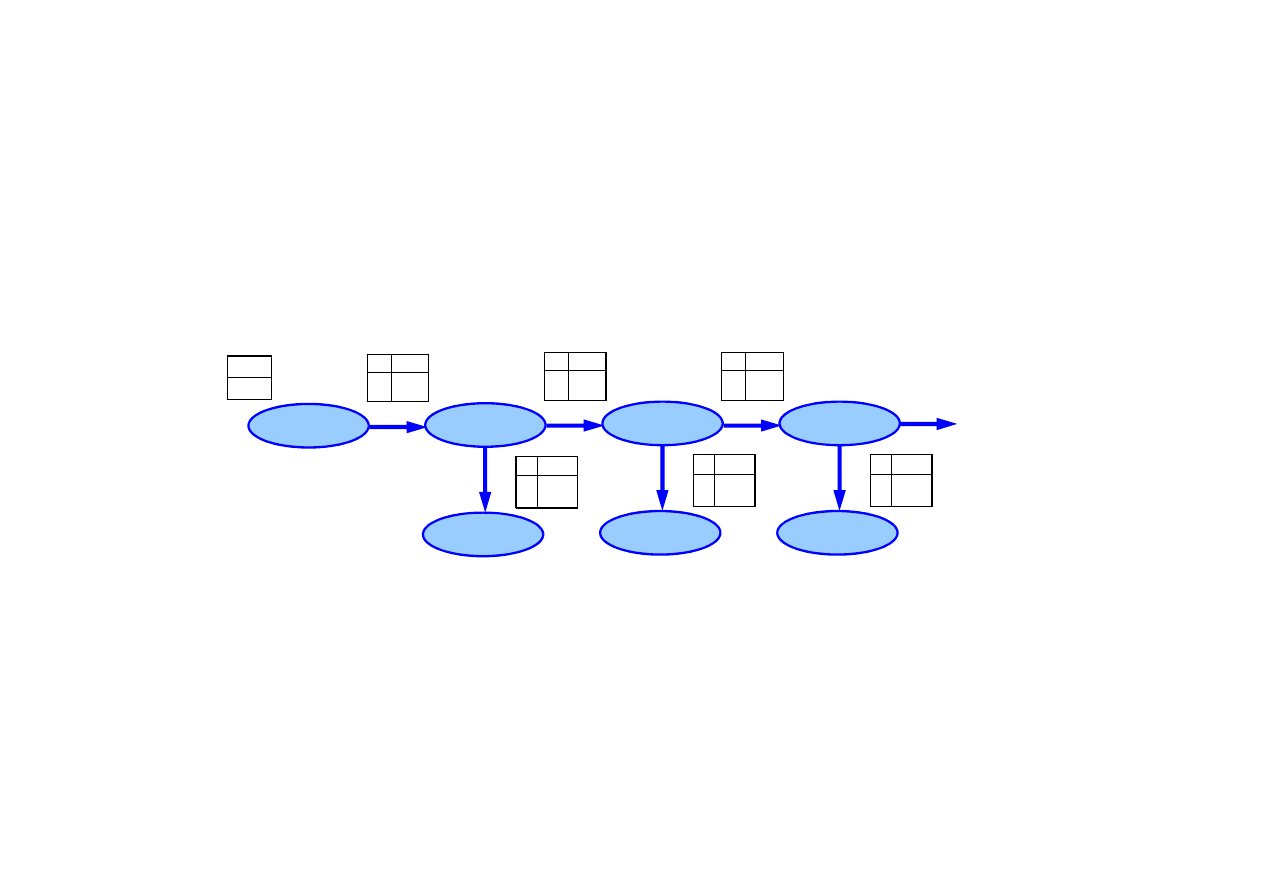
Słowa
Słowo jest okre
ś
lone rozkładem prawdopodobie
ń
stwa
P(X
1:t
| word )
w którym
X
i
jest fonemem w i-tej ramce.
Model słowa
- rozkład prawdopodobie
ń
stwa dla słowa -
okre
ś
lony jest przez
modelu wymowy
oraz
model fonemu
.
Model wymowy okre
ś
la rozkład prawdopodobie
ń
stwa dla
słowa wzgl
ę
dem fonemów, bez uwzgl
ę
dnienia ramek i czasu.
Słowo mo
Ŝ
e mie
ć
kilka modeli wymowy, np. słowo „tomato”
ma nast
ę
puj
ą
ce cztery modele:
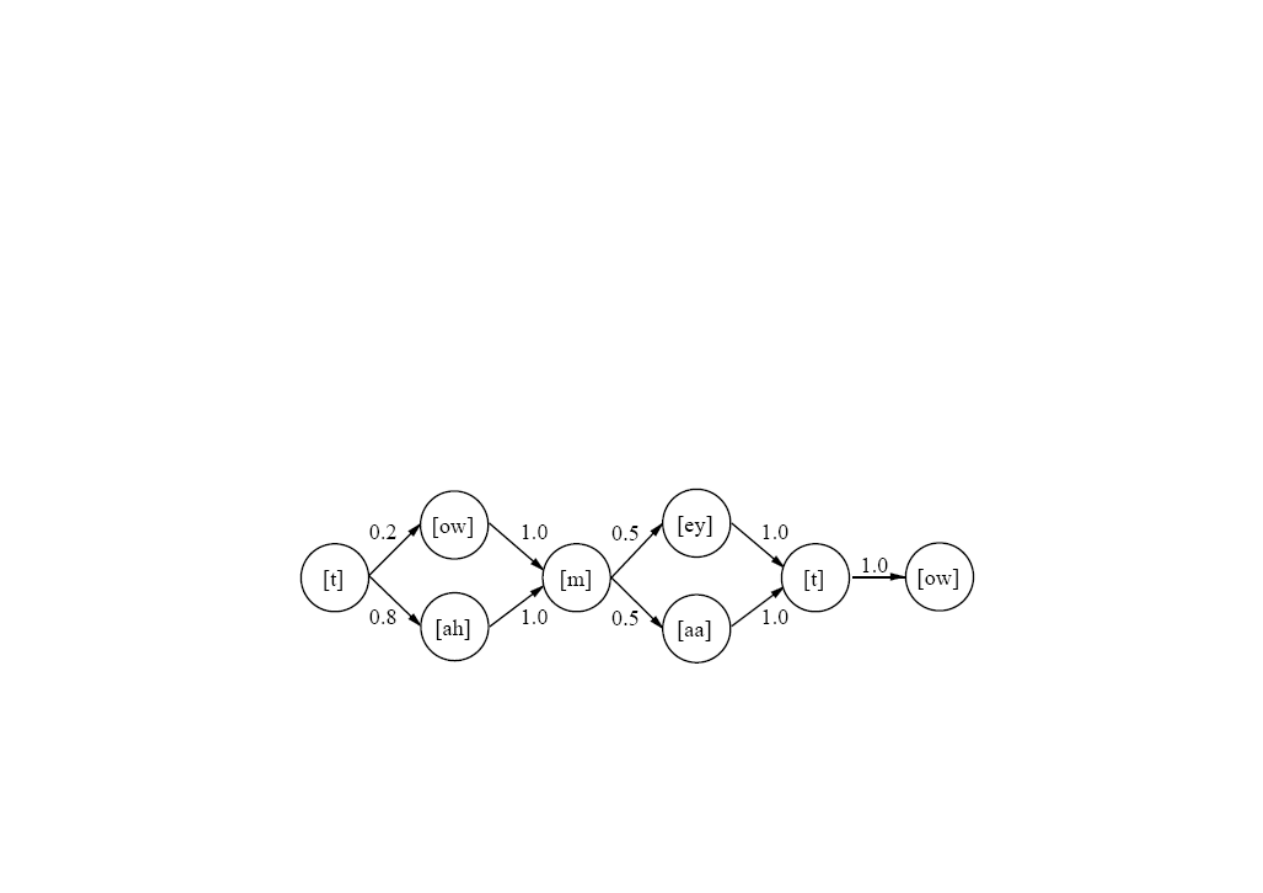
15.6. Rozpoznawanie mowy
© F.A. Dul 2007
ma nast
ę
puj
ą
ce cztery modele:
P( [t ow m ey t ow] |”tomato” ) = 0.1
P( [t ow m aa t ow] |”tomato” ) = 0.1
P( [t ah m ey t ow] |”tomato” ) = 0.4
P([t ah m aa t ow] |”tomato” ) = 0.4
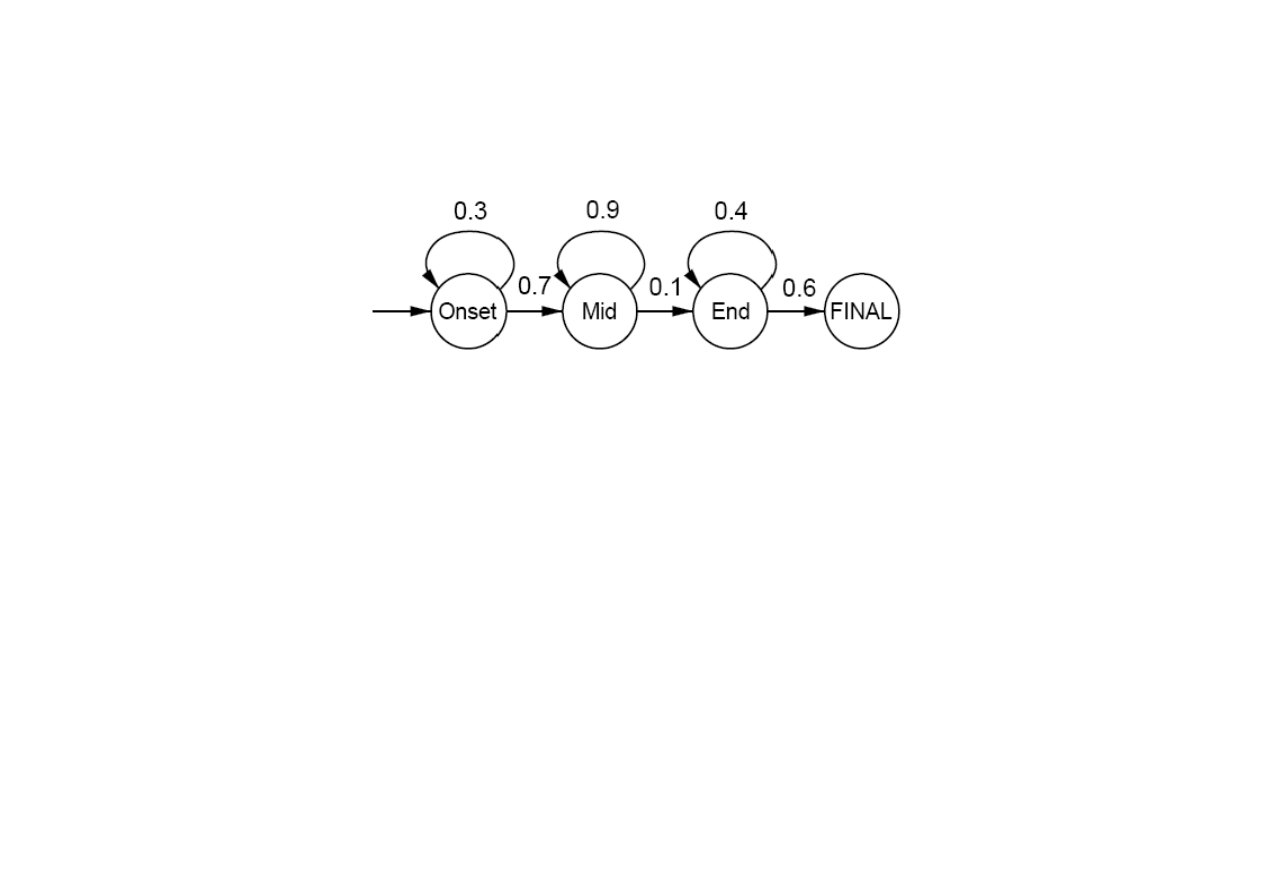
Modele fonemów okre
ś
laj
ą
odwzorowanie fonemów na ramki.
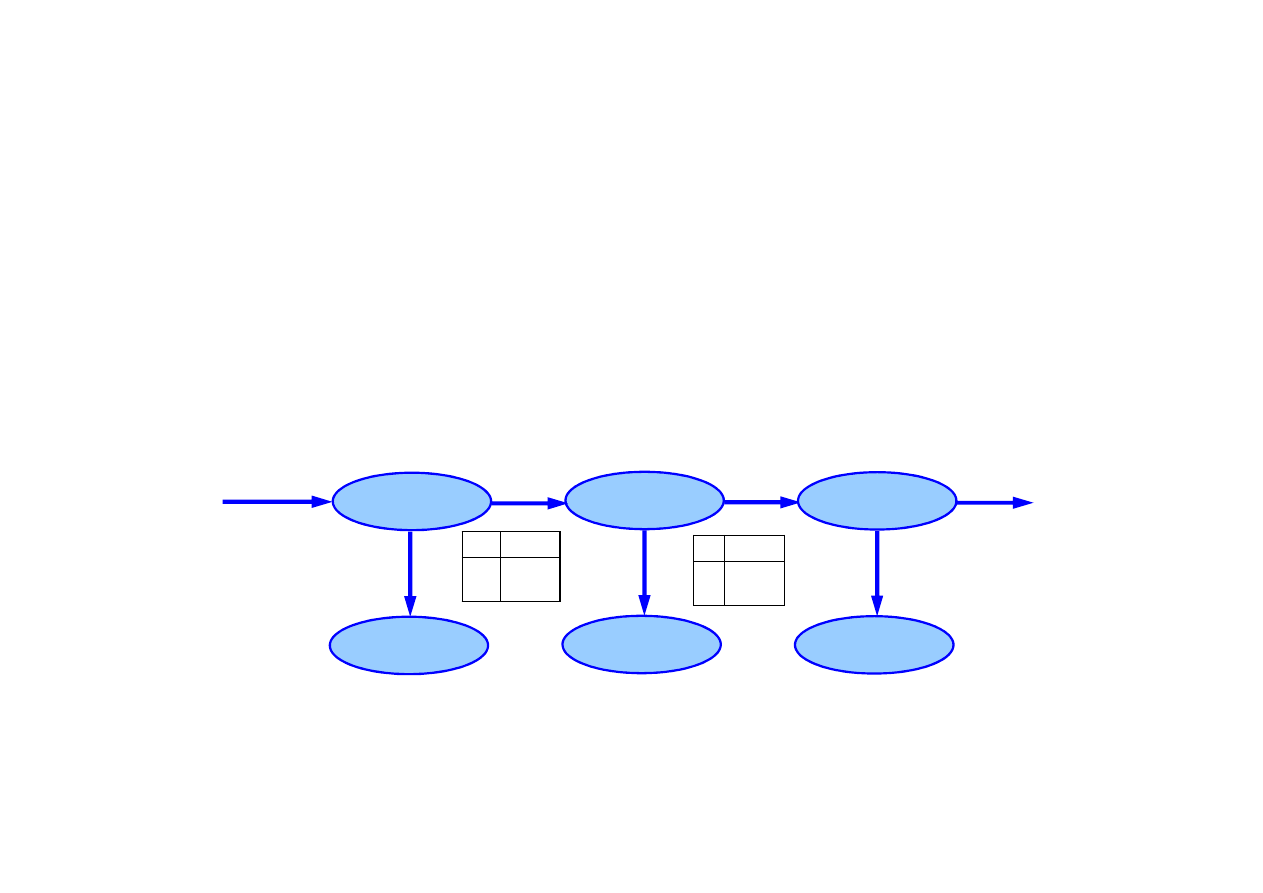
Przykład modelu trójstanowego dla fonemu [m]
15.6. Rozpoznawanie mowy
Modele stanów Onset, Mid i End okre
ś
laj
ą
realizacj
ę
akustyczn
ą
fonemu poprzez prawdopodobie
ń
stwa trwania
stanów (p
ę
tle).
© F.A. Dul 2007
akustyczn
ą
fonemu poprzez prawdopodobie
ń
stwa trwania
stanów (p
ę
tle).
Model słowa w poł
ą
czeniu z modelem fonemu okre
ś
la
wiarygodno
ść
dla słowa izolowanego,
P(word | e
1:t
) =
α
P(e
1:t
| word ) P(word )
Prawdopodobie
ń
stwo a priori
P(word )
wyznacza si
ę
zliczaj
ą
c
cz
ę
sto
ść
wyst
ę
powania słowa, za
ś
P(e
1:t
| word )
mo
Ŝ
na
obliczy
ć
rekurencyjnie
∑
=
t
X
t
t
t
e
X
word
e
P
)
,
(
)
|
(
:
1
:
1
P
Wypowiedzi
Dialog wymaga zrozumienia wypowiedzi ci
ą
głej.
Zrozumienie ci
ą
głej wypowiedzi wymaga
segmentacji
–
wła
ś
ciwego podziału ła
ń
cucha wypowiedzi na słowa.
Wypowied
ź
ci
ą
gła nie jest jednak prost
ą
sum
ą
ci
ą
gu słów –
sekwencja najbardziej prawdopodobnych słów nie jest
najbardziej prawdopodobn
ą
sekwencj
ą
słów.
Model j
ę
zyka
okre
ś
la prawdopodobie
ń
stwo ła
ń
cucha jako
ci
ą
gu kolejnych słów
15.6. Rozpoznawanie mowy
© F.A. Dul 2007
ci
ą
gu kolejnych słów
)
...
|
(
...
)
|
(
)
(
)
...
(
1
1
1
2
1
1
−
=
n
n
n
w
w
w
P
w
w
P
w
P
w
w
P
)
|
(
)
...
|
(
1
1
1
−
−
≈
i
i
i
i
w
w
P
w
w
w
P
W praktyce u
Ŝ
ywa si
ę
przybli
Ŝ
enia
bigram
dla dwóch słów
Prawdopodobie
ń
stwa modelu bigram mog
ą
by
ć
wyznaczone
poprzez zliczanie wyst
ą
pie
ń
w du
Ŝ
ym zbiorze wypowiedzi.
Przybli
Ŝ
enia u
Ŝ
ywaj
ą
ce trzech lub wi
ę
cej słów s
ą
du
Ŝ
o
dokładniejsze, lecz trudniejsze do oszacowania.
∏
=
−
=
n
i
i
i
w
w
w
P
1
1
1
)
...
|
(
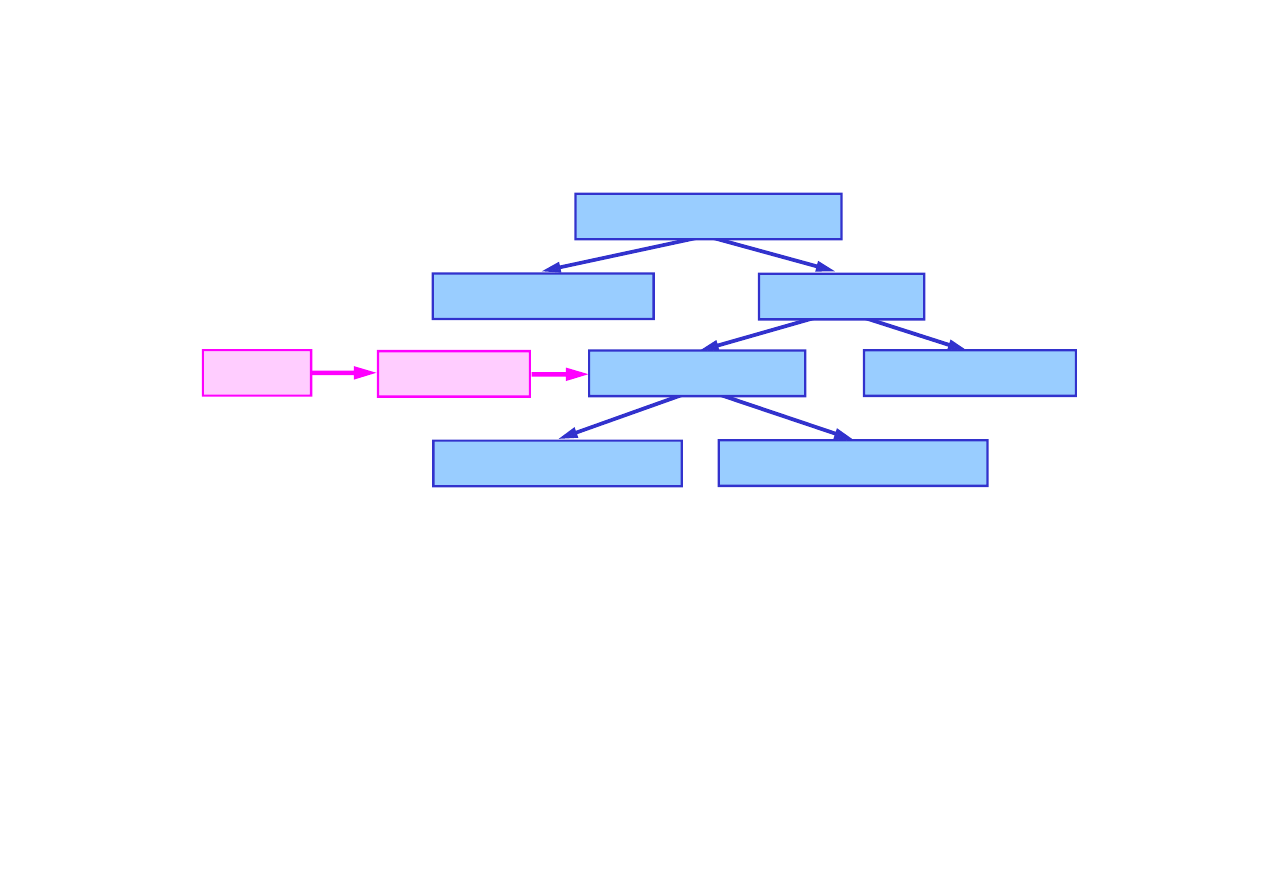
Model wypowiedzi
w postaci ukrytego modelu Markowa
(HMM) dla tworzy si
ę
z modeli nast
ę
puj
ą
co:
15.6. Rozpoznawanie mowy
Model wypowiedzi
Model j
ę
zyka
Model słów
Model wymowy
Model fonemów
Własno
ś
ci
Ramki
© F.A. Dul 2007
Najbardziej prawdopodobny ci
ą
g słów dla danego ła
ń
cucha,
wyznacza si
ę
na podstawie modelu wypowiedzi np. za
pomoc
ą
algorytmu Viterbiego.
Segmentacji ła
ń
cucha dokonuje si
ę
na podstawie tak
wyznaczonego ci
ą
gu słów.
Najbardziej prawdopodobny ci
ą
g słów w wypowiedzi mo
Ŝ
na
wyznaczy
ć
bardzo efektywnie za pomoc
ą
dekodera A*
,
uzupełnionego odpowiedni
ą
heurystyk
ą
.
Model trójfonemowy
Model trójstanowy
Budowa systemów rozpoznawania mowy
Jako
ść
systemów rozpoznawania mowy zale
Ŝ
y od jako
ś
ci
wszystkich elementów: modelu j
ę
zyka, modeli wymowy słów,
modeli fonemów, algorytmów przetwarzania sygnałów mowy
oraz obszerno
ś
ci słowników wymowy słów.
Rozkłady prawdopodobie
ń
stw mog
ą
zawiera
ć
nawet miliony
parametrów definiuj
ą
cych modele sygnałów.
Parametry te mog
ą
by
ć
okre
ś
lone w ró
Ŝ
ny sposób, ale
najlepsze rezultaty osi
ą
ga si
ę
poprzez
uczenie
modelu.
15.6. Rozpoznawanie mowy
© F.A. Dul 2007
najlepsze rezultaty osi
ą
ga si
ę
poprzez
uczenie
modelu.
Uczenie polega na dostrajaniu parametrów na podstawie
du
Ŝ
ej liczby wypowiedzi.
Zaawansowane systemy rozpoznawania mowy u
Ŝ
ywaj
ą
do treningu modeli ogromnych zbiorów wypowiedzi.
Do uczenia słu
Ŝ
y algorytm maksymalizacji warto
ś
ci
oczekiwanej (expectation-maximization, EM).
Algorytm ten gwarantuje znaczn
ą
popraw
ę
jako
ś
ci modeli
w porównaniu z modelami nie uczonymi.
Systemy rozpoznawania mowy s
ą
rozwijane intensywnie,
zwłaszcza w ostatniej dekadzie, nie osi
ą
gn
ę
ły jednak jeszcze
zadowalaj
ą
cej skuteczno
ś
ci.
Niezawodno
ść
systemów rozpoznawania mowy zale
Ŝ
y
od warunków akustycznych i sposobu wypowiedzi.
Wypowied
ź
jednej osoby, zło
Ŝ
ona z pojedy
ń
czych słów z
niewielkiego słownika, odbywaj
ą
ca si
ę
w dobrych warunkach
akustycznych, bez du
Ŝ
ych zakłóce
ń
, rozpoznawana jest
z dokładno
ś
ci
ą
95-99%.
15.6. Rozpoznawanie mowy
© F.A. Dul 2007
z dokładno
ś
ci
ą
95-99%.
W przypadku dowolnych wypowiedzi wielu osób typowa
dokładno
ść
rozpoznania wynosi 60-80%, nawet w dobrych
warunkach akustycznych.
Gdy warunki akustyczne s
ą
złe, dokładno
ść
jest mniejsza.
Niektóre systemy rozpoznawania mowy:
• w medycznych systemach diagnostycznych,
• w pakiecie Microsft Office,
• w telefonii komórkowej, bankowo
ś
ci, itp.
Wnioskowanie stochastyczne dynamiczne
Metody dynamicznego wnioskowania stochastyczne-
nego stanowi
ą
wa
Ŝ
ne narz
ę
dzie analizy
rzeczywisto
ś
ci.
Filtr Kalmana umo
Ŝ
liwił realizacj
ę
lotów na Ksi
ęŜ
yc
i jest powszechnie u
Ŝ
ywany w nawigacji, sterowaniu
oraz wielu innych dziedzinach.
Dynamiczne sieci Bayesa pozwalaj
ą
modelowa
ć
©
F.A. Dul 2007
Dynamiczne sieci Bayesa pozwalaj
ą
modelowa
ć
zło
Ŝ
one zjawiska stochastyczne.
Rozpoznawanie mowy jest wa
Ŝ
nym zagadnieniem
komunikacji człowiek-maszyna.
Podsumowanie
• Zmiany stanu
ś
wiata w czasie mog
ą
by
ć
opisane zmiennymi
losowymi zale
Ŝ
nymi od czasu.
• Modele procesów Markowa pozwalaj
ą
zwi
ęź
le modelowa
ć
stacjonarne procesy stochastyczne.
• Stochastyczny model dynamiczny składa si
ę
z modelu
przej
ś
cia i modelu obserwacji.
• Głównymi zadaniami wnioskowania stochastycznego
w czasie s
ą
: filtracja, predykcja, wygładzanie oraz
wyznaczanie najbardziej wiarygodnego wyja
ś
nienia.
© F.A. Dul 2007
wyznaczanie najbardziej wiarygodnego wyja
ś
nienia.
• Podstawowymi modelami dynamicznymi s
ą
sieci Bayesa
oraz ich szczególne przypadki: ukryte modele Markowa
oraz filtr Kalmana.
• Filtr Kalmana stanowi podstawowe narz
ę
dzie wnioskowania
stochastycznego dla układów dynamicznych.
• Zastosowanie Filtrów Kalmana jest bardzo szerokie:
nawigacja, sterowanie, uczenie, rozpoznawanie obrazów,…
• Rozpoznawanie mowy jest wa
Ŝ
nym zadaniem wnioskowania
stochastycznego.