WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

15. WNIOSKOWANIE

PROBABILISTYCZNE

EWOLUCYJNE

EWOLUCYJNE

© F.A. Dul 2007

Wnioskowanie probabilistyczne ewolucyjne

Poka

ż

emy,

ż

e agent wnioskuj

ą

cy

probabilistycznie mo

ż

e mimo

niepewno

ś

ci zrozumie

ć

, co działo si

ę

w przeszło

ś

ci, wła

ś

ciwie zinterpretowa

ć

w przeszło

ś

ci, wła

ś

ciwie zinterpretowa

ć

tera

ź

niejszo

ść

, a nawet przewidzie

ć

przyszło

ść

.

© F.A. Dul 2007

• Niepewno

ść

i czas

• Wnioskowanie w modelach czasowych

• Ukryte modele Markowa

• Filtracja Kalmana

• Dynamiczne sieci Bayesa

•

Zastosowanie - Rozpoznawanie mowy

Plan rozdziału

© F.A. Dul 2007

15.1. Niepewno

ść

i czas

Ś

wiat jest niepewny i zmienia si

ę

w czasie.

Opis probabilistyczny zjawisk zmieniaj

ą

cych si

ę

w czasie

polega na wyznaczeniu w ka

ż

dej chwili czasu zmiennych

losowych, z których pewne s

ą

obserwowalne, a inne – nie:

• X

t

–

zmienne stanu

, nieobserwowane,

• E

t

–

zmienne obserwowanle

(evidence variables).

Zbiór warto

ś

ci

E

t

= e

t

w chwili

t

okre

ś

la zmienne obserwowalne.

Procesy stacjonarne

© F.A. Dul 2007

Procesy stacjonarne

Procesy stacjonarne

to takie, w których rozkłady g

ę

sto

ś

ci

prawdopodobie

ń

stwa zmiennych losowych

X

nie zmieniaj

ą

si

ę

wraz z czasem.

Parametry procesu stacjonarnego, takie jak warto

ść

ś

rednia

m

X

i wariancja

W

X

nie zale

żą

od czasu.

x(t)

t

m

X

= 0

W

X

= const

15.1. Niepewno

ść

i czas

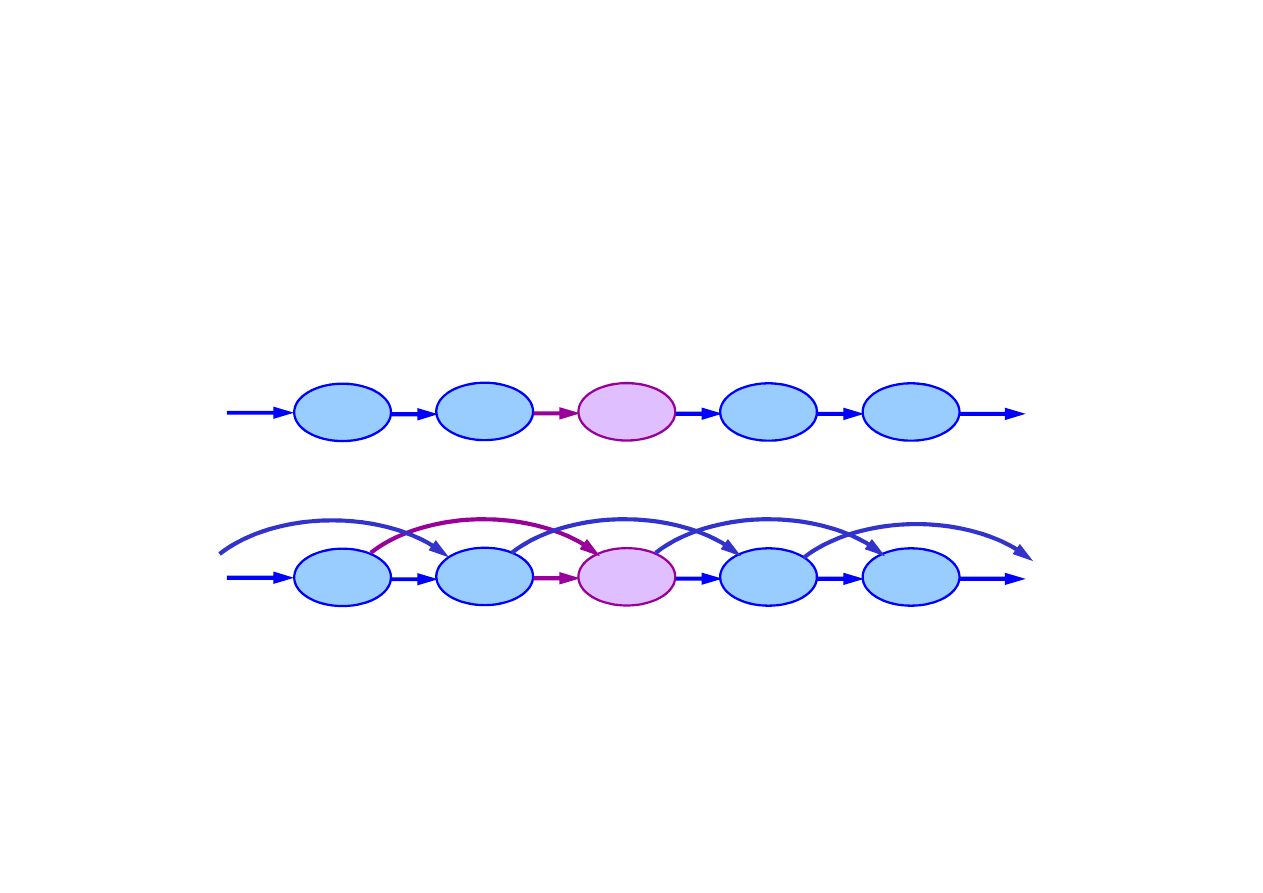
Procesy Markowa

Zało

ż

enie Markowa

– stan bie

żą

cy zale

ż

y tylko od sko

ń

czonej

liczby stanów poprzednich.

Proces (ła

ń

cuch) Markowa

pierwszego rz

ę

du – taki w którym

stan bie

żą

cy zale

ż

y tylko od stanu poprzedniego i nie zale

ż

y

od innych stanów wcze

ś

niejszych.

Sie

ć

Bayesa dla procesu Markowa pierwszego rz

ę

du

X

t-1

X

t

X

t+1

X

t+2

X

t-2

© F.A. Dul 2007

)

|

(

)

|

(

1

1

:

0

−

−

=

∀

t

t

t

t

t

X

X

P

X

X

P

Ewolucja stanu w procesie Markowa jest opisana całkowicie
rozkładem warunkowym

P

(

X

t

|

X

t-1

), który jest nazywany

modelem przej

ś

cia

.

Sie

ć

Bayesa dla procesu Markowa drugiego rz

ę

du

X

t-1

X

t

X

t+1

X

t+2

X

t-2

Prawdopodobie

ń

stwo warunkowe dla ła

ń

cucha Markowa

15.1. Niepewno

ść

i czas

)

|

(

)

,

|

(

1

:

0

:

0

t

t

t

t

t

X

E

P

E

X

E

P

=

−

Rozkład warunkowy

P

(

E

t

|

X

t

) nazywany jest

modelem

czujników

lub

modelem obserwacji

.

Zało

ż

enie dla procesu Markowa: zmienne zaobserwowane

E

t

zale

żą

tylko od stanu bie

żą

cego

Rozkład ł

ą

czny prawdopodobie

ń

stwa zmiennych stanu

i obserwowalnych przy zało

ż

eniu,

ż

e proces jest procesem

Markowa pierwszego rz

ę

du

© F.A. Dul 2007

Markowa pierwszego rz

ę

du

∏

=

−

=

t

i

i

i

i

i

t

t

1

1

1

0

1

0

)

|

(

)

|

(

)

,...,

,

,

,...,

,

(

X

E

P

X

X

P

E

E

E

X

X

X

P

Proces Markowa pierwszego rz

ę

du jest jedynie przybli

ż

eniem

procesów rzeczywistych.
Lepsze przybli

ż

enia uzyskuje si

ę

stosuj

ą

c procesy Markowa

wy

ż

szych rz

ę

dów, ale ich analiza jest bardziej zło

ż

ona.

15.2. Wnioskowanie w modelach czasowych

Główne zadania wnioskowania probabilistycznego w czasie:

• Filtracja

(monitorowanie)

Wyznaczenie stanu wiarygodnego - rozkładu a posteriori

stanu bie

żą

cego

na podstawie wszystkich obserwacji

do chwili bie

żą

cej,

P

(

X

t

|

e

1:t

).

• Predykcja

(prognozowanie)

Wyznaczenie rozkładu a posteriori

stanu przyszłego

na podstawie wszystkich obserwacji do chwili bie

żą

cej,

© F.A. Dul 2007

na podstawie wszystkich obserwacji do chwili bie

żą

cej,

P

(

X

t+k

|

e

1:t

),

k > 0

.

• Wygładzanie

Wyznaczenie rozkładu a posteriori

stanu przeszłego

na podstawie wszystkich obserwacji do chwili bie

żą

cej,

P

(

X

k

|

e

1:t

),

1

≤

k < t

.

• Najbardziej wiarygodne wyja

ś

nienie

Wyznaczenie stanów najbardziej wiarygodne generuj

ą

cych

dane obserwacje,

.

)

|

(

max

arg

:

1

:

1

:

1

t

t

t

e

x

P

x

15.2. Wnioskowanie w modelach czasowych

Filtracja
Je

ż

eli znane s

ą

wyniki filtracji do chwili

t - 1,

to rozkład

prawdopodobie

ń

stwa zmiennej

X

t

mo

ż

na wyznaczy

ć

na podstawie obserwacji

e

t

, za pomoc

ą

estymacji

∑

−

−

−

−

=

1

)

|

(

)

|

(

)

|

(

)

|

(

1

:

1

1

1

:

1

t

t

t

t

t

t

t

t

t

P

x

e

x

x

X

P

X

e

P

e

X

P

α

Funkcja

f

1:t

=

P

(

X

t

|

e

1:t

) opisuje propagacj

ę

informacji –

„wiadomo

ść

” – wzdłu

ż

ci

ą

gu zmiennych stanu i obserwacji.

© F.A. Dul 2007

)

|

(

1

:

1

:

1

t

t

t

e

f

f

−

=

Forward

α

„wiadomo

ść

” – wzdłu

ż

ci

ą

gu zmiennych stanu i obserwacji.

Rozkład prawdopodobie

ń

stwa zmiennej stanu przy danych

obserwacjach mo

ż

na zapisa

ć

w postaci rekurencyjnej

15.2. Wnioskowanie w modelach czasowych

Predykcja
Predykcja mo

ż

e by

ć

uwa

ż

ana za filtracj

ę

w której pomini

ę

to

k ostatnich obserwacji,

e

t-k:t.

Rozkłady prawdopodobie

ń

stw zmiennych

X

t+k+1

mo

ż

na

wyznaczy

ć

na podstawie obserwacji

e

t

, za pomoc

ą

estymacji

∑

+

+

+

+

+

+

+

=

k

t

t

k

t

k

t

k

t

t

k

t

P

x

e

x

x

X

P

e

X

P

)

|

(

)

|

(

)

|

(

:

1

1

:

1

1

Wiarygodno

ść

© F.A. Dul 2007

∑

=

=

t

t

t

t

t

P

L

x

x

e

)

(

)

(

:

1

:

1

:

1

l

Wiarygodno

ść

Wiarygodno

ść

ci

ą

gu obserwacji

P(e

1:t

)

jest wielko

ś

ci

ą

u

ż

yteczn

ą

w wielu zastosowaniach.

Funkcja

ℓ

l

1:t

=

P

(

X

t

,

e

1:t

) opisuj

ą

ca „wiadomo

ść

” – propagacj

ę

wiarygodno

ś

ci mo

ż

e by

ć

przedstawione w postaci

rekurencyjnej

)

|

(

1

:

1

1

:

1

+

+

=

t

t

t

e

l

l

Forward

α

Wiarygodno

ść

wyra

ż

a si

ę

wzorem

15.2. Wnioskowanie w modelach czasowych

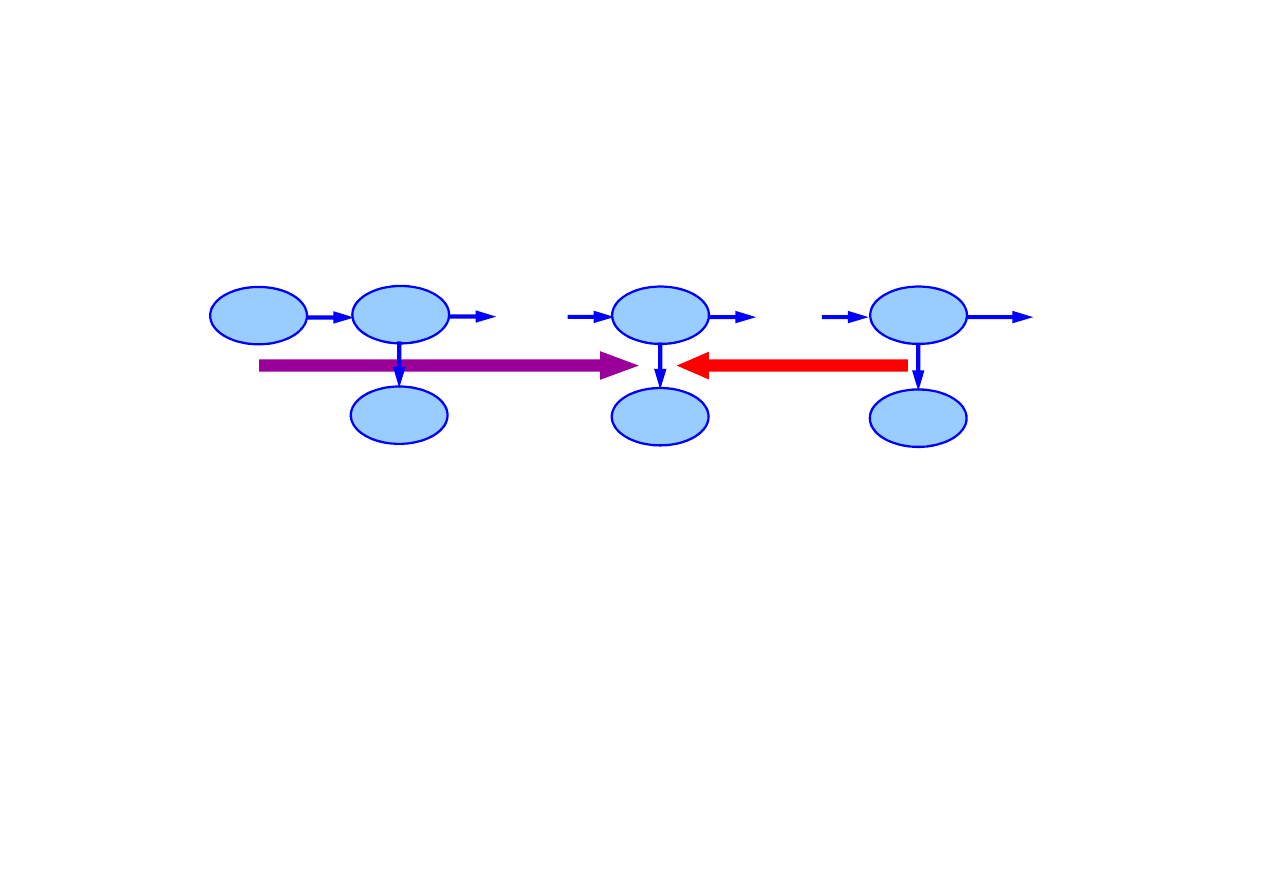
Wygładzanie
Wygładzanie polega na wyznaczeniu rozkładu a posteriori
stanów przeszłych

1

≤

k < t

na podstawie wszystkich

obserwacji do chwili bie

żą

cej,

P

(

X

k

|

e

1:t

),.

X

1

X

k

X

t

X

0

E

1

E

k

E

t

. . .

. . .

© F.A. Dul 2007

t

k

k

t

k

:

1

:

1

:

1

)

|

(

+

=

b

f

e

X

P

α

1

b

e

b

b

=

=

+

+

+

+

t

t

t

k

t

k

t

k

:

1

:

1

:

2

:

1

,

)

,

(

Backward

oraz

wstecz

, od k+1 do t

Rozkłady prawdopodobie

ń

stw wygładzanych zmiennych

X

k

dane s

ą

wzorem rekurencyjnym

Wygładzanie przebiega w dwu etapach:

w przód

od 1 do k

)

|

(

1

:

1

:

1

k

k

k

e

f

f

−

=

Forward

15.2. Wnioskowanie w modelach czasowych

Najbardziej wiarygodne wyja

ś

nienie

Rozkłady prawdopodobie

ń

stw kolejnych obserwacji pozwalaj

ą

wyznaczy

ć

wiarygodno

ść

kolejnych stanów.

Jednak wiarygodno

ść

ci

ą

gu stanów nie jest równa wiarygod-

no

ś

ci stanów oddzielnych, gdy

ż

s

ą

one na ogół zale

ż

ne.

Wiarygodno

ść

ci

ą

gu stanów polega na wyznaczeniu ł

ą

cznego

rozkładu prawdopodobie

ń

stwa dla wszystkich chwil

k = 1,...,t

.

Istnieje zale

ż

no

ść

rekurencyjna pomi

ę

dzy najbardziej

wiarygodnymi

ś

cie

ż

kami do stanów

x

t+1

i

x

t

© F.A. Dul 2007

)

)

|

,

...

(

max

)

|

(

(

max

)

|

(

:

1

1

1

...

1

1

1

1

1

t

t

t

t

t

t

t

P

t

t

e

x

x

x

x

X

P

X

e

P

x

x

x

−

+

+

+

−

=

α

Zale

ż

no

ść

ta jest identyczna z zale

ż

no

ś

ci

ą

dla filtracji

po zast

ą

pieniu funkcji

f

1:t

=

P

(

X

t

|

e

1:t

) funkcja

Wyznaczenie najbardziej wiarygodnego ci

ą

gu stanów przy

pomocy

algorytmu Viterbiego

przebiega tak, jak przy filtracji.

wiarygodnymi

ś

cie

ż

kami do stanów

x

t+1

i

x

t

=

+

+

)

|

,

...

(

max

1

:

1

1

1

...

1

t

t

t

t

e

X

x

x

P

x

x

)

|

,

...

(

max

:

1

1

1

...

:

1

1

1

t

t

t

t

t

e

X

x

x

P

m

x

x

−

−

=

Przykład
Stra

ż

nik tajnych instalacji ukrytych pod ziemi

ą

mo

ż

e

wnioskowa

ć

o pogodzie wył

ą

cznie na podstawie obserwacji

czy szef przychodzi rano z parasolem, czy te

ż

bez.

Dla ka

ż

dego dnia

t

zbiór zmiennych obserwowalnych

E

t

zawiera jedn

ą

zmienn

ą

U

t

okre

ś

laj

ą

c

ą

obserwacj

ę

parasola,

za

ś

zbiór zmiennych stanu

X

t

zawiera jedn

ą

zmienn

ą

R

t

okre

ś

laj

ą

c

ą

, czy pada deszcz.

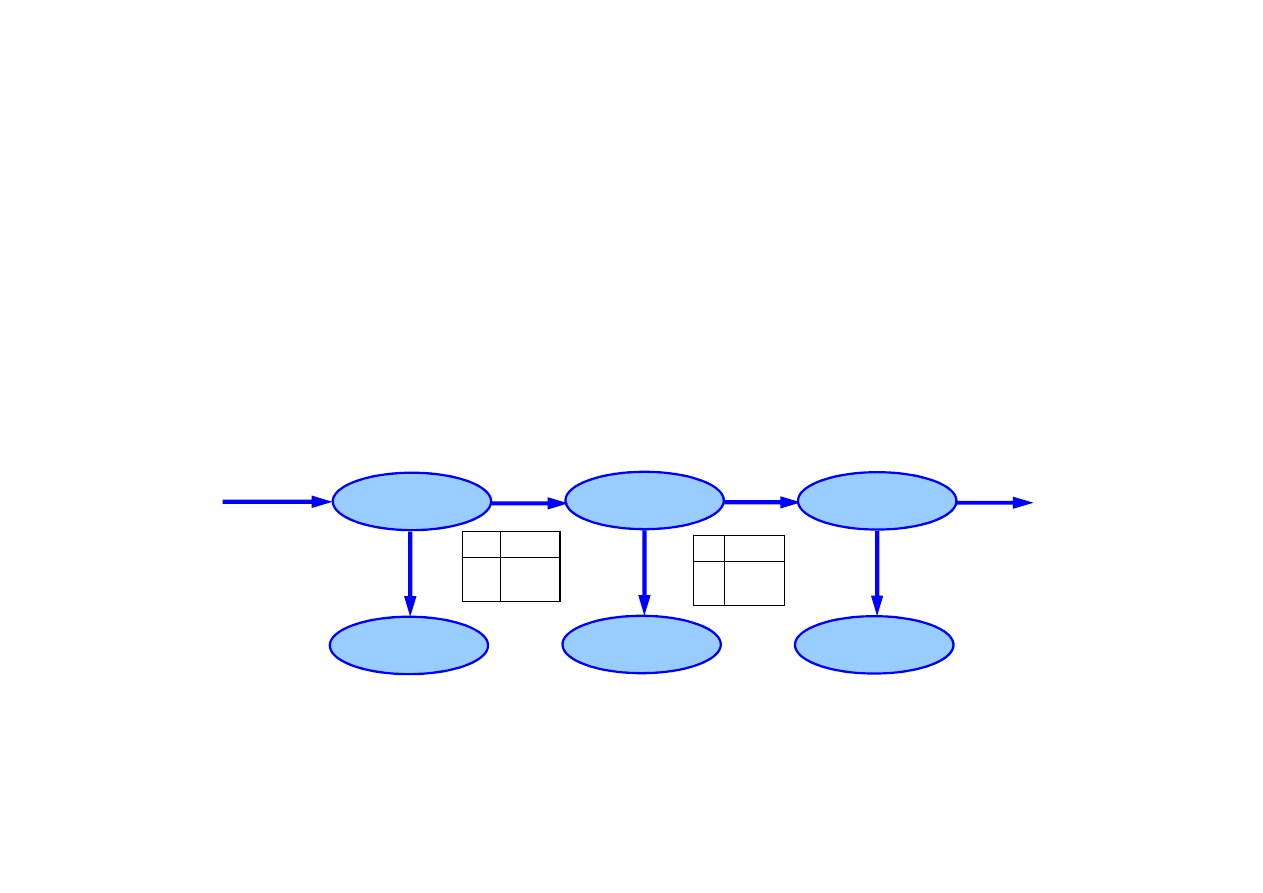
15.2. Wnioskowanie w modelach czasowych

Sie

ć

Bayesa oraz rozkład prawdopodobie

ń

stw warunkowych

© F.A. Dul 2007

Deszcz

t

Deszcz

t+1

Deszcz

t-1

R

t

P(U

t

)

t

f

0.90
0.20

Parasol

t

Parasol

t+1

Parasol

t-1

R

t-1

P(U

t

)

t

f

0.70
0.30

Sie

ć

Bayesa oraz rozkład prawdopodobie

ń

stw warunkowych

15.3. Ukryte modele Markowa

Ukryte modele Markowa

(Hidden Markov Models, HMM)

s

ą

to modele probabilistyczne w których stan procesu opisuje

pojedy

ń

cza

dyskretna zmienna losowa

X

t

.

Ukryty model Markowa posiada proste reprezentacje modeli
przej

ś

cia, obserwacji oraz funkcji propagacji informacji.

Je

ż

eli zmienna stanu

X

t

ma S warto

ś

ci, to model przej

ś

cia

T = P

(

X

t

|

X

t 1

) ma posta

ć

macierzy S

×

S której elementy

)

|

(

1

i

X

j

X

P

t

t

ij

=

=

=

−

T

© F.A. Dul 2007

1

t

t

ij

−

opisuj

ą

prawdopodobie

ń

stwo przej

ś

cia ze stanu i do stanu j.

Model obserwacji ma posta

ć

macierzy diagonalnej

O

t

której

elementy s

ą

równe

)

|

(

i

X

e

P

t

t

ii

=

=

O

Funkcje propagacji informacji w przód i wstecz maj

ą

postacie

wektorów

,

:

1

1

1

:

1

t

T

t

t

f

T

O

f

+

+

=

α

t

k

k

t

k

:

2

2

:

1

+

+

+

=

b

O

T

b

Ukryte modele Markowa umo

ż

liwiaj

ą

zbudowanie efektywnych

algorytmów filtracji i wygładzania, w tym równie

ż

on-line.

15.4. Filtracja Kalmana

W technice cz

ę

sto spotyka si

ę

zagadnienia dynamiczne

obarczone niepewno

ś

ci

ą

modelu lub obserwacji, np:

– wyznaczanie trajektorii ciał niebieskich

na podstawie niedokładnych obserwacji;

–

ś

ledzenie ruchu obiektów przy silnie

zakłóconych obserwacjach;

– nawigacja pojazdami

Program “Apollo” - lot na Ksi

ęż

yc!

Rudolph E. Kalman

© F.A. Dul 2007

S

ą

to problemy estymacji stanu obiektów (poło

ż

enia i pr

ę

dko-

ś

ci) na podstawie zakłóconych (zaszumionch) obserwacji.

Do analizy takich dynamicznych zagadnie

ń

stochastycznych

u

ż

ywa si

ę

powszechnie

filtracji Kalmana

.

Filtracja Kalmana jest to wnioskowanie w probabilistycznym
modelu dynamicznym zło

ż

onym z losowego modelu zjawiska

fizycznego i losowego modelu obserwacji (pomiarów).
Filtracja Kalmana jest szczególnie przydatna w mechanice.

15.4. Filtracja Kalmana

Idea filtracji Kalmana
Filtracja Kalmana ma na celu oszacowanie przyszłego stanu
układu x(t

)

na podstawie modelu układu, znanego stanu

poprzedniego x(t–

∆

t

)

oraz aktualnej obserwacji z(t

)

.

Filtracja Kalmana ma posta

ć

liniowej kombinacji wa

ż

onej:

• predykcji stanu x(t

)

na podstawie (zaszumionego) modelu

i stanu poprzedniego x(t–

∆

t

)

,

• niepewnej (zaszumionej) obserwacji z(t),

)

(

)

(

~

)

(

t

a

t

t

a

t

z

x

x

+

∆

−

© F.A. Dul 2007

• Je

ż

eli obserwacje s

ą

niepewne (du

ż

e warto

ś

ci wariancji

obserwacji), to estymacja stanu przyszłego zawiera
wi

ę

cej stanu, a

x

> a

z

.

• Je

ż

eli predykcja stanu jest bardziej niepewna (du

ż

e

warto

ś

ci wariancji zmiennej stanu), to estymacja stanu

przyszłego zawiera wi

ę

cej obserwacji, a

z

> a

x

;

Filtracja Kalmana pozwala ponadto wyznaczy

ć

wariancje

zmiennych stanu i obserwacji.

)

(

)

(

~

)

(

t

a

t

t

a

t

z

x

z

x

x

+

∆

−

15.4. Filtracja Kalmana

,

)

(

)

(

t

t

t

∆

−

=

x

F

x

Rozkład prawdopodobie

ń

stwa warunkowego dla stanu

w chwili t jest równy

]

))

(

)

((

exp[

)

)(

,

(

1

2

1

µ

x

Q

µ

x

x

Q

µ

−

−

−

=

−

T

N

α

µµµµ

- wektor warto

ś

ci

ś

rednich, Q - macierz kowariancji białego szumu.

Filtracja Kalmana opiera si

ę

na dwóch zało

ż

eniach:

• model obiektu jest liniowy,

• zakłócenia modelu i pomiarów maj

ą

rozkład normalny,

© F.A. Dul 2007

Liniowo

ść

modelu gwarantuje,

ż

e estymacje stanu w kolejnych

chwilach czasu maj

ą

rozkład

normalny.

)

(

)

),

(

(

)

)

(

)

(

|

)

(

)

(

(

t

t

t

N

t

t

t

t

t

t

P

x

Fx

x

X

x

X

σ

∆

−

=

∆

−

=

∆

−

=

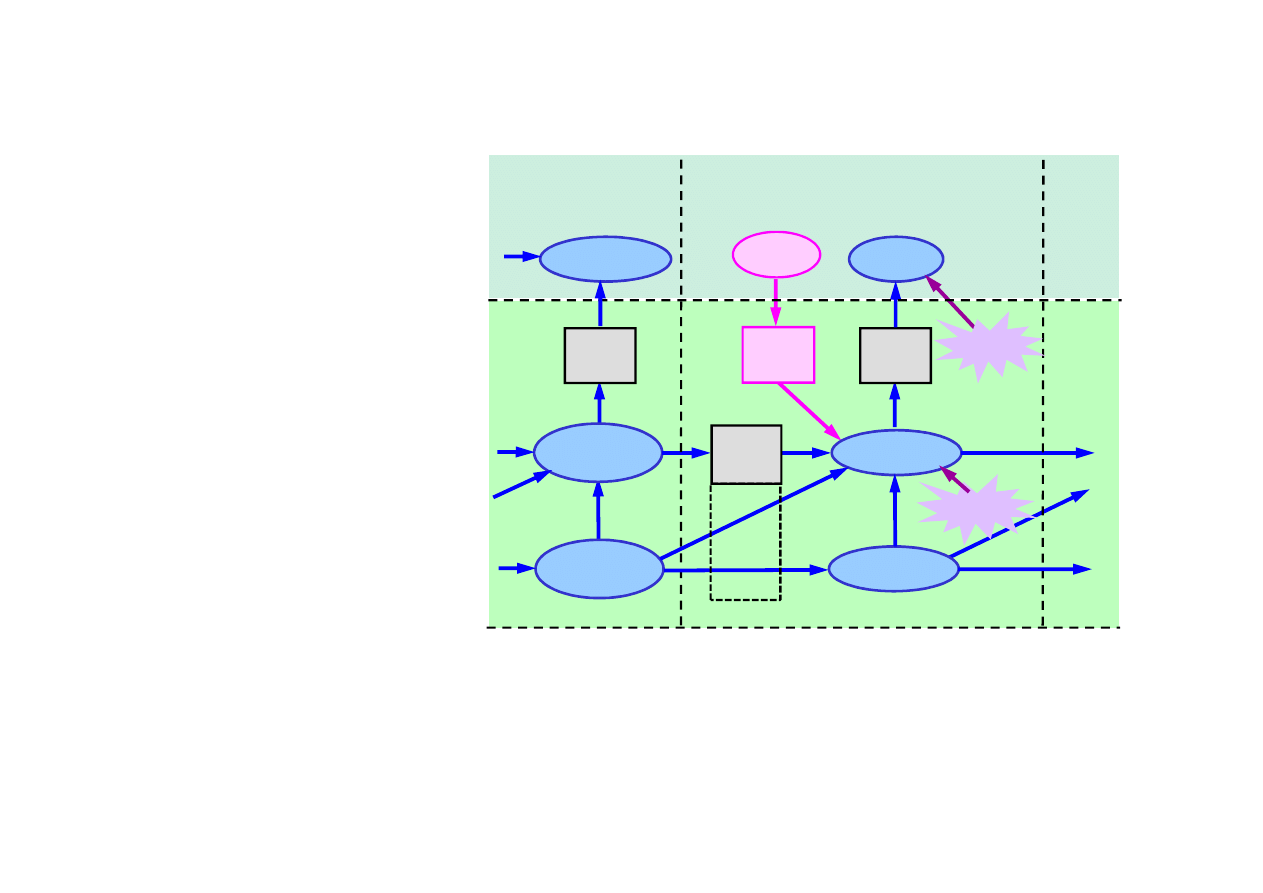
w chwili t jest równy

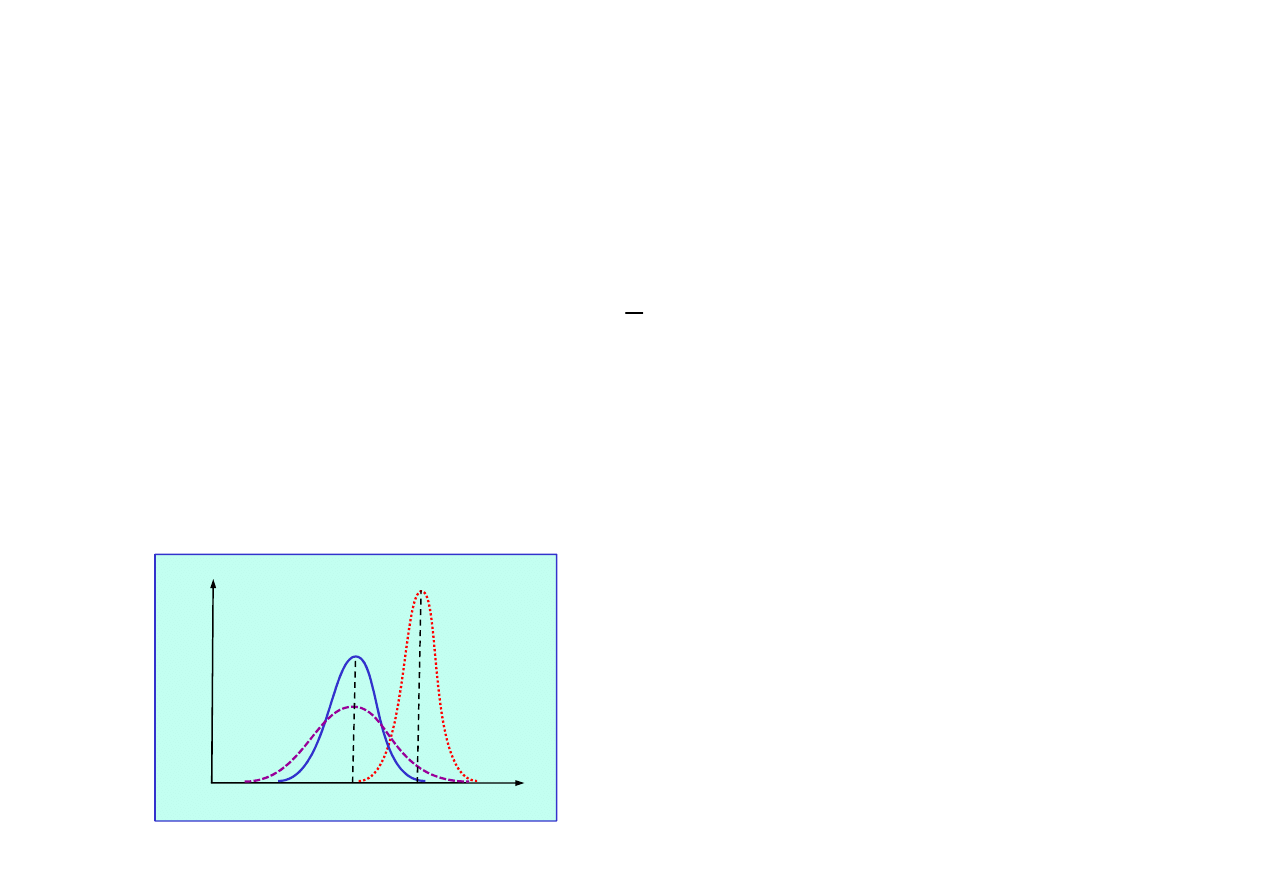
Kolejne predykcje stanu s

ą

spłaszczane przez szumy
pomiarów i modelu.

P(x

0

|z

1

=2,5)

P(x

0

)

P(x

1

)

-5 -2.5 0 2.5 x

5.0

0

0

.2

0

.4

0

.6

P

(x

)

15.4. Filtracja Kalmana

Sie

ć

Bayesa dla filtru Kalmana

Cz

ęść

widoczna:

B

)

(t

U

Cz

ęść

ukryta:

)

(

t

t

∆

−

X

)

(t

X

F

H

)

(t

Z

t -

∆

t

(k – 1)

t +

∆

t

(k+1)

t

(k)

)

(

t

R

w

)

(

t

t

∆

−

Z

H

• obserwacje Z(t),
• sterowanie U(t).

• stan X(t),
• zakłócenia

© F.A. Dul 2007

Modele układu i obserwacji maj

ą

posta

ć

)

(

)

(

)

(

t

t

t

t

Q

n

Fx

x

+

∆

−

=

)

(

)

(

)

(

t

t

t

R

w

Hx

z

+

=

+ Bu(t)

)

(

t

t

∆

−

X

)

(t

X

)

(

t

Q

n

F

)

(t

X

&

)

(

t

t

∆

−

X

&

• zakłócenia

stanu n(Q

t

),

• zakłócenia

obserwacji w(R

t

).

15.4. Filtracja Kalmana

Dla filtracja Kalmana ze stałym krokiem czasowym

t

k

t

k

∆

=

)

(

k

k

k

R

w

Hx

z

+

=

Zakłócenia stanu i pomiarów s

ą

opisane rozkładami

normalnymi Gaussa

1

x

Q

x

x

Q

0

Q

n

−

−

=

=

T

α

modele układu i obserwacji maj

ą

posta

ć

k

k

k

k

Bu

Q

n

Fx

x

+

+

=

−

)

(

1

© F.A. Dul 2007

k

k |

ˆx

Filtr Kalmana u

ż

ywa nast

ę

puj

ą

cych zmiennych roboczych:

- estymacja stanu w chwili k.

k

k |

P

- estymacja macierzy kowariancji bł

ę

du stanu,

]

)

(

exp[

)

)(

,

(

)

(

1

2

1

x

Q

x

x

Q

0

Q

n

−

−

=

=

k

T

n

k

k

N

α

]

)

(

exp[

)

)(

,

(

)

(

1

2

1

x

R

x

x

R

0

R

w

−

−

=

=

k

T

w

k

k

N

α

k

k|

S

- estymacja macierzy kowariancji bł

ę

du pomiaru,

k

K

- macierz wzmocnienia optymalnego.

15.4. Filtracja Kalmana

Filtr Kalmana wyznacza estymacje stanu minimalizuj

ą

ce

warto

ść

oczekiwan

ą

E kwadratu bł

ę

du

min

]

)

ˆ

[(

2

|

→

−

k

k

k

E

x

x

Jest to równowa

ż

ne minimalizacji

ś

ladu macierzy kowariancji

bł

ę

du P

k|k

wzgl

ę

dem macierzy wzmocnienia optymalnego K

k

0

2

)

(

2

)

(

tr

1

|

|

=

+

−

=

∂

∂

−

k

k

T

k

k

k

k

k

S

K

P

H

P

1

1

|

−

−

=

k

T

k

k

k

k

S

H

P

K

T

k

k

k

T

k

T

k

k

k

k

k

k

k

k

k

k

k

K

S

K

K

H

P

P

H

K

P

P

+

−

−

=

−

−

−

1

|

1

|

1

|

|

© F.A. Dul 2007

0

2

)

(

2

1

|

=

+

−

=

∂

−

k

k

k

k

k

k

S

K

P

H

K

1

|

−

=

k

k

k

k

k

S

H

P

K

Własno

ś

ci estymat otrzymanych za pomoc

ą

filtru Kalmana

0

]

ˆ

[

]

ˆ

[

1

|

|

=

−

=

−

−

k

k

k

k

k

k

E

E

x

x

x

x

0

]

[

=

k

E e

)

ˆ

cov(

|

|

k

k

k

k

k

x

x

P

−

=

)

ˆ

cov(

1

|

1

|

−

−

−

=

k

k

k

k

k

x

x

P

)

cov(

k

k

e

S

=

15.4. Filtracja Kalmana

k

T

k

k

k

k

k

k

Q

F

P

F

P

+

=

−

−

−

1

|

1

1

|

k

k

k

k

k

k

k

u

B

x

F

x

+

=

−

−

−

1

|

1

1

|

ˆ

ˆ

(predykcja stanu)

(predykcja macierzy kowariancji)

Filtracja Kalmana składa si

ę

z dwóch faz:

• predykcji

, która polega na wyznaczeniu estymat stanu

i macierzy kowariancji bł

ę

du na podstawie ich warto

ś

ci

w chwili poprzedniej.

• aktualizacji

, w której wykorzystuje si

ę

pomiary w chwili

bie

żą

cej do poprawienia estymat uzyskanych w predykcji

© F.A. Dul 2007

k

T

k

k

k

k

k

R

H

P

H

S

+

=

−

1

|

1

|

ˆ

−

−

=

k

k

k

k

k

x

H

z

e

1

|

|

)

(

−

−

=

k

k

k

k

k

k

P

H

K

I

P

k

k

k

k

k

k

e

K

x

x

+

=

−

1

|

|

ˆ

ˆ

(aktualizacja bł

ę

du pomiaru)

(aktualizacja kowariancji bł

ę

du pomiaru)

(aktualizacja estymacji stanu)

(aktualizacja kowariancji bł

ę

du stanu)

1

1

|

−

−

=

k

T

k

k

k

k

S

H

P

K

(macierz wzmocnienia optymalnego)

bie

żą

cej do poprawienia estymat uzyskanych w predykcji

w celu otrzymania dokładniejszych warto

ś

ci stanu

i macierzy kowariancji bł

ę

du.

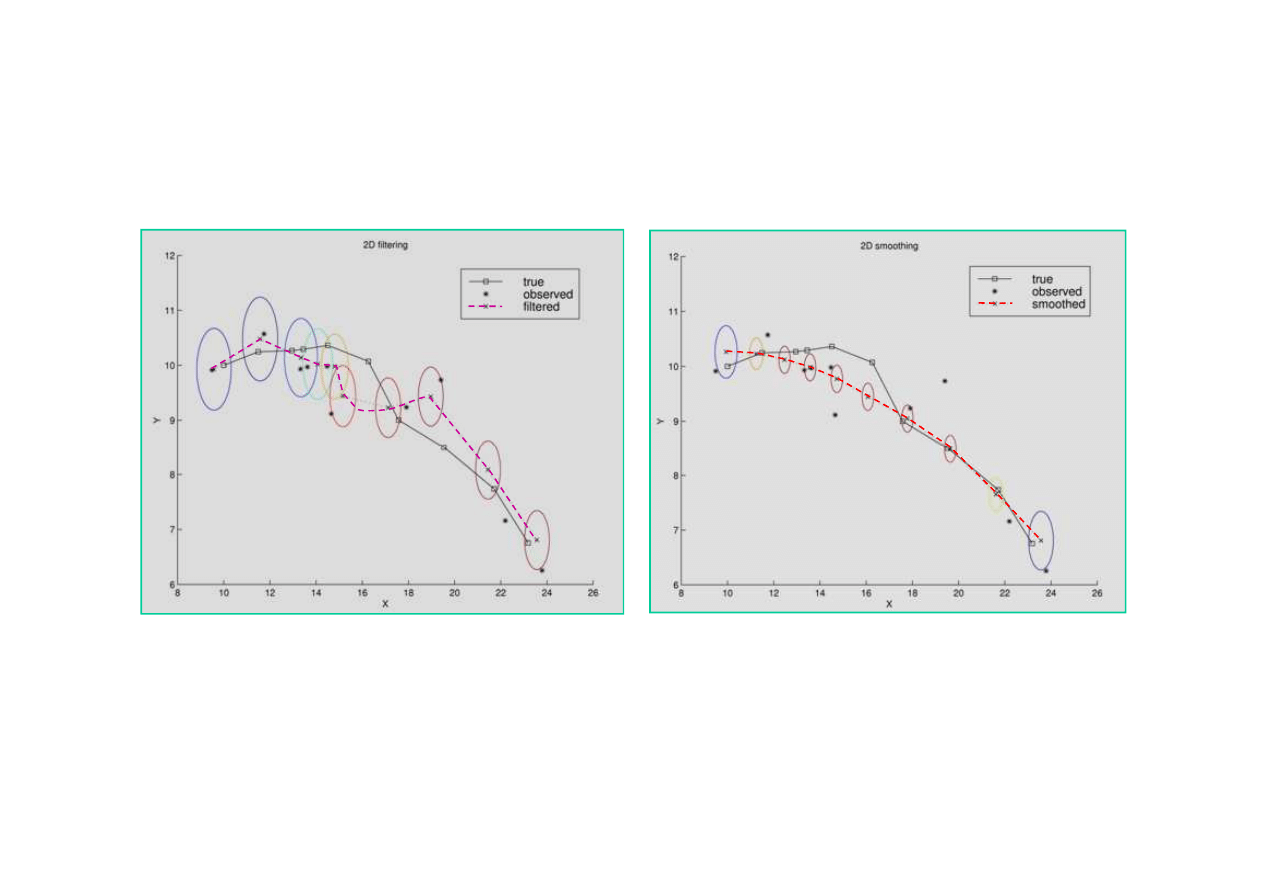
15.4. Filtracja Kalmana

Przykład
Zastosowanie filtracji Kalmana do

ś

ledzenia ruchu obiektu

w płaszczy

ź

nie X-Y. Stan obiektu - X(t) = [ X, Y, V

X

,V

Y

]

T

.

© F.A. Dul 2007

Wygładzanie

Filtracja

Filtracja Kalmana zapewnia
poprawne

ś

ledzenie ruchu.

Wariancja bł

ę

dów pomiaru

szybko si

ę

stabilizuje.

Filtracja Kalmana zapewnia
wygładzenie toru i znaczn

ą

redukcj

ę

wariancji bł

ę

dów

pomiaru.

15.4. Filtracja Kalmana

Przykład filtracji Kalmana

Sterowanie pojazdem

(Dan Simon,

www.embedded.com

)

k

k

k

k

dt

dt

dt

n

u

x

x

+













+













=

−

2

2

1

1

1

0

1

[

]

k

k

k

w

x

z

+

=

0

1

Nale

ż

y wyznaczy

ć

estymacje poło

ż

enia i pr

ę

dko

ś

ci pojazdu

opisanego modelem

© F.A. Dul 2007

Poło

ż

enie pojazdu jest mierzone 10 razy na sekund

ę

, dt = 0.1,

z dokładno

ś

ci

ą

σ

z

= 3 m.

Przy

ś

pieszenie sterowania jest stałe i równe a = 0.33 m/s

2

.

Szum przy

ś

pieszenia wynosi

σ

a

= 0.07 m/s

2

.

Ze wzgl

ę

du na du

ż

y szum pomiarowy u

ż

ycie filtru Kalmana

powinno znacznie poprawi

ć

estymacj

ę

poło

ż

enia w stosunku

do warto

ś

ci zmierzonych.

gdzie:

x(t) = [x,v]

T

– stan pojazdu,

u(t) = [a]

– sterowanie (stałe przy

ś

pieszenie).

15.4. Filtracja Kalmana

k

k

k

k

n

u

x

x

+













+













=

−

1

.

0

005

.

0

1

0

1

.

0

1

1

Model ruchu pojazdu dla przyj

ę

tych warto

ś

ci

Macierz kowariancji bł

ę

du stanu jest równa

[

]

=













=













=

=

]

[

]

[

]

[

2

2

v

v

v

v

v

x

x

x

E

x

x

E

E

T

k

xx

Q

=









⋅

⋅

⋅

⋅

=

2

2

1

2

2

2

2

1

)

)

((

)

(

)

(

a

a

a

dt

dt

dt

σ

σ

σ

© F.A. Dul 2007

=









⋅

⋅

⋅

⋅

=

2

2

2

2

1

)

(

)

(

)

)

((

a

a

a

dt

dt

dt

σ

σ

σ

[ ] [ ]

[ ]

9

3

]

[

2

2

=

=

=

=

z

T

k

E

σ

zz

R

Macierz kowariancji bł

ę

du obserwacji jest równa

=













⋅

⋅

⋅

⋅

⋅

⋅

=

2

2

2

2

2

2

)

07

.

0

(

)

1

.

0

(

)

07

.

0

(

)

1

.

0

(

)

005

.

0

(

)

07

.

0

(

)

1

.

0

(

)

005

.

0

(

)

07

.

0

(

)

005

.

0

(













⋅

⋅

⋅

⋅

=

−

−

−

−

5

6

6

7

10

90

.

4

10

45

.

2

10

45

.

2

10

225

.

1

P

o

ło

ż

e

n

ie

(f

t)

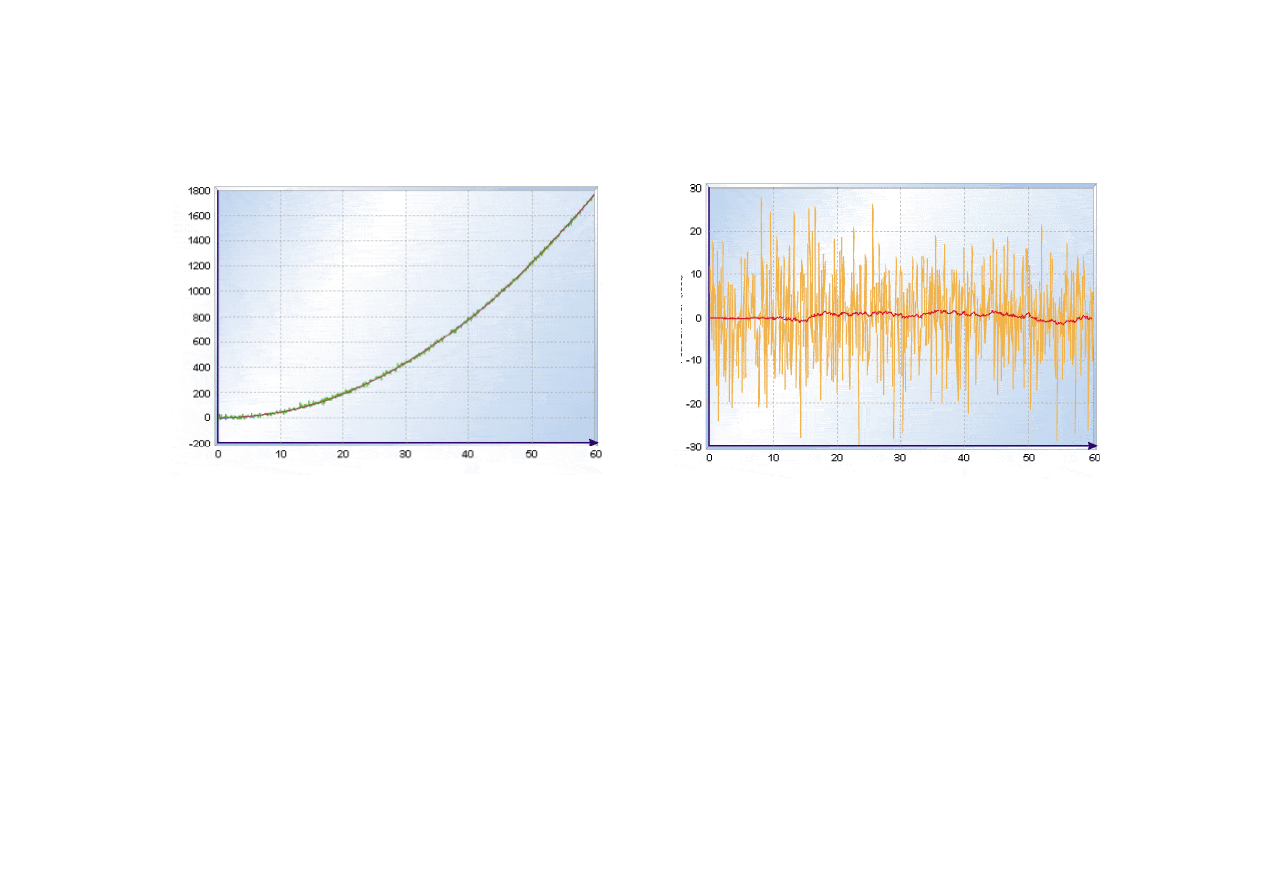
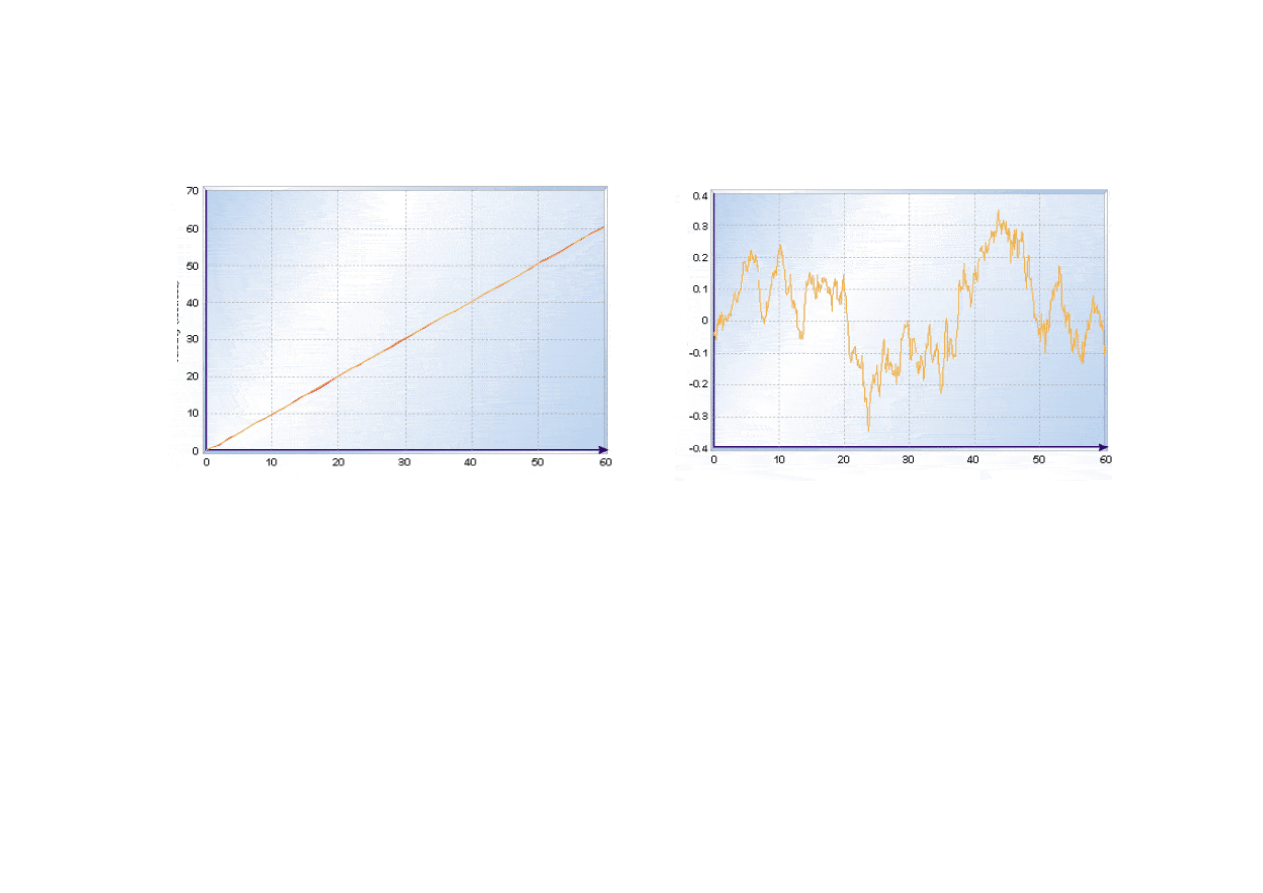
15.4. Filtracja Kalmana

Poło

ż

enie dokładne, zmierzone i estymacja poło

ż

enia

B

ł

ą

d

p

o

ło

ż

e

n

ia

(

ft

)

Czas (s)

© F.A. Dul 2007

Poło

ż

enie dokładne i jego

estymacja

s

ą

bardzo bliskie.

Poło

ż

enie

zmierzone

jest silnie

zaszumione.

Czas (s)

U

ż

ycie filtru Kalmana znacznie (~10 razy) poprawiło

estymacj

ę

poło

ż

enia w stosunku do warto

ś

ci zmierzonych.

Odchylenie standardowe

bł

ę

du

estymacji

poło

ż

enia ~0.7 m.

Odchylenie standardowe

bł

ę

du

pomiaru

poło

ż

enia ~3

÷

10 m.

15.4. Filtracja Kalmana

Pr

ę

dko

ść

dokładna i jej estymacja

P

r

ę

d

k

o

ś

ć

(

ft

/s

)

B

ł

ą

d

p

r

ę

d

k

o

ś

c

i

(f

t/

s

)

© F.A. Dul 2007

Pr

ę

dko

ść

dokładna

oraz jej

estymacja

s

ą

bardzo bliskie

Czas (s)

Wida

ć

tutaj dodatkow

ą

zalet

ę

filtru Kalmana - pozwala on

uzyska

ć

poprawn

ą

estymat

ę

pr

ę

dko

ś

ci

bez konieczno

ś

ci

pomiaru samej pr

ę

dko

ś

ci

.

Czas (s)

Odchylenie standardowe

bł

ę

du pomiaru

pr

ę

dko

ś

ci

~0.35 m/s.

• model obiektu musi by

ć

liniowy,

• bł

ę

dy modelu i pomiarów musz

ą

mie

ć

rozkład normalny

Gaussa.

15.4. Filtracja Kalmana

Ograniczenia klasycznej filtracji Kalmana

Mimo swoich niezaprzeczalnych zalet klasyczny filtr Kalmana
ma dwa powa

ż

ne ograniczenia:

Liniowo

ść

układu i gaussowski rozkład bł

ę

dów s

ą

w praktyce

ograniczeniami istotnymi.
Przykład

Wła

ś

ciwa estymacja poło

ż

enia powinna

umo

ż

liwi

ć

omini

ę

cie drzewa.

© F.A. Dul 2007

Przykład
Estymacja poło

ż

enia lec

ą

cego ptaka przy

zało

ż

eniu rozkładu Gaussa dla bł

ę

dów

modelu lotu sugeruje lot wprost na drzewo.

Wymaga to jednak u

ż

ycia modelu nieliniowego.

Rozszerzony filtr Kalmana

(extended

Kalman filter) pozwala analizowa

ć

modele

nieliniowe o ile nieliniowo

ś

ci nie s

ą

zbyt silne.

• Nawigacja kosmiczna, lotnicza, l

ą

dowa i morska.

• Systemy nawigacji satelitarnej.
• Systemy naprowadzania bezwładno

ś

ciowego.

• Systemy autopilotów.
• Układy

ś

ledzenia radarowego i sonarowego.

• Wyznaczanie trajektorii cz

ą

stek elementarnych.

• Numeryczne prognozowanie pogody.
• Modelowanie cyrkulacji oceanów i atmosfery na podstawie

obrazów satelitarnych.

15.4. Filtracja Kalmana

Zastosowania filtracji Kalmana

obrazów satelitarnych.

• Równoczesna lokalizacja i tworzenie mapy (eksploracja

przez roboty nieznanego

ś

rodowiska).

• Sterowanie procesami produkcyjnymi.
• Nadzór elektrowni atomowych.
• Modelowanie demografii.
• Detekcja radioaktywno

ś

ci ziemskiej.

• Uczenie w logice rozmytej i sieciach neuronowych.
• Ekonomia, w szczególno

ś

ci makroekonomia, ekonometria.

• Rozpoznawanie obrazów.

© F.A. Dul 2007

Filtry Kalmana

Znaczenie filtru Kalmana jest trudne do przecenienia.

Filtr Kalmana umo

ż

liwił realizacj

ę

lotów na Ksi

ęż

yc

i jest powszechnie u

ż

ywany w nawigacji, sterowaniu

oraz wielu innych dziedzinach.

Wynalezienie filtru Kalmana przyczyniło si

ę

w stopniu

zasadniczym do rozwoju powy

ż

szych dziedzin.

©

F.A. Dul 2007

Chocia

ż

filtr Kalmana posiada ograniczenia, to jest

w dalszym ci

ą

gu podstawowym narz

ę

dziem

stochastycznego wnioskowania dynamicznego.

Ograniczenia filtracji Kalmana mo

ż

na omin

ąć

stosuj

ą

c bardziej ogólne

dynamiczne sieci Bayesa

.

15.5. Dynamiczne sieci Bayesa

Dynamiczna sie

ć

Bayesa

(dynamic Bayesian network, DBN)

słu

ż

y do reprezentacji dowolnych dynamicznych modeli

probabilistycznych.

Ka

ż

dy ukryty model Markowa mo

ż

e by

ć

reprezentowany

przez dynamiczn

ą

sie

ć

Bayesa, za

ś

ka

ż

dy HMM mo

ż

e by

ć

przekształcony do postaci DBN.

Ka

ż

dy filtr Kalmana mo

ż

e by

ć

reprezentowany przez

dynamiczn

ą

sie

ć

Bayesa, ale nie an odwrót.

© F.A. Dul 2007

dynamiczn

ą

sie

ć

Bayesa, ale nie an odwrót.

Dynamiczna sie

ć

Bayesa mo

ż

e reprezentowa

ć

zmienne

losowe z wieloma maksimami lokalnymi, czego nie mo

ż

na

osi

ą

gn

ąć

przy pomocy rozkładu Gaussa.

Dynamczne sieci Bayesa

Ukryte modele Markowa

Filtr Kalmana

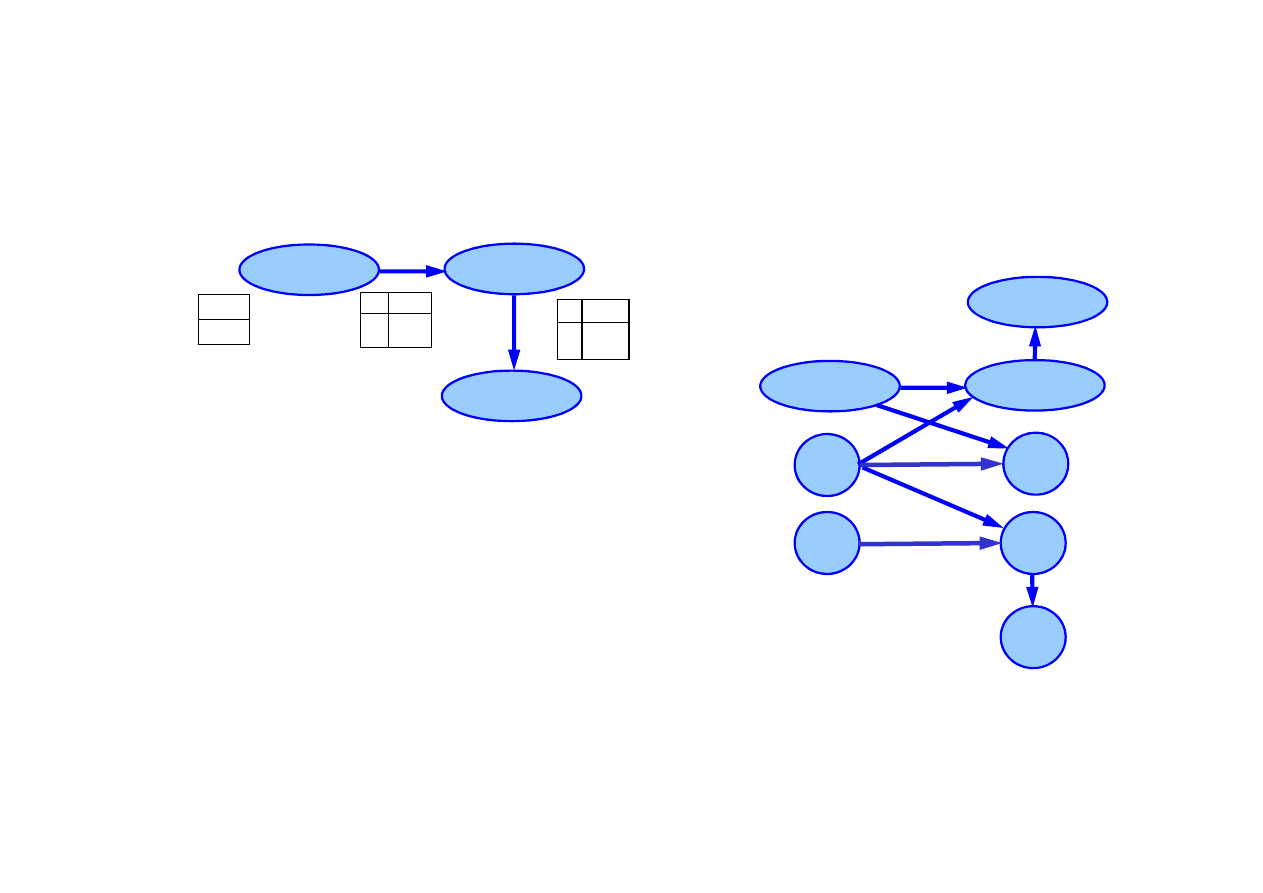
15.5. Dynamiczne sieci Bayesa

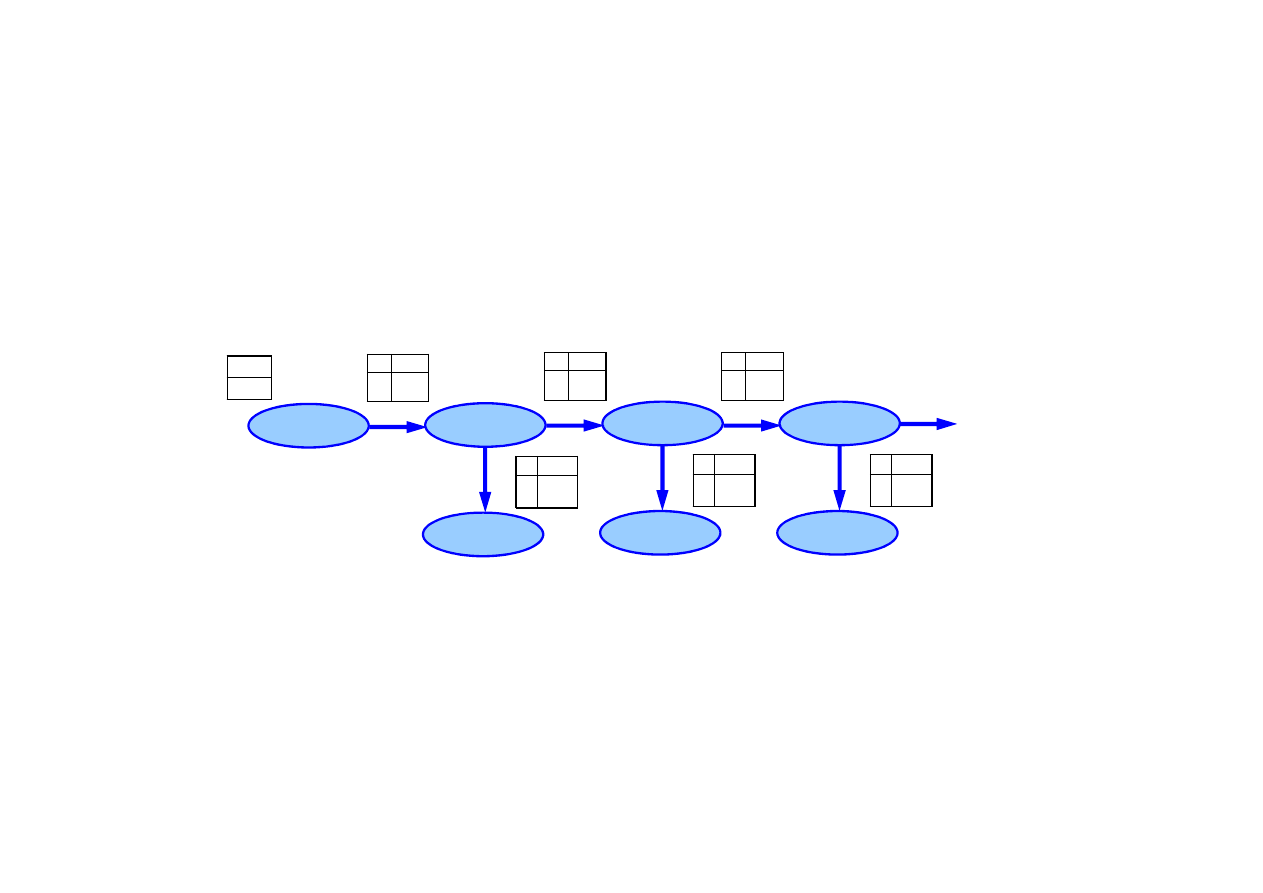
Przykłady dynamicznych sieci Bayesa

DBN dla zadania z parasolem

DBN dla ruchu robota

w płaszczy

ź

nie X-Y

Deszcz

1

Deszcz

0

R

1

P(U

1

)

t

f

0.90
0.20

Parasol

1

R

-0

P(R

0

)

t

f

0.70
0.30

P(R

0

)

0.70

Bateria

1

Bateria

0

MiernikB

1

© F.A. Dul 2007

V

0

V

1

Z

1

X

0

X

1

Do budowy DBN potrzebne s

ą

:

• rozkład prawdopodobie

ń

stwa

pocz

ą

tkowego zmiennej stanu

P

(

X

0

),

• model przej

ś

cia

P

(

X

t

|

X

t-1

),

• model obserwacji

P

(

E

t

|

X

t

),

• topologia sieci.

15.5. Dynamiczne sieci Bayesa

Wnioskowane

ś

cisłe w dynamicznych sieciach Bayesa

Wnioskowanie w DBN mo

ż

e by

ć

przeprowadzone tak, jak

w zwykłej sieci Bayesa.

Nale

ż

y w tym celu rozwin

ąć

sie

ć

powielaj

ą

c wielokrotnie

warstw

ę

pocz

ą

tkow

ą

(unrolling)

Deszcz

1

Deszcz

0

R

-0

P(R

0

)

t

f

0.70
0.30

P(R

0

)

0.70

Deszcz

2

R

-0

P(R

0

)

t

f

0.70
0.30

Deszcz

3

R

-0

P(R

0

)

t

f

0.70
0.30

. . .

© F.A. Dul 2007

R

1

P(U

1

)

t

f

0.90
0.20

Parasol

1

R

1

P(U

1

)

t

f

0.90
0.20

Parasol

2

R

1

P(U

1

)

t

f

0.90
0.20

Parasol

3

Rozwini

ę

ta DBN umo

ż

liwia reprezentowanie nawet bardzo

zło

ż

onych procesów w zwi

ę

zły sposób.

Wnioskowanie

ś

cisłe w sieci rozwini

ę

tej jest jednak bardzo

kosztowne, co praktycznie uniemo

ż

liwia u

ż

ycie metod

stosowanych w zwykłych sieciach Bayesa.

15.5. Dynamiczne sieci Bayesa

Wnioskowane przybli

ż

one w dynamicznych sieciach

Bayesa

Wnioskowanie przybli

ż

one w dynamicznych sieciach Bayesa

polega na zastosowaniu ogólnej zasady filtracji oddzielnie
dla ka

ż

dej warstwy czasowej bez rozwijania sieci.

Tak wyznaczone zmienne stanu stanowi

ą

reprezentacj

ę

przybli

ż

on

ą

rzeczywistego (

ś

cisłego) rozkładu stanu.

Do wnioskowania przybli

ż

onego słu

żą

do tego

algorytmy

filtrowania cz

ą

stkowego

.

• Na podstawie rozkładu P(X ) tworzy si

ę

zbiór N próbek

© F.A. Dul 2007

• Na podstawie rozkładu P(X

0

) tworzy si

ę

zbiór N próbek

X

0

(i), i = 1,...N.

• Za pomoc

ą

modelu przej

ś

cia

P(X

t+1

|X

t

) d

la ka

ż

dej próbki

wyznaczany jest stan nast

ę

pny.

• Ka

ż

da próbka jest wa

ż

ona za pomoc

ą

wiarygodno

ś

ci

okre

ś

laj

ą

cej jej wkład do nowych obserwacji P(e

t+1

|x

t+1

).

• Nowa populacja próbek jest generowana za pomoc

ą

modelu przej

ś

cia z uwzgl

ę

dnieniem wag próbek.

Przy wystarczaj

ą

cej liczbie N próbek wnioskowanie przybli

ż

one

prowadzi do wyników

ś

cisłych, N(x

t

|e

1:t

)/N = P(x

t

|e

1:t

).

15.6. Rozpoznawanie mowy

Rozpoznawanie mowy

pozwala komputerowi wyposa

ż

onemu

w urz

ą

dzenie do rejestracji d

ź

wi

ę

ku (mikrofon) interpretowa

ć

mow

ę

ludzk

ą

.

Rozpoznawanie mowy pełni wa

ż

n

ą

rol

ę

w wielu dziedzinach:

• interakcja człowieka z systemami komputerowymi,
• obsługa urz

ą

dze

ń

gospodarstwa domowego,

• sterowanie pojazdami – samochodami, samolotami,

statkami kosmicznymi,...

© F.A. Dul 2007

statkami kosmicznymi,...

• automatyczne notowanie.

Rozpoznawanie mowy polega na identyfikacji ci

ą

gu słów

wypowiedzianych przez mówc

ę

na podstawie zarejestrowane-

go sygnału akustycznego.

Zrozumienie

wypowiedzi jest krokiem nast

ę

pnym.

Zadaniem komplementarnym jest

synteza mowy

.

Jest to zadanie du

ż

o łatwiejsze ni

ż

rozpoznawanie mowy

(podobnie jak rysowanie obiektów jest znacznie łatwiejsze
ni

ż

ich rozpoznawanie).

Mowa naturalna jest bardzo trudna do analizy, gdy

ż

:

15.6. Rozpoznawanie mowy

• ten sam mówca mo

ż

e ró

ż

nie wypowiada

ć

to samo słowo,

• ró

ż

ne słowa mog

ą

brzmie

ć

podobnie,

• ró

ż

ni mówcy mog

ą

wymawia

ć

słowo w ró

ż

ny sposób,

• tempo, intonacja i gło

ś

no

ść

mog

ą

zmienia

ć

si

ę

nawet w tej

samej wypowiedzi,

• gdy mówi wiele osób pojawiaj

ą

si

ę

interferencje słów,

• w płynnej wypowiedzi słowa zlewaj

ą

si

ę

,

• mowa mo

ż

e by

ć

zaszumiona, zniekształcona.

© F.A. Dul 2007

• mowa mo

ż

e by

ć

zaszumiona, zniekształcona.

Rozpoznawanie mowy jest wi

ę

c zadaniem wnioskowania

probabilistycznego.

Rozpoznawanie mowy jest najwa

ż

niejszym zastosowaniem

czasowych modeli probabilistycznych.

Sformułowanie zadania rozpoznawania mowy

Words

– zmienna losowa opisuj

ą

ca wszystkie mo

ż

liwe słowa.

signal

– obserwowany ci

ą

g sygnałów akustycznych.

Najbardziej prawdopodobn

ą

interpretacj

ą

wypowiedzi jest

warto

ść

zmiennej

Words

maksymalizuj

ą

ca

P(words | signal).

Z reguły Bayesa

15.6. Rozpoznawanie mowy

)

(

)

|

(

)

|

(

Words

P

Words

signal

P

signal

Words

P

α

=

P(signal |Words)

okre

ś

la

model akustyczny

opisuj

ą

cy

© F.A. Dul 2007

P(signal |Words)

okre

ś

la

model akustyczny

opisuj

ą

cy

brzmienie słów.

P(Words)

okre

ś

la

model j

ę

zyka

– prawdopodobie

ń

stwo

ka

ż

dej wypowiedzi.

Modele j

ę

zyka okre

ś

laj

ą

prawdopodobie

ń

stwa wyst

ą

pienia

ci

ą

gu słów:

- bigram: prawdopodobie

ń

stwa dwóch kolejnych słów.

- trigram: prawdopodobie

ń

stwa trzech kolejnych słów, itd.

Np.:

P(”It is”) = 0.96, P(”It this”) = 0.001.

Fonem (phoneme) jest najmniejsz

ą

jednostk

ą

mowy

rozró

ż

nian

ą

przez u

ż

ytkowników danego j

ę

zyka.

Alfabet j

ę

zyka liczy zwykle 40-50 fonemów, np. International

Phonetic Alphabet (IPA), czy ARPAbet (American English):

[t] –

t

en, [ow] – b

oa

t, [m] –

m

et, [aa] – c

o

t, ...

Słowo „

tomato”

ma reprezentacj

ę

fonetyczn

ą

[t ow m aa t ow ].

Fonemy umo

ż

liwiaj

ą

podział modelu akustycznego na

model

wymowy

oraz

model fonemów

.

Model wymowy okre

ś

la rozkład prawdopodobie

ń

stwa

15.6. Rozpoznawanie mowy

© F.A. Dul 2007

Model wymowy okre

ś

la rozkład prawdopodobie

ń

stwa

ka

ż

dego słowa wzgl

ę

dem zbioru wszystkich fonemów.

Zmienna X

t

okre

ś

la fonem wypowiedziany w chwili t.

Model fonemów okre

ś

la sposób realizacji fonemów jako

sygnałów akustycznych.
Zmienna ukrytego modelu Markowa E

t

okre

ś

la własno

ś

ci

sygnału w chwili t.

Model fonemów okre

ś

la prawdopodobie

ń

stwo

P(E

t

|X

t

)

pojawienia si

ę

w chwili t własno

ś

ci E

t

w sygnale je

ż

eli

wypowiedziany został fonem X

t

.

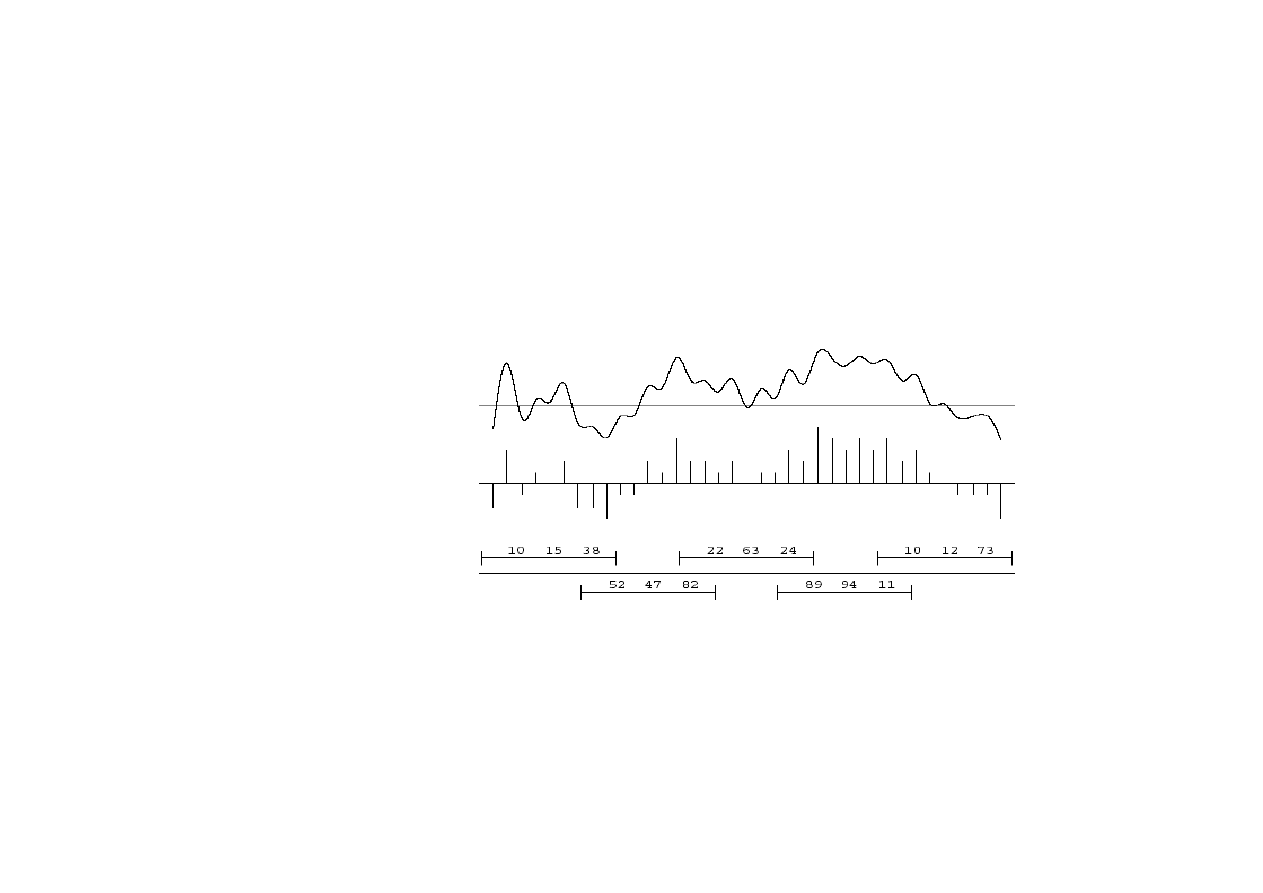
Reprezentacja sygnału mowy
Próbkowanie sygnału odbywa si

ę

z cz

ę

stotliwo

ś

ci

ą

8-16 kHz.

Sygnał rejestrowany jest z rozdzielczo

ś

ci

ą

8-12 bitów.

Wymagana pami

ęć

jest du

ż

a – 1 MBajt / minut

ę

wypowiedzi,

wi

ę

c wyznaczenie

P(signal | phone)

nie jest praktyczne.

15.6. Rozpoznawanie mowy

Sygnał analogowy

© F.A. Dul 2007

Sygnał próbkowany

dyskretny

Ramki z własno

ś

ciami

Mowa reprezentowana jest wi

ę

c poprzez

ramki

(frames)

opisuj

ą

ce

n

własno

ś

ci

sygnału (features) w małych

przedziałach czasu (~50-100 próbek).

Własno

ś

ciami mog

ą

by

ć

np. energie d

ź

wi

ę

ku, formanty, itp.

Własno

ś

ci w ramkach s

ą

reprezentowane w zwartej postaci

za pomoc

ą

:

15.6. Rozpoznawanie mowy

• kwantyzacji wektorowej VC (obecnie rzadziej u

ż

ywana),

• mieszanek Gaussa.

Mieszanka Gaussa to zbiór

k

rozkładów Gaussa z ró

ż

nymi

warto

ś

ciami

ś

rednimi i wariancjami dobranymi tak, aby jak

najlepiej reprezentowały rozkład prawdopodobie

ń

stwa

P(features | phone)

w obszarze ramki.

Struktura czasowa fonemu opisywana jest

modelem

© F.A. Dul 2007

Struktura czasowa fonemu opisywana jest

modelem

trójstanowym

: ka

ż

dy fonem składa si

ę

z trzech faz: Pocz

ą

tek,

Ś

rodek, Koniec (Onset, Mid, End).

Kontekst w którym pojawia si

ę

fonem opisywany jest

modelem trójfonemowym

: model akustyczny fonemu

uwzgl

ę

dnia trójk

ę

fonemów: poprzedni, bie

żą

cy i nast

ę

pny.

Kombinacja modeli trójstanowego i trójfonemowego pozwala
zwi

ę

kszy

ć

liczb

ę

mo

ż

liwych stanów z

n

do

3n

3

, co znacznie

poprawia dokładno

ść

reprezentacji sygnału akustycznego.

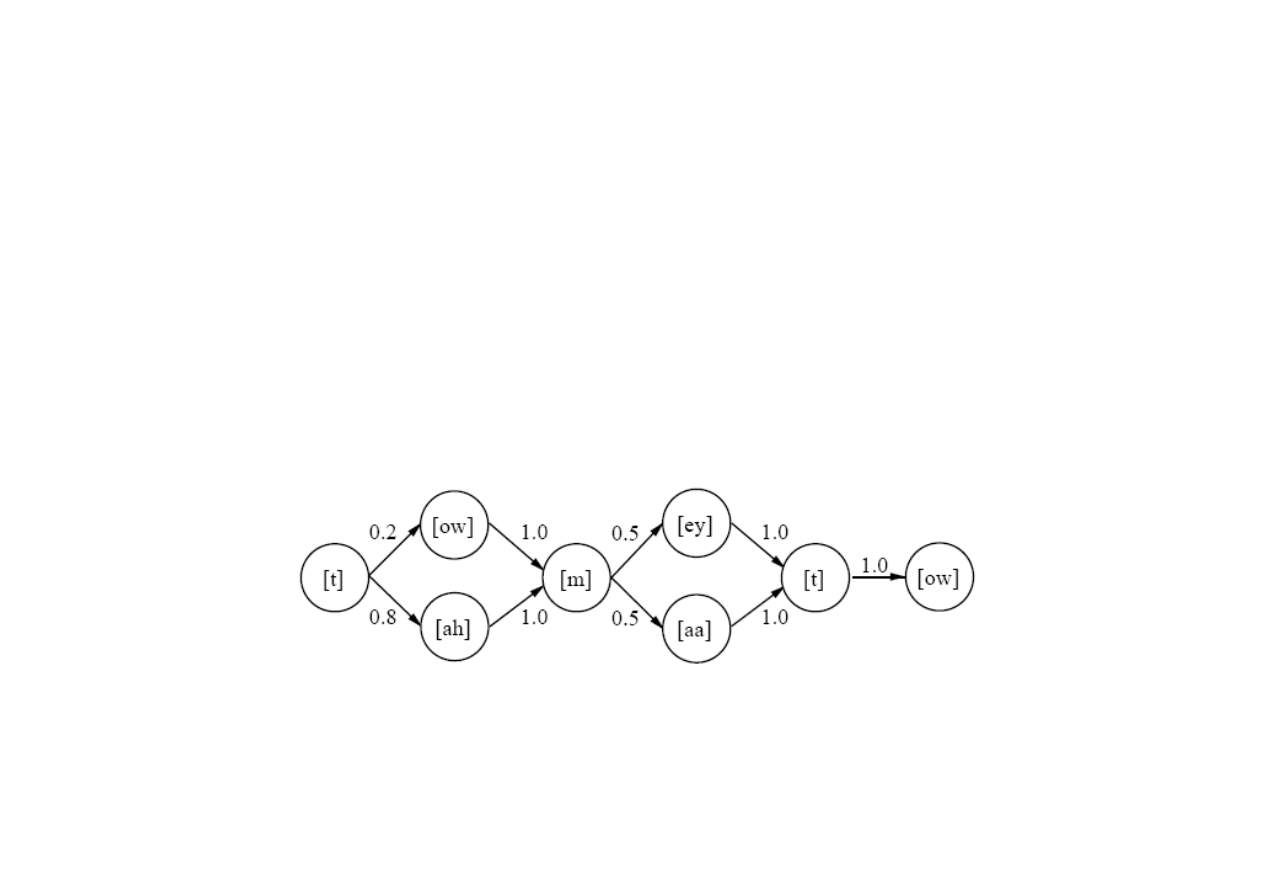
Słowa
Słowo jest okre

ś

lone rozkładem prawdopodobie

ń

stwa

P(X

1:t

| word )

w którym

X

i

jest fonemem w i-tej ramce.

Model słowa

- rozkład prawdopodobie

ń

stwa dla słowa -

okre

ś

lony jest przez

modelu wymowy

oraz

model fonemu

.

Model wymowy okre

ś

la rozkład prawdopodobie

ń

stwa dla

słowa wzgl

ę

dem fonemów, bez uwzgl

ę

dnienia ramek i czasu.

Słowo mo

ż

e mie

ć

kilka modeli wymowy, np. słowo „tomato”

ma nast

ę

puj

ą

ce cztery modele:

15.6. Rozpoznawanie mowy

© F.A. Dul 2007

ma nast

ę

puj

ą

ce cztery modele:

P( [t ow m ey t ow] |”tomato” ) = 0.1
P( [t ow m aa t ow] |”tomato” ) = 0.1
P( [t ah m ey t ow] |”tomato” ) = 0.4
P([t ah m aa t ow] |”tomato” ) = 0.4

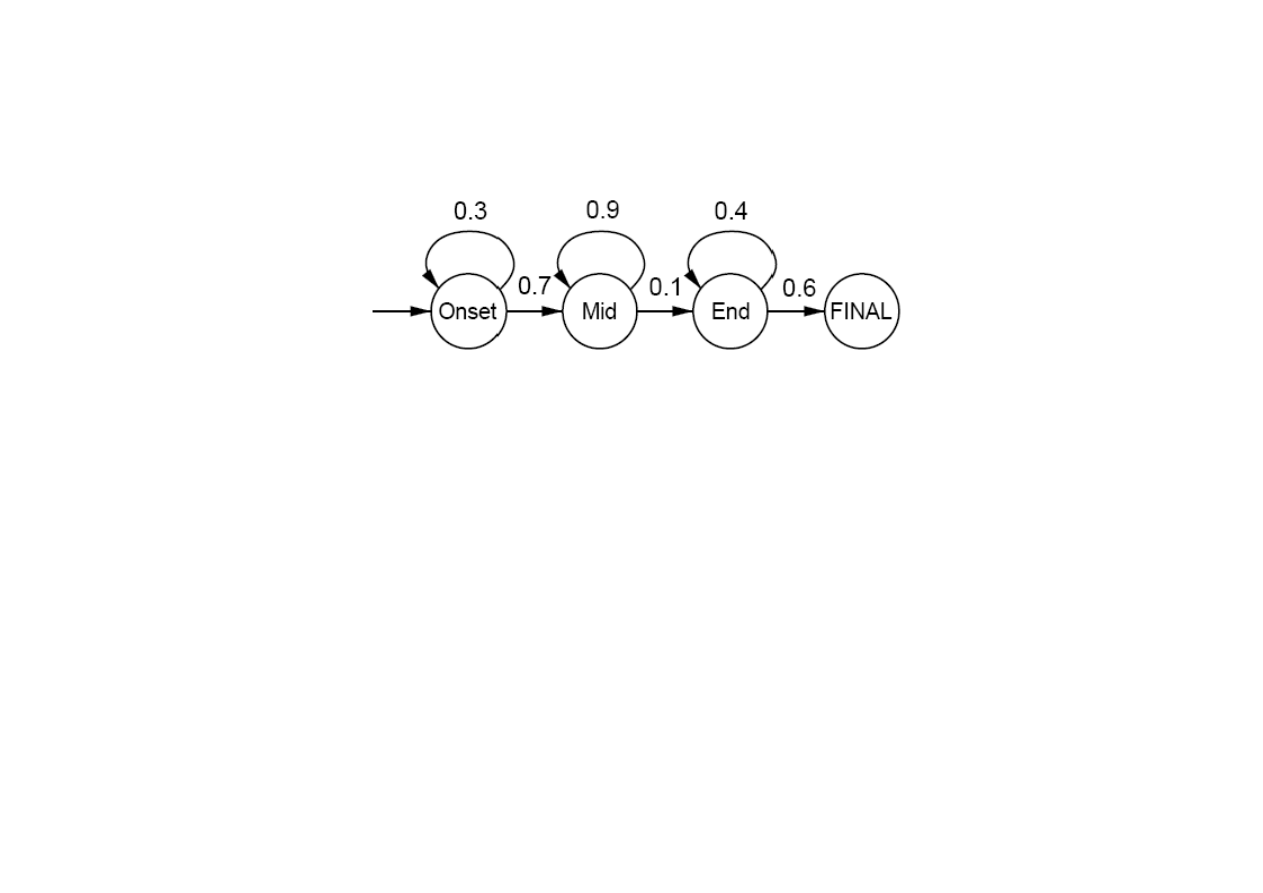
Modele fonemów okre

ś

laj

ą

odwzorowanie fonemów na ramki.

Przykład modelu trójstanowego dla fonemu [m]

15.6. Rozpoznawanie mowy

Modele stanów Onset, Mid i End okre

ś

laj

ą

realizacj

ę

akustyczn

ą

fonemu poprzez prawdopodobie

ń

stwa trwania

stanów (p

ę

tle).

© F.A. Dul 2007

akustyczn

ą

fonemu poprzez prawdopodobie

ń

stwa trwania

stanów (p

ę

tle).

Model słowa w poł

ą

czeniu z modelem fonemu okre

ś

la

wiarygodno

ść

dla słowa izolowanego,

P(word | e

1:t

) =

α

P(e

1:t

| word ) P(word )

Prawdopodobie

ń

stwo a priori

P(word )

wyznacza si

ę

zliczaj

ą

c

cz

ę

sto

ść

wyst

ę

powania słowa, za

ś

P(e

1:t

| word )

mo

ż

na

obliczy

ć

rekurencyjnie

∑

=

t

X

t

t

t

e

X

word

e

P

)

,

(

)

|

(

:

1

:

1

P

Wypowiedzi
Dialog wymaga zrozumienia wypowiedzi ci

ą

głej.

Zrozumienie ci

ą

głej wypowiedzi wymaga

segmentacji

–

wła

ś

ciwego podziału ła

ń

cucha wypowiedzi na słowa.

Wypowied

ź

ci

ą

gła nie jest jednak prost

ą

sum

ą

ci

ą

gu słów –

sekwencja najbardziej prawdopodobnych słów nie jest
najbardziej prawdopodobn

ą

sekwencj

ą

słów.

Model j

ę

zyka

okre

ś

la prawdopodobie

ń

stwo ła

ń

cucha jako

ci

ą

gu kolejnych słów

15.6. Rozpoznawanie mowy

© F.A. Dul 2007

ci

ą

gu kolejnych słów

)

...

|

(

...

)

|

(

)

(

)

...

(

1

1

1

2

1

1

−

=

n

n

n

w

w

w

P

w

w

P

w

P

w

w

P

)

|

(

)

...

|

(

1

1

1

−

−

≈

i

i

i

i

w

w

P

w

w

w

P

W praktyce u

ż

ywa si

ę

przybli

ż

enia

bigram

dla dwóch słów

Prawdopodobie

ń

stwa modelu bigram mog

ą

by

ć

wyznaczone

poprzez zliczanie wyst

ą

pie

ń

w du

ż

ym zbiorze wypowiedzi.

Przybli

ż

enia u

ż

ywaj

ą

ce trzech lub wi

ę

cej słów s

ą

du

ż

o

dokładniejsze, lecz trudniejsze do oszacowania.

∏

=

−

=

n

i

i

i

w

w

w

P

1

1

1

)

...

|

(

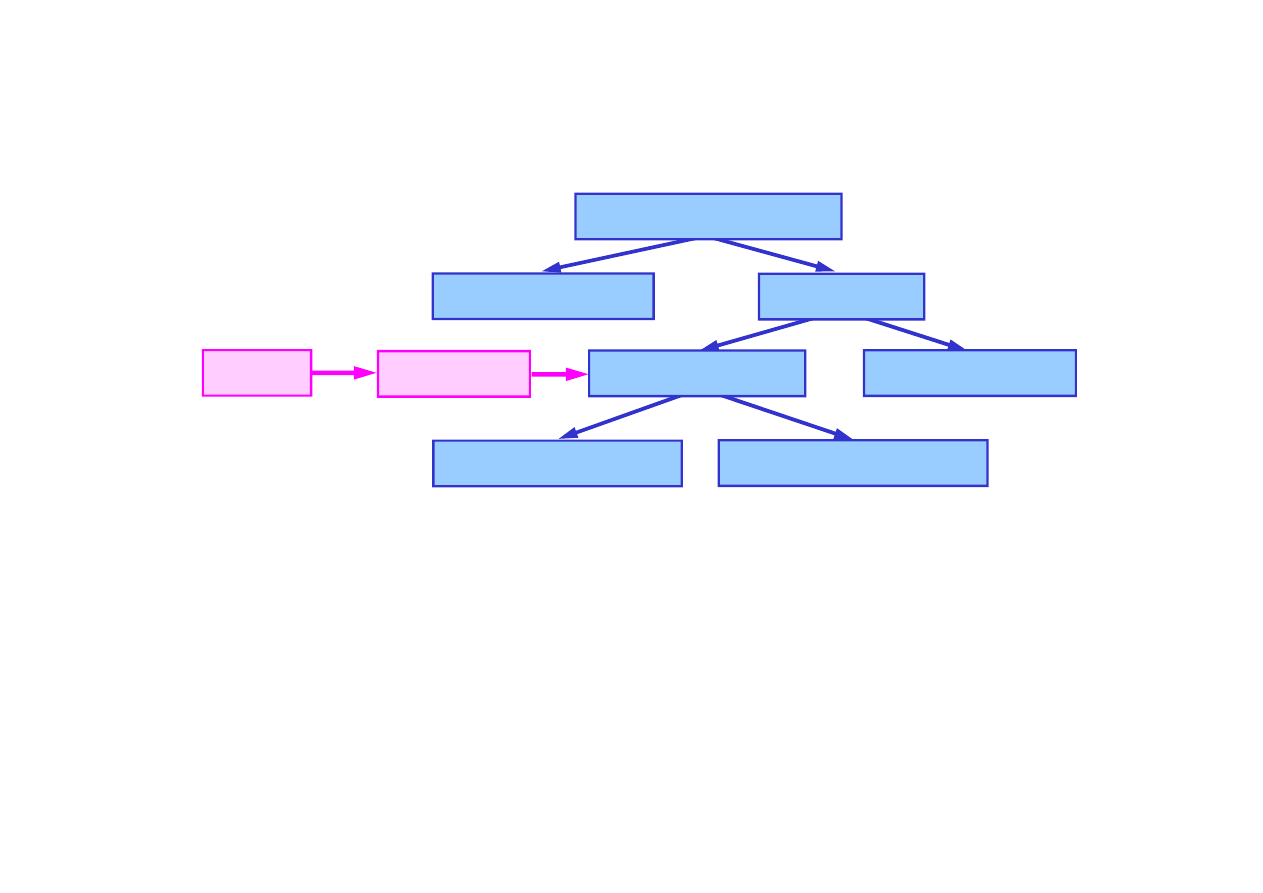
Model wypowiedzi

w postaci ukrytego modelu Markowa

(HMM) dla tworzy si

ę

z modeli nast

ę

puj

ą

co:

15.6. Rozpoznawanie mowy

Model wypowiedzi

Model j

ę

zyka

Model słów

Model wymowy

Model fonemów

Własno

ś

ci

Ramki

© F.A. Dul 2007

Najbardziej prawdopodobny ci

ą

g słów dla danego ła

ń

cucha,

wyznacza si

ę

na podstawie modelu wypowiedzi np. za

pomoc

ą

algorytmu Viterbiego.

Segmentacji ła

ń

cucha dokonuje si

ę

na podstawie tak

wyznaczonego ci

ą

gu słów.

Najbardziej prawdopodobny ci

ą

g słów w wypowiedzi mo

ż

na

wyznaczy

ć

bardzo efektywnie za pomoc

ą

dekodera A*

,

uzupełnionego odpowiedni

ą

heurystyk

ą

.

Model trójfonemowy

Model trójstanowy

Budowa systemów rozpoznawania mowy
Jako

ść

systemów rozpoznawania mowy zale

ż

y od jako

ś

ci

wszystkich elementów: modelu j

ę

zyka, modeli wymowy słów,

modeli fonemów, algorytmów przetwarzania sygnałów mowy
oraz obszerno

ś

ci słowników wymowy słów.

Rozkłady prawdopodobie

ń

stw mog

ą

zawiera

ć

nawet miliony

parametrów definiuj

ą

cych modele sygnałów.

Parametry te mog

ą

by

ć

okre

ś

lone w ró

ż

ny sposób, ale

najlepsze rezultaty osi

ą

ga si

ę

poprzez

uczenie

modelu.

15.6. Rozpoznawanie mowy

© F.A. Dul 2007

najlepsze rezultaty osi

ą

ga si

ę

poprzez

uczenie

modelu.

Uczenie polega na dostrajaniu parametrów na podstawie
du

ż

ej liczby wypowiedzi.

Zaawansowane systemy rozpoznawania mowy u

ż

ywaj

ą

do treningu modeli ogromnych zbiorów wypowiedzi.

Do uczenia słu

ż

y algorytm maksymalizacji warto

ś

ci

oczekiwanej (expectation-maximization, EM).

Algorytm ten gwarantuje znaczn

ą

popraw

ę

jako

ś

ci modeli

w porównaniu z modelami nie uczonymi.

Systemy rozpoznawania mowy s

ą

rozwijane intensywnie,

zwłaszcza w ostatniej dekadzie, nie osi

ą

gn

ę

ły jednak jeszcze

zadowalaj

ą

cej skuteczno

ś

ci.

Niezawodno

ść

systemów rozpoznawania mowy zale

ż

y

od warunków akustycznych i sposobu wypowiedzi.

Wypowied

ź

jednej osoby, zło

ż

ona z pojedy

ń

czych słów z

niewielkiego słownika, odbywaj

ą

ca si

ę

w dobrych warunkach

akustycznych, bez du

ż

ych zakłóce

ń

, rozpoznawana jest

z dokładno

ś

ci

ą

95-99%.

15.6. Rozpoznawanie mowy

© F.A. Dul 2007

z dokładno

ś

ci

ą

95-99%.

W przypadku dowolnych wypowiedzi wielu osób typowa
dokładno

ść

rozpoznania wynosi 60-80%, nawet w dobrych

warunkach akustycznych.

Gdy warunki akustyczne s

ą

złe, dokładno

ść

jest mniejsza.

Niektóre systemy rozpoznawania mowy:

• w medycznych systemach diagnostycznych,
• w pakiecie Microsft Office,
• w telefonii komórkowej, bankowo

ś

ci, itp.

Wnioskowanie stochastyczne dynamiczne

Metody dynamicznego wnioskowania stochastyczne-
nego stanowi

ą

wa

ż

ne narz

ę

dzie analizy

rzeczywisto

ś

ci.

Filtr Kalmana umo

ż

liwił realizacj

ę

lotów na Ksi

ęż

yc

i jest powszechnie u

ż

ywany w nawigacji, sterowaniu

oraz wielu innych dziedzinach.

Dynamiczne sieci Bayesa pozwalaj

ą

modelowa

ć

©

F.A. Dul 2007

Dynamiczne sieci Bayesa pozwalaj

ą

modelowa

ć

zło

ż

one zjawiska stochastyczne.

Rozpoznawanie mowy jest wa

ż

nym zagadnieniem

komunikacji człowiek-maszyna.

Podsumowanie

• Zmiany stanu

ś

wiata w czasie mog

ą

by

ć

opisane zmiennymi

losowymi zale

ż

nymi od czasu.

• Modele procesów Markowa pozwalaj

ą

zwi

ęź

le modelowa

ć

stacjonarne procesy stochastyczne.

• Stochastyczny model dynamiczny składa si

ę

z modelu

przej

ś

cia i modelu obserwacji.

• Głównymi zadaniami wnioskowania stochastycznego

w czasie s

ą

: filtracja, predykcja, wygładzanie oraz

wyznaczanie najbardziej wiarygodnego wyja

ś

nienia.

© F.A. Dul 2007

wyznaczanie najbardziej wiarygodnego wyja

ś

nienia.

• Podstawowymi modelami dynamicznymi s

ą

sieci Bayesa

oraz ich szczególne przypadki: ukryte modele Markowa
oraz filtr Kalmana.

• Filtr Kalmana stanowi podstawowe narz

ę

dzie wnioskowania

stochastycznego dla układów dynamicznych.

• Zastosowanie Filtrów Kalmana jest bardzo szerokie:

nawigacja, sterowanie, uczenie, rozpoznawanie obrazów,…

• Rozpoznawanie mowy jest wa

ż

nym zadaniem wnioskowania

stochastycznego.