Tomasz Kowalski
Wykłady z matematyki dla studentów kierunków ekonomicznych
Wykład 10
ASYMPTOTY WYKRESU FUNKCJI
1. Asymptoty pionowe
Prostą
jest asymptotą pionową (obustronną) jeżeli obie granice:
0
x
x
0
lim ( )
x
x
f x
oraz
0
lim ( )
x
x
f x
są
niewłaściwe.
Jeżeli dokładnie jedna z powyższych granic jest niewłaściwa, to prosta
0
x
x
jest asymptotą pionową
jednostronną. Precyzyjniej:
1. Jeżeli
albo
0
lim ( )
x
x
f x
0
lim ( )
x
x
f x
, to prosta
0
x
x
jest asymptotą pionową lewostronną.
2. Jeżeli
albo
0
lim ( )
x
x
f x
0
lim ( )
x
x
f x
, to prosta
0
x
x
jest asymptotą pionową prawostronną
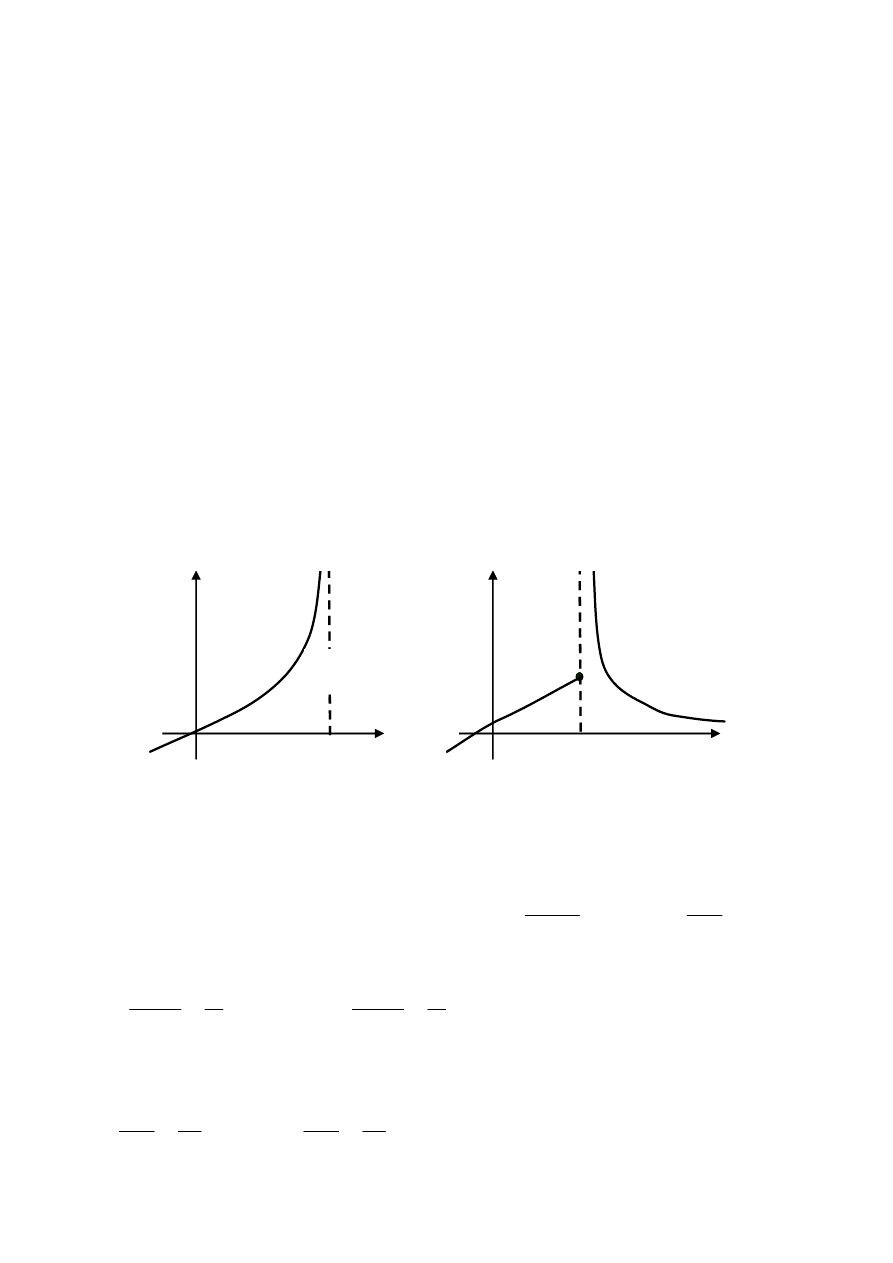
Ilustrację jednostronnych asymptot pionowych przedstawia rys. 1.
Prosta
0
x
x
jest asymptotą pionową lewostronną
Y
X
0
x
)
(x
f
y
)
(
lim
0
x
f
x
x
Prosta
0
x
x
jest asymptotą pionową prawostronną
Y
X
0
x
)
(x
f
y
)
(
lim
0
x
f
x
x
Rys. 1.
Twierdzenie. Funkcja elementarna może mieć asymptotę pionową tylko w skończonym krańcu
dziedziny, który do niej nie należy.
Przykład 1. Wyznaczyć asymptoty pionowe funkcji a)
2
)
3
(
1
)
(
x
x
f
, b)
2
)
(
2
x
x
x
f
.
Rozwiązanie.
a) Ponieważ
, to obliczamy granice:
}
3
{
\
R
D
f
2
3
1
1
lim
(
3)
0
[ ]
x
x
oraz
2
3
1
1
lim
(
3)
0
[ ]
x
x
.
Oznacza to, że prosta
jest asymptotą pionową wykresu danej funkcji. Wykres funkcji w sąsiedztwie
punktu
przedstawia rys.2.
3
x
3
0
x
b) . Obliczając granice jednostronne funkcji w punkcie
}
2
{
\
R
D
f
2
0
x
otrzymujemy:
]
[
0
4
2
lim
2
2
+
x
x
x
,
]
[
0
4
2
lim
2
2
-
x
x
x
.
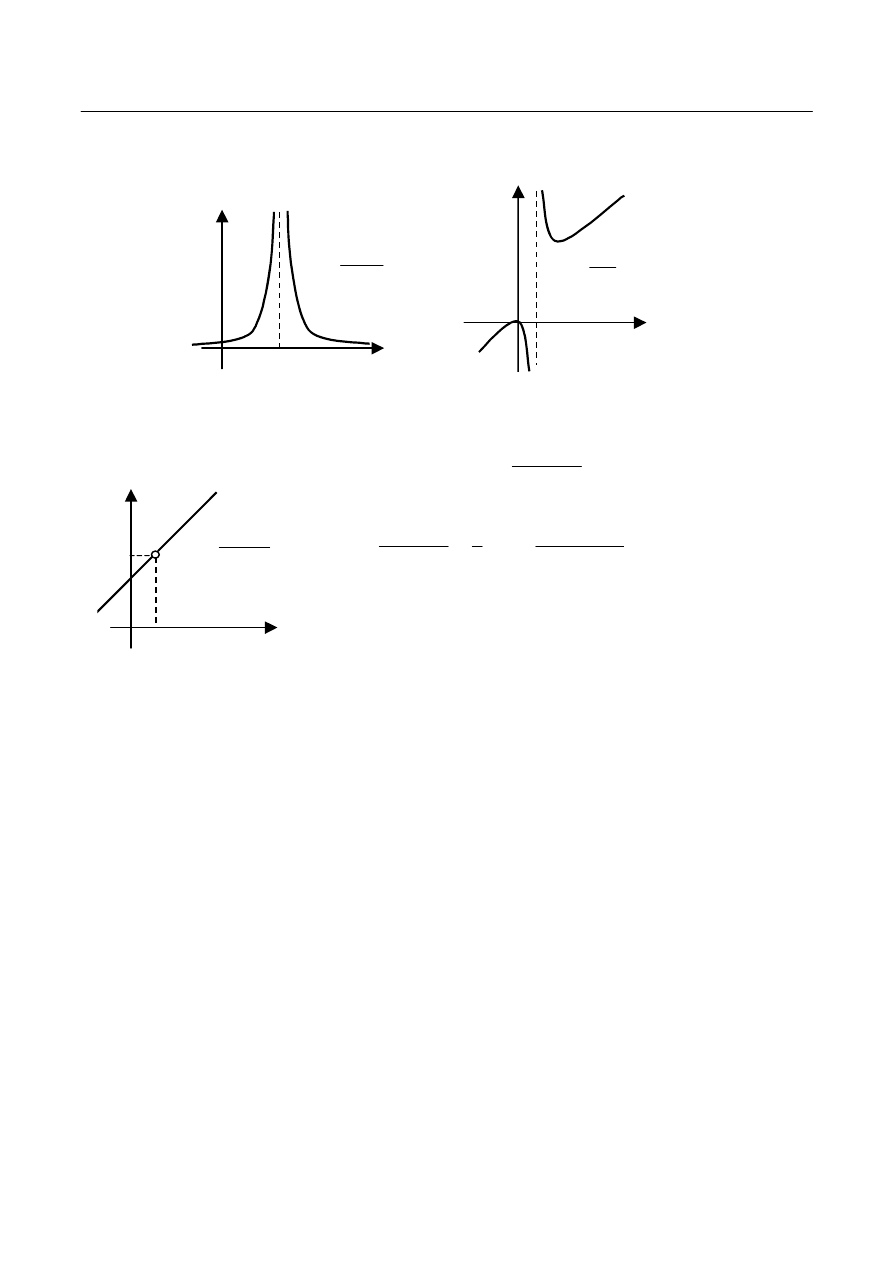
Wykład 10. Asymptoty wykresu funkcji
2
Oznacza to, że prosta
jest asymptotą pionową obustronną. Asymptota oraz wykres funkcji
w sąsiedztwie punktu
zostały przedstawione na rys.3.
2
x
2
0
x
X
f x
x
( )
(
)
1
3
2
Y
3
Rys. 2.
X
2
)
(
2
x
x
x
f
Y
2
Rys. 3.
Uwaga. Jeżeli , to z tego nie należy wnioskować, że prosta
}
{
\
0
x
R
D
f
0
x
x
jest asymptotą
pionową.
Przykład 2.
Wyznaczyć asymptoty pionowe funkcji
1
2
)
(
2
x
x
x
x
f
.
X
1
2
)
(
2
x
x
x
x
f
Y
1
3
Rys. 4.
Rozwiązanie. Mamy tutaj
}
1
{
\
R
D
f
. Jednocześnie
3
2)
(
lim
1
2
)(
1
(
lim
1
x
x
x
)
0
0
1
2
lim
1
2
1
]
[
x
x
x
x
x
x
x
.
Oznacza to, że wykres funkcji nie posiada asymptot pionowych.
Wykres funkcji w sąsiedztwie punktu
1
0
x
(równej
2
)
(
x
x
g
) przedstawia rys.4.
2. Granice właściwe funkcji w nieskończoności. Asymptoty poziome
Niech
f
będzie funkcją określoną w przedziale
)
;
(
a
.
Jeżeli dla każdego ciągu o wyrazach należących do przedziału
)
(
n
x
)
;
(
a
i rozbieżnego do
, ciąg
wartości funkcji
jest zbieżny do
))
(
(
n
x
f
g
, to mówimy, że funkcja
f
posiada w
granicę g
.
Zapisujemy wówczas
.
g
x
)
f
(
lim
x
Podobnie, niech
f
będzie funkcją określoną w przedziale
)
;
(
a
.
Jeżeli dla każdego ciągu o wyrazach należących do przedziału
)
(
n
x
)
;
(
a
i rozbieżnego do
, ciąg
wartości funkcji
jest zbieżny do
))
(
(
n
x
f
g
, to mówimy, że funkcja
f
posiada w
granicę g
zapisujemy
).
g
x
f
)
(
x
lim
Prostą
g
y
nazywamy asymptotą poziomą prawostronną jeżeli
g
x
f
x
)
(
lim
.
Podobnie, prosta
g
y
jest asymptotą poziomą lewostronną, jeżeli
g
x
f
x
)
(
lim
.
Jeżeli prosta
g
y
jest jednocześnie asymptotą poziomą prawostronną i lewostronną krzywej
)
(
x
f
y
,
to nazywamy ją asymptotą poziomą (obustronną).
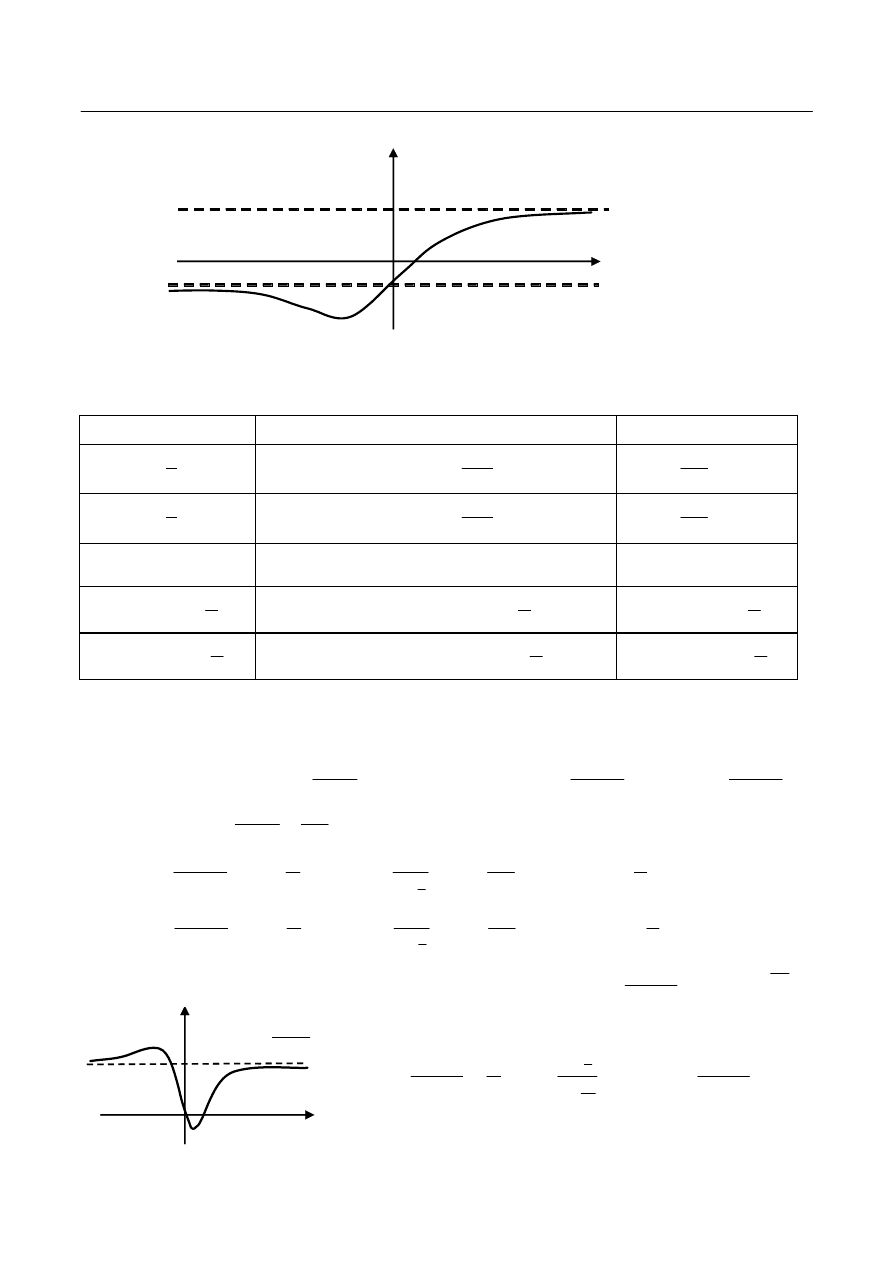
Na rys. 4 przedstawiony został wykres funcji posiadającej różne skończone granice w punktach
niewłaściwych i tym samym posiadającej różne asymptoty poziome jednostronne.
Wykład 10. Asymptoty wykresu funkcji
3
Prosta
g
y
jest asymptotą poziomą lewostronną, prosta
h
y
asymptotą prawostronną
Y
X
)
(x
f
y
g
x
f
x
)
(
lim
h
x
f
x
)
(
lim
h
g
Rys. 4.
Wykaz niektórych granic właściwych w nieskończoności zapisanych w postaci symbolicznej
Granica Uogólnienie
Zapis
symboliczny
0
1
lim
x
x
Jeżeli
)
(
lim
...
x
u
x
, to
0
)
(
1
lim
...
x
u
x
.
0
1
]
[
0
1
lim
x
x
Jeżeli
)
(
lim
...
x
u
x
, to
0
)
(
1
lim
...
x
u
x
.
0
1
]
[
0
lim
x
x
e
Jeżeli
)
(
lim
...
x
u
x
, to
.
0
lim
)
(
...
x
u
x
e
0
]
[
e
2
arctg
lim
x
x
Jeżeli
)
(
lim
...
x
u
x
, to
2
arctg
lim
...
x
x
.
2
)
(
arctg
]
[
2
arctg
lim
x
x
Jeżeli
)
(
lim
...
x
u
x
, to
2
arctg
lim
...
x
x
.
2
)
(
arctg
]
[
Uwaga. Zapis
...
x
w powyższej tabelce oznacza dowolne z przejść granicznych:
,
,
,
0
x
x
0
x
x
0
x
x
x
,
x
.
Przykład 3.
Obliczyć: a)
4
5
lim
2
x
x
, b)
, c)
4
-
2
lim
x
x
e
2
4
arctg
lim
2
x
x
x
x
, d)
2
4
arctg
lim
2
x
x
x
x
.
Rozwiązanie. a)
0
]
5
[
4
5
lim
2
x
x
, b)
,
0
lim
]
[
4
-
2
e
e
x
x
c)
2
)
arctg(
1
arctg
1
4
arctg
lim
arctg
2
4
arctg
lim
]
[
]
[
]
[
2
2
x
x
x
x
x
x
x
,
d)
2
)
arctg(
1
arctg
1
4
arctg
lim
arctg
2
4
arctg
lim
]
[
]
[
]
[
2
2
x
x
x
x
x
x
x
.
Przykład 4.
Wyznaczyć, jeżeli istnieją asymptoty poziome funkcji: a)
10
3
)
(
2
2
x
x
x
x
f
, b)
2
3
)
(
x
x
e
x
f
.
X
10
3
)
(
2
2
x
x
x
x
f
Y
1
y
Rozwiązanie. a) Mamy tutaj
R
D
f
.
1
1
1
2
10
3
x
x
lim
10
3
lim
2
2
]
[
x
x
x
x
x
1
10
3
lim
2
2
x
x
x
x
.
oraz
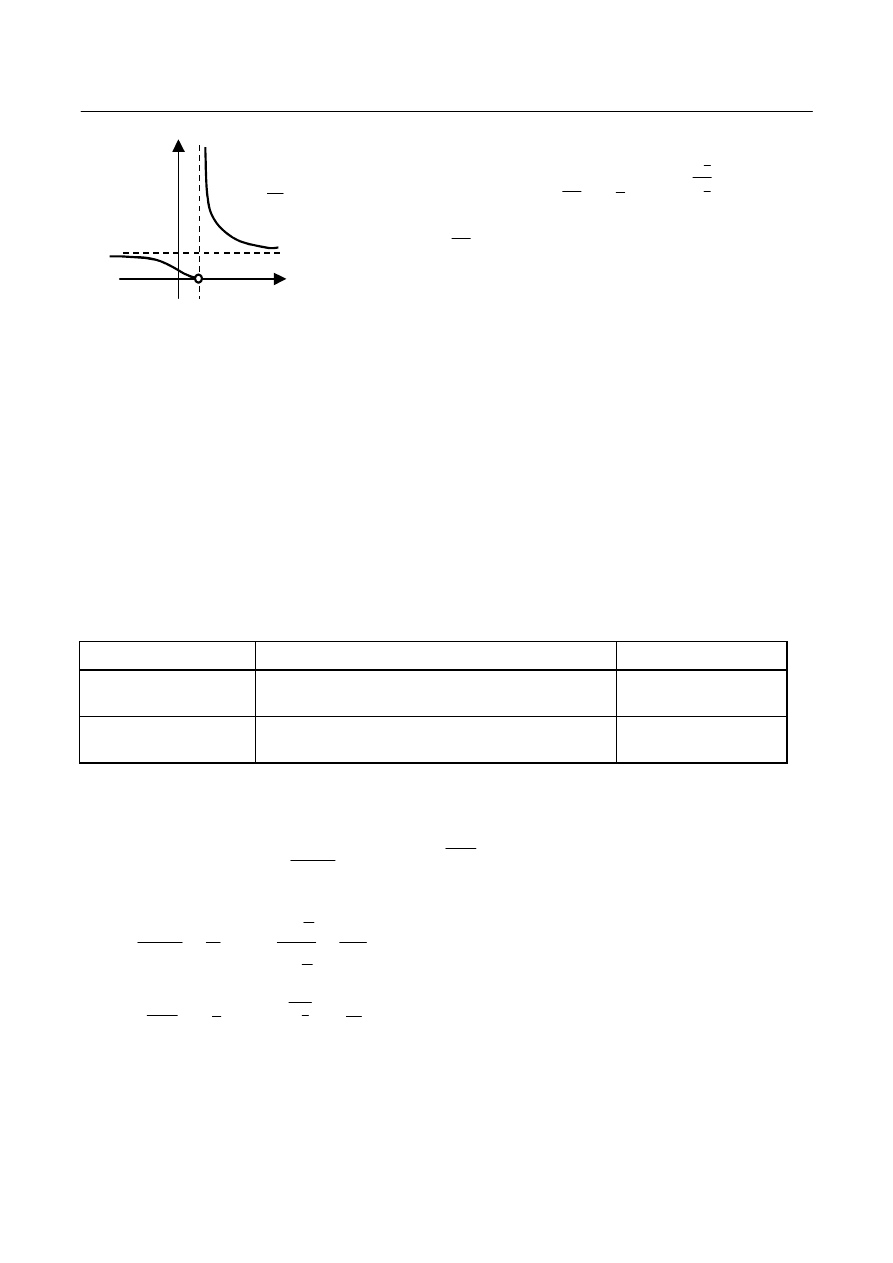
Prosta 1
y
jest asymptotą poziomą obustronną.
Ilustrację graficzną przedstawia rys.5.
Rys. 5
.
Wykład 10. Asymptoty wykresu funkcji
4
X
2
3
)
(
x
x
e
x
f
Y
2
y= e
e
e
e
e
x
x
x
x
x
x
2
1
3
1
2
3
lim
lim
]
[
b) . Mamy tutaj
}
2
{
\
R
D
f
oraz
analogicznie
e
e
x
2
x
3
e
y
x
lim
. Oznacza to, że prosta
jest asymptotą
poziomą obustronną. Wykres funkcji i asymptotę przedstawia rys.6.
Rys. 6.
3. Granice niewłaściwe funkcji w nieskończoności. Asymptoty ukośne
Niech f będzie funkcją określoną w przedziale
)
;
(
a
.
Jeżeli dla każdego ciągu o wyrazach należących do tego przedziału i rozbieżnego do
, ciąg
wartości funkcji
jest rozbieżny do
)
(
n
x
))
(
(
n
x
f
, to mówimy, że funkcja f posiada w
granicę
niewłaściwą
i zapisujemy
)
(
lim
x
f
x
.
Uwaga.
Podobnie definiujemy granicę
)
(
lim
x
f
x
oraz przy założeniu o określoności funkcji f
w przedziale
granice:
)
;
(
a
)
(
lim
x
f
x
,
)
(
lim
x
f
x
.
Wykaz niektórych granic niewłaściwych w nieskończoności zapisanych w postaci symbolicznej
Granica Uogólnienie
Zapis
symboliczny
x
x
e
lim
Jeżeli
)
(
lim
...
x
u
x
, to
.
)
(
...
lim
x
u
x
e
]
[
e
x
x
ln
lim
Jeżeli
)
(
lim
...
x
u
x
, to
)
(
ln
lim
...
x
u
x
.
]
[
)
ln(
Uwaga.
Zapis
...
x
oznacza dowolne z przejść granicznych:
,
,
,
0
x
x
0
x
x
0
x
x
x
,
x
.
Przykład 5.
Obliczyć: a)
5
lim
2
x
x
x
x
, b)
1
4
2
lim
x
x
x
x
e
, c)
.
)
4
ln(
lim
x
e
x
x
Rozwiązanie.
a)
]
[
]
[
1
5
1
1
lim
5
lim
2
x
x
x
x
x
x
x
x
,
b)
]
[
]
[
]
[
1
1
1
1
4
1
4
lim
lim
2
e
e
e
e
e
x
x
x
x
x
x
x
,
c)
.
]
[
]
[
]
[
)
ln(
)
ln(
)
ln(
)
4
ln(
lim
e
x
e
x
x
Wykład 10. Asymptoty wykresu funkcji
5
Niech f będzie funkcją określoną w przedziale
)
;
(
a
. Prostą o równaniu
n
mx
y
nazywamy:
asymptotą ukośną lewostronną
krzywej
)
(x
f
y
, wtedy i tylko wtedy, gdy
0
)]
(
)
(
[
lim
n
mx
x
f
x
.
Podobnie, jeżeli f jest funkcją określoną w przedziale
)
;
(
a
), to p
rostą o równaniu
n
mx
y
nazywamy asymptotą ukośną prawostronną krzywej )
(x
f
y
, wtedy i tylko wtedy, gdy
.
0
)]
(
)
(
[
lim
n
mx
x
f
x
Jeżeli prosta
jest jednocześnie asymptotą ukośną lewostronną i prawostronną krzywej
, to nazywamy ją asymptotą ukośną (obustronną) tej krzywej (rys. 7.).
n
mx
y
)
(x
f
y
Prosta
n
mx
y
jest asymptotą ukośną obustronną
Y
X
)
(x
f
y
0
)]
(
)
(
[
lim
n
mx
x
f
x
0
)]
(
)
(
[
lim
n
mx
x
f
x
n
mx
y
Rys. 7.
Uwaga.
Asymptoty poziome można traktować jako szczególny przypadek asymptot ukośnych (
0
m
).
Twierdzenie.
1. Jeżeli istnieją skończone granice:
)
(
lim
x
x
f
m
x
oraz
)
)
(
(
lim
mx
x
f
n
x
, to prosta
n
mx
jest
asymptotą ukośną lewostronną krzywej
)
(x
f
y
y
.
2. Jeżeli istnieją skończone granice:
x
x
f
m
x
)
(
lim
i
)
)
(
(
lim
mx
x
f
n
x
, to prosta
n
mx
stanowi
asymptotę ukośną prawostronną krzywej
)
(x
f
y
y
.
Uwaga.
Z powyższego twierdzenia wynika, że krzywa może mieć co najwyżej jedną asymptotę ukośną
lewostronną (wliczając w to asymptotę poziomą lewostronną) oraz co najwyżej jedną prawostronną
(wliczając w to poziomą prawostronną).
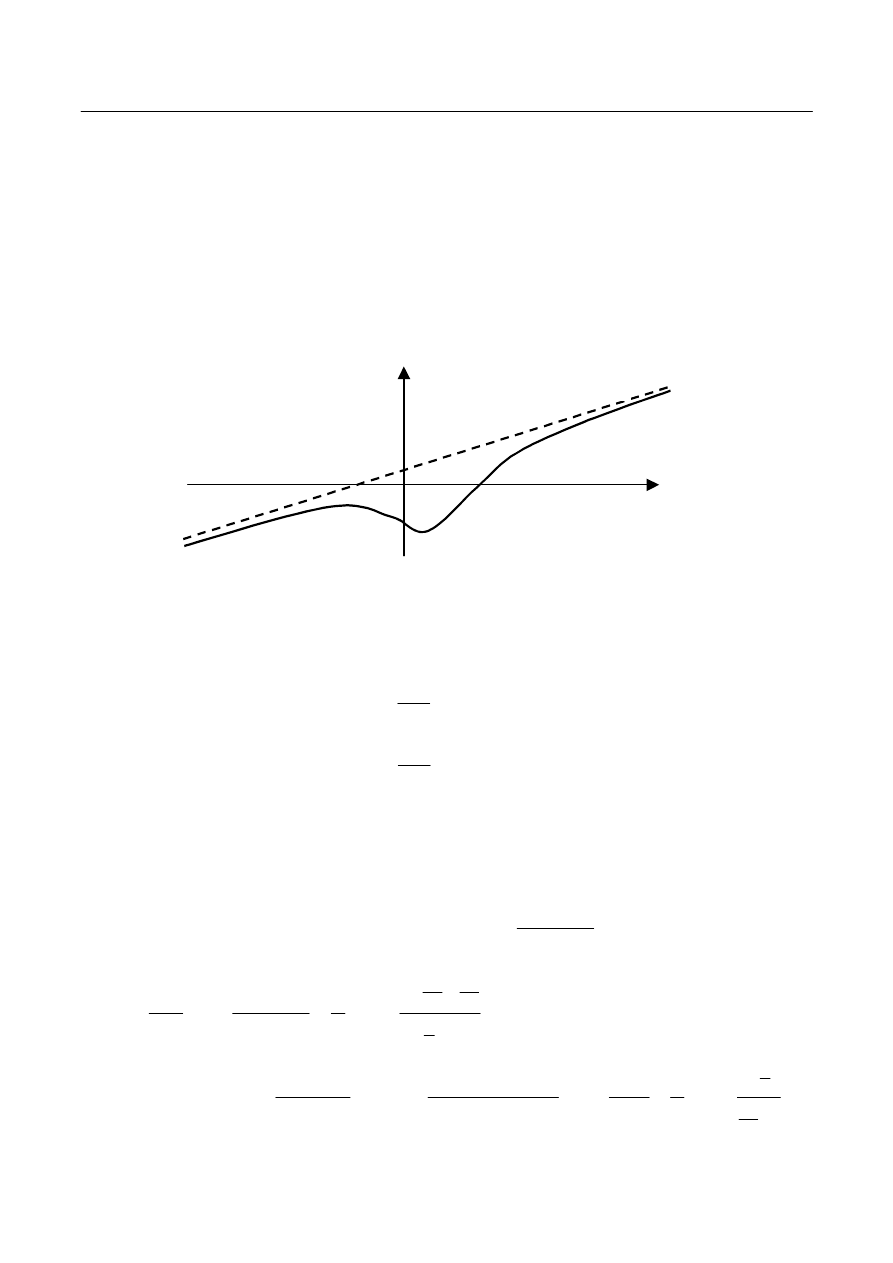
Przykład 6.
Wyznaczyć asymptoty ukośne krzywej: a)
2
3
1
4
6
)
(
x
x
x
x
f
, b)
.
x
x
x
f
arctg
)
(
Rozwiązanie. a) Badamy najpierw istnienie asymptoty ukośnej lewostronnej. Ponieważ
1
1
1
4
6
1
lim
]
[
4
6
lim
)
(
lim
3
2
3
3
x
x
x
x
x
x
x
x
x
f
m
x
x
x
,
2
2
1
lim
)
1
(
lim
]
)
(
[
lim
x
x
x
mx
x
f
n
x
x
x
3
3
3
4
6
4
6
x
x
x
x
x
x
0
1
1
7
lim
]
[
1
7
lim
2
2
x
x
x
x
x
x
Wykład 10. Asymptoty wykresu funkcji
6
Y
X
y
x
y
x
x
x
3
2
6
4
1
Rys. 8.
oraz analogicznie:
1
4
6
lim
)
(
lim
3
3
x
x
x
x
x
x
f
m
x
x
i
0
)
1
4
6
(
lim
]
)
(
[
lim
2
3
x
x
x
x
mx
x
f
n
x
x
, to
asymptotą ukośną (obustronną) jest prosta
x
y
. Wykres
funkcji wraz z jej asymptotą przedstawiony został na rys.8.
b) Szukając asymptoty ukośnej prawostronnej dostajemy
1
0
1
1
)
arctg
1
(
lim
arctg
lim
)
(
lim
]
[
]
[
2
x
x
x
x
x
x
x
f
m
x
x
x
oraz
2
)
(
arctg
arctg
lim
]
)
arctg
[(
lim
]
)
(
[
lim
]
[
x
x
x
x
mx
x
f
n
x
x
x
.
Podobnie w przypadku asymptoty ukośnej lewostronnej mamy
1
0
1
1
)
arctg
1
(
lim
arctg
lim
)
(
lim
]
[
]
[
2
x
x
x
x
x
x
x
f
m
x
x
x
,
2
)
(
arctg
arctg
lim
]
)
arctg
[(
lim
]
)
(
[
lim
]
[
x
x
x
x
mx
x
f
n
x
x
x
.
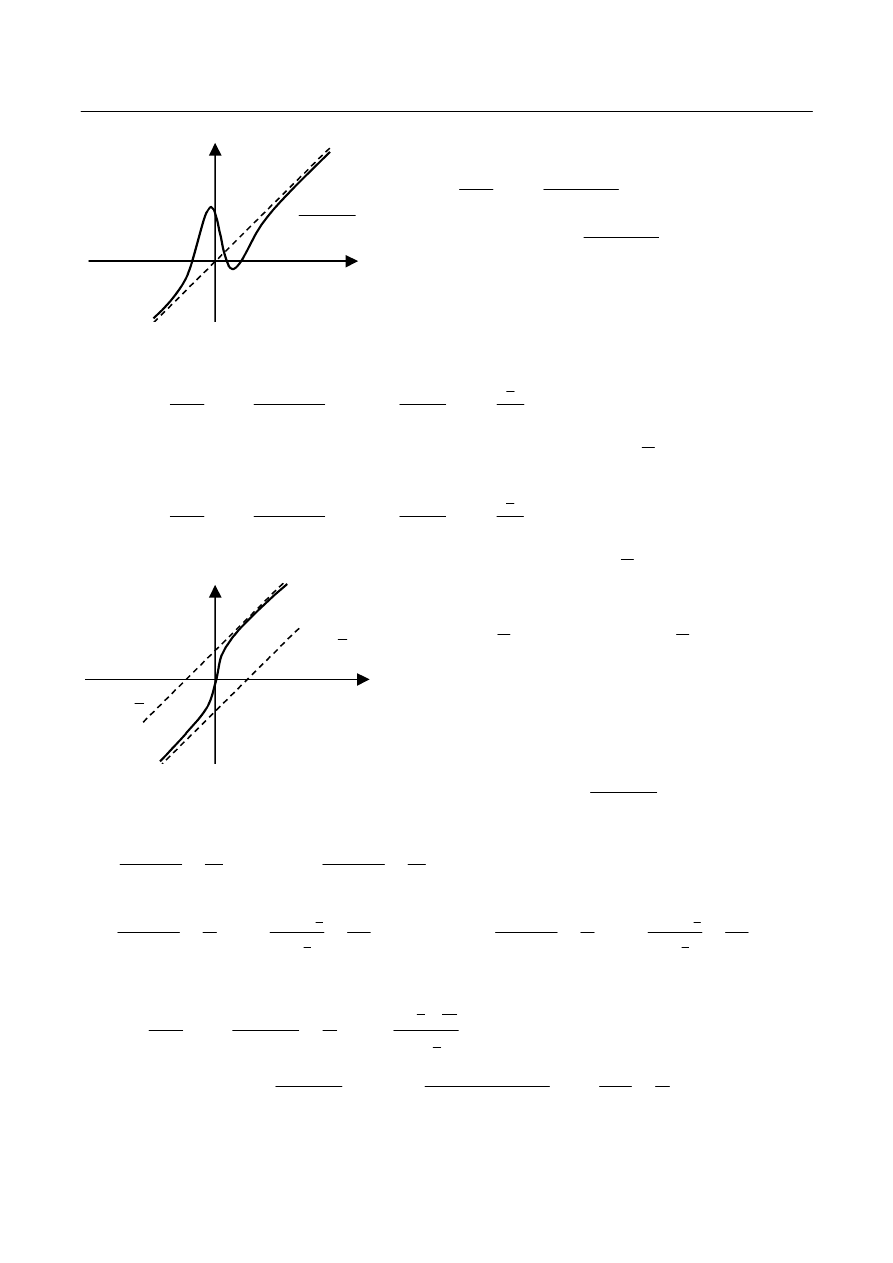
Y
X
2
x
y
x
x
x
f
arctg
)
(
2
x
y
Rys.9.
Funkcja posiada asymptotę ukośną prawostronną
2
x
y
2
x
y
i lewostronną
. Proste te są
do siebie równoległe, gdyż mają ten sam
współczynnik kierunkowy. Ilustrację graficzną
przedstawia rys.9.
Przykład 7. Wyznaczyć równania wszystkich asymptot funkcji:
1
1
)
(
2
x
x
x
x
f
.
Rozwiązanie. Mamy tutaj
.
\ { 1}
f
D
R
2
1
1
1
lim
1
0
[ ]
x
x
x
x
,
2
1
1
1
lim
1
0
[ ]
x
x
x
x
. Oznacza to, że funkcja posiada asymptotę
pionową o równaniu
.
1
x
1
2
1
1
1
lim
lim
1
1
1
[ ]
[ ]
x
x
x
x
x
x
x
x
oraz
1
2
1
1
1
lim
lim
1
1
1
[ ]
[ ]
x
x
x
x
x
x
x
x
.
Wynika stąd, że funkcja nie posiada asymptot poziomych, może natomiast posiadać asymptoty ukośne.
Poszukując asymptot ukośnych mamy
1
1
1
lim
1
lim
)
(
lim
1
2
1
1
2
2
]
[
x
x
x
x
x
x
x
x
x
x
x
x
f
m
,
0
1
1
1
lim
1
1
lim
1
1
lim
]
)
(
[
lim
]
[
)
(
2
2
2
x
x
x
x
x
x
x
x
x
x
mx
x
f
n
x
x
x
x
.
Analogiczne granice otrzymujemy przy
x
. Oznacza to, że funkcja posiada asymptotę ukośną
x
y
.