Tomasz Kowalski
Wykłady z matematyki dla studentów kierunków ekonomicznych
Wykład 12
PODSTAWOWE TWIERDZENIA RACHUNKU RÓŻNICZKOWEGO
FUNKCJI JEDNEJ ZMIENNEJ
1. Różniczka funkcji i jej zastosowania
Niech
f będzie funkcją mającą pochodną w punkcie x. Różny od zera przyrost
x
zmiennej niezależnej
nazywamy różniczką tej zmiennej i oznaczamy symbolem dx.
Różniczką df funkcji f w punkcie x dla przyrostu dx nazywamy iloczyn
.
dx
x
f
df
)
(
0
/
Wzory na różniczki otrzymujemy więc dopisując do pochodnych wyrażenie dx.
Przykład 1.
Obliczyć różniczki funkcji: a)
x
x
x
f
cos
)
(
, b)
.
x
x
e
x
f
4
2
)
(
Rozwiązanie.
a) Ponieważ
, to
x
x
x
x
x
x
f
sin
cos
)
cos
(
)
(
/
/
dx
x
x
x
df
)
sin
(cos
.
b) Mamy tutaj
i tym samym
.
)
4
2
(
)
(
)
(
4
/
4
/
x
e
e
x
f
x
x
x
x
2
2
dx
x
e
df
x
x
)
4
2
(
4
2
Z definicji pochodnej funkcji w punkcie wynika, że w przypadku, gdy pochodna w punkcie
istnieje,
to dla małyc
x
ma miejsce przybliżony wzó
0
x
h
r:
)
0
x
(
)
(
)
(
/
0
0
f
x
x
f
x
x
f
, z którego otrzymujemy
x
x
f
x
f
x
x
f
)
(
)
(
)
(
0
/
0
0
.
Wzór ten służy do przybliżonych obliczeń.
Zapisując w powyższym wzorze przyrost
x
jako
0
x
x
dostajemy następujący wariant wzoru:
.
)
)(
(
)
(
)
(
0
0
/
0
x
x
x
f
x
f
x
f
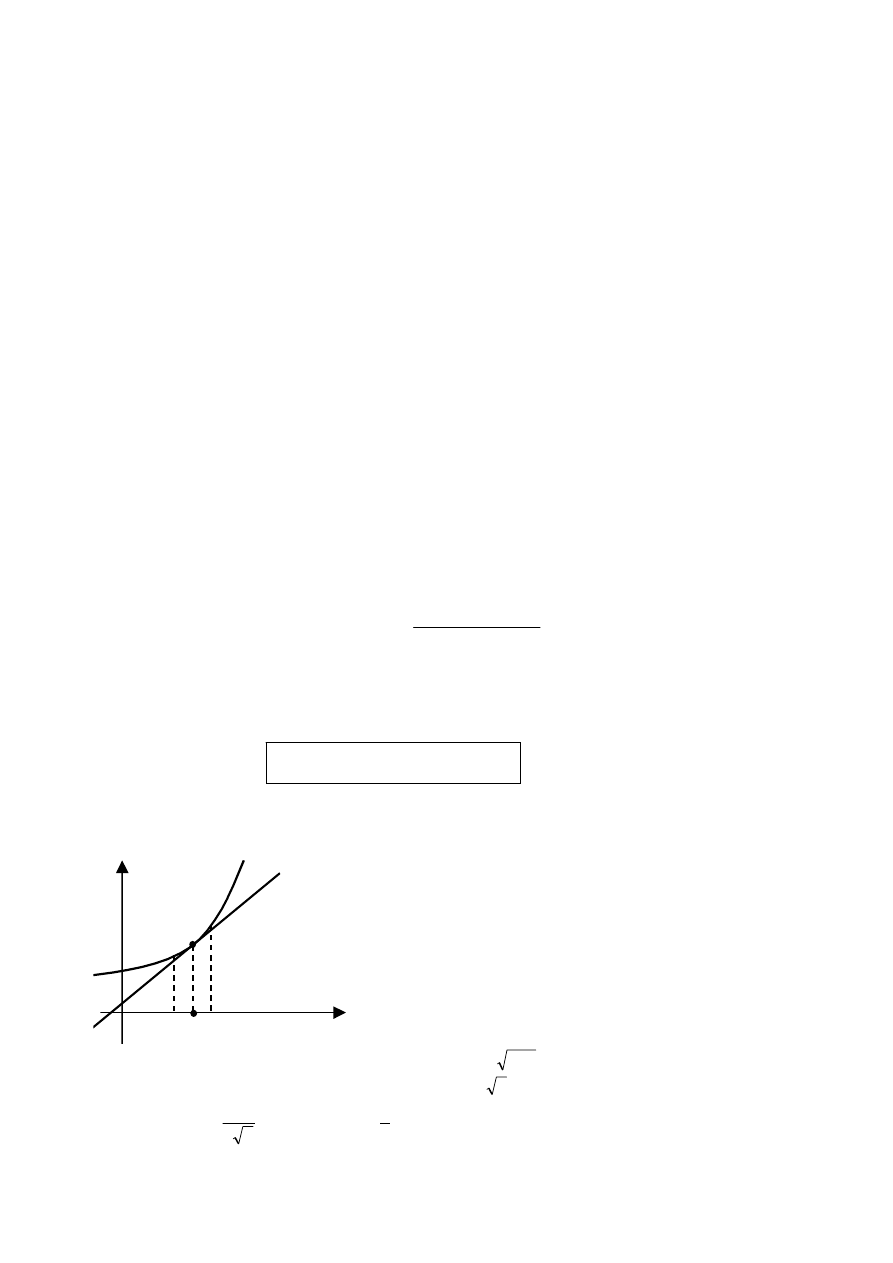
Interpretację geometryczną tego wzoru przedstawia rys.1. Wynika z niej, że w pewnym przedziale zawie-
rającym
funkcję f można przybliżyć odpowiednią styczną do jej wykresu.
0
x
Uwaga.
Aby obliczyć przybliżoną wartość
należy możliwie blisko punktu x znaleźć
taki punkt
, aby
oraz
dały się
łatwo obliczyć, a następnie zastosować podany
wyżej wzór.
)
(x
f
y
)
)(
(
)
(
0
0
/
0
x
x
x
f
x
f
y
X
Y
0
x
Rys. 1.
)
(x
f
)
(
0
/
x
f
0
x
)
(
0
x
f
Przykład 2.
Obliczyć przybliżoną wartość wyrażenia: a)
4
,
16 , b)
.
8
,
0
arctg
Rozwiązanie. a) Wyrażenie to jest wartością funkcji
x
x
f
)
(
dla
4
,
16
x
. Przyjmując
mamy
,
16
0
x
4
)
(
0
x
f
x
x
f
2
1
)
(
/
i dalej
8
1
)
(
0
/
x
f
. Zatem po wstawieniu do wzoru
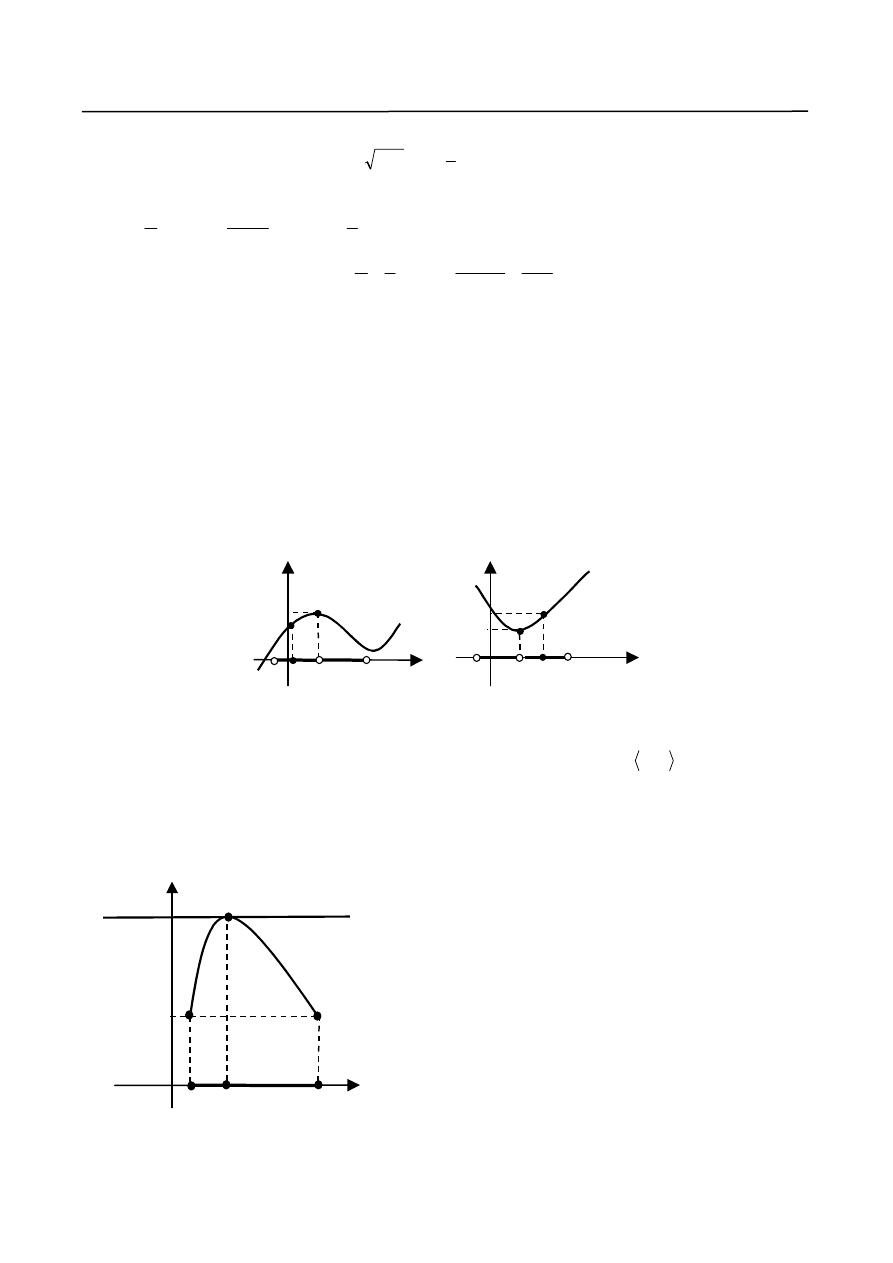
Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
2
05
,
4
4
,
0
8
1
4
4
,
16
.
b) Wyrażenie jest wartością funkcji
8
,
0
arctg
x
x
f
arctg
)
(
dla
8
,
0
x
. Przyjmując
mamy
1
0
x
4
)
(
0
x
f
,
2
/
1
)
(x
1
x
f
,
2
1
)
(
0
/
x
f
. Stąd wstawiając do wzoru otrzymujemy
685
,
0
4
74
,
2
4
4
,
0
)
2
,
0
(
2
1
4
8
,
0
arctg
.
2.
Monotoniczność funkcji. Ekstrema
Niech f będzie funkcją określoną w punkcie
. Jeżeli istnieje takie sąsiedztwo S tego punktu, że
funkcja jest w nim określona i spełnia warunek
x
0
)
x
)
(
(
0
x
f
f
dla każdego
S
x
, to mówimy, że posiada
ona w punkcie
maksimum właściwe. Podobnie, jeżeli spełnia warunek
, to mówimy, że
posiada w punkcie
minimum właściwe.
x
0
)
(
0
x
f
)
(x
f
x
0
Maksima i minima nazywamy ekstremami.
Na rys.2. przedstawiona została ilustracja graficzna ekstremów.
maksimum właściwe
Y
y
f x
( )
X
S
f x
f x
( )
( )
0
x
0
x
minimum właściwe
Y
y
f x
( )
X
S
)
(
)
(
0
x
f
x
f
x
0
x
Rys. 2.
Twierdzenie
(Rolle'a).
Jeżeli f jest funkcją ciągłą na przedziale domkniętym
b
a
; , różniczkowalną
wewnątrz tego przedziału i przyjmującą na jego końcach równe wartości
)
)
(
)
(
(
b
f
a
f
, to istnieje taki
punkt
)
;
( b
a
, że
.
0
)
(
/
f
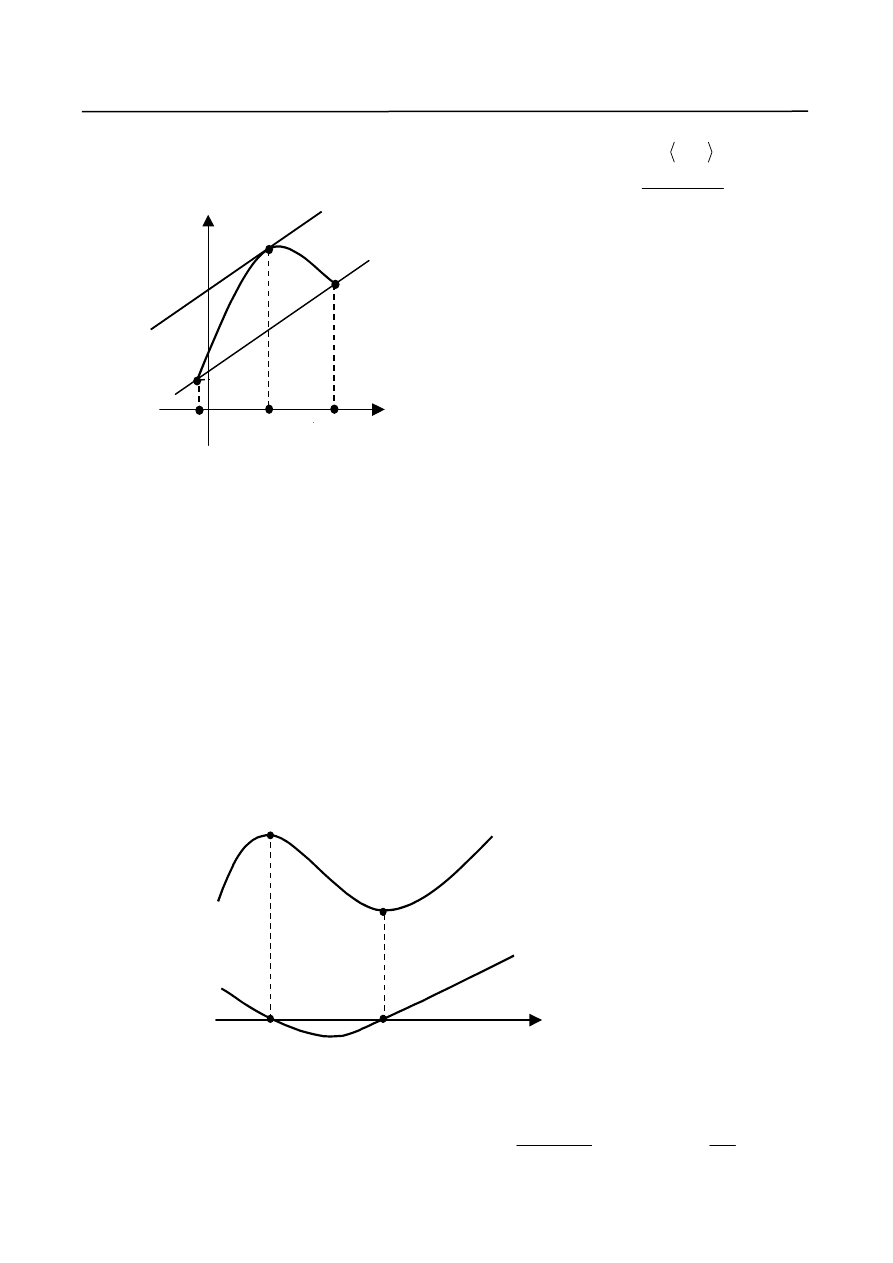
Rys.3. przedstawia interpretację geometryczną tego twierdzenia.
f a
f b
( )
( )
a
b
y
f x
( )
P
f
( , ( ))
Y
X
Rys. 3
Istnieje punkt
t. że współczynnik kierunkowy
stycznej do wykresu funkcji w punkcie
jest rów-
ny zeru, tzn. styczna jest równoległa do osi
OX
.
( , )
a b
P
f
( , ( ))
Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
3
Twierdzenie (Lagrange'a).
Jeżeli f jest funkcją ciągłą na przedziale domkniętym
b
a
;
i różnicz-
kowalną wewnątrz tego przedziału, to istnieje taki punkt
)
;
(
b
a
, że
a
b
a
f
b
f
f
)
(
)
(
)
(
/
.
a
b
X
y
f x
( )
P a f a
1
( , ( ))
P b f b
2
( , ( ))
P
f
( , ( ))
Y
Rys. 4.
Na rys.4. przedstawiona została interpretacja gra-
ficzna tego twierdzenia.
Istnieje punkt
t. że styczna do wykresu funkcji
( , )
a b
y
f x
( ) w punkcie P
f
( , ( ))
ma współczynnik kierunkowy
identyczny jak prosta przechodząca przez punkty
,
, tzn. styczna jest równoległa do siecznej przechodzą-
cej przez punkty i
.
P a f a
1
( , ( ))
P b f b
2
( , ( ))
P
1
P
2
Z
powyższych twierdzeń wynikają następujące twierdzenia dotyczące monotoniczności i ekstremów
funkcji:
Twierdzenie.
Jeżeli dla
, to f jest funkcją stałą na tym przedziale.
0
)
(
/
x
f
)
;
( b
a
x
Jeżeli dla
, to f jest funkcją rosnącą na tym przedziale, jeżeli natomiast
dla
, to f jest funkcją malejącą na tym przedziale.
0
)
(
/
x
f
)
;b
)
;
( b
a
x
0
)
(
/
x
f
(a
x
Twierdzenie.
Jeżeli f jest funkcją ciągłą w punkcie
i różniczkowalną w pewnym jego sąsiedztwie
x
0
)
;
(
0
x
S
S
przy czym
1.
, to w punkcie
występuje maksimum.
0
/
0
/
dla
0
)
(
oraz
dla
0
)
(
x
x
x
f
x
x
x
f
x
0
2.
, to w punkcie
występuje minimum.
0
/
0
/
dla
0
)
(
oraz
dla
0
)
(
x
x
x
f
x
x
x
f
x
0
Uwaga.
W samym punkcie
pochodna może nie istnieć, jeżeli jednak
istnieje to równa się
zeru.
x
0
)
(
0
/
x
f
Ilustrację graficzną powyższych twierdzeń przedstawia rys.5.
y
f x
( )
Znak
)
(
/
x
f
+
+
funkcja maleje
funkcja rośnie
maksimum
minimum
x
0
//
x
0
/
funkcja
rośnie
X
Rys. 5.
Przykład 3.
Wyznaczyć przedziały monotoniczności oraz ekstrema funkcji:
a) , b)
, c)
5
9
6
)
(
2
3
x
x
x
x
f
x
xe
x
f
3
)
(
2
5
4
)
(
2
x
x
x
x
f
, d)
x
x
x
f
ln
)
(
.
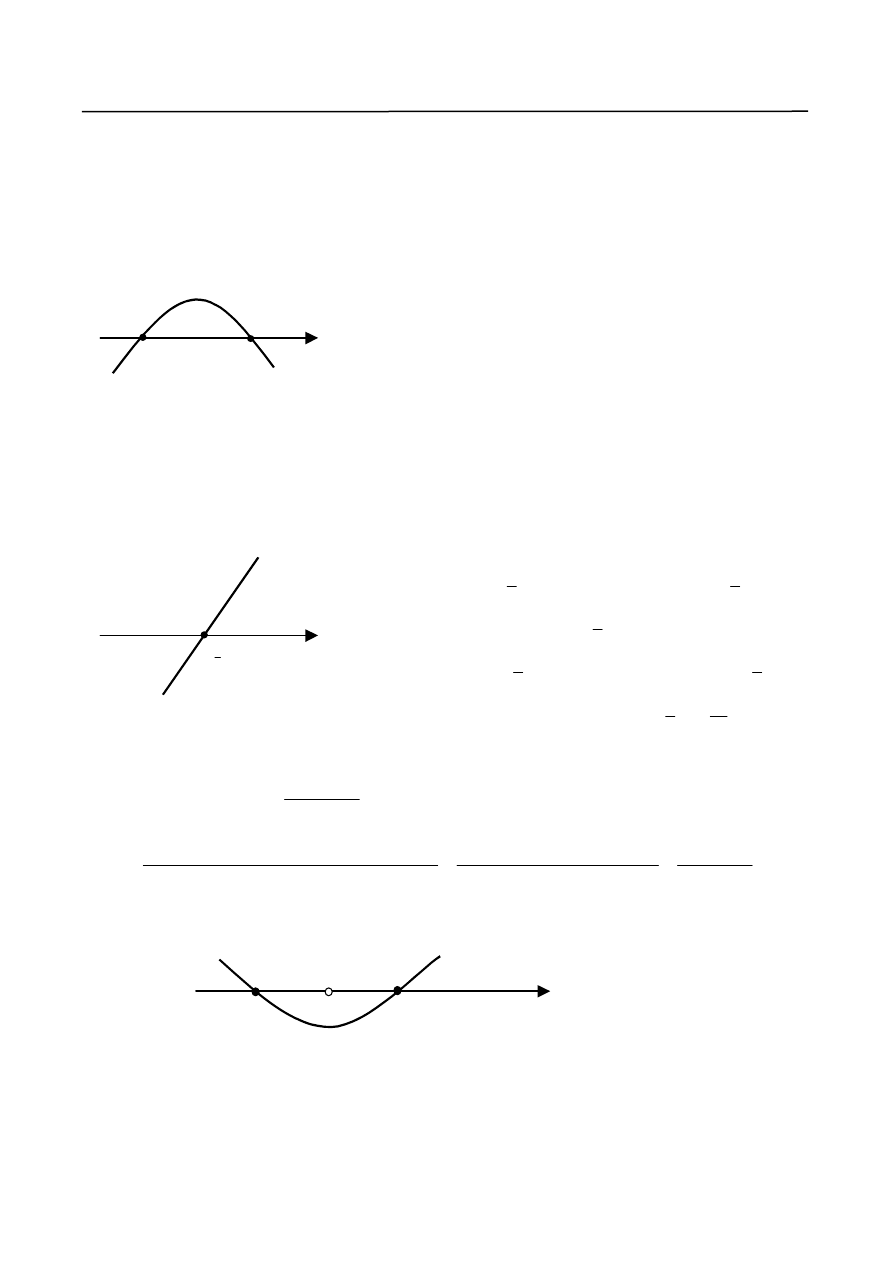
Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
4
Rozwiązanie.
a) Dziedziną funkcji jest
R
D
f
. Pochodną funkcji jest
)
3
4
.
(
3
9
12
3
)
(
2
2
/
x
x
x
x
x
f
Oznacza to, że znak pochodnej jest taki sam jak znak funkcji
, której szkic wykresu
przedstawiony jest na rys.6.
3
4
)
(
2
x
x
x
g
)
3
;
1
(
0
)
(
/
x
x
f
1
;
(
0
)
(
/
x
x
f
)
3
;
1
(
)
;
3
(
),
1
;
(
,
. Na podstawie po-
wyższych twierdzeń wnioskujemy, że funkcja rośnie
w przedziale
, maleje w przedziałach:
X
3
4
)
(
2
x
x
x
g
Znak
f x
/
( )
_ _
+ + +
_ _
1
3
)
;
3
(
)
. W punkcie
1
1
x
1
osiąga minimum
wynoszące
Rys. 6.
b) Dziedziną funkcji jest
. Obliczamy pochodną funkcji:
.
R
D
f
)
3
1
(
3
)
(
3
3
3
/
x
e
xe
e
x
f
x
x
x
Ponieważ
dla każdego
, zatem znak pochodnej jest identyczny w zbiorze R jak znak funk-
cji , której szkic wykresu przedstawiony jest na rys.7.
0
3
x
e
1
3
x
R
x
)
(
x
g
X
y
x
3
1
1
3
Znak
f x
/
( )
+ + +
_ _ _
c) Dziedziną funkcji
2
5
4
)
(
2
x
x
x
x
f
jest
)
;
2
(
)
2
;
(
f
D
.
Obliczamy pochodną funkcji:
2
/
2
/
2
/
)
2
(
)
2
)(
5
4
(
)
2
(
)
5
4
(
)
(
x
x
x
x
x
x
x
x
f
2
2
)
2
(
)
5
4
(
)
2
)(
4
2
(
x
x
x
x
x
2
2
)
2
(
3
4
x
x
x
.
W rozpatrywanej dziedzinie mianownik wyrażenia jest dodatni, zatem znak pochodnej i miejsca zerowe są
identyczne jak w przypadku funkcji
, której szkic wykresu przedstawiony jest na rys.8.
3
4
)
(
2
x
x
x
g
x
1
1
x
2
3
X
+
+
Znak
f x
/
( )
2
Rys. 8.
Wynika z niego, że funkcja rośnie w przedziałach: )
;
3
(
,
)
1
;
(
, maleje natomiast w przedziałach:
. W punkcie
funkcja osiąga maksimum równe
)
3
;
2
(
,
)
2
;
1
(
x
1
1
f
f
x
( )
ma
1
2 , w punkcie x
2
3
minimum równe
.
f
f
min
( )
3
2
)
;
3
1
(
0
)
(
/
x
x
f
,
)
3
1
;
(
0
)
(
/
x
x
f
.
Wynika stąd że w przedziale
)
;
3
1
(
funkcja rośnie,
w przedziale
)
3
1
;
(
funkcja maleje, w punkcie
3
1
x
funkcja osiąga minimum równe
e
f
f
3
1
)
3
1
(
min
.
Rys. 7.
)
1
(
min
f
f
max
, w punkcie
maksi-
mum wynoszące
3
2
x
.
f
f
5
)
3
(

Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
5
d) Dziedziną funkcji
x
x
x
f
ln
)
(
jest
)
;
0
(
f
D
. Obliczamy pochodną funkcji:
2
2
ln
1
ln
x
x
x
2
/
/
/
1
)
(
ln
)
(ln
)
(
x
x
x
x
x
x
x
x
x
f
.
W rozpatrywanej dziedzinie znak pochodnej jest identyczny jak znak funkcji
, której wykres
przedstawiony jest na rys.9.
x
x
g
ln
1
)
(
Ponieważ
X
Y
e
g x
x
( )
ln
1
)
;
0
(
0
)
(
/
e
x
x
f
,
,
)
;
(
0
)
(
/
e
x
x
f
to w przedziale
funkcja rośnie, a w przedziale
maleje.
W punkcie
)
;
0
(
e
)
;
(
e
Rys. 9.
3. Wklęsłość i wypukłość krzywej. Punkty przegięcia
Niech
f będzie funkcją mającą pochodną w przedziale I. Jeżeli wykres funkcji leży poniżej każdej
stycznej poprowadzonej do niego w dowolnym punkcie o odciętej
I
x
0
, to funkcję (krzywą)
nazywamy w tym przedziale wklęsłą, ( wypukłą w górę). Jeżeli natomiast leży powyżej, to funkcję nazywa-
my wypukłą (wypukłą w dół ).
)
(x
f
y
Jeżeli krzywa
jest wklęsła w pewnym sąsiedztwie
punktu
i wypukła w sąsiedztwie
(lub na odwrót), to punkt
nazywamy punktem przegięcia krzywej.
)
(x
f
y
P
S
x
0
S
))
(
,
(
0
0
x
f
x
Ilustrację tych pojęć przedstawia rys.10.
a
b
x
0
y
f x
( )
funkcja wklęsła
(wypukła w górę)
X
Y
a
b
x
0
y
f x
( )
funkcja wypukła
(wypukła w dół)
X
Y
x
0
y
f x
( )
X
Y
P x f x
( , ( ))
0
0
punkt przegięcia
Rys. 10.
Twierdzenie.
Jeżeli dla punktów przedziału I zachodzi warunek
, to krzywa o równaniu
jest w tym przedziale wklęsła, jeżeli natomiast warunek
, to wypukła.
)
0
)
(
//
x
f
0
)
(
//
x
)
(x
f
y
f
Twierdzenie.
Jeżeli f jest funkcją mającą pochodną w punkcie
i posiadającą drugą pochodną w
pewnym jego sąsiedztwie, przy czym
(lub na odwrót),
x
0
f
0
//
0
//
dla
0
)
(
oraz
dla
0
)
(
x
x
x
x
x
x
f
to
jest punktem przegięcia.
))
(
,
(
0
0
x
f
x
P
e
x
e
e
f
f
1
)
(
min
.
funkcja osiąga minimum
a

Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
6
Przykład 3.
Wyznaczyć punkty przegięcia oraz przedziały, w których funkcja jest wklęsła lub wypukła:
a)
, b)
,
c)
x
f (
3
3
4
)
(
x
x
x
f
x
xe
x
f
2
)
(
x
x ln
)
2
.
Rozwiązanie.
a)
R
D
. Kolejne pochodne są równe
,
.
2
/
3
/
3
3
)
3
4
(
)
(
x
x
x
x
f
x
x
x
f
6
)
3
3
(
)
(
/
2
//
Szkic wykresu funkcji
przedstawia rys.11.
)
(
//
x
f
y
0
Znak f
x
//
( )
+ +
- - -
X
Z wykresu wynika, że oraz
. Oznacza to, na podstawie po-
wyższych twierdzeń, że funkcja jest wypukła w przedziale:
i wklęsła w przedziale (
)
0
;
(
0
)
(
//
x
x
f
)
)
;
0
;
0
(
0
)
(
//
x
x
f
)
0
;
(
. Ponieważ
4
)
0
(
f
P
, to punkt
jest punktem przegięcia.
)
4
,
0
(
Rys. 11.
b) Dziedziną funkcji jest zbiór R. Pierwsza pochodna jest równa
,
)
2
1
(
)
2
(
)
(
2
2
2
/
x
e
xe
e
x
f
x
x
x
druga .
)
4
4
(
)
2
4
2
(
)
2
(
)
2
1
)(
2
(
)
(
2
2
2
2
//
x
e
x
e
e
x
e
x
f
x
x
x
x
Znak drugiej pochodnej jest w rozpatrywanej dziedzinie identyczny jak znak funkcji liniowej
4
4
)
(
x
x
h
,
której wykres (uwzględniający jedynie położenie względem osi OX ) przedstawiony został na rys.12.
Funkcja jest wypukła w przedziale (
)
;
1
, wklęsła w przedziale
. Punkt
jest punktem przegięcia.
1
Znak f
x
//
( )
+ +
- - -
X
)
,
1
(
2
e
P
)
1
;
(
Rys. 12.
c)
. Kolejno mamy tutaj
,
)
;
0
(
D
x
x
x
x
x
x
x
x
x
x
f
ln
2
)
(ln
ln
)
(
)
ln
(
)
(
/
2
/
2
/
2
/
)
2
3
(ln
2
3
ln
2
)
(
)
(ln
2
ln
)
(
2
)
/
/
/
/
x
x
x
x
x
x
x
x
ln
2
(
)
(
//
x
x
x
f
.
W rozpatrywanej dziedzinie znak drugiej pochodnej jest identyczny jak znak funkcji
2
3
ln
)
(
x
x
h
, któ-
rej szkic wykresu funkcji przedstawia rys. 13.
X
Znak f
x
//
( )
+ +
-
1
e e
Y
Obliczenia pomocnicze:
ln
ln
x
x
x e
e e
3
2
0
3
2
1
3
2
Rys. 13.
Z wykresu wynika, że
)
;
1
(
0
)
(
//
e
e
x
x
f
oraz
)
1
;
0
(
0
)
(
//
e
e
x
x
f
. Oznacza to, że funk-
cja jest wypukła w przedziale:
)
;
1
(
e
e
i wklęsła w przedziale
)
1
;
0
(
e
e
. Ponieważ
f
e e
e
e e
e
(
)
ln
1
1
1
3
2
3
3
, to punkt
)
2
3
,
1
(
3
e
e
e
P
jest punktem przegięcia.
Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
7
4. Reguła de l’Hospitala
Twierdzenie.
Jeżeli funkcje
)
(
)
(
x
g
x
f
i
)
(
)
(
/
/
x
g
x
f
są określone w pewnym sąsiedztwie S punktu
oraz
x
0
1.
albo obie granice
są niewłaściwe,
0
)
(
lim
)
(
lim
0
0
x
g
x
f
x
x
x
x
)
(
lim
),
(
lim
0
0
x
g
x
f
x
x
x
x
2. istnieje granica
)
(
)
(
lim
/
/
0
x
g
x
f
x
x
(właściwa lub niewłaściwa),
to istnieje także granica
)
(
)
(
lim
0
x
g
x
f
x
x
, przy czym
)
(
)
(
lim
)
(
)
(
lim
/
/
0
0
x
g
x
f
x
g
x
f
x
x
x
x
.
Uwagi
1. Twierdzenie pozostaje prawdziwe dla granic jednostronnych oraz dla granic w nieskończoności.
2. Jeżeli przy obliczaniu granicy
)
(
)
(
lim
/
/
0
x
g
x
f
x
x
otrzymamy symbol nieoznaczony typu
]
[
0
0
lub
]
[
, to moż-
na
stosować regułę de l'Hospitala ponownie.
3. Z twierdzenia tego można korzystać przy obliczaniu granic w przypadku pozostałych symboli
nieoznaczonych:
]
[
]
[
]
[
]
[
]
[
0
0
,
1
,
0
,
0
,
po uprzednim sprowadzeniu tych granic do granic typu
]
[
0
0
lub
]
[
.
Przykład 4.
Obliczyć granice stosując regułę de l’Hospitala: a)
1
ln
lim
1
x
x
x
,
b)
x
x
x
)
1
ln(
lim
2
,
c)
1
cos
1
lim
2
0
x
e
x
x
, d)
)
1
(
lim
1
x
x
e
x
, e)
x
x
x
tg
)
2
(
lim
2
, f)
)
sin
1
1
(
lim
0
x
x
x
, g)
)
1
1
1
(
lim
0
x
e
x
x
.
Rozwiązanie.
a) Stosując bezpośrednio regułę de l’Hospitala mamy:
1
1
1
lim
)
1
(
)
(ln
lim
0
0
1
ln
lim
1
/
/
1
1
]
[
x
x
x
x
x
x
x
x
.
b) Podobnie stosując dwukrotnie regułę de l’Hospitala dostajemy
1
1
2
lim
)
(
))
1
(ln(
lim
)
1
ln(
lim
2
/
/
2
2
]
[
x
x
x
x
x
x
x
x
x
/
2
/
2
)
1
(
)
2
(
lim
1
2
lim
]
[
x
x
x
x
x
x
0
2
2
2
lim
]
[
x
x
.
W dalszych przykładach litera H nad znakiem równości oznacza powołanie się na twierdzenie de
l’Hospitala.
c)
2
cos
)
2
(
2
lim
0
0
sin
2
lim
0
0
1
cos
1
lim
2
2
2
2
0
0
2
0
]
[
]
[
x
e
x
e
x
xe
x
e
x
x
x
H
x
x
H
x
x
.

Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
8
d)
2
2
1
1
1
1
)
1
(
lim
0
0
1
lim
0
)
1
(
lim
]
[
]
[
1
x
x
e
e
e
x
x
x
H
x
x
x
x
x
1
lim
0
e
e
x
x
1
.
e)
1
sin
1
1
lim
0
0
ctg
2
lim
0
tg
)
2
(
lim
2
2
2
2
]
[
]
[
x
x
x
x
x
x
H
x
x
.
f)
H
x
H
x
x
x
x
x
x
x
x
x
x
x
x
cos
sin
1
cos
lim
0
0
sin
sin
lim
)
sin
1
1
(
lim
0
0
0
]
[
]
[
0
2
0
sin
cos
cos
sin
lim
0
x
x
x
x
x
x
.
g)
H
x
x
x
x
x
e
x
e
x
x
e
]
[
]
[
0
0
)
1
(
1
lim
)
1
1
1
(
lim
0
0
2
1
lim
0
0
1
1
lim
0
0
]
[
x
x
x
x
x
H
x
x
x
x
xe
e
e
e
xe
e
e
.
5. Wzór Taylora i Maclaurina
Uogólnienie wzoru do obliczeń przybliżonych z użyciem równania stycznej podaje następujące twierdze-
nie Taylora:
Jeżeli f jest funkcją mającą ciągłą pochodną rzędu n + 1 na pewnym przedziale I o środku x0 i długości
2d, to dla każdego x z tego przedziału zachodzi wzór:
/
//
( )
2
0
0
0
0
0
0
( )
( )
( )
( )
( )
(
)
(
)
...
(
1!
2!
!
n
n
f x
f
x
f
x
0
)
f x
f x
x x
x x
x x
n
,
przy czym błąd przybliżenia nie przekracza
(
1)
( )
max
(
1)!
n
n
x I
f
x
d
n
.
Dla każdej funkcji elementarnej wielkość
zmierza do zera, gdy n dąży do nieskończoności, a to ozna-
cza, że wybierając dostatecznie duże n we wzorze można uzyskać żądaną dokładność.
Przyjmując x0 = 0 we wzorze Taylora otrzymujemy następujący tzw. wzór Maclaurina:
/
//
( )
2
(0)
(0)
(0)
( )
(0)
...
1!
2!
!
n
n
f
f
f
f x
f
x
x
x
n
,
przy czym błąd przybliżenia nie przekracza
(
1)
( )
max
(
1)!
n
n
x I
f
x
d
n
.
Uwaga.
Wyrażenie występujące po prawej stronie wzoru Maclaurina jest wielomianem stopnia n. Oznacza to, że
wzór ten pozwala zastępować funkcję odpowiednim wielomianem. Dokładność przybliżenia jest tym lepsza
im większe n zostanie użyte we wzorze.
Przykład 5.
Zastosować wzór Maclaurina dla funkcji ( )
x
f x
e
przyjmując
5
n
, a następnie z jego
pomocą obliczyć e.
Wykład 12. Podstawowe twierdzenia rachunku różniczkowego
9
Rozwiązanie.
Ponieważ
/
//
( )
( )
( ) ....
( )
V
x
f x
f x
f
x
f
x
e
, to
/
//
0
(0)
(0)
(0) ....
(0)
1
V
f
f
f
f
e
, to wzór
Maclaurina przyjmie postać:
2
3
4
1
1
1
1
1
1
1!
2!
3!
4!
5!
x
e
x
x
x
x
5
x .
Przyjmując w tym wzorze
1
x
otrzymamy
1
1
1
1
1
1 1
1
1
120 120 60 20 5 1 326
1
1 1
2,71667
1! 2! 3! 4! 5!
2 6
24 120
120
120
e
.
Przykład 6.
Dla funkcji
na przedziale
x
x
f
sin
)
(
2
;
2
znaleźć przybliżenie wielomianem stop-
nia 5 posługując się wzorem Maclaurina, a następnie oszacować błąd przybliżenia.
Rozwiązanie. Mamy tutaj
,
,
sin
)
(
,
cos
)
(
//
/
x
x
f
x
x
f
x
x
f
cos
)
(
///
(4)
( ) sin
f
x
x
,
(5)
( ) cos
f
x
x
,
(6)
( )
sin
f
x
x
x
0
0
. Zatem przyjmując
otrzymujemy
,
,
0
( ) sin 0 0
f x
/
0
( ) cos 0
f x
1
//
0
( )
f
x
sin 0 0
///
0
( )
cos0
f
x
,
1
(4)
0
( ) sin
f
x
,
0 0
(5)
0
( )
f
x
,
Stąd po wstawieniu do wzoru Maclaurina otrzymujemy:
cos0 1
2
3
4
1
0
1
0
1
sin
0
1!
2!
3!
4!
5!
5
x
x
x
x
x
x
,
czyli
3
5
1
1
sin
6
120
x x
x
x
.
Błąd przybliżenia nie przekracza
6
6
;
2 2
sin
1
max
( )
( )
0,02
6!
2
6! 2
x
x
.
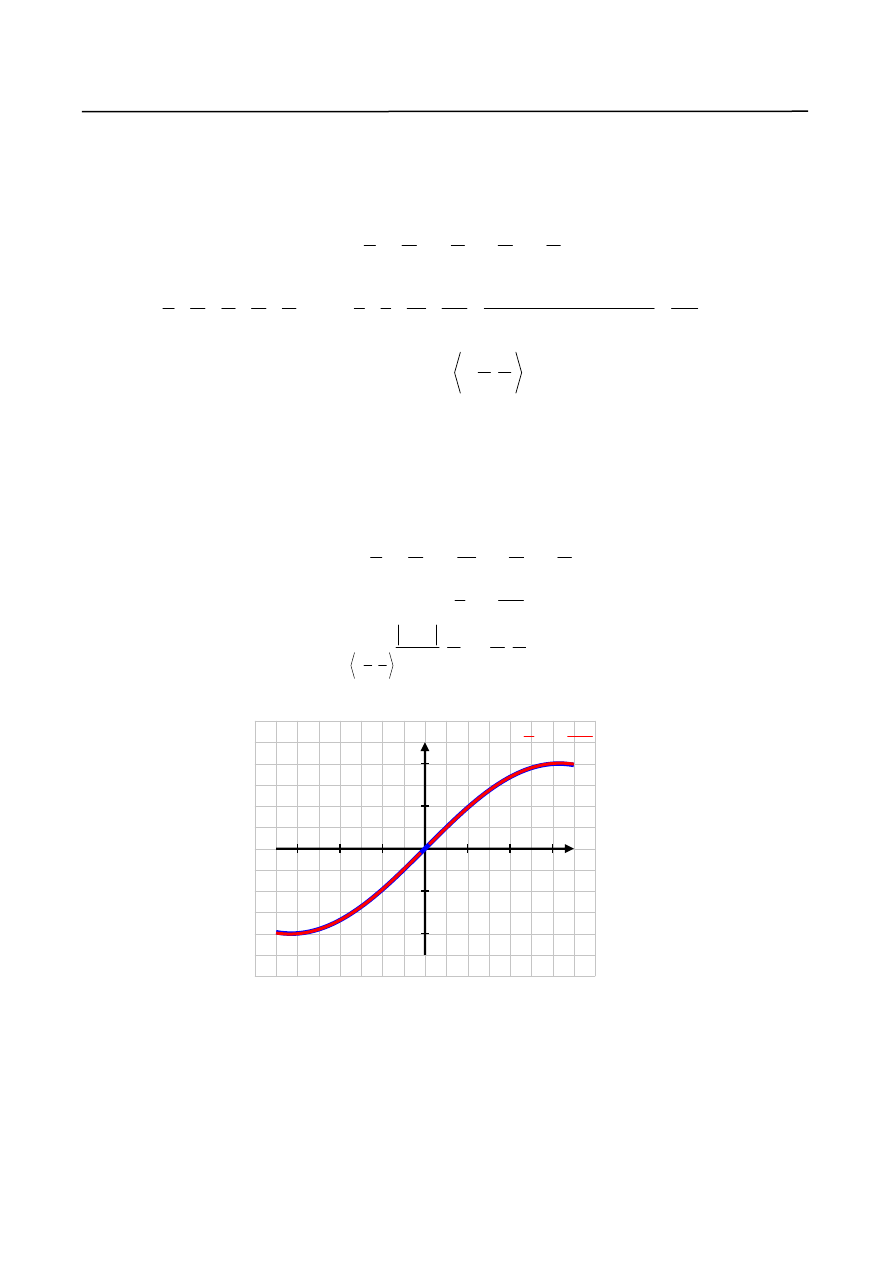
Interpretację graficzną zadania przedstawia rys.14.
-1.5 -1
-0,5
0,5
1
1.5
-1
-0,5
0,5
1
X
Y
sin
y
x
3
5
5
1
1
( )
6
120
W x
x
x
x
Rys.14
.
Wyszukiwarka
Podobne podstrony:
FiR matma L13 id 172577 Nieznany
FiR matma 10 id 172572 Nieznany
lab1 12 id 258878 Nieznany
II CSK 330 12 1 id 209820 Nieznany
Cwiczenie 12 id 99084 Nieznany
Calki, IB i IS, 2011 12 id 1073 Nieznany
zestaw 12 id 587976 Nieznany
ldm rozmaite 12 id 264070 Nieznany
IMG 12 id 210985 Nieznany
Instrukcja 12 id 215508 Nieznany
pamieci 12 id 348557 Nieznany
LITERATURA 12 id 270804 Nieznany
Fizyka i astronomia 12 id 17675 Nieznany
matma zad 1 id 288062 Nieznany
img 12 id 211037 Nieznany
KPG 433 12 id 249386 Nieznany
PMWEU 12 id 363556 Nieznany
BiolMol 12 id 87437 Nieznany (2)
więcej podobnych podstron