CPS 1

2006/2007

SYGNAŁY DYSKRETNE

Definicje:

U

Sygnały dyskretne w czasie

U

reprezentowane są przez ciągi liczb i oznaczane

jako {x[n]}

Elementy tych ciągów nazywa się

U

próbkami

U

, wartości próbek sygnałów oznacza

się jako x[n] dla n całkowitych w zakresie

n

−∞ < < ∞

Sygnały dyskretne w czasie mogą być zapisane:

1. jako zależności pozwalające obliczyć n-tą wartość ciągu. Na przykład:

( )

1

3

0

0

0

n

n

x n

⎧⎪

⎡ ⎤ ⎨

⎣ ⎦

⎪⎩

≥

<

=

lub

{ }

( )

1 1

1

3 9

3

1, , , ,

,

n

x n

⎧

⎫

⎡ ⎤

⎨

⎬

⎣ ⎦

⎩

⎭

=

…

…

2. jako listy wartości ciągów. Na przykład:

{ }

{

}

,1.1, 0.2,2.1,3.0, 1.2,

x n

↑

⎡ ⎤

⎣ ⎦

=

−

−

…

…

gdzie strzałka oznacza próbkę o indeksie

n=0,

lub

1

0.2,

0

2.1, 1

3.0

x

x

x

⎡ ⎤

⎡ ⎤

⎡ ⎤

⎣ ⎦

⎣ ⎦

⎣ ⎦

− = −

=

=

…

…

U

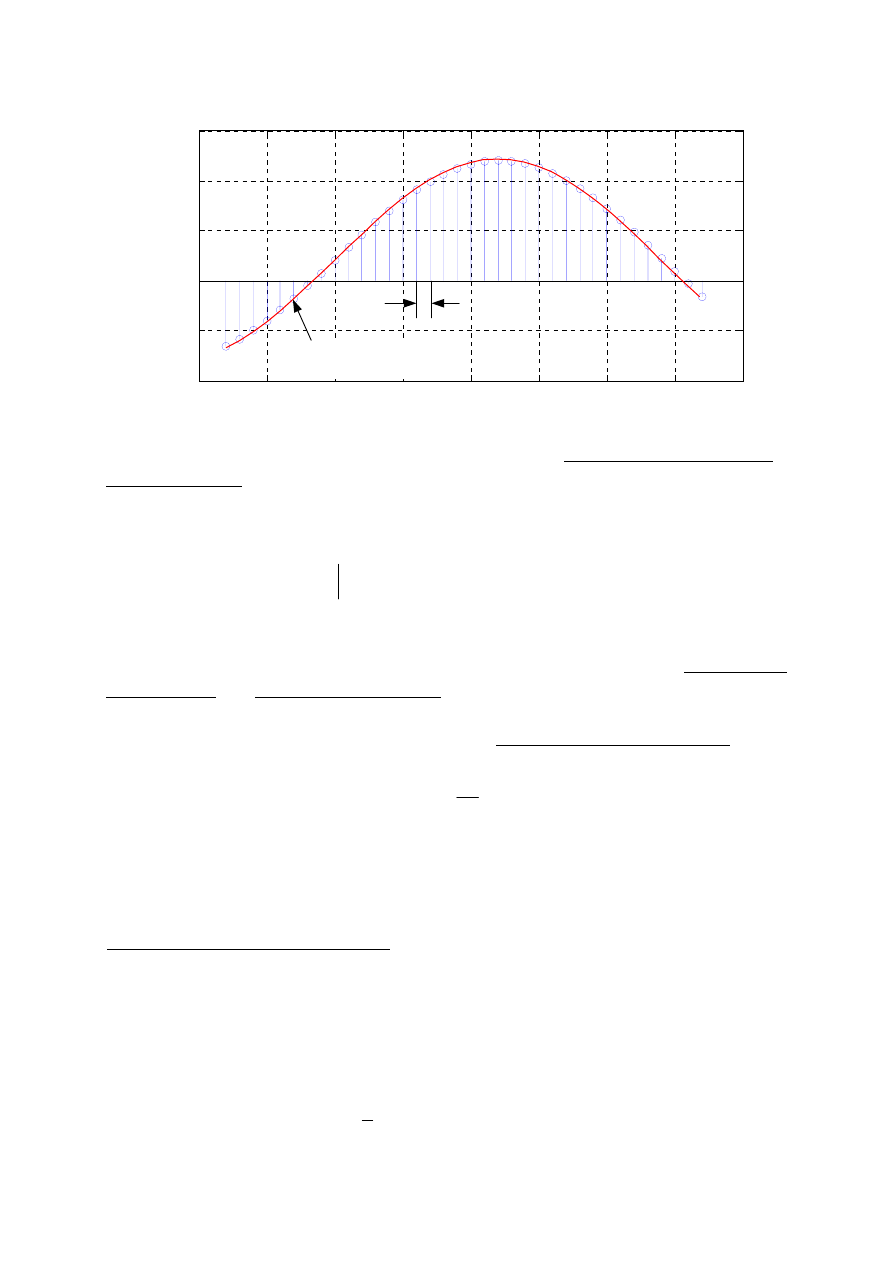
Graficzna reprezentacja sygnału dyskretnego w czasie

U

:

MATLAB

c

lear;

n=-8:1:27;
x=0.2+sin(0.13*n);
plot(n,x);
grid

CPS 2

2006/2007

-10

-5

0

5

10

15

20

25

30

-1

-0.5

0

0.5

1

1.5

n

T

x[-3]=x

a

(-3T)

Sygnał dyskretny najczęściej otrzymuje się w wyniku

U

próbkowania w równych

odstępach czasu

U

sygnału ciągłego w czasie (analogowego).

Wtedy n-tą próbkę opisuje zależność:

( )

( )

,

, 2, 1,0,1,2,

p

p

a

a

t nT

x n

x t

x nT

n

=

⎡ ⎤

⎣ ⎦

=

=

=

− −

…

…

Odległość między kolejnymi próbkami (

T

B

p

B

) nazywa się

U

przedziałem

próbkowania

U

lub

U

okresem próbkowania

U

.

Odwrotność okresu próbkowania nosi nazwę

U

częstotliwości próbkowania

U

i

oznacza się jako

f

B

p

B

1

p

p

f

T

=

Klasyfikacja:

U

Rzeczywiste i zespolone sygnały:

Ze względu na typ wartości próbek sygnały dzielimy rzeczywiste i zespolone.
W

wielu aplikacjach cyfrowego przetwarzania sygnały zespolone mają duże

zastosowanie. Sygnały zespolone wyraża się jako sumę części rzeczywistej i
urojonej:

n

n

jy

z

x

n

⎡ ⎤

⎡ ⎤

⎡ ⎤

⎣ ⎦

⎣ ⎦

⎣ ⎦

+

=

CPS 3

2006/2007

lub w postaci wykładniczej:

( )

arg

j

z n

e

n

n

z

z

⎡ ⎤

⎣ ⎦

⎡ ⎤

⎡ ⎤

⎣ ⎦

⎣ ⎦

=

U

Deterministyczne i przypadkowe

Sygnały

U

deterministyczne

U

są sygnałami, których wartości są znane dla każdej

chwili czasu. Sygnały takie można zamodelować jako funkcje czasu. Sygnały

U

przypadkowe

U

posiadają przypadkowe wartości i muszą być opisywane

statystycznie. Program wykładu nie obejmuje klasy sygnałów przypadkowych.

U

Parzyste i nieparzyste

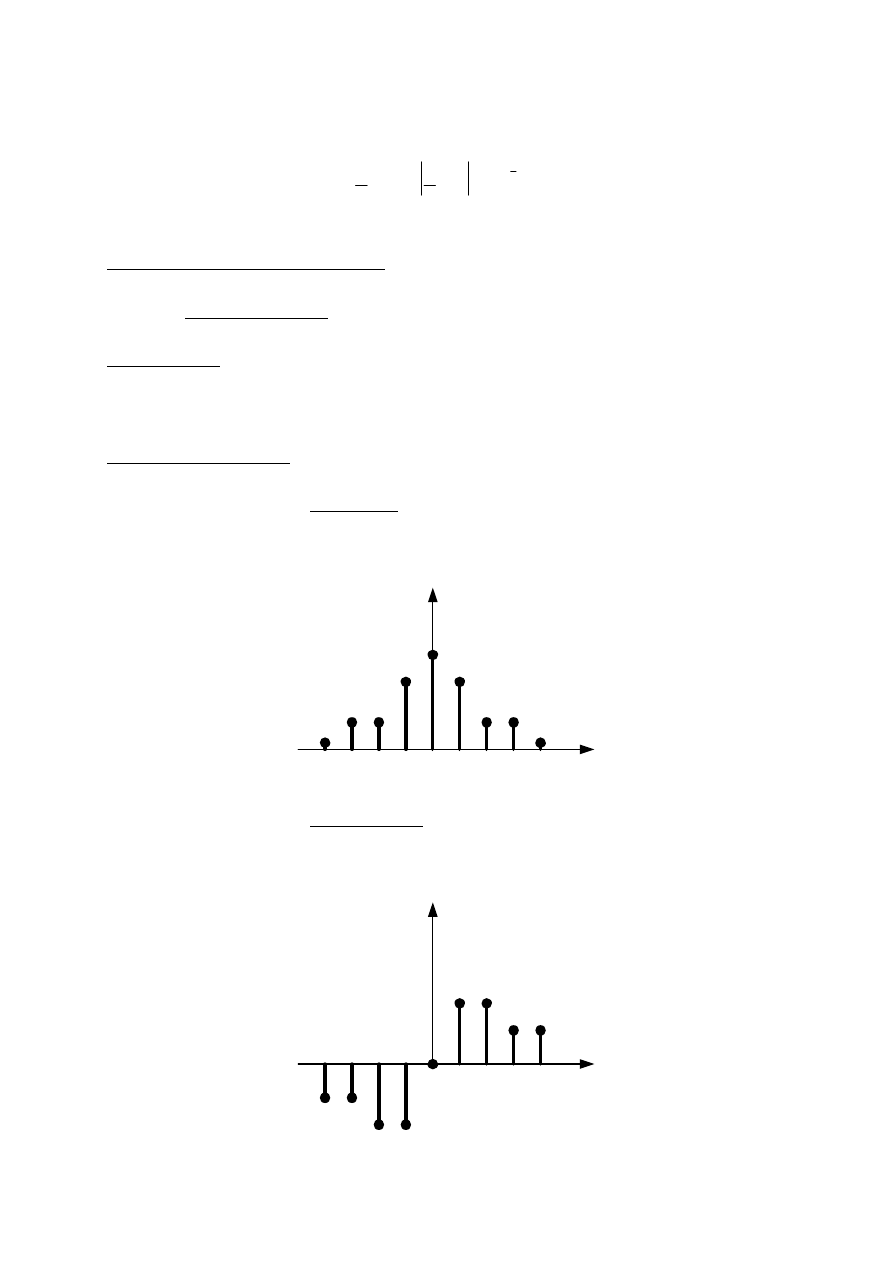
Sygnał x[n] nazywa się

U

parzystym

U

jeżeli:

x

n

n

x

⎡

⎤

⎡ ⎤

⎣

⎦

⎣ ⎦

−

=

x[n]

n

0 1 2 3 4

-1

-2

-3

-4

Sygnał x[n] nazywa się

U

nieparzystym

U

jeżeli:

x

n

n

x

⎡

⎤

⎡ ⎤

⎣

⎦

⎣ ⎦

−

= −

x[n]

n

0 1 2 3 4

-1

-2

-3

-4

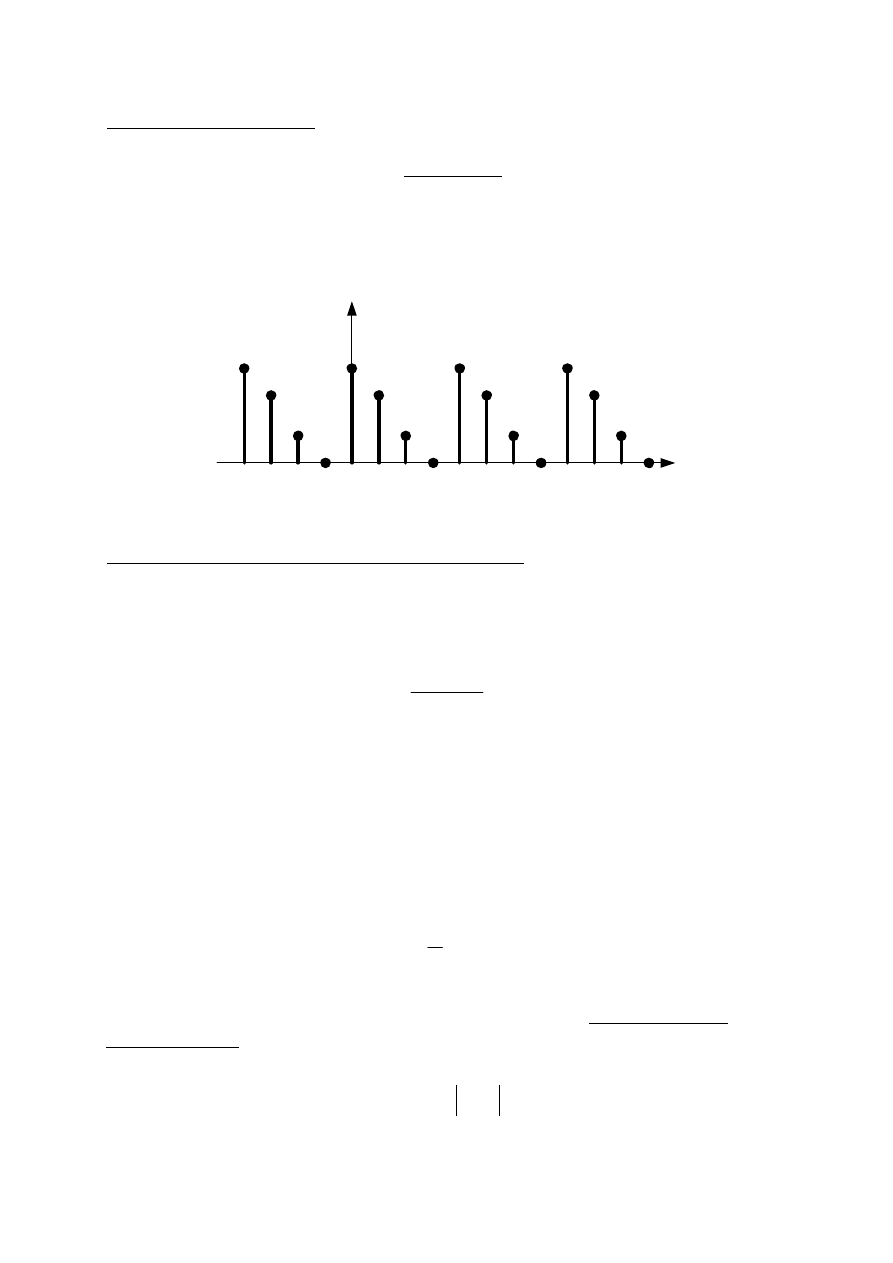
CPS 4

2006/2007

U

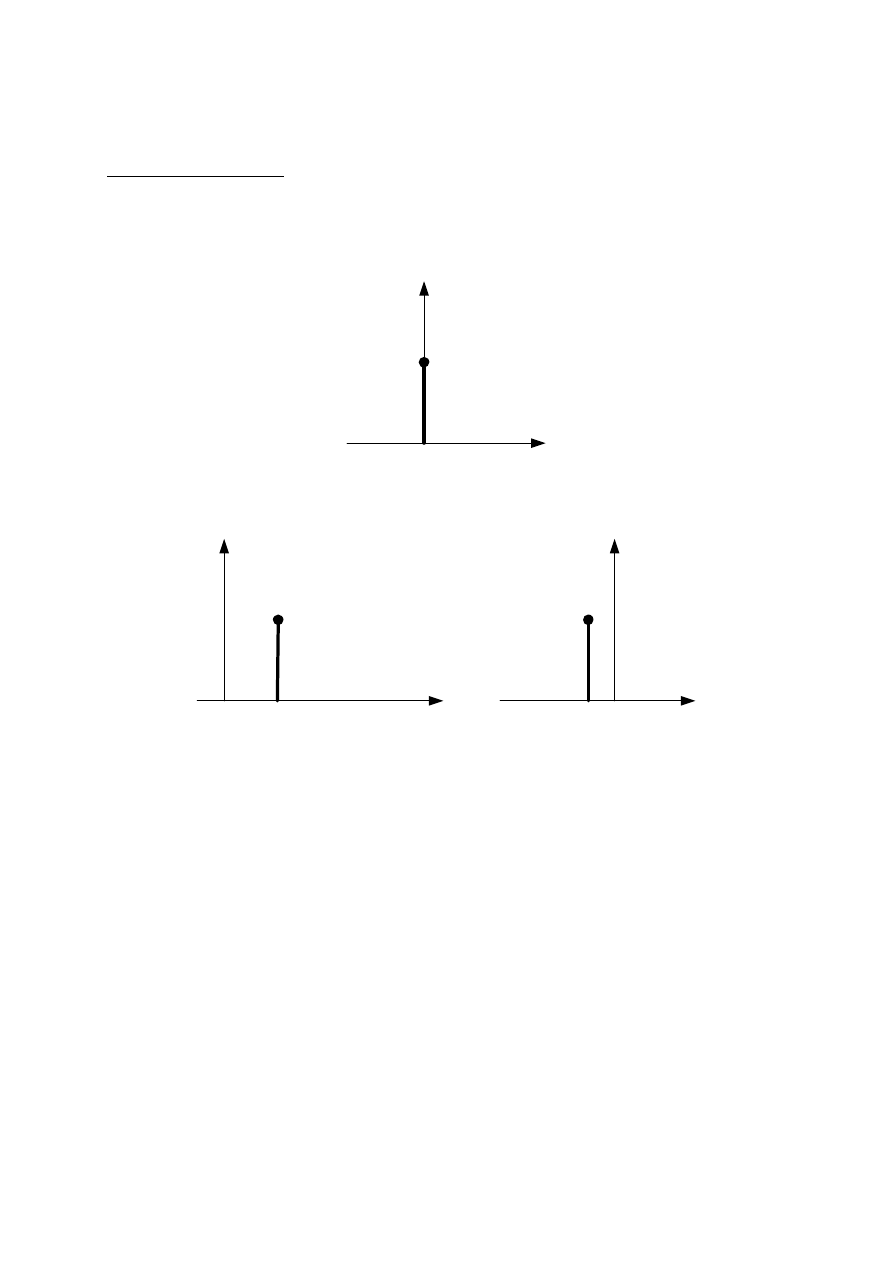
Okresowe i nieokresowe

Sygnał dyskretny x[n] nazywa się

U

okresowym

U

z okresem N (N jest dodatnią

liczbą całkowitą) jeżeli:

x

n N

n

x

⎡

⎤

⎡ ⎤

⎣ ⎦

⎣

⎦

+

=

dla wszystkich n

x[n]

0

N

-N

2N

n

U

Sygnały o skończonej energii i skończonej mocy:

Jeżeli prąd „i” płynący przez rezystor o wartości „R” wywołuje spadek napięcia
„u” to chwilowa moc na jednostkę rezystancji jest definiowana jako:

( ) ( ) ( )

( )

2

i t u t

p t

i t

R

⋅

=

=

Wtedy energia całkowita na jednostkę rezystancji wynosi:

( )

2

E

dt

i t

∞

−∞

= ∫

oraz średnia moc na jednostkę rezystancji wynosi:

( )

/ 2

/ 2

2

1

lim

T

T

T

P

d

T

i t

→∞

−

=

∫

t

Analogicznie, dla sygnału dyskretnego x[n] definiuje się

U

znormalizowaną

energię sygnału

U

jako:

2

n

E

x n

∞

=−∞

⎡ ⎤

⎣ ⎦

= ∑

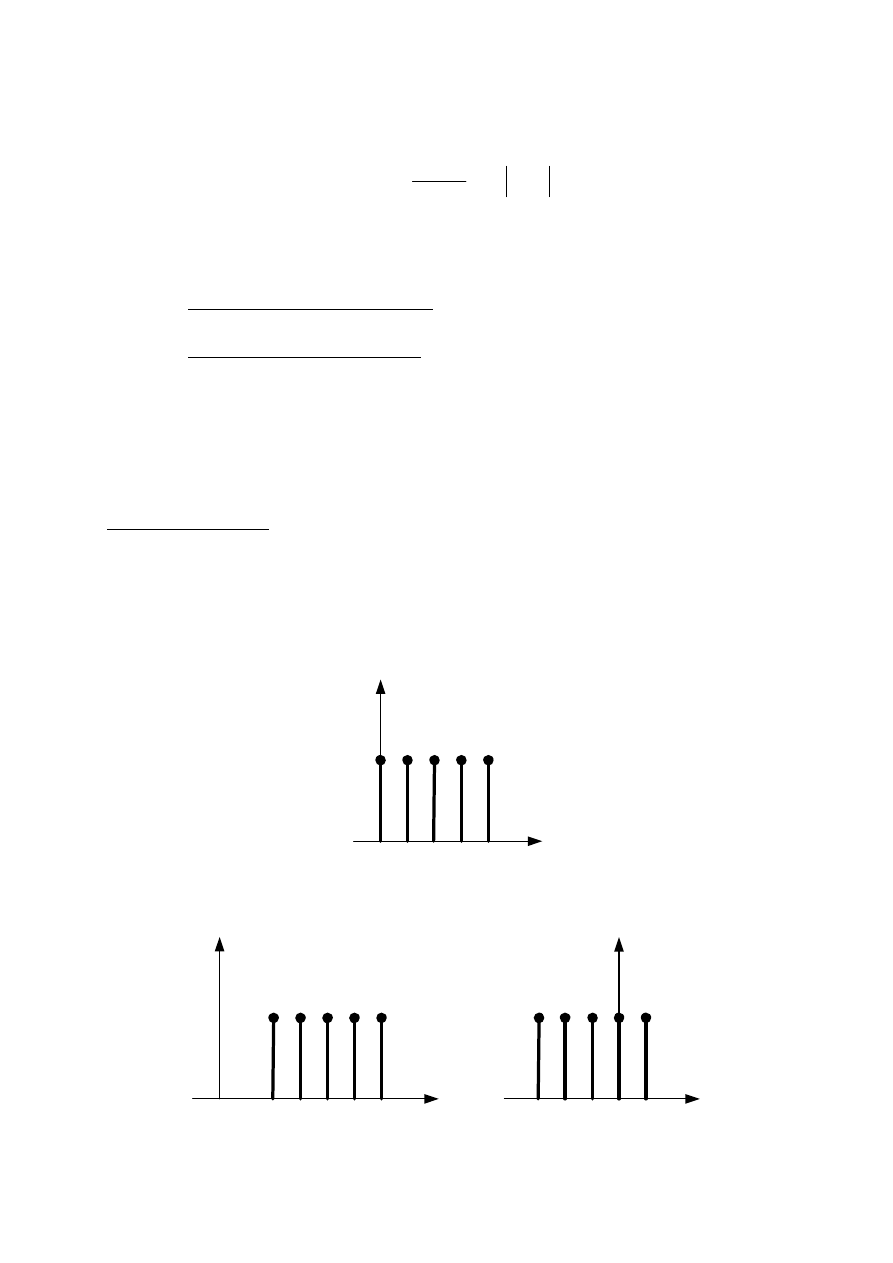
CPS 5

2006/2007

oraz znormalizowaną moc średnią sygnału dyskretnego:

2

1

2

1

lim

N

n

N

N

P

x

N

=−

→−∞

n

⎡ ⎤

⎣ ⎦

+

=

∑

Bazując na tych definicjach sygnały dzieli się na:

-

U

sygnały o skończonej energii

U

, jeżeli

0 E

< ∞

<

oraz P=0;

-

U

sygnały o skończonej mocy

U

0 P

< ∞

<

oraz

E

∞

=

Podstawowe przebiegi dyskretne:

U

Skok jednostkowy:

[ ]

1,

0

1

0,

0

n

n

n

≥

⎧

= ⎨

<

⎩

1[n]

n

0 1 2 3 4

...

1

1[n-2]

n

0 1 2 3 4

...

5 6

1

1[-n+1]

n

0 1 2

-1

-2

...

1

CPS 6

2006/2007

U

Impuls jednostkowy:

[ ]

1,

0

0,

0

n

n

n

δ

=

⎧

= ⎨

≠

⎩

δ

[n]

n

0 1 2 3

-1

n

0 1 2 3 4 5 6

δ

[n-2]

n

0 1 2

-1

-2

δ

[n+1]

Z definicji skoku jednostkowego i impulsu jednostkowego wynikają następujące
zależności:

0

x n

n

x

n

δ

δ

⎡ ⎤

⎡ ⎤ ⎡ ⎤

⎡ ⎤

⎣ ⎦ ⎣ ⎦

⎣ ⎦

⎣ ⎦

=

x n

n k

x k

n k

δ

δ

⎡

⎤

⎡ ⎤ ⎡

⎡ ⎤

⎣ ⎦

⎤

⎣

⎦

⎣ ⎦ ⎣

⎦

−

=

−

oraz:

1

1

n

n

n 1

δ

⎡

⎤

⎡ ⎤

⎡ ⎤ −

⎣ ⎦

⎣ ⎦

⎣

⎦

=

−

1

n

k

n

k

δ

=−∞

⎡ ⎤

⎡ ⎤

⎣ ⎦

⎣ ⎦

=

∑

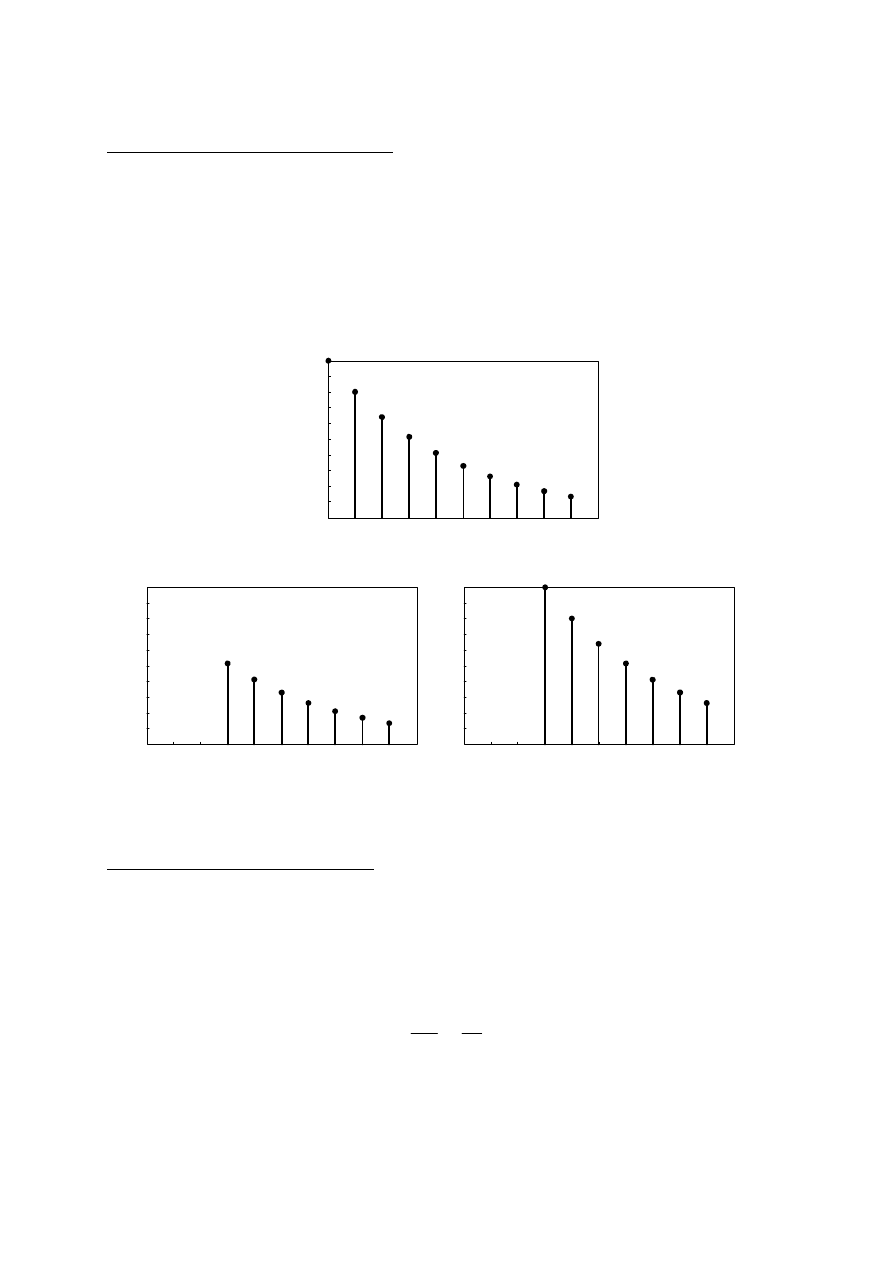
CPS 7

2006/2007

U

Rzeczywisty sygnał wykładniczy:

n

a

x n

⎡ ⎤

⎣ ⎦

=

dla

n

−∞ < < ∞

Często analizowane są sygnały wykładnicze jednostronne:

[ ]

[ ]

1

n

n

n

a

x

⋅

=

0 1 2 3 4 5 6 7 8 9

1

n

0.5

x[n]=(0.8)

n

1[n]

0 1 2 3 4 5 6 7 8 9

1

n

0.5

x[n]=(0.8)

n

1[n-3]

0 1 2 3 4 5 6 7 8 9

1

n

0.5

x[n]=(0.8)

(n-3)

1[n-3]

U

Zespolony sygnał wykładniczy:

0

j n

e

x n

ω

⎡ ⎤

⎣ ⎦

=

dla

n

−∞ < < ∞

Tak opisany sygnał jest okresowy z okresem N jeżeli spełniony jest warunek:

0

2

m
N

ω

π

=

gdzie m jest liczbą całkowitą dodatnią

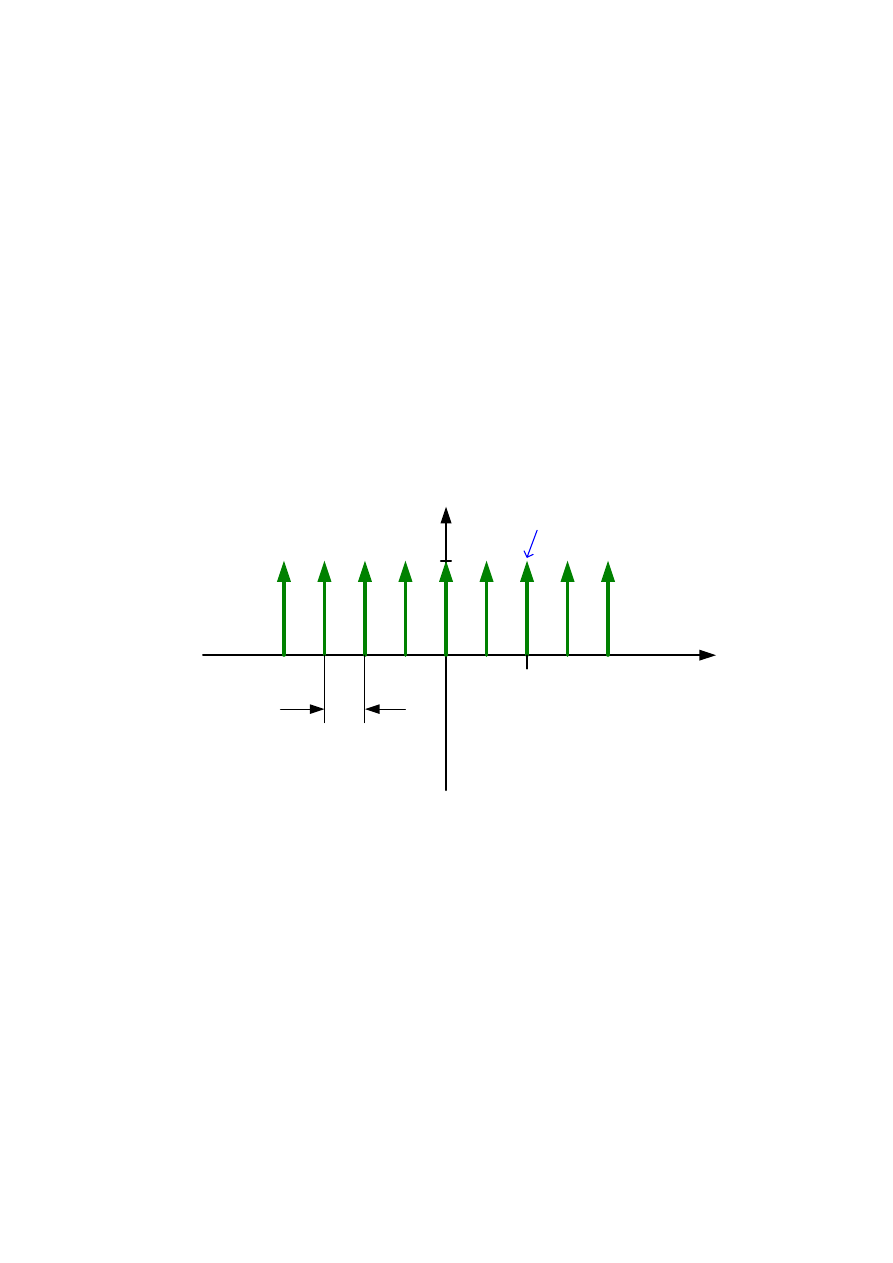
CPS 8

2006/2007

Konwersja analogowo-cyfrowa:

Proces próbkowania opisuje się jako mnożenie sygnału analogowego f(t) i
nieskończonego szeregu impulsów (delt) Diraca d(t). Impulsy w takim szeregu
powtarzają się z okresem próbkowania T

B

p

B

.

Szereg impulsów Diraca opisuje zależność:

( )

(

)

p

d t

t nT

δ

∞

−∞

=

−

∑

Na wykresie przedstawia się taki szereg w postaci strzałek o jednostkowej
długości ( jest to miara pola powierzchni delty), oddalonych od siebie o stały
przedział czasu równy Tp (okres próbkowania).

0

t

d(t)

1

T

p

(

)

p

nT

t

−

δ

p

nT

t

=

0

Oznaczając sygnał spróbkowany jako:

( )

( ) ( )

*

f

t

f t d t

=

⋅

( )

( )

(

)

*

p

f

t

f t

t nT

δ

∞

−∞

=

⋅

−

∑

i wykorzystując własność filtracyjną delty Diraca otrzymujemy wyrażenie
opisujące sygnał dyskretny:

( )

( ) (

*

p

p

)

f

t

f nT

t nT

δ

∞

−∞

=

⋅

−

∑

CPS 9

2006/2007

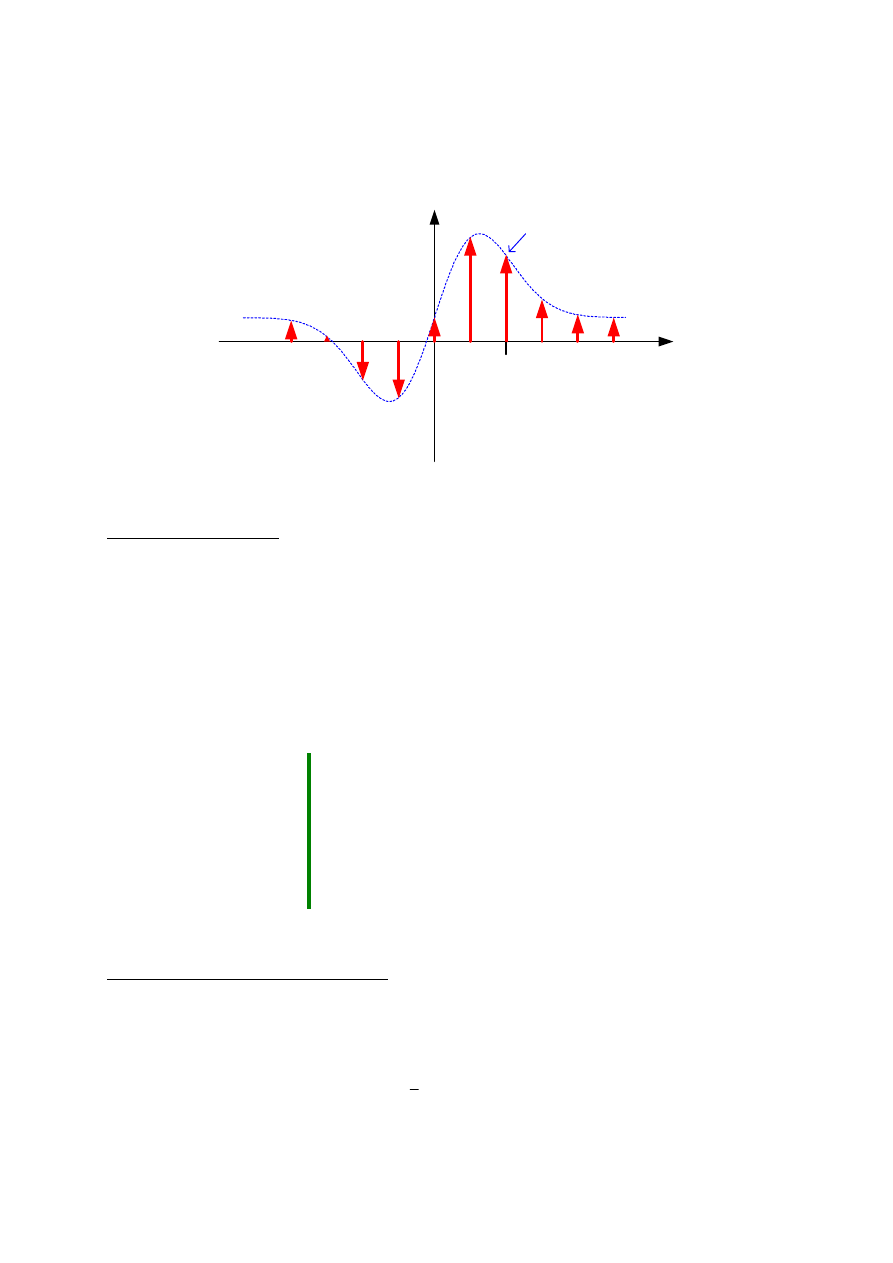
Zapis ten należy interpretować jako szereg impulsów Diraca o polach równych
wartościom próbkowanej funkcji analogowej w punktach, w których znajdują
się impulsy szeregu d(t).

0

t

f*(t)

( ) (

)

p

p

nT

t

nT

f

−

⋅

δ

p

nT

t

=

0

U

Widmo delty Diraca

U

zgodnie z definicją przekształcenia Fouriera wynosi:

( )

{ }

( )

1

j t

t

t e

dt

ω

δ

δ

∞

−

−∞

=

=

∫

F

( )

1

t

δ

⎯⎯→

F

Inne pary transformat Fouriera:

(

)

j T

t T

e

ω

δ

−

−

⎯⎯→

F

( )

1

2

πδ ω

⎯⎯→

F

(

)

0

0

2

j t

e

ω

πδ ω ω

⎯⎯→

−

F

U

Widmo przebiegu okresowego.

U

Do wyznaczenia wykorzystamy zespolony

szereg Fouriera
Przebieg okresowy f(t) w postaci zespolonego szeregu Fouriera ma postać

( )

0

jk t

k

k

f t

c e

ω

∞

=−∞

=

∑

CPS 10

2006/2007

Jego transformata Fouriera

( )

{

}

0

jk t

k

k

F j

c e

ω

ω

∞

=−∞

=

∑

F

( )

{ }

0

jk t

k

k

F j

c

e

ω

ω

∞

=−∞

=

∑

F

ostatecznie:

( )

(

0

2

k

k

F j

c

k

)

ω

π

δ ω

ω

∞

=−∞

=

∑

+

(**)

gdzie

( )

0

0

0

0

1

T

jk t

k

c

f t e

T

ω

−

=

∫

dt

współczynniki szeregu Fouriera

0

0

2

T

π

ω

=

odstęp między impulsami widma

t

ω

t

ω

Wniosek:

Widmo dowolnego sygnału okresowego, opisuje szereg impulsów

Diraca oddalonych od siebie o stałą wartość

ω

B

0

B

i o polach równych odpowiednio

2

k

c

π

.

Sygnał okresowy posiada dyskretne widmo

.

Wykorzystując właściwość symetrii przekształcenia Fouriera można stwierdzić,
że

sygnał dyskretny posiada okresowe widmo

.

Ta właściwość charakterystyki widmowej sygnału dyskretnego, ma swoje
ważne konsekwencje w teorii próbkowania.

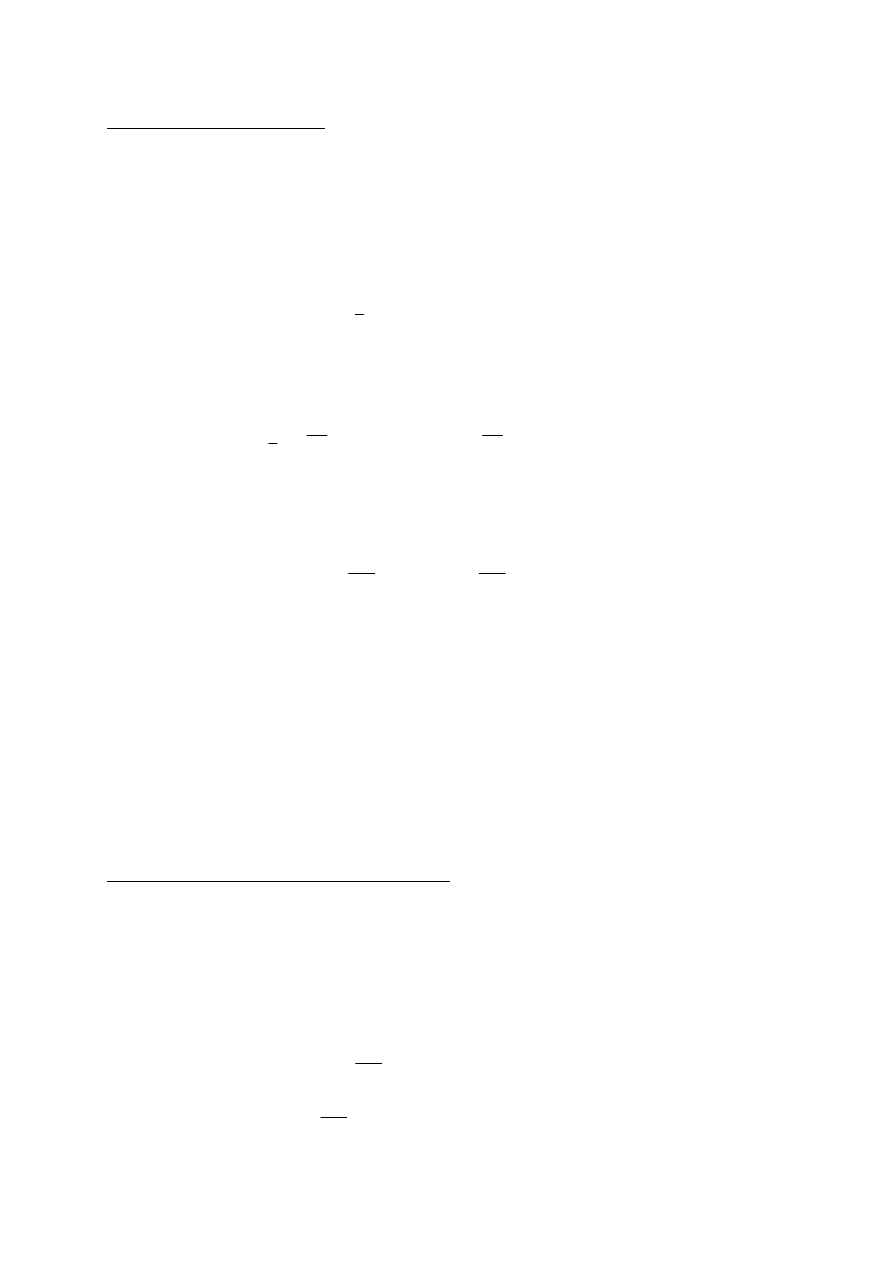
CPS 11

2006/2007

U

Szereg impulsów Diraca

U

rozpatrzymy jako szczególny przypadek przebiegu

okresowego

( )

(

)

p

k

d t

t kT

δ

∞

=−∞

=

−

∑

Po przedstawieniu

d(t)

w postaci szeregu Fouriera

( )

p

jk

t

k

k

d t

c e

ω

∞

=−∞

=

∑

współczynniki tego szeregu wynoszą

( )

/ 2

/ 2

1

1

p

p

p

T

j

kt

k

T

p

p

c

t e

d

T

T

ω

δ

−

−

=

=

∫

t

Stąd charakterystyka widmowa szeregu impulsów Diraca przyjmuje postać (**)

( )

2

2

k

p

p

D j

k

T

T

π

π

ω

δ ω

∞

=−∞

⎛

⎞

=

+

⎜

⎟

⎜

⎟

⎝

⎠

∑

Transformata Fouriera szeregu impulsów powtarzających się z okresem

T

B

p

B

(w dziedzinie czasu) jest również szeregiem impulsów powtarzających się z

okresem 2 /

p

T

π

(w dziedzinie częstotliwości).

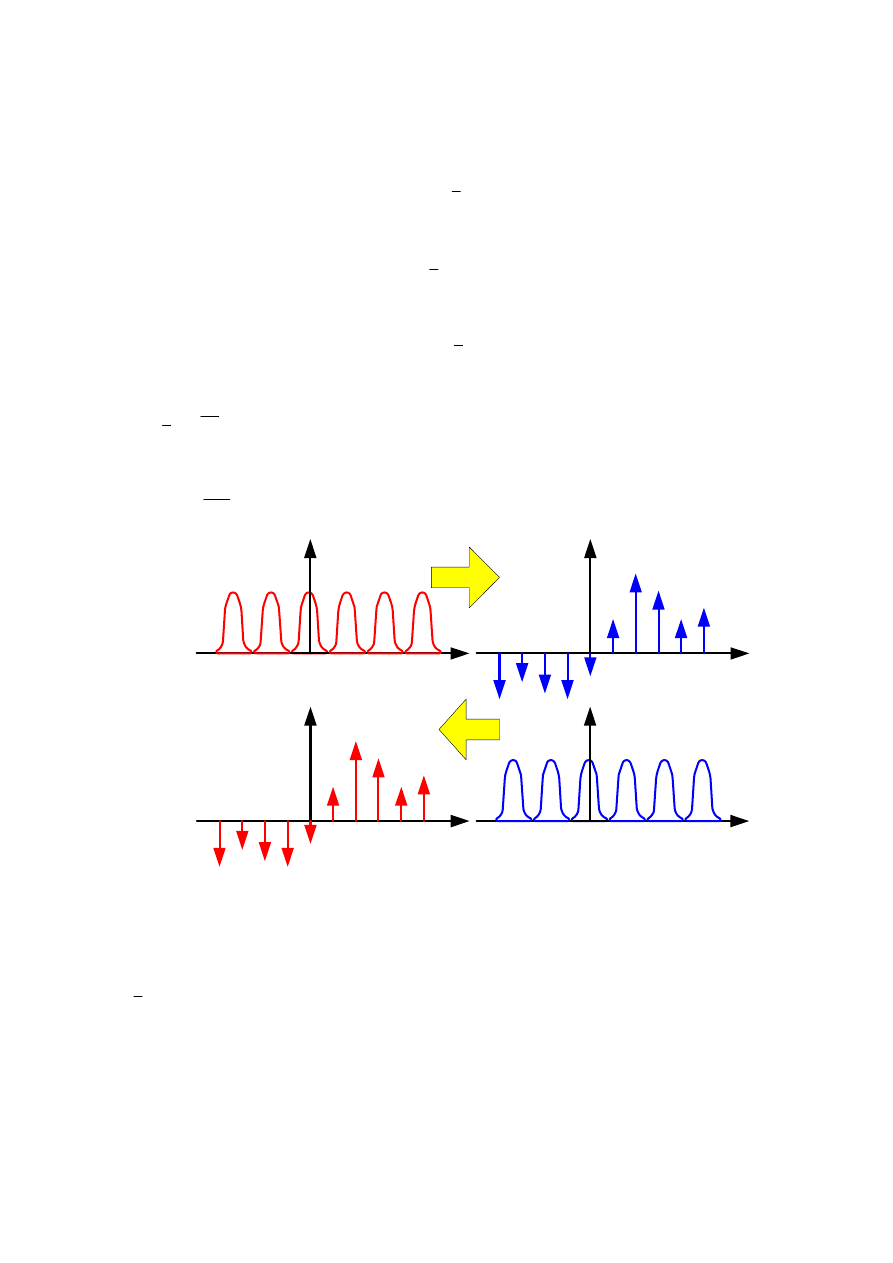
Zmniejszając odstępy między impulsami w dziedzinie czasu ( większa

częstotliwość próbkowania ) zwiększają się odstępy miedzy impulsami w
dziedzinie częstotliwości (i odwrotnie). Ta prosta zależność ma fundamentalne
znaczenie podczas realizacji zadania próbkowania przebiegów analogowych.

{

U

Obliczenia widma sygnału dyskretnego

U

( )

}

f * t

F

Analiza sygnałów w dziedzinie częstotliwości pozwala lepiej rozumieć
zagadnienia przetwarzania sygnałów.

Transformata Fouriera iloczynu dwóch przebiegów ( twierdzenie o splocie z
dziedzinie częstotliwości ):

( ) ( )

{

}

( )

{

}

( )

{ }

1

2

f t d t

f t

d t

π

⋅

=

∗

F

F

F

( )

{

}

( )

{

}

( )

{ }

1

*

2

f

t

f t

π

=

∗

F

F

F d t

CPS 12

2006/2007

W uproszczonej postaci zapiszemy transformatę Fouriera sygnału dyskretnego
jako

( )

( )

( )

1

*

2

F

j

F j

D j

ω

ω

ω

π

=

∗

oraz znając transformatę szeregu impulsów Diraca otrzymamy:

( )

( )

1

2

*

k

p

p

F

j

F j

k

T

T

π

ω

ω

δ ω

∞

=−∞

⎛

⎞

=

∗

+

⎜

⎟

⎜

⎟

⎝

⎠

∑

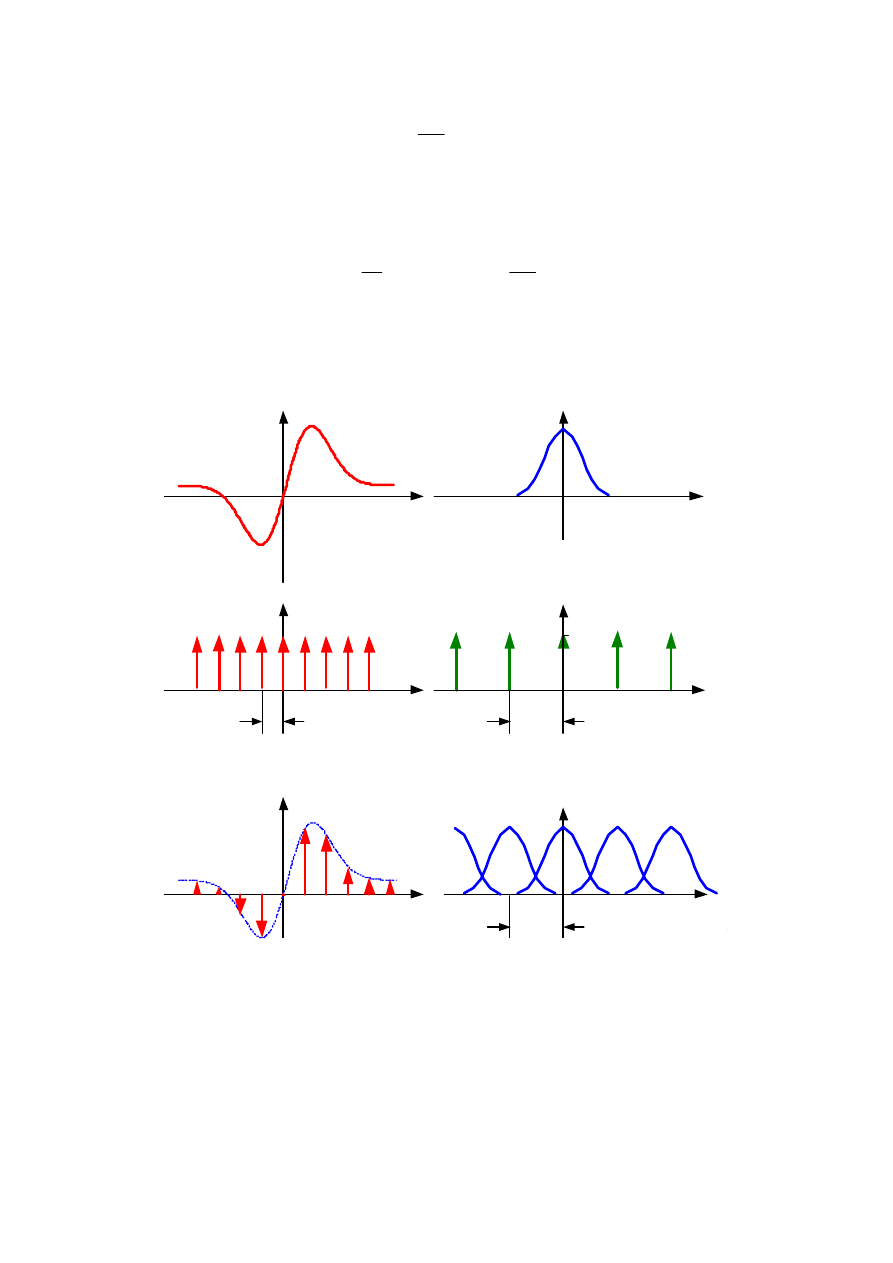
Pamiętamy, że splot funkcji z impulsem Diraca powoduje przesunięcie tej
funkcji do punktu, w którym znajduje się delta.

( ) (

)

(

)

0

0

T

T

f t

t t

f t t

δ

∗

−

=

−

( )

t

f

T

t

A

0

T

(

)

0

t

t

−

δ

0

t

przesunięcie

(

)

0

t

t

f

T

−

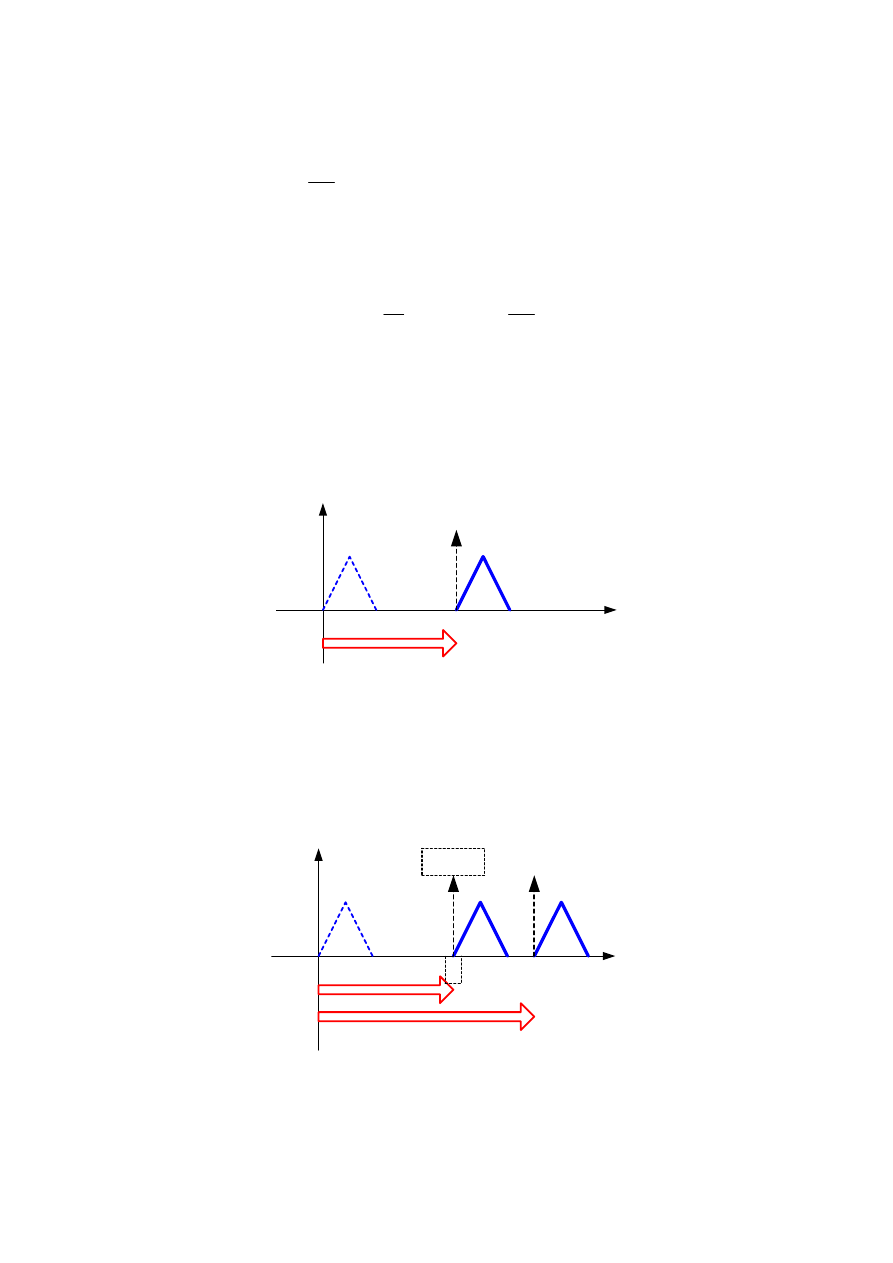
Dodatkowo jeżeli funkcja splatana jest z szeregiem impulsów, to następuje
powielanie tej funkcji i przesuwanie powieleń do miejsc, w których znajdują się
impulsy Diraca.

( ) (

) (

)

(

)

(

)

(

)

1

0

1

0

t

t

f

t

t

f

t

t

t

t

t

f

T

T

T

−

+

−

=

−

+

−

∗

δ

δ

t

A

0

T

(

)

0

t

t

−

δ

0

t

(

)

1

t

t

−

δ

1

t

przesunięcie i powielenie

(

)

0

t

t

f

T

−

(

)

1

t

t

f

T

−

( )

t

f

T

Wnioskujemy zatem, że widmo sygnału dyskretnego powstaje w wyniku
powielania widma sygnału analogowego nieskończoną ilość razy i przesuwania
tych powieleń o wielokrotności

ω

B

p.

CPS 13

2006/2007

2

p

p

T

π

ω

=

Transformata Fouriera sygnału dyskretnego ma zatem następującą postać:

( )

1

2

*

k

p

p

F

j

F j

jk

T

T

π

ω

ω

∞

=−∞

⎛

⎞

=

+

⎜

⎟

⎜

⎟

⎝

⎠

∑

Operację próbkowania sygnału analogowego f(t) można przedstawić graficznie
w postaci wykresów w dziedzinie czasu i częstotliwości.

0

t

f*(t)

0

t

f(t)

0

0

t

d(t)

1

T

p

ω

0

D(

ω

)

ω

p

ω

0

F*(

ω

)

2

π

ω

p

ω

ω

F( )

Jak wynika z wyprowadzeń postać widma sygnału dyskretnego zależy od

częstotliwości próbkowania.

W niektórych wypadkach w wyniku powieleń i przesunięć widma sygnału

analogowego, może występować nakładanie się powieleń.

CPS 14

2006/2007

SYSTEMY DYSKRETNE

Definicja:

W systemie dyskretnym, przetwarzanie obejmuje operacje arytmetyczne
przeprowadzane na sygnale wejściowym x[n], w wyniku, których na wyjściu
systemu otrzymuje się sygnał wyjściowy y[n] w postaci ciągu liczb.

W większości przypadków systemy czasu dyskretnego są systemami o jednym
wejściu i jednym wyjściu.

System dyskretny

x[n]

y[n]

Sygnał

wejściowy

Sygnał

wyjściowy

Systemy dyskretne można opisywać, podobnie jak układy analogowe, w
konwencji wejście-wyjście, do opisu stosuje się w tym przypadku

U

równania

różnicowe

U

, stanowiące algebraiczną zależność między ciągiem wejściowym i

wyjściowym.

Klasyfikacja:

Systemy dyskretne można klasyfikować ze względu następujących własności:

Liniowość

Stacjonarność

Pamięć

Przyczynowość

Stabilność

Pasywność

CPS 15

2006/2007

U

Liniowość:

U

Definicja: Jeżeli

[ ]

1

y n

jest sygnałem wyjściowym systemu zależnym od sygnału

wejściowego

[ ]

1

x n

oraz

[ ]

2

y n

jest sygnałem wyjściowym dla sygnału

wejściowego

[ ]

2

x n

to dla sygnału wejściowego:

1

2

x n

x n

x n

α

β

⎡ ⎤

⎡ ⎤

⎡ ⎤

⎣ ⎦

⎣ ⎦

⎣ ⎦

=

+

na wyjściu systemu otrzymamy

[ ]

[ ]

[ ]

1

2

y n

y n

y n

α

β

=

+

Zależność powyższa zachodzi dla dowolnie wybranych stałych

,

α β

oraz

dowolnych sygnałów wejściowych

[ ]

1

x n ,

[ ]

2

x n

Przykład systemu liniowego:

[ ]

[ ]

2

x n

y n

= −

[ ]

1

sin(

)

p

x n

nT

ω

=

o częstotliwości f=1Hz próbkowany z f

B

p

B

=20Hz

[ ]

2

sin(3

)

p

x n

nT

ω

=

o częstotliwości f=3Hz próbkowany z f

B

p

B

=20Hz

Superpozycja sygnałów wejściowych

[ ]

[ ]

[ ]

1

2

sin(

) sin(3

)

p

p

x n

x n

x n

nT

nT

ω

ω

=

+

=

+

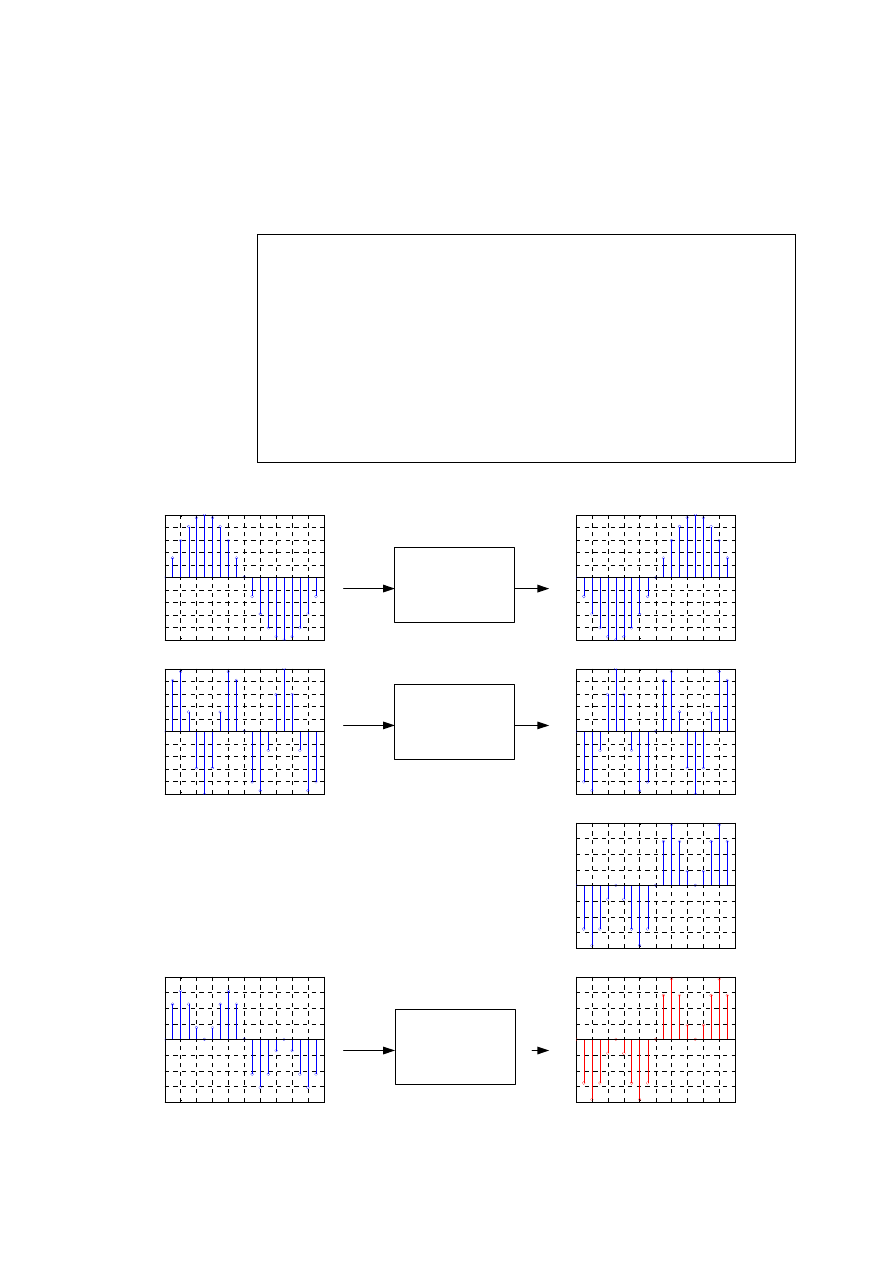
Na wyjściu systemu dla kolejnych sygnałów wejściowych otrzymamy:

[ ]

1

2

1

sin(

)

p

y n

nT

ω

= −

[ ]

1

2

2

sin(3

)

p

y n

nT

ω

= −

[ ]

[ ]

[ ]

1

1

2

2

1

2

sin(

)

sin(3

)

p

p

y n

y n

y n

nT

nT

ω

ω

=

+

= −

−

oraz inaczej

[ ]

[ ]

[ ]

(

)

(

)

1

1

2

2

0

1

2

sin(

) sin(3

)

p

p

y n

x n

x n

nT

nT

ω

ω

= −

+

= −

+

CPS 16

2006/2007

Dla sygnału liniowego zachodzi równość:

[ ]

[ ]

0

y n

y n

=

MATLAB

clear;
fp=20; T=1/fp; f=1;
omega=2*pi*f;
t=0:T:1-T;
x1=sin(omega*t); figure(1); stem(t,x1); grid
y1=-x1/2; figure(2); stem(t,y1); grid
x2=sin(3*omega*t); figure(3); stem(t,x2); grid
y2=-x2/2; figure(4); stem(t,y2); grid
x=x1+x2; figure(5); stem(t,x); grid
y=y1+y2; figure(6); stem(t,y); grid
yy=-x/2; figure(7); stem(t,yy,'-r'); grid

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

x

1

[n]

y

1

[n]

x

2

[n]

y

2

[n]

x[n]=x

1

[n]+x

2

[n]

y

1

[n]+y

2

[n]

y[n]

system

system

system

CPS 17

2006/2007

Przykład systemu nieliniowego:

[ ]

[ ]

(

)

2

y n

x n

=

[ ]

1

sin(

)

p

x n

nT

ω

=

o częstotliwości f=1Hz próbkowany z f

B

p

B

=20Hz

[ ]

2

sin(3

)

p

x n

nT

ω

=

o częstotliwości f=3Hz próbkowany z f

B

p

B

=20Hz

Superpozycja sygnałów wejściowych

[ ]

[ ]

[ ]

1

2

sin(

) sin(3

)

p

p

x n

x n

x n

nT

nT

ω

ω

=

+

=

+

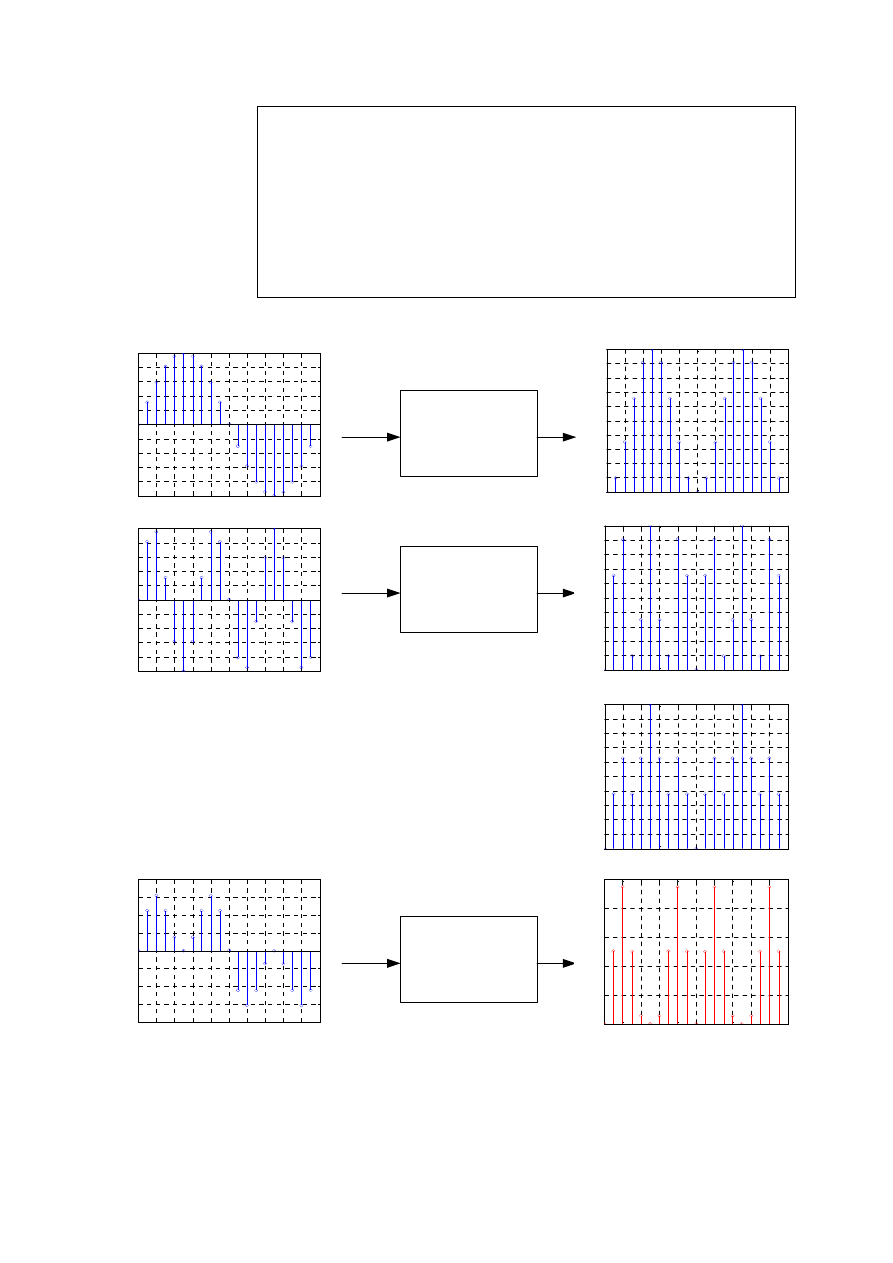
Na wyjściu systemu otrzymamy:

[ ]

1

1

1 cos(2

)

2

p

y n

nT

ω

⎡

⎤

=

−

⎣

⎦

[ ]

2

1

1 cos(6

)

2

p

y n

nT

ω

⎡

⎤

=

−

⎣

⎦

Sygnał jako suma sygnałów wyjściowych

[ ]

1

1

2

2

1

cos(2

)

cos(6

)

p

p

y n

nT

nT

ω

ω

= −

−

oraz jako sygnał wyjściowy sumy sygnałów wejściowych

[ ]

1

1

2

2

0

1

cos(2

) cos(4

)

cos(6

)

p

p

y n

nT

nT

nT

p

ω

ω

ω

= +

−

−

Nierówność

[ ]

[ ]

0

y n

y n

≠

wskazuje na nieliniowość systemu

MATLAB

clear;
fp=20; T=1/fp; f=1;
omega=2*pi*f;

CPS 18

2006/2007

t=0:T:1-T;
x1=sin(omega*t); figure(1); stem(t,x1); grid
y1=x1.^2; figure(2); stem(t,y1); grid
x2=sin(3*omega*t); figure(3); stem(t,x2); grid
y2=x2.^2; figure(4); stem(t,y2); grid
x=x1+x2; figure(5); stem(t,x); grid
y=y1+y2; figure(6); stem(t,y); grid
yy=x.^2; figure(7); stem(t,yy,'-r'); grid

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

x

1

[n]

x

2

[n]

x[n]=x

1

[n]+x

2

[n]

system

system

system

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

y

2

[n]

y

1

[n]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

y

1

[n]+y

2

[n]

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.5

1

1.5

2

2.5

y[n]

CPS 19

2006/2007

Stacjonarność

W systemie stacjonarnym przesunięcie w czasie w ciągu wejściowym powoduje
równoważne przesunięcie w ciągu wyjściowym

Jeżeli na wymuszenie x odpowiedź wynosi y

[ ]

[ ]

system

x n

y n

⎯⎯⎯

→

to na wymuszenie x przesunięte w czasie o k próbek układ odpowie sygnałem y
tak samo przesuniętym

[

]

[

]

system

x n k

y n k

− ⎯⎯⎯

→

−

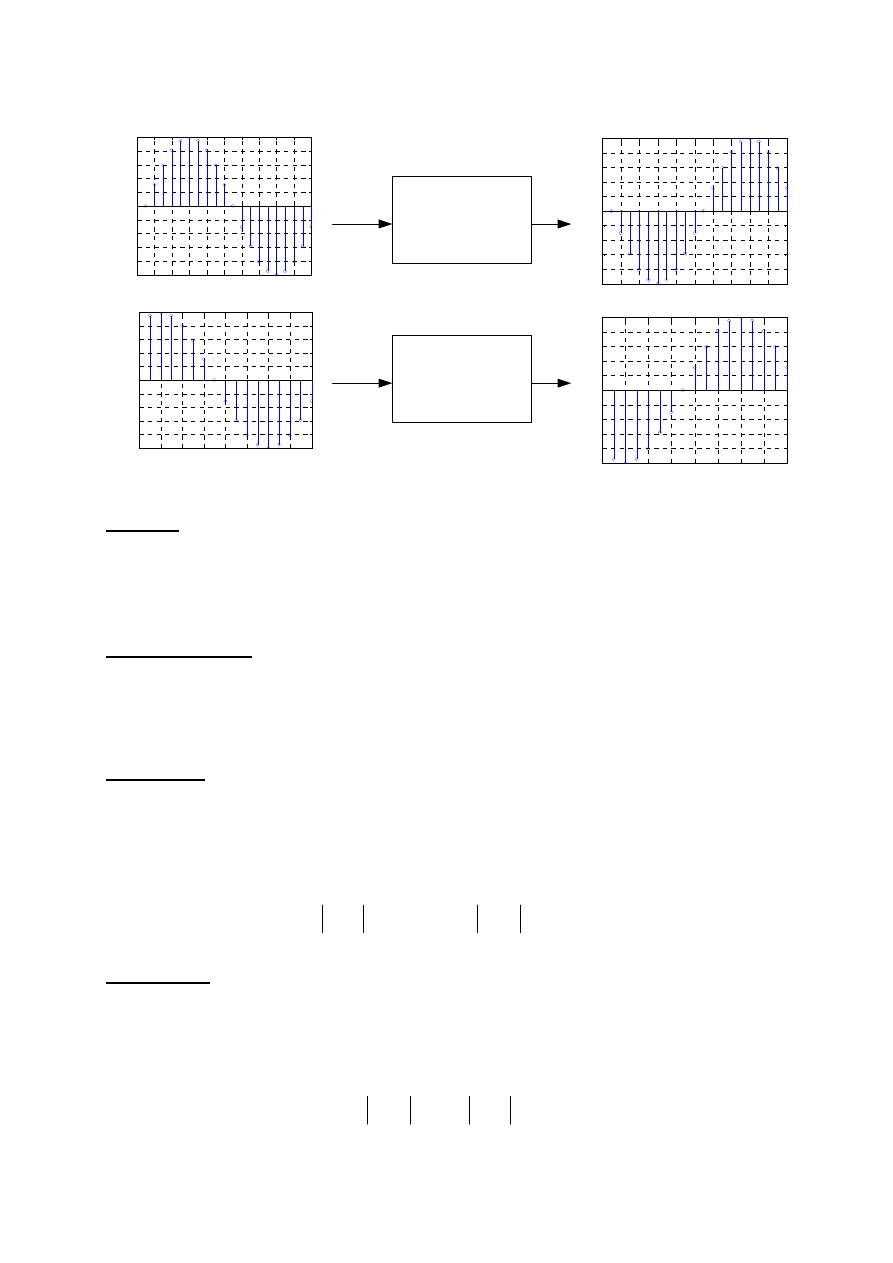
Przykład systemu stacjonarnego

[ ]

[ ]

2

x n

y n

= −

[ ]

[

]

[ ]

[

]

2

2

n 4

n 4

system

x n

x

y n

y

=

+ ⎯⎯⎯

→

=

+

MATLAB

clear;
fp=20; T=1/fp; f=1;
omega=2*pi*f;
t=0:T:1-T;
x1=sin(omega*t); figure(1); stem(x1); grid
y1=-x1/2; figure(2); stem(y1); grid
x2=x1(5:20);figure(3); stem(x2); grid
y2=-x2/2; figure(4); stem(y2); grid

CPS 20

2006/2007

0

2

4

6

8

10

12

14

16

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

0

2

4

6

8

10

12

14

16

18

20

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

0

2

4

6

8

10

12

14

16

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

x

1

[n]

x

2

[n]

system

system

y

2

[n]

y

1

[n]

Pamięć:

W układach bez pamięci odpowiedź systemu y[n] zależy tylko od teraźniejszych
wartości wymuszenia x[n].

Przyczynowość

:

Odpowiedź systemu przyczynowego y[n] zależy tylko od przeszłych i
teraźniejszych wartości sygnału wymuszenia x[n].

Stabilność:

Układ jest stabilny w sensie BIBO (bounded input, bounded output), jeżeli przy
ograniczonym sygnale wejściowym x[n] sygnał wyjściowy y[n] jest także
ograniczony. Formalnie można warunek zapisać:

[ ]

[ ]

x

y

x n

M

y n

M

≤

< ∞ ⇒

≤

< ∞

Pasywność:

System dyskretny jest pasywny jeżeli dla każdego sygnału wejściowego x[n] o
skończonej energii sygnał wyjściowy y[n] posiada energię mniejszą lub równą
energii x[n].

[ ]

[ ]

2

2

k

k

y k

x k

∞

∞

=−∞

=−∞

≤

< ∞

∑

∑