Mirosław Tomera

Katedra Automatyki Okrętowej

Wydział Elektryczny

Akademia Morska w Gdyni

http://vega.am.gdynia.pl/~tomera/

Podstawy Automatyki

Wprowadzenie

22 luty 2014 r.

Plan wykładu

• Literatura
• Układ dwóch zbiorników połączonych kaskadowo
• Modelowanie matematyczne elementów składowych

– charakterystyka pompy
– dynamiki zbiorników
– charakterystyki czujników

• Nieliniowe równania dynamiczne opisujące dynamikę układu kaskadowego
• Linearyzacja modelu nieliniowego
• Wyznaczenie transmitancji obiektu
• Synteza sterowania poziomem w górnym zbiorniku
• Badania zaprojektowanego układu sterowania w Simulinku
• Sterowanie obiektem rzeczywistym

Podstawy Automatyki

2

© M. Tomera

Literatura

• Tomera M.: Materiały pomocnicze do nauki teorii sterowania,

Strona internetowa:

vega.am.gdynia.pl/~tomera/teoria_sterowania.htm

• Brzózka J.: Regulatory i układy automatyki, Wydawnictwo MIKOM, 2004.
• Kowal J.: Podstawy automatyki, Uczelniane wydawnictwa Naukowo-

Dydaktyczne Akademii Górniczo-Hutniczej w Krakowie, 2004.

• Mazurek J., Vogt H., Żydanowicz W.: Podstawy automatyki, Oficyna

Wydawnicza Politechniki Warszawskiej, 2002.

3

© M. Tomera

Podstawy Automatyki

Widok stanowiska laboratoryjnego

4

© M. Tomera

Podstawy Automatyki

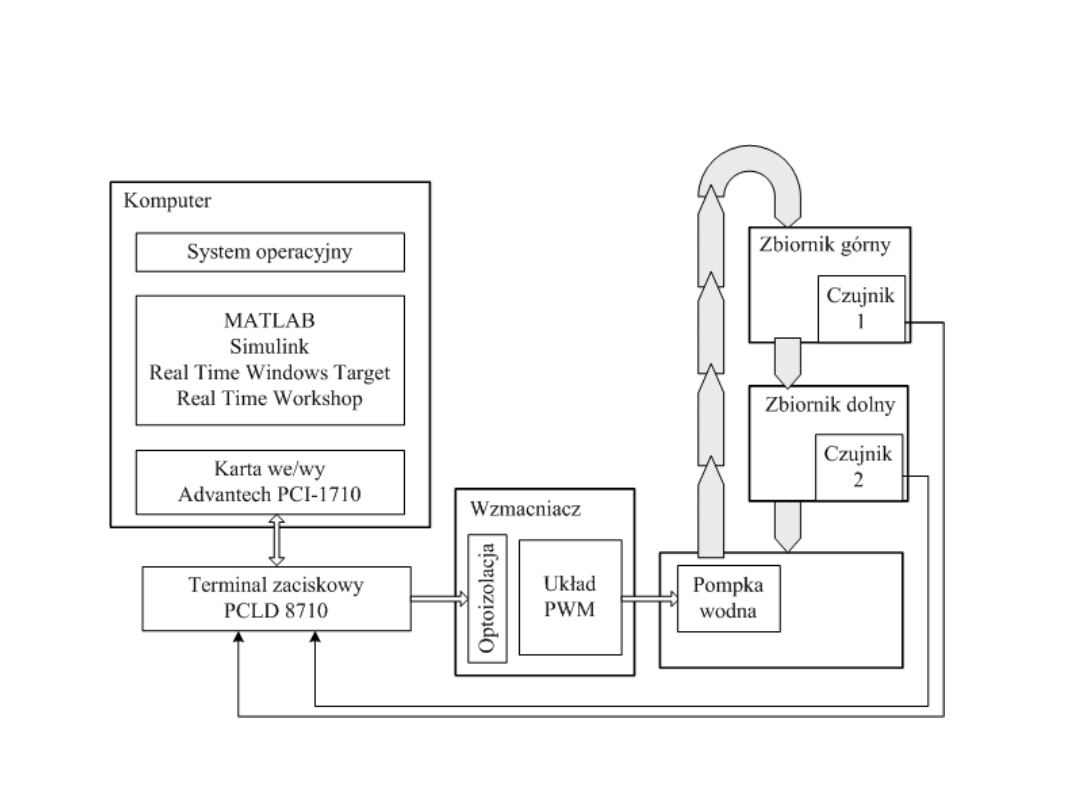
Sterowanie obiektem rzeczywistym - RTWT

5

© M. Tomera

Podstawy Automatyki

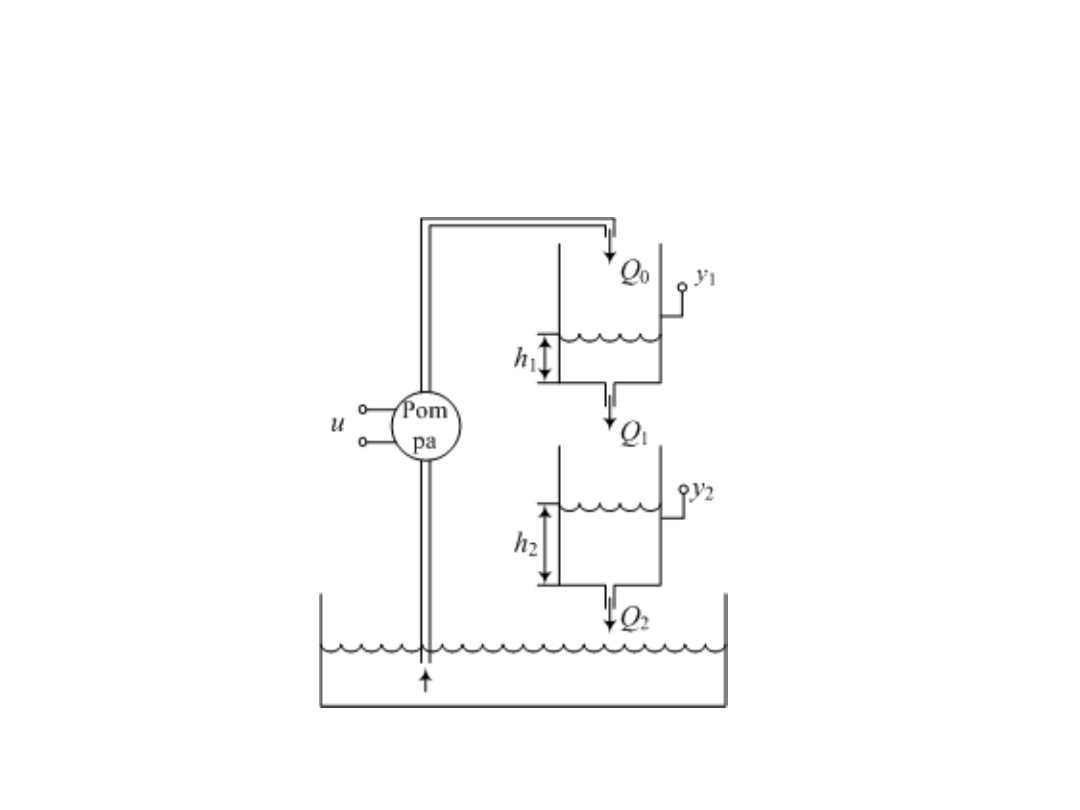
Układ kaskadowy dwóch zbiorników

6

© M. Tomera

Struktura układu

Podstawy Automatyki

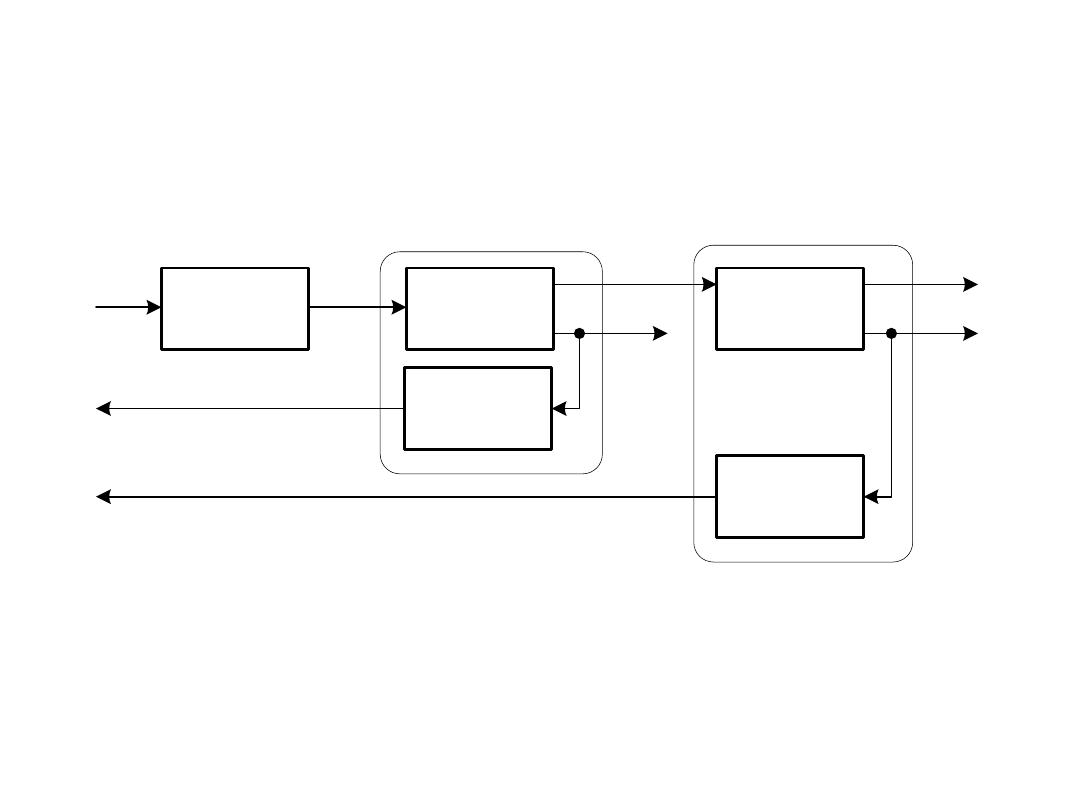
Schemat blokowy

7

© M. Tomera

Schemat blokowy układu kaskadowego dwóch zbiorników

Pompa

Zbiornik

górny

Czujnik 2

Zbiornik

dolny

h

1

Czujnik 1

Q

1

h

2

Q

2

u

1zm

u

2zm

Q

0

U

s

Podstawy Automatyki

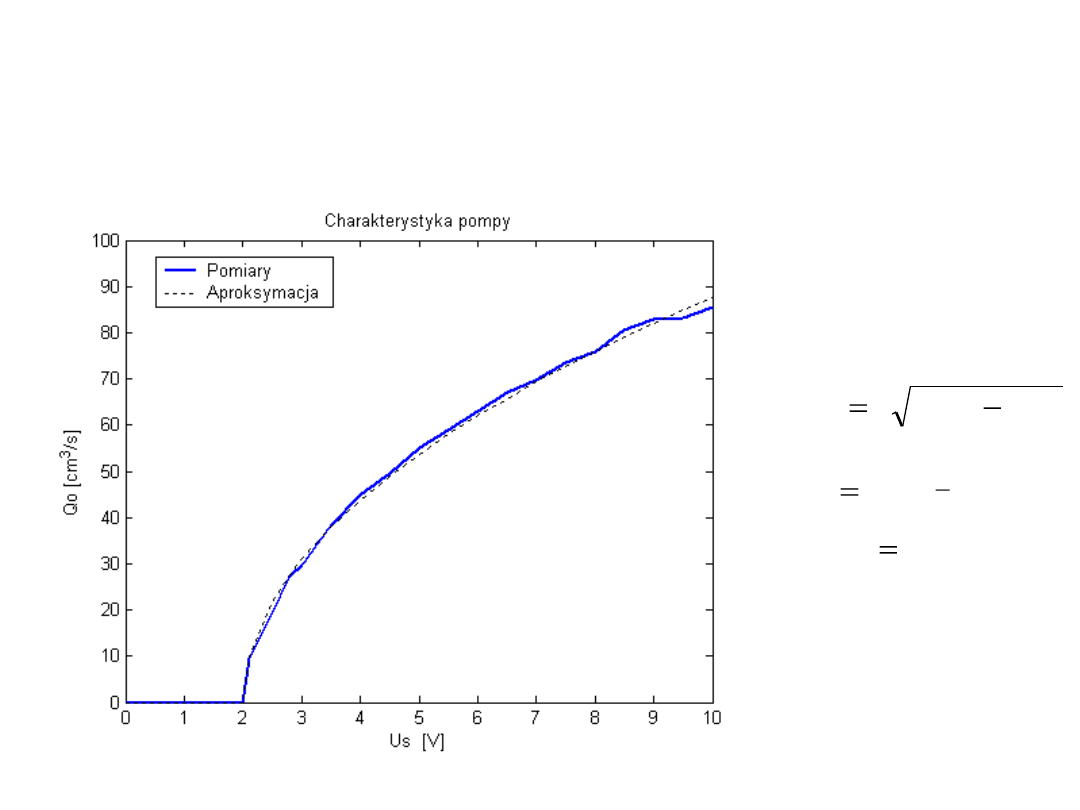
Model matematyczny pompy

8

© M. Tomera

Charakterystyka pompy

min

0

)

(

)

(

U

t

U

a

t

Q

s

0

.

19

a

0

.

2

m in

U

]

V

[

]

[

Podstawy Automatyki

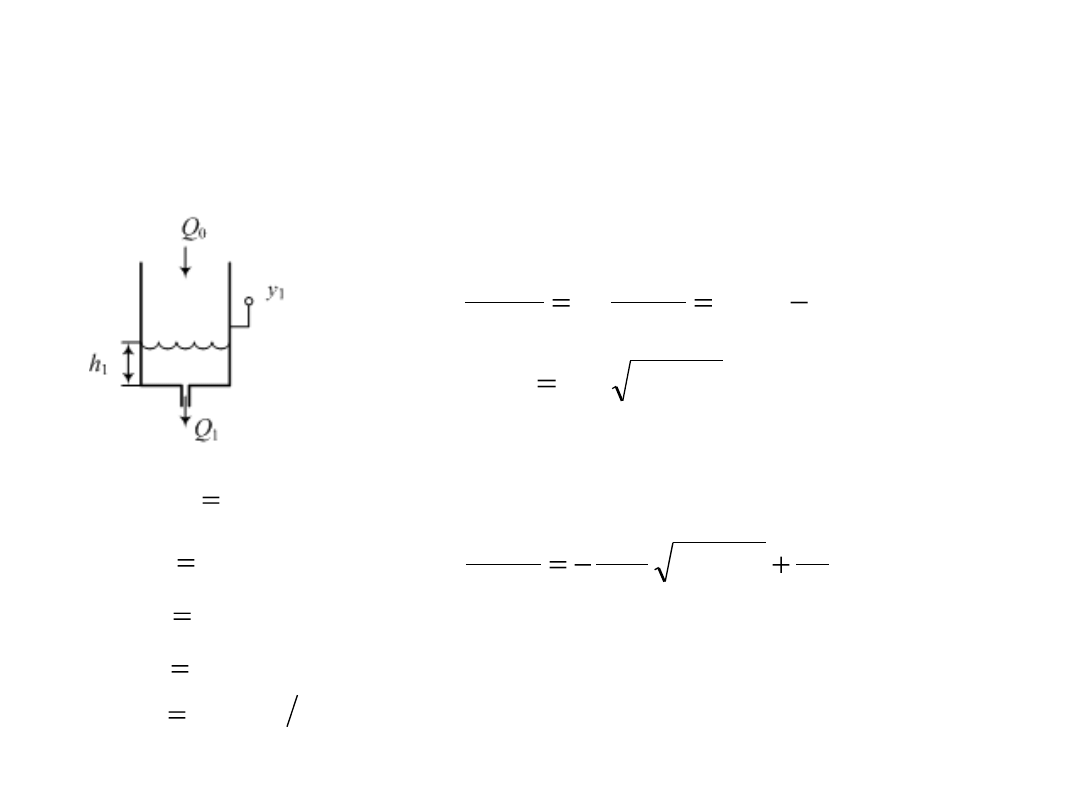
Model matematyczny górnego zbiornika

9

© M. Tomera

Definicja zmiennych

)

(

)

(

)

(

)

(

1

0

1

1

1

t

Q

t

Q

dt

t

dh

A

dt

t

dV

Równanie różniczkowe – bilans objętości

81

1

A

19635

.

0

1

S

25

m ax

h

)

(

2

)

(

1

1

1

1

t

gh

S

c

t

Q

Równanie dynamiki w górnym zbiorniku

)

(

1

)

(

2

)

(

0

1

1

1

1

1

1

t

Q

A

t

gh

A

S

c

dt

t

dh

1

1

c

981

g

]

cm

[

]

cm

[

2

]

cm

[

2

]

s

cm

[

2

]

-

[

Podstawy Automatyki

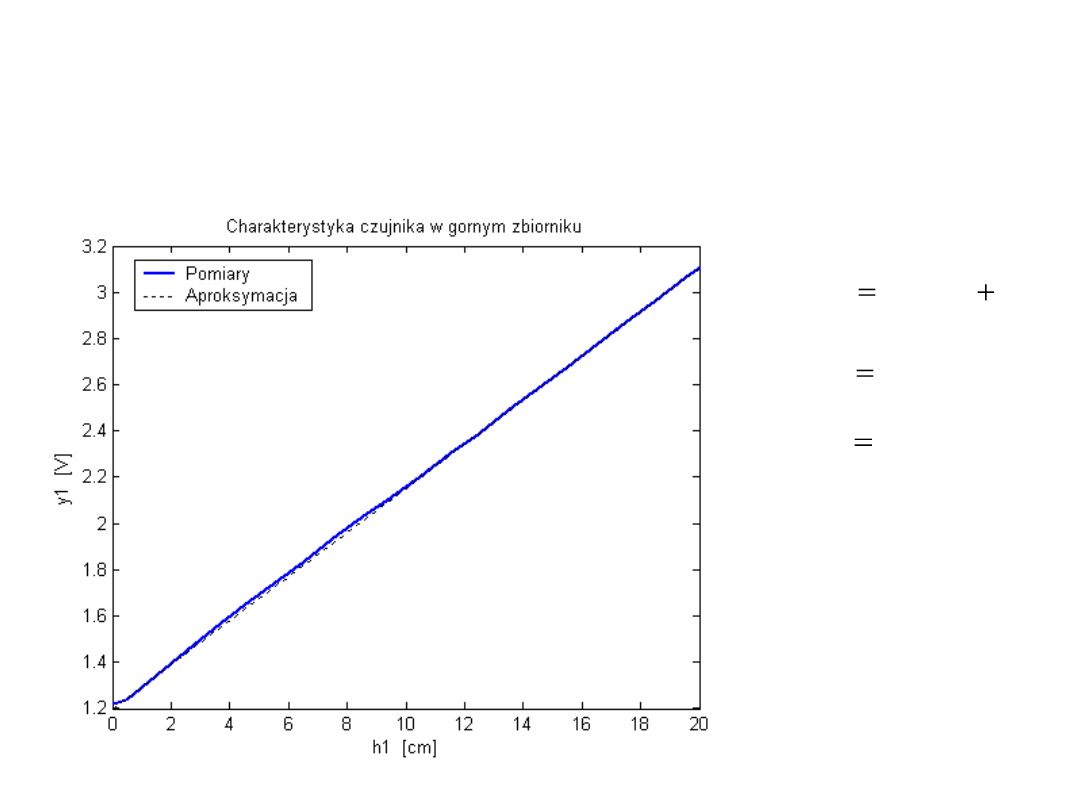
Model matematyczny czujnika w górnym zbiorniku

10

© M. Tomera

Charakterystyka czujnika w górnym zbiorniku

1

1

1

1

)

(

)

(

b

t

h

k

t

y

c

0952

.

0

1

c

k

1991

.

1

1

b

Podstawy Automatyki

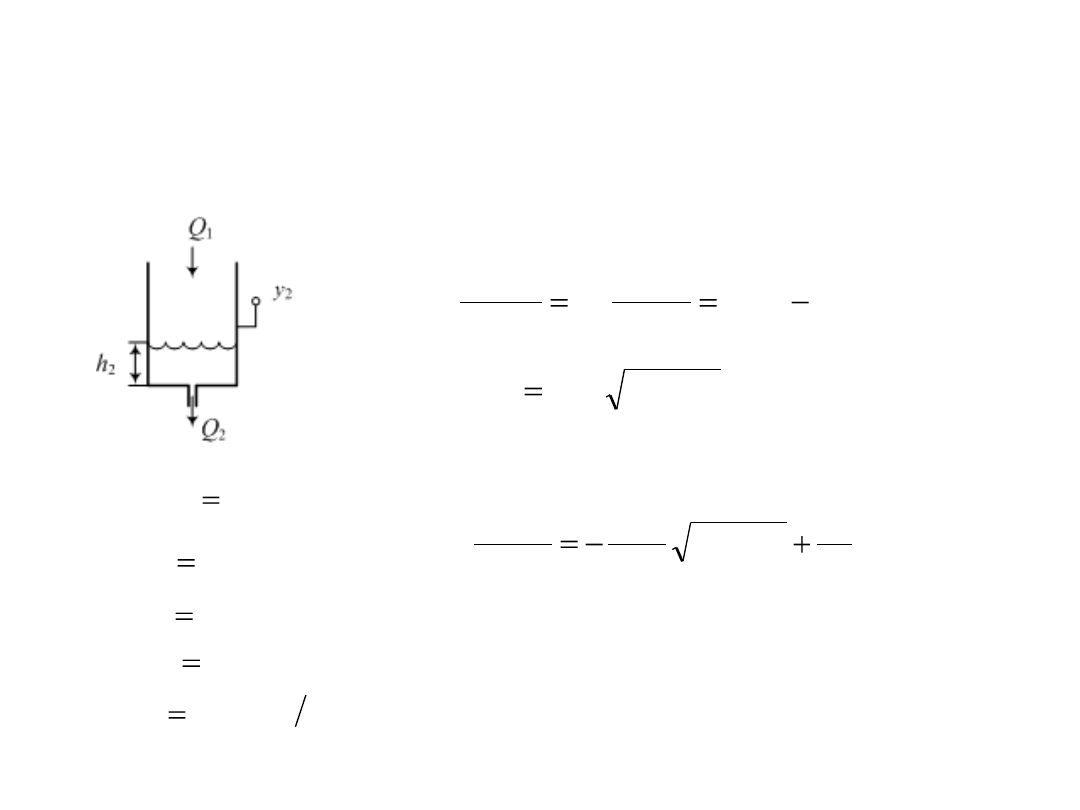
Model matematyczny dolnego zbiornika

11

© M. Tomera

Definicja zmiennych

)

(

)

(

)

(

)

(

2

1

2

2

2

t

Q

t

Q

dt

t

dh

A

dt

t

dV

Równanie różniczkowe – bilans objętości

81

2

A

19635

.

0

2

S

25

m ax

h

Równanie dynamiki w dolnym zbiorniku

)

(

1

)

(

2

)

(

1

2

2

2

2

2

2

t

Q

A

t

gh

A

S

c

dt

t

dh

99

.

0

2

c

981

g

)

(

2

)

(

2

2

2

2

t

gh

S

c

t

Q

]

cm

[

]

cm

[

2

]

s

cm

[

2

]

-

[

]

cm

[

2

Podstawy Automatyki

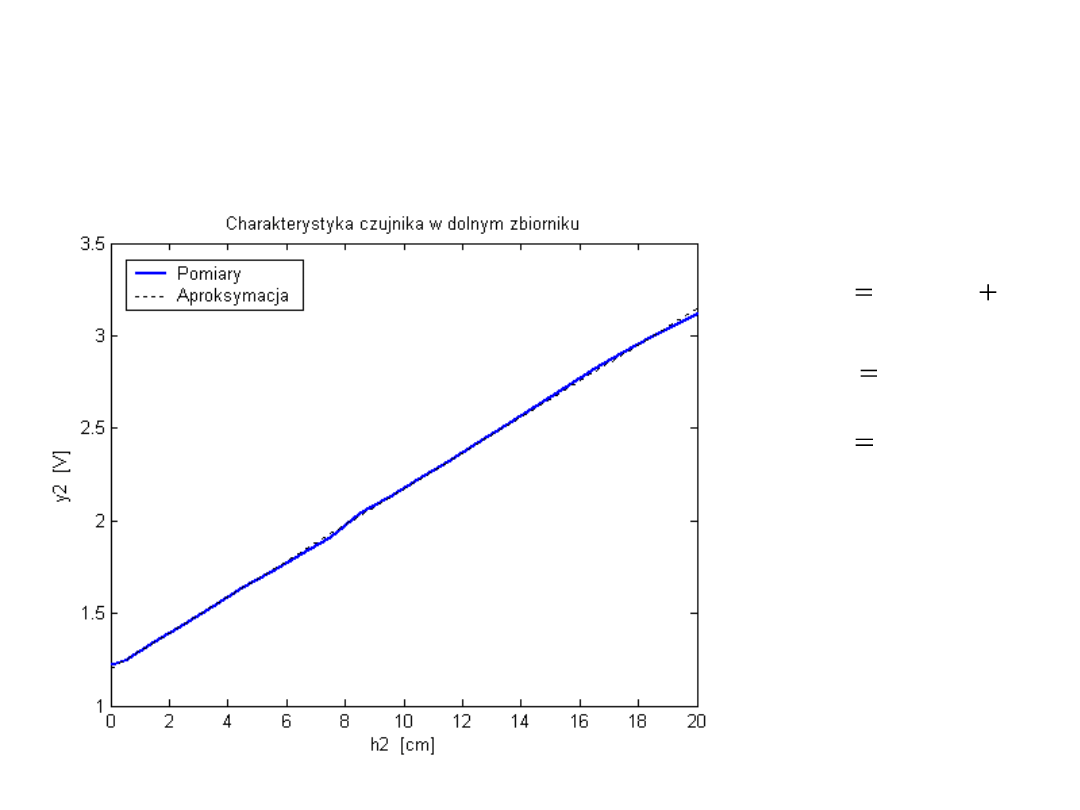
Model matematyczny czujnika w dolnym zbiorniku

12

© M. Tomera

Charakterystyka czujnika w dolnym zbiorniku

2

2

2

2

)

(

)

(

b

t

h

k

t

y

c

0973

.

0

2

c

k

1991

.

1

2

b

Podstawy Automatyki

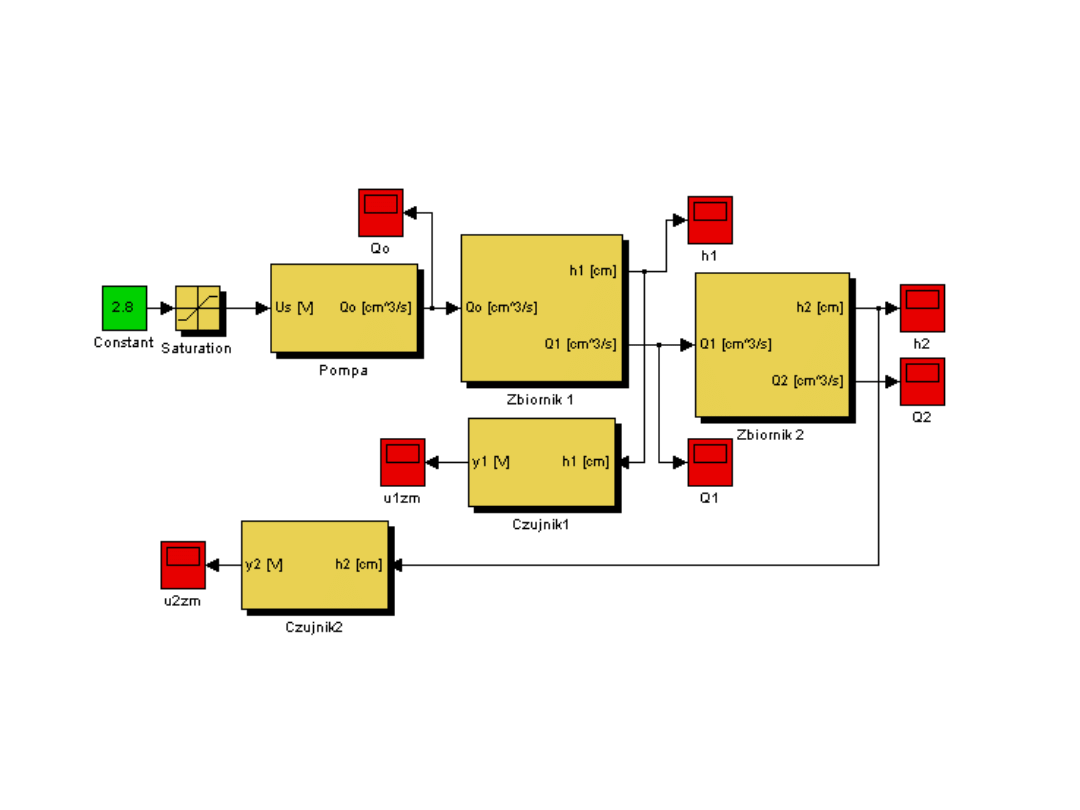
Implementacja układu kaskadowego w Simulinku

13

© M. Tomera

Podstawy Automatyki

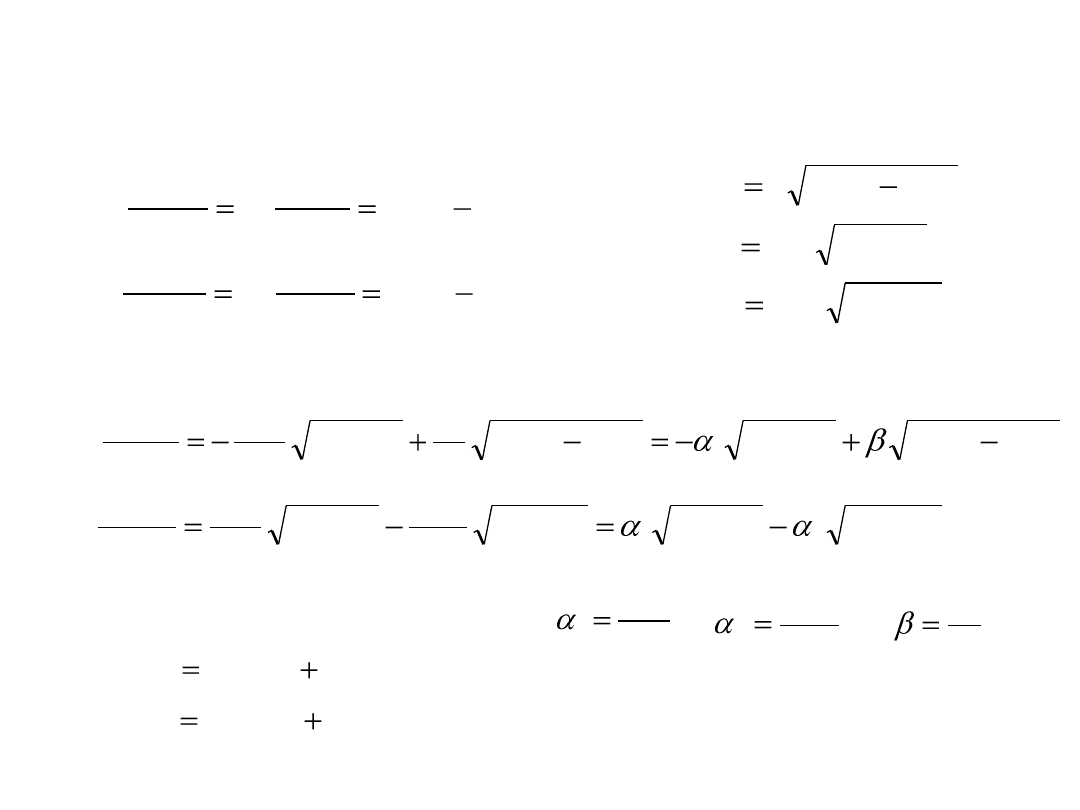
Model matematyczny układu kaskadowego

14

© M. Tomera

Równania bilansu objętości

)

(

)

(

)

(

)

(

1

0

1

1

1

t

Q

t

Q

dt

t

dh

A

dt

t

dV

Równania stanu

m in

1

1

m in

1

1

1

1

1

1

)

(

)

(

2

)

(

)

(

2

)

(

U

t

U

t

gh

U

t

U

A

a

t

gh

A

S

c

dt

t

dh

s

s

)

(

)

(

)

(

)

(

2

1

2

2

2

t

Q

t

Q

dt

t

dh

A

dt

t

dV

)

(

2

)

(

1

1

1

1

t

gh

S

c

t

Q

)

(

2

)

(

2

2

2

2

t

gh

S

c

t

Q

min

0

)

(

)

(

U

t

U

a

t

Q

s

)

(

2

)

(

2

)

(

2

)

(

2

)

(

2

2

1

1

2

2

2

2

1

1

1

1

2

t

gh

t

gh

t

gh

A

S

c

t

gh

A

S

c

dt

t

dh

Równania wyjścia

1

1

1

1

)

(

)

(

b

t

h

k

t

y

c

2

2

2

2

)

(

)

(

b

t

h

k

t

y

c

1

1

1

1

A

S

c

2

2

2

2

A

S

c

1

A

a

Podstawy Automatyki

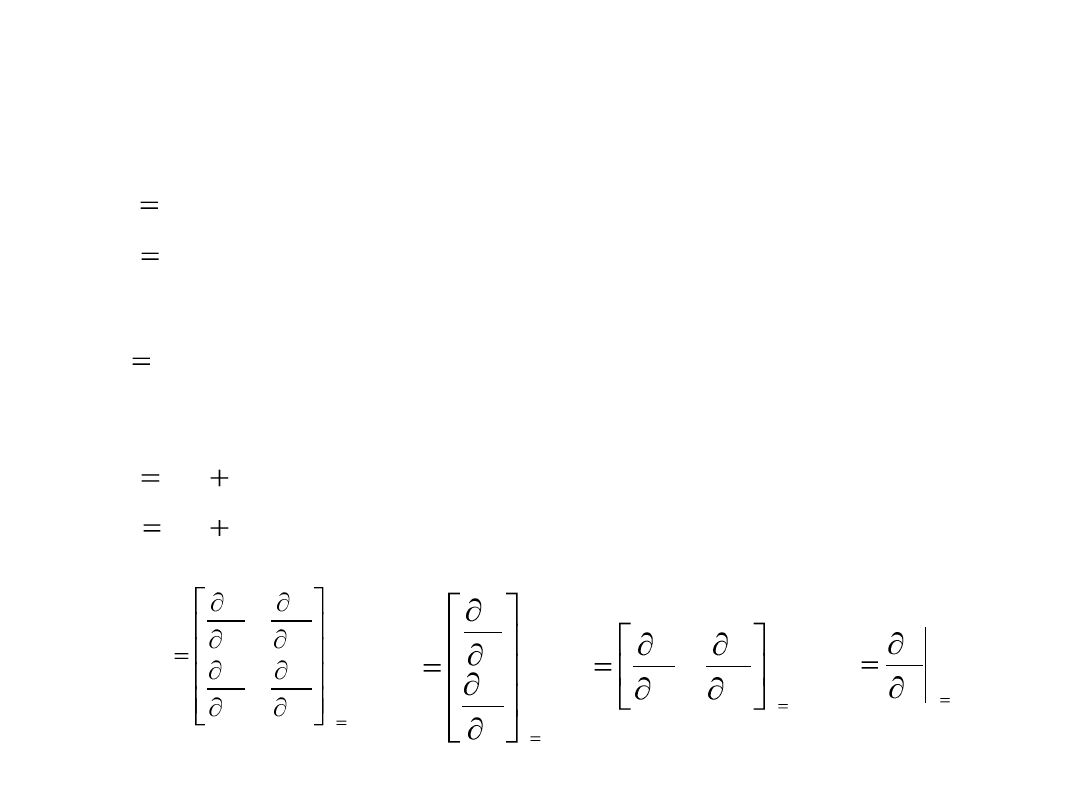
Linearyzacja modelu matematycznego

15

© M. Tomera

Nieliniowe równania stanu

)

,

,

(

2

1

1

1

u

x

x

f

x

Liniowy model matematyczny obiektu

)

,

,

(

2

1

2

2

u

x

x

f

x

Nieliniowe równanie wyjścia

)

,

,

(

2

1

u

x

x

g

y

u

B

Αx

x



Du

y

Cx

gdzie:

0

2

2

1

2

2

1

1

1

x

Α

x

f

x

f

x

f

x

f

0

2

1

u

u

f

u

f

B

0

2

1

x

C

x

g

x

g

0

u

u

g

D

Podstawy Automatyki

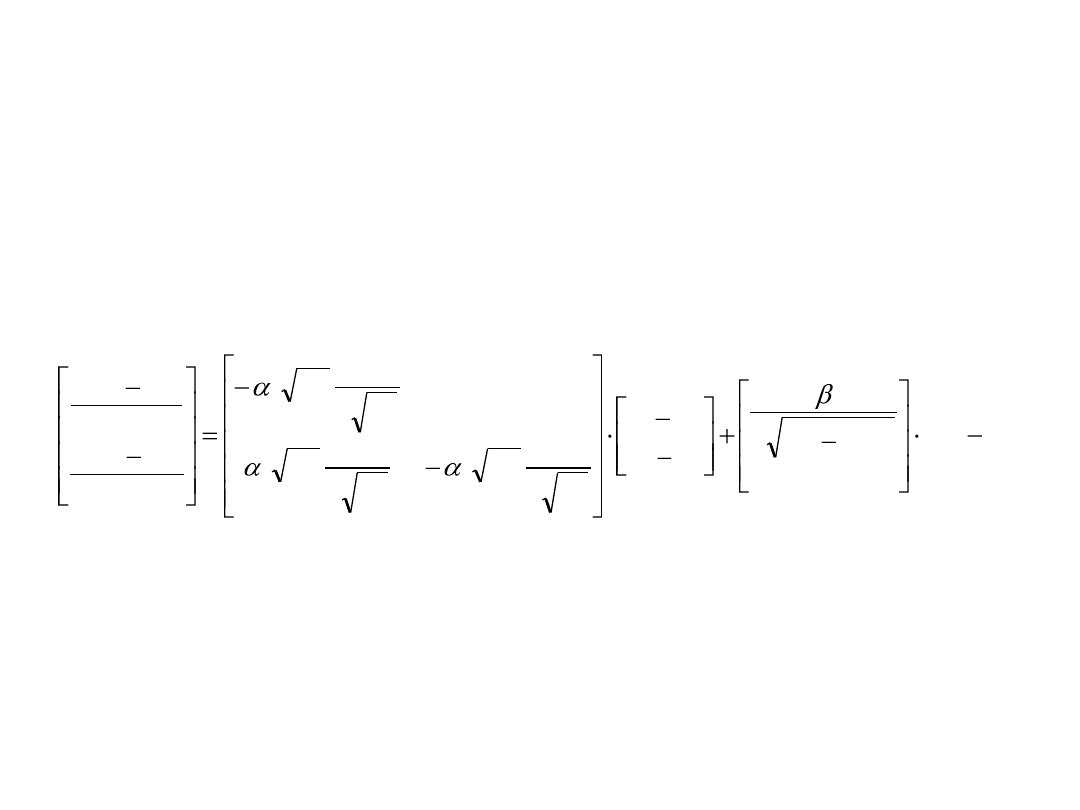
Linearyzacja układu kaskadowego

16

© M. Tomera

Punkt pracy

)

,

,

,

,

(

0

2

0

1

0

0

2

0

1

zm

zm

s

y

y

U

h

h

Model matematyczny układu kaskadowego dwóch zbiorników zapisany w postaci
macierzowych równań stanu

)

(

0

2

2

1

2

2

1

2

0

2

1

2

)

(

)

(

0

min

0

0

2

2

0

1

1

0

2

1

0

1

1

0

1

1

0

2

2

0

1

1

s

s

s

U

U

U

U

h

h

h

h

h

g

h

g

h

g

dt

h

h

d

dt

h

h

d

Podstawy Automatyki

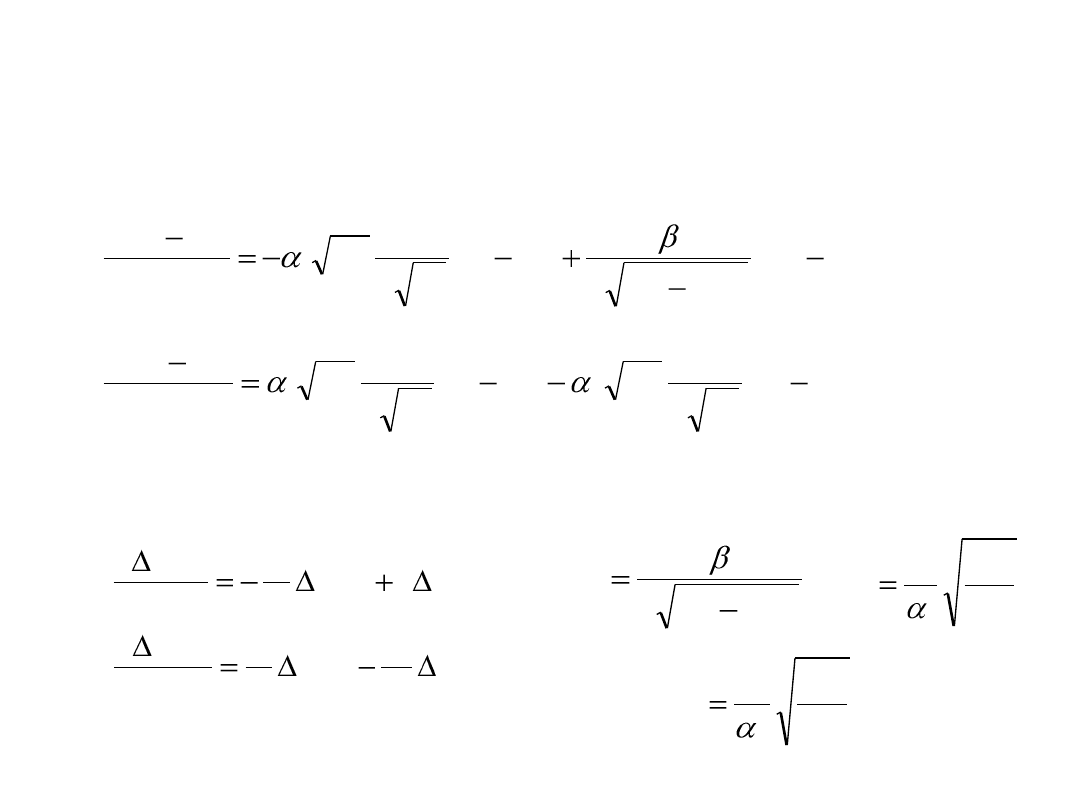
Zlinearyzowany układ kaskadowy

17

© M. Tomera

Równania stanu po zlikwidowaniu opisu macierzowego

)

(

2

)

(

2

1

2

)

(

0

m in

0

0

1

1

0

1

1

0

1

1

s

s

s

U

U

U

U

h

h

h

g

dt

h

h

d

)

(

2

1

2

)

(

2

1

2

)

(

0

2

2

0

2

2

0

1

1

0

1

1

0

2

2

h

h

h

g

h

h

h

g

dt

h

h

d

Zlinearyzowany model matematyczny układu kaskadowego dwóch zbiorników

)

(

)

(

1

)

(

1

1

1

t

U

k

t

h

T

dt

t

h

d

s

)

(

1

)

(

1

)

(

2

2

1

1

2

t

h

T

t

h

T

dt

t

h

d

min

0

2

U

U

k

s

g

h

T

0

1

1

1

2

1

g

h

T

0

2

2

2

2

1

Podstawy Automatyki

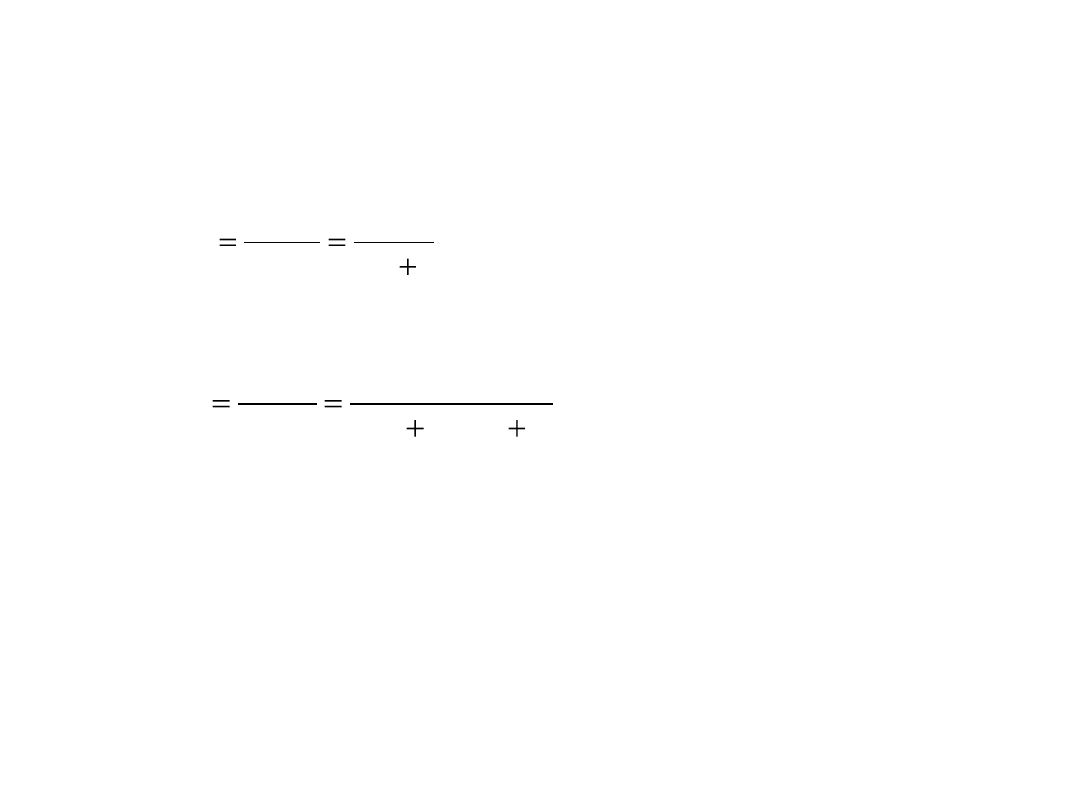
Uzyskane transmitancje operatorowe

18

© M. Tomera

• dla górnego zbiornika

1

)

(

)

(

)

(

1

1

1

1

sT

kT

s

U

s

H

s

G

s

• dla dolnego zbiornika

)

1

)(

1

(

)

(

)

(

)

(

2

1

2

2

2

sT

sT

kT

s

U

s

H

s

G

s

Podstawy Automatyki

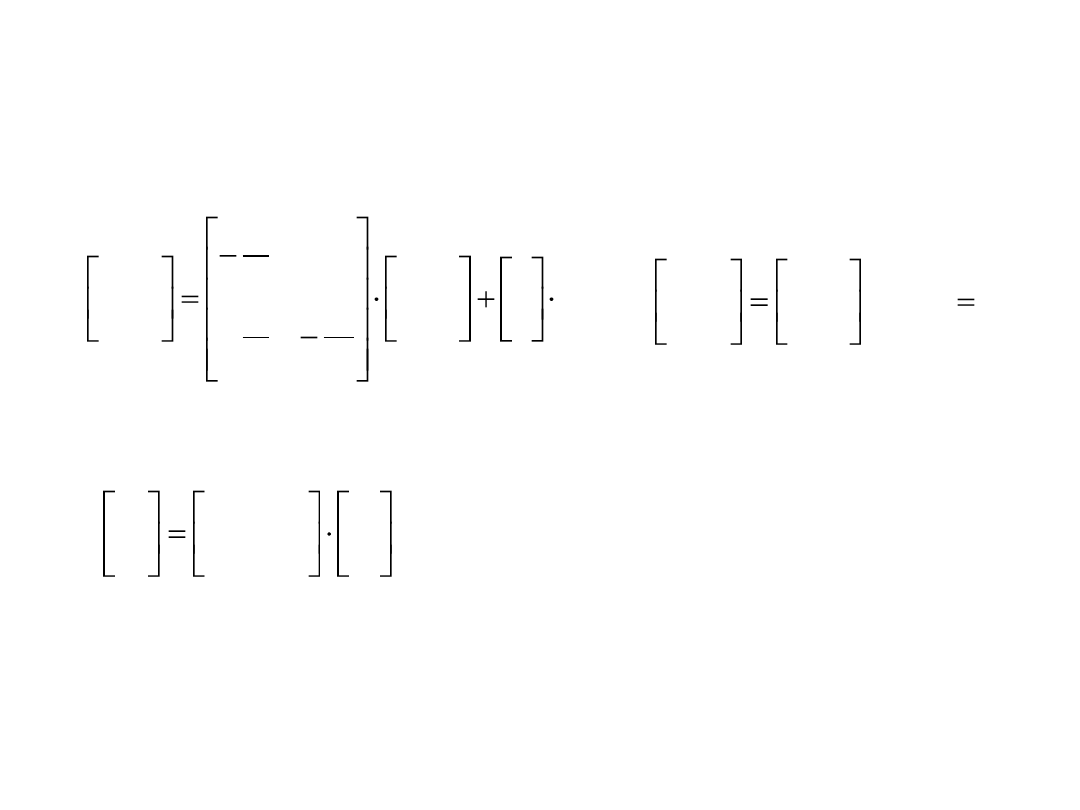
Uzyskane zlinearyzowane równania dynamiczne

19

© M. Tomera

• równania stanu

• równania wyjścia

u

k

t

x

t

x

T

T

T

t

x

t

x

0

)

(

)

(

1

1

0

1

)

(

)

(

2

1

2

1

1

2

1





2

1

2

1

2

1

0

0

x

x

k

k

y

y

c

c

)

(

)

(

)

(

)

(

2

1

2

1

t

h

t

h

t

x

t

x

)

(

)

(

t

U

t

u

s

Podstawy Automatyki

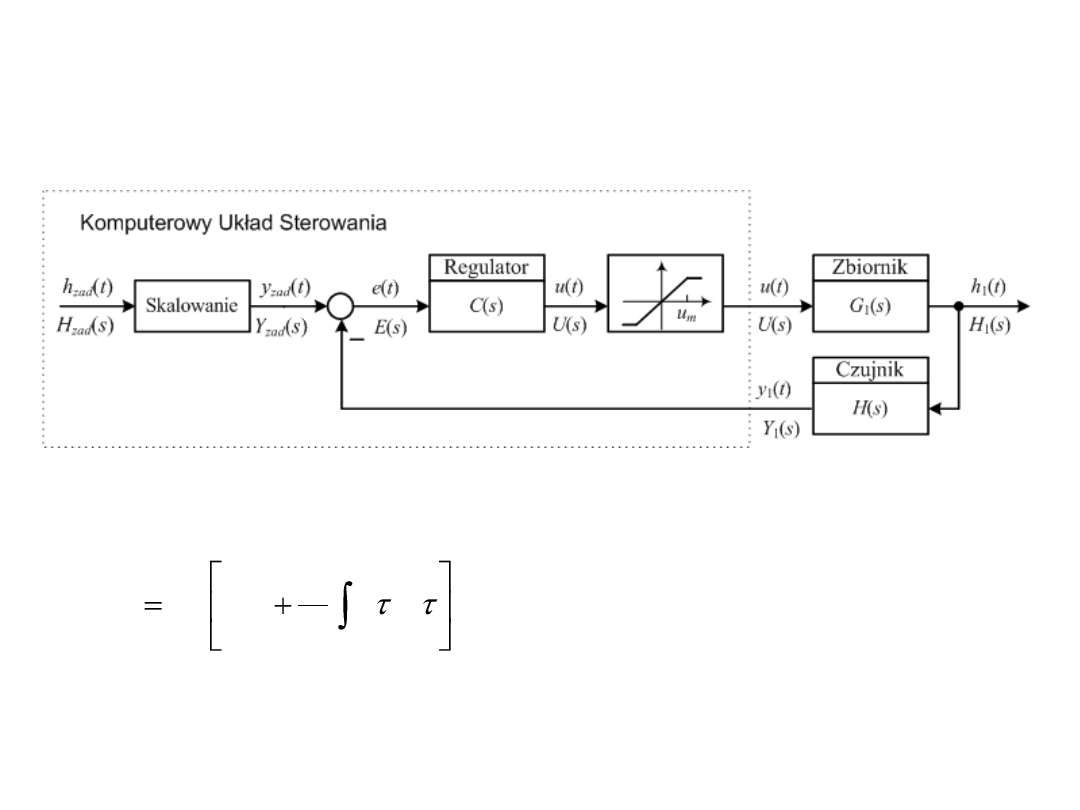
Model układu sterowania

20

© M. Tomera

Schemat blokowy układu sterowania poziomem wody w górnym zbiorniku

Algorytm regulatora ciągłego PI

t

I

P

d

e

T

t

e

K

t

u

0

)

(

1

)

(

)

(

Podstawy Automatyki

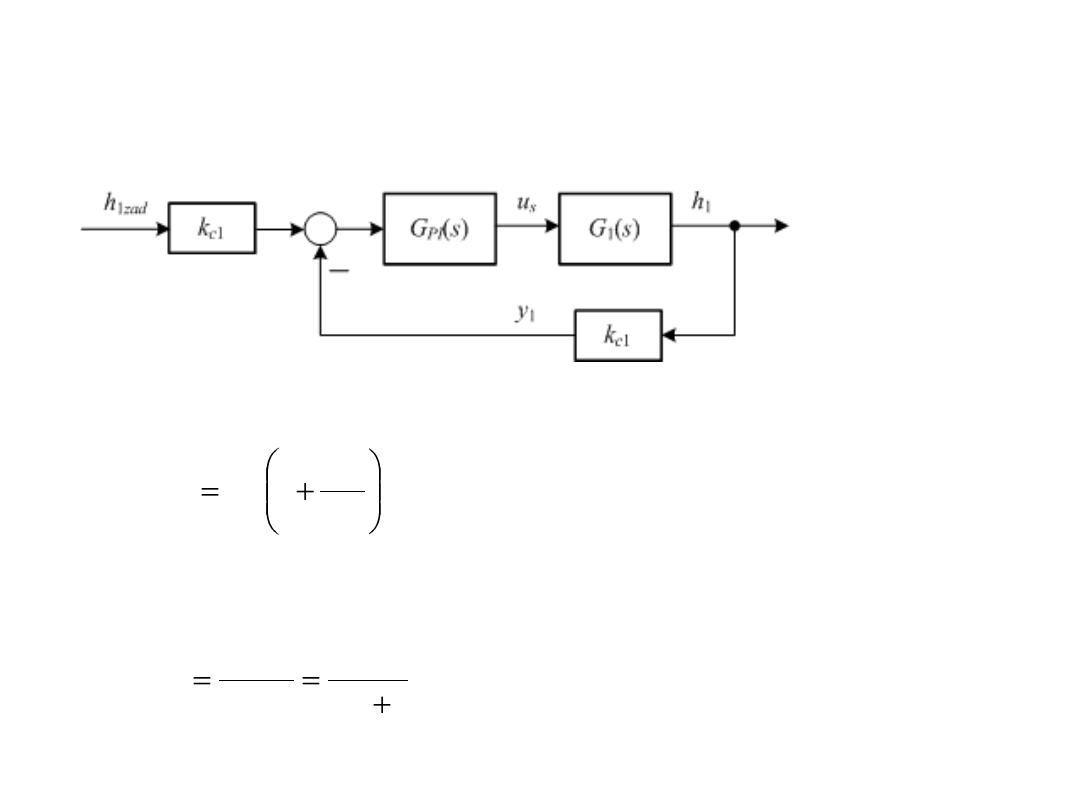
Synteza sterowania poziomem w górnym zbiorniku

21

© M. Tomera

Schemat blokowy układu

I

P

PI

sT

K

s

G

1

1

)

(

Transmitancja regulatora PI

Transmitancja górnego zbiornika

1

)

(

)

(

)

(

1

1

1

1

1

sT

T

k

s

U

s

H

s

G

s

Podstawy Automatyki

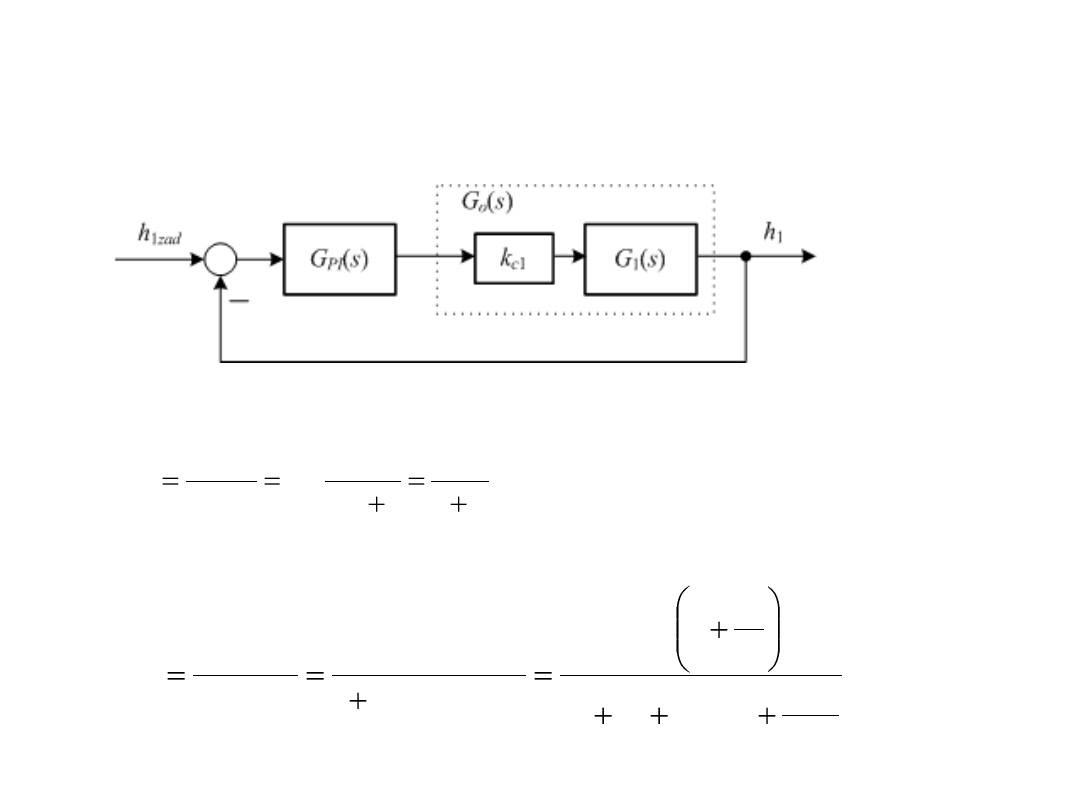
Synteza regulatora PI

22

© M. Tomera

Schemat blokowy układu

I

P

P

I

P

o

PI

o

PI

zad

T

bK

s

bK

a

s

T

s

bK

s

G

s

G

s

G

s

G

s

H

s

H

s

T

)

(

1

)

(

)

(

1

)

(

)

(

)

(

)

(

)

(

2

1

1

Transmitancja obiektu

Transmitancja wypadkowa całego układu

a

s

b

sT

T

k

k

s

U

s

H

s

G

c

s

o

1

)

(

)

(

)

(

1

1

1

1

1

Podstawy Automatyki

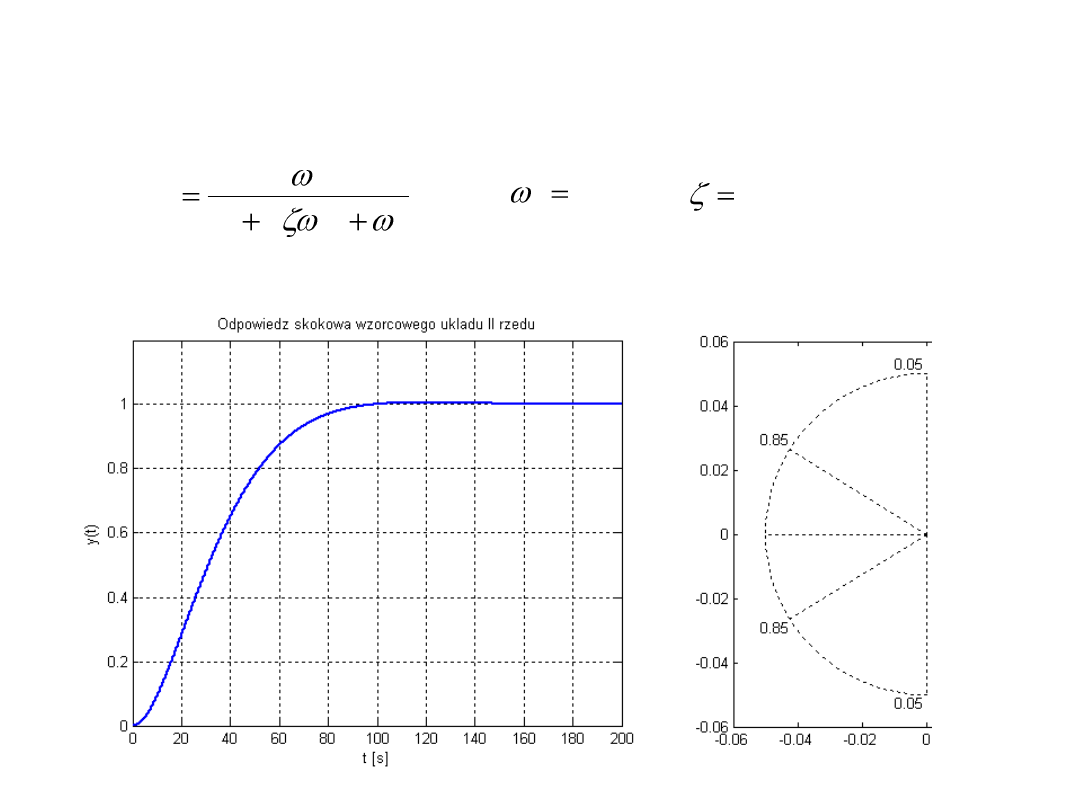
Wzorcowy układ II rzędu

23

© M. Tomera

Transmitancja operatorowa

Odpowiedź skokowa i rozkład biegunów

2

2

2

2

)

(

n

n

n

s

s

s

T

05

.

0

n

85

.

0

Podstawy Automatyki

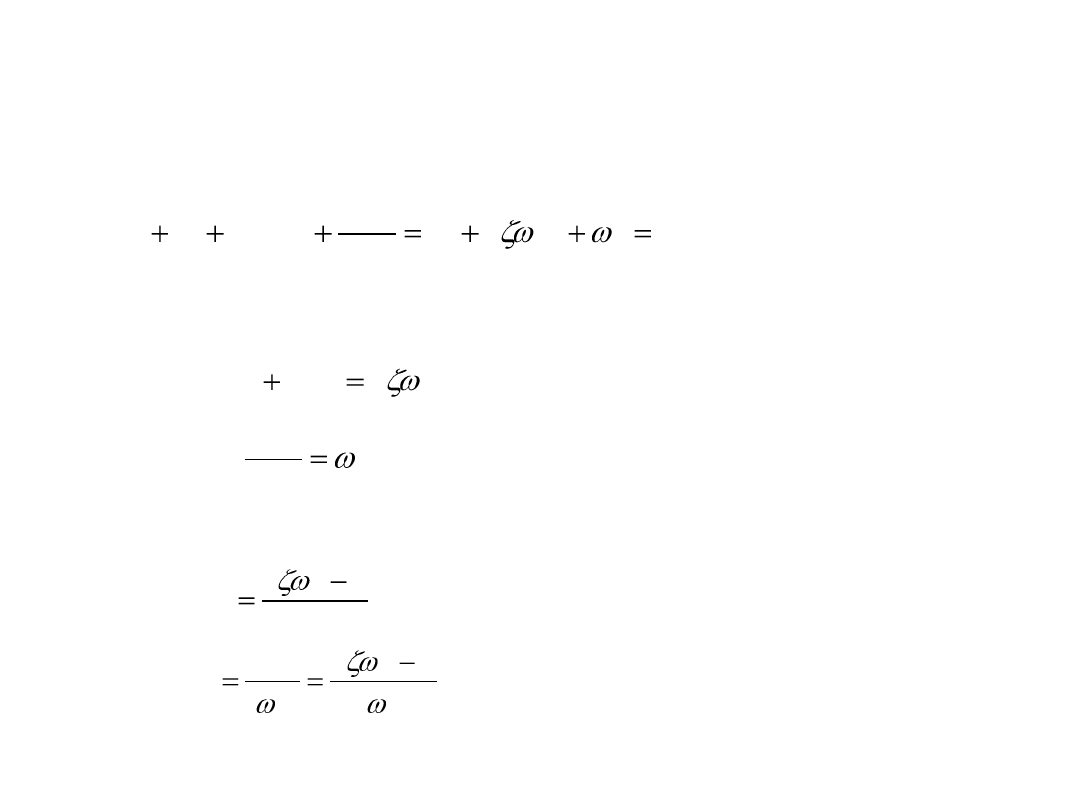
Dobór parametrów regulatora PI

24

© M. Tomera

Metoda lokowania biegunów

0

2

)

(

2

2

2

n

n

I

P

P

s

s

T

bK

s

bK

a

s

Z porównania współczynników równania charakterystycznego

Poszukiwane parametry regulatora PI

n

P

bK

a

s

2

:

1

2

0

:

n

I

P

T

bK

s

b

a

K

n

P

2

2

2

2

n

n

n

P

I

a

bK

T

Podstawy Automatyki

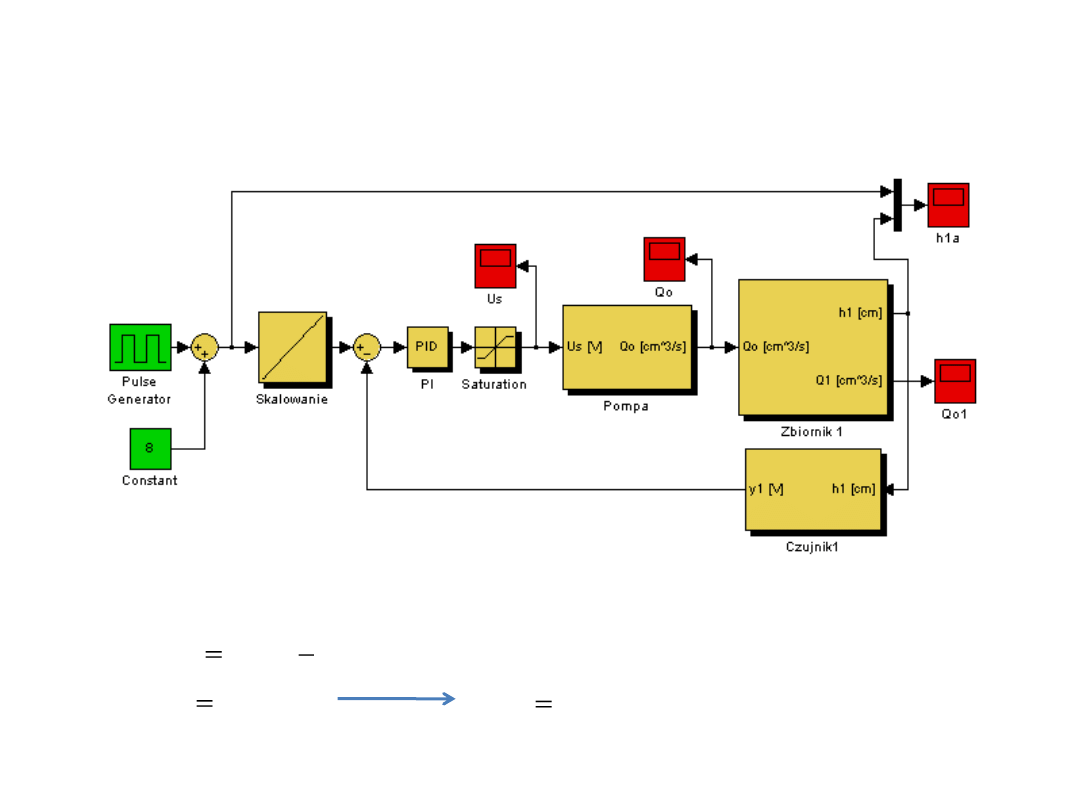
Implementacja układu sterowania w Simulinku

25

© M. Tomera

Podstawy Automatyki

03

.

4

P

K

4

.

22

I

T

]

[s

]

[

Model symulacyjny

Parametry regulatora PI

18

.

0

I

K

]

/

1

[ s

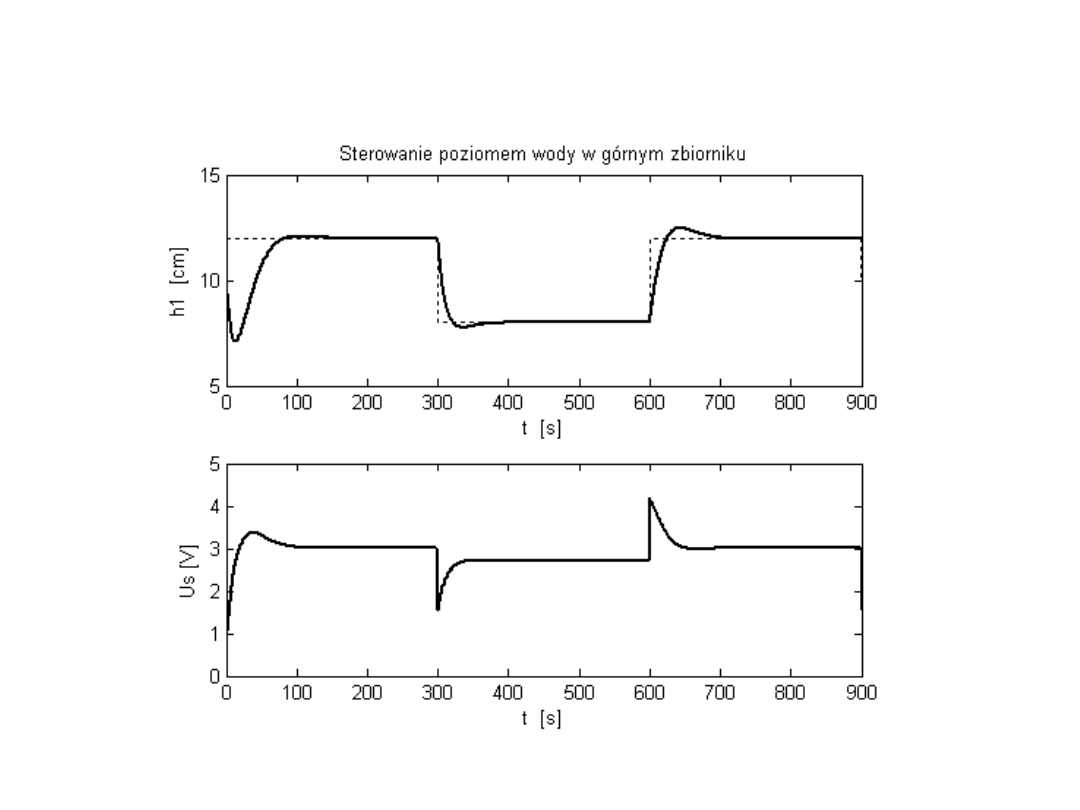
Wyniki badań symulacyjnych

26

© M. Tomera

Podstawy Automatyki

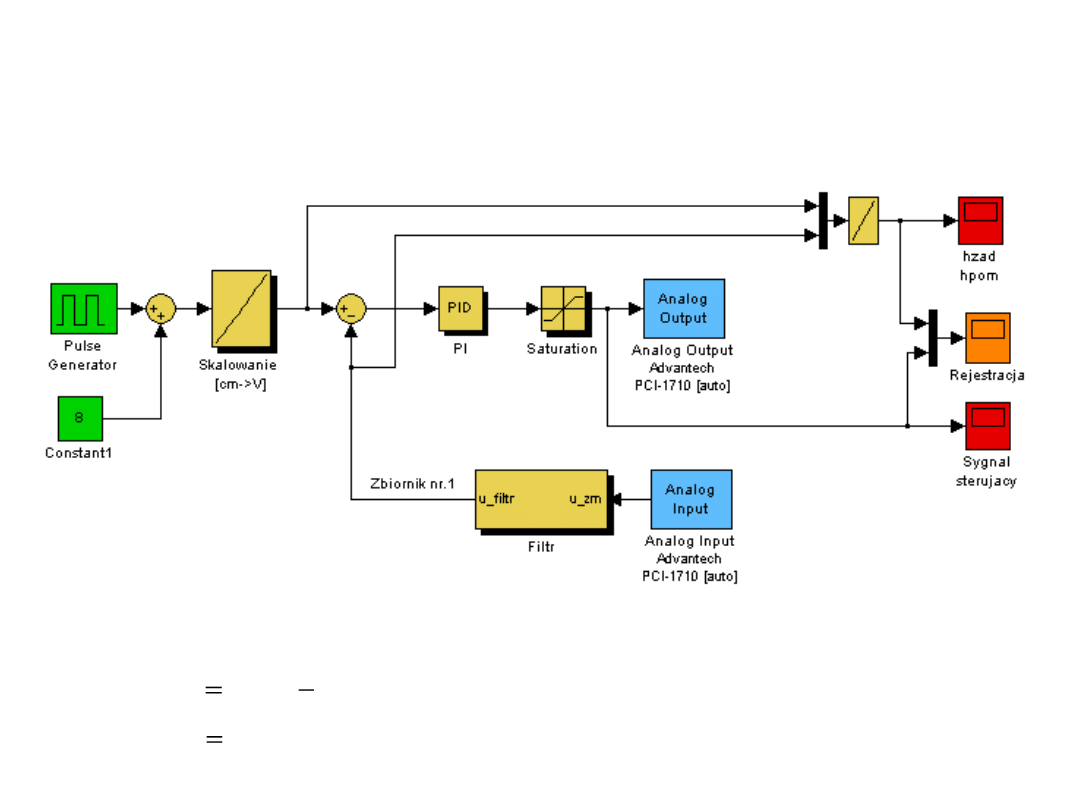
Implementacja układu sterowania w Simulinku - RTWT

27

© M. Tomera

03

.

4

P

K

]

[

Model układu regulacji do sterowania w czasie rzeczywistym

Parametry regulatora PI

Podstawy Automatyki

18

.

0

I

K

]

/

1

[ s

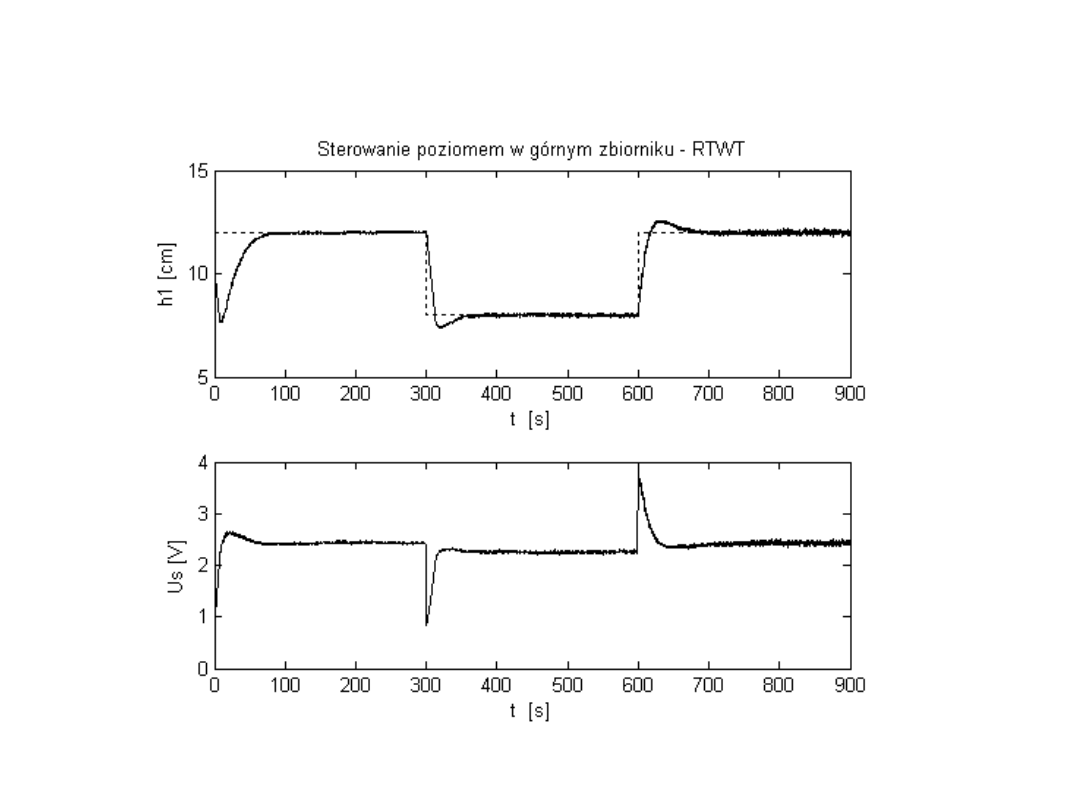
Weryfikacja na obiekcie rzeczywistym - RTWT

28

© M. Tomera

Podstawy Automatyki