J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

1

PROGRAMOWANIE NIELINIOWE

Jeżeli wektor zmiennych decyzyjnych

n



x R

, tzn. jego składowe są liczbami a nie funkcjami,

wtedy klasyfikacja problemu optymalizacji zależy od postaci funkcji celu

 

Q x

i funkcji ograni-

czeo

 

i

g x

:

Zadanie programowania nieliniowego: występuje wtedy, gdy co najmniej jedna z funkcji jest

nieliniowa względem wektora

x

,

Uwaga:

Zadanie programowania liniowego można potraktować jako szczególny przypadek zadania

programowania nieliniowego. Jednak z uwagi na trudność rozwiązywania nie jest to racjo-

nalne.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

2

METODY ANALITYCZNE

ZADANIE PROGRAMOWANIA NIELINIOWEGO BEZ OGRANICZEO

Zbiorem dopuszczalnym jest cała przestrzeo

n

R

.

Punkt

ˆx

jest minimum lokalnym funkcji

 

Q x

w przestrzeni

n

R

, jeżeli istnieje takie otwarte

otoczenie

n

U R

punktu

ˆx

, że

   

ˆ

,

U

Q

Q

 



x

x

x

, przy czym jeżeli nierównośd jest

ostra

   

ˆ

Q

Q



x

x

, to jest to ścisłe minimum lokalne.

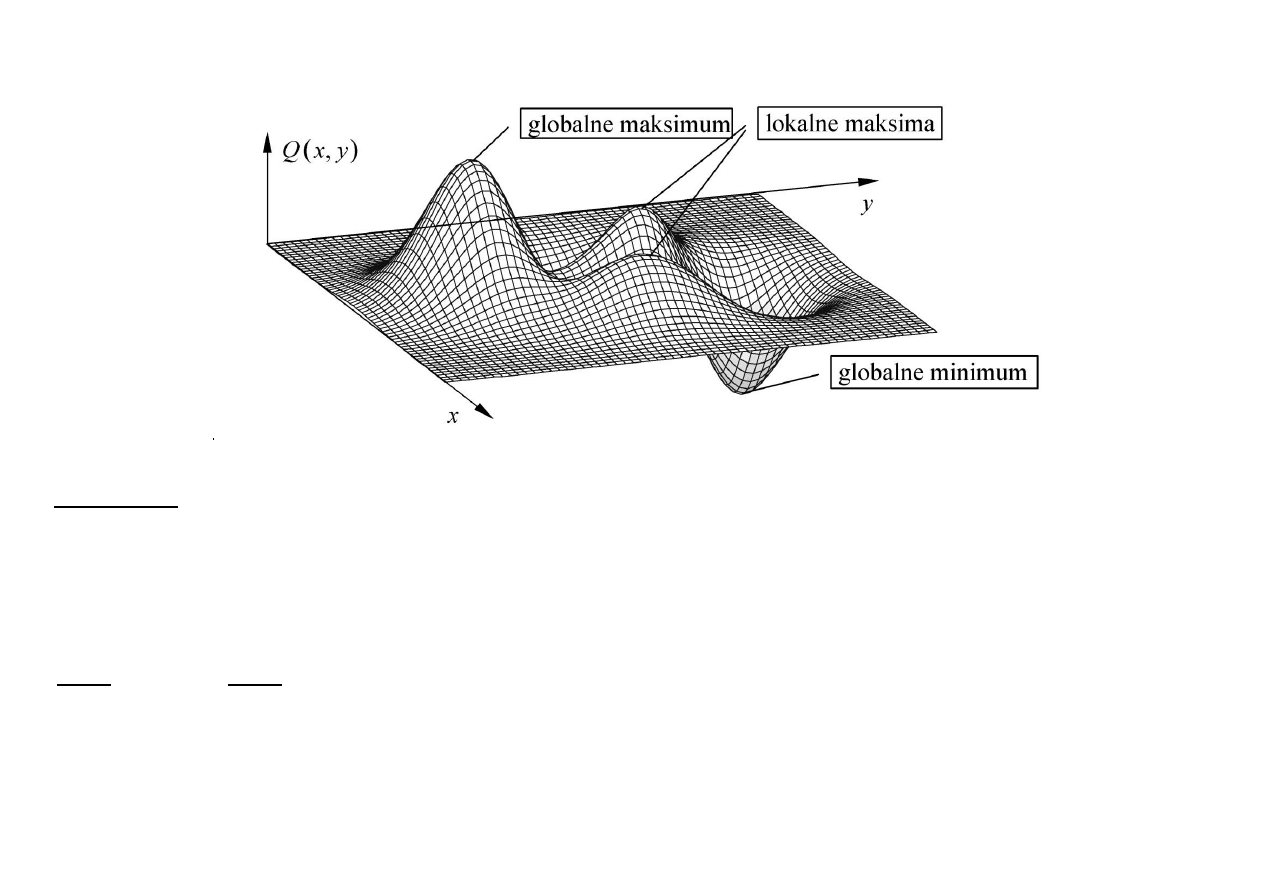
Punkt

ˆx

jest minimum globalnym funkcji

 

Q x

w przestrzeni

n

R

, jeżeli

   

ˆ

,

n

Q

Q

 



x R

x

x

, przy czym jeżeli nierównośd jest ostra

   

ˆ

Q

Q



x

x

, to jest to

ścisłe minimum globalne.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

3

Założenie:

 

,

Q x y

określona w przestrzeni

2

R

, jest klasy C

2

Def.

 

,

Q x y

ma punkt stacjonarny w punkcie

 

ˆ ˆ

,

x y

jeżeli

 

 

 

 

ˆ ˆ

ˆ ˆ

ˆ ˆ

ˆ ˆ

,

,

0

,

,

0

x

y

Q

Q

x y

x y

Q x y

Q x y

x

y























Jest to zarazem warunek konieczny istnienia ekstremum lokalnego

 

,

Q x y

w punkcie

 

ˆ ˆ

,

x y

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

4

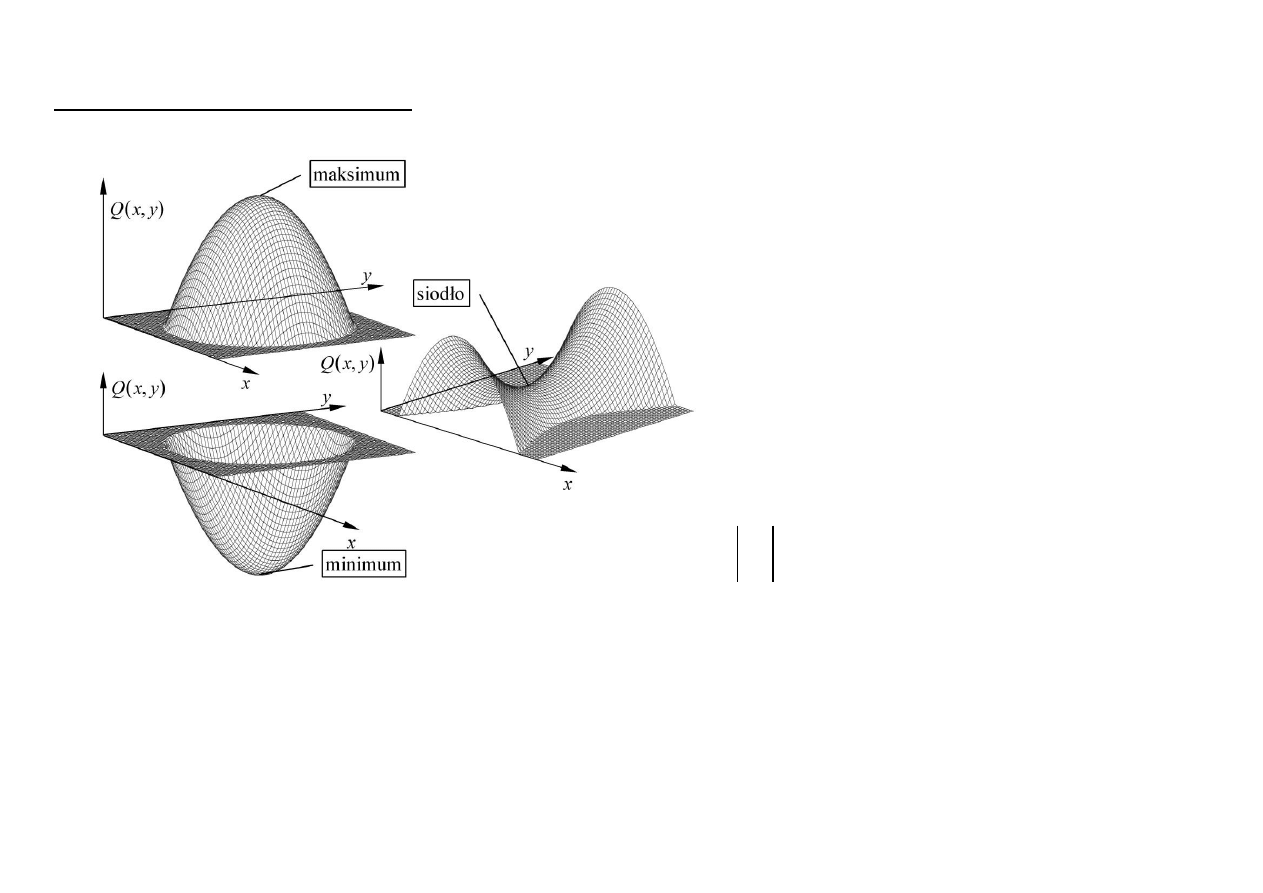
Typy punktów stacjonarnych:

Utwórzmy macierz drugich pochod-
nych (hesjan):

 

 

 

 

,

,

,

,

xx

xy

yx

yy

Q

x y Q

x y

Q

x y Q

x y













  

  



 













H

,

której wyznacznik w punkcie

 

ˆ ˆ

,

x y

wynosi:

   

 

2

ˆ

ˆ ˆ

ˆ ˆ

ˆ ˆ

,

,

,

xx

yy

xy

Q

x y Q

x y Q

x y











H

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

5

Tw.

Jeśli

 

ˆ ˆ

,

x y

jest punktem stacjonarnym

 

,

Q x y

, wtedy:

a)

jeżeli

 

ˆ

ˆ ˆ

,

0 i

0

xx

Q

x y







H

to

 

,

Q x y

ma lokalne maksimum w punkcie

 

ˆ ˆ

,

x y

,

b)

jeżeli

 

ˆ

ˆ ˆ

,

0 i

0

xx

Q

x y







H

to

 

,

Q x y

ma lokalne minimum w punkcie

 

ˆ ˆ

,

x y

,

c)

jeżeli

ˆ

0



H

to

 

,

Q x y

ma siodło w punkcie

 

ˆ ˆ

,

x y

.

Jeżeli

ˆ

0



H

to problem pozostaje nierozstrzygnięty.

Dowód:

Zbadajmy

 

,

Q x y

w otoczeniu





ˆ

ˆ

,

x u y v





.

Rozwijając

 

,

Q x y

w szereg Taylora otoczeniu





ˆ

ˆ

,

x u y v





:



  

 

 

 

 

 

2

2

ˆ

ˆ

ˆ ˆ

ˆ ˆ

ˆ ˆ

,

,

,

,

1

ˆ ˆ

ˆ ˆ

ˆ ˆ

,

2

,

,

2

x

y

xx

xy

Q x u y v

Q x y

uQ x y

vQ x y

u Q

x y

uvQ

x y

v Q x y







 































Ponieważ

 

ˆ ˆ

,

x y

jest punktem stacjonarnym :

 

 

ˆ ˆ

ˆ ˆ

,

,

0

x

y

uQ x y

vQ x y









J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

6

Przyrost



  





2

2

1

ˆ

ˆ

ˆ ˆ

,

,

2

2

Q Q x u y v

Q x y

Au

Buv Cv

 



 







gdzie:

 

 

 

ˆ ˆ

ˆ ˆ

ˆ ˆ

,

,

,

xx

xy

yy

A Q

x y

B Q

x y

C Q

x y













2

2

2

2

2

2

2

2

Bv

B

Bv

Au

Buv Cv

A u

C

v

A u

v

A

A

A

A













 























































































 





gdzie:

2

ˆ

CA B





 H

( wyznacznik hesjanu)

a)

jeśli

 

0 i

0

0

,

A

Q

Q x y



    

ma lokalne minimum w punkcie

 

ˆ ˆ

,

x y

,

b)

jeśli

 

0 i

0

0

,

A

Q

Q x y



    

ma lokalne maksimum w punkcie

 

ˆ ˆ

,

x y

c)

jeśli

0



to

 

,

Q x y

ma w punkcie

 

ˆ ˆ

,

x y

punkt siodłowy.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

7

PRZYKŁAD:

 

2

2

,

Q x y

x

y

 

 

 

   

,

2

0

ˆ ˆ

,

0, 0

,

2

0

x

y

Q x y

x

x y

Q x y

y













 

 

2 0

ˆ

ˆ ˆ

4 0

,

0

2

x y



 





H

jest siodłem.

Uwaga:
Przeprowadzone rozumowanie można uogólnid na funkcję wielu zmiennych.

Założenie:

  



1

2

, , ,

n

Q

Q x x

x



x



określona w przestrzeni

n

R

, jest klasy C

2

.

Def.

 

Q x

ma punkt stacjonarny w punkcie

  



1

2

ˆ

ˆ ˆ

ˆ

, , ,

n

x x

x



x



jeżeli

 

 

 

 

1

2

ˆ

ˆ

ˆ

ˆ

0

n

Q

Q

Q

grad Q

x

x

x











 









x

x

x

x



Jest to zarazem warunek konieczny istnienia ekstremum lokalnego

 

Q x

w punkcie

 

ˆx

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

8

Utwórzmy macierz drugich pochodnych (hesjan):

 

 

 

 

 

 

 

 

 

 

2

2

2

2

1

2

1

1

2

2

2

2

2

1

2

2

2

2

2

2

1

2

n

n

n

n

n

Q

Q

Q

x x

x x

x

Q

Q

Q

x x

x x

x

Q

Q

Q

x x

x x

x







 

 









 

 









 

 





























 







 































x

x

x

x

x

x

H x

x

x

x















którą w punkcie

 

ˆx

oznaczymy jako

 

ˆ













H x

.

Oznaczmy podwyznaczniki (minory) główne, które można utworzyd z hesjanu

 

ˆ













H x

jako:

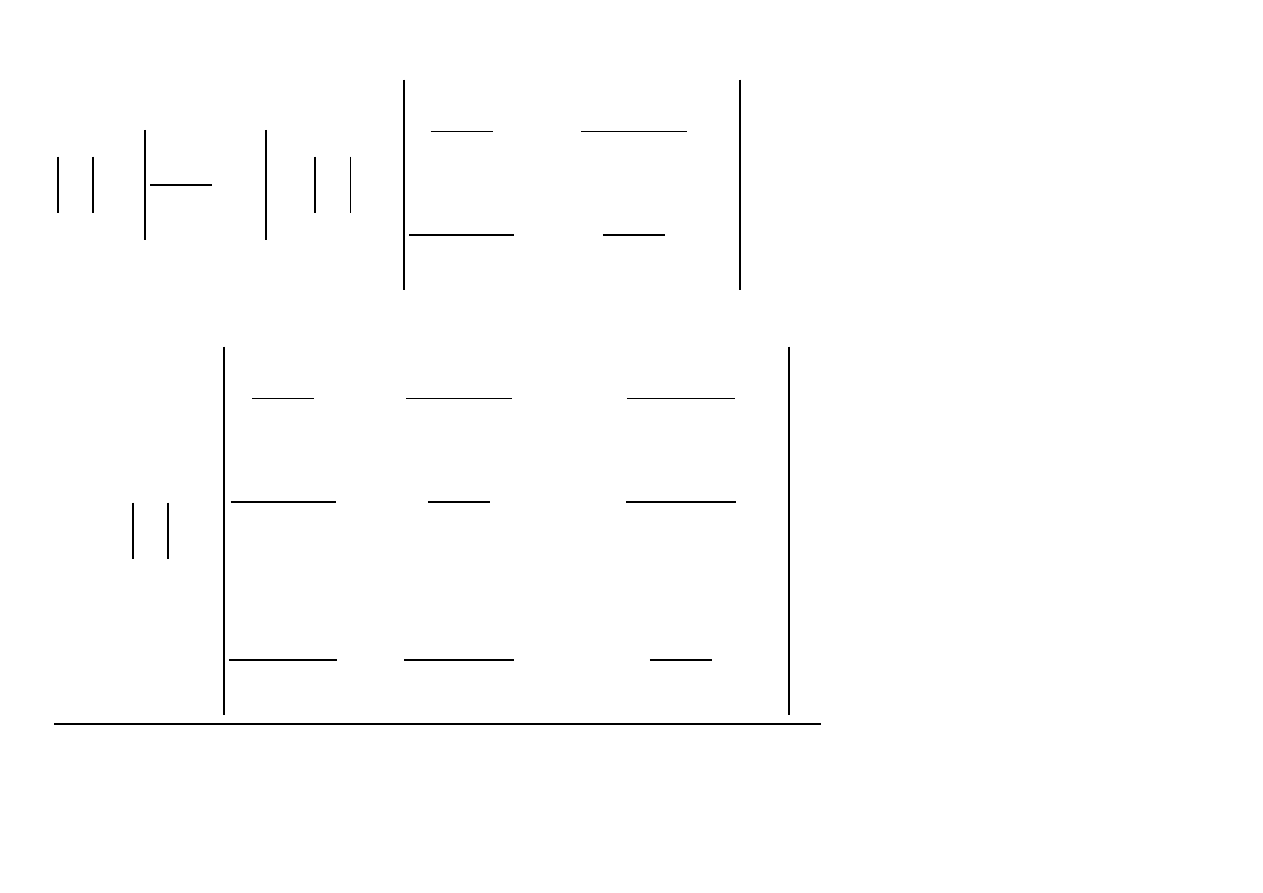
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

2

2

1

2

1

2

2

2

1

2

1

2

2

1

2

2

2

2

2

1

2

1

1

2

2

2

2

2

1

2

2

2

2

2

2

1

2

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

n

n

n

n

n

n

Q

Q

x x

Q

x

Q

Q

x

x x

x

Q

Q

Q

x x

x x

x

Q

Q

Q

x x

x x

x

Q

Q

Q

x x

x x

x





 











 









 

 









 

 









 

 









x

x

H

x

H

x

x

x

x

x

x

x

x

H

x

x

x



















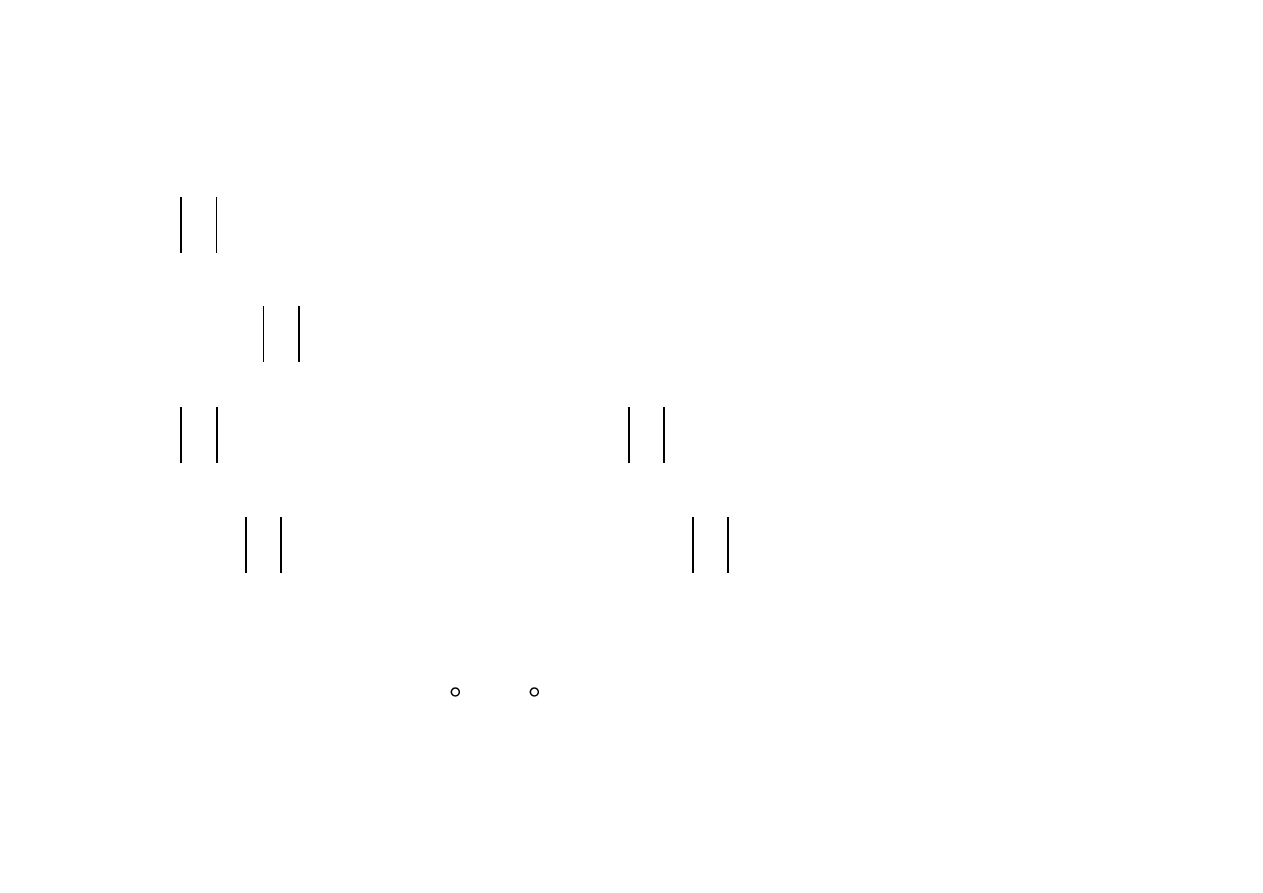
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

10

Tw.

Jeśli

 

ˆx

jest punktem stacjonarnym

 

Q x

, wtedy:

a)

jeżeli

ˆ

0 dla

1, ,

i

i

n





H



to

 

Q x

ma minimum w punkcie

ˆx

(hesjan jest określo-

ny dodatnio),

b)

jeżeli

 

ˆ

1

0 dla

1, ,

n

i

i

n







H



to

 

Q x

ma maksimum w punkcie

ˆx

(hesjan jest

określony ujemnie),

c)

jeżeli

ˆ

ˆ

0 dla

1, ,

1 oraz

0

i

n

i

n









H

H



(hesjan jest określony półdodatnio),

lub

 

ˆ

ˆ

1

0 dla

1, ,

1 oraz

0

n

i

i

i

n











H

H



(hesjan określony półujemnie),to nie można rozstrzygnąd o istnieniu ekstremum w punk-
cie

ˆx

,

Jeżeli nie są spełnione warunki 2 lub 3 (hesjan jest nieokreślony) to

 

Q x

nie ma ekstre-

mum w punkcie

ˆx

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

11

PRZYKŁAD:

Mając 36mb kształtownika, zbudowad otwarty zbiornik o największej
objętości.





















1

2

1 2

1

2

1

2

1

2

1 2

1

2

,

1

2

4

36

9

2

1

,

9

2

Q x x

x x c

max

x

x

c

c

x

x

Q x x

x x

x

x

max







 



 



































2

1

2

2

1 2

2

1

2

1

2

1

1

1 2

2

1

,

9

0

2

1

,

9

0

2

Q

x x

x

x x

x

x

Q

x x

x

x

x x

x













 

















 





x

2

x

1

c

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

12

 



 



2

2

2

1 2

2

1

1

1 2

2

2

2

2

2

2

1

1

2

1

1

1

9

9

2

2

2

18

18

9

9

x

x x

x

x

x

x x

x

x

x

x

x

x











 















Zatem:



 



ą

ł ż

2

1

2

1

2

1

2

1

1

1

9

9

lub

9

9

lub

18

(to rozwi zanie prowadzi do wyniku

6

co jest sprzeczne z za o eniem

>0)

x

x

x

x

x

x

x

x

x

x

  



 





 



 





2

2

1

1

1

1

1

1

1

2

1

9

0 :

0

2

3

1

9

6

6

9

6 6

3

2

2

x

x

x

x

bo

x

x

x

x

c



















 

 

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

13

 

2

1

2

1

1

1

(6,6)

2

2

1

max

9

6

3

ˆ

36 9 27

9

3

6

ˆ

ˆ

0

i

0

6 6

jest maksimum

6, 6

6 6 3 108

T

x

x

x

x

x

x

Q

x

Q

Q



 

 





  

 



 













  









   

H

H

x

ZADANIE PROGRAMOWANIA NIELINIOWEGO Z OGRANICZENIAMI W RÓWNOŚCIOWYMI

Problem:

Dana jest funkcja

 

Q x

klasy C

1

, w zbiorze dopuszczalnym

n

R

. Zbiór dopuszczalny okre-

ślony jest przez ograniczenia równościowe

 

0

j

h



x

. Znajdź minimum funkcji celu.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

14

Tw. (zasada Lagrange’a)

Niech dane będą stałe

1

2

, , , , ,

j

m

 



 R





takie, że w punkcie

ˆ

n



x R

funkcja

 

 

1

ˆ

ˆ

m

j j

j

Q

h









x

x

ma minimum bez ograniczeo (bezwarunkowe). Wtedy punkt

ˆx

jest mi-

nimum (warunkowym) funkcji

 

Q x

w zbiorze dopuszczalnym określonym przez ograniczenia

równościowe

 

0 dla

1, ,

j

h

j

m





x



.

Dowód:

Przyjmijmy, że

ˆx

jest lokalnym minimum funkcji

 

 

1

ˆ

ˆ

m

j j

j

Q

h









x

x

. Oznacza to, że istnieje

otoczenie

U

punktu

ˆx

takie, że:

 

   

 

1

1

ˆ

ˆ

,

m

m

j j

j j

j

j

U Q

h

Q

h









 











x

x

x

x

x

Ponieważ dla

 

 

ˆ

ˆ

,

,

0 oraz

0

j

j

U

h

h

 





x x

x

x

, prawdziwe jest

   

ˆ

Q

Q



x

x

oznacza to, że

 

Q x

ma minimum w punkcie

ˆ



x

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

15

Uwaga:

Podobne rozumowanie można przeprowadzid dla zadania maksymalizacji. Podstawiając

 

Q

 x

zamiast

 

Q x

otrzymamy taki sam rezultat dla zadania maksymalizacji.

Wniosek:

Pierwotny problem

n

– wymiarowy minimalizacji funkcji

 

Q x

z ograniczeniami równościo-

wymi

 

0

j

h



x

został zastąpiony

n m



– wymiarowym problemem minimalizacji zastęp-

czej funkcji

 

 

1

m

j j

j

Q

h









x

x

bez ograniczeo.

Taki sposób postępowania to metoda mnożników Lagrange’a.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

16

Metoda mnożników Lagrange’a

Dana jest funkcja celu

 

Q x

klasy C

1

i zbiór dopuszczalny utworzony jest przez ograniczenia

równościowe (funkcjonalne).

 





:

0;

1,..., ;

;

n

j

h

j

m m n











x

x

R

Φ

gdzie:

m

- liczba ograniczeo równościowych,

n

- liczba zmiennych decyzyjnych.

Funkcje

 

j

h x

są również klasy C

1

.

Utwórzmy funkcję:

   

 

 

 

1 1

2 2

...

m m

L

Q

h

h

h













 

x,

x

x

x

x

λ

gdzie:

1

2

,...,

T

m

 







 







λ

- wektor mnożników Lagrange’a.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

17

Warunkiem koniecznym istnienia ekstremum lokalnego funkcji

 

,

L x λ

w punkcie

 

ˆx

dla

wektora mnożników

ˆλ

jest:

 

 

 

ˆ

ˆ,

0

1,...,

ˆ

ˆ,

0

ˆ,

0

1,...,

i

j

L

i

n

x

L

L

j

m





































x

x

x

λ

λ

λ

Rozwiązując układ (6)

n m



równao znajdujemy punkt

ˆx

i wektor

ˆλ

, dla których zeruje się

gradient a zatem punkt, w którym występują punkty stacjonarne.

Jeśli

 

Q x

jest klasy C

2

badając hesjan

 

ˆ













H x

możemy rozstrzygnąd o typie punktu stacjo-

narnego.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

18

PRZYKŁAD:

Dane zadania jak w przykładzie poprzednim.







 























1

2

1 2

1

2

1

2

1

2

1

2

1

2

1

2

1 2

1

2

, ,

, ,

2

4

36 0

, , ,

, ,

, ,

, , ,

2

4

36

Q x x c

x x c

max

h x x c

x

x

c

L x x c

Q x x c

h x x c

max

L x x c

x x c

x

x

c

max

















  

















 















2

1

1

1

1 2

1

2

2

0

(1)

2

0

(2)

4

0

(3)

2

4

36 0 (4)

L

x c

x

L

x c

x
L

x x

c

L

x

x

c









 













 



































  





J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

19





1

2

1

2

2

2

2

2

1

1

1

2

(1)=(2)

bo

(5)

z (2)

(6)

(5) i (6) do (3)

bo

(7)

(7) do (2)

bo

(8)

(5) i (8) do (4)

0

2

2

4

0

0

0

2

0

2

0

2 2

2

4

36

3

6

x

x

c

x

c

c

c

c

x c

c

x

c

c

c

c

c

c

x

x















 



 











  

  





















  







 

 

 

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

20

ZADANIE PROGRAMOWANIA NIELINIOWEGO Z OGRANICZENIAMI NIERÓWNOŚCIOWYMI

Zadanie, w którym funkcja celu jest wypukła i zbiór dopuszczalny jest wypukły, nazywamy za-
daniem programowania wypukłego.

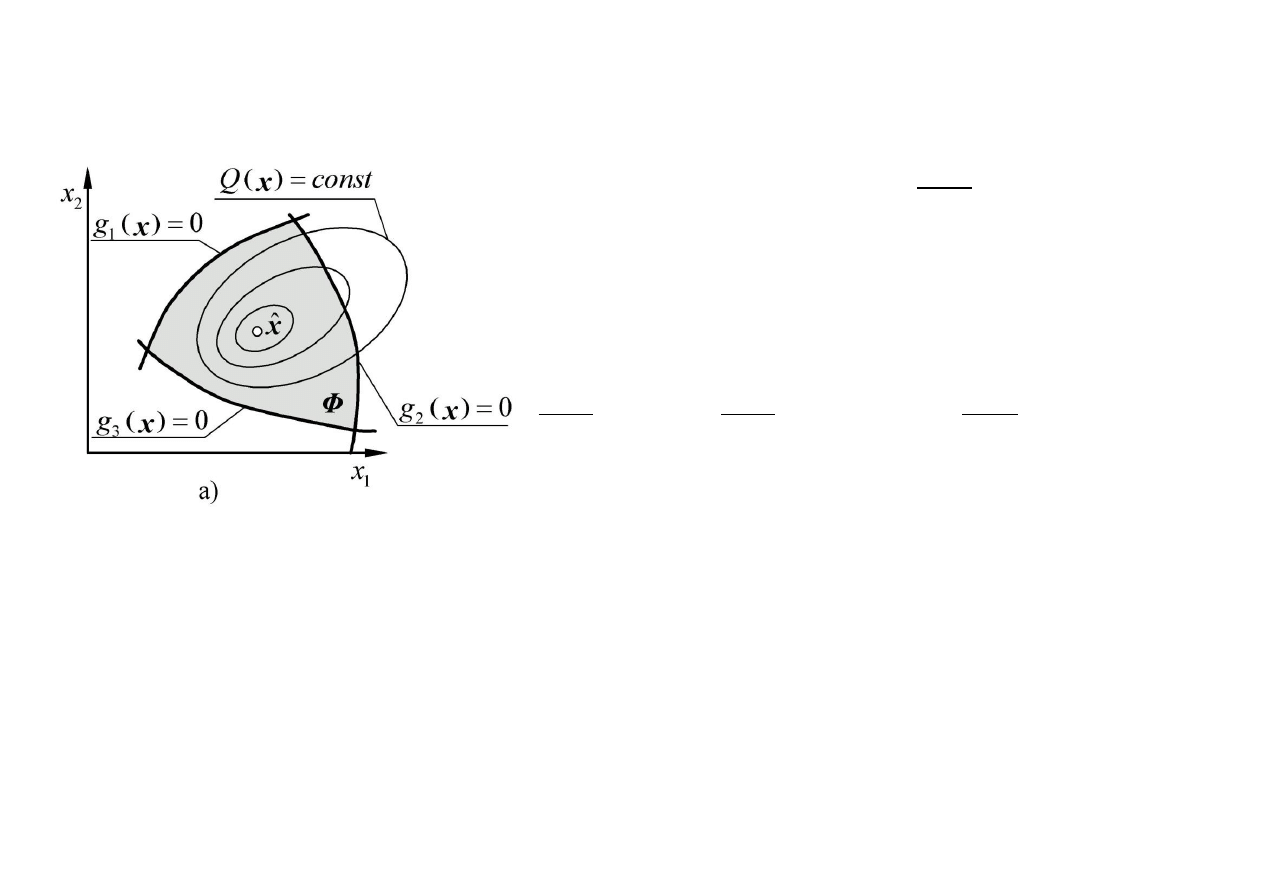
Rozważmy dwuwymiarowe zadanie programowania wypukłego

 

 





2

1

2

min,

,

:

0,

1,2, 3

T

j

Q

x x

g

j

























x

x

x

x

R

w którym

 

Q x

jest klasy C

1

.

Utwórzmy funkcję Lagrange’a:

   

 

 

   

 

λ

3

1 1

2 2

3 3

1

j j

j

L

Q

g

g

g

Q

g

























x,

x

x

x

x

x

x

Możliwe są trzy położenia minimum

ˆx

wg zbioru



J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

21

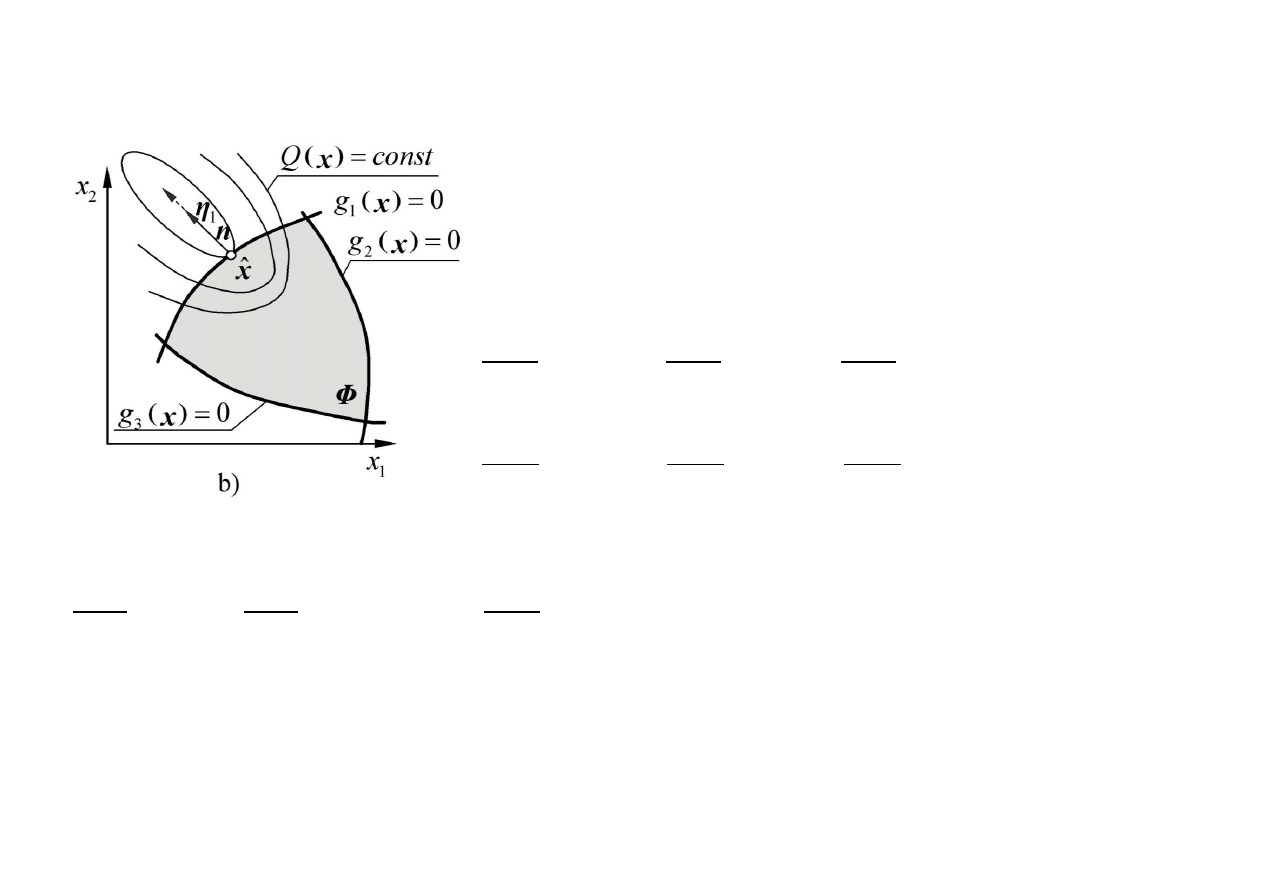
a)

 

Q x

ma minimum w

ˆx

leżącym wewnątrz



,

Wtedy

 





 

ˆ

ˆ

0

0

i

Q

grad Q

x



 





x

x

oraz

 

ˆ

0,

1,2, 3

j

g

j





x

.

Co można wyrazid za pomocą funkcji Lagrange’a

 

 

 

λ

3

1

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

j

j

j

i

i

i

g

L

Q

x

x

x

























x

x

x

jeśli

ˆ

0,

1,2, 3

j

j

 



.

Warunek

 

ˆ

0

j

g



x

jest aktywny w punkcie

ˆx

, jeżeli

 

ˆ

0

j

g



x

.

Warunek

 

ˆ

0

j

g



x

jest nieaktywny w punkcie

ˆx

, jeżeli

 

ˆ

0

j

g



x

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

22

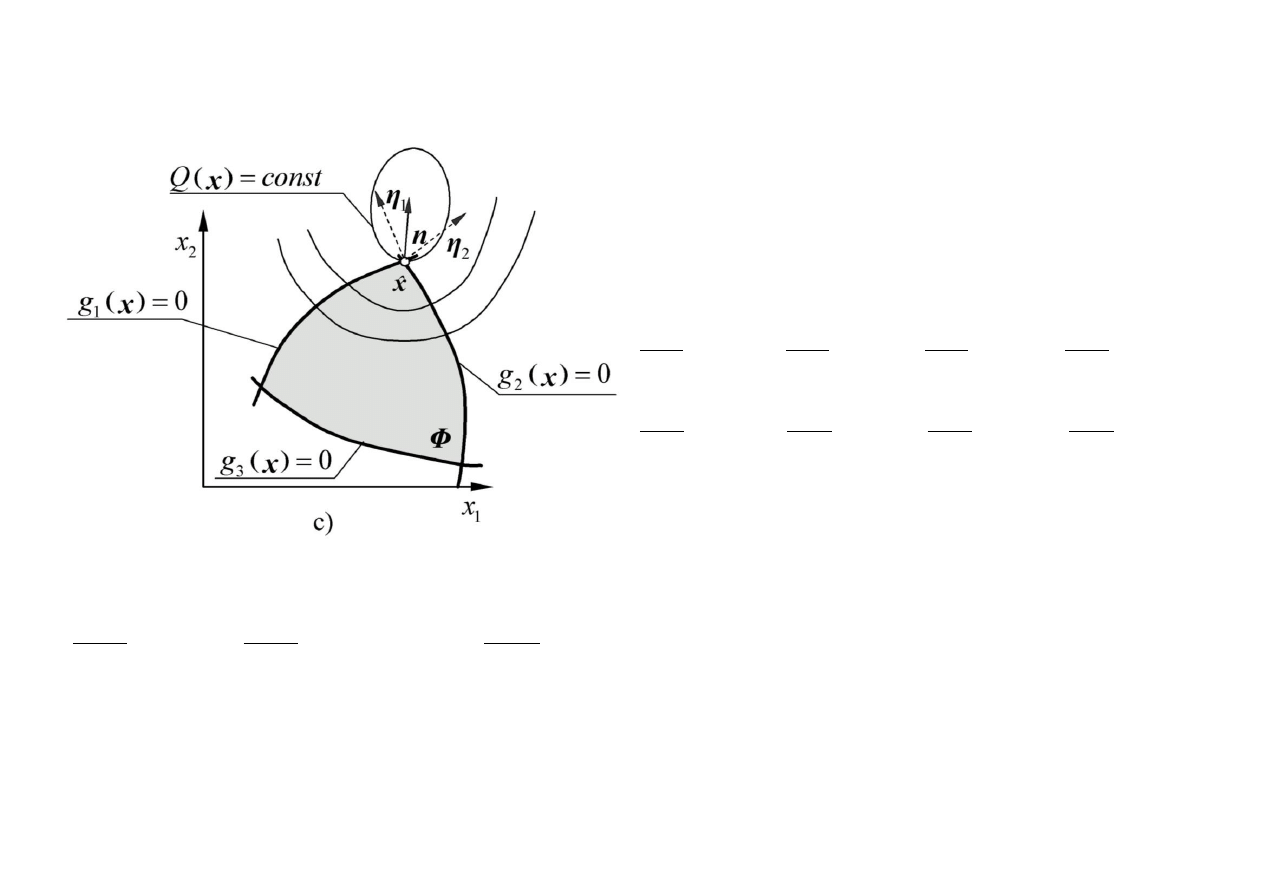
b)

 

Q x

ma minimum w

ˆx

leżącym na brzegu



(np. ograniczenie

1

g

jest aktywne),

Wtedy

 

 

 

1

2

3

ˆ

ˆ

ˆ

0,

0,

0,

g

g

g







x

x

x

Zatem w dostatecznie małym otoczeniu

ˆx

zadanie jest

równoważne problemowi optymalizacji z ograniczeniem
równościowym.

 

 

 

 

 

 

1

1

1

1

1

1

1

1

1

2

2

2

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

g

L

Q

x

x

x

g

L

Q

x

x

x













































x

x

x

x

x

x

Co można wyrazid za pomocą funkcji Lagrange’a

 

 

 

λ

3

1

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

j

j

j

i

i

i

g

L

Q

x

x

x

























x

x

x

jeśli

1

2

3

ˆ

ˆ

ˆ

0,

0









 

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

23

c)

 

Q x

ma minimum w

ˆx

leżącym w narożu



(np. ograniczenia

1

g

i

2

g

są aktywne),

Wtedy

 

 

 

1

2

3

ˆ

ˆ

ˆ

0,

0,

0,

g

g

g







x

x

x

Zatem w dostatecznie małym otoczeniu

ˆx

za-

danie jest równoważne problemowi optymali-
zacji z dwoma ograniczeniami równościowymi.

 

 

 

 

 

 

 

 

1

2

1

1

2

1

1

1

1

1

1

1

1

2

2

2

2

2

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

g

g

L

Q

x

x

x

x

g

g

L

Q

x

x

x

x





























































x

x

x

x

x

x

x

x

Co można wyrazid za pomocą funkcji Lagrange’a

 

 

 

λ

3

1

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

j

j

j

i

i

i

g

L

Q

x

x

x

























x

x

x

jeśli

1

2

3

ˆ ˆ

ˆ

,

0,

0

 







J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

24

Podsumujmy przypadki a), b), c):

Zawsze dla

ˆ

1,2, 3

0

j

j







, ponadto:

1° jeżeli

 

ˆ

0

j

g



x

(warunek nieaktywny), to

ˆ

0

j

 

,

2° jeżeli

 

ˆ

0

j

g



x

(warunek aktywny), to

ˆ

0

j

 

.

Zatem punkt

ˆx

jest rozwiązaniem zadania, gdy:

 

 

 

1

ˆ

ˆ

ˆ

ˆ

ˆ

,

0

m

j

j

j

i

i

i

g

L

Q

x

x

x

























x

x

x

λ

,

 

ˆ

ˆ

0

i

0

j

j

g







x

( spełnia wszystkie ograniczenia),

 

ˆ

ˆ

0

j j

g





x

(co oznacza warunki 1° i 2°).

Powyższe warunki są warunkami koniecznymi istnienia rozwiązania zadania programowania

nieliniowego z ograniczeniami nierównościowymi zwanymi warunkami Kuhna-Tuckera (WKT).

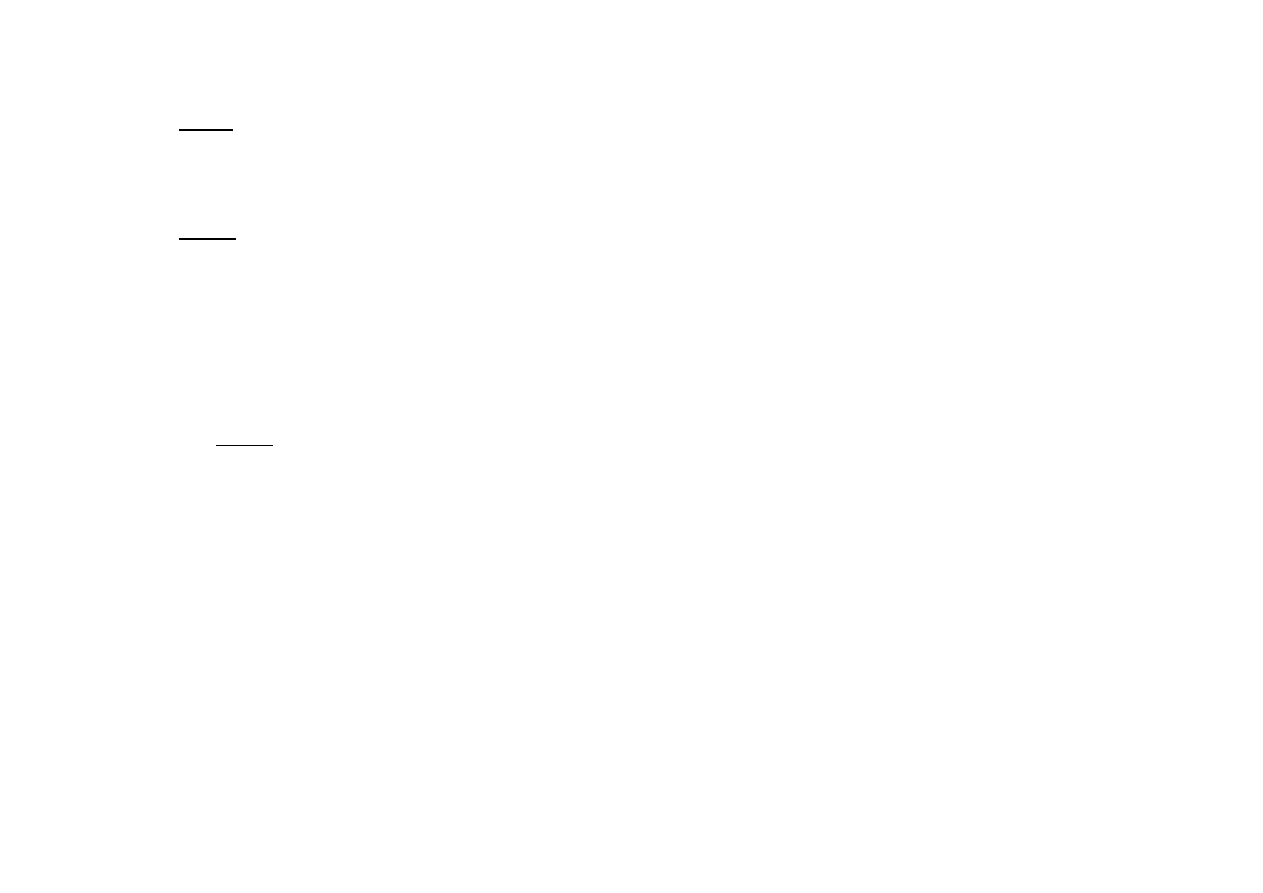
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

25

Inaczej:

 

 

 

ˆ

ˆ,

0

1, ,

ˆ

0

ˆ

0

1, ,

ˆ

ˆ

0

i

j

j

j

j

L

i

n

x

L

j

m

L



























































 













































x

x

x





λ

Uwaga:

Jeżeli w zadaniu występowałyby jednocześnie ograniczenia typu nierównościowego i równo-

ściowego, to każdą z równości

 

0

j

g



x

można zastąpid dwoma nierównościami

 

1

0

j

g



x

i

 

2

0

j

g





x

.

O tym czy punkt

ˆx

jest minimum

 

Q x

można rozstrzygnąd badając hesjan

ˆ

 

 

 

H

.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

26

PRZYKŁAD:

  

 



2

2

,

1

1

min

Q x y

y x

x

 

 

 

(dolina Rosenbrocka)

przy ograniczeniach:

 

 

1

2

1

,

1 0

1

,

1 0

y x

g x y

y x

y

x

g x y

y x

 



   

 



   



  

 

 



 











1

2

1 1

2 2

2

2

1

2

, , ,

,

,

,

1

1

1

1

L x y

Q x y

g x y

g x y

y x

x

y x

y x

 















 

 

 

  

  



 







1

2

1

1

1

1

1

2

2 1

0

1 0

1

0

1

0

L

y x

x

x

L

y x

L

y x





















 

   







   







 



 





  

 



J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

27









1

2

2

2

2

2

2

2

0

1 0

2

0

1

0

L

y x

y

L

y x

L

y x





















   









   







 











   

 



Warunki 1°1 i 2°1 tworzą układ równao:

1

2

1

2

2

2

2 2

0

2

2

0

y

x

x

y

x









      





   



Załóżmy, że ograniczenia

 

1

,

0

g x y 

,

 

2

,

0

g x y 

są nieaktywne, tj.

1

2

,

0

  

.

Wtedy:

2

4

2 0

2

2

ˆ

ˆ

1

1

2

2

0

y

x

x

x

y

y

x

y x

   







 





 

 



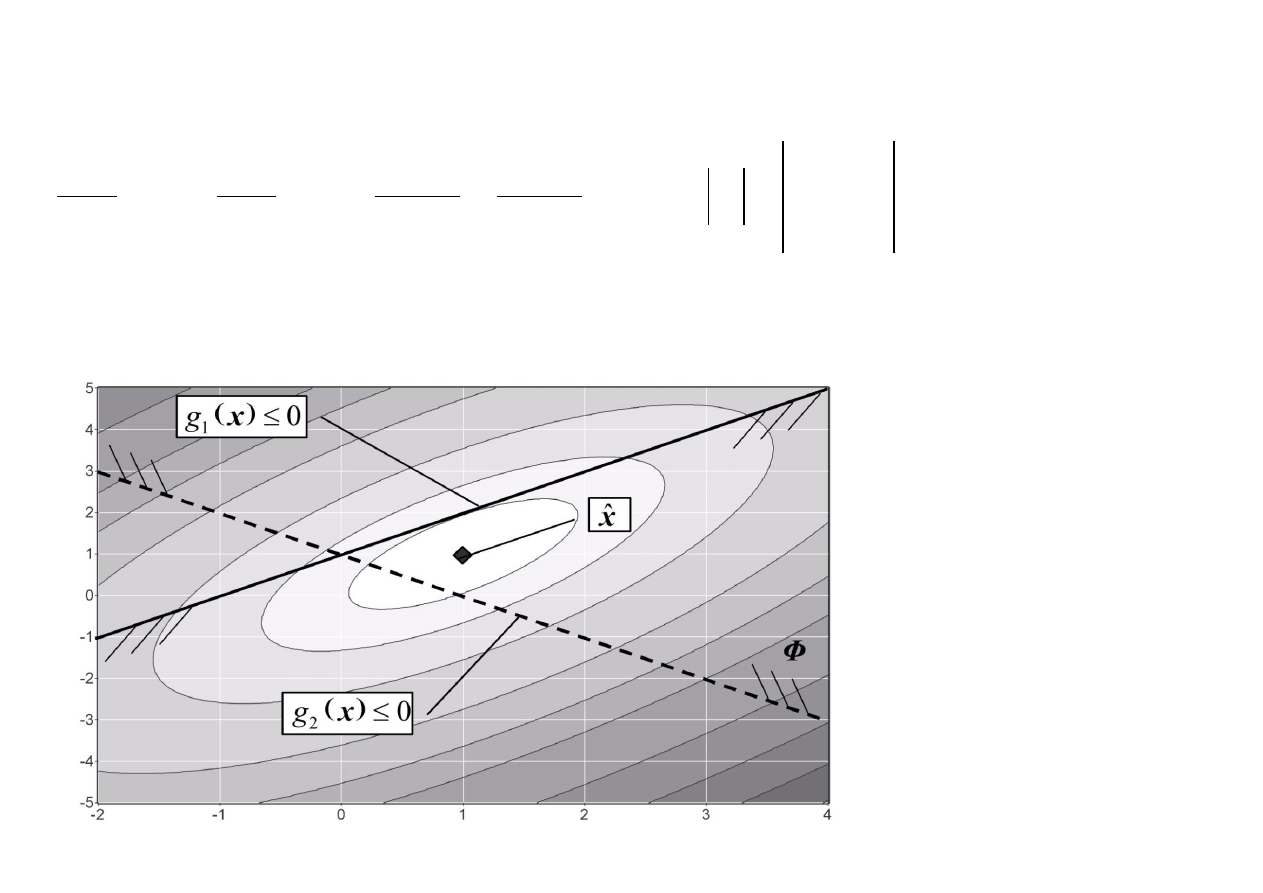
Łatwo sprawdzid, że pozostałe warunki KT w punkcie

   

ˆ ˆ

,

1,1

x y 

są spełnione.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

28

Obliczmy hesjan w punkcie

   

ˆ ˆ

,

1,1

x y 

.

2

2

2

2

2

2

4

2

ˆ

4

2

2

16 4 12 0

2 4

L

L

L

L

x y

y x

x

y





















   



 

 





H

Zatem w punkcie

   

ˆ ˆ

,

1,1

x y 

funkcja celu

 

,

Q x y

ma minimum przy ograniczeniach

 

1

,

0

g x y 

,

 

2

,

0

g x y 

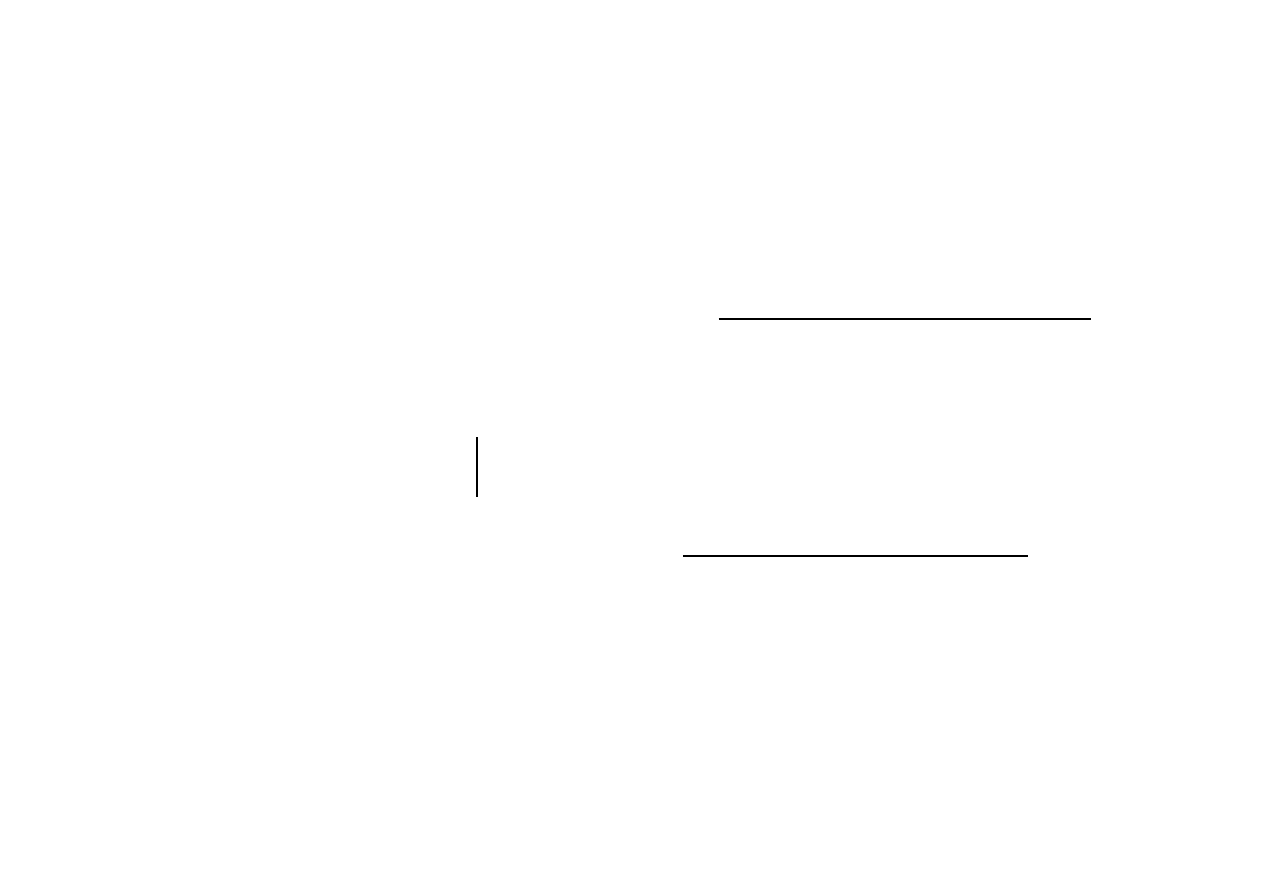
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

29

Zmieomy warunek

 

2

,

0

g x y 

na następujący:

 

2

3

,

3 0

y

x

g x y

y x



 



   

Wtedy:

1

2

1

2

1

2

1

2

2

2

2

2 2

0

2 2

4

0

2

2

0

2

2

0

2 2

2

0

y

x

x

y

x

y

x

y

x

x



























      

  

  















   

   











  



Stąd:

2

1 x

  

 

1

2

1

2

1

2

1

2

1

2 2

4

0

2 2

4

0

1

2

2

0

2

2

0

2 4

6

2

0

y

x

y

x

y

x

y

x

y

x

 





















     

  

  

 

















   

   









  



Stąd:

1

3

2

1

x

y

   

Sprawdzamy pozostałe warunki KT:

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

30







1

1

3

2

1

1

0

3

2

1 0

1 0

3

1

1

2

2

L

x

y

y x

x

y

y x

y

x

y x









 

  



  



  









 

Stąd:

   

ˆ ˆ

,

3, 4

x y 

,

1

3 3 2 4 1 0

      

,

2

1 3

2 0

    

(warunek niespełniony)







2

2

1

3

0

1

0

3 0

1

3

L

x

y x

x

y x

x

y

x







 

   



 



   







 

Stąd:

   

ˆ ˆ

,

1,2

x y 

1

3 2 2 1 1 3 0

       

,

2

1 1 0

   

1

2 1 1 0

L





   



,

2

2 1 3 0

L





   



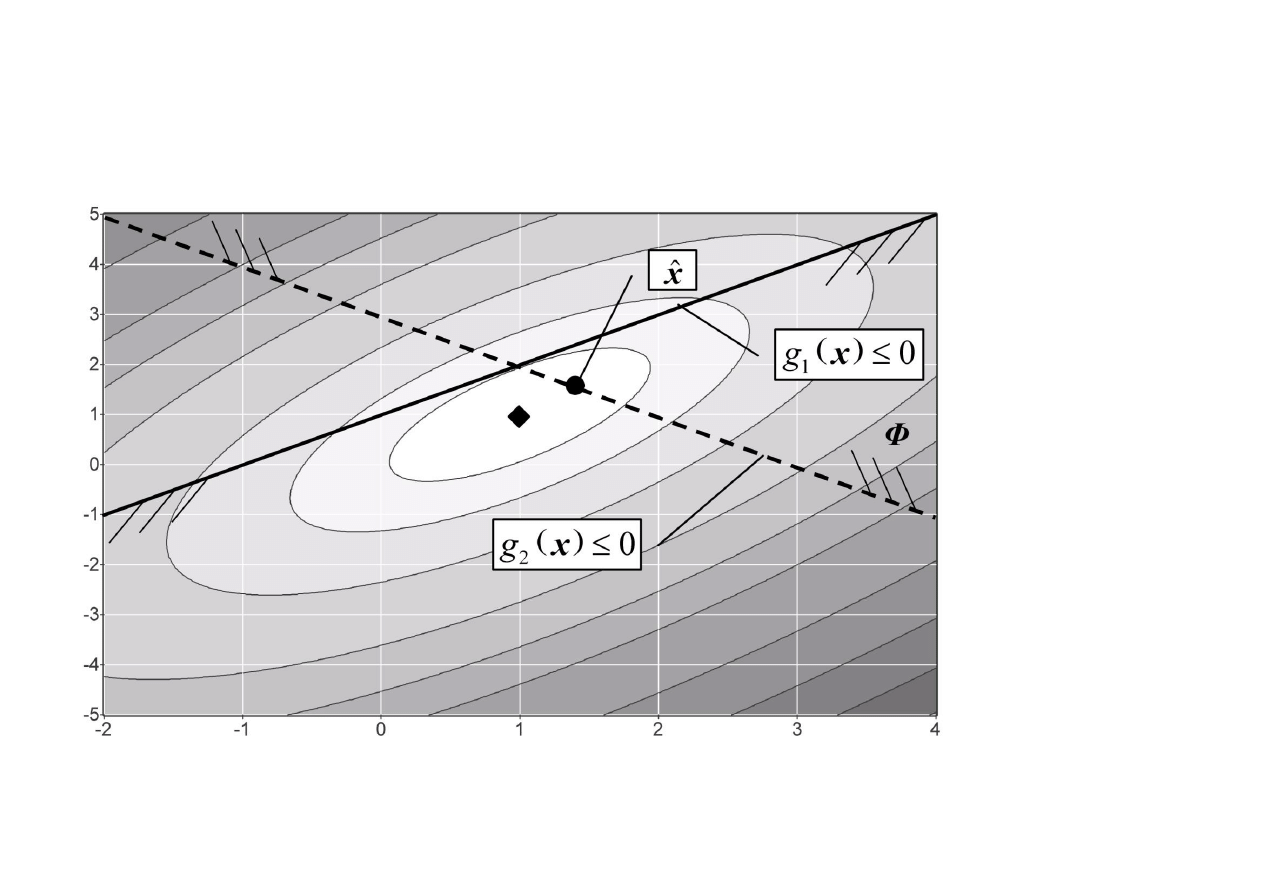
Zatem punkt

   

ˆ ˆ

,

1,2

x y 

spełnia warunki konieczne rozwiązania zadania.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd3: PROGRAMOWANIE NIELINIOWE – metody analityczne

31

Hesjan

ˆ

 

 

 

H

nie zmienia się, dlatego w punkcie

   

ˆ ˆ

,

1,2

x y 

funkcja celu

 

,

Q x y

ma mini-

mum przy ograniczeniach

 

1

,

0

g x y 

,

 

2

,

0

g x y





.