g

c

cc

g

c

cc

g

c

cc

1

2

3

4

8

9

10

1

2

3

4

9

Nr

ci

ą

gów

v

x

p

i

v

x

v

x

p

i

v

x

Suma k

ą

tów

lewych lub prawych

Niewyrównany

azymut w

ę

złowy A

i

Nr-y

ci

ą

gów

Punkt

pocz

ą

t

kowy

Ilo

ść

k

ą

tów

(n

i

)

Waga

odcinka

p

i

=10/n

i

n - ilość

odcinków obl.

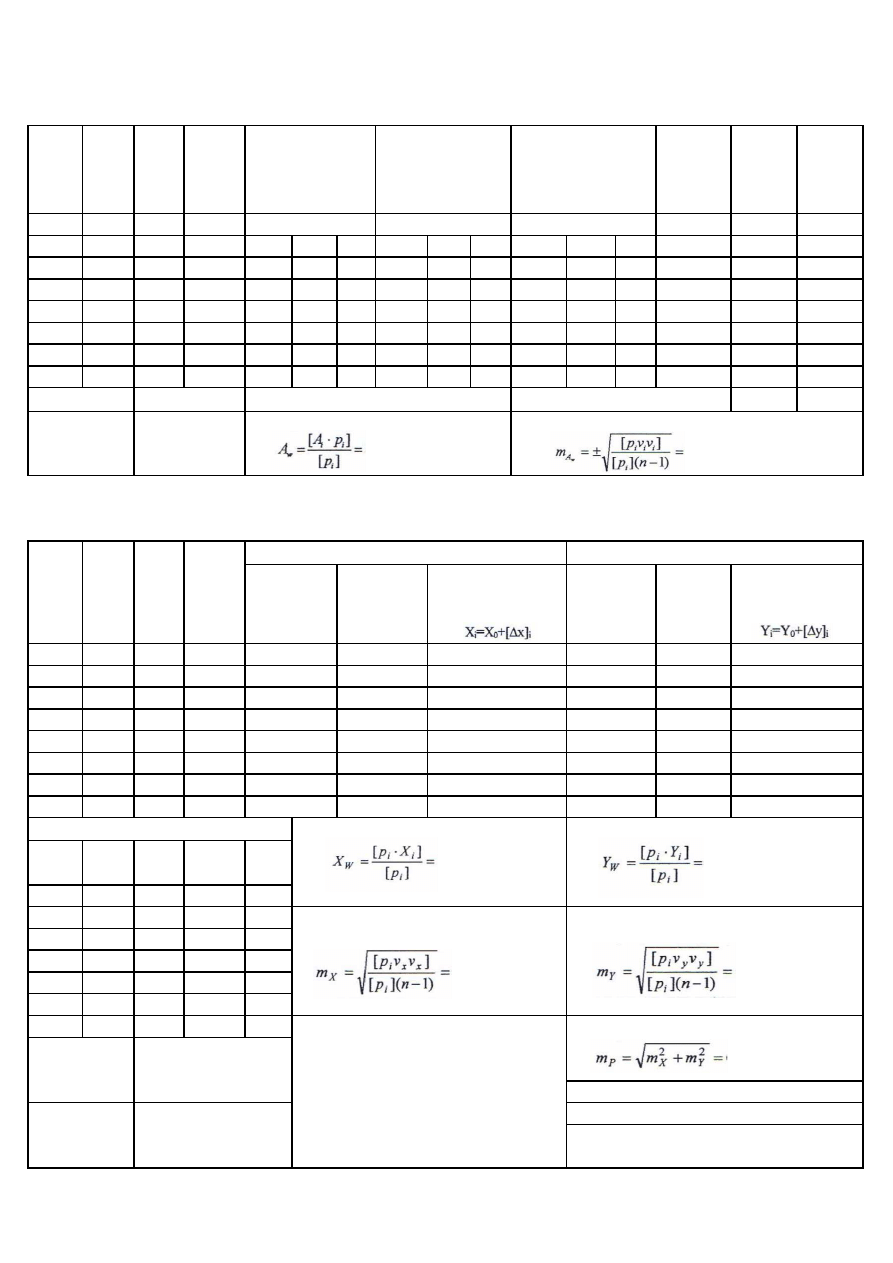
A

w

n

i

- ilość kątów

odcinka

Azymut wyrównany:

Błąd średni azymutu wyrównanego:

OBLICZENIE AZYMUTU WĘZŁOWEGO:

n =

[p

i

] =

[p

i

](n-1)=

Sumy:

Poprawki

v

i

=A

w

-A

i

Iloczyny

A

i*

p

i

Iloczyny

p

i*

v

i

5

6

7

Azymut wyj

ś

ciowy

A

0

10

Współrz

ę

dna

punktu

nawi

ą

zania

Y

0

Współrzędna Y

Niewyrównana

współrz

ę

dna punktu

w

ę

złowego

8

7

Suma

przyrostów

[

Δ

y]

i

Niewyrównana

współrz

ę

dna

punktu w

ę

złowego

Suma

przyrostów

[

Δ

x]i

Współrz

ę

dna

punktu

nawi

ą

zania X

0

Współrzędna X

Nr-y

ci

ą

gów

Punkt

nawi

ą

z

ania

Długo

ść

ci

ą

gu

L

i

Waga

ci

ą

gu p

i

6

5

[p

i

]=

Współrz

ę

dna wyrównana X :

Współrz

ę

dna wyrównana Y :

[p

i

v

x

]=

[p

i

v

x

v

x

]=

[p

i

v

y

]=

[p

i

v

y

v

y

]=

OBLICZENIE WSPÓŁRZĘDNYCH WĘZŁOWYCH PUNKTU:

Ś

redni bł

ą

d wyrównanej współrz

ę

dnej X:

Ś

redni bł

ą

d wyrównanej współrz

ę

dnej Y:

Uwagi

Bł

ą

d

ś

redni poło

ż

enia p. w

ę

złowego

Obliczył:

Data:

Podpis: