1
NIEPEWNOŚĆ
1. Podstawy
2. Teoria prawdopodobieństwa i preferencje względem ryzyka
2.1. Prawdopodobieństwo obiektywne i subiektywne
2.2. Wartość oczekiwana i wariancja
2.3. Niezależność
2.4. Własności prawdopodobieństwa
2.5. Paradoks Petersburski
3. Użyteczność oczekiwana i funkcja użyteczności von Neumann’a
– Morgenstern’a
3.1. Twierdzenia dotyczące użyteczności oczekiwanej
3.2. Wskaźnik von Neumann’a – Morgenstern’a
3.3. Postawa wobec ryzyka
4. Rynek ubezpieczeniowy
4.1. Model zakupu ubezpieczenia
4.2. Wykup pełnego ubezpieczenia i pewna konsumpcja
4.3. Ubezpieczenie i prawo wielkich liczb
5. Kontrakty futures i inne kontrakty długoterminowe jako forma
ubezpieczenia
6. Roszczenia warunkowe (
Contingent claims
) i model preferencji
zależnych od stanu (
the state-preference model
)
6.1.
Dobra warunkowe (
Contingent commodities
)
i roszczenia
warunkowe (
contingent claims
)
6.2.
Krzywe obojętności zależne od stanu (
State-contingent
indifference curve
)
6.3. Malejąca MRS i awersja wobec ryzyka
6.4. Linia ograniczenia budżetowego zależna od stanu i maxU
6.5. Dzielenie ryzyka między konsumentami na rynku roszczeń
warunkowych
6.6. Pełne ubezpieczenie konsumenta neutralnego względem
ryzyka
2
Własności prawdopodobieństwa
Zał.: za każdym razem rezultat jest jednym z n niezależnych
i różnych wyników.
Niech:
x
i
: wartość i-tego wyniku
ρ
i
: prawdopodobieństwo zaistnienia i-tego wyniku
Dwie własności p-stwa:
1.
1
=
∑
n
i
i
ρ
2. p-stwo x
i
oraz x
j
= (ρ
i
)( ρ
j
)
Dwie definicje:
1. Wartość oczekiwana = E{x} =
x
x
i
n
i
i
=
∑
ρ
2. Wariancja = var{x} =
2
)
(
x
x
i
n
i
i
−
∑
ρ
Paradoks Petersburski
Masz możliwość zapłacić $100 i wziąć udział w jednej z
trzech (sprawiedliwych) gier:
1. Otrzymujesz z powrotem $100;
2. Rzucam sprawiedliwą monetą. Ty otrzymujesz:
$200 jeżeli jest to orzeł
0 jeżeli jest to reszka
3. Rzucam sprawiedliwą kością. Ty otrzymujesz:
$400 jeżeli jest to 1
$70 : 2
$55 : 3
$25 : 4
$40 : 5
$10 : 6
3
Wszystkie te gry mają wartość oczekiwaną $100, ale różne
wariancje:
1. 0
2. ½ (200 – 100)
2
+ ½ (0 - 100)
2
= 10.000
3. (1/6)(300
2
+ 30
2
+ 45
2
+ 75
2
+ 60
2
+ 90
2
) = 18.375
Tą kwestię ilustruje Paradoks Petersburski sformułowany
przez Beronulli’ego Zaproponował on wariancję następującej
gry. Rzucamy kostką aż do otrzymania orła. Wygrana zależy
od liczby rzutów zanim pojawi się orzeł. Rzuty sprawiedliwą
kostką są niezależne i prawdopodobieństwo jest iloczynem
prawdopodobieństw kolejnych rzutów.
Wygrane w tej grze są konstruowane następująco:
$2 : jeżeli orzeł pojawi się przy pierwszym rzucie (ρ = ½ )
$4 : jeżeli orzeł pojawi się przy drugim rzucie (ρ = 1/4)
$8 : jeżeli orzeł pojawi się przy trzecim rzucie (ρ = 1/8)
$16 : jeżeli orzeł pojawi się przy czwartym rzucie (ρ = 1/16)
$2
n
: jeżeli orzeł pojawi się przy n-tym rzucie (1/2
n
)
Wartość oczekiwana gry =
½ 2 + (1/4)4 + ... =
∑
∞
=1
2
2
1
n
n
n
= 1 + 1 + .... = ∞
Nikt nie zapłaci nieskończenie wiele aby wziąć udział w tej
grze. Niewiele osób zapłaci więcej niż kilka $ aby wziąć
udział w tej grze. Przyczyną jest wariancja również równa ∞,
a większość osób preferuje mniejsze wariancje – mniejszą
niepewność.
4
Użyteczność oczekiwana i funkcja użyteczności von
Neumann’a – Morgernstern’a
Z Paradoksu Petersburskiego wynika, że potrzebujemy
czegoś więcej niż wartość oczekiwana do analizowania
decyzji podejmowanych przez ludzi w warunkach ryzyka:
Użyteczność oczekiwana : przedstawia preferencje w
warunkach niepewności w ujęciu wartości oczekiwanej zbioru
użyteczności względem możliwych wyników, x
i
:
E{U} =
)
(
i
n
i
i
x
U
∑
ρ
(liniowa względem p-stwa)
Twierdzenia dotyczące użyteczności oczekiwanej: 1- 6.
Wskaźnik użyteczności von Neumann’a – Morgenstern’a
Konstruowany jest w sposób następujący: Wszystkie możliwe
wyniki są uporządkowane zgodnie z twierdzeniem o użyteczności
oczekiwanej (preferencje dotyczące możliwych wyników: x
1
, ... ,
x
n
są spójne, zwrotne i przechodnie), czyli: x
2
jest preferowane
względem x
1
, x
3
jest preferowane względem x
2
i x
n
jest
preferowane względem x
n-1
.
Następnie najmniej preferowanemu wynikowi przypisuje się
użyteczność = 0, a najbardziej: = 1. Wszystkie pozostałe wyniki
(x
i
) mają użyteczność równą ρ
i
, gdzie x
i
to ekwiwalent pewności
gry dotyczącej x
n
z p-stwem ρ
i
i x
1
z p-stwem (1 - ρ
i
):
U(x
1
) ≡ 0, U(x
n
) ≡ 1, U(x
i
) ≡ ρ
i
. (*)
Zbiór tych wskaźników użyteczności jest równoważny do
obliczenia oczekiwanych wartości użyteczności x
n
i x
1
przy
wykorzystaniu prawdopodobieństw ρ
i
i (1 - ρ
i
)związanych z grą, w
której x
i
jest ekwiwalentem pewności dla każdego x
i
włączając x
1
i x
n
:
U(x
i
) = ρ
i
U(x
n
) + (1 - ρ
i
)U(x
1
) = ρ
i
+ 0 = ρ
i
. (**)
Wskaźniki użyteczności opisane (*) i (**) zachowują zależność
ekwiwalentu pewności przy przekształceniu tożsamościowym.
Możemy więc wybrać dowolne nieujemne wartości użyteczności
5
dla x
1
i x
n
(U(x
n
) > U(x
1
)) i przedstawić U(x
i
) jako użyteczność
oczekiwaną gry.
Np. V(x
1
) = a, V(x
n
) = b, b > a ≥ 0,
V(x
i
) = ρ
i
b + (1 - ρ
i
)a.
Aby stwierdzić, że liniowe przekształcenie zachowuje ekwiwalent
pewności dla uporządkowania (*) dla zdefiniowanego U(x):
V(x) = c + dU(x),
a więc: V(x
1
) = c + d0 = c i V(x
n
) = c + d1 = c + d,
z czego wynika, że: V(x
i
) = ρ
i
(c + d) + (1 - ρ
i
)c = c + dρ
i
.
Wartość V(x
i
) jest więc taka sama jak przekształcona
użyteczność x
i
otrzymana z prostego podstawienia za U(x
i
) z (*)
w równaniu V(x) = c + dU(x). Zachowana więc zostaje zależność
ekwiwalentu pewności.
Postawa wobec ryzyka
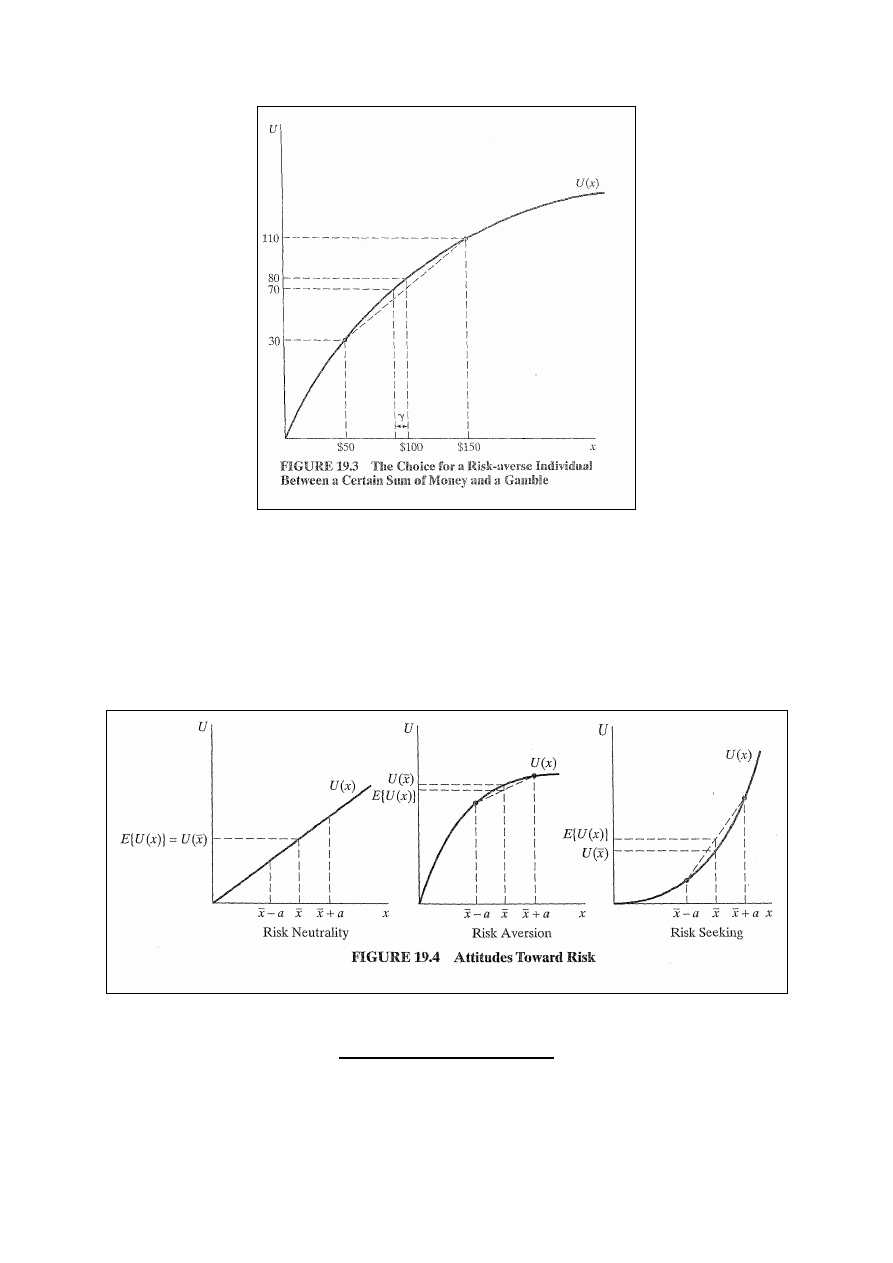
Zał.: możliwe są trzy wyniki i dwie działalności.
Wyniki są następujące:
•
Wynik 1: $50 i U = 30
•
Wynik 2: $100 i U = 80
•
Wynik 3: $150 i U = 110
Czyli: U($50) = 30, U($100) = 80, U($150) = 110.
Dwie działalności dają
te
wyniki
z
różnymi
prawdopodobieństwami:
•
Działalność A daje $100 na pewno: E{U(A)} = (1)U(100) =
80
•
Działalność B daje $50 z p-stwem ½ i $150 z p-stwem ½
: E{U(B)} = ½ U(50) + ½ U(150) = 70 < 80.
A więc, pomimo że każda z działalności daje oczekiwaną
wygraną = $100, to użyteczność oczekiwana B < od
użyteczności oczekiwanej A.
6
Rys. 19.3: U=70 < U=80: osoba jest niechętna wobec ryzyka.
Co więcej osoba ta będzie gotowa zapłacić γ aby uniknąć
ryzyka. Przy niższej wypłacie ($100 - γ) jednostka w dalszym
ciągu ma U = 70 i nie musi podejmować ryzyka. Kwotę γ
nazywamy składką od ryzyka (risk premium).
Rys. 19.4.
Rynek ubezpieczeń
Zastosowaniem teorii awersji wobec ryzyka jest rynek
ubezpieczeń. Ubezpieczenie jest sposobem ochrony przeciw
7
ryzyku i jednostki niechętne wobec ryzyka chcą zapłacić
składkę od ryzyka aby je uniknąć.
Przykład
Posiadasz budynek wart $50.000 i inne aktywa warte
$50.000. Z p-stwem 10% budynek ulegnie zniszczeniu . A
więc z p-stwem 10% masz aktywa o wartości $50.000 i 90%
- $100.000.
Użyteczność oczekiwana gry:
E{U} = (0,10)U(50.000) + (0,90)U(100.000);
Wartość oczekiwana:
E{x} = 0,10(50.000) + 0,90(100.000) = 95.000.
Rys.19.5: E{U} można obliczyć rysując linię prostą między
50.000 i 100.000 (liniowa kombinacja użyteczności tych
wartości). Użyteczność oczekiwana jest w 9/10 odległości od
50.000 i 100.000 wzdłuż tej linii. Przy awersji wobec ryzyka
użyteczność oczekiwana gry o $95.000 jest mniejsza od
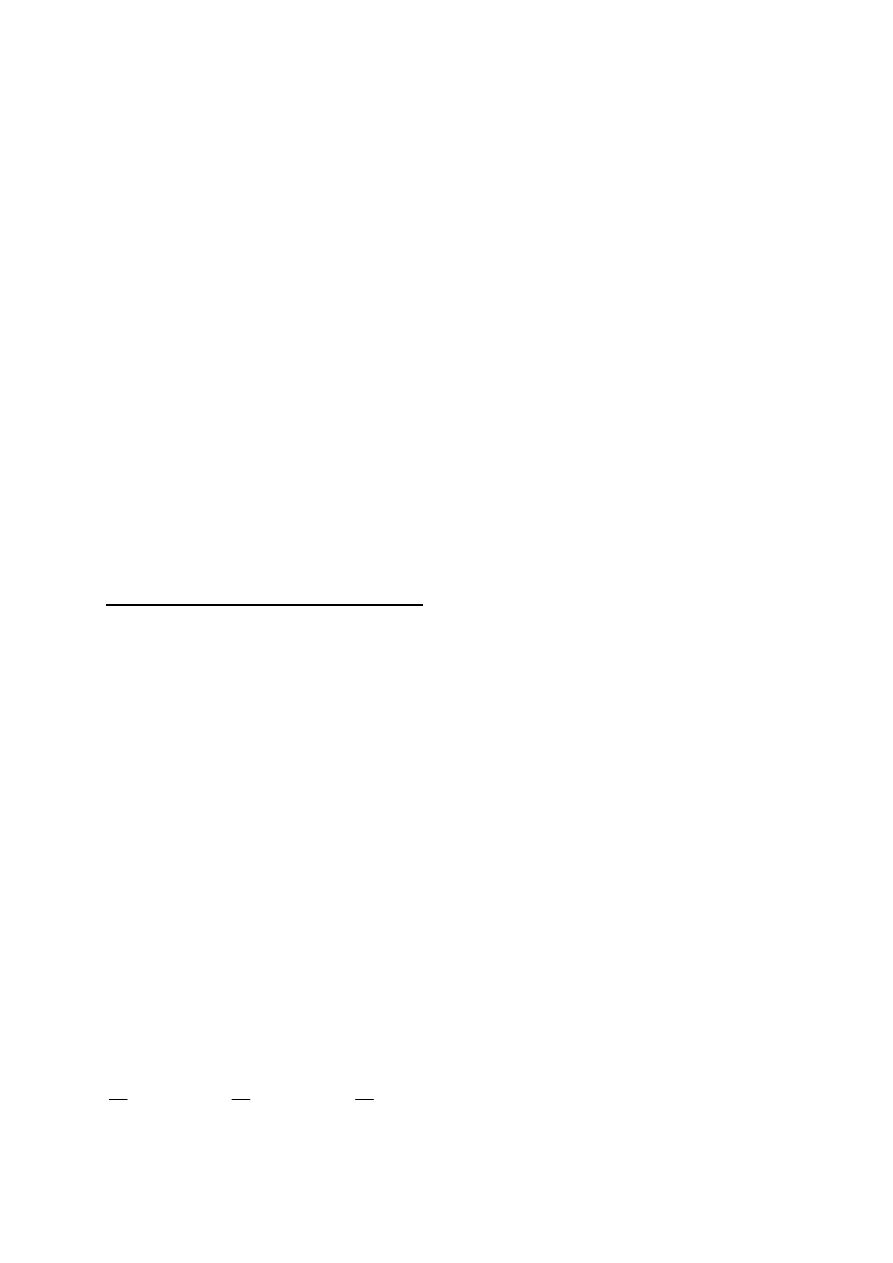
8
posiadania $95.000 na pewno. Co więcej przy wartości
oczekiwanej gry o $95.000 chcesz zapłacić pewną składkę od
ryzyka γ aby uniknąć gry.
Jeżeli masz możliwość wykupienia ubezpieczenia musisz
zapłacić składkę ubezpieczeniową (insurance premium). W
przypadku zaistnienia strat firma ubezpieczeniowa wypłaci
wcześniej uzgodnione odszkodowanie. Zał.: składka = wartość
oczekiwana straty = 0,10 (50.000) = $5.000.
Mówimy, że składka jest aktuarialnie sprawiedliwa jeżeli
równa się wartości oczekiwanej straty.
Kolejny problem: Jakie ubezpieczenie wykupi osoba
niechętna ryzyku?
Model wykupu ubezpieczenia
Oznaczenia:
X
0
: aktywa bez straty
L : strata
ρ
: p-stwo straty
A : odszkodowanie
Jeżeli składka ubezpieczeniowa jest sprawiedliwa:
ρ
A = oczekiwane odszkodowanie = całkowita składka
ubezpieczeniowa
x
l
= x
0
– L + A - ρA = aktywa po stracie
x
n
= x
0
- ρA = aktywa bez straty
Zał.: użyteczność zależy wyłącznie od aktywa. Użyteczność
oczekiwana: E{U} = ρU(x
l
) + (1 - ρ)U(x
n
).
Aby wyznaczyć optymalne ubezpieczenie różniczkujemy E{U}
względem A i przyrównujemy do 0:
0
)
(
)
1
(
)
(
)
1
(
}
{
=
∂
∂
−
−
∂
∂
−
=
∂
∂
n
l
x
U
A
x
U
A
U
E
A
ρ
ρ
ρ
ρ
.
9
Po uproszczeniu:
)
(
)
(
n
l
x
U
A
x
U
A
∂
∂
=
∂
∂
.
Przy funkcji ściśle wklęsłej pierwsze pochodne są takie
same, gdyż są wyznaczane dla tych samych aktywów netto
przy stracie i bez niej. A więc użyteczności i aktywa netto
muszą być takie same w każdej sytuacji:
x
0
– L + A - ρA = x
0
- ρA.
Po rozwiązaniu: A* = L.
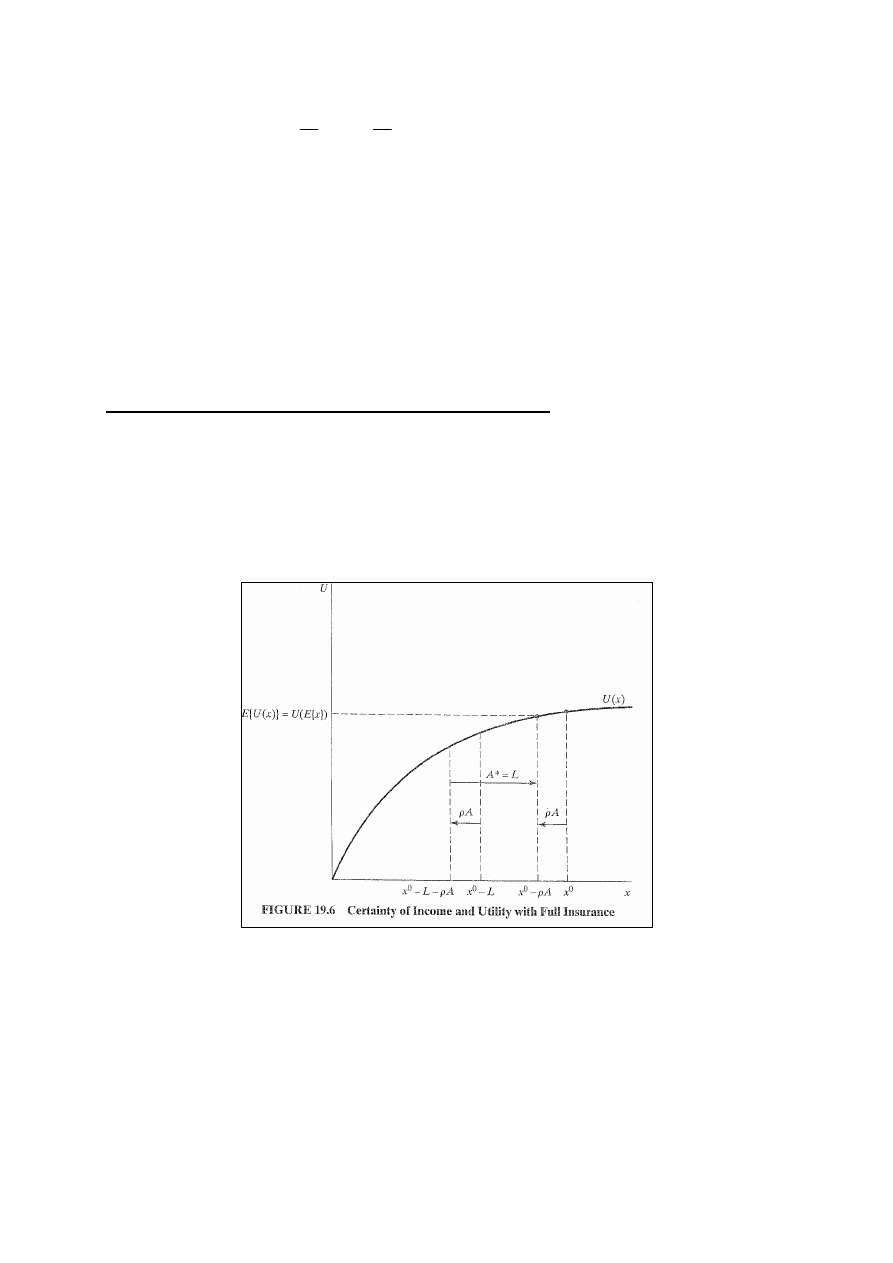
Pełne ubezpieczenie i pewna konsumpcja
Przy aktuarialnie sprawiedliwym ubezpieczeniu konsument
zamienia potencjalną stratę na pewien wynik (taką samą
wartość aktyw niezależnie od zaistnienia straty). Oznacza
to, że użyteczność oczekiwana będzie równała się
użyteczności wartości oczekiwanej (rys. 19.6).
Dzięki wykupowi pełnego ubezpieczenia konsument może
konsumować x
n
w obu sytuacjach:
x
l
= x
0
– A + A - ρA = x
0
- ρA = x
n
,
czyli konsument otrzymuje x
n
na pewno, a więc użyteczność
oczekiwana jest użytecznością odpowiadającą x
n
.
10
Ubezpieczenie i prawo wielkich liczb
Rys.19.7.
Kontrakty futures i inne kontrakty długoterminowe jako
forma ubezpieczenia
Konsumenci mogą nabywać ubezpieczenie także i inną drogą
niż poprzez rynek ubezpieczeniowy. Np. przy transakcjach
określenie wysokość ceny w przyszłości jest formą
ubezpieczenia.
Kontrakty futures
Kontrahenci uzgadniają wysokość ceny (
future price
). Dzięki
temu kupujący nie ponoszą ryzyka związanego z wysokością
rzeczywistych cen w przyszłości (
spot price
) Przyjmując, że
kupujący jest niechętny ryzyku będzie on kupował po cenie
future tak długo, jak różnica między ceną future i średnią
cen spot nie jest większa od premii od ryzyka.
Rys. 19.8: Na osi poziomej jest mierzony dochód po
dokonaniu transakcji. Średnia cen spot to
p
i kupujące ma
szanse 50/50 otrzymania p
1
lub p
2
, dla p
1
> p
2
. Ponieważ
kupowana jest tylko jedna jednostka dobra, to konsument ma
dochód x
0
– p
1
lub x
0
– p
2
przy średnim dochodzie x
0
-
p
i
użyteczności oczekiwanej = E{U(x)}. Jeżeli konsument kupi
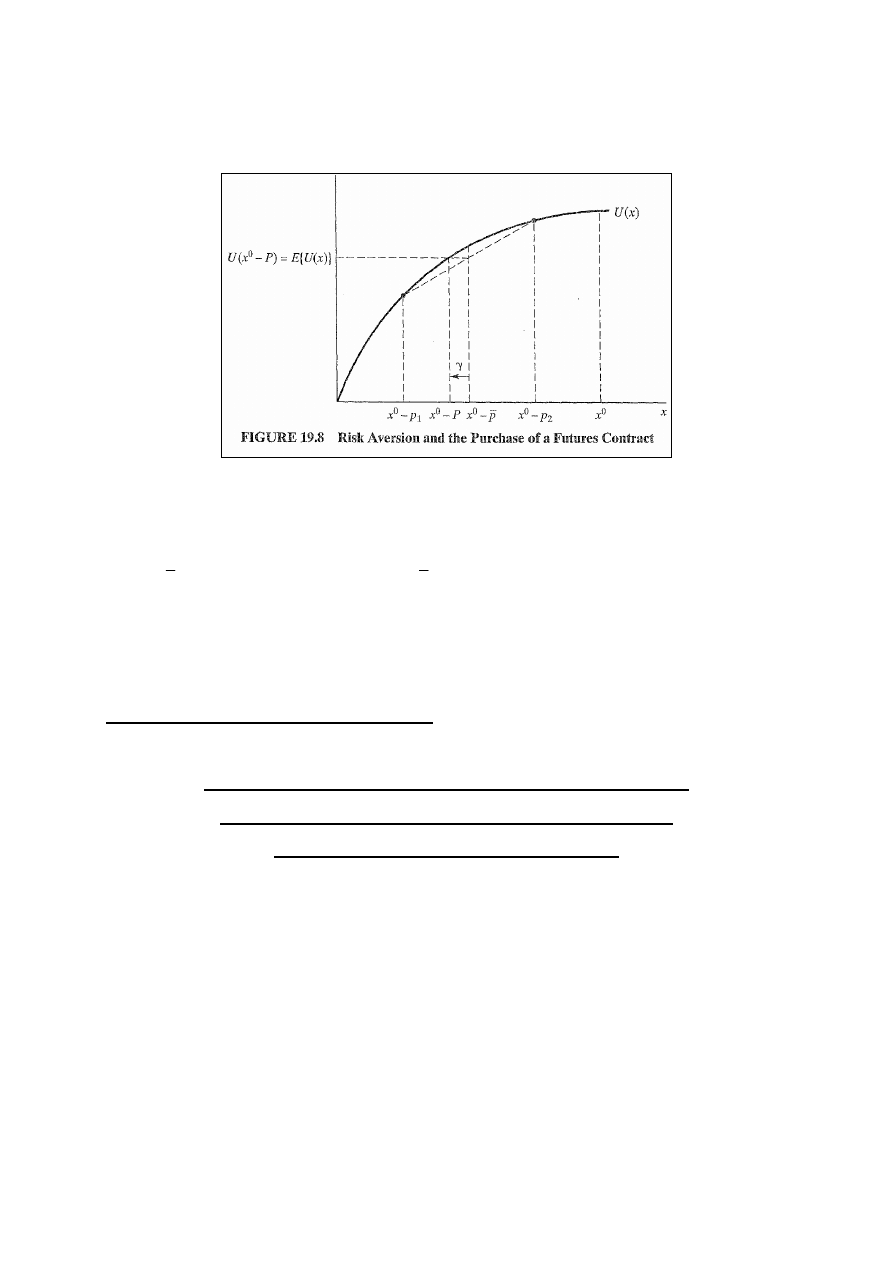
11
jednostkę dobra po cenie P na rynku futures, to może
osiągnąć tą samą użyteczność na pewno: U(x
0
– P) = E{U(x)}.
Na rysunku różnica między oczekiwanym dochodem i pewnym
dochodem kontraktu futures jest premią za ryzyko
konsumenta, γ:
(x
0
-
p
) – (x
0
– P) = γ ⇒ P -
p
= γ.
Dla niższej P konsument płaci mniej niż γ i preferuje
kontrakt future.
Długookresowe umowy o płacy
Roszczenia warunkowe (
Contingent claims
)
i model preferencji zależnych od stanu
(
the state-preference model
)
Alternatywnym sposobem modelowania decyzji w warunkach
niepewności jest model preferencji zależnych od stanu
(state preference model).
Ex ante
myślimy o różnych
wynikach osiąganych w różnych stanach, gdyż nie wiemy, jaki
stan nastąpi. Chcemy jednak być pewni, że będziemy mieli
dobra konsumpcyjne w każdym stanie.
12
Dobra warunkowe i warunkowe roszczenia
(Contingent
commodities & contingent claims)
W dotychczasowym modelu przyjmowaliśmy, że x
1
to
konsumpcja w stanie 1, a x
2
to konsumpcja w stanie 2. Dobro,
które będzie dostarczone tylko w jednym ze stanów
nazywamy (
state – contingent commodity
) dobrem
otrzymanym pod warunkiem zaistnienia danego stanu –
dobrem warunkowym. Jeżeli istnieje n różnych dóbr i m
stanów, to istnieje (m • n) różnych dóbr warunkowych.
Zał.: jedno dobro – konsumpcja i dwa stany – dobry i zły, a
więc są dwa dobra warunkowe.
W modelu preferencji zależnych od stanu konsumenci
handlują warunkowymi roszczeniami, czyli prawami do
konsumpcji jeśli tylko dany stan zaistnieje. Czyli:
x
1
: ilość dóbr, jaką otrzyma konsument w stanie 1;
x
2
: ilość dóbr, jaką otrzyma konsument w stanie2.
Jeżeli konsument chce konsumować niezależnie od stanu, to
musi mieć roszczenia do x
1
i x
2
.
Jeden ze sposobów wyobrażenia sobie rynku warunkowych
roszczeń jest porównanie go do zakładów podczas końskich
gonitw. Stan świata odpowiada różnym miejscom zajętym
przez konie, a roszczenie odpowiada np.. zakładowi, że koń
wygra. Jeżeli twój koń wygra, to dostaniesz wypłatę
proporcjonalną do liczby wykupionych zakładów. Ale jedynym
sposobem zagwarantowania wypłaty w każdym stanie jest
wykupienie zakładów na zwycięstwo każdego konia.
13
Warunkowe krzywe obojętności (
state - contingent
indifference curve
)
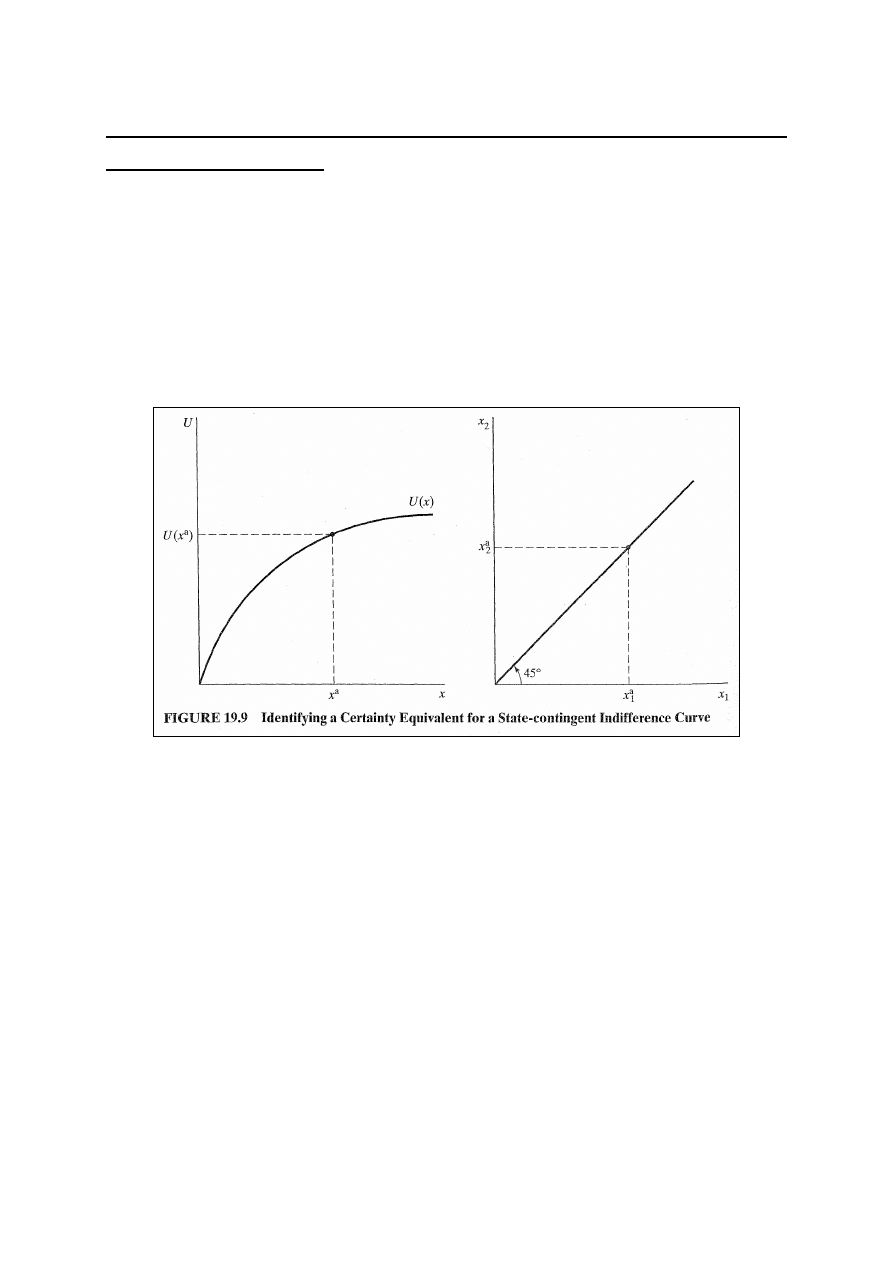
Aby analizować rynek warunkowych roszczeń znajdujemy
najwyższą osiągalną krzywą obojętności przy ograniczeniu
budżetowym. Aby skonstruować mapę obojętności zaczniemy
od „normalnej” funkcji użyteczności U(x). Punkt x
a
wzdłuż
tej funkcji reprezentuje x
a
otrzymywane na pewno, a U(x
a
)
to odpowiadająca użyteczność. Jest to równoważne z
osiągnięciem x
a
w obu stanach (x
a
1
= x
a
2
).
Rys. 19.9: na lewym wykresie: x
a
generuje użyteczność U(x
a
)
na pewno. Na prawym rysunku: x
a
1
= x
a
2
wzdłuż promienia
wychodzącego pod kątem 45
0
. Reprezentuje to punkt z
krzywej obojętności, dla którego: E{U(x)} = U(x
a
), a x
a
jest
ekwiwalentem pewności tej krzywej obojętności.
Zał.: p-stwo zaistnienia stanu 1 : 2/3, a stanu 2 : 1/3.
Szukamy kombinacji x
1
i x
2
(x
b
1
i x
b
2
), która jest obojętna
konsumentowi względem x
a
otrzymywanym na pewno.
Ponieważ konsument jest obojętny między x
a
i grą , to punkt
(x
b
1
i x
b
2
) również znajduje się w zbiorze krzywych
obojętności U(x
a
).
14
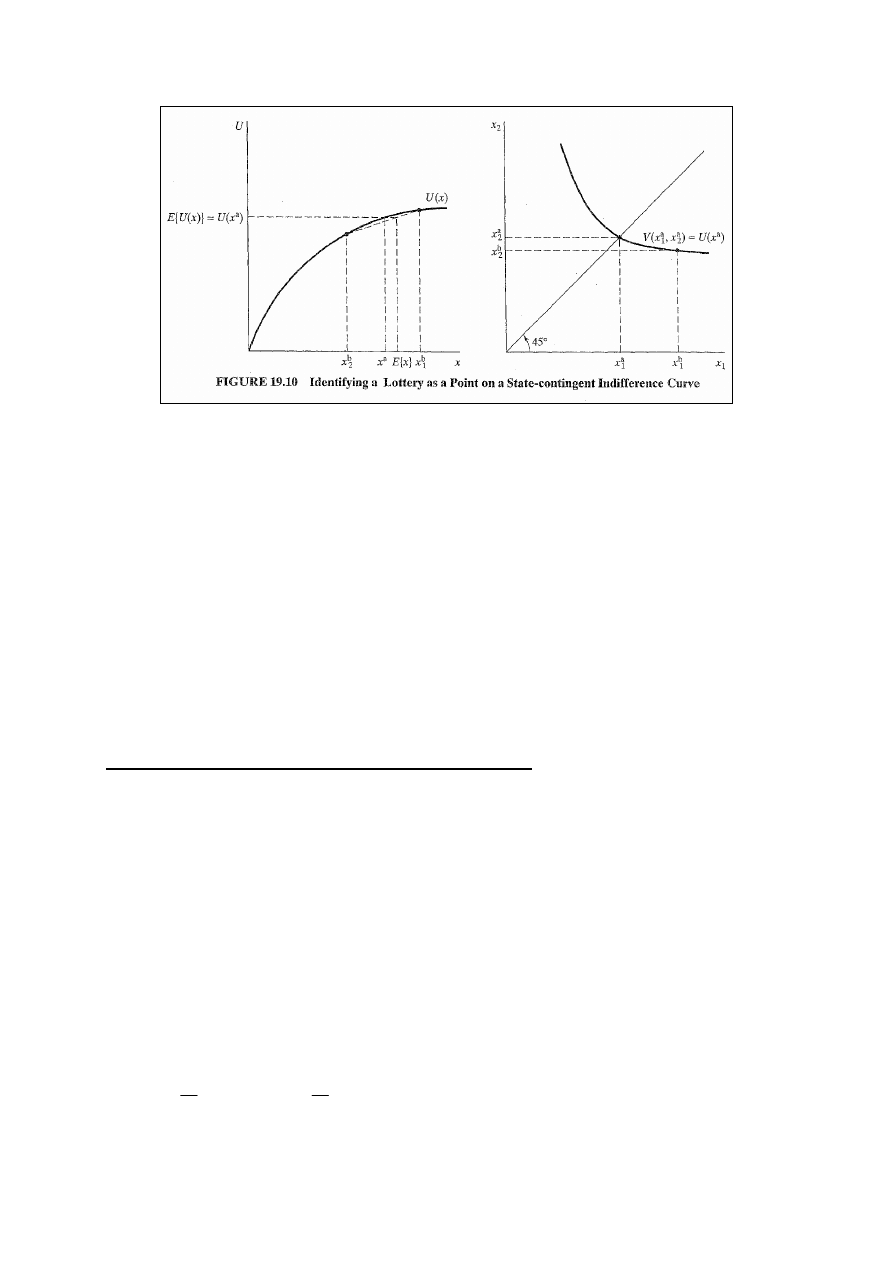
Rys. 19.10: na lewym rysunku: użyteczność oczekiwana gry =
użyteczności x
a
. Użyteczność oczekiwaną oznaczamy: V(x
a
1
,
x
a
2
):
(2/3)U(x
b
1
) + (1/3) U(x
b
2
) = U(x
a
) = V(x
a
1
, x
a
2
).
Aby skonstruować krzywą obojętności znajdujemy wszystkie
możliwe kombinacje ilości dóbr konsumowanych w stanie 1 i
2, takie, że konsument jest obojętny między x
a
konsumowanym na pewno i grą, w której stan 1 zaistnieje z p-
stwem 2/3 i stan 2 zaistnieje z p-stwem 1/3.
Malejąca MRS i awersja wobec ryzyka
Przyjrzyjmy się tej krzywej obojętności. Zawiera ona
kombinację x
1
i x
2
, taką że:
ρ
U(x
1
) + (1 - ρ)U(x
2
) = U(x
a
) = V(x
a
1
, x
a
2
),
gdzie ρ to p-stwo zaistnienia stanu 1.
MRS wzdłuż warunkowej krzywej obojętności określa
stosunek, w jakim konsument chce zrezygnować z konsumpcji
w jednym stanie w celu zwiększenia konsumpcji w drugim
stanie. Aby wyznaczyć MRS różniczkę zupełną powyższego
równania przyrównujemy do 0:
2
2
1
1
)
(
)
1
(
)
(
0
dx
x
U
dx
d
dx
x
U
dx
d
dV
ρ
ρ
−
+
=
=
.
Rozwiązując dla nachylenia krzywej obojętności:
15
( )
[
]
( )
[
]
0
)
(
'
)
1
(
)
(
'
/
)
1
(
/
2
1
2
1
1
2
<
−
−
=
−
−
=
x
U
x
U
dx
x
dU
dx
x
dU
dx
dx
ρ
ρ
ρ
ρ
.
Należy spostrzec, że MRS jest wzdłuż promienia
wychodzącego z początku układu pod kątem 45
0
, gdzie x
1
=
x
2
:
MRS = ρ/(1 -ρ),
gdyż dU(x
1
)/dx = dU(x
2
)/dx gdy x
1
= x
2
. Ponadto chcemy
określić kształt krzywej obojętności. Obliczmy więc drugą
pochodną:
2
2
1
1
2
2
2
1
2
1
2
2
)]
(
'
)
1
[(
)
(
'
)[
/
)(
(
''
)
1
(
)]
(
'
)
1
)[(
(
''
x
U
x
U
dx
dx
x
U
x
U
x
U
dx
x
d
ρ
ρ
ρ
ρ
ρ
−
−
−
−
−
=
.
Ponieważ pierwsza pochodna funkcji użyteczności i p-stwa są
dodatnie i nachylenie krzywej jest ujemne, to wyrażenie w
powyższym równaniu będzie dodatnie w każdym punkcie
krzywej obojętności (prowadząc do malejącej MRS) wtedy i
tylko wtedy, gdy druga pochodna funkcji użyteczności jest
ujemna w każdym punkcie. Jeżeli druga pochodna funkcji
użyteczności jest wszędzie ujemna, to powyższe wyrażenie
jest dodatnie. Jeżeli druga pochodna wszędzie = 0, to
wyrażenie powyższe = 0 i jeżeli druga pochodna jest
wszędzie dodatnia, to powyższe wyrażenie jest ujemne.
Wiemy jednak, że wklęsła funkcja użyteczności (druga
pochodna ujemna) oznacza, że jednostka jest niechętna
ryzyku. Z powyższego argumentu wynika więc, że w modelu
preferencji zależnych od stanu, awersja wobec ryzyka jest
warunkiem koniecznym i wystarczającym aby warunkowe
krzywe obojętności wykazywały malejącą MRS . Jeżeli
jednostka jest neutralna względem ryzyka (druga pochodna
= 0), to krzywa obojętności jest prosta. Jeżeli jednostka
lubi ryzyko (druga pochodna jest dodatnia), to krzywe
obojętności mają przeciwne wybrzuszenie.
16
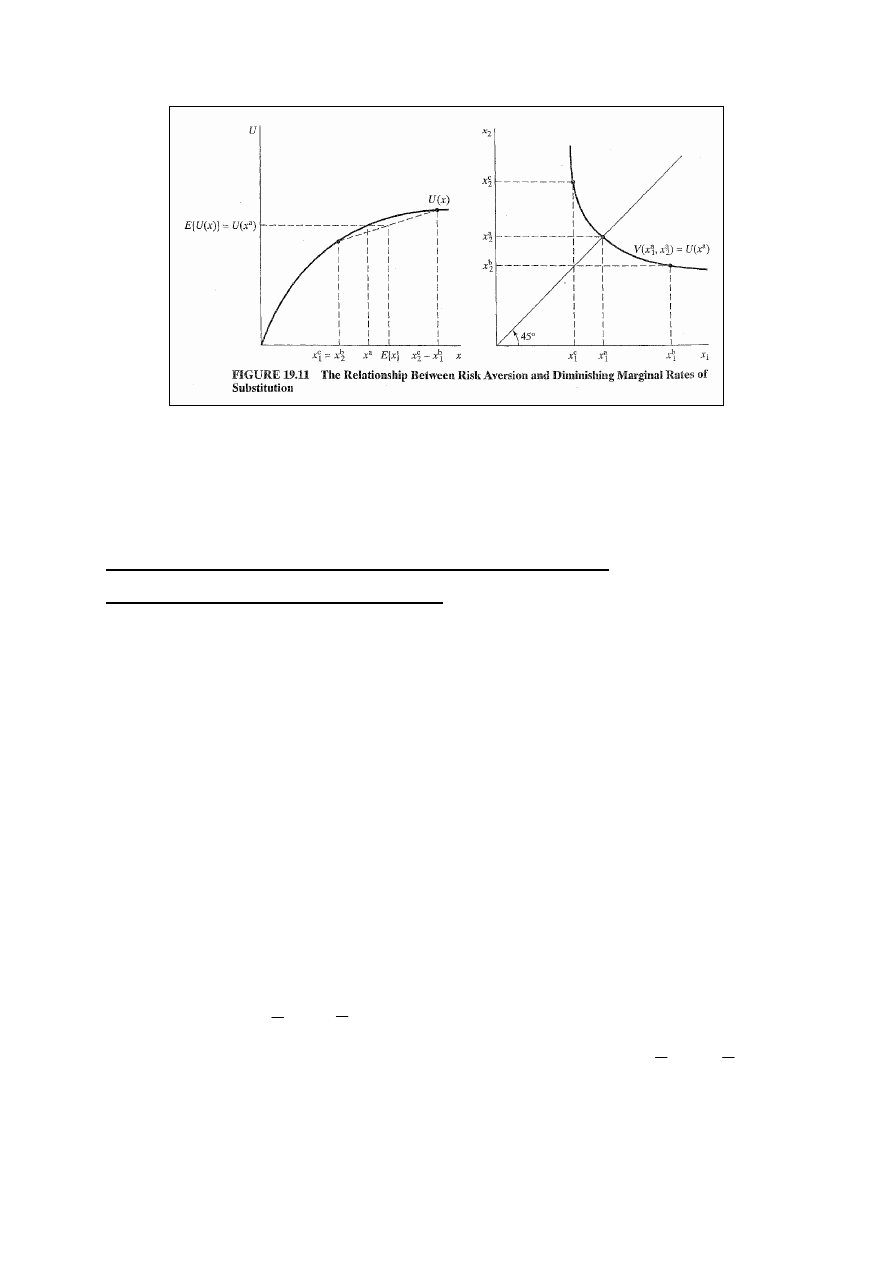
Rys. 19.11: osoba niechętna ryzyku, Ściśle wklęsła funkcja
użyteczności oznacza, że krzywe obojętności są wklęsłe
względem początku układu współrzędnych.
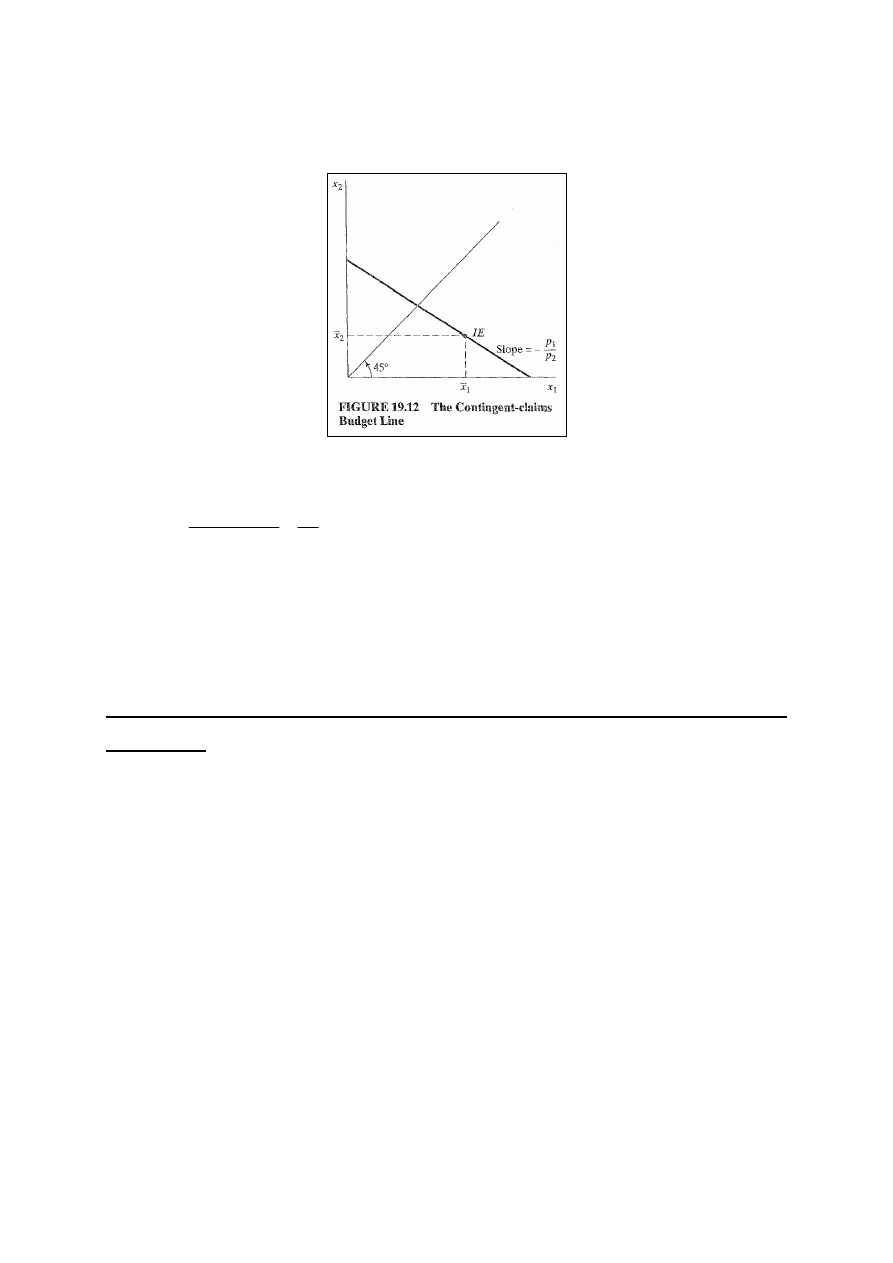
Linia warunkowego ograniczenia budżetowego
i maksymalizacja użyteczności
Aby skonstruować linię ograniczenia budżetowego zaczynamy
od spostrzeżenia, że zaistnienie stanu 1 lub 2 oznacza, że
dostępna będzie określona ilość dobra konsumpcyjnego.
Poprzez oznaczenie stanu 1 jako „dobry”, a stanu 2 jako „zły”
przyjmujemy, że początkowe wyposażenie w stanie 1 będzie
większe niż początkowe wyposażenie w stanie 2. Tak więc
wyposażenie początkowe znajduje się pod promieniem 45
0
.
Wiedząc, że mamy wyposażenie początkowe możemy
skonstruować linię ograniczenia budżetowego . Wartości
warunkowych roszczeń nabytych nie mogą być większe od
wartości roszczeń w punkcie wyposażenia początkowego
jednostki:
p
1
x
1
+ p
2
x
2
≤ p
1 1
x
+
p
2 2
x
,
gdzie: p
1
i p
2
to ceny warunkowych żądań i
1
x
i
2
x
to
wyposażenia początkowe. Linia wyposażenia początkowego
17
jest więc linią prostą o nachyleniu p
1
/p
2
przechodzącą przez
punkt wyposażenia początkowego – rys. 19.12.
Maksymalizacja użyteczności wymaga więc zrównania MRS
ze stosunkiem cen:
MRS =
2
1
2
1
)
(
'
)
1
(
)
(
'
p
p
x
U
x
U
=
−
ρ
ρ
.
Powyższy warunek informuje nas, że stosunek cen
warunkowych równa się stosunkowi użyteczności krańcowych
ważonych stosunkiem subiektywnych prawdopodobieństw.
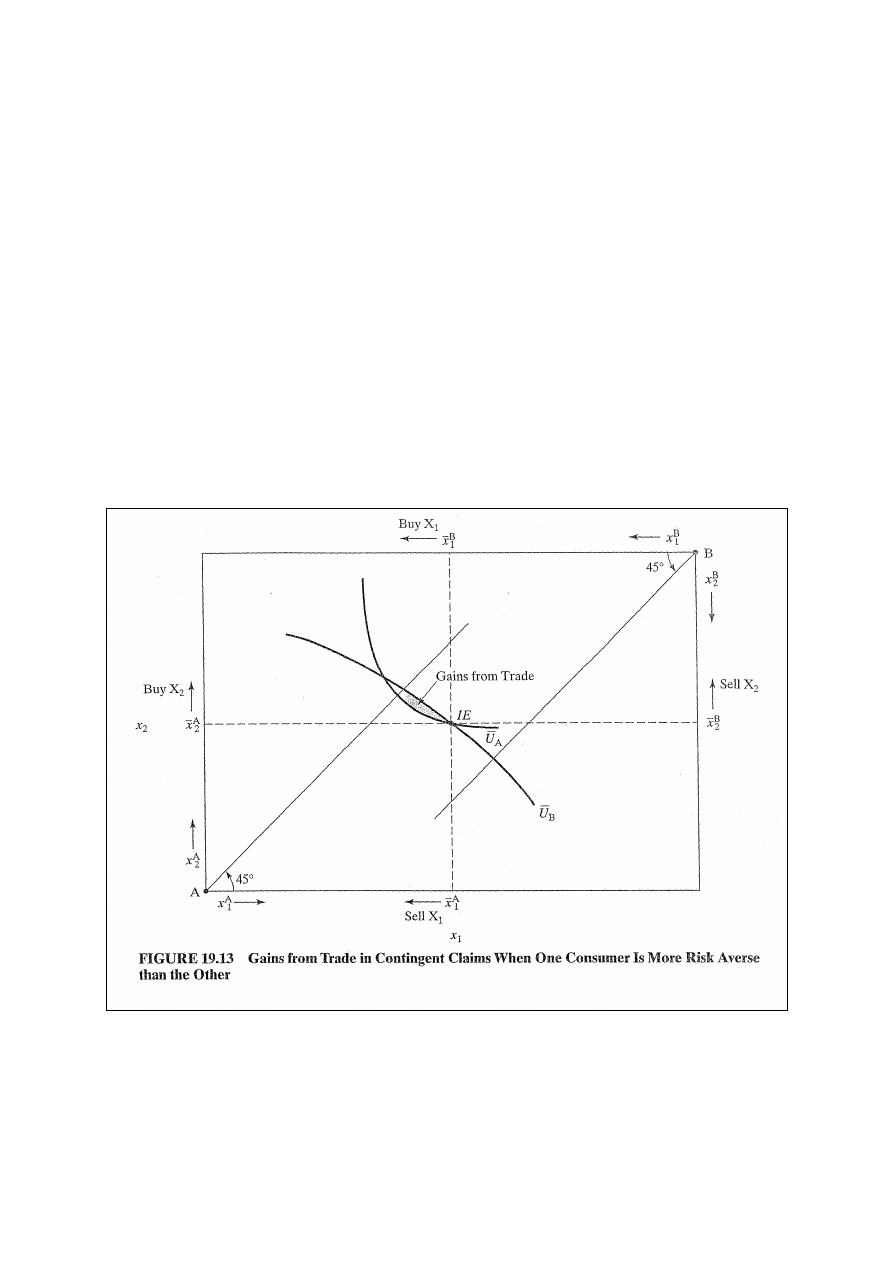
Dzielenie ryzyka między konsumentów i rynek warunkowych
roszczeń
Przyjmujmy, że są dwie jednostki o różnym stosunku wobec
ryzyka i o jednakowym wyposażeniu w dobra konsumpcyjne w
stanie 1 i stanie 2. Z doskonale konkurencyjnym rynkiem
roszczeń warunkowych osoba o mniejszej niechęci wobec
ryzyka będzie chciała sprzedać roszczenia w „złym” stanie
osobie o większej skłonności do ryzyka w zamian za prawo
zwiększenia konsumpcji w „dobrym” stanie. Pomimo że obie
osoby mogą charakteryzować się awersją wobec ryzyka, to
zróżnicowanie ich awersji powoduje, że osoba bardziej
niechętna do ryzyka gotowa jest zapłacić osobie mniej
niechętnej wobec ryzyka za zrezygnowanie z roszczeń do
konsumpcji w „złym” stanie.
18
Dzielenie ryzyka pokazane jest w skrzynce Edgeworth’a (rys.
19.13): Mniejsza ilość jest dostępna w stanie 2, co ujawnia,
że stan 2 jest „zły”. Jeżeli obaj konsumenci są uposażeni tak
samo, to wyposażenie początkowe znajduje się w środku
skrzynki (IE). Konsument A jest bardziej niechętny do
ryzyka niż konsument B, z czego wynika, że krzywe
obojętności konsumenta A są bardziej wypukłe. Krańcowe
stopy substytucji obu konsumentów równają się stosunkom
ich subiektywnych prawdopodobieństw wzdłuż promieni
wychodzących z początków układu współrzędnych, jak w
równaniu: MRS = ρ/(1 -ρ).
Ponieważ krzywe obojętności konsumenta A są bardziej
wypukłe, to obszar pokazujący korzyści z handlu leży na
północny - zachód od punktu wyposażenia początkowego.
Wynika z tego, że przy dzieleniu ryzyka efektywnym w
19
sensie Pareto, osoba z większą awersją wobec ryzyka kupuje
prawa do konsumpcji bardziej równomiernie w obu stanach.
Osoba z mniejszą niechęcią wobec ryzyka gotowa jest
zrezygnować z części konsumpcji w stanie 2 („złym”) za
względnie duży transfer roszczenia warunkowego stanu 1 od
osoby bardziej niechętnej ryzyku. Osoba o mniejszej awersji
konsumuje względnie więcej w stanie 1 („dobrym”).
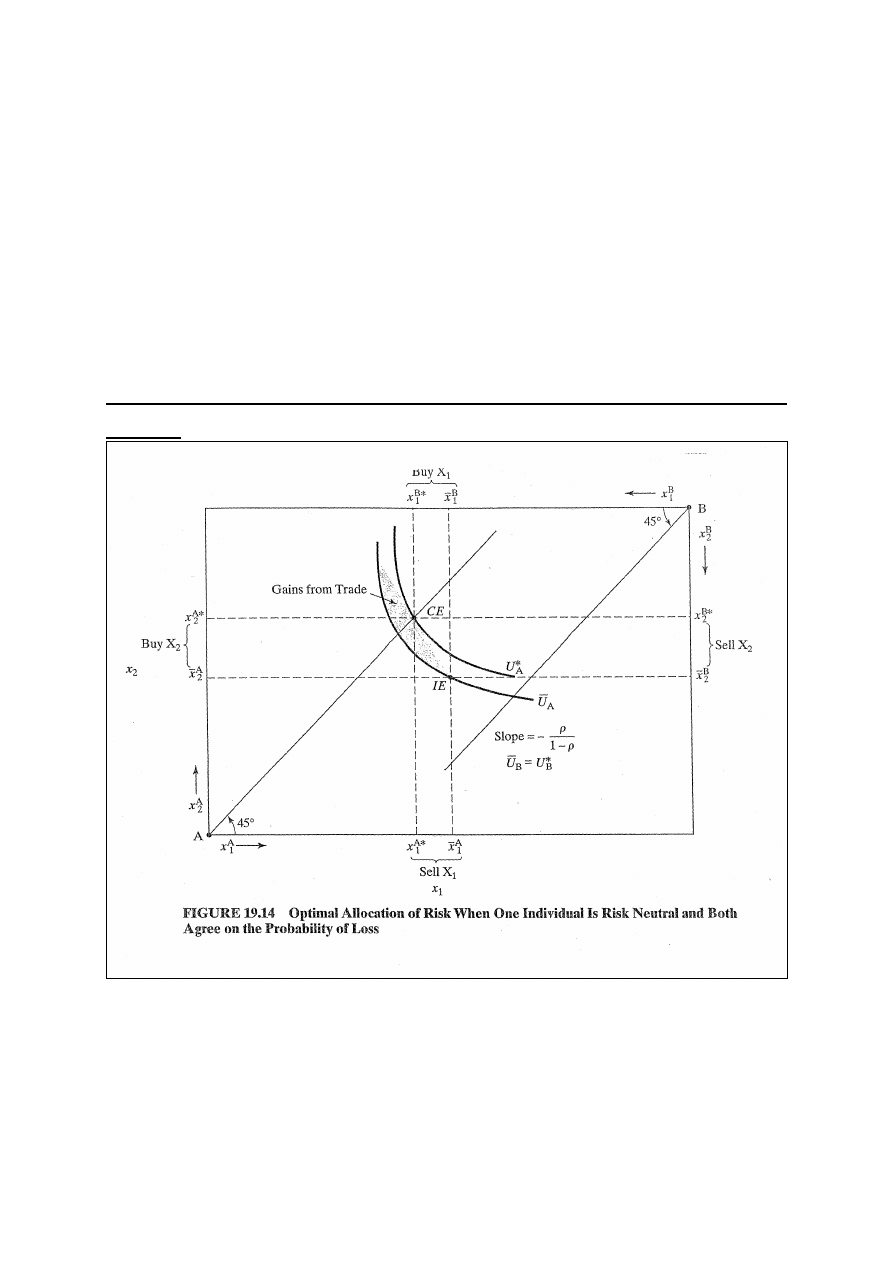
Pełne ubezpieczenie konsumenta neutralnego względem
ryzyka
Rys. 19.14: optymalne dzielenie ryzyka gdy jeden z
konsumentów jest neutralny względem ryzyka, a drugi jest
niechętny ryzyku i zgadzają się co do subiektywnego
prawdopodobieństwa straty. Krzywe obojętności konsumenta
neutralnego wobec ryzyka, konsumenta B, są liniowe i
20
przechodzą przez punkt wyposażenia początkowego. Jego
MRS = stosunkowi prawdopodobieństw. Funkcja użyteczności
oczekiwanej konsumenta neutralnego względem ryzyka:
E{U} = ρx
1
+ (1 - ρ)x
2
,
a MRS:
ρ
ρ
−
=
∂
∂
∂
∂
=
1
/
}
{
/
}
{
2
1
x
U
E
x
U
E
MRS
.
Ponieważ krzywe obojętności konsumenta neutralnego
względem ryzyka są liniowe, to nachylenie krzywej
obojętności, stosunek obiektywnych prawdopodobieństw
staje się stosunkiem cen roszczeń warunkowych. W
równowadze doskonale konkurencyjnej konsument niechętny
względem ryzyka kupuje tak wiele roszczeń, ile tylko chce
przy tym stosunku cen. Co więcej ponieważ stosunek cen
równa się stosunkowi prawdopodobieństw, to konsument
niechętny wobec ryzyka maxU dzięki zakupowi ilości
roszczeń zapewniającej jednakową konsumpcję w obu
stanach. Dziej się tak, gdyż MRS = stosunkowi
prawdopodobieństw wzdłuż promienia 45
0
wychodzącego z
początku układu współrzędnych. (Taki wynik otrzymaliśmy na
rynku ubezpieczeń, gdy firma ubezpieczeniowa oferowała
pełne ubezpieczenie przy aktuarialnie sprawiedliwych
stawkach. Tutaj, zrównanie wielkości konsumpcji w obu
stanach jest identyczne z zakupem pełnego ubezpieczenia.
Tak więc zakup pełnego ubezpieczenia przy aktuarialnych
stawkach sprawiedliwych jest optimum Pareto, gdy firmy
ubezpieczeniowe są neutralne wobec ryzyka, a konsumenci są
niechętni ryzyku i obydwaj zgadzają się na
prawdopodobieństwo straty.